10 в степени минус 23: 6 умножить на 10 в 23 степени равняется

Содержание

Числительные в немецком языке. Zahlwörter. Мобильное приложение по немецкому языку | SpeakASAP®

Знание и умение ориентироваться в числах – штука крайне полезная и важная в иностранном языке.

Мы с вами познакомимся с самыми основными количественными числительными, благодаря которым вы сможете говорить о своем возрасте, спрашивать цены в магазинах, воспринимать на слух информацию на вокзалах и так далее.

От 0 до 9	От 10 до 19	От 20 до 29	Десятки
0 – null	10 – zehn	20 – zwanzig	10 – zehn
1 – eins	11 – elf	21 – einundzwanzig (1 и 20)	20 – zwanzig
2 – zwei	12 – zwölf	22 – zweiundzwanzig (2 и 20)	30 – dreißig
3 – drei	13 – dreizehn (3,10)	23 – dreiundzwanzig (3 и 20)	40 – vierzig
4 – vier	14 – vierzehn (4,10)	24 – vierundzwanzig	50 – fünfzig
5 – fünf	15 – fünfzehn (5,10)	25 – fünfundzwanzig	60 – sechzig
6 – sechs	16 – sechzehn	26 – sechsundzwanzig	70 – siebzig
7 – sieben	17 – siebzehn	27 – siebenundzwanzig	80 – achtzig
8 – acht	18 – achtzehn	28 – achtundzwanzig	90 – neunzig
9 – neun	19 – neunzehn	29 – neunundzwanzig	100 – hundert

После того как вы выучили глагол sein, вы можете говорить о возрасте:

Ich bin sechsundzwanzig (26) Jahre alt. – Мне 26 лет. (дословно: «Я есть 26 лет старый»)
Er ist vierzig(40) Jahre alt. – Ему 40 лет.
Du bist zwanzig(20) Jahre alt. – Тебе 20 лет.

Числительные в немецком языке – особый разговор. Мало того, что числа от 21 до 99 пишутся и читаются наоборот, так еще числа после 101 пишутся слитно и получаются просто огромными по длине.

500 – fünfhundert – пятьсот
4000 – viertausend – четыре тысячи
341 – dreihunderteinundvierzig
40.000 – vierzigtausend
400.000 – vierhunderttausend
1.000.000 – eine Million
3.300.400

– drei Millionen dreihunderttausendvierhundert

Если нужно назвать четырехзначное число, то сначала называется количество тысяч, затем количество сотен, а затем уже двухзначное число – десятки и единицы.

Например:

1571 = eintausendfünfhunderteinundsiebzig

Если разбить слово на образующие, то получим:

eintausend + fünfhundert + ein + und + siebzig
(одна тысяча) (пятьсот) (один) (и) (семьдесят)

Числительные отвечают на один из W-вопросов, так называемых W-Fragen.

Указание количества – Wie viel? Wie viele?

Wie viel? – сколько для неисчисляемых
Wie viele? – сколько для исчисляемых

Wie viele Kinder haben Sie? – Сколько у Вас детей?
Ich habe drei Kinder, davon zwei Söhne und eine Tochter. – У меня трое детей, из них двое сыновей и одна дочь.

Wie viel kosten die Tickets? – Сколько стоят билеты?

Sie kosten 54 Euro und 25 Cent. – Они стоят 54 евро и 25 центов.

Wie viele Blumensträuße hast du gekauft? – Сколько букетов цветов ты купил?
3 Sträuße mit je 11 Rosen. – 3 букета по 11 роз.

Указание времени – Wann? Um wie viel Uhr?

Wann hast du Geburtstag? – Когда у тебя день рождения?
Am Mittwoch, dem 23.05. – В среду, 23.05.

Um wie viel Uhr fängt die Stunde an? – В котором часу начинается урок?
Um 8 Uhr kommt der Lehrer und die Stunde beginnt. – В 8 часов приходит учитель, и урок начинается.

Wie lange wartet ihr hier schon? – Как долго вы здесь ждете?
Nur 10 Minuten, wir haben noch Zeit.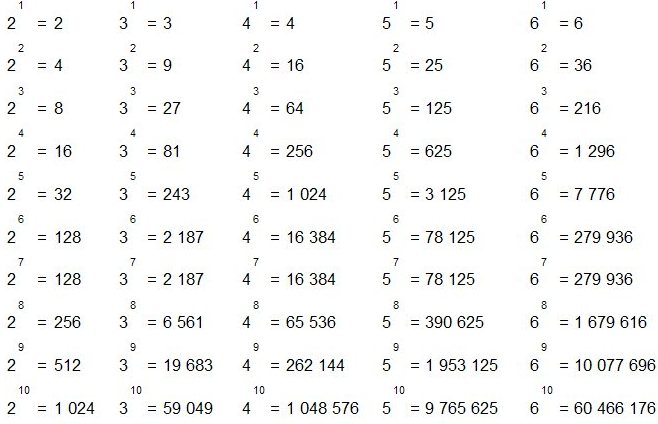 – Только 10 минут, у нас еще есть время.

Различают:

Количественные числительные. Kardinalzahlen

eins, zwei, drei, zehn, (ein) hundert, fünftausend, eine Million, zehn Milliarden, …

Порядковые числительные. Ordinalzahlen

1., 2., 3., 4., … /erste, zweite, dritte, vierte, …

Дробные числительные. Bruchzahlen

ein halb, eineinhalb, ein Drittel, drei Fünftel, sieben Zehntel, …

Числительные, которые указывают на действие умножения (дважды, трижды и т.д.). Multiplikationswörter

einfach, zweifach, doppelt, dreifach, fünffach, dreißigfach, tausendfach, zigfach, …

Количественные числительные

Цифра 1 (произносится: eins)

Склоняется как неопределенный артикль, если в предложении заменяет существительное.

Haben Sie Kulis? – У Вас есть ручки?

Без указания на существительное: Ja, einen. – Да, одна.
С указанием на существительное: Ja, einen blauen Kuli und einen roten Kuli. – Да, одна синяя ручка и одна красная ручка.

Ich habe nur ein Auto und nicht drei (Autos)! – У меня одна машина, а не три!

Если eins используется в предложении вместе с определенным артиклем, то в этом случае eins склоняется как имя прилагательное.

Warum hören Sie das eine und nicht das andere Lied? – Почему Вы слушаете одну, а не другую песню?

Du musst aufpassen, was der eine sagt und was der andere tut. – Ты должен обращать внимание на то, что один говорит и что другой делает.

Цифры 2 и 3 склоняются только в падеже датив и генитив. Все остальные количественные числительные не склоняются.

Beno und Anke sind glückluiche Eltern zweier Zwillinge. – Бено и Анке счастливые родители двух близнецов.
Ich gehe ins Kino mit dreien besten Freunden. – Я иду в кино с тремя лучшими друзьями.

Числительные, которые выступают в роли существительных.

die Million, fünf Millionen
die Milliarde, acht Milliarden
die Billion, drei Billionen

Порядковые числительные

Порядковые числительные пишутся цифрами, после них всегда стоит точка («. «). Но могут писаться и буквами: erste, zweite, dritte, neunte, dreizehnte, …

Порядковые числительные от 2 до 19 образуются с помощью -t:

acht-, zehnt-, vierzehnt-, fünfzehnt-, … + их окончания склоняются как у прилагательных.

Порядковые числительные от 20 образуются с помощью -st:

zwanzigst-, sechsundvierzigst-, neunundsiebzigst-… + их окончания склоняются как у прилагательных.

Обозначение порядка начинается со слов der /die /das erste и заканчивается словами der /die /das letzte.

Die erste Sehenswürdigkeit in Deutschland war für Tim das Brandenburger Tor.
Der letzte Brief von dir bekam ich am Dienstag.

Существует всего несколько исключений в образовании порядковых числительных:

1. = der erste
3. = der dritte

7. = der siebte
8. = der achte
16. = der sechzehnte
17. = der siebzehnte

Для порядковых числительных действует правила склонения прилагательных.

In der neunten Ausgabe dieser Zeitschrift finden Sie einen Bericht über die Weltreise von Michael Braun. – В девятом выпуске этого журнала Вы найдете сообщение о кругосветном путешествии Михаэля Брауна.
2012 feiert man das zweihundertste Jubiläum der Märchen von Gebrüdern Grimm. – В 2012 году празднуется двухсотлетний юбилей сказок братьев Гримм.

Порядковые числительные могут быть в предложении существительными.

Er kam als Zweiter zum Ziel. – Он пришел вторым (как второй) к финишу.
Der Erste in der Klasse war Klaus, er war auch der Klassensprecher. – Первым в классе был Клаус, он также был старостой.

Обозначение дат.

Der wie vielte ist morgen? – Morgen ist Sonntag, der 10.09.2011 /zehnte September zweitausendelf.

Den wie vielten hatten wir gestern? – Gestern hatten wir den 5.01. /den fünften Januar (после глагола haben слова стоят в падеже аккузатив)

Использование числительных в обозначении массы, длины, %, долей и так далее

70% / siebzig Prozent

Die Preisen stiegen um 70%. – Цены выросли на 70%.

30,12% / dreißig Komma eins zwei Prozent

30,12% der Summe ist schon ausgegeben.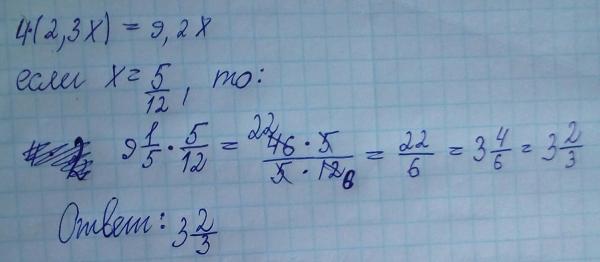 – 30,12% суммы уже потрачено.

0,3‰ / null Komma drei Promille

Der Busfahrer hatte 0,3‰ Alkohol im Blut. – Водитель автобуса имел 0,3‰ алкоголя в крови.

¼ / ein Viertel

¼ der Stunde dauert 15 Minuten. – ¼ часа длится 15 минут.

½ / ein halb

Wir haben eine halbe Torte gegessen. – Мы съели половину торта.

¾ / drei Viertel

Etwa ¾ der Touristen verbringen ihre Zeit am Strand. – Примерно ¾ туристов проводят свое время на пляже.

1½ kg / eineinhalb = anderthalb Kilogramm

Für diesen riesigen Kuchen brauchen wir 1½ kg Äpfel. – Для этого огромного пирога нам понадобится 1½ кг яблок.

1 Pfd. / ein Pfund

1 Pfd. Mehl nimmt sie, um einen Pflaumenkuchen zu backen. – 1 фунт муки берет она, чтоб испечь сливовый пирог.

100 ml / einhundert Milliliter

Du musst noch 100 ml Milch hinzufügen. – Ты должен добавить еще 100 мл молока.

200 km/h / zweihundert Stundenkilometer

Der neue Wagen von BMW kann schneller als 200 km/h fahren. – Новая машина BMW может ехать быстрее 200 км/ч.

19 m² / neunzehn Quadratmeter

Die Wohnfläche dieser Wohnung beträgt 19 m². – Жилая площадь этой квартиры составляет 19 м².

50 l³ / fünfzig Kubikliter

Sie haben zu Hause ein Aquarium für 50 l³ Wasser. – Дома у них аквариум на 50 л³ воды.

30°C / dreißig Grad Celsius

Anfang der Woche liegen die Tagestemperaturen im ganzen Land bei 30°C. – В начале недели дневные температуры по всей стране будут около 30°C.

-15°C / minus fünfzehn Grad / fünfzehn Grad unter Null

Die kälteste Temperatur in unserer Stadt war -15°C. – Самая холодная температура в нашем городе была -15°C.

am 23.07.1978 / am dreiundzwanzigsten siebten neunzehnhundertachtundsiebzig

Dieser junge Schriftsteller ist am 3.11.1989 geboren. – Этот молодой писатель родился 3.11.1989.

Методическая разработка занятия с одаренными детьми «Степень с натуральным показателем. Сравнение степеней» (6–7-е классы)

Основная цель занятия — продолжить работу по углублению и расширению знаний учащихся по теме “Натуральные числа, степени с натуральным показателем, свойств натуральных чисел” изученных в предыдущем учебном году, развитию познавательного интереса учащихся к изучению темы. Ознакомить учащихся с новыми методами решения задач на сравнение степеней с натуральными показателями, на определение цифры, на которую оканчивается число, рассмотреть задачи на делимость выражений, содержащих степени с натуральным показателем. Продолжить формирование навыков исследовательской, самостоятельной работы.

Изучение данной темы в младших классах способствует лучшему усвоению тем связанных со степенями в старших классах, формирует познавательный интерес к изучению.

Данная методическая разработка прошла апробацию на занятиях районной очно-заочной математической школы 2006–2009 учебных годах.

План

Лекционное занятие – 1 час
Малая олимпиада (индивидуальное решение задач) – 1 час
Заочное решение задач (домашнее задание) – 2 часа

Ход занятияЛекционное занятие с учащимися
В математике господствуют две стихии – числа и фигуры с их бесконечным многообразием свойств и взаимосвязей.
Мы будем заниматься стихией чисел.
Возникновение понятия числа – одно из гениальнейших проявлений человеческого разума. Действительные числа не только измеряют, сравнивают, вычисляют, но даже рисуют, играют, сочиняют.
Самые древние по происхождению числа натуральные: 1,2,3,4,5………Обозначаются N.
В прошлом учебном году мы рассматривали ряд задач на натуральные числа. В этом году будем продолжать знакомство со свойствами натуральных чисел.
Вспомним какие арифметические действия можно выполнять во множестве натуральных чисел?
Сложение.

Вычитание.

Умножение.

Деление.

– Какие из этих действий выполняются всегда? Ответ: сложение, умножение.
– А какие не выполняются? Ответ: не всегда: 15–20, 15:8.
5 • 5 • 5 • 5 • 5 • 5 =
– Как короче записать это произведение? Ответ: 5⁶.
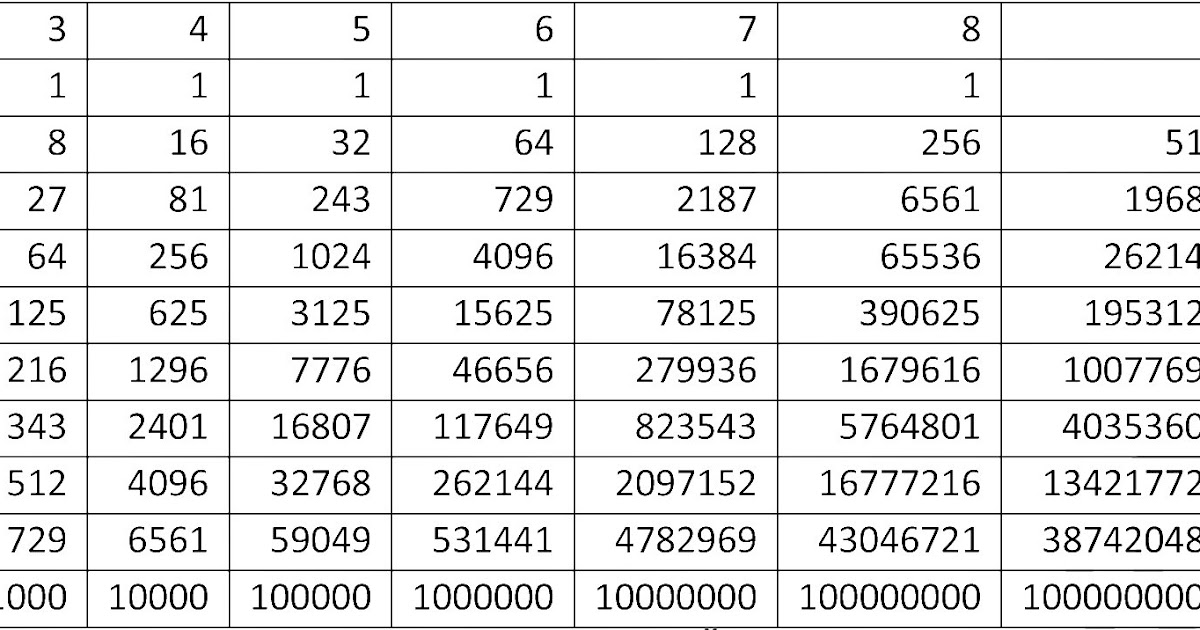
– Говорят, что это шестая степень числа пять.
Вообще: а^п=а а а а а а … а, .
Записываем свойства в тетрадь:
aⁿbⁿ=(ab)ⁿ.

aⁿa^m=a^n+m.

(aⁿ)^m=a^nm.

1. Сегодня мы рассмотрим ряд задач на сравнение степеней с натуральными показателями.

Задача 1

Сравнить 31¹¹ и 17¹⁴.

Решение:
Числа 31 и 17 находятся рядом со степенями числа “2” (32=2⁵, 16=2⁴).

31¹¹<32¹¹= (2⁵)¹¹=2⁵⁵, т.е. 31¹¹< 2⁵⁵.

16<17 ; 16¹⁴<17¹⁴, (2⁴)¹⁴<17¹⁴.

31¹¹<2⁵⁵<2⁵⁶<17¹⁴ следовательно 31¹¹<17¹⁴.

Задача 2

Сравнить 9997¹⁰ и 100003⁸.

Решение:
9997¹⁰<10000¹⁰=(10⁴)¹⁰=10⁴⁰.
9997¹⁰<10⁴⁰.

10⁴⁰=(10⁵)⁸=100000⁸/

100000⁸<100003⁸.

Значит, 9997¹⁰<100003⁸.

Задача 3

Что больше 5³⁰⁰ или 3⁵⁰⁰?

Решение:
5³⁰⁰=5^3 100=(5³)¹⁰⁰=(5 5 5)¹⁰⁰=125¹⁰⁰.

3⁵⁰⁰=3^5 100=(3 3 3 3 3)¹⁰⁰=243¹⁰⁰.

125<243 следовательно 125¹⁰⁰<243¹⁰⁰ следовательно 5³⁰⁰<3⁵⁰⁰.

Ответ: 5³⁰⁰<3⁵⁰⁰.
2. Задачи на определение цифры, на которую оканчивается число.
Натуральные числа обладают следующим свойством: при умножении ряда чисел, оканчивающихся единицей или “5”, получается число, оканчивающиеся той же цифрой. Например:

22375 • 12735 = ……..5.
281 • 381 = ……….1

581²⁸⁹¹¹=581 581…581 = ………..1.
28911 раз

Всякая степень числа оканчивающаяся на “5”, тоже оканчивается на “5”.
Если число оканчивается “6”, то всякая степень числа оканчивается “6”.

286¹²³⁷ оканчивается “6”.

Если число оканчивается 76, то любая его степень оканчивается “76”.

2876⁴оканчивается 76.

Если число оканчивается 25, то любая его степень оканчивается “25”.
Рассмотрим задачи такого типа.
Задача 1
Какой цифрой оканчивается число 3²⁰⁰⁴?
Решение:
3¹=3
3²=9
3³=27
3⁴=81
3⁵=243
3⁶=729.

Заметим, что 3¹ и3⁵ оканчиваются на одну цифру “3”, 3²и 3⁶ – тоже на одну цифру “9”.
Последняя цифра повторяется через 4, т.е. в общем виде число 3^4m+nзаканчивается той же цифрой, что и 3ⁿ
2004=4 х501=2000+4=4 х 500 +4.

3²⁰⁰⁴=3^{4 х 500 +4}оканчивается той же цифрой, что 3⁴, т.е. на 1.

Ответ: на 1.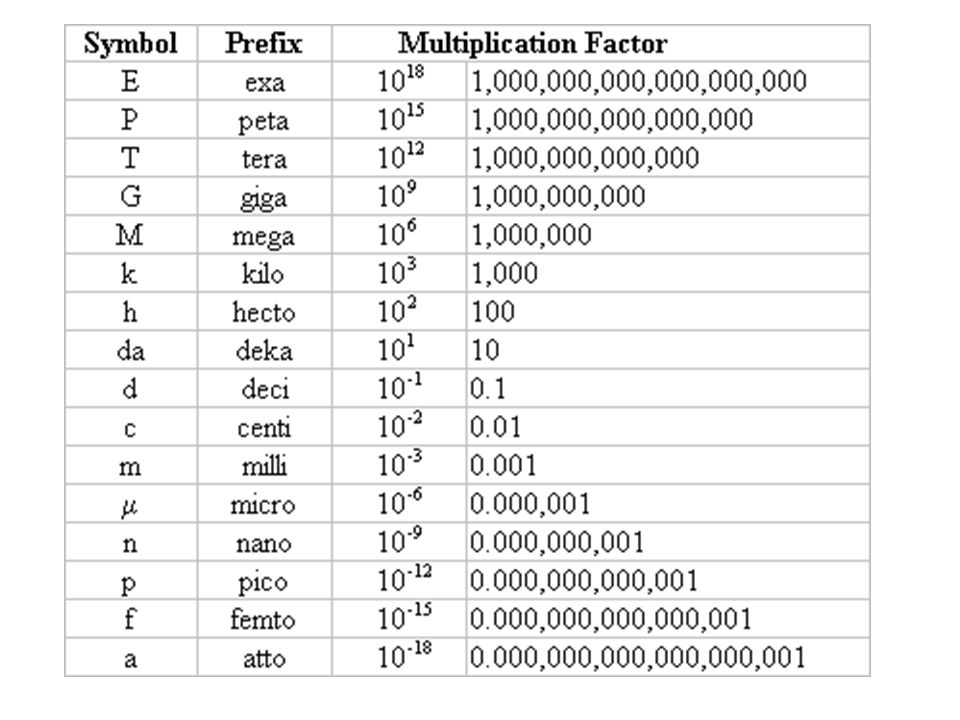

Задача 2

На какую цифру оканчивается число 3²⁰⁰⁴+4²⁰⁰⁵?

Решение:
3²⁰⁰⁴

оканчивается на 1 (первая задача).
4¹=4
4²=16
4³=64
4⁴=256
4⁵=924

Если степень числа 4 – нечётное число, то число оканчивается на “4”, если степень чётная, на “6”. 2005 – нечётное число, значит 4²⁰⁰⁵ оканчивается на “4”.
3²⁰⁰⁴+4²⁰⁰⁵

оканчивается на “5” (1+4=5).

Задачи на делимость

Задача 1

Выяснить, делится ли на 3 число 1+2+2²+2³+2⁴+…+2²⁰⁰³+2²⁰⁰⁴?

Решение:

Сгруппируем слагаемые:

Первое слагаемое делится на 3, второе нет, значит, сумма не делится на 3.

Задача 2

Доказать, что разность 999993¹⁹⁹⁹ – 777777¹⁹⁹⁷ кратна 5.

Решение:
Если оканчивается цифрой 3, то степени оканчиваются 3,9,7,1. Повторение через 4. в нашем случае 1999:4=499+3, 1999=4 х 499 +3. Значит число 999993¹⁹⁹⁹ оканчивается на ту же цифру, что число 3³, т.е. на 7.

Если число оканчивается на 7, то степень числа оканчивается на 7,9,3,1. повторение через 4.

7¹=7

7²=49

7³=343

7⁴=2401

7⁵=16807

1997:4=499+4

1997 = 4 х 499+1, значит 777777¹⁹⁹⁷ оканчивается на туже цифру, что и число 7¹, т.е. на 7.
3. Разность данных чисел оканчивается на 0 (7–7=0), 0:5, следовательно разность кратна “5”.

Задачи для индивидуального решения

Задача 1

Что больше 100²⁰ или 9000¹⁰?

Решение:
100²⁰=100^{2 х10}=(100²)¹⁰=(100 х100)¹⁰=1000¹⁰.

1000<9000 следовательно 10000¹⁰<9000¹⁰ следовательно 100²⁰<9000¹⁰.

Задача 2

Сравнить 127²³ и 513¹⁸.

Решение:
127<128; 127<2⁷; 127²³<2^{7 х23}=2¹⁶¹.

512<513; 2⁹<513; 2^{9 х18}<513¹⁸; 2¹⁶²<513¹⁸.

127²³<2¹⁶¹<2¹⁶²<513¹⁸ следовательно 127²³<513¹⁸.

Задача 3

Какая цифра будет последней в записи результата 953⁹⁹⁹⁹⁹?

Решение:
если число оканчивается на 3, то его степень оканчивается на 3, 9, 7, 1. Повторение через 4.

99999:4=24999 +(3 ост.).
99999=4 х 24999 +3.
Наше число имеет остаток такой же, что и 953³, т.е. число 7.

Задача 4

776⁷⁷⁶+777⁷⁷⁷+778⁷⁷⁸. Какой цифрой оканчивается сумма и кратна ли она 5.

Решение:
776⁷⁷⁶ оканчивается 6 (см. пред.задачи).

777⁷⁷⁷ оканчивается 7. если число оканчивается на 7, то его степени оканчиваются на 7,9,3,1, повторение через 4.
777=4 х 194+1.
Значит, 777⁷⁷⁷ имеет последней ту же цифру, что и 7¹, т. е. оканчивается на 7.

778⁷⁷⁸

8¹⁼⁸

8²=64

8³=512

8⁴=4096

8⁵=32768 Степени оканчиваются на 8,4,2,6. Повторение через 4. 778⁷⁷⁸ оканчивается на ту же цифру что и 8³, т.е. на 2. 778=4 х 194+3.

Наша сумма оканчивается на 5 (6+7+2=15).

Задачи для заочной работы

Задача 1

Какой цифрой оканчивается число ((9999⁹⁹⁹)⁹⁹)⁹.

Решение:
9¹=9

9²=81

9³=729 Если степень четная, то число оканчивается на 1, если степень нечетная, то на 9.

99⁹оканчивается на 9, т.к. 9 – нечетное число

число 99⁹ – нечетное, т.к. оканчивается на 9.

((999⁹⁹)⁹ оканчивается на 9, т.е. оно нечётное.

((999⁹⁹⁹)⁹⁹)⁹ оканчивается на 9, т.к. степень нечетная.

Задача 2

Что больше: 2⁷⁰⁰или5³⁰⁰? 2³⁰⁰или 3²⁰⁰.

Решение:
2⁷⁰⁰=(2⁷)¹⁰⁰=128¹⁰⁰.

5³⁰⁰=(5³)¹⁰⁰=125¹⁰⁰.

128>125 следовательно 128¹⁰⁰>125¹⁰⁰ следовательно 2⁷⁰⁰>5³⁰⁰.

1. 2³⁰⁰=8¹⁰⁰ 3²⁰⁰=9¹⁰⁰.
8¹⁰⁰<9¹⁰⁰ следовательно 2³⁰⁰<3²⁰⁰.

Задача 3

Найти последнюю цифру числа 8²⁰⁰⁶.

Решение:
если число оканчивается на 8, то его степени оканчиваются на 8,4,2,6. Повторение через 4.

а^4т+п имеет последней ту же цифру, что число а^п.

2006=501 х 4 +2.

8²⁰⁰⁶=8^{4 х 501+2}, значит это число имеет ту же цифру, что и 8², т.е. оканчивается на 4.

Задача 4

Что больше или
Найти несколько способов решения.

Решение:

Литература

Гусев В.А. и др. Внеклассная работа по математике в 6–8 классах. М.: Просвещение, 1984.
Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. М.: Просвещение, 1984.
Кордемский В.А. Ахадов А.А. Удивительный мир чисел. М.: Просвещение, 1986.
Перельман Я.И. Занимательная алгебра. М.: Наука, 1978.
Пичурин Л.Ф. За страницами учебника алгебры. М.: Просвещение, 1990.
Фарков А.В. Математические кружки в школе. М.: Айрис-пресс, 2007.
Сколько будет 23 в 10-й степени?
Итак, вы хотите знать, сколько будет 23 в 10-й степени, не так ли? В этой статье мы объясним, как именно выполнить математическую операцию под названием «возведение в степень 23 в степени 10». Это может показаться фантастическим, но мы объясним это без жаргона! Давай сделаем это.
Что такое возведение в степень?
Давайте сначала зафиксируем наши термины, а затем посмотрим, как вычислить, сколько будет 23 в 10-й степени.
Когда мы говорим об возведении в степень, все, что мы на самом деле имеем в виду, это то, что мы умножаем число, которое мы называем 9) для обозначения показателя степени. Знак вставки полезен в ситуациях, когда вы не хотите или не нуждаетесь в использовании надстрочного индекса.
Итак, мы упомянули, что возведение в степень означает умножение базового числа само на себя для получения показателя степени число раз. Давайте посмотрим на это более наглядно:
23 в 10-й степени = 23 x … x 23 (10 раз)
Итак, каков ответ?
Теперь, когда мы объяснили теорию, лежащую в основе этого, давайте посчитаем числа и выясним, чему равно 23 в 10-й степени:
23 в степени 10 = 23 ¹⁰ = 41 426 511 213 649
Почему мы вообще используем возведение в степень 23 ¹⁰? Что ж, нам намного проще писать умножения и выполнять математические операции как с большими, так и с маленькими числами, когда вы работаете с числами с большим количеством конечных нулей или большим количеством десятичных знаков.
Надеюсь, эта статья помогла вам понять, как и почему мы используем возведение в степень, и дала вам ответ, который вы изначально искали. Теперь, когда вы знаете, что такое 23 в 10-й степени, вы можете продолжить свой веселый путь.
Не стесняйтесь поделиться этой статьей с другом, если вы считаете, что она поможет ему, или перейдите вниз, чтобы найти еще несколько примеров.
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
Сколько будет 23 в 10-й степени?
«Сколько будет 23 в 10-й степени?». VisualFractions.com . По состоянию на 5 октября 2022 г. http://visualfractions.com/calculator/exponent/what-is-23-to-the-10th-power/.
«Сколько будет 23 в 10-й степени?». VisualFractions. com , http://visualfractions.com/calculator/exponent/what-is-23-to-the-10th-power/. По состоянию на 5 октября 2022 г.
Сколько будет 23 в 10-й степени?. VisualFractions.com. Получено с http://visualfractions.com/calculator/exponent/what-is-23-to-the-10th-power/.
Калькулятор возведения в степень
Хотите найти решение еще одной задачи? Введите число и мощность ниже и нажмите «Рассчитать».
Вычисление возведения в степень
Случайный список примеров возведения в степень
Если вы добрались до этого места, вам должно быть ДЕЙСТВИТЕЛЬНО нравится возведение в степень! Вот несколько случайных вычислений:
Сколько будет 73 в 35-й степени?
Сколько будет 85 в 67-й степени?
Сколько будет 29 в 54-й степени?
Сколько будет 17 в 7-й степени?
Сколько будет 55 в 44-й степени?
Сколько будет 9 в 73-й степени?
Сколько будет 21 в 80-й степени?
Сколько будет 73 в 67-й степени?
Сколько будет 31 в 78-й степени?
Сколько будет 97 в 11-й степени?
Сколько будет 76 в 10-й степени?
Сколько будет 25 в 98-й степени?
Сколько будет 14 в 67-й степени?
Сколько будет 3 в 80-й степени?
Сколько будет 2 в 35-й степени?
Сколько будет 42 в 52 степени?
Сколько будет 74 в 54-й степени?
Сколько будет 19 в 46-й степени?
Сколько будет 37 в 95-й степени?
Сколько будет 68 в 64-й степени?
Сколько будет 37 в 85-й степени?
Сколько будет 85 в 75-й степени?
Сколько будет 53 в 39-й степени?
Сколько будет 89 в 6-й степени?
Сколько будет 36 в 74-й степени?
Сколько будет 20 в 75-й степени?
Сколько будет 3 в 98-я сила?
Сколько будет 90 в 88-й степени?
Сколько будет 95 в 32-й степени?
Сколько будет 4 в 29-й степени?
Сколько будет 59 в 66-й степени?
Сколько будет 11 в 14-й степени?
Сколько будет 21 в 71-й степени?
Сколько будет 37 в 21-й степени?
Сколько будет 48 в 23-й степени?
Сколько будет 38 в 78-й степени?
Сколько будет 89 в 85-й степени?
Сколько будет 35 в 87-й степени?
Что такое 91 в 59-й степени?
Сколько будет 61 в 38-й степени?
Сколько будет 52 в 71-й степени?
Сколько будет 89 в 29-й степени?
Сколько будет 47 в 37-й степени?
Сколько будет 70 в 69-й степени?
Сколько будет 14 в 38-й степени?
Сколько будет 47 в 85-й степени?
Сколько будет 49 в 6-й степени?
Сколько будет 94 в 43-й степени?
Сколько будет 25 в 69-й степени?
Сколько будет 13 в 22-й степени?
Сколько будет 23 в 92 степени?
Сколько будет 36 в 60-й степени?
Сколько будет 64 в 99-й степени?
Сколько будет 26 в 32-й степени?
Сколько будет 86 в 51-й степени?
Сколько будет 83 в 47-й степени?
Сколько будет 79 в 28-й степени?
Сколько будет 9 в 64-й степени?
Сколько будет 56 в 93-й степени?
Сколько будет 88 в 43-й степени?
Сколько будет 30 в 76-й степени?
Сколько будет 2 в 90-й степени?
Сколько будет 33 в 95-й степени?
Сколько будет 44 в 59-й степени?
Сколько будет 61 в 82-й степени?
Сколько будет 49 в 17-й степени?
Сколько будет 92 в 73-й степени?
Сколько будет 32 в 4-й степени?
Сколько будет 68 в 72-й степени?
Сколько будет 63 в 70-й степени?
Сколько будет 78 в 50-й степени?
Сколько будет 27 в сотой степени?
Сколько будет 78 в 20-й степени?
Сколько будет 78 в 46-й степени?
Сколько будет 70 в 89-й степени?
Сколько будет 59 в 42-й степени?
Сколько будет 7 в 46-й степени?
Сколько будет 36 в 58-й степени?
Сколько будет 69 в 63-й степени?
Сколько будет 89 в 25-й степени?
Сколько будет 61 в 94-й степени?
Сколько будет 70 в 76-й степени?
Сколько будет 53 в 22-й степени?
Сколько будет 30 в 26-й степени?
Сколько будет 70 в 50-й степени?
Сколько будет 40 в 93-я власть?
Сколько будет 50 в 86-й степени?
Сколько будет 51 в 24-й степени?
Сколько будет 62 в 77-й степени?
Сколько будет 29 в 60-й степени?
Сколько будет 38 в сотой степени?
Сколько будет 86 в 87-й степени?
Сколько будет 85 в 33-й степени?
Сколько будет 83 в 27-й степени?
Сколько будет 35 в 94-й степени?
Сколько будет 24 в 33-й степени?
Сколько будет 46 в 73-й степени?
Сколько будет 88 в 55-й степени?
Сколько будет 56 в 92-й степени?
Сколько будет 40 в 53-й степени?
Сколько будет 67 в 66-й степени?
Калькулятор научных обозначений
Создано Даниэлем Трояновски и Войцехом Сас, кандидатом наук
Отредактировано Богной Шик и Джеком Боуотером
Последнее обновление: 21 июля 2022 г.
Содержание:
Что такое научное обозначение?
Правила научной записи
Как преобразовать число в научную запись?
Как пользоваться конвертером экспоненциальной записи?
Часто задаваемые вопросы
Калькулятор экспоненциального представления принимает любое десятичное значение и преобразует его в экспоненциальное представление. Здесь мы не только расскажем вам, что такое научная запись, но также объясним правила научной записи и обсудим небольшие вариации, которые могут появиться в разных областях, где люди используют научную запись.
Что такое научная запись?
Научная нотация обычно используется с очень большими или очень маленькими числами в таких приложениях, как физика, инженерия и химия. Он сжимает числа в число a между 1 (включено) и 10 (исключено), умноженное на 10 , возведенное в степень, обозначаемое как a × 10ⁿ .
Правила научной записи
При преобразовании числа в научную запись мы должны помнить несколько правил. Во-первых, десятичная дробь должна находиться между первыми двумя ненулевыми числами. Число перед символом умножения известно как значащее или мантисса. Количество цифр в значащих зависит от приложения и называется значащими цифрами. Калькулятор значащих цифр может помочь в этой ситуации. Значение показателя степени зависит от того, сдвинут ли десятичный разряд вправо или влево, чтобы вернуться к исходному числу. Пример того, как преобразовать число в экспоненциальное представление, приведен в следующем разделе.
Чтобы лучше понять эти правила научной записи, давайте обсудим пример.
Как преобразовать число в экспоненциальное представление?
Предположим, мы хотим преобразовать 0,00345 в экспоненциальное представление:
Поместите десятичную дробь между первыми двумя ненулевыми числами, чтобы мы получили 3,45 .
Подсчитайте количество перемещенных знаков после запятой, в данном случае это 3 .
Определите, нужно ли переместить десятичную точку влево или вправо, чтобы вернуться к исходному числу.
Если десятичная дробь сдвинута вправо, показатель степени будет отрицательным. Если десятичная дробь сдвинута влево, показатель степени положительный.
Запишите в виде a × 10ⁿ , в данном случае 3,45 × 10⁻³ .
Проверьте этот результат с помощью нашего калькулятора научных представлений! Если вы хотите, чтобы в ответе было две значащие цифры, вам придется округлить значащую до 3,5 . Калькулятор округления — отличный инструмент для решения этой задачи. Также полезным при преобразовании чисел в экспоненциальное представление является калькулятор экспоненты.
Как пользоваться конвертером экспоненциальной записи?
Пользоваться калькулятором экспоненциальной записи Omni очень просто: просто введите число, а наш конвертер сделает все остальное.
Обратите внимание, что этот преобразователь экспоненты использует e плюс или минус показатель степени вместо 10, возведенных в степень. В зависимости от приложения используется несколько различных обозначений. Компьютерные языки, инженерные и математические приложения используют схожие, но разные способы представления научных обозначений.
Если вы ищете полезные математические калькуляторы, не стесняйтесь взглянуть на калькулятор кубического корня, который позволяет вычислять не только кубический корень, но и корни любой степени.
Часто задаваемые вопросы
Как умножать и делить в экспоненциальном представлении?
Предположим, у вас есть два числа, записанные в экспоненциальном представлении: a × 10ⁿ и b × 10ᵐ .
На умножить их, умножить коэффициенты и сложить показатели степени: (a×b) × 10ⁿ⁺ᵐ .
Чтобы разделить первое на второе, разделить коэффициенты и вычесть показатели степени: (a/b) × 10ⁿ⁻ᵐ .
Результат не обязательно должен быть в экспоненциальном представлении! Рекомендуется проверить, так ли это, и при необходимости выполнить преобразование. Вы можете использовать калькулятор экспоненциальной записи Omni, чтобы быстро и легко выполнить эту задачу.
Что такое 4500 в экспоненциальном представлении?
4,5×10³ или эквивалентно 4,5e3. Это потому, что мы хотим записать 4500 как 9.0311 a × 10ⁿ , где a ∈ [1,10) и n целое число.
Что такое 0,00057 в экспоненциальном представлении?
5,7×10⁻⁴ или эквивалентно 5,7e-4. Таким образом, мы записали наше число как a × 10ⁿ , где a ∈ [1,10) , а n — целое число.
Даниэль Трояновски и Войцех Сас, кандидат наук
Введите десятичную или экспоненциальную систему счисления
Число
Ознакомьтесь с 61 похожим арифметическим калькулятором ➗
Абсолютное значениеСложениеАссоциативное свойство… Еще 58
Показатели: Научное представление | Purplemath
Основные правилаNegativeEng. Not’nFractional
Purplemath
Используя показатели степени, мы можем переформатировать числа. Это может быть полезно почти так же, как полезно (то есть проще) писать «двенадцать триллионов», а не 12 000 000 000 000, или «тридцать нанометров», а не «0,00000003 метра».
Для очень больших или очень малых чисел иногда проще использовать «научную нотацию» (так называемую, потому что ученые часто имеют дело с очень большими и очень маленькими числами).
Формат записи числа в экспоненциальном представлении довольно прост: (первая цифра числа), затем (десятичная точка), а затем (все остальные цифры числа), умножить (10 в соответствующей степени). ).
Содержание продолжается ниже
MathHelp.com
Научное обозначение
Преобразование довольно простое.
Это не очень большое число, но для примера оно подойдет. Чтобы преобразовать это в научное представление, я сначала преобразую «124» в «1,24». Это не то число, которое мне дали, а (1,24)(100) = 124, а 100 = 10 ² .
Тогда в экспоненциальной записи число 124 записывается как 1,24 × 10 ² .
На самом деле преобразование между «обычной» записью и научной записью еще проще, чем я только что показал, потому что все, что вам действительно нужно сделать, это подсчитать десятичные разряды. Чтобы выполнить преобразование для предыдущего примера, я бы подсчитал количество знаков после запятой, на которое я передвинул десятичную точку. Поскольку я переместил его на два места, я имел бы дело со степенью 2 на 10. Но должна ли она быть положительной или отрицательной степенью 2? Поскольку исходное число (124) было больше преобразованной формы (1,24), то мощность должна быть положительной.
Так как показатель степени 10 положительный, я знаю, что они ищут БОЛЬШОЕ число, поэтому мне нужно переместить десятичную точку вправо, чтобы сделать число БОЛЬШЕ. Поскольку показатель степени числа 10 равен «12», мне нужно переместить десятичную точку на двенадцать разрядов.
Во-первых, я переставлю десятичную точку на двенадцать разрядов. Я делаю маленькие циклы, когда считаю места, чтобы отслеживать:
Затем я заполняю циклы нулями:
Другими словами, число равно 3 600 000 000 000, или 3,6 триллиона
Идиоматическое примечание: «Триллион» означает тысячу миллиардов, то есть тысячу тысяч миллионов, на американском языке; британско-английский термин для американского «миллиарда» будет «миллиардом», поэтому американский «триллион» (выше) будет британским «тысяча миллиардов».
В экспоненциальной записи числовая часть (в отличие от десятичной части) будет «4,36». Итак, я посчитаю, на сколько знаков десятичная точка должна переместиться, чтобы попасть из того места, где она сейчас, туда, где она должна быть:
Тогда степень числа 10 должна быть равна −11: «одиннадцать», потому что на столько знаков нужно переместить десятичную точку, и «минус», потому что я имею дело с МАЛЕНЬКИМ числом.
Итак, в экспоненциальной записи число записывается как 4,36 × 10 ⁻¹¹
Поскольку показатель степени у 10 отрицательный, я ищу небольшое число. Поскольку показатель степени равен семи, я буду перемещать десятичную точку на семь знаков. Поскольку мне нужно переместить точку, чтобы получить небольшое число, я буду перемещать ее влево.
Ответ: 0,000 000 42
Это небольшое число, поэтому показатель степени 10 будет отрицательным. Первая «интересная» цифра в этом числе — 5, так что именно там должна быть десятичная точка. Чтобы перейти от того места, где оно находится, сразу после 5, десятичная точка должна будет переместиться на девять знаков вправо. (Отсчитайте их, если вы не уверены!)
Тогда степень числа 10 будет отрицательной 9, и ответ будет 5,78 × 10 ⁻⁹
Это большое число, поэтому показатель степени на 10 будет положительным. Первая «интересная» цифра в этом числе — старшая 9., так что там должна быть десятичная точка. Чтобы перейти от того места, где оно находится, сразу после 9, десятичная точка должна будет переместиться на семь знаков влево.
Тогда степень числа 10 будет равна 7, и ответ будет равен 9,3 × 10 ⁷
Помните: на сколько делений вы переместили десятичную дробь, это степень числа 10. Если у вас есть небольшое число в десятичной форме (меньше 1 по абсолютной величине), то степень отрицательна для научной записи; если это большое десятичное число (больше 1 по абсолютной величине), то показатель степени положителен для научного представления.
Предупреждение: Отрицательное значение показателя степени и отрицательное значение числа означают две очень разных вещей! Например:
-0,00036 = -3,6 × 10 ^-4
0,00036 = 3,6 × 10 ⁻⁴
36 000 = 3,6 × 10 ⁴
−36 000 = −3,6 × 10 ⁴
Не путайте!
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании обычного числа в экспоненциальное представление. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку «бумажный самолетик», чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок. )
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажмите здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.)
Вас могут попросить умножить и разделить числа в экспоненциальном представлении. Я никогда не видел смысла в этом, так как в «реальной жизни» вы бы имели дело с этими беспорядочными числами, используя калькулятор, но вот процесс, если вам нужно «показать свою работу»:
Поскольку я умножаю, я могу легко перемещать вещи и упрощать некоторые из них:
(2,6 × 10 ⁵ ) (9,2 × 10 ⁻¹³ )
= (2.6) (10 ⁵ ) (9.2) (10 ⁻¹³ )
= (2,6) (9,2) (10 ⁵ ) (10 ⁻¹³ )
= (2,6) (9,2) (10 ⁵⁻¹³ )
= (2,6) (9,2) (10 ⁻⁸ )
Хорошо; Я упростил десятую часть. Теперь я должен иметь дело с 2,6 умножить на 9.2, не забывая преобразовать произведение в экспоненциальное представление:
2,6 × 9,2 = 23,92 = 2,392 × 10 = 2,392 × 10 ¹
Собрав все вместе, у меня есть:
(2,6 × 10 5
02) (9,2 × 10 ⁻¹³ )
= (2,6) (9,2) (10 ⁻⁸ )
= (2,392 × 10 ¹ ) (10 ⁻⁸ )
= (2,392)(10 ¹ ) (10 ⁻⁸ )
= (2,392) (10 ¹⁻⁸ )
= 2,392 × 10 ⁻⁷
Тогда (2,6 × 10 ⁵ ) (9,2 × 10 ⁻¹³ ) = 2,392 × 10 ⁻⁷
90
Во-первых, я разберусь со степенями десяти:
(1,247 × 10 ⁻³ ) ÷ (2,9 × 10 ⁻² )
= (1,247 ÷ 2,9) (10 ⁻³ ÷ 10 ⁻² )
= (1,247 ÷ 2,9) (10 ⁻³ × 10 ² )
= (1,247 ÷ 2,9) (10 ⁻¹ )
Теперь я займусь делением:
1,247 ÷ 2,9 = 0,43 = 4,3 × 10 ⁻¹
Собираем все вместе: 90, я получаю3: 90, я получаю3
(1,247 × 10 ⁻³ ) ÷ (2,9 × 10 ⁻² )
= (1,247 ÷ 2,9) (10 ⁻¹ )
= (4,3 × 10−1) (10 ⁻¹ )
= (4.
No related posts.