Замечательный пределы: Математическое Бюро. Страница 404

Второй замечательный предел — примеры решений

Применяемые формулы, свойства и теоремы

Здесь мы рассмотрим примеры решений задач на вычисление пределов, в которых используется второй замечательный предел и его следствия.
Ниже перечислены формулы, свойства и теоремы, которые наиболее часто применяются в подобного рода вычислениях.

• Второй замечательный предел и его следствия:

  ,     ,     ,     .
  Стоит отметить еще одну формулу (см. пример ниже ⇓):
  , где α – действительное число.

• Свойства и формулы показательной функции, формулы логарифмов, свойства экспоненты и натурального логарифма.
• Арифметические свойства предела функции.
• Теоремы о пределе и непрерывности сложной функции.

Здесь мы будем иметь дело со степенно-показательной функцией, у которой основание и показатель являются функциями от некоторой переменной: . Ее удобно представить как экспоненту: . В этой связи полезна следующая лемма.

Лемма о пределе степенно-показательной функции
Пусть – функции переменной x, имеющие конечные пределы:
. Здесь .
Тогда
.
Доказательство ⇓

В случае бесконечных пределов, или когда , мы проводим исследование произведения , применяя свойства пределов бесконечно больших и малых функций.

В случае и , мы имеем неопределенность вида единица в степени бесконечность. Для ее раскрытия используется второй замечательный предел.

Раскрытие неопределенности 1 в степени бесконечность

Пусть u и v есть функции от переменной x: . И пусть при . Тогда выражение является неопределенным при . Для раскрытия этой неопределенности, мы вводим переменную t из соотношения
.
Тогда . При .
;
.

Таким образом задача сводится к вычислению предела .

Доказательство леммы о пределе степенно-показательной функции

Формулировка ⇑

Представим степенно-показательную функцию в виде показательной функции:
.
Поскольку логарифмическая функция непрерывна на своей области определения, то по теореме о пределе непрерывной функции от функции,
.
По теореме о пределе произведения двух функций,
.
Поскольку показательная функция непрерывна на всей числовой оси, то по теореме о пределе непрерывной функции от функции,
.

Лемма доказана.

Примеры решений

Все примеры Далее мы приводим подробные решения с объяснениями следующих пределов:
⇓,   ⇓,   ⇓,   ⇓,   ⇓.

Пример 1

Все примеры ⇑ Найти предел:
.

Решение

При ,   . Это неопределенность вида один в степени бесконечность.

Выполняем преобразования.
;
.

Сделаем замену переменной . При . Применим второй замечательный предел:
.

Находим предел дроби, разделив числитель и знаменатель на x:
.

Применяем лемму о пределе степенно-показательной функции ⇑
.

Ответ

.

Пример 2

Все примеры ⇑ Найдите предел:
.

Решение

При ,   .   при . Это неопределенность вида один в степени бесконечность. Раскрываем ее с помощью второго замечательного предела.

Введем переменную t из соотношения: . Тогда при ,
.
.

Применим второй замечательный предел к основанию степени:
.

Найдем предел показателя степени. Для этого применим тригонометрическую формулу

и первый замечательный предел:

.

Применяем лемму о пределе степенно-показательной функции ⇑ учитывая, что при :
.

Ответ

.

Пример 3

Все примеры ⇑ Найти предел последовательности:
.

Решение

При . Элементы последовательности равны единице. Поэтому . Рассмотрим случай .

При . Это неопределенность вида единица в степени бесконечность. Для ее раскрытия применим второй замечательный предел.

Введем переменную t из соотношения: . Тогда при ,
.
.

Применим второй замечательный предел к основанию степени:
.

Найдем предел показателя степени. Для этого применим тригонометрическую формулу

и первый замечательный предел:

.

Применяем лемму о пределе степенно-показательной функции ⇑ учитывая, что при :
.
Эта формула справедлива и при .

Ответ

.

Пример 4

Все примеры ⇑ Найти предел:
.

Решение

Пусть . Рассмотрим функцию в проколотой окрестности точки , на которой . Для определения предела, функция должна быть определена на любой проколотой окрестности этой точки. Считаем, что . Тогда . При . Поэтому .
Теперь рассмотрим предел при .

При . У нас неопределенность вида 0/0.

Для ее раскрытия приведем степенно-показательную функцию к основанию e учитывая, что :
.
Согласно следствию второго замечательного предела:
.
В последнем множителе сделаем замену переменной:
.
При . Кроме этого, при . Тогда
.

Применяем арифметические свойства предела функции:
.
Это же значение является правильным и при .

Ответ

.

Пример 5

Все примеры ⇑ Найдите предел функции:
.

Решение с помощью второго замечательного предела и его следствий

При . Это неопределенность вида 0/0. Для ее раскрытия, применим следствия второго замечательного предела.

Преобразуем числитель дроби:

.
Преобразуем знаменатель:
.

Разделим числитель и знаменатель на x:
.
Чтобы не загромождать формулы, мы ввели обозначение .

Применяя первый замечательный предел и следствия второго, имеем:
;   ;   ;   ;   .
Применяем арифметические свойства предела функции:
.

Решение с помощью эквивалентных функций

Мы можем упростить решение, если применим теорему о замене функций эквивалентными в пределе частного. Считаем, что предел существует. Тогда мы можем заменить знаменатель эквивалентной функцией при . Из таблицы эквивалентных функций находим:
.

Получаем более простой предел:
.
Далее делаем преобразования аналогично предыдущему:
.
Поскольку при , то применяем следствие второго замечательного предела:
;
.
В дробях и заменим функции в числителе эквивалентными:
;
.

Применяем арифметические свойства предела функции:
.

Ответ

.

Первый и второй замечательные пределы и способы их вычисления. (Семинар 6)

Похожие презентации:

Второй замечательный предел

Замечательные пределы

Замечательные пределы

Первый замечательный предел

Первый замечательный предел

Вычисление пределов функции. Предел функции на бесконечности. Два замечательных предела. Вычисление числа «е»

Два замечательных предела

Бесконечно малые, бесконечно большие функции, их свойства. Теоремы о пределе функции, замечательные пределы

Замечательные кривые в математике

Основные теоремы о пределах. Способы вычисления пределов функций. (Семинар 5)

Семинар 6. Первый и второй замечательные пределы и способы их вычисления
Первый замечательный предел
(предел отношения синуса бесконечно малой дуги к самой дуге)
Теорема Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной
в радианах, равен единице, то есть lim
x 0
sin x
1
x
(1)
Доказательство
B
C
O
A
Рассмотрим в координатной плоскости круг радиуса R с центром в начале координат

OA R, AOB x,0 x , AC OA
2
x
1
S AOB S сект. 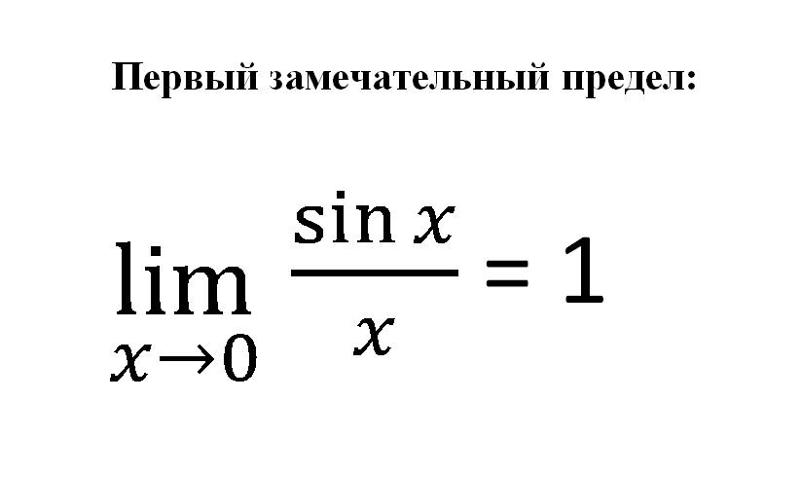AOB S AOC , то есть 1 R 2 sin x 1 R 2 x 1 R 2tgx или 1
.
sin
x
cos
x
2
2
2
1
x
В силу четности функций
это неравенство справедливо и для интервала
и
cos x
sin x
2
x 0 . Перейдя в этом неравенстве к пределу при x 0 и заметив, что в силу
непрерывности функции cosx при х=0 имеет место равенство lim x 0 cos x 1 получим
x
sin x
lim x 0
1 , что равносильно lim x 0
1.
sin x
x
Второй замечательный предел
n
Рассмотрим выражение 1 1 , где n – натуральное число.
n
n
Задаем для n неограниченно возрастающие значения и вычисляем 1 1 . Получим
следующий результат
n
n
1
1
n
n
1
2
10
100
1000
10000
2
2,25
2,594
2,705
2,717
2,718
1
Как видно из таблицы при увеличении n выражение 1
n
n
изменяется все медленнее и стремится к некоторому пределу, приближенно равному 2,718.
Теорема
n
1
Последовательность 1 стремится к конечному пределу, заключенному между 2 и 3.
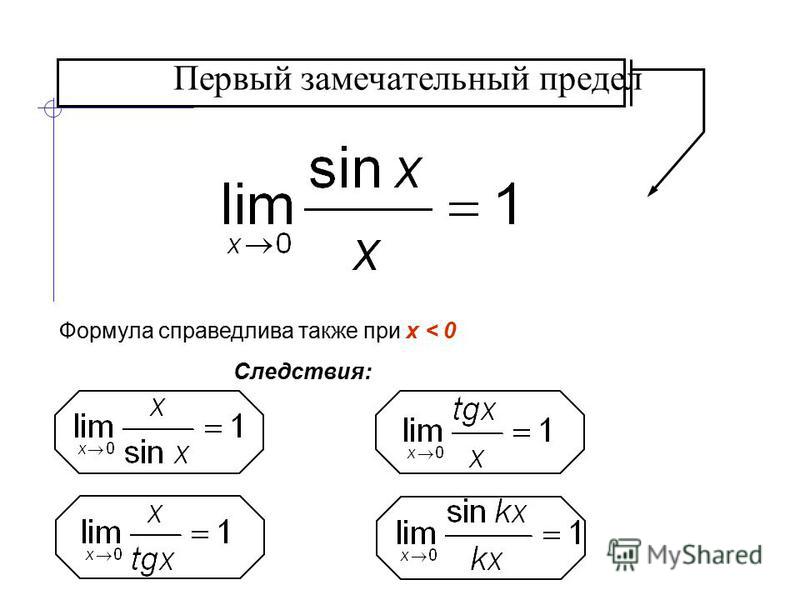
n
(Доказательство на основании разложения по биному Ньютона). Этот предел
называется числом e. Итак
n
1
e lim n 1 , е=2,7182818284…
n
x
1
Рассмотрим функцию 1 , где ( x ( , 1) (0, )) . Можно доказать, что
e lim
x
1
x 1 .
x
x
Другое выражение для числа е. Полагая , 1 ( 1) будем иметь e lim 0 1
x
1
При вычислении пределом полезно применять следующие формулы:
k
ln( 1 x)
lim x (1 ) x e k ; lim x 0 (1 kx) x e k ; lim x 0
1.
x
x
1
Данные формулы легко получаются из двух основных формул.
Примеры с решениями
sin mx
x 0
x
1.Найти lim
Решение. Используя первый замечательный предел, имеем
m sin mx
sin mx
sin mx
lim
lim
m
lim
= x 0
x 0
mx = x 0 mx m
x
1 cos 5 x
2. Найти lim
x 0
x2
2
2 sin 2 (5 x / 2)
1 cos 5 x
sin(
5
x
/
2
)
5
2
Решение. Имеем lim
= lim
= 2 lim (
) 2 25 / 2
2
x 0
x 0
x2
x 0
x
x
2
cos 3 x cos 7 x
x 0
x2
3. Найти lim
cos 3 x cos 7 x
2 sin 5 x sin 2 x
=
lim
2 5 2 20
x 0
x2
x 0
x x
Решение. Имеем lim
arcsin x
x 0
x
4. Найти lim
Решение. Сделаем замену
t arcsin x x sin t t 0
. Тогда получим
arcsin x
t
= lim
1
x 0
t
0
x
sin t
5. Найти lim 1 cos x
x 0
x2
lim
Решение. Умножим числитель и знаменатель на сопряженное, то есть
x
1 cos x
1 cos x lim (1 cos x )(1 cos x)
2
lim
=
= lim
=
lim
2
2
2
x
0
2
x
0
x 0
x (1 cos x)
x
x (1 cos x ) x 0 x (1 cos x )
2 sin 2
2
x
sin
1
1
2
lim
x 0
x 2(1 cos x ) 4
2
x
x
6. Найти lim
x x 1
Решение. Преобразуем выражение в скобках и выделим второй замечательный предел.
x
x = lim 1 1
lim
x 1 1 / x
x x 1
e
x 2
x 1
lim
7. Найти
x x 3
x
Решение. Преобразуем выражение в скобках и выделим второй замечательный предел.
x 1
lim
x x 3
x 2
e 1 1
1 1/ x 1 1/ x
3 e 4
= lim
x 1 3 / x
e 1
1 3/ x
x
x 5x 4
lim 2
x x 3 x 7
2
8. Найти
x
2
Решение. Делением числителя дроби на знаменатель выделим целую часть, а именно
x 2 5x 4
8x 3
. Таким образом, при x данная функция представляет
1
x 2 3x 7
x 2 3x 7
собой степень, основание которой стремится к единице, а показатель к бесконечности
(неопределенность вида 1 ). Преобразуем функцию так, чтобы использовать второй
замечательный предел.
x ( 8 x 3)
x
x 3 x 7 x 2 3 x 7
x 2 5x 4
8x 3
8x 3
= lim 1 2
lim 2
lim (1 2
) 8 x 3
=
=
x x 3 x 7
x
x
x
3
x
7
x
3
x
7
8 3 / x
x
2
x 3 x 7 1 3 / x 7 / x 2
8
x
3
lim (1 2
) 8 x 3
8x 3
. Так как
x
0 , при x , то
x
3
x
7
2
x 3x 7
x 2 3 x 7
8
x
3
lim (1 2
) 8 x 3 e
8 3/ x
x
. Принимая во внимание, что lim
8,
x
3
x
7
x 1 3 / x 7 / x 2
2
x
x 2 5x 4
окончательно получаем lim 2
e 8 .
x x 3 x 7
x
9. Найти lim e 1
x 0
x
Решение. Сделав замену e x 1 z, x ln( 1 z ), z 0 , получим второй
замечательный предел, а именно
ex 1
z
lim
x 0
x
lim
z 0
ln( 1 z )
1
Примеры для самостоятельного решения.
Найти пределы:
tgx sin x
2) lim
x 0
x3
tg (mx)
1) lim
x 0 sin( nx )
sin 2 x
x 0 ln( 1 x)
4) lim
x 1
7) lim
x x 2
x
a x 1
9) lim
x 0
x
1 cos 5 x
x 0 1 cos 3 x
3) lim
x 1
6) lim 2
x
x
ln( x 2) ln 2
8) lim
x 0
x
arctg 2 x
5) lim
x 0 sin 3 x
e ax e bx
10) lim
x 0
x
2
x2 2

English     Русский Правила

Основные теоремы о пределах. Замечательные пределы.

Стр 1 из 6Следующая ⇒

Теорема 1. , где С = const.

Теорема 2.

Теорема 3.

Следствие.

Теорема 4. при

Теорема 5. Если f(x)>0 вблизи точки х = а и , то А>0.

Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.

Теорема 6. Если g(x) £ f(x) £ u(x) вблизи точки х = а и , то и .

Таблица пределов

Замечательные пределы.

Первый замечательный предел ,

Второй замечательный предел

Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.

Кроме, изложенных выше, пределов можно записать следующие полезные на практике соотношения:

 

 

Пример. Найти предел:

Пример. Найти предел:

 

Пример.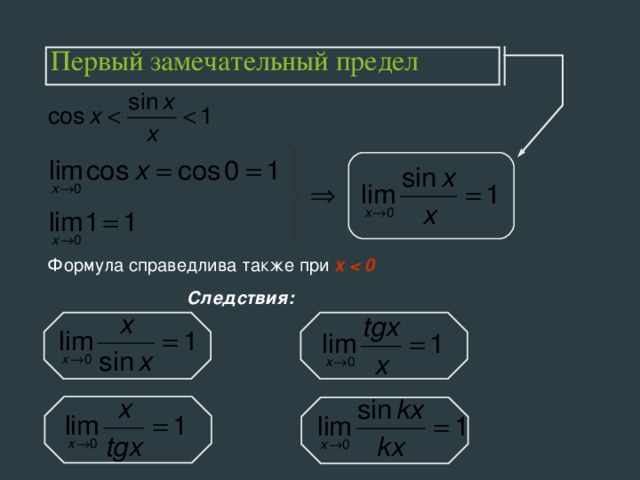 Найти предел: .

Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.

Тогда

 

Пример. Найти предел: .

Домножим числитель и знаменатель дроби на сопряженное выражение: = .

Пример. Найти предел:

Пример. Найти предел:

Разложим числитель и знаменатель на множители, тогда

 

 

Производная функции и дифференциал.

Дифференциал функции равен произведению производной на дифференциал аргумента

независимо от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.

Например, дифференциал сложной функции.

Пример. Задана функция . Найти

 

 

Задания для выполнения контрольной работы по теме 1.

Задание 1. Вычислить пределы (выбрать один вариант):

 

1 вариант	а)	б)
2 вариант	a)	б)
3 вариант	а)	б)
4 вариант	а)	б)
5 вариант	а)	б)
6 вариант	а)	б)
7 вариант	а)	б)
8 вариант	а)	б)
9 вариант	а)	б)
10 вариант	а)	б)

 

Задание 2.Найти производные первого порядка данных функций, используя таблицу производных правила вычисления производных (выбрать один вариант):

1 вариант а) y = б) y =

в) y = г) y = д) y =

2 вариант а) у = б) у =

в) у = г) у = д) у =

3 вариант а) б)

в) г) д)

4 вариант а) б)

в) г) д)

5 вариант а) б)

в) г) д)

6 вариант а) б)

в) г) д)

7 вариант а) б)

в) г) д)

8 вариант а) б)

в) г) д)

9 вариант а) б)

в) г) д)

10 вариант а) б)

в) г) д)

ТЕМА 2: НЕОПРЕДЕЛЁННОЕ ИНТЕГРИРОВАНИЕ. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.

План:

1. Понятие неопределенного интеграла.

2. Свойства неопределенного интеграла. Таблица интегралов. Непосредственное интегрирование.

3. Основные методы интегрирования в неопределенном интеграле: замена переменной в неопределенном интеграле, интегрирование по частям в неопределенном интеграле, интегрирование рациональных дробей.

4. Определенный интеграл и его свойства. Формула Ньютона-Лейбница.

5. Основные методы интегрирования в определенном интеграле: замена переменной в неопределенном интеграле, интегрирование по частям в неопределенном интеграле.

Понятие неопределенного интеграла.

Определение.Функция называется первообразнойфункции заданной на интервале , если она дифференцируема и для любого из этого интервала .

Определение. Совокупность всех первообразных функции на интервале называется неопределенным интегралом от функции и обозначается .

называется подынтегральной функцией, – подынтегральным выражением, – переменной интегрирования.

 

Свойства неопределенного интеграла. Таблица интегралов. Непосредственное интегрирование.

Свойства неопределенного интеграла.

Пусть – одна из первообразных .

1. .

2. .

3. .

 

Таблица интегралов:

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.
11.	12.
13.	14.
15.	16.
17.	18.
19.	20.
21.	22.

Непосредственное интегрирование.

3. Основныеметоды интегрирования в неопределенном интеграле:

Замена переменной в неопределенном интеграле (или метод подстановки)

Пусть требуется найти неопределенный интеграл , но непосредственно подобрать первообразную для не удается, хотя известно, что она существует. Во многих случаях введением вместо переменной интегрирования некоторой новой переменной можно данный интеграл свести к другому, который или содержится в таблице основных интегралов или легко вычисляется другим способом.

Такой метод называется методом замены переменной (метод подстановки), или методом подстановки.

Итак, введем новую переменную по формуле – дифференцируемая функция на некотором интервале, при этом функция непрерывна на соответствующем интервале изменения . Тогда – формула замены переменной в неопределенном интеграле.

Пример. Найти .

Сделаем замену переменной по формуле:

.

123456Следующая ⇒

великолепных пределов (Original Mix) Ады Ванвельдхуиз на Beatport

Трек

Ссылка:

Вставить:

художников Ада Ванвельдхейз

Выпускать
• 99″ data-ec-variant=»album» data-ec-id=»3802700″ data-ec-d1=»Ada Vanveldhuize»>

• Длина 4:45
• Вышел 2022-07-29
• ударов в минуту 87
• Ключ В ♭ мин
• Жанр Жесткий танец / Хардкор
• Этикетка DistroKid

• Трахни свой разум Расширенный микс

  Спиады

• 29″ data-ec-variant=»track» data-ec-id=»16729456″ data-ec-d1=»NSD» data-ec-d3=»Hard Dance / Hardcore» data-ec-d4=»Terror»>

  Террор Дрен Закрытые Оригинальный микс

  НРД

• Давайте глупо Оригинальный микс

  атмосфера, Тоншифтерз, код черный, Команда TAC

• 29″ data-ec-variant=»track» data-ec-id=»16718725″ data-ec-d1=»The Empire» data-ec-d3=»Hard Dance / Hardcore»>

  Темные экраны Оригинальный микс

  Империя

• КАНЬЕ Оригинальный микс

  Левенхан

• 29″ data-ec-variant=»track» data-ec-id=»16715403″ data-ec-d1=»Audiotricz» data-ec-d3=»Hard Dance / Hardcore» data-ec-d4=»Hardstyle»>

  Животные Расширенный микс

  Аудиотрикс

• До встречи Оригинальный микс

  Рейгин, Сбой системы

• 29″ data-ec-variant=»track» data-ec-id=»16703172″ data-ec-d1=»Calixto» data-ec-d3=»Hard Dance / Hardcore» data-ec-d4=»Hardstyle»>

  Сила истины Оригинальный микс

  Каликсто

• Один раз Оригинальный микс

  Ральфи Ди

• 29″ data-ec-variant=»track» data-ec-id=»16692170″ data-ec-d1=»Hypnose» data-ec-d3=»Hard Dance / Hardcore» data-ec-d4=»Hardstyle»>

  Огонь Оригинальный микс

  Гипноз

• Только один Расширенный микс

  Мисс Темпо

• 29″ data-ec-variant=»track» data-ec-id=»16677593″ data-ec-d1=»Dr. Rude, Lune, Kane Scott» data-ec-d3=»Hard Dance / Hardcore» data-ec-d4=»UK / Happy Hardcore»>

  Беги бесплатно Расширенный микс

  Доктор Руд, Луна, Кейн Скотт

• Аврора Оригинальный микс

  ХОТА, Сиа, Питу и Ческ

• Museo» data-ec-creative=»Recommended Tracks» data-ec-brand=»Notebook Records» data-ec-category=»Tracks» data-ec-list=»Recommended Tracks» data-ec-price=»1.29″ data-ec-variant=»track» data-ec-id=»16669433″ data-ec-d1=»Nothing But Requiem, Museo» data-ec-d3=»Hard Dance / Hardcore» data-ec-d4=»Uptempo»>

  feat. музей Оригинальный микс

  Ничего, кроме Реквиема, музей

• Подземные круги Оригинальный микс

  D-рецептор, Тайфон

• 29″ data-ec-variant=»track» data-ec-id=»16623123″ data-ec-d1=»TotenKore» data-ec-d3=»Hard Dance / Hardcore»>

  Смерть (ваш единственный выход) Оригинальный микс

  ТотенКоре

• Рэйверс Грув Оригинальный микс

  Бумер

• 29″ data-ec-variant=»track» data-ec-id=»16620544″ data-ec-d1=»Vandalize» data-ec-d3=»Hard Dance / Hardcore»>

  В мой ритм Оригинальный микс

  Вандализм

• Гимн беглеца Оригинальный микс

  Микки Моделл, Жана, DJ Кунос

• 29″ data-ec-variant=»track» data-ec-id=»16620532″ data-ec-d1=»Jay F» data-ec-d3=»Hard Dance / Hardcore»>

  Покажите мне Оригинальный микс

  Джей Ф

Смотри, играй, рисуй, пробуй — без ограничений

Опубликовано:

9 ноября 2021 г.

От космоса до путешествий в человеческом теле — вовлеките своих учеников в содержательные дискуссии на научные темы с помощью этой серии видеороликов и рабочей тетради.

Языки:

Английский

итальянский

Возраст:

8-9

9-12

12-15

15-18

Школьный предмет:

Физика

Химия

Технология

Формат:

Видео

Область исследования:

Информатика и инженерия

Физика

Увеличить

Подробная информация об этом задании

Это задание доступно на 2 языках

Super Science me

Этот материал вовлекает учеников в беспристрастные дебаты в классе со своими учителями на такие темы, как:

• персонаж исследователь
• роль науки в повседневной жизни
• делать ошибки
• мечтать о невозможном
• проснуться, чтобы сбылись мечты

Также можно использовать для дистанционного обучения и вообще для всех интересующихся наукой.

Материал включает виньетки (8-12 лет) и шесть видеороликов, в которых сурдопереводчик помогает глухим учащимся понимать.

1 и 2 (до)интервью с астронавтом ЕКА Паоло Несполи (8-18)

3. История путешествия во времени (8-12)

4. Научное путешествие в человеческом теле (8-12)

5. Путешествие через серию экспериментов (8-12)

6. Космическая миссия (8–12)

Информация для учителей

• Продолжительность занятия:  Виньетка: 20 мин.
  • Видео 1: 3’33’’
  • Видео 2: 51’35’’
  • Видео 3: 14’24’’
  • Видео 4: 24’36’’
  • Видео 5: 22’03’’
  • Видео 6: 37’24’’
• Рекомендуемый размер группы: Класс А
• Рекомендуемое место: В помещении, в школьном классе, даже при онлайн-обучении
• Требуется подготовка учителя: Да, распечатать виньетку для каждого ученика
• Необходимые дополнительные материалы: Нет

Super Science me

Questo materiale coinvolge gli alunni e i loro insegnanti in dibattiti in classe «senza pregiudizi» su argomenti quali:

• ла фигура ди чи фа рисерка
• иль Руоло делла Сциенца Нелла Вита Котидиана
• ошибка тарифа
• sognare cose impossibili
• «svegliarsi» для визуализации, которые могут быть реализованы.

Questo materiale può essere utilizzato anche per l’apprendimento a distanza e in generale da tutti coloro che sono appassionati alla scienza.

Материал включает виньетку (8-12 лет) и 6 видео на языке CUI Uninterprete della lingua dei segni aiuta la comprensione degli Studenti audiolesi:

1. e 2. (pre)interviste dell’astronauta dell’ESA Paolo Nespoli (8-18 лет)

3. Viaggio nel tempo (8-12 лет)

4. Viaggio nel corpo umano (8-12 лет) anni)

5. Специализированная школа (8-12 лет)

6. Missione Spaziale (8-12 лет)

Informazioni per gli insegnanti
• Продолжительность: 2:00012
• ;
  • Видео 1: 3’33’’;
  • Видео 2: 51’35’’;
  • Видео 3: 14’24’’;
  • Видео 4: 24’36’’;
  • Видео 5: 22’03’’;
  • Видео 6: 37’24’’
• Нумерация группы поддержки: в одном классе
• Предложение: Единый класс средней школы, а также коллега в DAD
• Необходимость подготовки к участию в розыгрыше: штемпеля для копии виньетки для всех
• Необходимые дополнительные материалы: nessuno

Проект MSCA, стоящий за этой деятельностью

Имя : SuperScienceMe: REsearch is your R-Evolution — European Researchers’ Night

Исследователи : Франческо Валентини и Андреа Лука Аттанасио

Веб-сайт Super Science Me

Хотите оставить отзыв об этой странице?

1. Вы нашли эту страницу полезной? (обязательно)

В чем была основная проблема?- Пожалуйста, выберите один вариант -Информация на странице нечеткая, неполная или неточная Проблема с переводомНе могу найти нужную мне информациюНеработающие ссылкиСтраница отображается плохоДругая техническая проблемаСтраница или ее часть недоступнаДругое

Пожалуйста, объясните свой выбор.

Пожалуйста, объясните свой выбор.

---

2. Проблема с этой страницей? (обязательно)

Пожалуйста, опишите проблему в поле ниже

---

3. Помогите нам стать лучше

Пожалуйста, расскажите нам больше о контексте.

Пожалуйста, ответьте на все обязательные вопросы

Река Гуадалупе

Река Гуадалупе Нью-Браунфелс – правила и информация о трубах

Нью-Браунфелс является домом не для одной, а для двух прекрасных рек — Гваделупе и Комала. Техас известен своим отдыхом на воде, но ничто не сравнится с жарой, как плавание!

  Река Гваделупе берет начало в истоках недалеко от Керрвилля, штат Техас. Река течет на протяжении 230 миль, вплоть до залива Сан-Антонио в Мексиканском заливе. Нижняя Гваделупа начинается у плотины Каньон-Лейк и проходит через Техас-Хилл-Кантри в Нью-Браунфелс.

Река Гваделупа извивается через несколько городов, но Нью-Браунфелс является эпицентром летнего речного тюбинга в Техасе! Река Гуадалупе предлагает живописные виды на природу и достаточно времени, чтобы впитать все это. Ищете более короткий поплавок? Попробуйте реку Комал!

Катание на тюбингах — самое популярное занятие на «Гуаде», но многие искатели приключений также любят рафтинг, греблю на каноэ, каяках и байдарках. Наслаждайтесь долгим днем, исследуя парк Ланда, играя в два шага в старейшем танцевальном зале в Техасе и совершая покупки. Когда ваши ноги начинают болеть, пусть прохладные течения реки Гуадалупе помогут вам расслабиться.

Веселье не прекращается, когда заканчивается жаркое техасское лето. Река Гуадалупе также является одним из популярных мест в стране для круглогодичной рыбалки нахлыстом. Каждую зиму тысячи радужных форелей выпускают на волю по всему Техасу, в том числе прямо здесь, в Нью-Браунфелсе!

Многие посетители Техас-Хилл-Кантри останавливаются в кемпингах или арендуют коттеджи вдоль Ривер-роуд в Нью-Браунфелсе. Живописный участок дороги проходит вдоль воды с несколькими переходами через реку между Нью-Браунфелсом и озером Каньон. Этот участок известен как Побережье Хилл-Кантри и предлагает замечательные достопримечательности и варианты проживания!

Наши реки открыты для сплава 7 дней в неделю, в зависимости от хорошего состояния тюбинга. Вода, сбрасываемая из озера Каньон в реку Гуадалупе, колеблется в зависимости от периодических засушливых условий. Речные условия, речной сток и уровень воды часто меняются.

Свяжитесь с одним из наших предпочитаемых New Braunfels  River Outfitters , чтобы узнать о текущем состоянии реки и времени плавания . Экипировщики упрощают плавание по реке, предлагая прокат труб, трансфер до вашего автомобиля и обратно и другие удобные услуги.

Правила и информация о реке Гуадалупе

ПРАВИЛА РЕКИ ГВАДАЛУПЕ – В ГРАНИЦАХ ГОРОДА НЬЮ-БРАУНФЕЛЬС

• Без одноразовых контейнеров
• Без стекла
• Без контейнеров для пены
• Не мусорить
• Спасательные жилеты рекомендуются для слабых пловцов и детей до восьми лет на реке Гуадалупе. Персональные плавучие средства будут бесплатно предоставляться клубням/гражданам с депозитом в пунктах снабжения реки Нью-Браунфелс
.
• Без объемных питьевых устройств
• Нет контейнеров объемом менее 5 унций жидкости.
• Шумовые устройства могут быть не слышны на расстоянии более 50 футов
• Запрещено прыгать с мостов, плотин или деревьев в реку Гуадалупе
• Кулеры должны иметь запорный механизм на крышке (молния, липучка, защелка, шнур). Максимальный объем 30 литров. Допускается 1 кулер на человека.
• Надувные устройства не могут превышать пяти футов в длину или ширину
• Длина судов на реке Гуадалупе не должна превышать 18 футов
• Когда скорость течения реки превышает 500 футов в секунду, все дети в возрасте до восьми лет обязаны носить спасательный жилет
• Когда скорость течения реки превышает 750 кубических футов в секунду, все лица обязаны носить спасательный жилет
.
• Когда речной сток превышает 1000 кубических футов в секунду, трубка не разрешена. Единственным разрешенным водным отдыхом на реке Гуадалупе являются сплавы на плотах и ​​каяках
.

ПРАВИЛА РЕКИ ГВАДАЛУПЕ – ЗА ПРЕДЕЛАМИ ГОРОДА НЬЮ-БРАУНФЕЛЬС

• Без стекла
• Без контейнеров для пены
• Не мусорить
• Нет контейнеров объемом менее 5 унций жидкости.
• Запрещено прыгать с мостов, плотин или деревьев в реку Гуадалупе

СТОИМОСТЬ ПРОВОДА ТРУБОПРОВОДА РЕКИ ГВАДАЛУПЕ

Ожидайте, что вы потратите 15–22 доллара США на человека, включая трансфер, аренду тюбинга и сборы. Большинству аутфиттеров требуется водительское удостоверение или кредитная карта в качестве залога за аренду.

ЧТО ВЗЯТЬ НА ДЕНЬ НА РЕКЕ ГВАДАЛУПЕ

1. Хорошее отношение — Мы понимаем, что нахождение под палящим солнцем в толпе может вызвать некоторые рудиментарные формы поведения. Будьте умны, сохраняйте хладнокровие и помните, что мы все здесь, чтобы хорошо провести время.
2. Надлежащая обувь — Река Гуадалупе представляет собой водоем с естественным течением. Таким образом, вы можете столкнуться с камнями, илом, плавающей растительностью, грязными насыпями и другими природными элементами.
3. Солнцезащитный крем и оттенок — наносите перед отплытием и во время плавания. Шляпа помогает сохранять прохладу и защищаться от солнца.
4. Увлажнение — Ответственное употребление холодного, приятного напитка — отличный способ насладиться нашими водными путями. Просто не забудьте дополнить его достаточным количеством h30 и электролитов.
5. Водонепроницаемый чехол для телефона/ремешок/сухой мешок — Река Гуадалупе — прекрасное место для воссоединения с природой. Однако мы знаем, что многие люди предпочитают брать с собой свои ценные вещи и электронику. Пожалуйста, пожалуйста, берите только то, что вам понадобится для вашего речного приключения. Оставьте украшения, запасные ключи и кошельки дома. Все, что вы приносите с собой, должно быть защищено от непогоды.

Экипировщики реки Гуадалупе

{{?:~равно(data.rankid, 2)}}

{{/}} {{:primary_image_is_default}} {{?}} {{/}}

{{/}} {{/}} {{?}} {{:нет изображения}}

{{:иДТН}}

Рекомендуемые

{{/isDTN}}

{{/}} {{/}}

{{:isFacilities}} {{#конференц-зал}}

{{/}} {{?}} {{:~равно(data.

No related posts.