Как привести к наименьшему общему знаменателю? — Спрашивалка
ЮК
Юлия Князева
- знаменатель
Ан
Анна
Чтобы привести дроби к наименьшему общему знаменателю, например 3/4 и 5/6, надо:
1) найти наименьшее общее кратное знаменателей этих дробей,
оно и будет их наименьшим общим знаменателем;
4 = 2 • 2 ; 6 = 2 • 3 ; НОК ( 4, 6 ) = 2 • 2 • 3 = 12 ;
НОЗ (наименьший общий знаменатель) = 12 ;
2) разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель;
дополнительный множитель для 3/4 равен 12 : 4 = 3 ;
дополнительный множитель для 5/6 равен 12 : 6 = 2 ;
3) умножить числитель и знаменатели каждой дроби на ее дополнительный множитель; 3/4 (3) = 9/12; 5/6 (2) = 10/12
Евгений Панов
выбери наименьшее общее кратное знаменателей
домножь числитель и знаменатель каждой дроби на дополнительный множитель
OB
Olga Baranowa
ну например надо привести к общему зн.
1:3и 1:2
Наименьшее число, на которое делится и 2 и 3, это 6.
Теперь нужно сделать так, чтобы у обоих дрбей был знаменатель 6. Чтобы в заменателне первой дроби было 6, нужно 3*2, ночтобы дробь не изменилась нужно числитель умножить на 2, получается 2:6
у второй дроби нужно знам. умножить на 3(т. к 2*3=6) и числитель умножить на 3, получается 3:6
Итак, дроби приведены к общему зн.
НВ
Настя Веряева
Как найти наименьший общий знаменатель
Знаменателем арифметической дроби a / b называют число b, показывающее размеры долей единицы, из которых составлена дробь. Знаменателем алгебраической дроби A / B называют алгебраическое выражение B. Для выполнения арифметических действий с дробями их необходимо привести к наименьшему общему знаменателю.
Инструкция
1
Рассмотрим приведение к наименьшему общему знаменателю двух арифметических дробей n/m и s/t, где n, m, s, t – целые числа. Понятно, что эти две дроби можно привести к любому знаменателю, делящемуся на m и на t.
2.
Полезный совет
После разложения чисел или многочленов на множители выполните проверку – посчитайте произведение всех множителей и убедитесь, что получились первоначальные значения.
Сергей
16 1/2 = 16 6/6 = 17
6 2/3 = 6 4/6
17- 6 4/6 = 16 6/6 — 6 4/6 = 10 2/6 = 10 1/3
Ал
Алексей
обьясни
Сергей
Алексей, спасибо огромное (чм)
Володимер Олiйник
Как найти наименьший общий знаменатель
Знаменателем арифметической дроби a / b называют число b, показывающее размеры долей единицы, из которых составлена дробь. Знаменателем алгебраической дроби A / B называют алгебраическое выражение B. Для выполнения арифметических действий с дробями их необходимо привести к наименьшему общему знаменателю.
Инструкция
1
Рассмотрим приведение к наименьшему общему знаменателю двух арифметических дробей n/m и s/t, где n, m, s, t – целые числа.
2.
Полезный совет
После разложения чисел или многочленов на множители выполните проверку – посчитайте произведение всех множителей и убедитесь, что получились первоначальные значения.
Na
Natali
Надо учится!
АС
Андрей Смирнов
Евгений
Чтобы привести дроби к наименьшему общему знаменателю, например 3/4 и 5/6, надо:
1) найти наименьшее общее кратное знаменателей этих дробей,
оно и будет их наименьшим общим знаменателем;
4 = 2 • 2 ; 6 = 2 • 3 ; НОК ( 4, 6 ) = 2 • 2 • 3 = 12 ;
НОЗ (наименьший общий знаменатель) = 12 ;
2) разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель;
дополнительный множитель для 3/4 равен 12 : 4 = 3 ;
дополнительный множитель для 5/6 равен 12 : 6 = 2 ;
3) умножить числитель и знаменатели каждой дроби на ее дополнительный множитель; 3/4 (3) = 9/12; 5/6 (2) = 10/12
ЕЗ
Елена Зозулина
хаха крузер
ИП
Ирина П
Чтобы привести дроби к наименьшему общему знаменателю, например 3/4 и 5/6, надо:
1) найти наименьшее общее кратное знаменателей этих дробей,
оно и будет их наименьшим общим знаменателем;
4 = 2 • 2 ; 6 = 2 • 3 ; НОК ( 4, 6 ) = 2 • 2 • 3 = 12 ;
НОЗ (наименьший общий знаменатель) = 12 ;
2) разделить наименьший общий знаменатель на знаменатели данных дробей, т.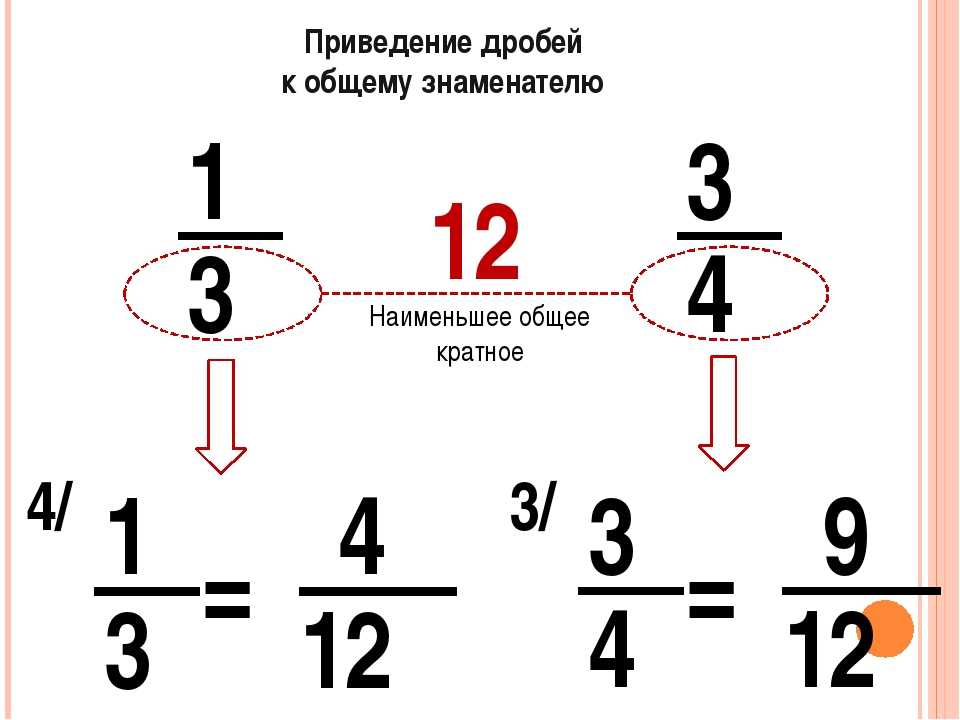
е. найти для каждой дроби дополнительный множитель;
дополнительный множитель для 3/4 равен 12 : 4 = 3 ;
дополнительный множитель для 5/6 равен 12 : 6 = 2 ;
3) умножить числитель и знаменатели каждой дроби на ее дополнительный множитель; 3/4 (3) = 9/12; 5/6 (2) = 10/12
ДЯ
Денис Яньшин
8 и 3 дробь и 5 12 8х12 ровно 96то 3 8 ровно 3х12 8 х12 ровно 36 96
Максим Журавков
гений
Александр П.
sdddddddd
УД
Урфин Джус
Чтобы совершать операции с дробями часто требуется привести дроби к общему знаменателю. Рассмотрим процесс приведения двух дробей дробь три восьмых и пять двенадцатых к наименьшему общему знаменателю :
1 Находим наименьшее общее кратное знаменателей: НОК (8, 12)=24. Число 24 является наименьшим общим знаменателем двух дробей, приведем обе дроби к данному знаменателю. Любые две дроби можно привести к одинаковому знаменателю.
2 Вычисляем дополнительный множитель первой дроби вычисляем дополнительный множитель для дроби 3/8. Умножаем числитель и знаменатель на дополнительный множитель 3, получаем дробь дробь 3/8 преобразуем в 9/24 путем умножения на 3.
3 Вычислим дополнительный множитель второй дроби вычисляем дополнительный множитель для дроби 5/12. Умножаем числитель и знаменатель на дополнительный множитель 2, получаем дробь дробь 5/12 преобразуем в 10/24 путем умножения на 2.
4 В результате получим дроби дробь 9/24 и дробь 10/24 с одинаковым знаменателем равным 24.
Пример Привести дроби дробь семь восемнадцатых и дробь три четвертых к наименьшему общему знаменателю
приведение дробей 7/18 и 3/4 к наименьшему общему знаменателю, нахождение дополнительного множетеля.
ОИ
Оксана Ивасюк-Наумова
Чтобы привести дроби к наименьшему общему знаменателю, например 3/4 и 5/6, надо:
1) найти наименьшее общее кратное знаменателей этих дробей,
оно и будет их наименьшим общим знаменателем;
4 = 2 • 2 ; 6 = 2 • 3 ; НОК ( 4, 6 ) = 2 • 2 • 3 = 12 ;
НОЗ (наименьший общий знаменатель) = 12 ;
2) разделить наименьший общий знаменатель на знаменатели данных дробей, т.
е. найти для каждой дроби дополнительный множитель;
дополнительный множитель для 3/4 равен 12 : 4 = 3 ;
дополнительный множитель для 5/6 равен 12 : 6 = 2 ;
3) умножить числитель и знаменатели каждой дроби на ее дополнительный множитель; 3/4 (3) = 9/12; 5/6 (2) = 10/12
AR
Alexey Ramazanov
Чтобы привести дроби к наименьшему общему знаменателю, например 3/4 и 5/6, надо:
1) найти наименьшее общее кратное знаменателей этих дробей,
оно и будет их наименьшим общим знаменателем;
4 = 2 • 2 ; 6 = 2 • 3 ; НОК ( 4, 6 ) = 2 • 2 • 3 = 12 ;
НОЗ (наименьший общий знаменатель) = 12 ;
2) разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель;
дополнительный множитель для 3/4 равен 12 : 4 = 3 ;
дополнительный множитель для 5/6 равен 12 : 6 = 2 ;
3) умножить числитель и знаменатели каждой дроби на ее дополнительный множитель; 3/4 (3) = 9/12; 5/6 (2) = 10/12
АТ
Аида Турсуналиева
тобы привести дроби к наименьшему общему знаменателю, например 3/4 и 5/6, надо:
1) найти наименьшее общее кратное знаменателей этих дробей,
4 = 2 • 2 ; 6 = 2 • 3 ; НОК ( 4, 6 ) = 2 • 2 • 3 = 12 ;
НОЗ (наименьший общий знаменатель) = 12 ;
2) разделить наименьший общий знаменатель на знаменатели данных дробей, т.
е. найти для каждой дроби дополнительный множитель;
дополнительный множитель для 3/4 равен 12 : 4 = 3 ;
дополнительный множитель для 5/6 равен 12 : 6 = 2 ;
3) умножить числитель и знаменатели каждой дроби на ее дополнительный множитель; 3/4 (3) = 9/12; 5/6 (2) = 10/12
ОМ
Олеся Молдавская
спс
Похожие вопросы
Привести дроби к общему знаменателю и сократить
Приведите дроби к наименьшему общему знаменателю:
Наименьший общий знаменатель
как привести дроби к наименьшему общему знаменателю предварительно сократив их
как найти наименьший общий знаменатель
Приведите дроби к наименьшему общему знаменателю?
Помогите! Скажите, как привести сразу 3 дроби к наименьшему общему знаменателю?
какой общий наименьший знаменатель у чисел 45 и 48? НАИМЕНЬШИЙ
Найди наименьший общий знаменатель, к которому можно привести дроби:
Как привести дроби к наименьшему общему знаменателю.
. 1/2,1/6и2/3?
GCF 11 и 20
На этой странице мы определим GCF 11 и 20, научим вас различным способам расчета GCF 11 и 20, и показать вам, для чего вы можете использовать GCF 11 и 20.
Что такое GCF 11 и 20?
GCF — это аббревиатура от Greatest Common Factor. Таким образом, GCF чисел 11 и 20 совпадает с наибольшим общим делителем.
из 11 и 20. GCF 11 и 20 является наибольшим положительным целым числом, на которое можно разделить как 11, так и 20.
Кроме того, и 11, и 20 имеют набор факторов, и GCF является наибольшим фактором, общим для 11 и 20.
Сравните множители, чтобы получить GCF 11 и 20
Согласно приведенному выше определению, чтобы найти GCF 11 и 20, вы можете сравнить коэффициенты 11 с
умножить на 20, чтобы узнать, какой из них больше. Когда мы это сделали, мы обнаружили
что наибольший общий делитель (НОК) чисел 11 и 20 равен 1.
Используйте НОК для получения НОД чисел 11 и 20
Наименьшее общее кратное (НОК) чисел 11 и 20 равно 220.
Вы можете найти НОД чисел 11 и 20, путем деления произведения 11 и 20 на НОК 11 и 20.
Вот формула и математика:
| = GCF |
| = 1 |
Используйте компьютерную таблицу, чтобы рассчитать GCF 11 и 20
Если у вас есть компьютер, вы также можете использовать электронную таблицу в Excel или Numbers для расчета GCF 11 и 20.
Вы хотите ввести
=gcf(11, 20) в ячейку, чтобы получить ответ.
gcf(11, 20) = 1
Используйте GCF 11 и 20, чтобы упростить дробь
GCF 11 и 20 можно использовать для многих целей. Вы можете, например, упростить дробь, разделив числитель и знаменатель на
GCF выглядит следующим образом:
| = |
Используйте GCF, равный 11 и 20, для упрощения отношения
Аналогично, вы можете использовать GCF, равный 11 и 20, для упрощения отношения, разделив каждую часть отношения на
= 11 : 20
= (11 ÷ 1) : (20 ÷ 1)
= 11 : 20
Используйте НГК 11 и 20, чтобы найти НОК 11 и 20
Поскольку использование наименьшего общего кратного (НОК) является одним из способов нахождения НОК 11 и 20, вы можете использовать НОК 11 и 20, чтобы найти НОК 11 и 20.
НОК 11 и 20 можно, например, использовать для сложения и вычитания дробей со знаменателем 11 и 20.
НОК 11 и 20 — это произведение 11 и 20, деленное на НГК 11 и 20. Вот математика:
| . | = LCM |
| = 220 |
Вот и все! Мы надеемся, что эта страница выполнила свою задачу по определению GCF 11 и 20, показав вам, как рассчитать GCF,
примеры его использования и его отношение к LCM.
Калькулятор GCF
Используйте Калькулятор GCF для решения задачи, аналогичной описанной на этой странице.
GCF 11 и 21
Вот следующий GCF в нашем списке, который мы рассчитали и объяснили для вас.
Авторское право | Политика конфиденциальности | Отказ от ответственности | Контакт
Наибольший общий делитель чисел 5, 11 и 20 (НОД 5, 11, 20)
Вы ищете НОД 5, 11 и 20? Так как вы находитесь на этой странице, я так думаю! В этом кратком руководстве мы расскажем, как вычислить наибольший общий делитель для любых чисел, которые вам нужно проверить. Давайте прыгать!
Хотите быстро узнать или показать учащимся, как найти НГК двух или более чисел? Включи это очень быстрое и веселое видео прямо сейчас!
Прежде всего, если вы торопитесь, вот ответ на вопрос «Каков GCF 5, 11 и 20?» :
GCF 5, 11 и 20 = 1
Что такое наибольший общий делитель?
Проще говоря, GCF набора целых чисел — это наибольшее положительное целое число (т.
е. целое число, а не десятичное), которое без остатка делится на все числа набора. Он также широко известен как:
- Наибольший общий знаменатель (GCD)
- Наивысший общий множитель (HCF)
- Наибольший общий делитель (НОД)
Существует несколько различных способов расчета GCF набора чисел в зависимости от того, сколько чисел у вас есть и насколько они велики.
Для меньших чисел вы можете просто посмотреть на множители или кратные для каждого числа и найти их наибольшее общее кратное.
Для 5, 11 и 20 эти коэффициенты выглядят следующим образом:
- Коэффициенты для 5: 1 и 5
- Коэффициенты для 11: 1 и 11
- Коэффициенты для 2, 2, 2, 29307 8 20 4, 5, 10 и 20
Как вы можете видеть, перечисляя множители каждого числа, 1 — это наибольшее число, на которое делятся 5, 11 и 20.
Простые множители
По мере того, как числа становятся больше, или вы хотите сравнить несколько чисел одновременно, чтобы найти GCF, вы можете увидеть, что перечисление всех факторов стало бы слишком большим.
Чтобы исправить это, вы можете использовать простые множители.
Перечислите все простые множители для каждого числа:
- Простые множители для 5: 5
- Простые множители для 11: 11
- Простые множители для 20: 2, 2 и 5
Теперь, когда у нас есть список простых множителей, нам нужно найти те, которые являются общими для каждого числа.
Поскольку нет общих простых множителей между приведенными выше числами, это означает, что наибольший общий множитель равен 1:
GCF = 1
Найдите GCF с помощью алгоритма Евклида
Окончательный метод расчета GCF 5, 11, и 20 — использовать алгоритм Евклида. Это более сложный способ вычисления наибольшего общего множителя, который на самом деле используется только калькуляторами НОД.
Если вы хотите узнать больше об алгоритме и, возможно, попробовать его самостоятельно, загляните на страницу Википедии.
Надеюсь, сегодня вы немного изучили математику и поняли, как вычислять НОД чисел.
Возьмите карандаш и бумагу и попробуйте сами. (или просто используйте наш калькулятор НОД — мы никому не скажем!)
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте инструмент ниже, чтобы убедитесь, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
«Наибольший общий делитель чисел 5, 11 и 20». VisualFractions.com . По состоянию на 17 декабря 2022 г. http://visualfractions.com/calculator/greatest-common-factor/gcf-of-5-11-and-20/.
«Наибольший общий делитель чисел 5, 11 и 20». VisualFractions.com , http://visualfractions.com/calculator/greatest-common-factor/gcf-of-5-11-and-20/. По состоянию на 17 декабря 2022 г.
