Таблица нахождения первообразных: Таблица первообразной — Интегралы,первообразные

Дистанционный репетитор — онлайн-репетиторы России и зарубежья

КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?

Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!

КАК ВЫБРАТЬ репетитора

Выбрать репетитора самостоятельно

ИЛИ

Позвонить и Вам поможет специалист

8 (800) 333 58 91

* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК

ПОДАТЬ ЗАЯВКУ

Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41

Выбранные репетиторы

Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.

Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных

Вы также можете воспользоваться
расширенной формой подачи заявки

Как оплачивать и СКОЛЬКО ЭТО СТОИТ

от
800 до 5000 ₽

за 60 мин.

и зависит

ОТ ОПЫТА и
квалификации
репетитора

ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)

ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)

Оплата непосредственно репетитору, удобным для Вас способом

Почему я выбираю DisTTutor

БЫСТРЫЙ ПОДБОР

РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД

ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА

ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ

НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.

ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА

ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО

376157 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор

И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах

Владимир Александрович Кузьмин

«

Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить. Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии. Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.

В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!

«

Вячеслав Юрьевич Матыкин

Чулпан Равилевна Насырова

«

Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!

«

Алина Крякина

Надежда Васильевна Токарева

«

Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.

«

Эльмира Есеноманова

Ольга Александровна Мухаметзянова

«

Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.

«

Оксана Александровна

Клиентам

• Репетиторы по математике
• Репетиторы по русскому языку
• Репетиторы по химии
• Репетиторы по биологии
• Репетиторы английского языка
• Репетиторы немецкого языка

Репетиторам

• Регистрация
• Публичная оферта
• Библиотека
• Бан-лист репетиторов

Партнеры

• ChemSchool
• PREPY. RU
• Class

Правила нахождения первообразных — презентация онлайн

Похожие презентации:

Правило нахождения первообразной

Понятие первообразной. Таблица первообразных. Правила нахождения первообразных

Первообразная. Правила нахождения первообразных

Первообразная. Правила нахождения первообразных

Первообразная. Правила нахождения первообразных

Первообразная и интеграл

Первообразная. Интеграл

Первообразная. Основное свойство первообразной

Первообразная

Первообразная. Формулы и правила нахождения первообразной

Тема урока:

Таблицу первообразных можно
составить , используя таблицу
производных.
(cosx)’ = — sinx
( — sinx)’ = — cosx
F(x)= — cosx + C
Таблица первообразных:
f(x)
F(x)
1
к
кх С
2
р
х р 1
С
р 1
3
х
р 1
р 0
р 1
(к х b)
4
1
х
5
1
кх в
р
х 0
к 0
(к х b) р 1
С
к(р 1)
lnх С
1
ln кх в С
к
Таблица первообразных:
f(x)
6
7
8
9
10
1
х
е
е
F(x)
2 х С
х
е С
х
к х в
1 кх в
е
С
к
х
ах
С
lna
а
а
к х в
а кх в
С
к lna
Таблица первообразных:
11
12
13
f(x)
F(x)
sinx
— cosх С
sin кx в
к 0
cosx
14
cos кx в
15
1
cos 2 х
16
1
sin 2 х
—
1
cos кх в С
к
sinх С
к 0
1
sin кх в С
к
tgх С
— ctgх С
Для нахождения первообразных нам понадобятся
кроме таблицы правила нахождения первообразных.
Правила интегрирования
1) Если F(x)– первообразная для функции f(x), а
G(x)– первообразная для функции g(x), то
F(x)+G(x)– первообразная
для функции
f(x)+g(x).
Первообразная
суммы
равна
сумме первообразных
2) Если F(x)– первообразная для функции f(x),
а а –константа, то аF(x)– первообразная
для функции аf(x).Постоянный множитель можно
выносить за знак первообразной
3) Если F(x) – первообразная для функции f(x), а k и b1
константы, причем k≠0, то F ( kx b )- первообразная для
k
функции f ( kx b ).
23.03.2021
7
Задача. Дана функция f(x). Найдите ее
первообразную, воспользовавшись таблицей
первообразных и правилами нахождения
первообразной и выполните проверку,
1)
2
f(x) 2
x
В таблице такой функции нет.
Коэффициент
Преобразуем
f(x):
Табличная
F( x ) ?
2
1
f( x) 2 2 2
x
x
1
F( x ) 2 2
x
x
Проверка:
функция
Используем таблицу
и второе правило.
1 2
2
1
F ( x ) 2 2 2 2 f ( x )
x x
x
x
F ( x ) первообразная
для
f(x)
Задача. Дана функция f(x). Найдите ее
первообразную, воспользовавшись таблицей
первообразных и правилами нахождения
первообразной
2)
f(x) x x
F( x ) ?
2
16
Табличная
функция
Табличная
функция
Используем таблицу
и первое правило.
x 2 1
x 16 1
x 3 x 17
F( x )
2 1 16 1
3 17
x
1 3 1
x
Проверка: F ( x )
( x )
( x 17 )
3
17
17
3
1
1
2
16
2
3x
17 x 16 x x f ( x )
3
17
3
17
F ( x ) первообразная
для
f(x)
Задача . Дана функция f(x). Найдите ее
первообразную, воспользовавшись таблицей
первообразных и правилами нахождения
первообразной
Коэффициент
Коэффициент
3)
f ( x ) 3 sin x 2 cos x Используем таблицу,
первое и второе правило.
F( x ) ?
Табличная
Табличная
F ( x ) 3( cos x ) 2 sin x
функция
функция
3 cos x 2 sin x
Проверка:
F ( x ) ( 3 cos x 2 sin x ) 3 sin x 2 cos x f ( x )
F ( x ) первообразная
для
f(x)
Задача . Дана функция f(x). Найдите ее
первообразную, воспользовавшись таблицей
первообразных и правилами нахождения
первообразной
4)
f ( x ) sin( 3 x ) Синус – табличная функция.
Табличная
Аргумент – линейная функция (k=3).
F
(
x
)
?
функция
Используем таблицу и третье правило.
1
1
F ( x ) ( cos( 3 x )) cos( 3 x )
3
3
Проверка:
1
1
F ( x ) cos( 3 x ) cos( 3 x )
3
3
1
1
( sin( 3 x ))( 3 x ) sin( 3 x ) 3 sin( 3 x )
3
3
f ( x ) F ( x ) первообразная
для
f(x)
№ 988-991(неч.).
№ 988-991
(чет.).

English     Русский Правила

исчисление — Таблицы примитивов с указанием метода решения

Я не думаю, что существует опубликованный справочник, который содержит столько деталей, сколько вы хотите, с очень элементарным интегралом, который вы привели в качестве примера (простой экспоненциальный раз многочлен, который является прототипом табличного метода), так как пример, который вы привели, был бы в пределах предполагаемого фона для читателя и потребовал бы слишком много времени и слишком загромождения, чтобы его стоило неоднократно упоминать (в публикации). Действительно, для поиска Google в моем последнем предложении я получил почти 9миллион просмотров для интеграции деталей табличным методом. Однако то, о чем вы просите, кажется разумным для программного обеспечения даже в настоящее время, и если что-то подобное еще не существует, я уверен, что оно будет в течение 10 лет.

Во всяком случае, некогда известная книга Peirce [7] (к вашему сведению, у меня есть копия издания 1957 года в твердом переплете, отредактированная Рональдом Мартином Фостером) дает краткое описание многих методов интеграции. Описания появляются в начале многих различных глав и разделов. Фактически, причина, по которой я получил копию этой книги (см. здесь, если вы заинтересованы в получении копии), заключалась в том, что я постоянно видел, как она снова и снова цитируется в старой литературе.

Существуют буквально сотни свободно доступных книг по математическому анализу 1800-х и начала 1900-х годов, в которых содержится подробная информация о различных методах интеграции, особенно о методах, которые были отредактированы из текстов по математическому анализу за последние 30-40 лет. Я знаю несколько наиболее полных методов лечения: [1] , [2] , [5] , [8] , [9] , [10] ниже.

Что касается книг, посвященных в первую очередь методам интегрирования в конечных формах, то лучшими из известных мне книг (которые не предназначены для исследователей современных компьютерных методов интегрирования в конечных формах) являются Fichtenholz [3] (единственный пункт ниже, насколько я могу судить, не находится в свободном доступе в Интернете), Hardy [4] и MacNeish [6] .

Что касается пунктов ниже, даты и ссылки относятся к последнему изданию, которое я смог найти в свободном доступе в Интернете. Я использую последние версии, чтобы свести к минимуму опечатки и ошибки, которые могли быть в ранней версии. В некоторых случаях (особенно в книге Тодхантера) дата намного позже, чем когда книга впервые появилась.

[1] Джозеф Эдвардс, Трактат по интегральному исчислению, том 1 (1921)

[2] Джозеф Эдвардс, Трактат по интегральному исчислению, том 2 90 0203 6 (10 02003 6) [3] Григорий Михайлович Фихтенгольц, Неопределенный интеграл (1971)

[4] Годфри Гарольд Харди, Интегрирование функций одной переменной (1916) 50 Hombrace

5 [4] ,

Элементарный курс бесконечно -максимального исчисления (1942)

[6] Харрис Франклин Макнейш, Алгебраическая техника интеграции (1952)

[7] Бенджамин Осгуд Пейрс, a Короткая таблица 666666 (7] Benjamin Osgood Peirce, a Talect of Table 666 (7] Бенджамин Осгуд Пейрс, A STAGTRALS 6 (7] Benjamin Osgood Peirce, A STAGTRALS 6 (7] .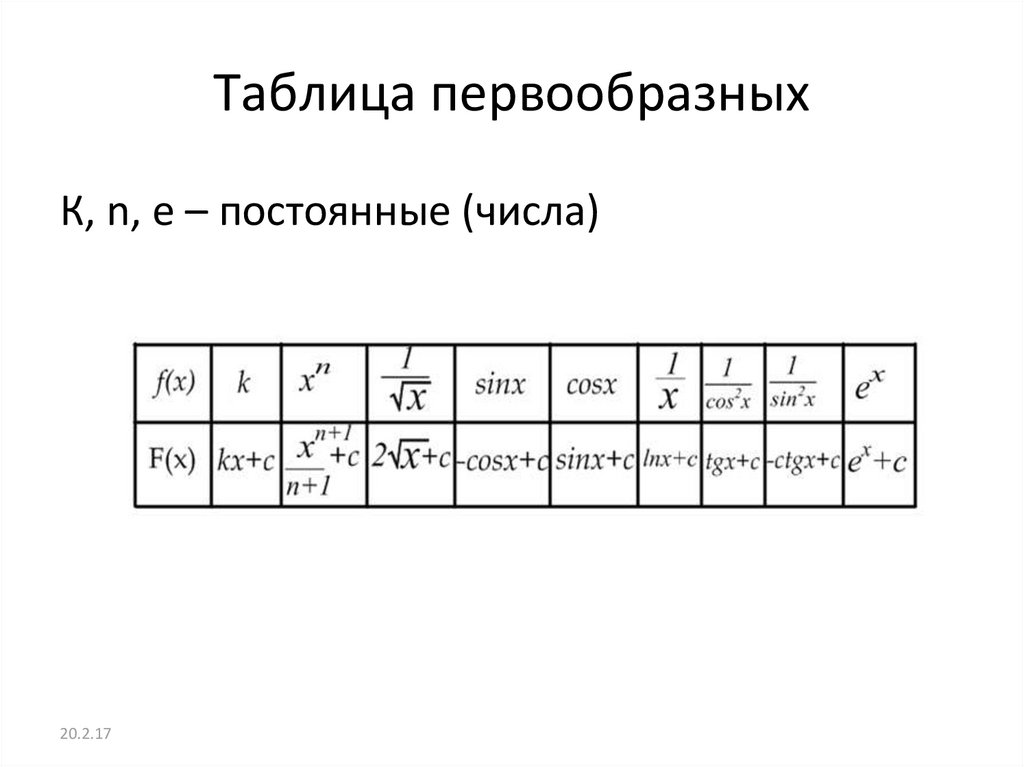 1914)

[8] Уильям Бенджамин Смит, InfinitesImalal Analysis (1898)

[9] Isaac Todhunter Tractiet по интегральному кольцу (1906)

[10] (1906)

[10]0006 Бенджамин Уильямсон, Элементарный трактат по интегральному исчислению (1888)

Таблица примитивов схемы по категориям

Простая схема: Таблица примитивов схемы по категориям Просто Схема : Введение в информатику 2/e Copyright (C) 1999 MIT

Брайан Харви Калифорнийский университет, Беркли Мэтью Райт Калифорнийский университет, Санта-Барбара Скачать PDF версию Назад к содержанию ЗАДНЯЯ ЧАСТЬ ветка главы [нет следующего] Массачусетский технологический институт Пресс-страница для Просто схема

---

Используйте эту таблицу, если вы забыли имя примитива. затем посмотрите в указателе, чтобы узнать больше о том, как использовать примитив.

^* Не входит в стандартную схему

Слова и предложения

появления ^*
раньше? ^*
бутпервый (бф) ^*
бутласт (бл) ^*
количество ^*
пустой? ^*
равно? ^*
первый ^*
деталь ^*
последний ^*
член? ^*
цитата
предложение (se) ^*
предложение? ^*
слово ^*
слово? ^*

Списки

добавить
доц.
автомобиль
CDR
к...р
минусы
фильтр ^*
для каждого
длина
список
список?
список-ссылка
карта
член
ноль?
уменьшить ^*

Деревья

дети ^*
датум ^*
make-node ^*

Арифметика

+ , - , *, /
< , <= , = , > , >=
абс
потолок
потому что
даже?
доб.

No related posts.