Калькулятор интегралов и производных: Производная интегрального калькулятора с шагами

Интегрирование по частям. Примеры решений

И снова, здравствуйте. Сегодня на уроке мы научимся интегрировать по частям. Метод интегрирования по частям – это один из краеугольных камней интегрального исчисления. На зачете, экзамене студенту почти всегда предлагают решить интегралы следующих типов: простейший интеграл (см. статью Неопределенный интеграл. Примеры решений) либо интеграл на замену переменной (см. статью Метод замены переменной в неопределенном интеграле) либо интеграл как раз на метод интегрирования по частям.

Для эффективного изучения темы необходимо хорошо ориентироваться в материалах двух вышеуказанных уроков. Если Вы чайник, и только-только начинаете погружение в удивительный мир интегралов, то читать далее не имеет особого смысла – следует начать с урока Неопределенный интеграл. Примеры решений.

Как всегда, под рукой должны быть: Таблица интегралов и Таблица производных

. Если у Вас до сих пор их нет, то, пожалуйста, посетите кладовку моего сайта: Математические формулы и таблицы. Не устану повторять – лучше всё распечатать. Весь материал я постараюсь изложить последовательно, просто и доступно, в интегрировании по частям нет особых трудностей.

Какую задачу решает метод интегрирования по частям? Метод интегрирования по частям решает очень важную задачу, он позволяет интегрировать некоторые функции, отсутствующие в таблице, произведение функций, а в ряде случаев – и частное. Как мы помним, нет удобной формулы: . Зато есть такая:   – формула интегрирования по частям собственной персоной. Знаю, знаю, ты одна такая – с ней мы и будет работать весь урок (уже легче).

И сразу список в студию. По частям берутся интегралы следующих видов:

1)  ,  ,   – логарифм, логарифм, умноженный на какой-нибудь многочлен.

2)  ,  – экспоненциальная функция, умноженная на какой-нибудь многочлен. Сюда же можно отнести интегралы вроде   – показательная функция, умноженная на многочлен, но на практике процентах так в 97, под интегралом красуется симпатичная буква «е».

… что-то лирической получается статья, ах да… весна же пришла.

3)  ,  ,   – тригонометрические функции, умноженные на какой-нибудь многочлен.

4)  ,   – обратные тригонометрические функции («арки»), «арки», умноженные на какой-нибудь многочлен.

Также по частям берутся некоторые дроби, соответствующие примеры мы тоже подробно рассмотрим.

Интегралы от логарифмов

Пример 1

Найти неопределенный интеграл.

 

Классика. Время от времени данный интеграл можно встретить в таблицах, но пользоваться готовым ответом нежелательно, так как у преподавателя весенний авитаминоз и он сильно заругается. Потому что рассматриваемый интеграл отнюдь не табличный – он берётся по частям. Решаем:

Прерываем решение на промежуточные объяснения.

Используем формулу интегрирования по частям: 

Формула применяется слева направо

Смотрим на левую часть:  . Очевидно, что в нашем примере   (и во всех остальных, которые мы рассмотрим) что-то нужно обозначить за  , а что-то за  .

В интегралах рассматриваемого типа за   всегда обозначается логарифм.

Технически оформление решения реализуется следующим образом, в столбик записываем:

То есть, за   мы обозначили логарифм, а за   – оставшуюся часть подынтегрального выражения.

Следующий этап: находим дифференциал  :

Дифференциал – это почти то же самое, что и производная, как его находить, мы уже разбирали на предыдущих уроках.

Теперь находим функцию  . Для того чтобы найти функцию   необходимо проинтегрировать

правую часть нижнего равенства  :

Теперь открываем наше решение и конструируем правую часть формулы:  . Вот кстати, и образец чистового решения с небольшими пометками:

Единственный момент, в произведении   я сразу переставил местами   и  , так как множитель   принято записывать перед логарифмом.

Как видите, применение формулы интегрирования по частям, по сути дела, свело наше решение к двум простым интегралам.

Обратите внимание, что в ряде случаев сразу после применения формулы, под оставшимся интегралом обязательно проводится упрощение – в рассматриваемом примере мы сократили подынтегральное выражение на «икс».

Выполним проверку. Для этого нужно взять производную от ответа:

Получена исходная подынтегральная функция, значит, интеграл решён правильно.

В ходе проверки мы использовали правило дифференцирования произведения:  . И это не случайно.

Формула интегрирования по частям   и формула   – это два взаимно обратных правила.

Пример 2

Найти неопределенный интеграл.

Подынтегральная функция представляет собой  произведение логарифма на многочлен. Решаем.

Я еще один раз подробно распишу порядок применения правила, в дальнейшем примеры будут оформляться более кратко, и, если у Вас возникнут трудности в самостоятельном решении, нужно вернуться обратно к первым двум примерам урока.

Как уже говорилось, за   необходимо обозначить  логарифм (то, что он в степени – значения не имеет). За   обозначаем оставшуюся часть подынтегрального выражения.

Записываем в столбик:

Сначала находим дифференциал  :

Здесь использовано правило дифференцирования сложной функции  . Не случайно, на самом первом уроке темы Неопределенный интеграл. Примеры решений я акцентировал внимание на том, что для того, чтобы освоить интегралы, необходимо «набить руку» на производных. С производными придется столкнуться еще не раз.

Теперь находим функцию  , для этого интегрируем правую часть нижнего равенства  :

 

Для интегрирования мы применили простейшую табличную формулу 

Теперь всё готово для применения формулы  . Открываем «звёздочкой» и «конструируем» решение в соответствии с правой частью  :

Под интегралом у нас снова многочлен на логарифм! Поэтому решение опять прерывается и правило интегрирования по частям применяется второй раз. Не забываем, что за   в похожих ситуациях всегда обозначается логарифм.

Хорошо бы, если к данному моменту простейшие интегралы и производные Вы умели находить устно.

 (1) Не путаемся в знаках! Очень часто здесь теряют минус, также обратите внимание, что минус  относится ко всей скобке  , и эти скобки нужно корректно раскрыть.

(2) Раскрываем скобки. Последний интеграл упрощаем.

(3) Берем последний интеграл.

(4) «Причесываем» ответ.

Необходимость дважды (а то и трижды) применять правило интегрирования по частям возникает не так уж и редко.

А сейчас пара примеров для самостоятельного решения:

Пример 3

Найти неопределенный интеграл.

Этот пример решается методом замены переменной (или подведением под знак дифференциала)! А почему бы и нет – можете попробовать взять его по частям, получится забавная вещь.

Пример 4

Найти неопределенный интеграл.

А вот этот интеграл интегрируется по частям (обещанная дробь).

Это примеры для самостоятельного решения, решения и ответы в конце урока.

Вроде бы в примерах 3,4 подынтегральные функции похожи, а вот методы решения – разные! В этом-то и состоит основная трудность освоения интегралов – если неправильно подобрать метод решения интеграла, то возиться с ним можно часами, как с самой настоящей головоломкой. Поэтому чем больше вы прорешаете различных интегралов – тем лучше, тем легче пройдут зачет и экзамен. Кроме того, на втором курсе будут дифференциальные уравнения, а без опыта решения интегралов и производных делать там нечего.

По логарифмам, пожалуй, более чем достаточно. На закуску могу еще вспомнить, что студенты-технари логарифмами называют женскую грудь =). Кстати, полезно знать графики основных элементарных функций: синуса, косинуса, арктангенса, экспоненты, многочлена четвертой степени и т.д. Нет, презерватив на глобус я натягивать не буду, но вы все прочитаете мой пост 

Графики и свойства элементарных функций  =).

Интегралы от экспоненты, умноженной на многочлен

Общее правило: за   всегда обозначается многочлен

Пример 5

Найти неопределенный интеграл.

Решение:

Используя знакомый алгоритм, интегрируем по частям:

Если возникли трудности с интегралом  , то следует вернуться к статье Метод замены переменной в неопределенном интеграле.

Единственное, что еще можно сделать, это «причесать» ответ:

Но если Ваша техника вычислений не очень хороша, то самый выгодный вариант оставить ответом   или даже 

То есть, пример считается решенным, когда взят последний интеграл. Ошибкой не будет, другое дело, что преподаватель может попросить упростить ответ.

Пример 6

Найти неопределенный интеграл.

Это пример для самостоятельного решения. Данный интеграл дважды интегрируется по частям. Особое внимание следует обратить на знаки – здесь легко в них запутаться, также помним, что   – сложная функция.

Больше про экспоненту рассказывать особо нечего. Могу только добавить, что экспонента и натуральный логарифм взаимно-обратные функции, это я к теме занимательных графиков высшей математики =) Стоп-стоп, не волнуемся, лектор трезв.

Интегралы от тригонометрических функций, умноженных на многочлен

Общее правило: за   всегда обозначается многочлен

Пример 7

Найти неопределенный интеграл.

Интегрируем по частям:

Хммм, …и комментировать нечего.

Пример 8

Найти неопределенный интеграл

Это пример для самостоятельного решения

Пример 9

Найти неопределенный интеграл

Еще один пример с дробью. Как и в двух предыдущих примерах за   обозначается многочлен.

Интегрируем по частям:

Если возникли трудности или недопонимание с нахождением интеграла  , то рекомендую посетить урок Интегралы от тригонометрических функций.

Пример 10

Найти неопределенный интеграл

Это пример для самостоятельного решения.

Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.

Вот, пожалуй, и всё в данном параграфе. Почему-то вспомнилась строчка из гимна физмата «А синуса график волна за волной по оси абсцисс пробегает»….

Интегралы от обратных тригонометрических функций. Интегралы от обратных тригонометрических функций, умноженных на многочлен

Общее правило: за   всегда обозначается обратная тригонометрическая функция.

Напоминаю, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи я буду называть их «арками»

Пример 11

Найти неопределенный интеграл.

Решаем.

Интегрируем по частям:

Интеграл   найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде. Аналогичный пример мы разбирали на уроке Метод замены переменной в неопределенном интеграле.

Таким образом, помимо «чистого» интегрирования по частям нередко требуется применять и другие методы, приёмы решения.

Пример 12

Найти неопределенный интеграл.

Это пример для самостоятельного решения

И заключительный пример сегодняшнего урока под счастливым номером тринадцать: «арк», умноженный на многочлен. Он сложнее, и предназначен для маньяков желающих лучше разобраться в методе интегрирования по частям. Пример, пожалуй, будет тоже для самостоятельного решения, поскольку меня немного утомил тот логарифм в квадрате.

Пример 13

Найти неопределенный интеграл.

Что касаемо интегрирования по частям, почти всё разобрали. Рассмотренный метод часто применяется в комбинации с другими приёмами решения интегралов. Читатели с хорошими навыками могут ознакомиться с такими примерами на уроке Сложные интегралы.

А сейчас, как любила говорить моя учительница по математике, пора кончать.

Желаю успехов!

Решения и ответы:

Пример 3: Решение:

Пример 4: Решение:

Интегрируем по частям:

Пример 6: Решение:

Дважды интегрируем по частям:

Пример 8: Решение:

Интегрируем по частям:

Пример 10: Решение:

Интегрируем по частям:

Примечание: Здесь мы использовали известную тригонометрическую формулу двойного угла . Её можно было использовать и сразу: , а  потом интегрировать по частям.

Похожим способом также решаются интегралы вроде ,  – в них необходимо (сразу или в ходе решения) понизить степень синуса (косинуса) с помощью соответствующих формул. Более подробно – см. Интегралы от тригонометрических функций.

Пример 12:

Интегрируем по частям:

Пример 13:

Интегрируем по частям:

Примечание: Если возникли трудности с интегралом , то следует посетить урок Интегрирование некоторых дробей. 

Поверхностные интегралы первого рода. Примеры решений

Наведем готовые ответы к заданиям на вычисление поверхностных интегралов первого рода.
Все примеры дополнены рисунками поверхностей по которых интегрируем, объяснено для чего нужна первая квадратичная форма и когда ее использовать.
Алгоритм вычисления поверхностных интегралов хорошо расписан на разных параметризующих поверхностях, поэтому нескольких примеров Вам будет достаточно, чтобы самостоятельно выполнить контрольную или расчетную работу!
Материал отвечает уровню подготовки студентов первых, вторых курсов вузов.

Пример 1 Вычислить поверхностный интеграл первого рода int[1/(1+x+y), S]

где S — предел тетраэдра x+y+z≤1, x≥0, y≥0, z≥0.
Решение: Прежде чем вычислять интеграл построим схематический вид тетраэдра

Заданный тетраэдр состоит из четырех плоскостей (поверхностей), поэтому заданный поверхностный интеграл будем считать по всем плоскостям отдельно, то есть

Поверхность 1: y=0.
Отсюда, дифференциал площади равен dS₁=dxdz.
Дальше расставляем пределы первой грани:
Учитывая, что y=0 уравнение x+y+z=1 упростится к виду x+z=1, отсюда z=1-x верхний предел по z.
Таким образом получим
0≤x≤1 и 0≤z≤1- x.
Осталось подставить y=0 в подынтегральную функцию и найти поверхностный интеграл первого рода

Далее аналогичные расчеты по остальных плоскостях.

Поверхность 2: x=0.
Дифференциал поверхности dS2=dydz, пределы 2-й грани:
0≤y≤1, 0≤z≤1-y.
Пределы и подынтегральная функция изменяются с учетом условия x=0.
Вычисляем кратный интеграл

Поверхность 3: z=0.
Отсюда dS3=dxdy, а пределы 3-й грани:
0≤x≤1, 0≤y≤1-x.
Проверьте правильность приведенных пределов поверхностного интеграла.
Напоследок, само интегрирование

 

Поверхность №4: x+y+z=1.
На поверхности уравнение равно z=1-x-y, поэтому частичные производные за двумя другими координатами отрицательны
z_x‘=-1, z_y‘=-1.
Дифференциал вычисляем по формуле

Пределы 4 грани:
0≤x≤1, 0≤y≤1-x.
Вычисляем еще один поверхностный интеграл

Конечное значение поверхностного интеграла первого рода по граням тетраэдра находим суммируя найденные значения:
Подобным образом можно рассчитывать поверхностный интеграл по граням любого ограниченного плоскостями тела.

 

Пример 2 Вычислить поверхностный интеграл первого рода int[x+y+z, S]

где S — поверхность сферы x²+y²+z²=a², z ≥0.

Решение: Имеем каноническое уравнение сферы в прямоугольной системе координат.
Интеграл нужно найти для верхнего его полушария (см. рисунок)

Запишем уравнение заданной сферы в параметрическом виде:

Эти формулы являются универсальными, поэтому их часто будете использовать для сферических тел.
Угол «пси» отвечает за положение точек на сфере при z>0.
Для нахождения коэффициента I квадратичной формы нужны производные параметрической записи координат по обоим углам.

Вычислим коэффициенты I квадратичной формы по формуле:

Формула первой квадратичной формы

Она служит дополнительным множителем, который возникает в результате параметризации координат.
Поверхностный интеграл первого рода находим за формулой:

Внимательно пересмотрите интегрирование тригонометрических функций. Здесь некоторые промежуточные вычисления пропущены, это все для того, чтобы побуждать Вас побольше работать самостоятельно.
С другой стороны все что видите следует проверять.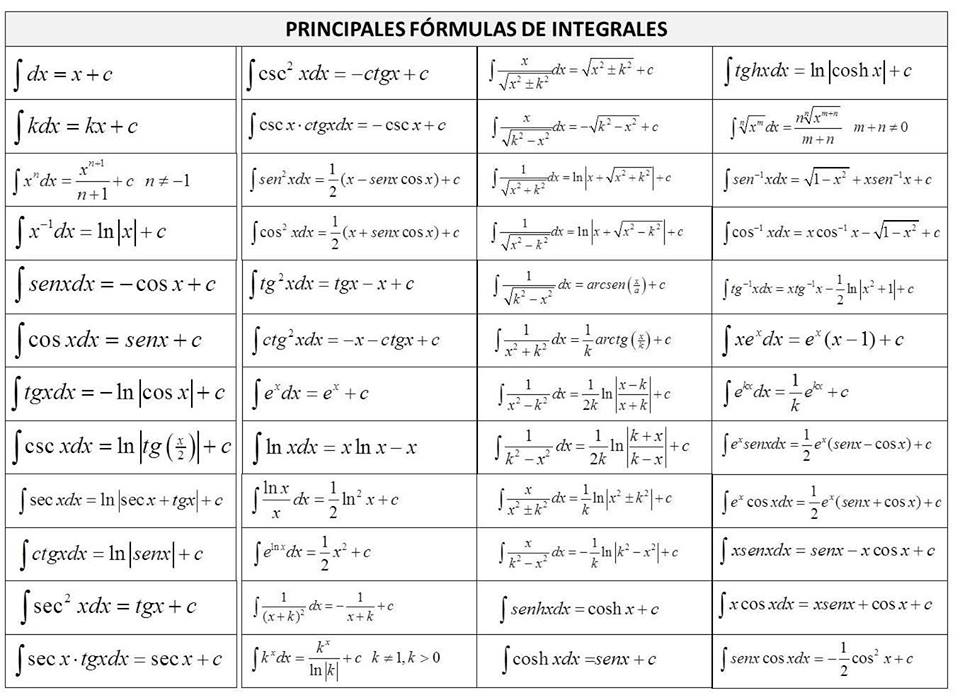

 

Пример 3 Вычислить поверхностный интеграл первого рода int[z², S]

где S — часть поверхности конуса
x=r-cos(φ)sin(alpha)
y=r-sin(φ)sin(alpha)
z=r-cos(alpha)
(0≤r≤a; 0≤φ≤2π) и a — постоянная 0≤alpha≤π/2).
Решение: Здесь первый шаг алгоритма вычислений поверхностного интеграла пропускаем, поскольку в условии уже имеем параметризованое уравнение конуса.

Найдем частичные производные по углу и радиус-вектор 

Далее за производными вычисляем коэффициенты I квадратичной формы

Поверхностный интеграл первого рода вычисляем по формуле

Сначала находим внутренний интеграл за радиусом вектором, а дальше по углу «фи».
В результате получили, что поверхностный интеграл зависит от угла между плоскостью основы и образующей конуса — «альфа».
Больше примеров на поверхностные интегралы первого рода ищите на страницах сайта.
Добавляйте сайт в закладки и делитесь ссылкой на учебные материалы с друзьями!

‎Integral_Calculator в App Store

Интегральный калькулятор поможет вам выполнить интеграционные расчеты

Этот интегральный калькулятор поможет вам выполнить интеграционные расчеты в кратчайшие сроки. Как мы знаем, всегда есть обратная операция для всех операций, таких как суммирование и вычитание, умножение и деление в математике. И этот обратный процесс известен как антидифференциация или простая интеграция процесса различения.

Интеграл – это заданная функция в производной, которая, когда мы ее выделяем и оцениваем площадь под кривой графика функции, определяет данную функцию.

Для расчета поля, длины, центральных точек и многих других полезных элементов можно использовать интегрирование. Вы можете легко решить интеграцию с помощью этого бесплатного калькулятора, но начать с функции поиска площади под кривой — это самый простой и быстрый способ решить интеграцию.
Типы интегралов

Существует множество типов интегралов, но наиболее часто используются следующие типы интегралов:

Определенные интегралы
Неопределенные интегралы

Этот онлайн-калькулятор интегрирования поможет вам найти оба типа интегралов, независимо от того, с каким типом вы работаете.
Как использовать этот калькулятор для интегральной оценки?
Этот интегральный калькулятор представляет собой бесплатное онлайн-приложение, которое может проиллюстрировать важность либо определенных интегралов, либо бесконечных интегралов всех интегральных функций. Поскольку он показывает результаты за доли секунд, это более простой способ измерения целых чисел.

Введите только интегральный тип, который вы хотите добавить, после установки этого приложения из магазина приложений на свой смартфон.

Калькулятор представит ваше введенное выражение графически, затем нажмите кнопку «Рассчитать», если оно точно такое же, как вы хотите.

На экране появятся результаты в секундах.

Хотя интегральные калькуляторы помогают вычислять как определенные, так и неопределенные функции нескольких переменных, в случае решения определенных интегралов необходимо сначала применить границы.

В конечном счете, это пошаговый метод решения и понимания интегралов, но этот решатель позволяет нам работать удаленно, поскольку он охватывает все методы интегрирования и даже специальные функции для получения общих решений.
Зачем использовать этот калькулятор для решения задачи интеграции?

Объяснения, почему вы должны использовать этот калькулятор интегралов для решения функций интегрирования, представлены ниже.

Этот интегральный калькулятор представляет собой бесплатное онлайн-приложение, которое позволяет очень легко вычислять интеграл в режиме онлайн и помогает проверять несколько переменных из
интегрирующие функции.

Это избавит вас от выполнения вычислений вручную, чтобы выяснить назначение тех или иных интегралов, и вы можете получить результаты с помощью онлайн-калькулятора интегралов.

Калькулятор интегралов не только помогает определить способ, обратный взятию производной, но также помогает выявить проблемы в полевых условиях.

Решение интеграционных функций может быть очень утомительной работой для студентов без технического образования. Это приложение сервисов поможет вам быстро и эффективно преодолеть эти проблемы.

Этот калькулятор также поможет вам при решении сложных уравнений интегрирования в исчислении и математике, поскольку он имеет стандартные методы интегрирования, а также специальные функции интегрирования.

Если вы пытаетесь найти интегралы, вы можете использовать этот калькулятор для поиска ответов. Таким образом, при выполнении домашних заданий и заданий это также побудит вас перепроверить свои ответы.
Возможности этого приложения — встроенный калькулятор или средство поиска интеграции Приложение:
дает мгновенные результаты
100% безопасное и надежное использование
экономит ваше время
Совершенно бесплатно
Поиск интеграции в режиме реального времени в магазине игр
предоставляет результаты, просто введя выражение интеграции
Если вы столкнетесь с какой-либо проблемой при загрузке или использовании нашего приложение калькулятора, пожалуйста, дайте нам знать, чтобы мы могли это исправить.

Производная интеграла — формула

Производная интеграла — это результат, полученный дифференцированием результата интеграла. Интеграция — это процесс нахождения «анти» производной, и, следовательно, дифференцирование интеграла должно привести к самой исходной функции. Но это не может быть сценарием со всеми определенными интегралами.

Давайте узнаем больше о производной интеграла (в разных случаях) вместе с другими примерами.

1.	Что такое производная интеграла?
2.	Дифференцирование неопределенного интеграла
3.	Производная определенного интеграла
4.	Часто задаваемые вопросы о производной интеграла

Что такое производная интеграла?

производная интеграла функции есть сама функция. Но это всегда верно только в случае неопределенных интегралов. Производная определенного интеграла функции есть сама функция только тогда, когда нижний предел интеграла есть константа, а верхний предел есть переменная, по которой мы дифференцируем. Подытожим:

• Производная неопределенного интеграла функции есть сама функция. т. е. d/dx ∫ f(x) dx = f(x)
• Производная определенного интеграла с постоянными пределами равна 0, т. е. d/dx ∫ _a ^b f(t) dt = 0
• Производная определенного интеграла, нижний предел которого — константа, а верхний предел — переменная, сама является функцией от данной переменной (верхняя граница).
  т. е. d/dx ∫ _a ^x f(t) dt = f(x), где a — константа, а x — переменная.

Давайте подробно рассмотрим каждый из этих случаев. Кроме того, давайте посмотрим, как вычислять определенные интегралы, которые не совпадают ни с одним из последних двух случаев.

Дифференцирование неопределенного интеграла

Рассмотрим неопределенный интеграл ∫ x ^3/2 dx. Если мы оценим это, используя степенное правило интегрирования, мы получим (2x ^5/2 )/5 + C. Если мы продифференцируем это, используя степенное правило дифференцирования, мы получим (2/5) (5/2) ( х ^3/2 ) + 0 = х ^3/2 . Если мы поместим это интегрирование и дифференцирование в один шаг, мы можем записать это как

d/dx ∫ x ^3/2 dx = x ^3/2 .

т. е. производная неопределенного интеграла равна самой исходной функции (это своего рода «символ производной и интеграла сокращаются друг с другом»). Таким образом, для любой функции f(x) можно написать

d/dx ∫ f(x) dx = f(x)

Производная определенного интеграла

Определенный интеграл имеет вид ∫ _a ^b f(t) dt. Но здесь пределы не всегда должны быть постоянными. Может быть 3 случая.

• Оба предела могут быть постоянными.
• Нижний предел — константа, а верхний предел — переменная.
• Оба ограничения могут включать переменные.

Мы изучим, как найти производную интеграла в каждом из этих случаев.

Когда оба предела являются константами

Рассмотрим определенный интеграл ∫ _a ^b f(x) dx, где и a, и b являются константами.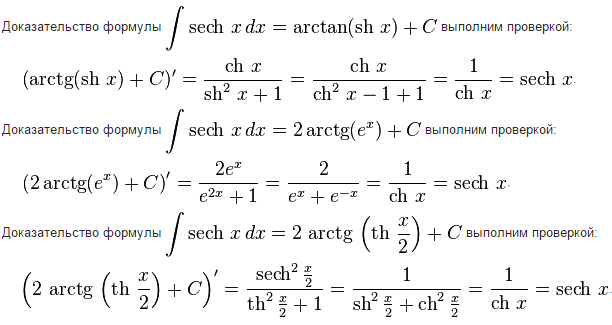 Тогда по второй фундаментальной теореме исчисления ∫ _a ^b f(x) dx = F(b) — F(a), где F(x) = ∫ f(t) dt. Теперь вычислим его производную. d/dx∫ _a ^b f(x) dx = d/dx [F(b) — F(a)] = 0 (поскольку F(b) и F(a) — константы). Таким образом, когда оба предела являются константами, производная определенного интеграла равна 0,

т. е. d/dx ∫ _a ^b f(t) dt = 0

Когда один из пределов является константой

Рассмотрим определенный интеграл ∫ _a ^x f(t) dt, где «a» — константа, а «x» — переменная. Тогда по первой фундаментальной теореме исчисления d/dx ∫ _а ^х f(t) dt = f(x). Это отражало бы тот факт, что производная интеграла является самой исходной функцией. Вот несколько примеров.

• d/dx ∫ ₂ ^x t ³ dt = x ³ .
• d/dx ∫ _-1 ^x sin t ² dt = sin x ² .

Обратите внимание, что здесь нижний предел должен быть постоянным. Если верхний предел — константа, а нижний предел — переменная, скажем, d/dx ∫ _x ² t ³ dt, то мы перепишем (используя свойство определенного интеграла) как — d/dx ∫ ₂ ^x t ³ dt и теперь его результат с использованием приведенных выше примеров равен -x ³ .

Когда оба предела имеют переменные

Рассмотрим интеграл ∫ _t² ^t³ log (x ³ + 1) dx. Здесь оба предела включают переменную t. В таких случаях мы применяем свойство определенного интеграла, которое гласит, что ∫ _a ^c f(t) dt = ∫ _a ^b f(t) dt + ∫ _b ^c f(t) dt, и при применении этого свойства мы предполагаем, что b является случайной константой. . Затем мы можем написать вышеуказанный интеграл как

∫ _T² ^T³ Log (x ³ + 1) DX = ∫ _T² ¹ Log (x ³ + 1) DX + ∫ ₁ 011101110111011101110111101 ^t³ log (x ³ + 1) dx

Теперь применим другое свойство определенных интегралов, которое гласит, что ∫ _a ^b f(t) dt = — ∫ _b ^a f(t) dt. Используя это, мы можем записать ∫ _t² ¹ log (x ³ + 1) dx как — ∫ ₁ ^t² log (x ³ + 1) dx. Теперь приведенный выше шаг становится:

= — ∫ ₁ ^T² log (x ³ + 1) DX + ∫ ₁ ^T³ Log (x ³ + 1) DX

Взятие деверной с обеих сторон,

d/dt ∫ _t² ^t³ Log (x ³ + 1) DX = — D/DT ∫ ₁ ^T² Log (x ³ + 1) DX + D/DT ∫ ₁ ^T³ Log (x ³ + 1) dx

Для первого интеграла положим t ² = u, а для второго интеграла положим t ³ = v. По цепному правилу можно записать

= — [ d/du ∫ ₁ ^u log (x ³ + 1) dx ] [ du/dt ] + [ d/dv ∫ ₁ ^v log (x ³ + 1) dx ]

= — [ d/du ∫ ₁ ^u log (x ³ + 1) dx ] [ 2t ] + [ d/dv ∫ ₁ ^v log (1 x 30 1) dx ] [ 3t ² ]

Поскольку нижний предел каждого интеграла является константой, а верхний предел — переменной, их производные равны функциям в терминах соответствующих переменных. т. е.

= [- log (u ³ + 1) ] [ 2t ] + [log (v ³ + 1) ] [ 3t ² ]

Замените u = t ² и v = t ³ здесь,

= — 2t log (t ⁶ + 1) + 3t ² log (t ^{9 0 904 04 + 1) Эта процедура очень полезно узнать производную интеграла.}

Производная формулы интеграла

Мы видели, что производная интеграла ∫ _t² ^t³ log (x ³ + 1) dx равна — 2t log (t ^{6 0} + 1 2 log (t ⁹ + 1), и это можно записать как 3t ² бревно (t ⁹ + 1) — 2т бревно (t ⁶ + 1). Обратите внимание, что производная от верхнего предела t ³ равна 3t ² , а производная от нижнего предела t ² равна 2t. Таким образом, мы можем вычислить производную интегральной формулы следующим образом:

∫ _g(t) ^h(t) f(x) dx = h'(t) · f(h(t)) — g'(t) · f(g(t))

, где f(h(t)) и f(g(t)) составные функции.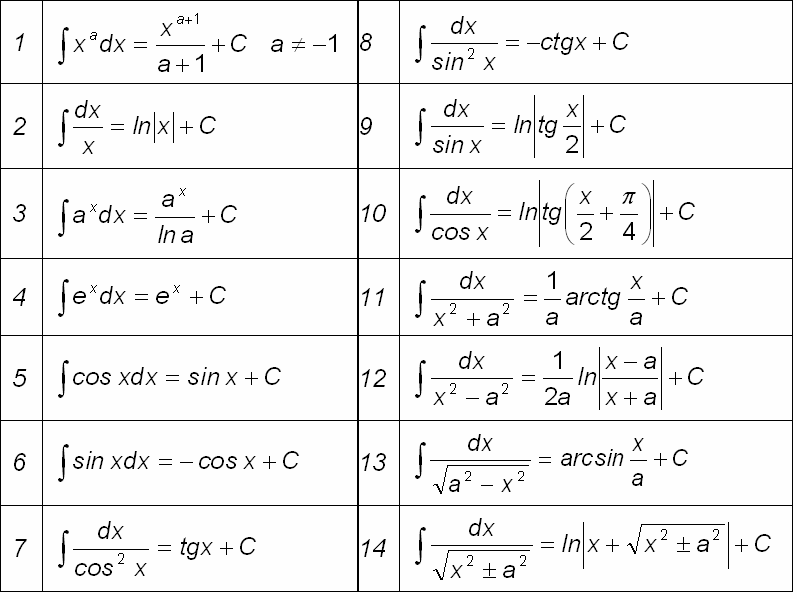 т. е. найти производную интеграла:

• Шаг 1: Найдите производную от верхнего предела и затем подставьте верхний предел в подынтегральное выражение. Умножьте оба результата.
• Шаг 2: Найдите производную от нижнего предела и подставьте нижний предел в подынтегральное выражение. Умножьте оба результата.
• Шаг 3: Вычтите приведенные выше результаты по порядку.

☛ Связанные темы:

• Калькулятор определенных интегралов
• Интегральный калькулятор
• Калькулятор неопределенных интегралов

Часто задаваемые вопросы о производной интеграла

Как найти производную интеграла?

Производная интеграла — это сама функция, когда нижний предел интеграла является константой, а верхний предел — просто переменной. т. е. d/dx ∫ _a ^x f(t) dt = f(x), где a — константа.

Какова производная интеграла, если предел не является константой?

Чтобы найти производную интеграла, когда оба предела определенного интеграла не являются постоянными, мы применяем следующие два свойства, чтобы разбить данный интеграл на два интеграла, каждый из которых имеет нижний предел, равный константе.

Также применяем метод подстановки интегрирования, если верхний предел каждого интеграла не является просто переменной. Тогда производная каждого из интегралов есть сама функция с точки зрения ее соответствующей верхней границы.

Что такое процесс дифференцирования интеграла?

Для дифференцирования интегралов:

• Проверьте, является ли нижний предел константой. Если это так, то производная интеграла является самой функцией (в терминах верхнего предела).
• Если оба предела не являются постоянными, то разделите интеграл на два интеграла, используя свойства определенных интегралов и записав нижний предел каждого из интегралов как константу.

  No related posts.