Внутренние накрест лежащие углы: Внутренние накрест лежащие углы | Треугольники

Вопрос 1

Теорема 4.2: если сумма внутренних односторонних углов равна 180 или внутренние накрест лежащие углы равны, то прямые параллельны.

Доказательство: Пусть прямые а иbобразуют с секущей АВ равные внутренние накрест лежащие углы. Допустим, что прямыеа иbне параллельны, а значит, пересекаются в некоторой точке С.

Секущая АВ разбивает плоскость на 2 полуплоскости. Построим треугольник ВАС₁, равный АВС, в другой полплоскости. Т. К. Соответствующие углы треугольников АВС и ВАС с вершинами А и В равны, то они совпадают с внутренним накрест лежащими углами. Значит прямая АС₁, совпадает с а, а прямая ВС₁ совпадает с b. А это невозможно, значит прямыепараллельны.

Вопрос 2

Для того, чтобы найти гипотенузу, надо использовать свойство синуса (косинуса), если угол противолежащий (прилежащий).

Потом теорема Пифагора.

Билет №5 1. Теорема об углах, образованных при пересечении двух параллельных прямых третьей.

2. Вывод формул площади треугольника:

Вопрос 1

Теорема 4.3-обратная теореме 4.2. — Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна

Доказательство:

Пусть а и b – параллельные прямые, и с – прямая, пересекающая их в точках А и В. Проведем через точку А прямую а₁ так, чтобы внутренние накрест лежащие углы, образованные секущей с прямыми а₁ и b, были равны.

По признаку параллельности прямых прямые а₁ и b параллельны. А так как через точку А проходит только одна прямая, параллельная прямой b, то прямая а совпадет с прямой а₁.

Значит, внутренние накрест лежащие углы, образованные секущей с параллельными прямыми а и b, равны.

Теорема доказана.

Из свойства углов, образованных при пересечении параллельных прямых секущей, следует, что если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна другой.

Вопрос 2

Пусть АВС данный треугольник. Дополним этот треугольник до параллелограмма АВСD, как указано на рисунке. Площадь параллелограмма равна сумме площадей треугольников АВС и CDA. Так как они равны, то площадь параллелограмма равна удвоенной площади треугольника АВС. Высота параллелограмма, соответствующая стороне АВ, равна высоте треугольника АВС, проведенной к стороне АВ. Отсюда следует, что площадь треугольника равна половине произведения его стороны на проведенную к ней сторону:

S = 0,5 * a * h.

Докажем теперь, что площадь треугольника равна половине произведения двух любых его сторон на sin угла между ними.

Проведем в треугольнике АВС высоту BD. Имеем

S = 0,5 * AC * BD

Из прямоугольного треугольника ABDBD = AB * sin (alpha). Если угол alpha острый и BD=AB*sin(180-alpha), если угол alpha тупой. В любом случае BD = AB * sin (alpha), следовательно, площадь треугольника S = 0,5 * AC * AB * sinA, что и требовалось доказать.

Выведем формулу Герона для площади треугольника:

a, b, с – длины сторон треугольника, р – полупериметр

Имеем:

Из теоремы косинусов следует:

Значит:

Отсюда следует, что:

Таким образом, получается, что:

Формулы совпадают.

Билет №6 1. Внешний угол треугольника(определение). Теорема о внешнем угле треугольника. Сумма внешних углов n-угольника. 2. Нахождение значений синуса, косинуса и тангенса угла 45°.

Углы — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. УГЛЫ

У́гол — геометрическая фигура, образованная
двумя лучами (сторонами угла), выходящими из
одной точки (которая называется вершиной угла)

3.

По величинеУГЛЫ
ОСТРЫЙ
ТУПОЙ
ПРЯМОЙ
РАЗВЁРНУТЫЙ

5. Центральный угол, угол с вершиной в центре окружности.

Центральный угол,
угол с вершиной в центре окружности.
Величина центрального угла равна
градусной мере дуги, заключённой между
сторонами этого угла.

6. Вписанный угол, угол, вершина которого лежит на окружности, а стороны пересекают эту окружность

Величина вписанного угла равна половине градусной
меры дуги, ограниченной его сторонами.
Все вписанные углы,
опирающиеся на одну и ту же дугу, равны.

7. Сопряжённые углы

Два угла, имеющие общие вершину и обе
стороны, но различающиеся внутренней
областью; они образуют вместе полный
угол; сумма их величин 360°.

8. Смежные углы

два угла с общей вершиной, одна из сторон
которых — общая, а оставшиеся стороны
лежат на одной прямой.
Сумма смежных углов равна 180°.
Биссектрисы смежных углов перпендикулярны.

9. Вертикальные углы

Углы, которые образуются при
пересечении двух прямых, эти углы не
имеют общих сторон.
Вертикальные углы равны.

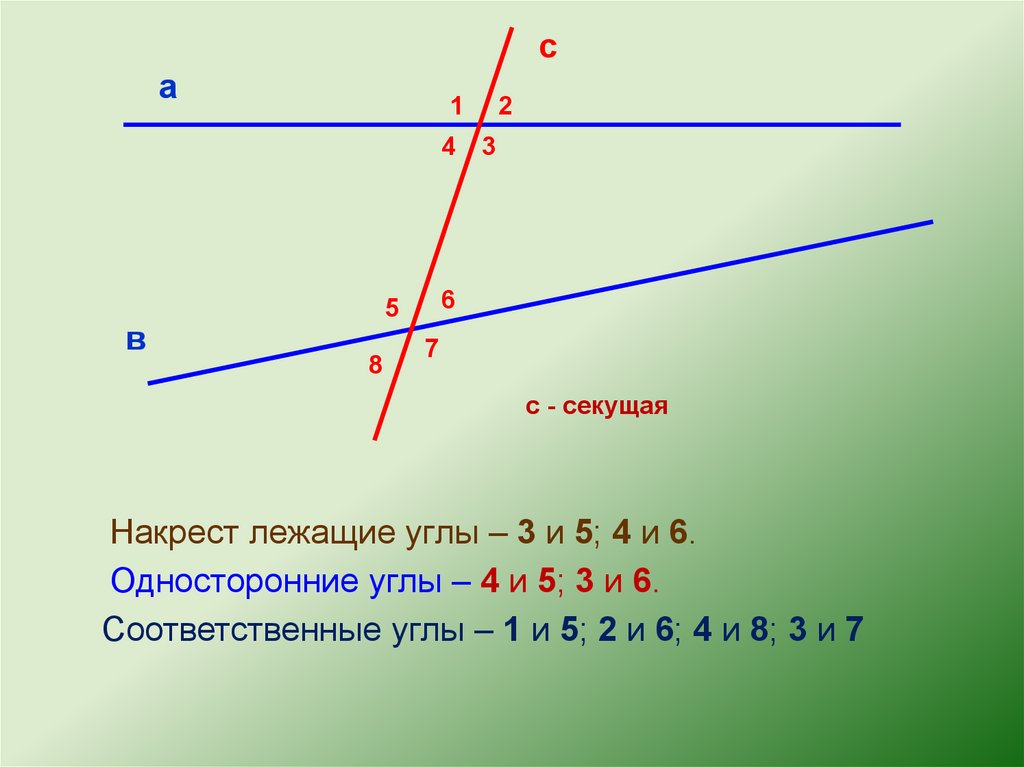
10. Внутренние односторонние углы при параллельных прямых.

Если две параллельные прямые пересечены
третьей прямой, то
сумма внутренних односторонних углов
равна 180°

11. Внутренние накрест лежащие углы при параллельных прямых.

Если две параллельные прямые пересечены
третьей прямой, то
внутренние накрест лежащие углы равны.

12. Соответственные углы при параллельных прямых.

Если две параллельные прямые пересечены
третьей прямой, то
соответственные углы равны.

13. Внешний угол треугольника

при данной вершине — это угол, смежный с
внутренним углом треугольника при этой
вершине.
Внешний угол треугольника равен сумме двух
внутренних углов, не смежных с ним.

14. Устная работа

№1 Найдите : y .
70°
y
a
110°
y — 10°
b
c
d
Ответ : 95°

15. Устная работа

№2 Найдите : x .
c
d
x
120°
a
60°
b
x + 10°
Ответ :85°.
Чему равен угол ВАС=?

18. СУММА УГЛОВ

Сумма внутренних углов
треугольника равна 180°.
Сумма внутренних углов
четырёхугольника равна 360°.
Сумма внутренних углов
n-угольника равна (n — 2)∙180°.
1. 37
2. 60
3. 70
4. 149
1
3
5
2
4
1. 100
2. 60
3. 35
4. 25
5. 65
6. 75
6

21. Задача

В треугольнике два угла равны 36⁰ и 73⁰.
Найдите его третий угол. Ответ дайте в
градусах.
Решение. Сумма углов треугольника равна
180⁰.
3 180 36 73 71
73⁰
?⁰
36⁰
№ 16
7 1
3
10 х
х

22. Задача

Один из острых углов прямоугольного
треугольника равен 57⁰. Найдите его другой
острый угол. Ответ дайте в градусах.
Решение.
Сумма острых углов прямоугольного
треугольника равна 90⁰.
3 90 57 33
57⁰
?⁰
№ 16
3 3
3
10 х
х

23. Задача

Один из углов равнобедренного треугольника равен
98⁰. Найдите один из других его углов. Ответ дайте в
градусах.
Решение.
Т.к. 98⁰- тупой угол, то это угол при
вершине равнобедренного треугольника,
А
поскольку углы при основании
равнобедренного треугольника
равны, а двух тупых углов у треугольника
быть не может.
А (180 98 ) : 2 41
№ 16
4 1
В
98⁰
3
10 х
С
х

24. Задача

В треугольнике АВС известно, что ∠ВАС = 64⁰,
AD – биссектриса. Найдите угол BAD. Ответ
дайте в градусах.
Решение.
Биссектриса треугольника
делит угол пополам.
BAD BAC : 2
BAD 64 : 2 32
№ 16
3 2
3
10 х
х
Ответ: 70
25
∠ВСА = 180° — 57° — 117°=6°
Ответ: 6
26
BAC BAL LAC 23 23 46
Ответ: 111
27

28. Четырёхугольники

Ответ: 7
∟А +∟С = ∟В +∟Д
Ответ: 100 и 120.
Углы
выпуклого
четырехугольника
пропорциональны числам 1, 2, 3, 4. Найдите
их.
Ответ: 36о, 72о, 108o, 144o.

35. В угол С величиной 75° вписана окружность, которая касается сторон угла в точках А и В, где О — центр окружности.

Найдите уголАОВ. Ответ дайте в градусах.

36. В окружности с центром О отрезки АС и BD — диаметры. Угол AOD равен 148°. Найдите угол АСВ. Ответ дайте в градусах.

АBCD – прямоугольник; М, K, Р, Т – середины его сторон, АВ =
6 см, AD = 12 см.
Найдите площадь четырехугольника МКРТ.
В
K
6см M
A
C
Р
T
12 см
D

English     Русский Правила

Как закрепить внутренний угол

Специальные приемы | Советы | Без категории

6 июня 2013 г. 16 июня 2022 г.

У меня есть простой способ скрепления внутреннего (перевернутого) угла, которым я хочу поделиться с вами сегодня.

Поскольку в моем следующем проекте к рождественской серии «Раз в месяц» есть внутренние углы, которые поначалу могут немного озадачить, я решил показать вам, насколько это может быть просто!

Вот краткий обзор не рождественской версии этого проекта (хотя теперь, когда я смотрю на нее, она может сойти за рождественскую). Это столешница с небольшой аппликацией, но ее очень легко сделать.

Полное руководство будет готово для вас 15 июня, а пока позвольте мне показать вам, как связать внутренние углы (их 8).

Шаг 1 . В каждом внутреннем углу маленькими ножницами обрежьте очень скудные 1/4 дюйма угла. Это позволит вам вытянуть края одеяла прямо на шагах 6 и 7.

Шаг 2 . Когда вы подходите к каждому внутреннему углу, нарисуйте линию 1/4″ от необработанного края вашей обвязочной полосы, которая находится на одном уровне с входящим краем, как показано на рисунке:

Шаг 3 . Нарисуйте линию на обвязочной ленте на расстоянии 1/4″ от необработанного края исходящего края, как показано, и пересеките с предыдущей нарисованной линией:

Шаг 4 . Нарисованные линии создадут опорную точку, например:

Шаг 5 . Когда вы сшиваете бейку, остановитесь, опустив иглу в этой точке поворота.

Шаг 6 . Потяните край одеяла перед иглой так, чтобы он был прямым и ровным с краем прижимной лапки.

Шаг 7 . Потяните край одеяла сзади иглы так, чтобы он также был прямым, образуя длинную прямую линию спереди назад.

Шаг 8 . Продолжайте шить, пока не дойдете до следующего угла.

Вот оно! Хитрость заключается в том, чтобы обрезать припуск на шов и повернуть в нужном месте.

Для этого конкретного проекта я пришила бейку к изнаночной стороне одеяла, а затем обернула ее спереди. Вот как будет выглядеть обратная сторона:

Вы не получите настоящую «складку» или «складку», как в случае с прямым углом. Просто легкость, которая позволяет уголку сгибаться и лежать ровно. Вот так будет выглядеть лицевая сторона:

Обвязку машинным способом я закончила. Я прошиваю как можно ближе к изгибу, и строчка на спине едва заметна (подходящей нитью).

Я часто обвязываю таким образом: пришиваю спинку, заворачиваю на перед и пришиваю на машине.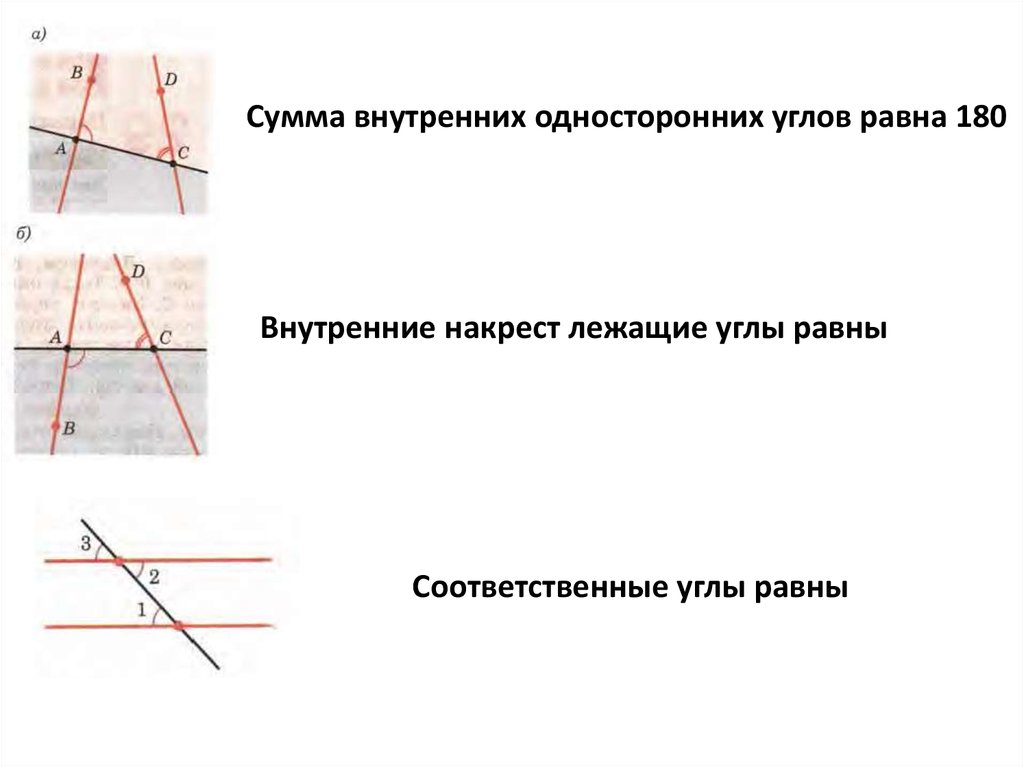 Быстро и просто!

Ради собственного удовольствия я должен показать вам фотографию своих ногтей.

Я всегда использую фотографии, на которых показаны ужасно выглядящие руки и ногти. У кого есть время привести ногти в порядок, когда они могли бы шить? Ну, я угостил себя на свой день рождения, так что я должен был показать вам! Эх, хотелось бы, чтобы они так и остались.

Счастливого квилтинга!

Синдром Якобсена: MedlinePlus Genetics

Описание

Синдром Якобсена — это состояние, вызванное потерей генетического материала из хромосомы 11. Поскольку эта делеция происходит на конце (конце) длинного (q) плеча хромосомы 11, синдром Якобсена также известен как синдром терминальной делеции 11q.

Признаки и симптомы синдрома Якобсена значительно различаются. У большинства больных наблюдается задержка развития, включая развитие речи и двигательных навыков (таких как сидение, стояние и ходьба). Большинство из них также имеют когнитивные нарушения и трудности в обучении. Сообщалось о поведенческих проблемах, включая компульсивное поведение (например, измельчение бумаги), короткую продолжительность концентрации внимания и легкую отвлекаемость. У многих людей с синдромом Якобсена был диагностирован синдром дефицита внимания/гиперактивности (СДВГ). Синдром Якобсена также связан с повышенной вероятностью расстройств аутистического спектра, которые характеризуются нарушением навыков общения и социализации.

Синдром Якобсена также характеризуется отличительными чертами лица. К ним относятся маленькие и низко посаженные уши, широко посаженные глаза (гипертелоризм) с опущенными веками (птоз), кожные складки, закрывающие внутренний угол глаз (эпикантальные складки), широкая переносица, опущенные вниз углы рта, тонкая верхняя губа и небольшая нижняя челюсть. Пораженные люди часто имеют большой размер головы (макроцефалия) и аномалию черепа, называемую тригоноцефалией, которая придает лбу заостренный вид.

Более 90 процентов людей с синдромом Якобсена страдают нарушением свертываемости крови, называемым синдромом Пэрис-Труссо.

Это состояние вызывает пожизненный риск аномального кровотечения и легкого образования синяков. Синдром Пэрис-Труссо — это нарушение тромбоцитов, клеток крови, необходимых для свертывания крови.

Другие признаки синдрома Якобсена могут включать пороки сердца, трудности с кормлением в младенчестве, низкий рост, частые инфекции уха и носовых пазух, а также скелетные аномалии. Расстройство может также повлиять на пищеварительную систему, почки и половые органы. Ожидаемая продолжительность жизни людей с синдромом Якобсена неизвестна, хотя больные доживают до зрелого возраста.

Частота

Предполагаемая частота синдрома Якобсена составляет 1 случай на 100 000 новорожденных. Сообщается о более чем 200 пострадавших.

Причины

Синдром Якобсена вызывается делецией генетического материала на конце длинного (q) плеча хромосомы 11. Размер делеции различается у разных людей, у большинства больных отсутствует от 5 до 16 миллионов строений ДНК. блоки (также пишется как от 5 Мб до 16 Мб).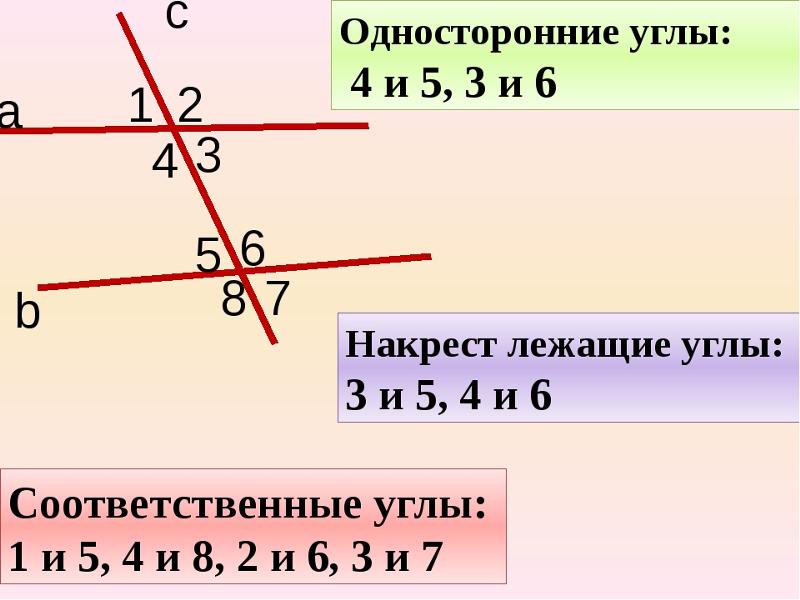

Почти у всех пораженных людей делеция включает кончик хромосомы 11. Более крупные делеции, как правило, вызывают более серьезные признаки и симптомы, чем мелкие делеции.

Особенности синдрома Якобсена, вероятно, связаны с потерей нескольких генов на хромосоме 11. В зависимости от размера удаленная область может содержать от 170 до более чем 340 генов. Многие из этих генов не были хорошо охарактеризованы. Однако гены в этой области, по-видимому, имеют решающее значение для нормального развития многих частей тела, включая мозг, черты лица и сердце. Только несколько генов были изучены как возможные факторы, влияющие на специфические черты синдрома Якобсена; исследователи работают над тем, чтобы определить, какие дополнительные гены могут быть связаны с этим заболеванием.

Наследование

В большинстве случаев синдром Якобсена не передается по наследству. Они возникают в результате хромосомной делеции, которая происходит как случайное событие во время формирования половых клеток (яйцеклеток или сперматозоидов) или на ранних стадиях развития плода.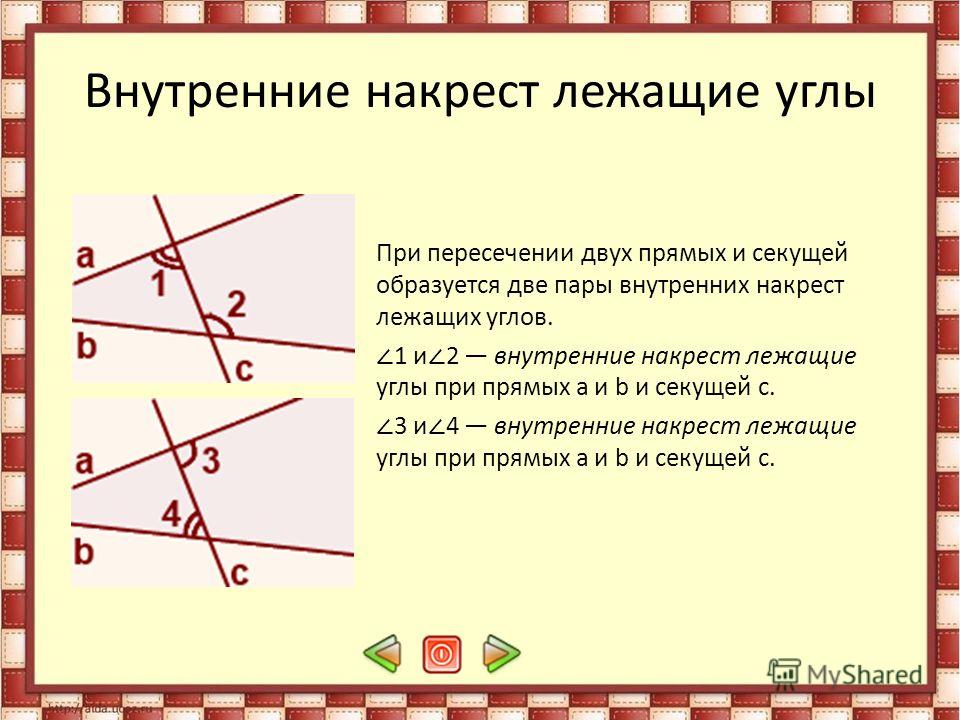 Пораженные люди, как правило, не имеют истории заболевания в своей семье, хотя они могут передать хромосомную делецию своим детям.

От 5 до 10 процентов людей с синдромом Якобсена наследуют хромосомную аномалию от здорового родителя. В этих случаях родитель несет хромосомную перестройку, называемую сбалансированной транслокацией, при которой сегмент хромосомы 11 поменялся местами с сегментом другой хромосомы. При сбалансированной транслокации генетический материал не приобретается и не теряется. Сбалансированные транслокации обычно не вызывают проблем со здоровьем; однако они могут стать несбалансированными при передаче следующему поколению.

Дети, унаследовавшие несбалансированную транслокацию, могут иметь хромосомную перестройку с отсутствующим генетическим материалом и дополнительным генетическим материалом. У людей с синдромом Якобсена, которые наследуют несбалансированную транслокацию, отсутствует генетический материал с конца длинного плеча хромосомы 11 и имеется дополнительный генетический материал из другой хромосомы. Эти хромосомные изменения приводят к проблемам со здоровьем, характерным для этого расстройства.

Другие названия для этого состояния

• Делеционное расстройство 11q
• 11q Делеционный синдром
• 11q Терминальное делеционное расстройство
• 11q- Делеционный синдром
• 11q23 Делеционное расстройство
• Тромбоцитопения Якобсена

Дополнительная информация и ресурсы

Информация о генетическом тестировании

• Реестр генетического тестирования: синдром частичной моносомии 11q

Информационный центр генетических и редких заболеваний

• Синдром Якобсена

Ресурсы поддержки и защиты интересов пациентов

• Поиск информации о заболеваниях
• Национальная организация редких заболеваний (NORD)

Научные исследования от ClinicalTrials.gov

• ClinicalTrials.gov

Каталог генов и болезней от OMIM

• СИНДРОМ ЯКОБСЕНА

Научные статьи в PubMed

• PubMed

Ссылки

• Акшомофф Н. , Маттсон С.Н., Гроссфельд П.Д. Доказательства расстройства аутистического спектра при синдроме Якобсена: идентификация гена-кандидата в дистальном отделе 11q. Жене Мед. 2015 Февраль; 17 (2): 143-8. doi: 10.1038/gim.2014.86. Epub 2014, 24 июля. Цитирование на PubMed
• Колдрен К.Д., Лай З., Шрагг П., Росси Э., Глайдвелл С.К., Зуффарди О., Маттина Т., Айви DD, Curfs LM, Mattson SN, Riley EP, Treier M, Grossfeld PD. хромосомный картирование микрочипов предполагает роль BSX и нейрогранина в нейрокогнитивных и поведенческие дефекты при синдроме терминальной делеции 11q (синдром Якобсена). Нейрогенетика. 2009 г.Апр;10(2):89-95. doi: 10.1007/s10048-008-0157-x. Электронная книга 2008 г. 15 октября. Цитирование в PubMed или бесплатная статья в PubMed Central
.
• Favier R, Akshoomoff N, Mattson S, Grossfeld P. Синдром Якобсена: достижения в наши знания о фенотипе и генотипе. Am J Med Genet C Semin Med Genet. 2015 Сен; 169 (3): 239-50. doi: 10. 1002/ajmg.c.31448. Epub 2015, 18 августа. Цитирование на PubMed
• Гроссфельд П.Д., Маттина Т., Лай З., Фавье Р., Джонс К.Л., Коттер Ф., Джонс К. 11q Терминальное делеционное расстройство: проспективное исследование 110 случаев. Am J Med Genet A. 2004 15 августа; 129А(1):51-61. doi: 10.1002/ajmg.a.30090. Цитата в PubMed
• Маттина Т., Перротта С.С., синдром Гроссфельда П. Якобсена. Orphanet J Rare Dis. 2009 7 марта; 4:9. дои: 10.1186/1750-1172-4-9. Цитирование в PubMed или бесплатная статья в PubMed Central
• Пенни Л.А., Делл’Акуила М., Джонс М.С., Бергоффен Дж., Каннифф С., Фринс Дж.П., Грейс Э., Грэм Дж. М. мл., Кусефф Б., Маттина Т. и др. Клинические и молекулярные характеристика пациентов с дистальными делециями 11q. Am J Hum Genet. 1995 Март; 56 (3): 676-83. Цитирование в PubMed или бесплатная статья в PubMed Central
• Тайсон С., Цяо И., Гарвард С., Лю Х, Бернье Ф.П., МакГилливрей Б.

  No related posts.