ГДЗ По Математике 6 Класс. Умножение дробей
Перейти к контенту
ГДЗ по Математике 6 класс Мерзляк А.Г. § 11. Умножение дробей
Вопросы к параграфу
1. Сформулируйте правило умножения дроби на натуральное число.
2. Какая дробь является произведением двух дробей?
3. Чему равно произведение дроби и числа 0?
4. Какие свойства умножения выполняются при умножении дробей?
Решаем устно
1. Найдите значение выражения:
2. Назовите неправильную дробь, которой равно смешанное число:
3. Найдите целую часть числа:
4. Упростите выражение:
5. Пешеход за ч проходит 1 км. За какое время он пройдет:
6. Назовите дроби со знаменателем 12, которые больше, чем , и меньше, чем .
Упражнения
333. Выполните умножение:
334. Выполните умножение:
335. Найдите произведение:
336. Найдите произведение:
337. Выполните умножение:
338. Выполните умножение:
339. Найдите произведение:
340. Выполните умножение:
341. Найдите значение выражения:
342. Найдите значение выражения:
343. Какой путь пройдёт поезд за ч, если его скорость составляет 66 км/ч?
344. Какое расстояние проедет автомобиль со скоростью 72 км/ч за ч?
345. Сколько стоят кг бананов, если цена 1 кг бананов составляет р.?
346. Сколько стоят кг конфет, если 1 кг конфет стоит р.?
347. Выполните умножение:
348. Выполните умножение:
349.
Найдите значение степени:
350. Найдите значение степени:
351. Найдите значение выражения:
352. Найдите значение выражения:
353. Найдите значение выражения, используя распределительное свойство умножения:
354. Найдите значение выражения, используя распределительное свойство умножения:
355. Вычислите значение выражения наиболее удобным способом:
356. Вычислите значение выражения наиболее удобным способом:
357. Упростите выражение:
358. Упростите выражение:
359. Упростите выражение:
360. Упростите выражение и найдите его значение:
361. Упростите выражение и найдите его значение:
362. Докажите, что значение выражения не зависит от значения переменной:
363. Раскройте скобки:
364.
Раскройте скобки:
365. Длина прямоугольного параллелепипеда равна см, что на см больше его ширины и в раза меньше его высоты. Вычислите объём прямоугольного параллелепипеда.
366. Одна из сторон прямоугольника равна м, а соседняя — в раза больше. Вычислите площадь прямоугольника.
367. Турист шёл пешком ч со скоростью км/ч и ехал на велосипеде ч со скоростью км/ч. Какое расстояние больше: то, которое турист преодолел пешком, или то, которое он проехал на велосипеде, и на сколько километров?
368. Мальвина купила кг апельсинов по цене сольдо за килограмм и кг яблок по цене сольдо. За какие фрукты — апельсины или яблоки — Мальвина заплатила больше и на сколько сольдо?
369. Велосипедист Андрей ехал со скоростью км/ч, а велосипедист Богдан — со скоростью в раза большей. Каким было расстояние между велосипедистами сначала, если Богдан догнал Андрея через ч после того, как они одновременно начали двигаться?
370.
Из двух городов одновременно навстречу друг другу отправились велосипедист и мотоциклист. Велосипедист ехал со скоростью км/ч, а мотоциклист — со скоростью и раза большей. Найдите расстояние между городами, если велосипедист и мотоциклист встретились через ч после начала движения.
371. Лодка плыла ч против течения реки и ч по течению. Какой путь преодолела лодка за всё время движения, если собственная скорость лодки равна 18 км/ч, а скорость течения — км/ч?
372. Теплоход шёл 3 ч против течения и ч по течению реки. На сколько километров меньше прошёл теплоход по течению, чем против течения, если скорость течения составляет км/ч, а собственная скорость теплохода — км/ч?
373. Одна швея может выполнить закал за 4 ч, а другая — за 6 ч. Какую часть заказа они выполнят за ч. работая вместе? Хватит ли им 3 ч, чтобы, работая вместе, выполнить заказ?
374. Один рабочий может выполнить производственное задание за 5 ч, а другой — за 15 ч.
Какую часть задания они выполнят, если будут работать вместе ч? Успеют ли они, работая вместе, выполнить задание за 3 ч?
375. Выполните умножение (буквами обозначены натуральные числа):
376. He выполняя умножения, сравните:
377. Не выполняя умножения сравните:
Упражнения для повторения
378. Игорь переложил из одного ящика в другой кг яблок, после чего в каждом ящике стало по 20 кг. Сколько килограммов яблок было в каждом ящике первоначально?
379. Запишите все правильные дроби с числителем 3, которые больше .
380. Фермер решил посадить кусты смородины. Он мог посадить их или в четыре ряда, или и шесть. Сколько кустов смородины он решил посадить. если известно, что их было больше 85, но меньше 100?
381. С одного аэродрома в одном направлении с интервалом 0,4 ч вылетели два самолёта. Первый самолёт летел со скоростью 640 км/ч, а второй — 720 км/ч.
Через сколько часов после своего вылета второй самолёт будет впереди первого на расстоянии 24 км?
382. Сколько равносторонних треугольников изображено на рисунке 9?
383. Сравните:
384. Сократите дробь:
385. Запишите в виде десятичной дроби:
386. Запишите в виде обыкновенной дроби:
387. Запишите в процентах:
Задача от мудрой совы
388. На доске написаны три двузначных числа. Первая слева цифра одного из них — 5, второго — 6, а третьего — 7. Учитель попросил троих учащихся сложить любые два из этих чисел. Первый учащийся получил в сумме число 147, второй и третий — разные трёхзначные числа, первые слева две цифры которых 1 и 2. Какие числа написаны на доске?
Этот сайт использует cookie для хранения данных.
Все школьные темы по математике для 6 класса | Wika
Loading
Навигация по разделам
- Обыкновенные дроби
- Десятичные дроби
- Натуральные числа
- Решение уравнений
- Координаты на плоскости
- Рациональные числа
- Умножение и деление обыкновенных дробей
- Отношения и пропорции
- Раскрытие скобок при упрощении
- Признаки делимости
Обыкновенные дроби
Определение прямой и обратной пропорциональной зависимости
Разложение числа на простые множители
Простые числа в математике
Как правильно сравнивать дроби с разными знаменателями
Нахождение дроби от числа
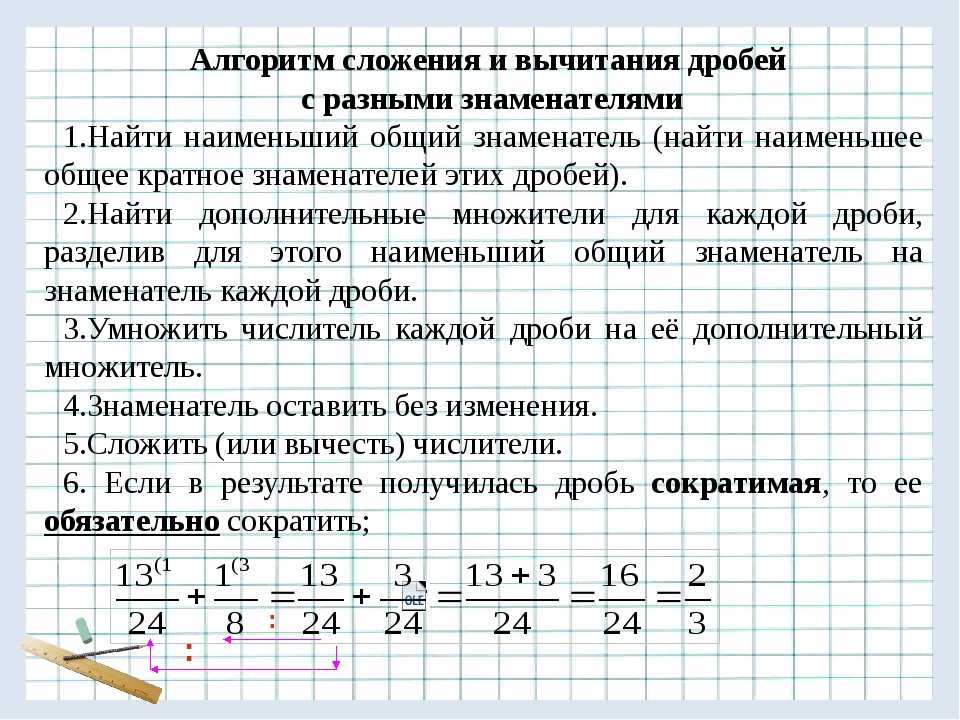
Как правильно складывать дроби с разными знаменателями
Основные сведения о признаках делимости чисел 2,4,5,10,25
Доказательство делимости числа на 3 и 9 — что важно знать
Объяснение дробных выражений для 6 класса
Основные сведения о взаимно обратных числах в математике
Десятичные дроби
Правило умножения десятичных дробей на натуральные числа
Как вычитать дроби с разными знаменателями
Натуральные числа
Умножение отрицательных чисел
Решение уравнений
Как решать задачи на составление уравнений
Координаты на плоскости
Основные сведения о столбчатых диаграммах
Рациональные числа
Сложение отрицательных чисел
Правила вычитания отрицательных чисел
Основные сведения о сложении чисел с разными знаками
Коэффициент в математике
Умножение и деление обыкновенных дробей
Как найти число по заданному значению его дроби
Как применять распределительной свойство умножения для решения задач
Отношения и пропорции
Составление и решение пропорций в математике
Что нужно знать об отношении двух чисел в математике за 6 класс
Длина окружности и площадь круга
Раскрытие скобок при упрощении
Как правильно раскрывать скобки в математических выражениях
Признаки делимости
Основные сведения о делимости произведения
Курс: США • 6 класс • Математика
Содержание
- Целые числа
- Урок: Целые числа
- Урок: Сравнение и упорядочивание целых чисел
- Урок: Абсолютные значения целых чисел
- Урок: Целые числа на числовой прямой
- Урок: Величайший общий фактор
- Урок: Наименьшее общее кратное
- Рациональное число
- Урок: Набор рациональных чисел
- Урок: Противоположности и абсолютное значение рациональных чисел
- Урок: Сравнение и упорядочивание рациональных чисел
- Операции с дробями
- Урок: Сложение дробей с разными знаменателями
- Урок: Умножение дробей
- Урок: Деление дробей
- Урок: Умножение смешанных чисел
- Урок: Деление смешанных чисел
- Урок: Деление целых чисел на дроби
- Урок: Деление дробей на целые числа
- Операции с десятичными дробями
- Урок: Деление трехзначных чисел на двузначные: длинное деление без остатка
- Урок: Деление трехзначных чисел на двузначные числа: длинное деление с остатками
- Урок: Сложение и вычитание десятичных дробей
- Урок: Умножение десятичных дробей
- Урок: Деление десятичных дробей
- Урок: Дроби, десятичные числа и проценты
- Урок: Деление целых чисел с десятичными дробями
- Урок: Взаимные отношения
- Проценты
- Урок: Введение в проценты
- Урок: Преобразование процентов в дроби
- Урок: дроби в процентах
- Урок: Преобразование процентов в десятичные дроби
- Урок: Перевод десятичных дробей в проценты
- Урок: Эквивалентные дроби, десятичные числа и проценты
- Урок: Проценты от числа
- Урок: Нахождение целого по части и проценту
- Урок: Оценка процента
- Соотношения
- Урок: Соотношения
- Урок: Эквивалентные отношения
- Урок: Сравнение отношений
- Урок: Сравнение правильных дробей
- Урок: Таблицы соотношений
- Урок: Графические отношения
- Ставки
- Урок: Использование ставок для прогнозирования
- Урок: Интерпретация отношений с помощью прямых линий
- Урок: Единица измерения
- Урок: Сравнение курсов
- Преобразование единиц измерения
- Урок: Преобразование и сравнение общепринятых единиц
- Урок: Преобразование и сравнение метрических единиц
- Урок: Преобразование между метрическими и обычными единицами измерения
- Числовые выражения
- Урок: Полномочия и показатели
- Урок: Факторизация простых чисел
- Урок: Факторизация простых чисел с показателями
- Урок: Порядок действий: оценка числовых выражений
- Урок: Порядок действий: десятичные дроби
- Урок: Порядок действий: экспоненты
- Урок: Свойства равенства
- Алгебраические выражения
- Урок: Части математического выражения
- Урок: Написание алгебраических выражений
- Урок: Вычисление алгебраических выражений
- Урок: Эквивалентные алгебраические выражения
- Урок: Упрощение выражений: объединение похожих терминов
- Урок: Упрощение выражений: коммутативные и ассоциативные свойства
- Уравнения
- Урок: Введение в уравнения
- Урок: Одношаговые уравнения: сложение и вычитание
- Урок: Одношаговые уравнения: умножение и деление
- Урок: сменный набор
- Урок: Переменные и константы
- Неравенства
- Урок: Неравенства на числовой прямой
- Урок: Введение в неравенства
- Урок: Определение истинности или ложности неравенства
- Урок: Одношаговые неравенства: сложение или вычитание
- Урок: Одношаговые неравенства: умножение или деление
- Отношения между двумя переменными
- Урок: Координатная плоскость: первый квадрант
- Урок: Координатная плоскость: четыре квадранта
- Урок: Зависимые и независимые переменные
- Урок: Заполнение таблиц функций
- Урок: Правила функций
- Урок: Графики линейных функций
- Урок: Связь таблиц, графиков и уравнений
- Области
- Урок: Площадь треугольника
- Урок: Равенство площадей двух треугольников
- Урок: Площади прямоугольников и квадратов
- Урок: Площадь параллелограмма
- Урок: Площадь трапеции
- Урок: Площадь квадрата по диагоналям
- Урок: Нахождение площади ромба с помощью диагоналей
- Урок: Площадь воздушного змея
- Урок: Площади составных многоугольников
- Расстояние и площадь в координатной плоскости
- Урок: Расстояние на координатной плоскости: по горизонтали и по вертикали
- Урок: Рисование многоугольников в координатной плоскости
- Урок: Прямоугольники на координатной плоскости
- Площадь поверхности и объем
- Урок: Сети трехмерных фигур
- Урок: Площади поверхностей прямоугольной призмы и кубов
- Урок: Объемы прямоугольных призм и кубов
- Урок: Площади поверхностей пирамид
- Меры центральной тенденции и изменчивости
- Урок: Среднее значение набора данных
- Урок: Медиана набора данных
- Урок: Режим набора данных
- Урок: Среднее, медиана и мода
- Урок: Лучшая мера центральной тенденции
- Урок: Среднее абсолютное отклонение
- Урок: Диапазон набора данных
- Урок: Межквартильный диапазон
- Урок: Лучшая мера изменчивости
- Отображение и анализ данных
- Урок: Типы переменных
- Урок: Сбор статистических данных
- Урок: Статистические и нестатистические вопросы
- Урок: Таблицы частот
- Урок: Сгруппированные таблицы частот
- Урок: Графики типа «ящик с усами»
- Урок: Статистические диаграммы
- Урок: Двойные гистограммы
- Урок: Точечные диаграммы
- Урок: Гистограммы
- Урок: Формы распределений
Математика 6 класс Математика | GreatSchools.
orgВ этом году ваш ребенок узнает много нового об отношениях, то есть между числами. Математика шестого класса изучает отношения и пропорции, отрицательные и положительные числа, эквивалентные уравнения и способы изображения трехмерных фигур в двух измерениях. Все это и X отмечают место для предварительной алгебры.
Вот 8 основных навыков, которые ваш ребенок должен освоить в шестом классе по математике:
- Использование соотношений для представления взаимосвязей между различными количествами, размерами и значениями.
- Решение текстовых задач с соотношениями путем их нанесения на диаграммы, графики и таблицы.
- Расчет процентов.
- Деление дробей на дроби.
- Понимание отрицательных чисел и их нанесение на числовые линии.
- Нахождение X (недостающего значения) в уравнениях как прелюдия к алгебре.
- Решение реальных математических задач на площадь, площадь поверхности и объем.
- Изучение основ статистики.
Коэффициенты
Коэффициенты нужны не только для того, чтобы похвастаться тем, что одна кофейня в два раза лучше всех остальных. Соотношения описывают отношения между количествами, размерами и значениями, которые можно измерить и отобразить на графике, в таблице или на диаграмме.
Например: На каждый дюйм роста ребенка она прибавляла 1½ фунта.
Шестиклассники учатся использовать пропорции для упрощения отношений.
Например: рецепт кекса требовал 1 чашку сахара на каждые 2 чашки муки, поэтому соотношение сахара и муки 1:2.
Студенты также работают со ставками, которые родственны пропорциям. Если на мойку одной машины уходит 10 минут, то это скорость 6 машин в час. Ставки обозначаются косой чертой 6/1, а соотношения — двоеточием 6:1.
Другой способ описания взаимосвязей — это проценты, которые описываются как доля от 100.
Например: Хэнк купил галлон молока и выпил его кварту. В этом случае галлон равен 100 процентам.
Кварта — это ¼ галлона, поэтому Хэнк выпил 25 процентов молока.
Разделяй дроби и властвуй
Шестиклассники переходят от умножения дробей к делению дробей. Они узнают, что для деления дроби требуется умножение. Кто это придумал, да?
Вот как это работает. У Инес есть 2 ⁄ 3 чашки замороженного йогурта, но она хочет съесть только 1 ⁄ 2 чашки. Вопрос в том, сколько порций по полстакана содержится в чашке 2 ⁄ 3 или что такое 2 ⁄ 3 9.0363 ÷ 1 ⁄ 2 ? Чтобы разделить фракции, вы переворачиваете Divisor (вторая фракция) и умножьте: 2 ⁄ 3 x 2 ⁄ 1 = 4 ⁄ 3 = 1 1 ⁄ 3 = 1 1 ⁄ 3 = 1 1 . Подними себе настроение и пойдем дальше.
Десятичные числа, множители и отрицательные числа
Шестиклассник должен уверенно складывать, вычитать, умножать и делить многозначные десятичные числа, например 43,57 + 0,75 и 238,437 ÷ 35,14.
Дети учатся использовать распределительное свойство для нахождения наибольшего общего делителя двух целых чисел, меньших или равных 100, и наименьших общих кратных двух целых чисел, меньших или равных 12.
Например: Используя распределительное свойство, 88 + 96 записывается как 8 x (11+12). Почему? Потому что наибольший общий делитель чисел 88 и 96 равен 8. 8 х 11 = 88 и 8 х 12 = 96. (И каждая разбивка дает 184.)
Шестиклассники работают как с положительными, так и с отрицательными числами. Они узнают, что 3 и -3 являются противоположностями и что на числовой прямой -3 находится на таком же расстоянии слева от 0, как 3 справа от 0.
Числовая прямая также показывает, что отрицательные числа имеют относительное значение. для другого. Например, -2 больше, чем -4. Подумайте о термометре. Температура -2 градуса чуть-чуть теплее, чем температура -4 градуса.
Выразите себя с помощью предварительной алгебры
Шестой класс — это год, когда ученики действительно начинают алгебру .
Они учатся читать, писать и вычислять алгебраических выражений и уравнений, в которых буква (также называемая переменной) заменяет неизвестное число. Например, они найдут значение X в уравнении X – 32 = 14.
Они будут работать с неизвестными, чтобы решать реальные задачи со словами с одной переменной.
Например: если Стив платит 75 долларов за свитер, который обычно стоит 9 долларов.0, какая скидка в долларах? (90 – y = 75)
Шестиклассники учатся использовать различные правила математики для составления уравнений , которые написаны по-разному, но эквивалентны .
Например: 9x – 3x – 4 эквивалентно 5x + x – 4. Ответ на оба вопроса будет одинаковым, независимо от того, какое число вставлено вместо x.
Ваш шестиклассник также узнает разницу между зависимой переменной и независимой переменной . Независимые переменные не изменяются другими факторами.
В школе с 20 классными комнатами по-прежнему будет 20 классных комнат, независимо от того, приходят ли новые ученики или уходят нынешние ученики. Но бюджет на содержание 20 учителей в этих классах будет меняться в зависимости от таких факторов, как заработная плата, льготы и рост стоимости жизни.
Геометрия
Помните, когда у вас закончились прямоугольные блоки при строительстве замка, вы сложили вместе два треугольника и надеялись, что один из них не развалится и не разрушит конструкцию? Геометрия в шестом классе немного похожа на эту.
В противоположных процессах, известных как составление и разложение , учащиеся соединяют фигуры и разделяют их, чтобы упростить нахождение площади и объема. Они применяют это для решения реальных математических задач.
Например: Рэй хочет посадить сад на Г-образном участке, и ему нужно знать площадь, чтобы купить нужное количество мульчи. Он использует разложение, чтобы разделить странную фигуру на прямоугольник и квадрат.
Теперь он может найти площадь каждой правильной фигуры и сложить их вместе, чтобы найти общую площадь. (8 х 8) + (10 х 24) = 304 квадратных фута.
Шестиклассники учатся находить объем трехмерных фигур с некоторой длиной в дробях путем заполнения их единичными кубами. Они также учатся применять формулы объем = длина x ширина x высота (V = lwh) или объем = основание x высота (v = bh), в зависимости от формы объекта.
Ваш ребенок также научится находить площадь поверхности трехмерных фигур, создавая двухмерные фигуры, называемые «сетками», которые показывают сплющенную форму до того, как она будет сложена в коробку или другую форму.
Например:
Это чистота…… из этого
Три из четырех учителей математики Жопают эти стандарты
Люди подходят в Статистику , особенно когда они просто сильные. Шестиклассники узнают, как должны собираться и анализироваться статистические данные, и что они основаны на изменчивости .