как объяснить ребенку деление в столбик
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3.
То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1.
А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять.
Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок.
Сколько каждый получит яблок, если нужно поделить их одинаково?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг .
Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение ( ), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов.
В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное.
Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ.
Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки.
Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера.
Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения.
Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе.
Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
- То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
- Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом.
Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082: 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой.
Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае.
Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
- Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.
- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится.
Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной.
Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения .
a = b ⋅ c + d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток.
Остаток меньше делителя 6
7⋅36+6=252+6=258
б) Делим столбиком:
1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1
Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873
Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.
Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток.
То есть ближайшее число к делителю. Это число 14.
Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)
Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22
б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107
Задача:
Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?
Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400
Ответ: 30 кусков получиться и 10 см.
проволоки останется.
Как делить десятичные дроби на натуральные числа? Рассмотрим правило и его применение на примерах.
Чтобы разделить десятичную дробь на натуральное число, надо:
1) разделить десятичную дробь на число, не обращая внимания на запятую;
2) когда закончится деление целой части, в частном поставить запятую.
Примеры.
Разделить десятичные дроби:
Чтобы разделить десятичную дробь на натуральное число, делим, не обращая внимания на запятую. 5 на 6 не делится, поэтому в частном ставим нуль. Деление целой части окончено, в частном ставим запятую. Сносим нуль. 50 делим на 6. Берем по 8. 6∙8=48. От 50 вычитаем 48, в остатке получаем 2. Сносим 4. 24 делим на 6. Получаем 4. В остатке — нуль, значит, деление окончено: 5,04: 6 = 0,84.
2) 19,26: 18
Делим десятичную дробь на натуральное число, не обращая внимания на запятую. Делим 19 на 18. Берем по 1. Деление целой части окончено, в частном ставим запятую. Вычитаем от 19 18.
В остатке — 1. Сносим 2. 12 на 18 не делится, в частном пишем нуль. Сносим 6. 126 делим на 18, получаем 7. Деление окончено: 19,26: 18 = 1,07.
Делим 86 на 25. Берем по 3. 25∙3=75. От 86 вычитаем 75. В остатке — 11. Деление целой части окончено, в частном ставим запятую. Сносим 5. Берем по 4. 25∙4=100. От 115 вычитаем 100. Остаток — 15. Сносим нуль. 150 делим на 25. Получаем 6. Деление окончено: 86,5: 25 = 3,46.
4) 0,1547: 17
Нуль на 17 не делится, в частном пишем нуль. Деление целой части окончено, в частном ставим запятую. Сносим 1. 1 на 17 не делится, в частном пишем нуль. Сносим 5. 15 на 17 не делится, в частном пишем нуль. Сносим 4. Делим 154 на 17. Берем по 9. 17∙9=153. От 154 вычитаем 153. В остатке — 1. Сносим 7. Делим 17 на 17. Получаем 1. Деление окончено: 0,1547: 17 = 0,0091.
5) Десятичная дробь может получиться и при делении двух натуральных чисел.
При делении 17 на 4 берем по 4. Деление целой части окончено, в частном ставим запятую. 4∙4=16. От 17 вычитаем 16.
Остаток — 1. Сносим нуль. 10 делим на 4. Берем по 2. 4∙2=8. От 10 вычитаем 8. В остатке — 2. Сносим нуль. 20 делим на 4. Берем по 5. Деление окончено: 17: 4 = 4,25.
И еще пара примеров на деление десятичных дробей на натуральные числа:
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия.
Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.
Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
ДЕЛЕНИЕ ДВУЗНАЧНОГО ЧИСЛА НА ДВУЗНАЧНОЕ — КиберПедия
Образец:
48 : 12 Решаем пример методом подбора.
Пробуем 2 ( 12 • 2 = 24) – не подходит. Пробуем 3 ( 12 • 3 = 36) – не подходит. Пробуем 4 ( 12 • 4 = 48) – подходит.
Значит, 48 : 12 = 4.
1. Реши примеры.
| 39 : 13 | 36 : 12 | 26 : 13 |
| 24 : 12 | 30 : 15 | 28 : 14 |
4. Реши примеры.
| 95 : 19 | 54 : 18 | 42 : 14 |
| 38 : 19 | 60 : 12 | 91 : 13 |
| 70 : 14 | 36 : 18 | 52 : 13 |
5. Реши примеры.
| ||
| 56 : 14 | 78 : 13 | 85 : 17 |
| 65 : 13 | 57 : 19 | 51 : 17 |
| 90 : 15 | 98 : 14 | 72 : 12 |
| 6. Реши примеры. | ||
| 144 : 18 | 171 : 19 | 112 : 14 |
| 84 : 14 | 162 : 18 | 128 : 16 |
| 119 : 17 | 108 : 18 | 104 : 13 |
| 7. Реши примеры. | ||
| 114 : 19 | 126 : 18 | 144 : 16 |
| 72 : 12 | 105 : 15 | 96 : 16 |
| 117 : 13 | 126 : 14 | 96 : 12 |
8. Реши примеры.
| 108 : 12 | 153 : 17 | 133 : 19 |
| 171 : 19 | 36 : 12 | 112 : 14 |
1.
Запиши неравенство.
2. Реши примеры. Над знаком «разделить» надпиши ответы зелёным цветом.
Сравни выражения.
Сравни выражения.
42 : 14 … 44 : 11
45 : 15 … 64 : 16
38 : 19 … 77 : 11
56 : 14 … 42 : 14
Сравни выражения.
84 : 14 … 65 : 13
91 : 13 … 95 : 19
112 : 16 … 72 : 12
84 : 12 … 136 : 17
Сравни выражения.
Сравни выражения.
48 : 16 … 85 : 17
57 : 19 … 76 : 19
28 : 14 … 39 : 13
51 : 17 … 68 : 17
Сравни выражения.
45 : 15 … 80 : 16
95 : 19 … 36 : 12
76 : 19 … 90 : 18
26 : 13 … 48 : 16
Сравни выражения.
78 : 13 … 108 : 12
96 : 12 … 56 : 14
51 : 17 … 84 : 14
90 : 15 … 48 : 12
Сравни выражения.
56 : 14 … 64 : 16
78 : 13 … 91 : 13
ПРОВЕРКА УМНОЖЕНИЯ
1. Запиши пример.
Реши его.
Сделай проверку.
Если произведение разделить на первый множитель, то получится второй множи-тель.
Если произведение разделить на второй множитель, то получится первый множи-тель.
Образец:
27 • 3 =81 Проверка: 81 : 27 = 3
81 : 3 = 27
Вычисли и проверь решение делением.
12 • 7
48 • 2
19 • 4
Вычисли и проверь решение делением.
35 • 2
14 • 5
33 • 3
Вычисли и проверь решение делением.
24 • 4
34 • 2
64 : 4
Вычисли и проверь решение делением.
13 • 3
12 • 6
22 • 3
Вычисли и проверь решение делением.
42 • 2
23 • 2
29 • 2
Вычисли и проверь решение делением.
43 • 2
22 • 4
ПРОВЕРКА ДЕЛЕНИЯ
1. Запиши пример.
Реши его.
Сделай проверку.
Если частное умножить на делитель, то получится делимое.
Если делимое разделить на частное, то получим делитель.
Образец:
84 : 3 = 28 Проверка 28• 3 = 84
84 : 28 = 3
Вычисли и проверь решение.
51 : 17
72 : 4
Вычисли и проверь решение.
72 : 4
64 : 16
48 : 3
Вычисли и проверь решение.
75 : 15
78 : 13
51 : 3
Вычисли и проверь решение.
91 : 13
72 : 6
60 : 12
Вычисли и проверь решение.
56 : 14
95 : 5
64 : 16
Вычисли и проверь решение.
90 : 15
84 : 7
ДЕЛЕНИЕ С ОСТАТКОМ
Рассмотри рисунки.
2. Составь примеры на деление с остатком.
| 10 : 3 = 3 (остаток 1) | остаток | ||||
1. Составь примеры на деление с остатком
и реши их.
3. Составь примеры на деление с остатком
и реши их.
4. Составь примеры на деление с остатком
и реши их.
5. Составь примеры на деление с остатком
и реши их.
1. Запиши пример.
2. Сделай рисунок к каждому примеру.
10 : 3 = 3 (остаток 1)
Остаток
Выполни деление, сделай рисунки.
| 7 : | 10 : 4 | |
| : 5 | 14 : 6 |
Выполни деление, сделай рисунки.
| : 6 | 12 : 5 | |
| 9 : | 13 : 6 |
Выполни деление, сделай рисунки.
| 15 : 2 | 7 : | |
| 11 : 2 | : 9 |
Выполни деление, сделай рисунки.
Выполни деление, сделай рисунки.
| 15 : 4 | 5 : | |
| 17 : 4 | : 2 |
Выполни деление, сделай рисунки.
| 13 : 3 | 9 : | |
| 16 : 5 | : 2 |
Выполни деление, сделай рисунки.
| 14 : 3 | 17 : 5 |
| 13 : 2 | 15 : 7 |
Выполни деление, сделай рисунки.
| 16 : 3 | 19 : 4 |
| 13 : 6 | 18 : 5 |
Выполни деление, сделай рисунки.
| 25 : 4 | 32 : 7 |
| 18 : 7 | 42 : 9 |
Выполни деление, сделай рисунки.
Образец:
10 : 3 = 3 (остаток 1)
Рассуждаем так: 10 без остатка на 3 не де-лится.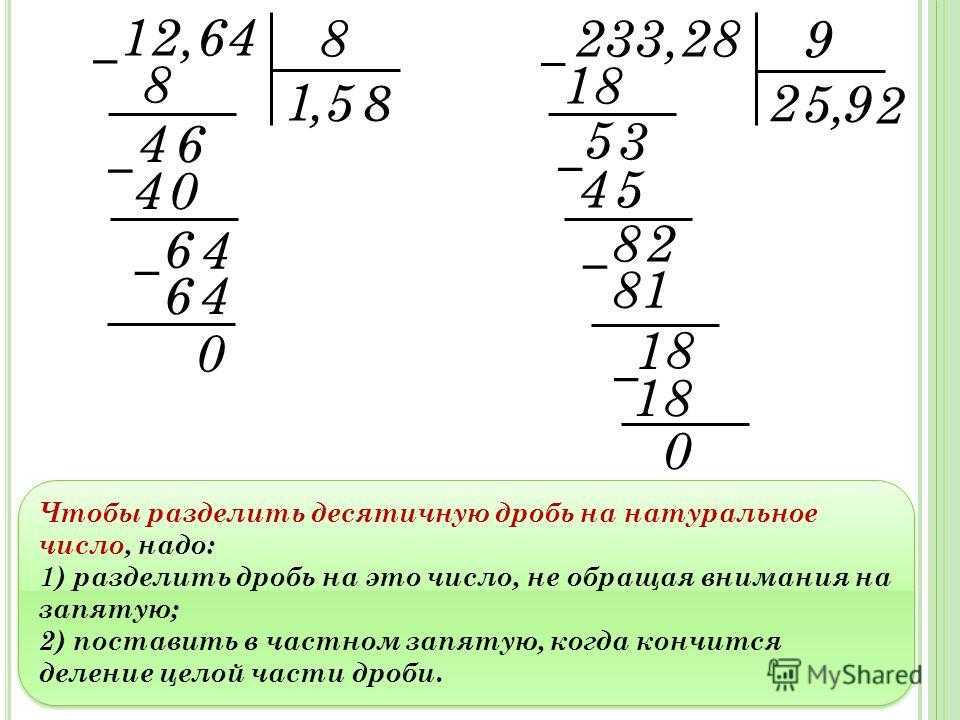
Подберём самое большое число, ко-торое меньше 10 и делится на 3 без остатка. Это число 9.
Делим 9 на 3. 9 : 3 = 3
Получили частное. Находим остаток: 10 – 9 = 1
Выполни деление.
| 26 : 5 | 70 : 8 | 17 : 3 |
| 41 : 5 | 23 : 7 | 32 : 5 |
| 55 : 9 | 19 : 3 | 29 : 8 |
Выполни деление.
| 28 : 9 | 60 : 8 | 52 : 6 |
| 73 : 9 | 48 : 5 | 67 : 9 |
Выполни деление.
| 85 : 9 | 57 : 6 | 19 : 7 |
| 26 : 6 | 13 : 2 | 88 : 9 |
| 22 : 3 | 31 : 8 | 43 : 6 |
6. Выполни деление.
| ||
| 83 : 9 | 32 : 7 | 18 : 7 |
| 49 : 5 | 57 : 9 | 71 : 9 |
| 16 : 6 | 20 : 8 | 41 : 7 |
| 7. Выполни деление. | ||
| 58 : 7 | 33 : 8 | 19 : 3 |
| 26 : 4 | 15 : 6 | 25 : 3 |
| 39 : 6 | 69 : 9 | 75 : 9 |
Выполни деление.
| 15 : 9 | 33 : 5 | 43 : 5 |
| 30 : 4 | 86 : 9 | 26 : 9 |
| 33 : 7 | 87 : 9 | 29 : 6 |
1. Запиши неравенство.
2. Реши примеры. Над знаками «разде-лить» надпиши ответы зелёным цветом.
Сравни выражения.
Сравни выражения.
16 : 5 … 13 : 3
74 : 8 … 10 : 4
56 : 6 … 34 : 8
68 : 9 … 60 : 7
Сравни выражения.
69 : 8 … 16 : 9
17 : 2 … 59 : 9
39 : 5 … 34 : 6
27 : 7 … 28 : 8
Сравни выражения.
Сравни выражения.
43 : 8 … 29 : 9
40 : 7 … 53 : 6
66 : 8 … 57 : 8
60 : 9 … 46 : 5
Сравни выражения.
78 : 8 … 27 : 4
13 : 5 … 22 : 9
48 : 9 … 61 : 7
50 : 6 … 22 : 5
Сравни выражения.
39 : 8 … 19 : 5
22 : 5 … 38 : 4
8 : 3 … 61 : 9
28 : 6 … 52 : 8
Сравни выражения.
21 : 9 … 11 : 4
13 : 6 … 34 : 5
Образец:
10 : 3 = 3 (ост. 1) Проверка 3•3 + 1 = 10
Рассуждаем так: 10 без остатка на 3 не де-лится. Подберём самое большое число, ко-торое меньше 10 и делится на 3 без остатка. Это число 9.
Делим 9 на 3. 9 : 3 = 3
Получили частное. Находим остаток: 10 – 9 = 1
Проверяем: чтобы получить делимое, ум-ножаем частное на делитель и прибавля-ем остаток.
Сколько 12 разделить на 48 с использованием длинного деления?
Запутались в длинном делении? К концу этой статьи вы сможете разделить 12 на 48, используя деление в длинную сторону, и сможете применить ту же технику к любой другой задаче на деление в длинную сторону! Давайте взглянем.
Хотите быстро научиться или показать учащимся, как решить деление числа 12 на 48 с помощью деления в большую сторону? Включи это очень быстрое и веселое видео прямо сейчас!
Итак, первое, что нам нужно сделать, это уточнить термины, чтобы вы знали, что представляет собой каждая часть деления:
- Первое число, 12, называется делимым.
- Второе число 48 называется делителем.
Здесь мы разберем каждый шаг процесса длинного деления на 12, деленное на 48, и объясним каждый из них, чтобы вы точно поняли, что происходит.
12 разделить на 48 пошаговое руководство
Шаг 1
Первый шаг — поставить задачу деления с делителем слева и делимым справа, как показано ниже:
Шаг 2
Мы можем вычислить, что делитель (48) входит в первую цифру делимого (1), 0 раз. Теперь мы это знаем, мы можем положить 0 вверху:
Шаг 3
Если мы умножим делитель на результат на предыдущем шаге (48 x 0 = 0), мы можем теперь добавить этот ответ под делимым:
| 0 | |||||||
| 4 | 8 | 1 | 2 | 0031 | 0 |
Шаг 4
Далее вычтем из второй цифры делимого результат предыдущего шага (1 — 0 = 1) и запишем, что ответ ниже: 3:90
| 0 | |||||||
| 4 | 8 | 1 | 2 | ||||
| — | 0 | ||||||
| 1 |
Step 5
Move the second digit of the dividend (2) down like so:
| 0 | |||||||
| 4 | 8 | 1 | 2 | ||||
| — | 0 | ||||||
| 1 | 2 |
Шаг 6
Делитель (48) входит в нижнее число (12), 0 раз, поэтому мы можем поставить 0 сверху:
| 0 | ||||||||
| 4 | 8 | 1 | 2 | |||||
| — | 0 | |||||||
| 1 | 2 |
Step 7
If we умножив делитель на результат предыдущего шага (48 x 0 = 0), теперь мы можем добавить этот ответ под делимым:
| 0 | 0 | ||||||
| 4 | 8 | 1 | 2 | ||||
| — | 0 | ||||||
| 1 | 2 | ||||||
| 0 |
Шаг 8
Далее, мы подчислим результат от предыдущего шага от третьего шага от DivIND от DivIND от DivIND от DivIND от DivIND от DivIND от DivIND.
) и запишите этот ответ ниже:
| 0 | 0 | ||||||
| 4 | 8 | 1 | 2 | ||||
| — | 0 | ||||||
| 1 | 2 | ||||||
| — | 0 | ||||||
| 1 | 2 |
Итак, чему равно 12 разделить на 48?
Если вы дочитали до этого урока, молодец! Больше не осталось цифр, чтобы двигаться вниз от делимого, а это значит, что мы решили задачу деления в длинную сторону.
Ваш ответ — это верхнее число, а любой остаток будет нижним числом. Итак, для 12, разделенных на 48, окончательное решение:
0
Остаток 12
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали.
Мы очень ценим вашу поддержку!
«Сколько 12 разделить на 48 с использованием длинного деления?». VisualFractions.com . По состоянию на 5 октября 2022 г. http://visualfractions.com/calculator/long-division/what-is-12-divided-by-48-using-long-division/.
«Сколько 12 разделить на 48 с использованием длинного деления?». VisualFractions.com , http://visualfractions.com/calculator/long-division/what-is-12-divided-by-48-using-long-division/. По состоянию на 5 октября 2022 г.
Сколько 12 разделить на 48 с использованием длинного деления?. VisualFractions.com. Получено с http://visualfractions.com/calculator/long-division/what-is-12-divided-by-48-using-long-division/.
Дополнительные вычисления для вас
Теперь вы изучили метод деления 12 на 48, вот несколько других способов, которыми вы можете выполнить вычисления:
- Используя калькулятор, если вы наберете 12, деленное на 48, вы получите 0,25.
- Вы также можете представить 12/48 в виде смешанной дроби: 0 12/48
- Если вы посмотрите на смешанную дробь 0 12/48, вы увидите, что числитель совпадает с остатком (12), знаменатель — это наш первоначальный делитель (48), а целое число — это наш окончательный ответ (0 ).
Калькулятор длинного деления
Введите другую задачу на длинное деление для решения
Следующая задача на длинное деление
Хотите более длинное деление, но не хотите вводить два числа в калькулятор выше? Без проблем. Вот следующая задача, которую вам нужно решить:
Сколько будет 12, разделенное на 49 с помощью деления в длинное число?
Случайные задачи на длинное деление
Если вы добрались до этого конца страницы, значит, вы ДЕЙСТВИТЕЛЬНО любите задачи на длинное деление, а? Ниже приведен набор случайно сгенерированных вычислений для вашего удовольствия от деления в длину:
Сколько будет 973, разделенное на 988 с помощью деления в длину?
Чему равно 798, разделенное на 972 в длинное деление?
Чему равно 377, разделенное на 613 в длинное деление?
Чему равно 737, разделенное на 768 с использованием длинного деления?
Чему равно 880, разделенное на 910 с использованием длинного деления?
Чему равно 446, разделенное на 844 в длинное деление?
Чему равно 20, разделенное на 818 с использованием длинного деления?
Чему равно 295, разделенное на 398 в длинном делении?
Чему равно 889, разделенное на 969 в длинное деление?
Сколько будет 587 разделить на 849?используя длинное деление?
Сколько 114 разделить на 462 в длинное деление?
Сколько 982 разделить на 993 в длинное деление?
Чему равно 342, разделенное на 658 с использованием длинного деления?
Чему равно 671, разделенное на 708 с использованием длинного деления?
Чему равно 246, разделенное на 934 в длинном делении?
Чему равно 787, разделенное на 968 в длинное деление?
Чему равно 757, разделенное на 818 с использованием длинного деления?
Чему равно 39, разделенное на 611 с использованием длинного деления?
Чему равно 755, разделенное на 927 с использованием длинного деления?
Сколько 218 разделить на 438 в длинное деление?
Чему равно 84, разделенное на 585 с использованием длинного деления?
Чему равно 871, разделенное на 964 в длинное деление?
Чему равно 262, разделенное на 737 в длинном делении?
Чему равно 135, разделенное на 540 с использованием длинного деления?
Чему равно 34, разделенное на 294 в длинное деление?
Сколько 58 разделить на 973 в длинное деление?
Сколько 43 разделить на 75 в длинное деление?
Чему равно 58, разделенное на 954 с использованием длинного деления?
Чему равно 466, разделенное на 877 в длинное деление?
Чему равно 630, разделенное на 963 с использованием длинного деления?
Сколько 767 разделить на 888 в длинное деление?
Чему равно 935, разделенное на 956 в длинное деление?
Чему равно 490, разделенное на 607 с использованием длинного деления?
Чему равно 825, разделенное на 974 в длинное деление?
Чему равно 57, разделенное на 707 в длинное деление?
Чему равно 53, разделенное на 685 в длинное деление?
Чему равно 826, разделенное на 875 в длинное деление?
Чему равно 541, разделенное на 859 с использованием длинного деления?
Чему равно 467, разделенное на 917 в длинное деление?
Чему равно 42, разделенное на 649 в длинное деление?
Чему равно 477, разделенное на 550 в длинное деление?
Чему равно 518, разделенное на 993 в длинное деление?
Чему равно 117, разделенное на 663 в длинное деление?
Чему равно 635, разделенное на 719 с использованием длинного деления?
Чему равно 477, разделенное на 627 в длинное деление?
Чему равно 127, разделенное на 314 в длинное деление?
Чему равно 191, разделенное на 454 в длинное деление?
Чему равно 369, разделенное на 703 с использованием длинного деления?
Чему равно 38, разделенное на 815 в длинное деление?
Сколько 11 разделить на 467 в длинное деление?
Чему равно 287, разделенное на 572 в длинное деление?
Сколько 833 разделить на 899 в длинное деление?
Сколько 21 разделить на 412 с помощью деления в большую сторону?
Что такое 892 разделить на 914 с использованием длинного деления?
Чему равно 15, разделенное на 234 с использованием длинного деления?
Чему равно 566, разделенное на 708 с использованием длинного деления?
Чему равно 540, разделенное на 879 с использованием длинного деления?
Чему равно 630, разделенное на 701 с использованием длинного деления?
Чему равно 81, разделенное на 849 в длинное деление?
Сколько 532 разделить на 767 в длинное деление?
Что такое 803, разделенное на 906 с использованием длинного деления?
Сколько будет 263 разделить на 629?используя длинное деление?
Чему равно 171, разделенное на 372 в длинное деление?
Чему равно 215, разделенное на 963 в длинное деление?
Чему равно 561, разделенное на 695 в длинное деление?
Чему равно 157, разделенное на 645 с использованием длинного деления?
Чему равно 717, разделенное на 979 с использованием длинного деления?
Чему равно 30, разделенное на 544 с использованием длинного деления?
Сколько 961 разделить на 972 в длинное деление?
Чему равно 871, разделенное на 928 в длинное деление?
Чему равно 222, разделенное на 948 с использованием длинного деления?
Чему равно 158, разделенное на 337 в длинное деление?
Чему равно 234, разделенное на 835 в длинное деление?
Чему равно 709, разделенное на 842 с использованием длинного деления?
Чему равно 782, разделенное на 833 с использованием длинного деления?
Сколько 173 разделить на 725 в длинное деление?
Чему равно 130, разделенное на 631 в длинное деление?
Сколько 14 разделить на 406 в длинное деление?
Сколько будет 413 разделить на 939 с использованием длинного деления?
Чему равно 983, разделенное на 990 в длинное деление?
Чему равно 402, разделенное на 545 с использованием длинного деления?
Чему равно 890, разделенное на 928 с использованием длинного деления?
Чему равно 452, разделенное на 646 в длинное деление?
Чему равно 922, разделенное на 940 с использованием длинного деления?
Чему равно 812, разделенное на 831 с использованием длинного деления?
Чему равно 793, разделенное на 987 с использованием длинного деления?
Чему равно 721, разделенное на 914 с использованием длинного деления?
Чему равно 321, разделенное на 712 с использованием длинного деления?
Чему равно 701, разделенное на 868 с использованием длинного деления?
Чему равно 562, разделенное на 894 в длинное деление?
Чему равно 181, разделенное на 996 в длинное деление?
Чему равно 945, разделенное на 986 с использованием длинного деления?
Чему равно 518, разделенное на 742 с использованием длинного деления?
Чему равно 335, разделенное на 376 в длинное деление?
Чему равно 327, разделенное на 624 в длинное деление?
Чему равно 60, разделенное на 447 в длинное деление?
Чему равно 64, разделенное на 809 с использованием длинного деления?
Чему равно 771, разделенное на 948 в длинное деление?
Сколько 914 разделить на 971 в длинное деление?
Чему равно 375, разделенное на 663 в длинное деление?
Чему равно 126, разделенное на 309 в длинное деление?
Факторы числа 48 — Найти простые факторизации/Множители числа 48
Факторы числа 48 — это список целых чисел, которые можно без остатка разделить на 48.
48 равны 2 и 3. Факторизация числа 48 равна 2·9.0624 4 × 3.
- Коэффициенты 48: 1, 2, 3, 4, 6, 8, 12, 16, 24 и 48
- Отрицательные коэффициенты 48: -1, -2, -3, -4, -6, -8, -12, -16, -24 и -48
- Простые множители числа 48: 2, 3
- Факторизация числа 48: 2 × 2 × 2 × 2 × 3 = 2 4 × 3
- Сумма коэффициентов 48: 124
| 1. | Какие множители числа 48? |
| 2. | Как рассчитать коэффициенты числа 48? |
| 3. | Советы и рекомендации |
| 4. | Коэффициенты 48 с помощью простой факторизации |
| 5. | Сложные вопросы |
| 6. | Коэффициенты 48 в парах |
| 7. | Важные примечания |
8. | Часто задаваемые вопросы о факторах 48 |
Какие множители числа 48?
Факторы 48 — это числа, которые при умножении дают 48. , мы говорим, что 6 и 8 являются множителями числа 48.
48 также имеет много других множителей, поскольку 6 и 8 сами имеют множители.
Чтобы найти их, вы можете расположить эти числа в массивах следующим образом.
Вы можете расположить 48 в массивах, как указано выше, и найти множители 48.
Как вычислить множители числа 48?
Шаг 1 : Запишите число, которое нужно разложить на множители, т. е. 48.
Это составное число. Это можно учитывать дальше.
Шаг 2 : Найдите два числа, произведение которых дает 48.
2 × 24 = 48. Итак, возьмем 2 и 24 как два множителя.
2 — простое число. Следовательно, он может быть факторизован только как 1 и само число.
1 × 2 = 2
Шаг 3: Поскольку 24 не простое число, давайте разобьем его на множители.
2 × 12 = 24. Итак, возьмем 2 и 12 как два множителя.
Опять же, 2 — простое число.
Шаг 4: Разбейте 12 на множители.
3 × 4 = 12
2 — простое число.
Шаг 5: Разбейте 4 на множители.
2 × 2 = 4
Мы остановимся здесь, так как мы нашли все делители числа 48.
Следовательно, делителей числа 48 равны 1, 2, 3, 4, 6, 8, 12, 16, 24, и 48.
Советы и рекомендации:
- 1 — наименьший делитель каждого числа.
- Каждое число имеет как минимум 2 множителя, то есть 1 и само число.
- Все четные числа всегда имеют 2 в качестве одного из своих множителей.
Исследуйте факторы с помощью иллюстраций и интерактивных примеров.
- Множители 36 — Множители 36 равны 1, 2, 3, 4, 6, 9, 12, 18, 36
- Коэффициенты 24 – множители 24 равны 1, 2, 3, 4, 6, 8, 12, 24
- Множители 15 — Множители 15 равны 1, 3, 5, 15
- Коэффициенты 45 – множители 45 равны 1, 3, 5, 9, 15, 45
- Множители 72 — Множители 72 равны 1, 2, 3, 4, 6, 8, 9 12, 18, 24, 36, 72
- Факторы 49 — множители 49 равны 1, 7, 49
Факторизация числа 48
Если множители числа являются простыми числами, то такие множители называются простыми множителями.
Факторизация простых чисел — это процесс записи числа как произведения его простых множителей.
Множители 48 путем простой факторизации даются с использованием следующих шагов.
Шаг 1: Запишите пару множителей, которые при умножении дают нужное число.
48 можно разложить на множители как произведение 6 и 8.
Шаг 2: Посмотрите на множители, независимо от того, является ли каждый из них простым или нет.
6 не является простым числом и может быть учтено как произведение 2 и 3.
8 не является простым числом и может быть учтено как произведение 2 и 4.
4 не является простым числом и может быть учтено как произведение 2 и 2.
Шаг 3: Согласно критерию,
Таким образом, 48 можно записать как:
.
48 = 6 × 8 = 2 × 3 × 2 × 2 × 2
Это также может быть записано как:
48 = 2 4 × 3 1
Мы также можем найти простые множители с помощью этого метода деления или метода факторного дерева.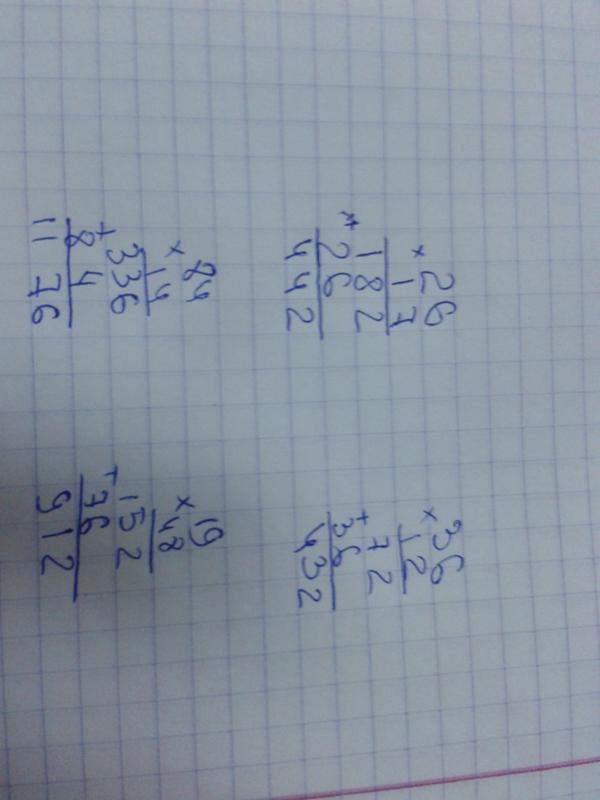
Факторы 48 методом деления
Мы каждый раз делим число таким образом, чтобы делитель был простым числом, как показано ниже.
48 = 2 4 × 3
Факторы 48 по методу факторного дерева
Можете ли вы нарисовать дерево совсем по-другому?
Наконец, вы получите ту же разложение на простые множители, что и 48 = 2 4 × 3 1
Задающие вопросы:
Каковы множители следующих чисел при использовании метода простого разложения?
- 96
- 245
- 6400
Факторы из 48 в парах
Пары факторов находятся в этом радужном методе .
Факторы положительной пары из 48
| Факторы | Парные множители |
|---|---|
| 1 × 48 = 48 | 1, 48 |
| 2 × 24 = 48 | 2, 24 |
| 3 × 16 = 48 | 3, 16 |
| 4 × 12 = 48 | 4, 12 |
| 6 × 8 = 48 | 6, 8 |
Отрицательная пара Факторы 48
| Факторы | Парные множители |
|---|---|
| -1 × -48 = 48 | -1, -48 |
| -2 × -24 = 48 | -2, -24 |
| -3 × -16 = 48 | -3, -16 |
| -4 × -12 = 48 | -4, -12 |
| -6 × -8 = 48 | -6, -8 |
Важные примечания:
- Делителями любого числа являются все возможные делимые числа. Это могут быть простые числа или составные числа.
- Факторы никогда не бывают дробями или десятичными числами.
- Коэффициенты могут быть отрицательными.
Это могут быть простые числа или составные числа.Коэффициенты 48 решенных примеров
Пример 1: Если Кайл тратит 48 часов, чтобы прочитать книгу за 8 дней, найдите, сколько часов она тратит в день?
Решение:
Находим, что 8 × ____ = 48
Теперь найдем недостающий множитель.
Используя факт умножения, мы знаем, что 8 × 6 = 48
Следовательно, Кайл тратит 6 часов в день.
Пример 2: Сможете ли вы найти общие делители чисел 45 и 48?
Решение:
Множители 45 равны 1, 5, 9, 45
Множители 48 равны 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Общий делитель равен 1
Следовательно, общий делитель равен 1.
Пример 3: Помогите Киту найти наибольший общий делитель чисел 18 и 12 путем разложения на простые множители.
Решение:
Запишите простую факторизацию для каждого числа.
18 = 2 × 3 × 3
12 = 2 × 2 × 3
Затем найдите общие делители обоих чисел.
Общие делители равны 2 × 3
Общий множитель равен 6.
Следовательно, наибольший общий делитель 18 и 12 равен 6.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о множителях 48
Что такое множители 48?
Множители числа 48 равны 1, 2, 3, 4, 6, 8, 12, 16, 24, 48, а его отрицательные множители равны -1, -2, -3, -4, -6, -8, — 12, -16, -24, -48.
Какой наибольший общий делитель чисел 48 и 13?
Делители числа 48 равны 1, 2, 3, 4, 6, 8, 12, 16, 24, 48, а делители числа 13 равны 1, 13.
48 и 13 имеют только один общий делитель, равный 1. Отсюда следует что 48 и 13 взаимно просты.
Следовательно, наибольший общий делитель (НОД) чисел 48 и 13 равен 1.
Какова сумма всех делителей числа 48?
Сумма всех множителей 48 = (2 4 + 1 — 1)/(2 — 1) × (3 1 + 1 — 1)/(3 — 1) = 124
Что такое парные множители числа 48?
Парные множители числа 48: (1, 48), (2, 24), (3, 16), (4, 12), (6, 8).
Сколько Факторов 48 также являются общими для Факторов 22?
Так как множители 48 равны 1, 2, 3, 4, 6, 8, 12, 16, 24, 48, а множители 22 равны 1, 2, 11, 22.
Следовательно, [1, 2] являются общими множителями 48 и 22.
Калькулятор дробей
Этот калькулятор дробей выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями.
Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически конвертируются в дроби — т.е. 1.45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|---|---|---|
| + | плюс знак | Дополнение | 1/2 + 1/3 |
| — | Минус. | multiplication | 2/3 * 3/4 |
| × | times sign | multiplication | 2/3 × 5/6 |
| : | division sign | division 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
|
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
Один и два плюс три и пять сотых