Определить строительный объем здания, сооружения, площадь застройки
Расчет объемов работ в строительстве играет важную роль. В проектной документации указывают разные величины, например, отапливаемый объем, общую площадь, жилую площадь и так далее. Как найти строительный объем здания, что это такое и зачем нужен показатель:
Общий строительный объем здания — что это такоеПравила подсчета показателя прописаны в СНиП 31-06-2009 года, а точнее — в их актуализированной редакции, СП 118.13330.2012 . В документе указано, что строительный объем здания определяется как сумма строительного объема выше отметки 0.00 — надземная часть — и ниже этой отметки — подземная часть. То есть величина — объем подземной и надземной части вместе. При этом учитываются все помещения — как жилые, так и нежилые, а фундамент не входит в формулы.
Строительный объем зданий указывают в кубических метрах. При подсчете полученные значения округляют до 1 м3. Например, если в результате получится цифра 4200,13 м3, то в проектной документации будет отражено значение 4200 м3.
Высота здания. Расстояние от проектной отметки земли до наивысшей точки отметки конструктивного элемента здания — например, конька или фронтона для скатных крыш.
Длина здания. Расстояние от одного торца здания до другого с учетом внешней отделки стен. В ряде случаев нужна внутренняя длина стен — ее измеряют от одного угла внешней стены до другого, без учета толщины внешних стен и отделки.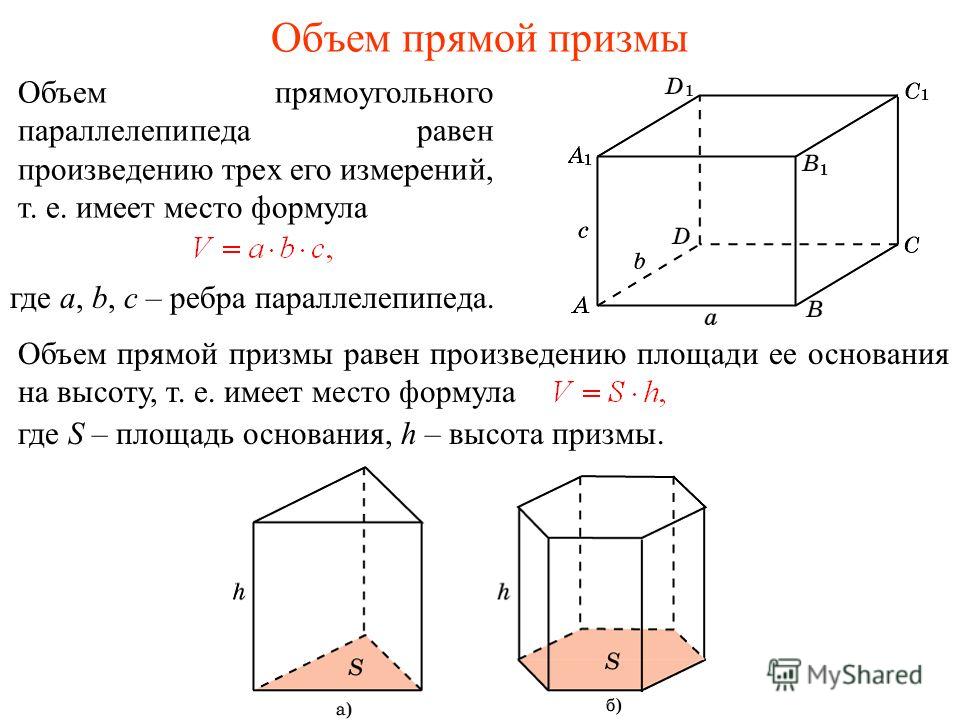
Общая площадь. Сумма площадей всех этажей, а также галерей, антресолей, веранд и других помещений, конструкций. Также в значение включают площадь открытых неотапливаемых планировочных элементов — например, наружных тамбуров или открытых лоджий.
Площадь застройки. Площадь горизонтального сечения по внешнему обводу здания по цоколю с учетом разных выступающих элементов, например, ступеней. Проезды под домом, площадь под ним, если здание расположено на столбах, выступающие элементы на уровне менее 4,5 м тоже включаются в площадь застройки. Если часть здания консольно выступает за пределы стены на высоте более 4,5 м, ее не учитывают.
Как считается строительный объем здания: основные правила
Самый простой способ узнать ориентировочный строительный объем — это умножить площадь застройки на высоту здания. Точное значение площади застройки можно посмотреть в технических документах, проектной декларации.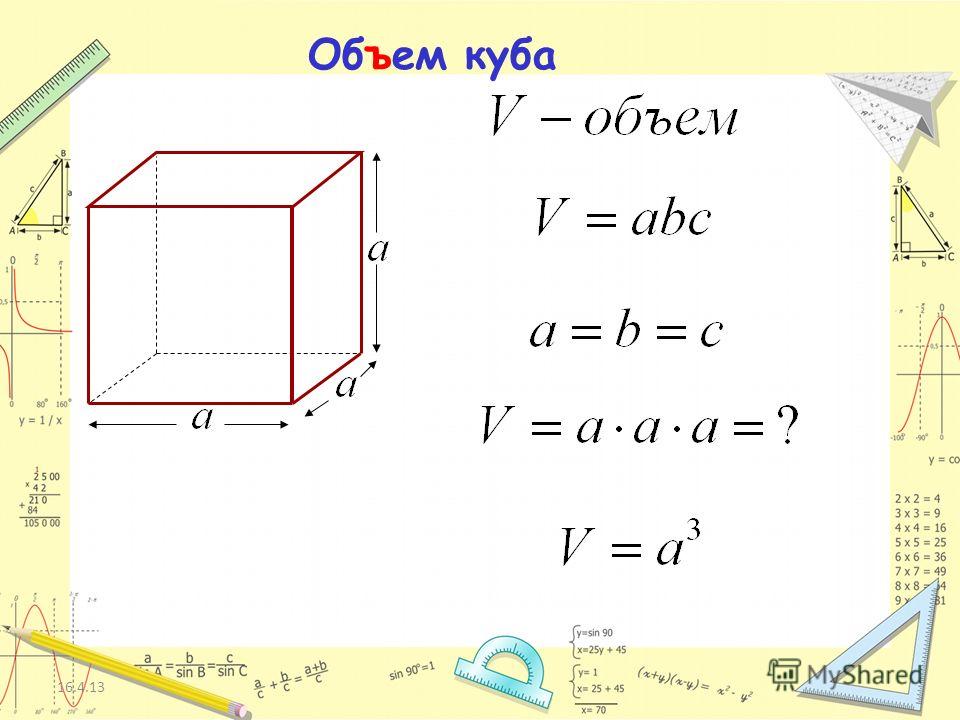 Если ее нет, можно использовать простую формулу: длину дома умножить на его ширину.
Если ее нет, можно использовать простую формулу: длину дома умножить на его ширину.
Например, есть рулетка для измерения длины, ширины и высоты здания. В результате измерений получились следующие данные:
- высота — 3,4 м;
- длина — 13 м;
- ширина — 8 м.
Сначала перемножаем длину и ширину, получаем площадь — 104 м3. Полученное значение умножаем на высоту: 3,4 м. Получаем 353,6 м3, округляем значение до 1 м3 и получаем строительный объем 353 м3.
Полученное значение далеко от реального результата, потому что не учитывает подземную часть, толщину перекрытий, толщину стен, индивидуальные особенности проектировки. Метод подсчета не соответствует требованиям к определению строительного объема, поэтому его нельзя использовать в проектной документации.
Более точный расчет строительного объемаПосчитать строительный объем дома точнее без специальных знаний и навыков помогут поправочные коэффициенты. В этом случае формула будет выглядеть так:
X = S1 x (h + 0,2) x 1,2,
где 0,2 и 1,2 — поправочные коэффициенты, S1 — общая площадь, а h — высота здания.
Как считать общую площадь здания, если она не указана в технической документации? Нужно найти площадь отдельно для каждого помещения, а потом сложить значения. Например, в доме есть 5 комнат площадью 10, 15, 10, 25 и 5 м2. Суммарная площадь составит 65 м2.
После того, как нашли площадь, нужно измерить или посмотреть высоту — допустим, она составляет 4,5 м. Добавляем к полученному значению 0,2 — примерную толщину перекрытий, получаем 4,7 м.
Теперь нужно перемножить полученные значения и умножить их на 1,2 — коэффициент перехода внутренней площади здания к внешней.
65 м2 x 4,7 м x 1,2 = 306,7 или 307 м3.
Этот способ расчета более достоверный по сравнению с первым, но тоже не дает точных результатов. Он не учитывает индивидуальные конструктивные особенности здания: толщину перекрытий и стен. Зато позволяет быстро посчитать строительный объем для зданий необычной формы — например, многоугольной.
Дома с подземной частью
Если в доме есть подвал, технический этаж или другие помещения под землей, нужно отдельно посчитать строительный объем подземной части здания и наземной, а потом сложить полученные значения.
Для определения объема подземной части нужно знать площадь застройки или площадь горизонтального сечения подвала. Например, для подвала правильной прямоугольной формы площадь горизонтального сечения можно легко найти: нужно умножить длину на ширину. Например, длина составляет 23 м, ширина — 10 м. Площадь застройки или сечения дальне нужно умножить на высоту — ее измеряют от уровня пола подвала до пола первого этажа. Например, она составляет 3 м. Перемножаем площадь 230 м? на высоту 3 м и получаем объем 690 м?.
Чтобы определить объем надземной части, тоже нужно выяснить площадь горизонтального сечения и высоту. Сечение измеряем по внешней части здания. Например, длина составляет 23,6 м, ширина — 10,3 м. Высоту измеряем от пола первого этажа до начала теплоизоляционного слоя чердачного помещения, а если крыша плоская — до середины чердака. Допустим, она составила 13 м. Точно также находим площадь — она составила 243,08 м2 — и умножаем ее на высоту. Получаем 3160,04 м3, или округленные 3160 м3.
Полученные значения складываем: прибавляем 690 м3 к 3160 м3 и получаем общий строительный объем: 3850 м3.
Здания без подвала
Если в доме нет подземной части, то строительный объем считается только по надземной части. Посчитать его можно по предыдущей формуле: находим сначала площадь горизонтального сечения, а затем умножаем ее на высоту.
Чтобы определить площадь поперечного сечения, тоже нужно проводить измерение по внешней части здания, с учетом штукатурки и облицовки. Если форма здания сложная, можно условно поделить его на отдельные геометрические фигуры. Например, если два параллельно расположенных здания соединены переходом в форме буквы «Н», можно рассчитать площадь отдельно каждого прямоугольника, а затем суммировать их и умножить на высоту.
Например, длина двух параллельных зданий — 30 м, их ширина — 15 м. Размеры перехода — 2,5 на 6 м. Значит, сначала нужно найти площадь одинаковых зданий: умножаем 15 на 30, получаем 450 м2. Площадь перехода — 15 м2. Складываем три площади: 450 + 450 + 15, получается 915 м2. Если высота здания составляет 3 м, то строительный объем будет 2745 м3.
Складываем три площади: 450 + 450 + 15, получается 915 м2. Если высота здания составляет 3 м, то строительный объем будет 2745 м3.
Здания с чердачными перекрытиями
Если в здании есть чердачное перекрытие, то строительный объем надземной части считают по особой формуле:
X = S1 x h.
В этом случае под S1 понимают площадь горизонтального сечения здания. Ее измеряют на уровне первого этажа выше цоколя, по внешнему обводу здания. Чтобы найти площадь, нужно также умножить ширину на длину здания, как и в расчетах по другим формулам.
Высоту h измеряют от верха чистого пола на первом этаже до верха засыпки чердачного перекрытия.
Допустим, площадь горизонтального сечения здания на уровне первого этажа составляет 420 м2. Высота составляет 25 м. В этом случае строительный объем будет равен 10500 м3.
Если у здания есть поздемная часть, ее объем считают так же, как и в предыдущих случаях, а затем оба значения складывают.
Дома без чердачного перекрытия
Строительный объем надземной части зданий без чердачных перекрытий считают по другой формуле:
X = S2 x L
S2 — тоже площадь поперечного сечения, но не горизонтального, а вертикального. Ее измеряют по наружным стенам, тоже с учетом слоя штукатурки и облицовки. В этом случае для определения площади нужна высота здания и его ширина.
Ее измеряют по наружным стенам, тоже с учетом слоя штукатурки и облицовки. В этом случае для определения площади нужна высота здания и его ширина.
L — это длина здания, перпендикулярная прямая относительно вертикального поперечного сечения. Ее измеряют от одного торца здания к другому, тоже с учетом штукатурки и облицовки, на уровне первого этажа либо цоколя.
Например, нужно рассчитать объем здания высотой 6 м, длиной 23 м и шириной 4 м. Площадь вертикального поперечного сечения в этом случае составит 24 м2, а строительный объем — 552 м3.
Если у здания есть подземная часть, ее также считают отдельно, а потом полученные значения суммируют.
Если известна общая площадь
Детальные данные, например, длину, высоту до определенных перекрытий и другие, не всегда указывают в технической документации. Поэтому строительный объем можно посчитать по другим формулам.
Если известна общая площадь, можно использовать формулу:
X = S x H x К
В этом случае S — сумма площадей всех этажей, или общая площадь. Ее измеряют по внутренней обводке наружных стен, то есть не учитывается их толщина. Кроме того, замеряют также площадь подвала, поэтому отдельных расчетов для подземной части не нужно.
Ее измеряют по внутренней обводке наружных стен, то есть не учитывается их толщина. Кроме того, замеряют также площадь подвала, поэтому отдельных расчетов для подземной части не нужно.
H в формуле — высота здания изнутри без учета перекрытий, так называемая высота в свету.
К — поправочный коэффициент, который учитывает толщину стен. Для жилых зданий он составляет 0,8.
То есть для расчета нужно знать всего два точных значения: общую площадь и высоту в свету. Допустим, площадь составляет 2 000 м2, а высота в свету — 15 м. В этом случае показатель составит 24000 м3 с учетом поправочного коэффициента.
Если известна площадь застройки
Если известна площадь застройки, можно использовать другую формулу. В ней больше переменных, и выглядит она так:
X = S1 x h2 + S2 x h3
S1 в этом случае — площадь общей застройки. Ее можно найти, представив здание в виде геометрической фигуры или нескольких таких фигур, если постройка сложной формы. h2 — высота дома, в которой можно не учитывать выступающие части крыши.
S2 и h3 — площадь и высота подвала соответственно. Площадь замеряют по внутренней обводке стен. Высоту — от верхней точки пола подвала до пола первого этажа.
Дома с мансардамиМансарда — этаж в чердачном пространстве, фасад которого частично либо полностью образован поверхностями наклонной крыши. Обязательное условие — линия пересечения плоскости крыши и фасада должна находиться не больше, чем на высоте 1,5 м от уровня пола в мансарде. Согласно нормативам, строительный объем мансарды считается отдельно.
Чтобы найти строительный объем мансарды, нужно умножить площадь ее поперечного вертикального сечения на длину дома.
Ширину и высоту нужно измерять по внешнему обводу, вертикаль — до начала перекрытий. Все эти данные понадобятся для того, чтобы найти площадь вертикального сечения. Она равна половине произведения ширины, то есть основания, на высоту. Например, высота мансарды — 1,5 м, ширина, то есть основание — 6 м. Тогда площадь составит 9 м2.
Полученное значение нужно умножить на длину дома. Например, она составляет 12 м. В этом случае строительный объем мансарды составит 108 м3.
Например, она составляет 12 м. В этом случае строительный объем мансарды составит 108 м3.
Оставшуюся надземную часть нужно считать по предыдущим формулам, но высоту измерять до начала основания мансарды, то есть до верхнего перекрытия. Объемы мансарды, надземной и подземной частей нужно просто сложить.
Если здание имеет сложную форму
Расчет строительного объема для зданий сложной формы — например, с мезонинами, башенками и различными пристроями — намного сложнее. В этом случае нужно сначала найти строительный объем каждого конструктивного элемента, а потом сложить полученные значения.
Полная формула расчета строительного объема зависит от исходных данных — есть ли подвал, предусмотрены ли чердачные перекрытия, построена ли мансарда. Чтобы получить точное значение, нужно провести тщательные замеры и использовать сложные схемы подсчета.
Формула вычисления объёма и площади прямоугольника
Форма объекта и его линейные размеры определяют один из важных с геометрической точки зрения параметров — объём. Формула для прямоугольника, позволяющая его вычислить, довольно проста и основана на знании стороны и высоты. Но при решении не всегда известны значения рёбер фигуры, поэтому приходится использовать свойства параллелограмма, а именно — способы нахождения площади.
Формула для прямоугольника, позволяющая его вычислить, довольно проста и основана на знании стороны и высоты. Но при решении не всегда известны значения рёбер фигуры, поэтому приходится использовать свойства параллелограмма, а именно — способы нахождения площади.
Общие сведения
По своей сути объём является количественной характеристикой пространства, которое занимает тело или вещество. Простыми словами, этот параметр показывает вместимость. В качестве единицы измерения, согласно СИ, принят кубический метр. За обозначение же объёма взята латинская буква V.
У тел, имеющих простую форму, характеристики находятся путём перемножения площади на высоту. Например, для куба он равен a3, прямоугольной призмы — h * b * a, пирамиды — (S * b * h) / 3. В эллипсоидных фигурах при расчётах используется радиус. Так, для конуса объём равен (p * R2 * h) / 3, сферы — (4 * p * R3) / 3, тора — 2 * p2 * R1 * R22.
Объём плоских фигур, таких как треугольник, круг, квадрат, прямоугольник, равен нулю. Но если их стороны или окружности имеют связанные с ними попарно параллельные линии, то они уже являются объёмными фигурами. Например, прямоугольник в пространстве называют параллелепипедом. Таким образом, чтобы найти объём прямоугольника, необходимо, чтобы он представлял собой прямоугольный параллелепипед, иначе действие будет бессмысленным.
Но если их стороны или окружности имеют связанные с ними попарно параллельные линии, то они уже являются объёмными фигурами. Например, прямоугольник в пространстве называют параллелепипедом. Таким образом, чтобы найти объём прямоугольника, необходимо, чтобы он представлял собой прямоугольный параллелепипед, иначе действие будет бессмысленным.
Определить объём — значит, знать две основные величины фигуры:
- площадь — двумерная характеристика, определяющая размер фигуры,
- высоту — это длина перпендикуляра, опущенного из вершины на основание в трёхмерном пространстве.
Так как площадь измеряется в метрах квадратных, а высота просто в метрах, то перемножение площади и высоты как раз и даст единицу измерения объёма — метр кубический.
Решение задач
На самом деле вычисление объёма не только выполняют на уроках математики. Это знание востребовано в довольно многих специальностях и науках. Например, при строительстве, в архитектуре, инженерии, физике, химии. Поэтому знание нахождения параметра может пригодиться не только в школе. Теорию обязательно необходимо закреплять на практике. Вот некоторые задачи, которые помогут усвоить рассматриваемый материал:
Поэтому знание нахождения параметра может пригодиться не только в школе. Теорию обязательно необходимо закреплять на практике. Вот некоторые задачи, которые помогут усвоить рассматриваемый материал:
- Пусть есть параллелепипед с прямыми сторонами. Его рёбра у основания равняются 19 и 20 сантиметрам. Размер же боковой грани составляет 10 сантиметров. Вычислить объём фигуры. Эта задача на одну формулу, все данные для подстановки в неё известны. Так, V = a * b * c = 19 * 20 * 10 = 3 800 см3 = 0,0038 м³.
- Пусть имеется параллелепипед с основанием 1 см на 1,2 см и высотой 0,8 см. Из него был удалено другое прямоугольное тело с размерами 0,3 x 0,55 x 0,5. Найти объём получившейся фигуры. Так как искомый параметр новой фигуры равен разнице изначального и удалённого объёмов, то зная формулу найти ответ не составит труда: V = 0,8 * 1 * 1,2 — 0,3 * 0,5 * 0,55 = 0,877 см3.
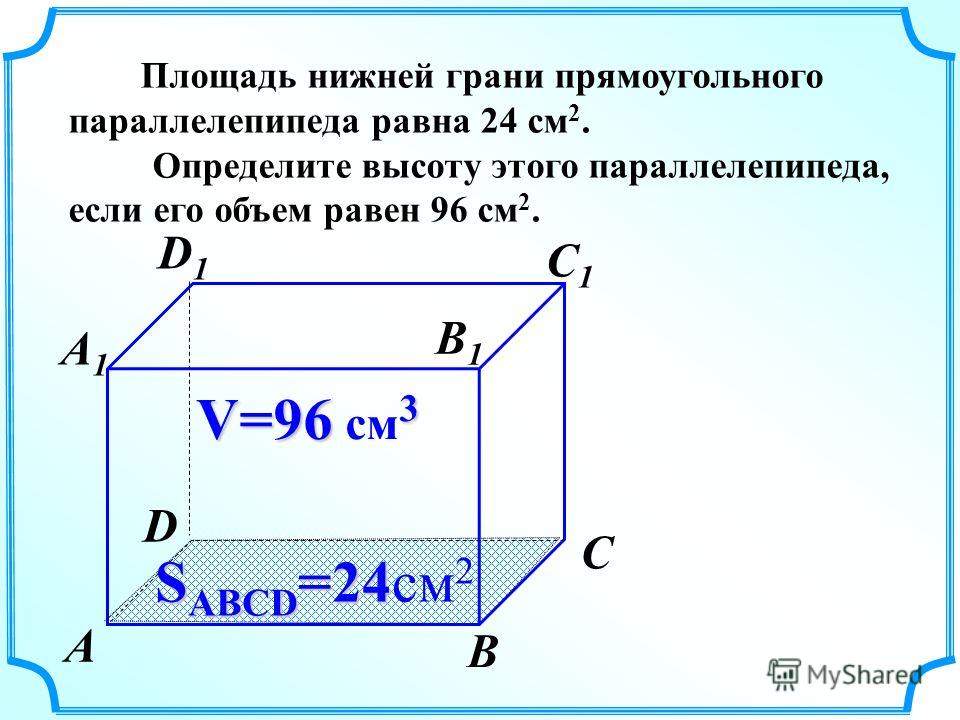
- Дан прямоугольный параллелепипед с вершинами ABCD и A1B1C1D1. Сравнить объём образованного в середине пирамиды AA1BD тела со значением фигуры.
 Для удобства решения стороны AB, AD, AA соответственно можно обозначить как x, y, z. Тогда объём прямоугольного тела будет равен Vп = Sп * AA1 = x * y * z. Если начертить условие на рисунке, то можно отметить, что площадь пирамиды вполовину меньше площади основания прямоугольника. То есть, Sabd = 0,5 * Sabd. Тогда V = Sabd * AA1 / 3 = x * y * z / 3 * 2 = x * y* z / 6. Значит, объём вписанной пирамиды меньше в шесть раз чем у фигуры.
Для удобства решения стороны AB, AD, AA соответственно можно обозначить как x, y, z. Тогда объём прямоугольного тела будет равен Vп = Sп * AA1 = x * y * z. Если начертить условие на рисунке, то можно отметить, что площадь пирамиды вполовину меньше площади основания прямоугольника. То есть, Sabd = 0,5 * Sabd. Тогда V = Sabd * AA1 / 3 = x * y * z / 3 * 2 = x * y* z / 6. Значит, объём вписанной пирамиды меньше в шесть раз чем у фигуры. - В гальванической ванне помещается три тысячи литров раствора. Высота наполнения ёмкости при этом достигает 75 сантиметров. В ванную поместили заготовку, после чего уровень поднялся на два сантиметра. Найти объём заготовки в метрах кубических. Итак, в одном кубическом метре содержится тысяча литров. Поэтому изначально в ёмкости было 3 м³ раствора. Значит, изначально в ванне раствор занимал: 3 = S * 75. Отсюда s = 3/75 = 1/25 см2. Объём детали составляет: V = S * 2 = (1/25) * 2 = 2 / 25 = 0,08 м³.
Использование калькулятора
Конечно же, на обычном калькуляторе объём прямоугольника не подсчитаешь. Разве что известны три его грани и формула нахождения параметра. Тогда нужно будет просто перемножить три числа. В других же случаях, когда нужно решить сложную задачу, связанную с громоздкими вычислениями, можно использовать математические сайты, имеющие название онлайн-калькуляторы.
Разве что известны три его грани и формула нахождения параметра. Тогда нужно будет просто перемножить три числа. В других же случаях, когда нужно решить сложную задачу, связанную с громоздкими вычислениями, можно использовать математические сайты, имеющие название онлайн-калькуляторы.
Это интернет-сервисы, предлагающие своим пользователям бесплатно воспользоваться услугами по вычислению объёма геометрических фигур и выполнить другие математические операции. Для того чтобы воспользоваться сайтами-решателями, нужно иметь любой гаджет с возможностью подключения его к интернету и установленным на него веб-обозревателем.
После загрузки онлайн-калькулятора все действия пользователя сводятся к заполнению специальной формы в которую вносится условие задания. Конечно же, такое решение не может называться самостоятельным, но для проверки полученного результата или выявления ошибок в расчёте подходит идеально. Кроме, непосредственно автоматического вычисления объёма большинство сайтов содержат на своих страницах теоретический материал, а также примеры решений типовых заданий. Так что при обучении учащихся их использование на первых порах вполне оправданно.
Так что при обучении учащихся их использование на первых порах вполне оправданно.
Как найти объём цилиндра зная площадь осевого сечения цил… -reshimne.ru
Новые вопросы
Ответы
Объем цилиндра равен произведению площади основания на высоту.
Диаметр основания = S сеч : h r= (S сеч : h)/2
Площадь основания = πr²=π(S сеч : h)/2)²
Объём цилиндра = h*π(S сеч : h)/2)²
Похожие вопросы
На рис. 68 BE=12см, AE=6, CE=2, DE=18. Докажите подобие треугольников ABE и DCE и найти отношение S₁:S₂….
Даю 44б. Помогите пожалуйста. Если мы возьмем произвольную точку в окружности, сможем ли мы построить диаметр?? Или это правильно только с центром окружности?…
Доказать: Треугольки ABO и СDO подобны.
Через вершину угла В прямоугольного треугольника АВС, катеты которого СВ = 3см и АС = 4см, проведено перпендикуляр ВМ к плоскости треугольника. Найдите расстояние от точки М до вершины А, если ВМ — 12см…
Точки М и Р лежат соответственно на сторонах АВ и ВС треугольника АВС, АВ • РВ = СВ • МВ. Докажите, что МР // АС. Помогите пожалуйста….
Помогите срочно!! В равнобедренном треугольнике основание меньше боковой стороны на 7 см, найдите длину боковой стороны, если перемиметр треугольника равен 62 см….
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Творческий проект для классов К-8
|
- 1869 Задача вступительного теста MIT
- Проблема «3N+1»
- Корзина, полная яиц
- Геометрическое доказательство теоремы Пифагора 9 «вырезать и вставить»0022
- Проблема для Молодые и старые ученики
- Проблема от русского Математическая олимпиада
- Доказательство Пифагора теорема с использованием подобных треугольников
- Головоломка с целыми числами от одного до шестнадцати
- Головоломка с номером 1089
- «Струнный рисунок», который мы можем нарисовать: ромб внутри шестиугольника
- Трехсторонний кот для рисования
- Путешественник на сетке 6 на 6
- Дополнительная плата
- Прибавление в детском саду и первый класс
- Арифметическое чудо из 1899 года
- Старый купец и его четверо детей
- Древний узел
- Анимации на TI
- Углы треугольника: геометрическое свойство посредством складывания бумаги
- Районы и границы
- Площадь и Периметр
- Арифметика с манипуляциями
- Средний балл за тест
- Мяч в коробке
- Банан
- Бочки, Бочки и другие фигурные контейнеры
- Большие числа АКА Зерна риса на шахматная доска
- Блочные дома
- Сборка собачьей будки в масштабе
- Создание ящика со скелетом в соответствии с к Спецификации
- Свечи
- Корзины для конфет
- Емкость
- Наутилус с камерой
- Проверка, является ли число простым номер
- Коробка с китайским календарем
- Хорды по кругу
- Круг, квадрат и треугольник
- Часы и время
- Монеты
- Раскрашивание линий в шестиугольнике
- Красочный Треугольники
- Конгруэнтность Треугольники
- Подсчет
- Счетная доска для детей учащиеся
- Счет до 100
- Бумага для биговки По кривым
- Кубики
- Куб со срезанным краем
- Кухня полоски
- Вырезание прямоугольника
- Вырезание треугольника
- Разрезание треугольника на две части куски равной площади и равного периметра
- Вырезание равностороннего треугольника
- Резка многогранников
- Цилиндр и конус одинаковой высоты и диаметра основания
- Вывод формулы для площадь треугольника
- Диагональ площади
- Разделение квадрата
- Деление с остатком на ТИ-108: Два экземпляра
- Собаки, кошки и мыши
- Точка за точкой
- Удвоение и деление пополам
- Чертеж прямоугольник
- Рисование простой фигуры из устных указаний
- Рисование треугольников
- Легкие квадраты
- Яичная дилемма (Часть 1)
- Возведение в степень
- Факторинг
- фантазии Конверты
- Нахождение дроби между двумя дроби
- Пятиконечный 3D Звезда
- переворачивание монеты
- Сложенный бумажный цветок С шестью лепестками
- Четыре жука
- Четыре карты
- Четыре кубика
- От миллиарда до нуля
- От одного до одного триллиона
- Игра кругов и звезд
- Игра в десятки
- Гигантская энчилада
- Шапка для Хэллоуина
- Орел или решка?
- Шестиугольная головоломка
- Праздник Орнамент
- Лошадь на продажу
- Как работает Калькулятор Вычислить квадратный корень из числа?
- Сколько пентамино?
- Сколько клеток на шахматной доске?
- Сколько треугольников? (Части 1 и 2)
- Сколько треугольников в этом треугольнике?
- Как измерить угол без транспортира
- Как превратить прямоугольник в другой прямоугольник
- Гиперболы и Эллипсы
- Я могу угадать твой возраст!
- Я могу угадать ваш возраст и номер дома!
- Невозможный объект
- Вписанный треугольник
- Проценты
- Введение в измерения (первый класс)
- Неправильные многоугольники
- Юлекурв АКА Валентайн Корзина
- Прыжок: игра в пасьянс с десятью жетонами
- Воздушные змеи
- Умножение решетки
- Дырявая крыша
- Ушастые твари
- Волшебные бобы
- Волшебный складной кубик
- Магический квадрат
- Создание животных Режущие полигональные пазлы
- Создание блоков из четырех Кубики
- Изготовление коробок
- Изготовление эвольвенты
- Лабиринт
- Мини-слот-машина
- Луны
- Больше задач «точка-точка»
- Больше старых словесных задач
- Умножения «Готово по Адаму Рису»
- Натан подбрасывает монету 20 раз
- Игра в числа с Кости
- Головоломка с числами
- Воля старого пастуха
- Олимпийские кольца
- Одна треть
- Покраска домов (и другие «рабочие» задачи)
- Парадокс средних
- Разделение квадрата
- Пентагон Пазлы
- Алгебра телефонных номеров
- Копилка
- Игра с формами
- Powerball 55
- Красивая подарочная коробка
- Простые числа: сито Эратосфена
- Свойства коробки
- Тыквы
- Пазл с камешками
- Пирамида на четверти
- Пирамида из кубиков
- Пирамида из мрамора
- Четырехугольники
- Прямоугольники
- Правильные многоугольники с равными Районы
- Связанные проблемы
- Прямоугольный треугольник
- Последовательности составных номера: конкурс
- Фигуры цифр
- Формы чисел с использованием треугольники
- Делиться хлебом
- Овца: Старая головоломка
- Шесть пирамид
- Шестнадцать Квадратные дюймы
- Печать Соломона
- Сортировочная игра
- Спираль (марки К-4)
- Спираль (5-8 классы)
- Спираль Феодора на Калькуляторе ТИ-83/84
- Квадратные и кубические единицы
- Квадрат в треугольнике
- Соломенные многогранники
- Алгоритм вычитания
- Вычитание со счетчиками
- Сумма всех 100 чисел в таблице умножения
- Сумма первых N целых чисел
- Сумма двух квадратов
- Выживший на шестиугольном острове
- Татами
- Чайные коробки
- Преобразование температуры
- Мозаика круга
- Задача о лестнице и ящике
- Сыр «Смеющаяся корова» Клиновые контейнеры
- Практическая ценность Доказательства
- Рейнберд Зуни
- Три четверти
- Круг из трех частей Пазл
- Бросание одного кубика
- Треугольник в квадрат: A шарнирный разборный
- Превращение прямоугольника в квадрат путем вскрытия
- Двенадцать простых фигур
- Двадцать четыре кубика
- Две старые проблемы
- Два брата-пастуха
- Понимание Длинная дивизия
- Необычный Контейнеры
- Что дальше?
- Что это за прямоугольник?
- Инь Ян
Отрыв
| Примечания | Кредиты
| Альбом | НМСУ
Курсы для учителей | Контакт
США
последнее изменение:
2 февраля 2022 г.
Объем прямоугольной призмы – формула, определение, примеры
Объем прямоугольной призмы – это измерение всего пространства внутри нее. Представьте себе прямоугольный сосуд, наполненный водой. В этом случае общее количество воды, которое может вместить контейнер, является его объемом. Призма – это многогранник с одинаковыми основаниями, плоскими прямоугольными боковыми гранями и одинаковым поперечным сечением по всей длине. Призмы классифицируются по форме основания. Прямоугольная призма классифицируется как трехмерная форма. У него шесть граней, и все грани призмы — прямоугольники. Давайте узнаем формулу, чтобы найти объем прямоугольной призмы в этой статье.
| 1. | Каков объем прямоугольной призмы? |
| 2. | Объем прямоугольной призмы Формула |
| 3. | Как найти объем прямоугольной призмы? |
| 4. | Часто задаваемые вопросы о прямоугольной призме |
Каков объем прямоугольной призмы?
Объем прямоугольной призмы определяется как пространство, занимаемое внутри прямоугольной призмы. Прямоугольная призма – это многогранник, имеющий две пары конгруэнтных и параллельных оснований. У него 6 граней (все прямоугольные), 12 сторон и 8 вершин. Поскольку прямоугольная призма представляет собой трехмерную форму (трехмерную форму), единицей измерения объема прямоугольной призмы является см 3 , м 3 и так далее. В математике любой многогранник, обладающий всеми такими характеристиками, может называться прямоугольным параллелепипедом.
Прямоугольная призма – это многогранник, имеющий две пары конгруэнтных и параллельных оснований. У него 6 граней (все прямоугольные), 12 сторон и 8 вершин. Поскольку прямоугольная призма представляет собой трехмерную форму (трехмерную форму), единицей измерения объема прямоугольной призмы является см 3 , м 3 и так далее. В математике любой многогранник, обладающий всеми такими характеристиками, может называться прямоугольным параллелепипедом.
Объем прямоугольной призмы Формула
Формула объема прямоугольной призмы = площадь основания × высота призмы. Поскольку основание прямоугольной призмы — прямоугольник, его площадь будет равна l × w. Затем эту площадь умножают на высоту призмы, чтобы получить объем призмы. Поэтому другой способ выразить эту формулу — умножить длину, ширину и высоту призмы и записать значение в кубических единицах (см 3 , м 3 , в 3 и т.д.).
Следовательно, формула для объема прямоугольной призмы: объем прямоугольной призмы (V) = l × w × h
, , где- «l» — длина основания
- «w» — ширина основания
- «h» — высота призмы
Чтобы найти объем прямоугольной призмы, мы умножаем длину, ширину и высоту, то есть площадь основания умножаем на высоту. Следует отметить, что объем измеряется в кубических единицах.
Следует отметить, что объем измеряется в кубических единицах.
Существует два типа прямоугольных призм — прямые прямоугольные призмы и наклонные призмы.
- Основания прямоугольной призмы перпендикулярны другим граням.
- В случае наклонной прямоугольной призмы основания не перпендикулярны другим граням. Таким образом, за ее высоту будет принят перпендикуляр, проведенный из вершины одного основания к другому основанию призмы.
Следует отметить, что мы можем применить одну и ту же формулу для расчета объема призмы, то есть формулу объема прямоугольной призмы, v = lwh, независимо от типа прямоугольной призмы.
Как найти объем прямоугольной призмы?
Прежде чем вычислить объем прямоугольной призмы по формуле, нужно убедиться, что все размеры в одних и тех же единицах измерения. Следующие шаги используются для вычисления объема прямоугольной призмы.
- Шаг 1: Определите тип основания и найдите его площадь, используя подходящую формулу (как описано в предыдущем разделе).

- Шаг 2: Определите высоту призмы, перпендикулярную от верхней вершины к основанию призмы.
- Шаг 3: Умножьте площадь основания и высоту призмы, чтобы получить объем прямоугольной призмы в кубических единицах. Объем = площадь основания × высота призмы
Пример: Рассчитайте объем прямоугольной призмы, высота которой равна 8 дюймов, а площадь основания равна 90 квадратных дюймов.
Решение: Мы можем вычислить объем прямоугольной призмы, используя следующие шаги:
- Шаг 1: Базовая площадь уже задана как 90 квадратных дюймов.
- Шаг 2: Высота призмы 8 дюймов.
- Шаг 3: Объем данной прямоугольной призмы = площадь основания × высота призмы = 90 × 8 = 720 кубических дюймов.
Объем прямоугольной призмы Примеры
Пример 1: Если объем прямоугольной призмы 40 кубических единиц, а площадь ее основания 10 квадратных единиц, какова ее высота?
Решение: Дан объем прямоугольной призмы = 40 кубических единиц; а площадь основания прямоугольной призмы = l × b = 10 квадратных единиц.

Используя формулу объема прямоугольной призмы, площадь основания × высота призмы = 40
Высота данной прямоугольной призмы = 10 × высота = 40.Таким образом, высота прямоугольной призмы = 40/10 = 4 единицы
Пример 2. Если длина основания прямоугольной призмы 8 дюймов, ширина основания 5 дюймов, а высота призмы 16 дюймов, найдите объем прямоугольной призмы.
Решение: Дано: длина основания прямоугольной призмы (l) = 8 дюймов, ширина основания (w) = 5 дюймов.
Таким образом, площадь основания = l × w = 8 × 5 = 40 кв. дюймов .
Высота призмы h = 16 дюймов.Используя формулу объема прямоугольной призмы, объем прямоугольной призмы = площадь основания × высота призмы = (40 × 16) = 640 кубических дюймов.
перейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика — это жизненный навык. Помогите своему ребенку усовершенствовать это с помощью реального приложения с Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по объему прямоугольной призмы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по объему прямоугольной призмы
Каков объем прямоугольной призмы?
Объем прямоугольной призмы — это емкость, которую она может вместить, или занимаемое ею пространство. Таким образом, объем прямоугольной призмы можно вычислить, умножив площадь ее основания на высоту. Формула, которая используется для нахождения объема прямоугольной призмы: Объем (V) = высота призмы × площадь основания. Он выражается в кубических единицах, таких как см 3 , m 3 , in 3 и т. д.
Какова формула объема прямоугольной призмы?
Формула объема прямоугольной призмы: Объем (V) = площадь основания × высота призмы. Другой способ выразить эту формулу: Объем = l × w × h; где «l» — длина, «w» — ширина, а «h» — высота призмы.
Как найти объем прямоугольной призмы?
Чтобы найти объем прямоугольной призмы, выполните следующие действия:
- Шаг 1: Определите длину (l) и ширину (w) основания призмы.

- Шаг 2: Найдите высоту (h) призмы.
- Шаг 3: Подставьте соответствующие значения в формулу, V = lwh
- Шаг 4: Найдите произведение этих значений, чтобы получить объем призмы в кубических единицах.
Как найти высоту прямоугольной призмы, зная объем прямоугольной призмы?
Высоту прямоугольной призмы можно рассчитать, если определить объем призмы по той же формуле: Объем (V) = площадь основания × высота призмы. Например, объем призмы равен 600 кубических единиц, а площадь ее основания равна 60 квадратных единиц. Тогда после подстановки значений в уравнение получаем 600 = 60 × высота призмы. Это означает, что высота = 600/60 = 10. Следовательно, высота равна 10 единицам.
Что произойдет с объемом прямоугольной призмы, если ее высоту удвоить?
Мы знаем, что объем прямоугольной призмы является произведением трех ее измерений, то есть объем = длина × ширина × высота. Если ее высоту удвоить, ее объем будет l × w × (2h) = 2lwh = 2 × v. Таким образом, мы можем сказать, что объем прямоугольной призмы также увеличивается вдвое, когда ее высота увеличивается вдвое.
Таким образом, мы можем сказать, что объем прямоугольной призмы также увеличивается вдвое, когда ее высота увеличивается вдвое.
Что произойдет с объемом прямоугольной призмы, если длину увеличить вдвое, а высоту уменьшить вдвое?
Формула для расчета объема прямоугольной призмы: объем = длина × ширина × высота. Если его длину удвоить, а высоту уменьшить вдвое, то его объем можно записать как V = (2l) × (w) × (1/2h). После упрощения мы получаем l × w × h, что является обычной формулой для объема. Таким образом, можно сказать, что объем прямоугольной призмы останется прежним, если ее длину увеличить вдвое, а высоту уменьшить вдвое.
Что произойдет с объемом прямоугольной призмы, если длину, ширину и высоту призмы удвоить?
Объем прямоугольной призмы равен произведению трех ее измерений, то есть объем = длина × ширина × высота. Если его длину, ширину и высоту удвоить, то его объем будет равен (2l) × (2w) × (2h) = 8lwh = 8 × v. Таким образом, мы можем заключить, что если его длину, ширину и высоту удвоить , объем прямоугольной призмы будет в 8 раз больше исходного значения.
Как найти объем прямоугольной призмы с дробями?
Объем прямоугольной призмы можно рассчитать, даже если значения указаны в дробях. Например, если длина прямоугольной призмы равна \(1\dfrac{3}{5}\) единиц, ширина 3/4, а высота 2/3 единиц, объем призмы = l × ш × ч = \ (1 \ dfrac {3} {5} \) × 3/4 × 2/3. Теперь переведем смешанную дробь в неправильную и перемножим все дроби. Сначала мы умножим числители, а затем знаменатели, а затем при необходимости сократим полученную дробь. Это означает, что Объем = 8/5 × 3/4 × 2/3 = 48/60 = 4/5. Следовательно, объем призмы равен 4/5 кубических единиц.
Нахождение объема и площади поверхности прямоугольных тел
Результаты обучения
- Нахождение объема и площади поверхности прямоугольного тела
Тренер группы поддержки просит команду раскрасить деревянные ящики школьными цветами, чтобы они стояли на играх. (См. изображение ниже). Количество краски, необходимое для покрытия внешней стороны каждой коробки, представляет собой площадь поверхности, квадратную меру общей площади всех сторон.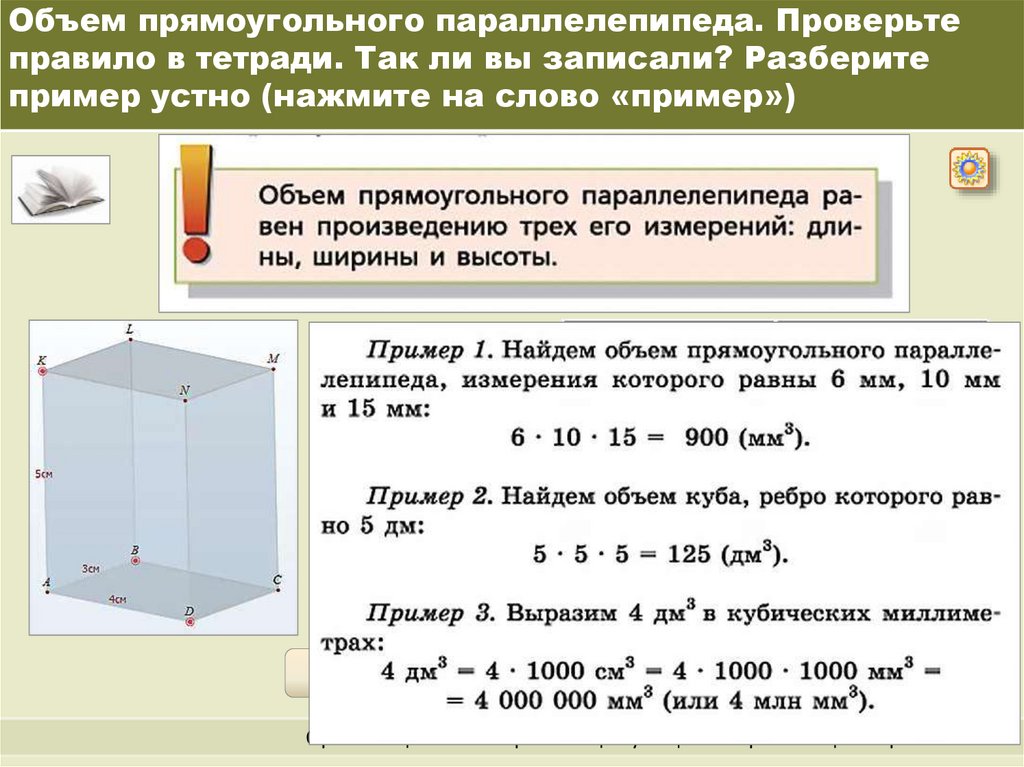 Объем пространства внутри ящика — это объем, кубическая мера.
Объем пространства внутри ящика — это объем, кубическая мера.
Этот деревянный ящик имеет форму прямоугольного тела.
Каждый ящик имеет форму прямоугольного тела. Его размерами являются длина, ширина и высота. Прямоугольное твердое тело, показанное на изображении ниже, имеет длину [латекс]4[/латекс], единицы ширины [латекс]2[/латекс] и высоту [латекс]3[/латекс]. Можете ли вы сказать, сколько всего кубических единиц? Смотрим слой за слоем.
Разбивка прямоугольного твердого тела на слои упрощает визуализацию количества содержащихся в нем кубических единиц. Это [латекс]4[/латекс] на [латекс]2[/латекс] на [латекс]3[/латекс] прямоугольное тело имеет [латекс]24[/латекс] кубических единиц.
Всего [латекс]24[/латекс] кубических единицы. Обратите внимание, что [латекс]24[/латекс] — это [латекс]\текст{длина}\times \текст{ширина}\times \text{высота}\текст{.}[/латекс]
Объем, [ латекс]V[/латекс] любого прямоугольного твердого тела является произведением длины, ширины и высоты.
[латекс]V=LWH[/латекс]
Мы могли бы также записать формулу объема прямоугольного тела через площадь основания. Площадь основания, [латекс]В[/латекс], равна [латекс]\текст{длина}\раз \текст{ширина}\текст{.}[/латекс]
[латекс]B=L\cdot W[/латекс]
Мы можем заменить [латекс]B[/латекс] на [латекс]L\cdot W[/латекс] в формуле объема, чтобы получить другую форму формула объема.
Теперь у нас есть другая версия формулы объема для прямоугольных тел. Давайте посмотрим, как это работает с прямоугольным телом [latex]4\times 2\times 3[/latex], с которого мы начали. См. изображение ниже.
Чтобы найти площадь поверхности прямоугольного тела, подумайте о нахождении площади каждой из его граней. Сколько граней у прямоугольного тела, показанного выше? Вы можете увидеть три из них.
[латекс]\begin{array}{ccccccc}{A}_{\text{front}}=L\times W\hfill & & & {A}_{\text{side}}=L\times W \hfill & & & {A}_{\text{top}}=L\times W\hfill \\ {A}_{\text{front}}=4\cdot 3\hfill & & & {A}_ {\ text {сторона}} = 2 \ cdot 3 \ hfill & & & {A} _ {\ text {верх}} = 4 \ cdot 2 \ hfill \\ {A} _ {\ text {спереди}} = 12 \hfill & & & {A}_{\text{side}}=6\hfill & & & {A}_{\text{top}}=8\hfill \end{массив}[/latex]
Уведомление для каждого из трех лиц, которые вы видите, есть идентичное противоположное лицо, которое не видно.
[латекс]\begin{array}{l}S=\left(\text{front}+\text{back}\right)\text{+}\left(\text{left side}+\text{ правая сторона}\справа)+\слева(\текст{сверху}+\текст{снизу}\справа)\\ S=\слева(2\cdot \текст{спереди}\справа)+\слева(\текст{2 }\cdot \text{слева}\справа)+\слева(\text{2}\cdot \text{сверху}\справа)\\ S=2\cdot 12+2\cdot 6+2\cdot 8\ \ S=24+12+16\\ S=52\text{кв. Units}\end{array}[/latex]
Площадь поверхности [latex]S[/latex] прямоугольного тела, показанного выше , составляет [latex]52[/latex] квадратных единиц.
В общем, чтобы найти площадь поверхности прямоугольного тела, помните, что каждая грань является прямоугольником, поэтому ее площадь является произведением ее длины и ширины (см. рисунок ниже). Найдите площадь каждого лица, которое вы видите, а затем умножьте каждую площадь на два, чтобы учесть лицо на противоположной стороне.
[латекс]S=2LH+2LW+2WH[/латекс]
Для каждой обращенной к вам грани прямоугольного твердого тела есть другая грань на противоположной стороне.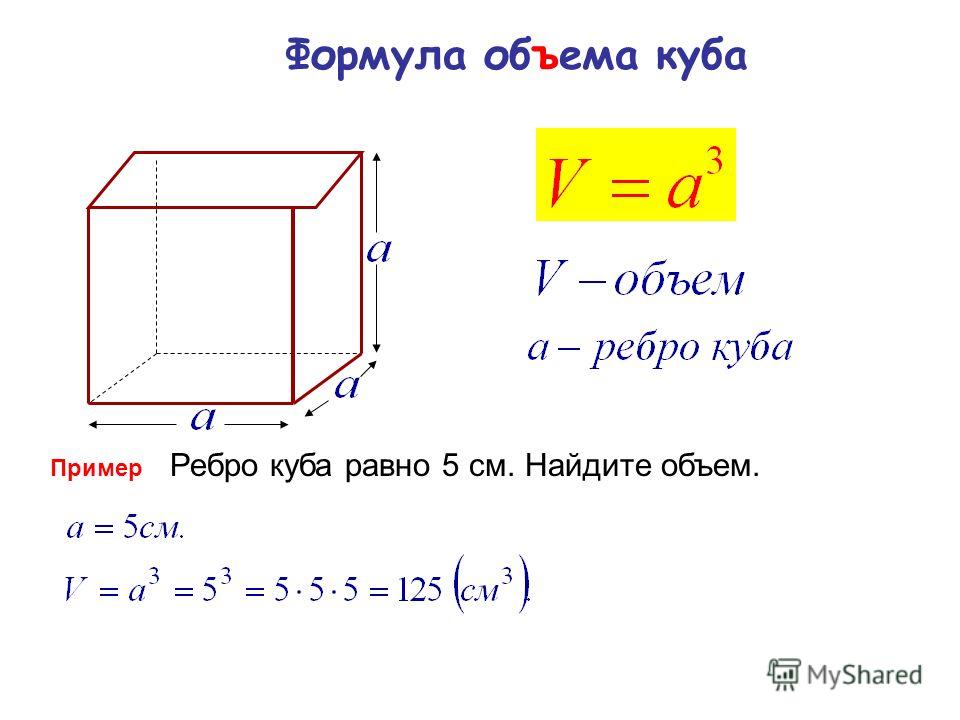 Всего [латексных]6[/латексных] лиц.
Всего [латексных]6[/латексных] лиц.
Объем и площадь поверхности прямоугольного тела
Для прямоугольного тела длиной [латекс]L[/латекс], шириной [латекс]W[/латекс] и высотой [латекс]Н:[/латекс]
Выполнение упражнения по манипулятивной математике «Раскрашенный куб» поможет вам лучше понять объем и площадь поверхности.
пример
Для прямоугольного твердого тела длиной [латекс]14[/латекс] см, высотой [латекс]17[/латекс] см и шириной [латекс]9[/латекс] см найдите 1. объем и 2. площадь поверхности.
Решение
Шаг 1 одинаков как для 1, так и для 2, поэтому мы покажем его только один раз.
| Шаг 1. Прочтите проблему. Нарисуйте фигуру и пометьте его данной информацией. |
| 1. | |
| Шаг 2. Определите , что вы ищете. | объем прямоугольного тела |
Шаг 3. Имя. Выберите переменную для ее представления. Имя. Выберите переменную для ее представления. | Пусть [латекс]V[/латекс] = объем |
| Шаг 4. Перевести. Напишите соответствующую формулу. Заменитель. | [латекс]V=LWH[/латекс] [латекс]V=\mathrm{14}\cdot 9\cdot 17[/латекс] |
| Шаг 5. Решите уравнение. | [латекс]V=2,142[/латекс] |
| Шаг 6. Проверка Мы оставляем вам возможность проверить ваши расчеты. | |
| Шаг 7. Ответьте на вопрос. | Площадь поверхности составляет [латекс]\текст{1,034}[/латекс] квадратных сантиметров. |
| 2. | |
| Шаг 2. Определить то, что вы ищете. | площадь поверхности твердого тела |
Шаг 3. Имя. Выберите переменную для ее представления. | Пусть [латекс]S[/латекс] = площадь поверхности |
| Шаг 4. Перевести. Напишите соответствующую формулу. Заменитель. | [латекс]S=2LH+2LW+2WH[/латекс] [латекс]S=2\левый(14\cdot 17\правый)+2\левый(14\cdot 9\правый)+2\левый(9\cdot 17\правый)[/латекс] |
| Шаг 5. Решите уравнение. | [латекс]S=1,034[/латекс] |
| Шаг 6. Проверка: Перепроверьте с помощью калькулятора. | |
| Шаг 7. Ответьте на вопрос. | Площадь поверхности [латекс]1034[/латекс] квадратных сантиметров. |
попробуйте
пример
Прямоугольный ящик имеет длину [латекс]30[/латекс] дюймов, ширину [латекс]25[/латекс] дюймов и высоту [латекс] 20[/латекс] дюймов. Найдите его 1. объем и 2. площадь поверхности.
Показать решение
попробуйте
Куб — это прямоугольное тело, длина, ширина и высота которого равны.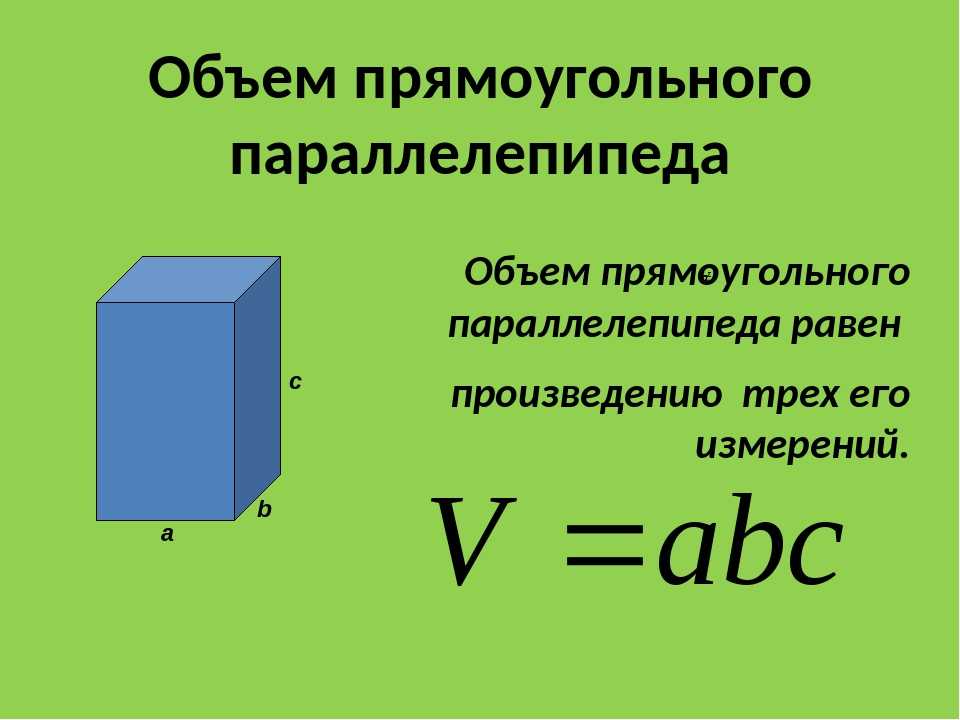 {2}\hfill \end{массив}[/latex] 9{2}[/латекс].
{2}\hfill \end{массив}[/latex] 9{2}[/латекс].
Объем и площадь поверхности куба
Для любого куба со сторонами длиной [латекс]s[/латекс],
пример
Куб имеет [латекс]2,5[/латекс] дюйма с каждой стороны. Найдите его 1. объем и 2. площадь поверхности.
Решение
Шаг 1 одинаков как для 1, так и для 2, поэтому мы покажем его только один раз.
| Шаг 1. Прочтите проблему. Нарисуйте фигуру и пометьте его данной информацией. 9{3}[/латекс] [латекс]V=15,625[/латекс] | |
| Шаг 6. Проверка: Проверьте свою работу. | |
| Шаг 7. Ответьте на вопрос. | Объем [латекс]15,625[/латекс] кубических дюймов. |
| 2. | |
| Шаг 2. Определите , что вы ищете. | площадь поверхности куба |
Шаг 3.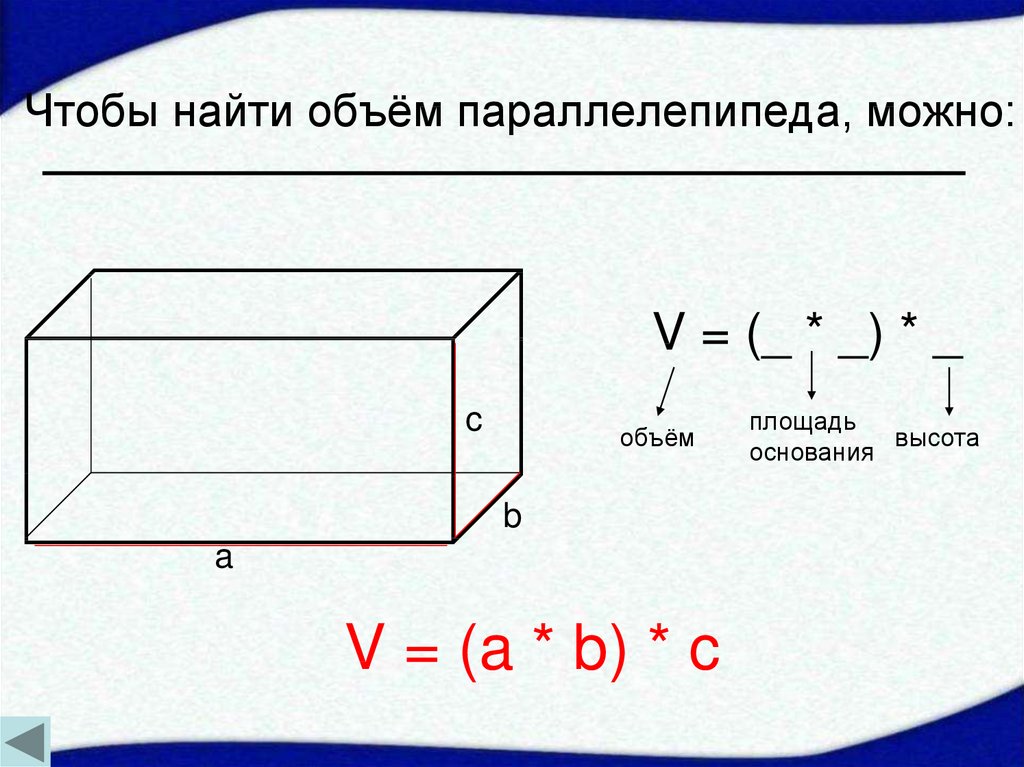 |

 Для удобства решения стороны AB, AD, AA соответственно можно обозначить как x, y, z. Тогда объём прямоугольного тела будет равен Vп = Sп * AA1 = x * y * z. Если начертить условие на рисунке, то можно отметить, что площадь пирамиды вполовину меньше площади основания прямоугольника. То есть, Sabd = 0,5 * Sabd. Тогда V = Sabd * AA1 / 3 = x * y * z / 3 * 2 = x * y* z / 6. Значит, объём вписанной пирамиды меньше в шесть раз чем у фигуры.
Для удобства решения стороны AB, AD, AA соответственно можно обозначить как x, y, z. Тогда объём прямоугольного тела будет равен Vп = Sп * AA1 = x * y * z. Если начертить условие на рисунке, то можно отметить, что площадь пирамиды вполовину меньше площади основания прямоугольника. То есть, Sabd = 0,5 * Sabd. Тогда V = Sabd * AA1 / 3 = x * y * z / 3 * 2 = x * y* z / 6. Значит, объём вписанной пирамиды меньше в шесть раз чем у фигуры.