Онлайн нахождение обратной функции: Калькулятор Обратных Функций

Содержание

Обратная функция — презентация онлайн

Похожие презентации:

Сложная функция

Сложная функция. 10 класс

Производная функции

Тригонометрические функции числового аргумента

Функции и их свойства. Предел последовательности и функции. Производная функции и дифференциал

Сложная функция

Рекурсивные функции

Производная сложной функции

Функции и их графики

Производная сложной функции

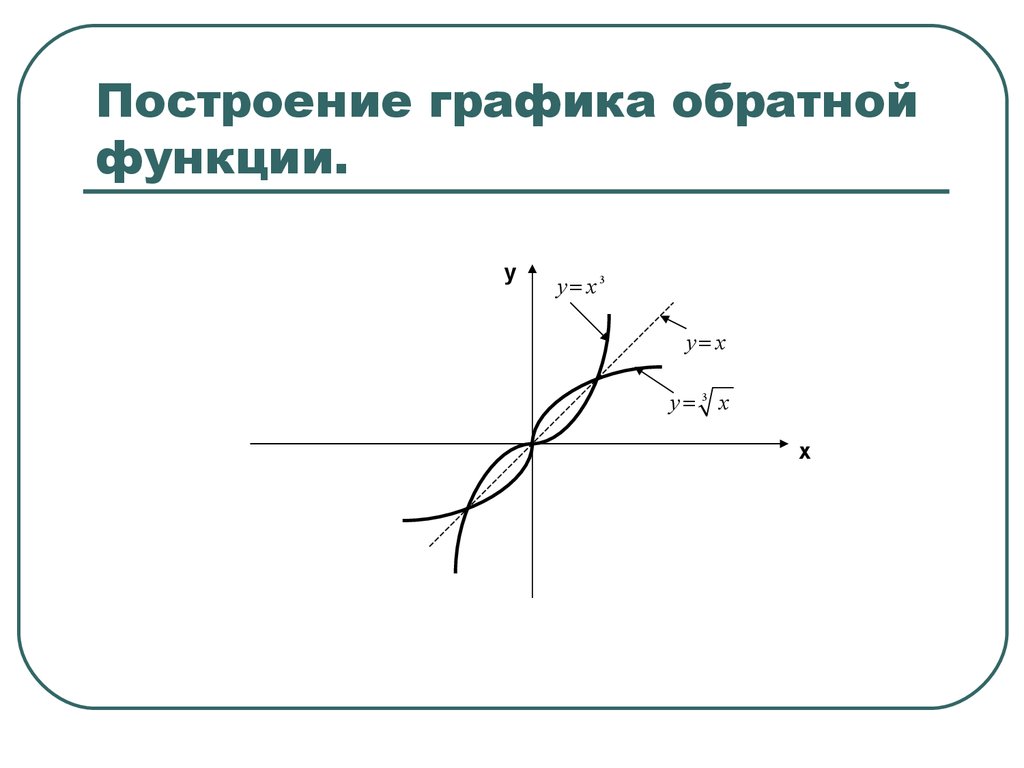
Обратная функция
https://www.youtube.com/watch?v=lffsY8VYv7U

3. Задание

Найдите функцию, обратную данной:
y 5x 2
3
y
x 1
постройте графики этих функций

4. СЛОЖНАЯ ФУНКЦИЯ

Сложная – не значит трудная!

5. Повторение.

Функция — это соответствие между двумя множествами,
при котором каждому элементу одного множества
соответствует единственный элемент другого
множества.
f(x)
x
у
0
0
X
y=f(x
)
Y
x0
y0
y0=f(x0)

6.

Сложная функция Композиция двух и более функцийy=f(g(x))
f(t)
g(x)
у
0
x
x
t
0
0
Y
T
X
0
x0
t0
y0

8. Определение: Функции, у которых аргумент в свою очередь также является функцией, называются сложной функций или композицией

функций.
Сложная
функция – функция от функции.

9. Формула для задания сложной функции

Пример.
y=f(g(x)) –
– сложная функция
у х 4
2
g(x) – внутренняя функция
g(x) = х2 — 4 –
внутренняя функция
f(t) – внешняя функция
f(t) = t – внешняя
функция

10. Примеры сложной функции y=f(g(x))

внешняя
функция
f(t)
внутренняя
функция
g(x)
1. y = sin2x
1. sin t
2. y = (x3 – 1 )5
2. t5
x3-1
3.
3. cos t
7x+2
4.
y = cos(7x + 2)
y=
1
x2 x
5. y = sin2x + sin x
4.
1
t
5. t2+t
2x
x2-x
sin x

11. Составьте сложную функцию ,если f(x)=x2, g(x)=2x-4, h(x)=sin x например: y=h(f(x))=sin x2

• y1=f(g(x))
• y2=g(f(x))
• y3= f(h(x))
• y4=h(g(x))

12.

Примеры построения графиковПример 1
у
х
2
4
Пример 2
y = sin 2x

13. Пример 1

у х2 4
1. Найдем область определения функции:
D(y) = (-∞; -2] U [2; +∞)
Функция четная.
2. Построим графики
внутренней и внешней функции:
g(x)=x2-4
f (t ) t
t
y
g(x)=x2-4
t0
-2
f (t ) t
y0
2
0
x0
0
х
t0
y
y0
0
x0
t0
2 x
0
х
y0
Как построить график
у х 4 ?
2
t
t
y
g(x)=x2-4
t0
-2
f (t ) t
y0
2
0
x0
0
х
t0
t
y
Изменение значений
x, t, y
y0
-2 0
2
x0
х
х
2; +∞
t
0;+∞
y
0;+∞
Использование четности:
график симметричен
относительно оси ординат
y
-2
0
2
у х 4
2
х

17. Пример 2

у sin 2 x
1. D(y) = R
Функция нечетная.
Функция периодическая, период: π.
2. Построим графики
внутренней и внешней функции:
g(x)=2х
f (t ) sin t
t
y
g(x)=2x
2
f (t ) sin t
1
0
4
0
х
y
0
х
Как построить график y = sin2x ?
2
π
t

19.

Таблица изменений значений x, t, yx
t
y
0 ;
4
;
4
2
3
2 ; 4
3
;
4
π
tt
y
g(x)=2x
2
f (t ) sin t
1
0
4
х
y
t
Изменение значений
x, t, y
1
0
π
2
0
4
х
4
2
х
0;
t
0;
y
0; 1
π
t
g(x)=2x
y
2
f (t ) sin t
1
0
4 2
х
2
0
y
t
Изменение значений
x, t, y
1
0
π
4 2
х
х
t
y
4
2
;
2
; π
1; 0
π
t
g(x)=2x
y
f (t ) sin t
3
2
1
0
3
2 4
х
y
3
2
1
0
4 2
π
2
0
t
Изменение значений
x, t, y
х
х
t
2
;
π;
3
4
3
2
y 0; -1
π
t
g(x)=2x
y
f (t ) sin t
3
2
1
0
3
2 4
х
2
0
y
3
2
1
0
4 2
2π х
2π
π
Изменение значений
x, t, y
х
t
3
π
;
4
3
2π
;
2
y -1 ; 0
t

24.

Таблица изменений значений x, t, y3
4 ;
π
π
3
2
3
2
2π
0;
-1
-1;
x
0 ;
4
;
4
2
3
2 ; 4
t
0 ;
2
; π
2
y
0 ;
1 ;
1
0
0
t
g(x)=2x
y
f (t ) sin t
3
2
1
0
х
0
2
3
2
2π
y
3
4
1
2
t
π
0
4 2
Y = sin2x
π
х

26. Нахождение множества значений сложной функции

Пример. Дана функция
y
1
3 sin x
Найдите Е(у).
Решение.
Внутренняя функция принимает значения от 2 до 4, так как 2≤3+sinx≤4.
Рассмотрим внешнюю функцию:
1
f (t )
t
Заметим, что она определена только при тех значениях t, для которых
2≤t≤4.

27. Множество значений сложной функции как множество значений внешней функции

Множество значений сложной функции
y
y
1
3 sin x
как множество значений внешней функции
1
f (t )
t
при 2≤t≤4
1
0,5
0,25
0
2
2 ≤ t ≤ 4, 0,25 ≤ y ≤ 0,5
4
t
E(y)=[0,25; 0,5]

РЕФЛЕКСИЯ
Я.

…………………………………. ознакомился.
Мне ……………………………… было нелегко.
Я ……………………………… усвоил
Я ………………………. …….запомнил.

English Русский Правила

Урок 12. Функции и их свойства. Теория 11 класс онлайн-подготовка на Ростелеком Лицей

Подготовка к ЕГЭ по математике

Эксперимент

Урок 12. Функции и их свойства

Теория

Конспект урока

Определение функции. Понятие ГМТ. Отличие функции от ГМТ

Мы начинаем с вами новую очень важную в математике тему «Функции». Школьный курс алгебры построен таким образом, что с понятием функция приходится встречаться очень часто на протяжении нескольких лет обучения. При этом, названия функций перекликаются с видами соответствующих им уравнений и неравенств. К примеру, когда речь идет о линейных функциях, то говорят и о линейных уравнениях и неравенствах, то же самое касается квадратичных, показательных, логарифмических и прочих функций. Для удобства мы с вами выделим обсуждение понятия «функция» и основных свойств функций в отдельную тему. Так что же такое функция? Вспомним определение.

Функция — этозакон соответствия между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует только одно определенное значение другой величины y (функции или зависимой переменной).

В указанном определении необходимо сразу обратить внимание на именно однозначное соответствие значений функции значениям аргумента.

Под функцией можно понимать как соответствие определенных чисел, так и других объектов. Например, каждому значению времени в минутах соответствует строго одно значение времени в секундах, при этом, закон соответствия этих величин нам известен – количество минут необходимо умножить на 60 и получится количество секунд. Скажем, в 3 минутах 180 секунд, а в 5 минутах 300 секунд. При этом каждому значению количества секунд соответствует строго одно определенное количество минут. Т.е. и зависимость секунд от минут и обратная зависимость являются функциями. Это мы привели пример числовой функции.

Примером нечисловой функции может быть однозначное соответствие человека и его фамилии. Обратите внимание, что у человека не может быть нескольких фамилий, но при этом есть однофамильцы, т.е. одной фамилии может соответствовать много разных человек, вспомните, например, сколько в России Ивановых. Это значит, что соответствие между человеком и фамилией однозначное, а обратное – нет. В первом случае соответствие будут называть функцией, а во втором нет.

Но не следует думать, что из приведенных примеров следует, что все числовые зависимости являются функциями, а нечисловые необязательно. Примером числовой зависимости, которая не является функцией, может быть соответствие между числом, на которое указывает стрелка часов, и временем суток. Например, часовая стрелка указывает на восьмерку, а это может означать как 8-00 утра так и 20-00 вечера.

Как же называть такие неоднозначные соответствия? Иногда их называют многозначными функциями, при этом, используя просто термин «функция» имеют в виду именно ее однозначность.

В математике нас, конечно же, будут интересовать именно числовые функции. Их удобно описывать именно графическим способом. При этом, графическое изображение однозначной функции называют построением графика функции, а изображение многозначной функции – построением геометрического места точек или ГМТ.

Давайте вспомним самые основные способы задания числовых функций:

1) Аналитический способ – задание функции с помощью формулы.

С таким способом мы сталкиваемся наиболее часто. Обозначать в общем виде такую формулу принято обычно как , где под понимают аргумент, а под значение функции. При этом, свободно используются, например, такие равноправные записи:

Что может означать указанная формула? Например, соответствие длины стены квадратной комнаты и ее площади.

С помощью такой функции можно легко ответить, что такой комнате со стороной 4 метра соответствует одна единственная площадь .

Кстати, стоит обратить внимание, что обозначение аргумента и функции латинскими буквами и не принципиально. То же самое касается и обозначения правила соответствия между этими переменными с помощью буквы (от слова «function»). Вполне нормальной будет запись функции в виде . Подумайте сами, какой буквой здесь что обозначено.

2) Табличныйспособ – задание функции с помощью таблицы связанных друг с другом значений. Такой способ зачастую используется, если не известно правило соотношения между аргументом и функцией. Примером такого задания функции может послужить таблица средних температур за несколько дней мая:

Число	1	2	3
Температура,	+14	+17	+16

3) Графический способ – задание функции с помощью изображения точек в системе координат, когда одной координате точек поставлена в однозначное соответствие другая ее координата. Например, в декартовой системе координат изображается множество точек, у которых поставлены в соответствие координаты по оси абсцисс (Ox) и координаты по оси ординат (Oy).

Если привести в пример график все той же функции , то он будет иметь вид не безызвестной вам параболы:

Такой способ задания функции очень наглядный и позволяет быстро анализировать различные ее свойства, например, монотонность, четность, периодичность и т.п. О них мы скоро поговорим.

Что касается различий в графических изображениях графиков функций и ГМТ многозначных функций, то существует быстрый способ их отличать друг от друга: любая вертикальная линия, проведенная в системе координат, пересекает график функции только в одной точке, а ГМТ многозначной функции в нескольких.

Изобразим это на рисунке.

График линейной функции – прямая или квадратичной – парабола:

ГМТ окружности или эллипса:

Область определения, область значений

Теперь рассмотрим основные свойства и характеристики функций. И одной из важнейших характеристик функции является ее область определения.

Область определения функции – это множество значений аргумента, для которых функция имеет смысл. Иными словами это допустимые значения икса. Это множество принято обозначать D или D(x).

При решении уравнений вы привыкли называть такое множество аргументов, которые в них входили, областью допустимых значений или ОДЗ. Для функций такой терминологией лучше не пользоваться, так как есть опасность перепутать областью допустимых значений аргумента с областью значений функции из-за схожести названий.

Искать область определения функции можно различными способами:

1) Если функция задана аналитически, как это чаще всего бывает, то в таком случае удобнее всего сначала найти те значения аргумента, при которых функция не имеет смысла, и исключить их из множества действительных чисел.

Например, для функции областью определения является , т.к. она определена при всех значениях икса, кроме нуля, поскольку на ноль делить нельзя.

Перечислим основные случаи, в которых необходимо искать не имеющие смысла для функции аргументы:

1. Наличие в функции деления на выражение, содержащее неизвестную. В таком случае исключаются те аргументы, при которых возникает деление на ноль. Например, в функции из области определения необходимо исключить аргументы, при которых , или сразу же наложить ограничение .

2. Присутствие в функции корня четной степени из выражения, содержащего неизвестную. При этом необходимо исключить аргументы, при которых подкоренное выражение отрицательно, в таком случае удобно сразу накладывать условие, что подкоренное выражение больше или равно нулю. Например, для функции областью определения будет решение неравенства .

Обратите внимание, что для корней нечетной степени, например, кубических такого ограничения нет.

3. Наличие в функции логарифмов, содержащих неизвестные выражения. В общем виде это можно записать так: если функция содержит , где и — это выражения, содержащие неизвестную, то областью определения будет решение системы неравенств

Например, для функции областью определения будет множество аргументов, которые удовлетворяют . Обратите внимание, что поскольку в данном примере основание логарифма – это константа, то она проверяется формально и это не записывается. Если бы в основании логарифма была, например , то функция в целом не имела бы смысла, и ее область определения не нужно искать.

Конечно же, функции могут содержать и композиции из указанных выражений, например, деление на логарифм от неизвестной. В таком случае для нахождения области определения записывается система из указанных ограничений. Кроме того, мы указали не все возможные ситуации, при которых необходимо искать ограничения на область определения. Чтобы вспомнить все подобные случаи повторите свойства функций, которые упоминались в нашем курсе ранее и в школьной программе. Например, тангенс имеет смысл не при всех значениях аргумента.

Функции, в которых нет действий, ограничивающих множество аргументов, областью определения является все множество действительных чисел. Это относится, например, к линейным и квадратичным функциям. Так для функции областью определения будет .

2) Для функций, заданных табличным способом, область определения явно указана в таблице – это все множество перечисленных аргументов.

Например, для функции, которая задана таблицей:

	-2		4,5
	7		1

Областью определения будет . Как видите, в случае табличного задания функции множество допустимых значений аргументов не является непрерывным и не может быть задано в виде промежутка, так как это определенный набор конкретных данных.

3) Если функция задана графически, т. е. изображен ее график, то областью определения будет множество значений координат точек графика по оси абсцисс. Иными словами необходимо искать все значения иксов, для которых изображены точки графика.

Например, для графика функции

Областью определения будет . Края отрезка не включены, т.к. на графике крайние точки выколоты.

Теперь рассмотрим такую характеристику функции как область значений.

Область значений функции – это множество значений функции, которые она принимает в своей области определения. Т.е. в стандартной записи функции это значения ее игрека. Множество значений функции принято обозначать E или E(y).

Задача на определение множества значений функции, как правило, более сложна, чем задача на поиск области определения. Дело в том, что в таком случае необходимо искать не ограничения на арифметические действия, а множество всех результатов этих действий, а это непросто.

Рассмотрим основные подходы к решению в данном случае.

1) Для функций, заданных аналитически, для поиска области значений можно использовать метод нахождения обратной функции, но этот способ не самый простой и не все функции однозначно обратимы. Для несложных примеров, обычно достаточно пользоваться заранее известными областями значений простейших функций. Перечислим такие самые часто встречающиеся функции:

1. Выражения, которые возводятся в четные степени, всегда неотрицательны. Например, или , для этих функций .

На нечетные степени указанное свойство не распространяется.

2. Функции, которые представляют собой корни четных степеней, также всегда имеют неотрицательные значения. Например, или , для них областью значений является .

Опять-таки, на корни нечетной степени это не распространяется, они могут иметь отрицательные значения.

3. Квадратичная функция тоже имеет ограниченную область значений. Это удобно увидеть на графике, изобразим, например, график функции . Проделаем это, опираясь на то, что вы помните из школьной программы. Конечно же, на следующем уроке мы отдельно подробно рассмотрим методы построения графиков таких функций. А пока воспользовавшись, к примеру, методом определения вершины параболы, получим такой график

Как видим, у функции из-за того, что ветки параболы направлены вниз, есть максимальное значение — восьмерка, а все остальные значения меньше. Таким образом, область значений этой функции . Для того чтобы получить этот ответ не обязательно рисовать график, достаточно просто уметь находить координату вершины параболы по оси ординат и помнить, что при положительном старшем коэффициенте функции, ее ветки направлены вверх, а при отрицательном вниз.

Таким образом, можно сформулировать алгоритм поиска области значений квадратичной функции: находим игрековую координату ее вершины и учитываем направление веток параболы по знаку старшего коэффициента, т.е. множителя при .

4. Показательная функция всегда принимает положительные значения. Например, , для нее .

5. Такие тригонометрические функции как синус и косинус имеют двухсторонние ограничения по области значений. Вспомним, что их значения ограничены промежутком .

При решении задач на определение области значений функции необходимо уметь использовать указанные ограничения на основные простейшие функции и преобразовывать их.

Мы привели не все известные нам ограниченные области значений простейших функций, вспомните, например, аркфункции. Для того чтобы не забыть такие ограничения, повторите все основные виды функций.

Нам известно множество функций, которые не имеют ограничения на область значений. Например, для линейных функций, которые не являются константами, областью значений является множество всех действительных чисел . Для примера вспомним, что к таким же функциям относится и тангенс с котангенсом.

Специфическим случаем является константная функция, для которой множеством значений является только одно число, хотя область определения не ограничена. Например, для функции : , а , т.е. функция всегда имеет одно и то же значение , что и указано в ее аналитической записи.

2) Для табличного способа задания функции нахождение области значений так же элементарно, как и области определения. Для этого просто достаточно перечислить все указанные в таблице значения функции. Выпишем область значений из таблицы, которую мы приводили для примера к области определения

	-2		4,5
	7		1

3) В случае графического способа задания функции область значений видна по графику, как и область определения. В данном случае необходимо указывать множество всех значений координат точек графика по оси ординат, т.е. всех игреков.

Приведем опять пример графика, по которому мы определяли область определения функции

Для него область значений .

Асимптоты функции, точки пересечения с осями

К области определения и значения функций имеют отношение такие вспомогательные элементы графика функций как асимптоты.

Асимптота графика функции – это прямая, расстояние от которой до графика функции при удалении на бесконечность стремится к нулю.

Хорошей наглядной демонстрацией асимптот является график стандартной дробно-рациональной функции , который называют гиперболой

Этот график демонстрирует два наиболее часто встречающихся типа асимптот: вертикальную и горизонтальную. На графике вертикальной асимптотой является ось , ее уравнение – к ней график прижимается по вертикали, а горизонтальной – ось , ее уравнение – к ней график прижимается по горизонтали.

Умение находить асимптоты полезно для построения графиков дробно-рациональных и других функций.

Как видим, асимптота является прямой линией, и для того, что бы ее найти, необходимо определить ее уравнение, т. е. соответствующую ей функцию.

Вертикальная асимптота образуется в той точке, где значение функции стремится к бесконечности. Это происходит при аргументах, при которых в функции возникает деление на ноль.

Уравнение вертикальной асимптоты удобно записать так:

аргументы, при которых в функции происходит деление на ноль.

Горизонтальная асимптота является значением, к которому функция стремится на бесконечности. Для ее определения в общем случае необходимо вводить понятие предела, но зачастую в несложных функциях достаточно просто логически посмотреть, к каким значениям функция приближается при увеличении аргумента до и при уменьшении до . В указанном примере с гиперболой несложно определить и без графика, что при увеличении икса до значение дроби стремится к нулю, то же само происходит и при уменьшении икса до .

Таким образом, уравнение горизонтальной асимптоты можно описать так:

значения, к которым функция приближается на .

Существует еще и наклонная асимптота, но она встречается редко и рассматривается обыкновенно в теме «исследование функций и построение графиков с помощью производной».

Для удобства построения графиков функций ее рассматривают такую их характеристику как точки пересечения с осями.

Точки пересечения с осями графика функции – это значения аргумента и функции, при которых одно из них равно нулю. Нулю могут равняться одновременно и аргумент с функцией, если график проходит через начало координат.

Для нахождения точек пересечения графика с осью необходимо подставить в функцию нулевое значение аргумента, т.е. .

Для нахождения точек пересечения графика с осью необходимо решить уравнение . В данном случае удобнее употреблять именно обозначение функции , а не , чтобы подчеркнуть, что к нулю необходимо приравнять именно формулу, которая задает функцию, а не просто игрек.

Например, для линейной функции точка пересечения с осью имеет координаты и , точка пересечения с осью координаты и , что можно увидеть на графике

Чётность и нечётность, периодичность

К важнейшим свойствам функций относится четность/нечетность.

Функция называется нечетной, если при изменении знака аргумента, она меняет свое значение на противоположное. Формульная запись этого выглядит так . Это значит, что после подстановки в функцию на место всех иксов значений «минус икс», функция изменит свой знак. График такой функции симметричен относительно начала координат.

Примерами нечетных функций являются и др.

Например, график действительно обладает симметричностью относительно начала координат:

Функция называется четной, если при изменении знака аргумента, она не меняет свое значение. Формульная запись этого выглядит так . Это значит, что после подстановки в функцию на место всех иксов значений «минус икс», функция в результате не изменится. График такой функции симметричен относительно оси .

Примерами четных функций являются и др.

К примеру, покажем симметричность графика относительно оси :

Если функция не относится ни к одному из указанных видов, то ее называют ни четной ни нечетной или функцией общего вида. У таких функций нет симметрии.

Такой функцией, например, является недавно рассмотренная нами линейная функция с графиком:

Особым свойством функций является периодичность. Дело в том, что периодичными функциями, которые рассматриваются в стандартной школьной программе, являются только тригонометрические функции. Мы уже подробно о них говорили при изучении соответствующей темы.

Периодичная функция – это функция, которая не меняет свои значения при добавлении к аргументу определенного постоянного ненулевого числа.

Такое минимальное число называют периодом функции и обозначают буквой .

Формульная запись этого выглядит следующим образом: .

Посмотрим на это свойство на примере графика синуса:

Вспомним, что периодом функций и является , а периодом и – .

Как мы уже знаем, для тригонометрических функций со сложным аргументом может быть нестандартный период. Речь идет о функциях вида:

У них период равен . И о функциях:

У них период равен .

Как видим, для вычисления нового периода стандартный период просто делится на множитель при аргументе. От остальных видоизменений функции он не зависит.

Промежутки монотонности функции

Очень важным свойством функции является ее монотонность. Зная это свойство различных специальных функций, можно определить поведение различных физических, экономических, социальных и многих других процессов.

Выделяют следующие виды монотонности функций:

1) функция возрастает, если на некотором интервале, если для любых двух точек и этого интервала таких, что выполнено, что . Т.е. большему значению аргумента соответствует большее значение функции;

2) функция убывает, если на некотором интервале, если для любых двух точек и этого интервала таких, что выполнено, что . Т.е. большему значению аргумента соответствует меньшее значение функции;

3) функция неубывает, если на некотором интервале, если для любых двух точек и этого интервала таких, что выполнено, что ;

4) функция невозрастает, если на некотором интервале, если для любых двух точек и этого интервала таких, что выполнено, что .

Для первых двух случаев еще применяют термин «строгая монотонность».

Два последних случая являются специфическими и задаются обычно в виде композиции из нескольких функций.

Отдельно отметим, что рассматривать возрастание и убывание графика функции следует именно слева-направо и никак иначе.

Обратные функции

Еще одним специфическим свойством функции является ее обратимость, т.е. наличие у нее обратной функции.

Обратная функция – это функция, которая обращает выбранную зависимость. Т.е. если функция каждому ставит в соответствие , то функция , которая каждому ставит в соответствие определенное , называется обратной к функции .

Умение искать обратные функции является крайне полезным во многих практических вопросах, например из умения находить площадь квадратной комнаты следует желание уметь вычислять длину ее стороны, зная площадь. Таким образом, для функции при вводится обратная функция .

Но не для всех функций существуют обратные. Более подробно смотрите об этом в «понятийном уроке» к нашей теме.

На этом уроке мы рассмотрели такое понятие как «функция» и все основные способы задания функций, их характеристики и свойства.

В практической части урока мы разберем примеры на определение свойств функций и займемся чтением их графиков.

Полезные ссылки:

1. http://interneturok.ru/ru/school/algebra/9-klass/chislovye-funktsii/nahozhdenie-oblasti-opredeleniya-i-oblasti-znacheniy-chislovoy-funktsii

2. http://interneturok.ru/ru/school/algebra/9-klass/chislovye-funktsii/zadachi-na-nahozhdenie-oblasti-opredeleniya-i-oblasti-znacheniy-funktsii-v-bolee-slozhnyh-sluchayah

3. http://interneturok.ru/ru/school/algebra/9-klass/chislovye-funktsii/analiticheskiy-sposob

4. http://interneturok.ru/ru/school/algebra/9-klass/chislovye-funktsii/graficheskiy-i-tablichnyy-sposoby

5. http://interneturok.ru/ru/school/algebra/9-klass/chislovye-funktsii/osnovnye-svoystva-chislovyh-funktsiy

6. http://interneturok.ru/ru/school/algebra/9-klass/chislovye-funktsii/opredeleniya-i-svoystva-chetnyh-i-nechetnyh-funktsiy

7. http://interneturok.ru/ru/school/algebra/9-klass/chislovye-funktsii/issledovanie-funktsiy-na-chetnost

Решение высшей математики онлайн

Теоретическая информация*

Функции и их графики
- Основные обозначения и определения
- Первый способ задания функции: табличный
- Второй способ задания функции: с помощью формулы
- Обзор некоторых элементарных функций
- Третий способ задания функции: указание процедуры вычисления
- Композиция функций
- Обратная функция
- Упражнения
Пределы
- Пределы при разных условиях. Некоторые частные случаи
- Общее определение предела
- Замена переменного и преобразование базы при такой замене
- Бесконечно малые и локально ограниченные величины и их свойства
- Общие свойства пределов
- Первый и второй замечательные пределы
- Бесконечно большие величины и бесконечные пределы
- Использование непрерывности функций при вычислении пределов
- Сравнение бесконечно малых
- Таблица эквивалентных бесконечно малых при
- Упражнения на вычисление пределов
Непрерывность функций и точки разрыва
- Определение непрерывности функции
- Определение точек разрыва
- Свойства функций, непрерывных в точке
- Непрерывность функции на интервале и на отрезке
- Равномерная непрерывность
- Непрерывность обратной функции
- Гиперболические функции и ареа-функции
- Примеры и упражнения
Производные и дифференциалы
- Мгновенная скорость при прямолинейном движении
- Касательная к кривой на плоскости
- Производная
- Свойства производных
- Производные некоторых элементарных функций
- Дифференциал
- Производная композиции
- Инвариантность дифференциала
- Производная обратной функции
- Производные некоторых элементарных функций (продолжение)
- Сводка основных результатов о производных
- Производные высших порядков
- Дифференциалы высших порядков и их неинвариантность
- Производные функции, заданной параметрически
- Производная функции, заданной неявно
- Приближённое вычисление производных
- Примеры и упражнения
Свойства дифференцируемых функций
- Четыре теоремы о дифференцируемых функциях
- Правило Лопиталя
- Сравнение бесконечно больших величин
Формула Тейлора
- Многочлен Тейлора
- Остаток в формуле Тейлора и его оценка
- Формула Тейлора для некоторых элементарных функций
- Оценки ошибок в формулах приближённого дифференцирования
- Упражнения
Исследование функций и построение графиков
- Асимптоты графика функции
- Возрастание и убывание функции
- Экстремум функции и необходимое условие экстремума
- Достаточные условия локального экстремума
- Выпуклость функции
- Общая схема исследования функции и построения её графика
- Примеры исследования функций и построения графиков
- Упражнения и задачи
Кривизна плоской кривой
- Кривизна графика функции
- Вершины кривых
- Радиус кривизны
- Упражнения
Приближённое нахождение корней уравнений и точек экстремума
- Отделение корней
- Метод простого перебора
- Метод половинного деления
- Метод простых итераций
- Метод секущих
- Метод одной касательной
- Метод Ньютона (метод касательных)
- Метод хорд (метод линейной интерполяции)
- Приближённое нахождение точки экстремума
- Метод простого перебора
- Метод почти половинного деления
- Метод золотого сечения и метод Фибоначчи
- Методы, связанные с приближённым нахождением корня производной
- Упражнения
Векторная алгебра
- Определение вектора
- Операции над векторами
- Разложение вектора по базису
- Линейная зависимость векторов
- Система координат и координаты вектора
- Проекции вектора
- Скалярное произведение
- Векторное произведение
- Выражение векторного произведения через координаты сомножителей
- Смешанное произведение
- Нахождение координат вектора в произвольном базисе
Прямые линии и плоскости
- Уравнение поверхности
- Уравнение плоскости
- Изображение плоскости
  - Все коэффициенты и свободный член в уравнении отличны от нуля
  - Коэффициенты при неизвестных отличны от нуля, а свободный член равен нулю
  - Один из коэффициентов при неизвестных равен нулю
  - Два коэффициента при переменных равны нулю
- Угол между плоскостями
- Расстояние от точки до плоскости
- Прямая на плоскости
- Прямая в пространстве
- Основные задачи на прямую и плоскость
Кривые второго порядка
- Окружность
- Эллипс
- Гипербола
- Парабола
- Параллельный перенос системы координат
Поверхности второго порядка
- Сфера
- Эллипсоид
- Гиперболоиды
- Конус
- Параболоиды
- Цилиндры
- Параллельный перенос системы координат
Матрицы
- Определение, обозначения и типы матриц
- Сложение матриц и умножение на число
- Символ суммирования
- Умножение матриц
- Транспонирование матрицы
- Определители
- Обратная матрица
- Ранг матрицы
Системы линейных уравнений
- Правило Крамера
- Существование решения системы линейных уравнений общего вида
- Однородная система уравнений
- Структура решений неоднородной системы линейных уравнений
- Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)
Алгебраические структуры
- Группы
- Кольца
- Поля
Комплексные числа
- Построение поля комплексных чисел
- Решение квадратных уравнений с вещественными коэффициентами
- Изображение комплексных чисел. Модуль и аргумент комплексного числа
- Тригонометрическая форма комплексного числа
- Показательная форма комплексного числа
- Извлечение корня из комплексного числа
- Корни многочленов
Многомерные пространства
- Линейные пространства
  - Определение и примеры
  - Базис и размерность пространства
  - Координаты векторов
  - Изменение координат вектора при изменении базиса
- Евклидово пространство
- Аффинное -мерное пространство
Линейные преобразования
- Определение и примеры
- Матрица линейного преобразования
- Изменение матрицы линейного преобразования при изменении базиса
- Собственные числа и собственные векторы
- Нахождение собственных чисел и собственных векторов матриц
- Матрица линейного преобразования в базисе из собственных векторов
- Приведение уравнения второго порядка к каноническому виду
Первообразная и неопределённый интеграл
- Определение первообразной и её свойства
- Неопределённый интеграл и таблица неопределённых интегралов
- Свойства неопределённого интеграла
- О «неберущихся» интегралах
- Приближённое нахождение первообразных
- Примеры и задачи
Нахождение неопределённых интегралов
- Интегрирование некоторых классов функций при помощи элементарных преобразований
- Формула понижения степени
- Рациональные функции и их интегрирование
- Интегралы, сводящиеся к интегралам от рациональных функций
- Интегралы от функций, рациональным образом зависящих от и
- Примеры и задачи
Определённый интеграл и его свойства
- Конструкция определённого интеграла и площадь криволинейной трапеции
- Свойства определённого интеграла
- Интеграл с переменным верхним пределом
- Определённый интеграл при произвольном соотношении между нижним и верхним пределами
- Некоторые приёмы нахождения определённых интегралов
- Проверка геометрического смысла интеграла при подсчёте площади части круга
- Примеры и задачи
Несобственные интегралы
- Несобственные интегралы первого рода
- Свойства несобственных интегралов первого рода
- Несобственные интегралы второго рода
- Свойства несобственных интегралов второго рода
- Несобственные интегралы с несколькими особенностями
- Примеры и задачи
Приближённое вычисление определённых интегралов
- Квадратурные формулы левых и правых прямоугольников
- Квадратурная формула центральных прямоугольников
- Квадратурная формула трапеций
- Оценки ошибок формул трапеций и центральных прямоугольников
- Квадратурная формула Симпсона (формула парабол)
- Квадратурные формулы более высокого порядка точности
- Практическая оценка погрешности при применении квадратурных формул
Приложения определённого интеграла к геометрическим вычислениям
- Площадь области, лежащей между двумя графиками
- Площадь в полярных координатах
- Нахождение объёма тела по площадям поперечных сечений
- Вычисление длины плоской линии
- Площадь поверхности вращения
- Примеры и задачи
Функции нескольких переменных и их дифференцирование
- Открытые и замкнутые области в
- Связные множества
- График функции нескольких переменных
- Пределы функций нескольких переменных
- Непрерывность функции
- Ограничения функции на данное множество
- Свойства функций, непрерывных в области
- Частные производные
- Частные производные высших порядков
- Дифференцируемость функции и дифференциал
- Связь дифференциала с частными производными
- Производная сложной функции
- Инвариантность дифференциала
- Равенство смешанных частных производных
- Теорема о неявной функции
- Производные неявно заданной функции
- Выпуклые множества и функции
- Касательная плоскость к графику функции
- Приближённые вычисления с помощью дифференциала
- Примеры и задачи
Градиент и производная по направлению
- Определение градиента и стационарных точек функции
- Производная по направлению
- Свойства градиента и производной по направлению
- Примеры и задачи
Формула Тейлора для функции нескольких переменных
- Вывод формулы Тейлора
- Матрица Гессе
- Примеры и задачи

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

▷Step by Step Приложения для TI-Nspire CX и CX CAS Скачать бесплатно.

Пройдите курсы по математике, естественным наукам и бизнесу

Подготовка к экзаменам по математике и естественным наукам, домашнее задание. Проверьте свою работу.

— Шаг за шагом к успеху. Приложения запускаются за считанные минуты. Сначала протестируйте наши бесплатные пробные версии.—


95% купили больше ПРИЛОЖЕНИЙ.	97% сообщили об улучшении показателей.	Рейтинг: 4,89 из 5 звезд.	Доступно 46 ПРИЛОЖЕНИЙ.

КОВИД СПЕЦИАЛЬНЫЙ

Купите 3 приложения Made Easy по цене 2 приложений.

Выберите 3 приложения. EasyBusiness Stats Made EasyCalculus with Physics Apps Calculo de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht Gemacht DiscreteMDisateM de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenie ur Mathematik Leicht GemachtFinance Made EasyКонечная математика Made EasyGeometry Made EasyGeometrie Leicht GmachtGeometria de Manera FacilLand Survey Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GmachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyЧисленный анализ Made EasyPhysik Leicht EasyPhysik Research Made EasyPhysik Research Made Easy GemachtFisica de Manera FacilPortfolio & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathSignals and Systems Made EasyStatistics and Probability Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatic and Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equation Solver Ecuaciones de Manera FacilПошаговый конвертер единиц измеренияThermodynamics Made EasyThermodynamik Leicht GemachtTrigonometry Made EasyTrigonometria de Manera FacilTr igonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht

Calculus Made EasyACT Made EasyAccounting Made EasyAerodynamics Made EasyAnalysis Leicht GemachtAnalysis mit PhysikAlgebra Made Easy CX CASAlgebra Made Easy CXAlgebra Leicht Gemacht CX CASAlgebra de Manera FacilAlgebra de Manera Facil CXApplications and Optimizations Made EasyBiology Made EasyBiostatistics AppBusiness Calculus Made EasyBusiness Stats with Physics with de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht GemachtDiscrete Math Made EasyMatematicas Discretas de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieur Mathematik Leicht GemachtFinance Mad e EasyFinite Math Made EasyGeometry Made EasyGeometrie Leicht GemachtGeometria de Manera FacilLand Surveying Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GemachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyNumerical Analysis Made EasyNumber Theory Made EasyProperties Research Made EasyPhysik Made EasyPhysik Leicht Gemacht & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathСигналы и системы Made EasyСтатистика и вероятность Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatik und Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equal SolverSolucionador de EcuacionesStep de Manera Facil by Step Unit ConverterThermodynamic Made EasyThermodynamik Leicht GemachtТригонометрия Made EasyTrigonometria de Manera FacilTrigonometrie Leicht GemachtВекторный расчет us Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht

Введите последние 8 цифр вашего 27-значного идентификатора продукта TI-Nspire.

Находится в разделе 5:Настройки → 4:Статус → О программе

ID может выглядеть так: 1008000007206E210B0 BD92F455 . ПОМОГИТЕ НАЙТИ ID.
Если бы это был ваш ID, вы бы набрали только BD92F455.

или на международном уровне:

В конце оплаты PayPal вам будет отправлено электронное письмо, содержащее ваш ключ и программное обеспечение.

Хотите купить TI-калькулятор?

Получите самые низкие цены на TI-Calculators
(со сравнением цен)

СРАВНИТЕ лучшие цены на Amazon, Ebay, Target, Walmart, Office Max, Best Buy.

Сравните лучшие цены на Amazon, Walmart, Ebay, Target, Best Buy и т. д.
Изучите историю цен калькуляторов за последние несколько месяцев.
Установите оповещение по электронной почте при снижении цен, чтобы получать уведомления.
Сравните различные модели, чтобы найти калькулятор, который лучше всего соответствует вашим потребностям.
Найдите новые, обновленные, восстановленные, подержанные калькуляторы.
Посмотрите обучающие видео и прочитайте руководства по калькуляторам.
Прочтите последние новости о калькуляторах в Интернете.

БЕСПЛАТНАЯ загрузка:
Решатель квадратных уравнений (шаг за шагом)

Загрузите пошаговый решатель квадратных уравнений

. Этот решатель является частью приложения Algebra Made Easy.

— Загрузите бесплатные пробные версии здесь.

— Срок действия пробных и платных приложений неограничен.

— Будущие обновления бесплатны — навсегда!

Онлайн-репетиторство по математике

Получите онлайн-репетиторство.

Репетиторы с отличными оценками по математике будут рады помочь вам.

Получите индивидуальную помощь по математике.

Мы используем Zoom для обучения онлайн, мы шаг за шагом объясняем, как решать математические задачи.

Репетиторы в настоящее время преподают алгебру, алгебру 2, предварительное исчисление, исчисление AP и BC, статистику AP, тригонометрию, дискретную математику.

Репетиторы работали более 10 лет в качестве читателей AP Calculus (те люди, которые оценивают экзамены AP Calculus).

Репетиторы также обучают навыкам сдачи тестов, которые так же важны, как и само содержание.

Наши преподаватели имеют более 20 лет опыта преподавания.

1. урок стоит 50$, после этого 100$ в час.
оптом: 540 долларов за 6 часов, 1000 долларов за 12 часов.

Забронируйте сеанс репетиторства по электронной почте: [email protected]

Для вопросов, заказов и т. д.: ОБЩАЙТЕСЬ С НАМИ.

Первый урок (50 долларов США)	Один урок (100 долларов США)	Несколько уроков

Как найти обратную функцию

Алгебра Учебники

Многие приложения в алгебре и исчислении зависят от знания того, как найти обратную функцию, и это тема данного руководства.

Прежде всего, нужно осознать, что прежде чем найти обратную функцию, нужно убедиться, что такая обратная существует.

Хорошая вещь в методе нахождения инверсии, который мы будем использовать, заключается в том, что мы найдем инверсию и выясним, существует ли она в то же время.

Готовый?? Тогда пристегнитесь.

Как узнать, есть ли у функции обратная функция?

Технически функция имеет обратную, когда она взаимно однозначна (инъективна) и сюръективна.

Однако решающим условием является то, что она должна быть взаимно однозначной, потому что функцию можно сделать сюръективной, ограничив ее диапазон собственным изображением.

Как узнать, является ли функция взаимно однозначной?

Ну, есть как минимум пара способов. Один из них — алгебраический, а другой — графический (держу пари, я знаю, какой из них вы предпочитаете, а?)

Алгебраический путь

Для алгебраического способа, чтобы функция $f$ была взаимно однозначной, нам нужно доказать, что каждый раз, когда $f(x) = f(y)$, нам нужно иметь это $х = у$.

Другими словами, нам нужно доказать, что

\[f(x) = f(y) \,\,\стрелка вправо \,\, x = y\]

Графический способ

Для графического способа нам нужно использовать тест горизонтальной линии : для любой горизонтальной линии, которую мы рисуем, график функции пересекает эту горизонтальную линию не более одного раза.

Графически:

Он проходит тест горизонтальной линии

Не проходит тест горизонтальной линии

Нахождение обратного

Чтобы найти обратную заданную функцию $f(x)$, вам нужно решить уравнение.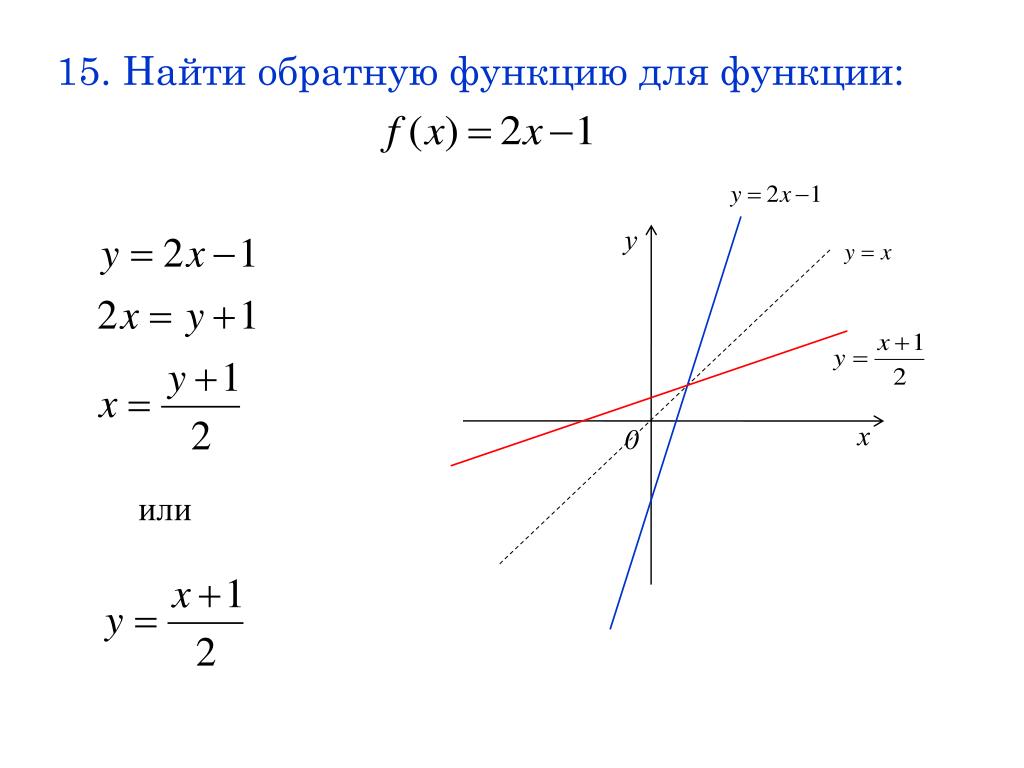

Действительно, у вас есть уравнение $f(x) = y$, вы принимаете $y$ за заданное число, и вам нужно решить его относительно $x$, и вам нужно убедиться, что решение УНИКАЛЬНОЕ.

Это все. Легко, правда??

Теперь о практических шагах:

Шаг 1: Для заданного $y$ задайте уравнение:

\[е(х) = у\]

и решить его относительно $x$.

Шаг 2: Обязательно обратите внимание на то, для каких $y$ на самом деле существует уникальное решение. 9{-1}(х)\).

ПРИМЕР 1

Найдите обратную функцию $f(x) = \sqrt x$

ОТВЕЧАТЬ:

Итак, мы принимаем $y$ как заданное и нам нужно решить $f(x) = y$, что в данном случае соответствует решению

\[\sqrt х = у\]

Обратите внимание, что квадратный корень всегда неотрицательный, поэтому для решения нам нужно, чтобы $y\ge 0$. 92\]

для $х\ge 0$.

ПРИМЕР 2

Найдите обратную функцию $f(x) = \displaystyle \frac{x}{x+1}$, для $x > -1$

ОТВЕЧАТЬ:

Снова считаем $у$ заданным, и теперь нам нужно решить относительно $х$ уравнение $f(x) = y$. Итак, у нас есть

\[\displaystyle \frac{x}{x+1} = y\] \[\Стрелка вправо \,\, х = у(х+1)\] \[\Стрелка вправо \,\, х = ух + у\] \[\Стрелка вправо \,\, х — ух = у\] \[\Стрелка вправо \,\, х(1 — у) = у\] \[\Rightarrow \displaystyle \,\, x = \frac{y}{1-y}\] 9{-1}(х)) = х\).

Подумайте о том, что говорит эта штука. Что-то вроде: «Функция, вычисляемая в обратном порядке, дает вам личность».

Или, другими словами, вычисление инверсии через функцию равносильно тому, чтобы ничего не делать с аргументом.

Или, как любят говорить некоторые люди: функция может каким-то образом отменять обратную.

Вы выбираете свою версию.

Как найти обратную квадратичную функцию? Не могли бы вы?

На самом деле, ответ таков: это зависит. Это потому, что если мы рассмотрим квадратичную функцию на всей реальной линии , то это не 1-к-1, так как он не проходит тест горизонтальной линии, как вы можете видеть на графике ниже:

Не проходя тест горизонтальной линии, мы можем видеть, что для заданного $y$ существует более одного значения $x$, так что $f(x) = y$, поэтому мы не можем «решить» для $x$, так как существует более одного $x$.

НО, если вы ограничите домен и рассмотрите, скажем, только положительные числа, мы получим следующее:

которая проходит тест горизонтальной прямой, и, следовательно, квадратичная функция обратима.

МОРАЛЬ ИСТОРИИ: чтобы проверить, обратимо ли что-то, нужно НЕ только функцию. Речь идет о функции И ее домен и диапазон .

Как быстро построить график обратных функций

Всегда требуется оценить, является ли функция $f(x)$ обратимой или нет (проверив, является ли она взаимно однозначной).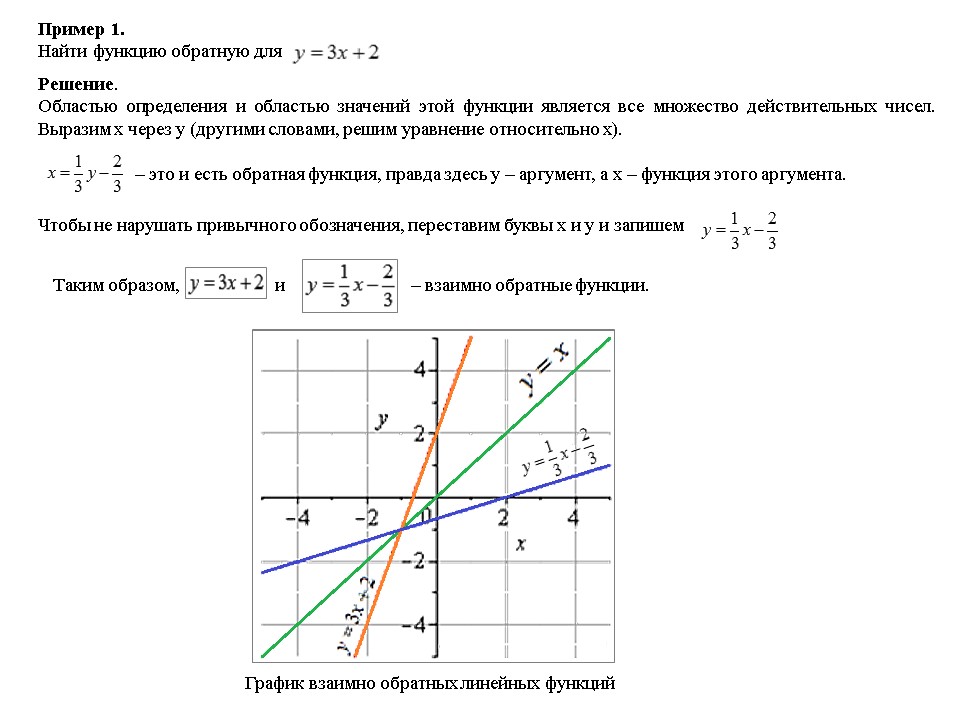 Но предполагая, что вы знаете, что оно обратимо, есть простой способ найти график обратного выражения.

Сначала начертите график заданной функции $f(x)$. 9{-1}(x) = \arcsinx\)

Другой способ увидеть это — использовать оригинал график и измените значение $x$ на значение $y$.

Есть ли способ, чтобы функция была сама себе инверсной?

Да, это действительно возможно, но это происходит только для функции тождества, т. е. с $f(x) = x$.

Учебник по алгебре График обратного Как найти обратную функцию Функции один к одному

Калькулятор обратной функции онлайн для студентов

В математике функция, которая может превратиться в другую функцию, называется обратной функцией, иногда называемой антифункцией. Рассмотрим функцию «f», которая преобразует x в y. Обратной функции «f» является y на x. Обозначается как f(x) = y ⇔ f− 1(y) = x. Учащиеся применяют калькулятор обратной функции, чтобы определить обратное значение функции, предоставленной в качестве входных данных.

Нахождение обратной функции без использования калькулятора обратной функции

В арифметике обратная функция — это тип функции, обращающий другую функцию. Калькулятор обратной функции — это веб-приложение, которое позволяет пользователям быстро находить обратную функцию. Придерживайтесь следующих методов вычисления обратных функций без использования калькулятора обратных функций, если вы не знаете об этом процессе.

Вы пытаетесь найти обратную функцию в отсутствие Калькулятор обратной функции ? Вы можете начать с замены функциональной переменной другой переменной. Затем, наконец, подставив обе переменные, вычислите другую переменную.

Пример 1
Определите обратную следующую функцию
f(x) = y = 4x-1
Ответ:
Начните с замены f(x) на f(y)
Следовательно, вы должны получить следующее уравнение
y= 4x-1
это можно записать как
x=4y-1
Теперь учащиеся должны найти значение y; что
y= (x+1) / 4
Следовательно, обратная функция y = (x+1)/4

Ниже приведена еще одна иллюстрация нахождения обратной функции без помощи калькулятора обратной функции .

Пример 2
Найдите обратную функцию
y=x+7/3x+5
Начните с замены x на y и наоборот
x = (y+7) / (3y+5)
или x (3y +5) = y+7
или 3xy+5x-y=7
или 3xy-y=7-5x
или y(3x-1) =7-5x
или y= (7-5x) / (3x- 1)
Следовательно, обратная функция y равна =(7-5x) / (3x-1)

Остались вопросы о том, как вычислить обратную функцию? Студенты могут использовать наш калькулятор обратной функции на нашей платформе для быстрых и простых расчетов.

Хотя вычисление обратной функции без использования калькулятора может быть для некоторых простым делом, они борются за то, чтобы понять фундаментальные концепции, и получают низкие оценки в своих работах. Поиск сложных обратных функций может потребовать использования калькулятора обратных функций.

Если вы хотите использовать Калькулятор обратной функции , обязательно соблюдайте приведенные ниже правила:

Нет необходимости зацикливаться на определении обратной функции. Вместо этого попробуйте наш калькулятор обратной функции, чтобы исключить шаги, которые не являются необходимыми, и получить быстрые результаты.

Представьте, что вы обсуждаете, воспользоваться ли помощью нашего калькулятора обратной функции. Затем бесплатно протестируйте наш калькулятор обратных уравнений и примите собственное решение.

Разница между обратными и обратными функциями

В математике фразы «обратный» и «обратный» часто используются и имеют сопоставимые значения. 1/a является мультипликативным обратным или обратным числом «a» и описывается как число, которое возвращает единицу при умножении на число (1). Это указывает на то, что обратная или мультипликативная обратная дробь x/y равна y/x. Если у вас есть действительное число, разделите его на 1, если вы хотите получить обратное или обратное число. Обратные числа — это любые два числа, произведение которых равно 1. Несмотря на тесную связь, обратная и обратная имеют некоторые отличия.

Работа по получению обратной дроби упрощается, потому что все, что нужно сделать, это поменять местами числитель и знаменатель.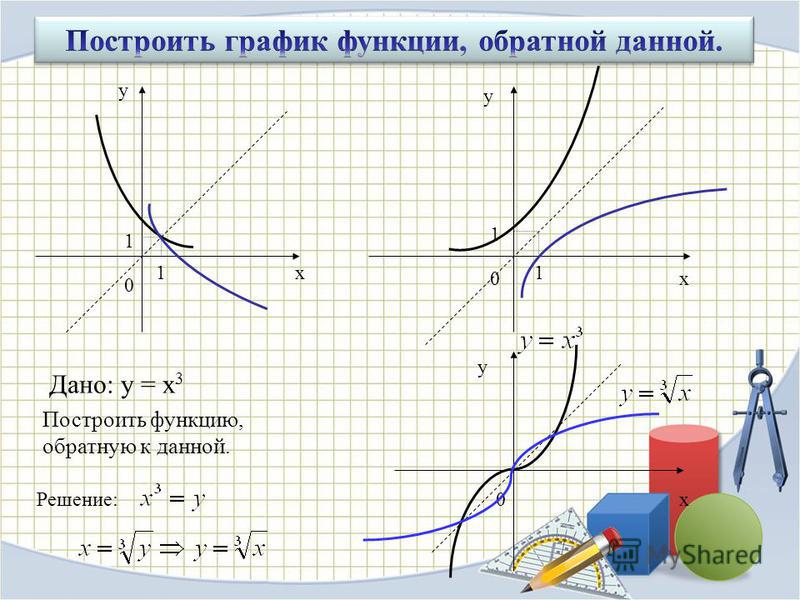 Концепция взаимности особенно полезна, поскольку упрощает многие арифметические задачи и позволяет решить задачу в уме.

Преимущества использования нашего уникального калькулятора обратной функции

Для получения отличных оценок по математике необходимы точные решения с подходящими шагами. Учащиеся, у которых недостаточно знаний или у которых жесткие сроки, должны использовать наш калькулятор уравнений и обратных функций, чтобы выполнять задания в срок. Другие преимущества использования нашего калькулятора обратной функции включают следующее.

Узнайте больше о нашем калькуляторе обратной функции и других академических инструментах.

Вооружившись нашим калькулятором обратной функции , учащиеся могут сделать вычисления проще и менее пугающими. С другой стороны, наши специалисты по математике помогут вам запомнить основы вычисления обратной функции без использования калькулятора.

Наши гуру математики являются настоящими экспертами в этой области, которые помогли тысячам учащихся преодолеть страх перед математикой и получить исключительные оценки, в дополнение к нашему совершенному калькулятору обратной функции и калькулятору уравнений.

Обратная функция — презентация онлайн

3. Задание

4. СЛОЖНАЯ ФУНКЦИЯ

5. Повторение.

6.

8. Определение: Функции, у которых аргумент в свою очередь также является функцией, называются сложной функций или композицией

9. Формула для задания сложной функции

10. Примеры сложной функции y=f(g(x))

11. Составьте сложную функцию ,если f(x)=x2, g(x)=2x-4, h(x)=sin x например: y=h(f(x))=sin x2

12.

13. Пример 1

17. Пример 2

19.

24.

26. Нахождение множества значений сложной функции

27. Множество значений сложной функции как множество значений внешней функции

Урок 12. Функции и их свойства. Теория 11 класс онлайн-подготовка на Ростелеком Лицей

Определение функции. Понятие ГМТ. Отличие функции от ГМТ

Область определения, область значений

Асимптоты функции, точки пересечения с осями

Чётность и нечётность, периодичность

Промежутки монотонности функции

Обратные функции

Решение высшей математики онлайн

▷Step by Step Приложения для TI-Nspire CX и CX CAS Скачать бесплатно.

Подготовка к экзаменам по математике и естественным наукам, домашнее задание. Проверьте свою работу.

— Шаг за шагом к успеху. Приложения запускаются за считанные минуты. Сначала протестируйте наши бесплатные пробные версии.—

Как найти обратную функцию

Как узнать, есть ли у функции обратная функция?

Нахождение обратного

ОТВЕЧАТЬ:

ОТВЕЧАТЬ:

Как найти обратную квадратичную функцию? Не могли бы вы?

Как быстро построить график обратных функций

Есть ли способ, чтобы функция была сама себе инверсной?

Калькулятор обратной функции онлайн для студентов

Добавить комментарий Отменить ответ