Расстояние между двумя точками онлайн
С помощю этого онлайн калькулятора можно найти расстояние между точками по известным координатам этих точек. Дается решение с пояснениями. Для нахождения расстояния между точками задайте размерность (2-если задача рассматривается в двухмерном пространстве, 3- если задача рассматривается в трехмерном пространстве), введите координаты точек в ячейки и нажмите на кнопку «Решить». Теоретическую часть смотрите ниже.
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между двумя точками на прямой
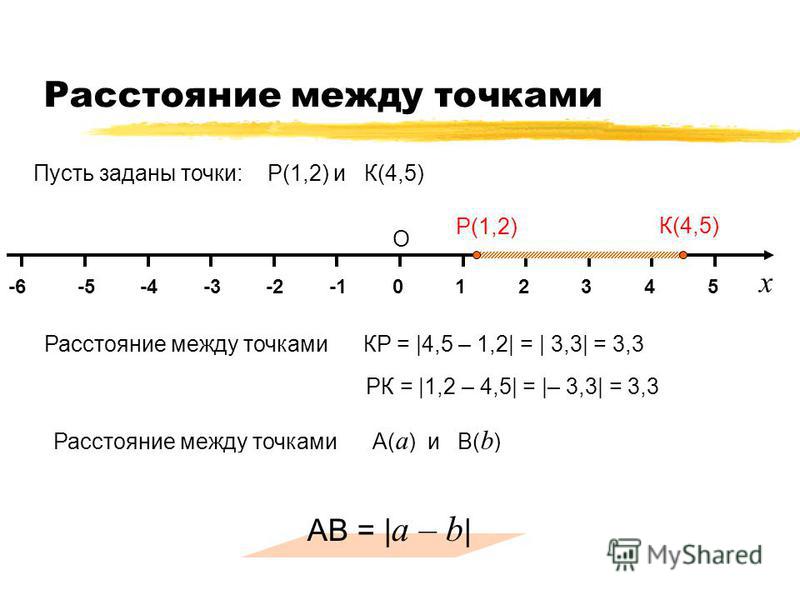
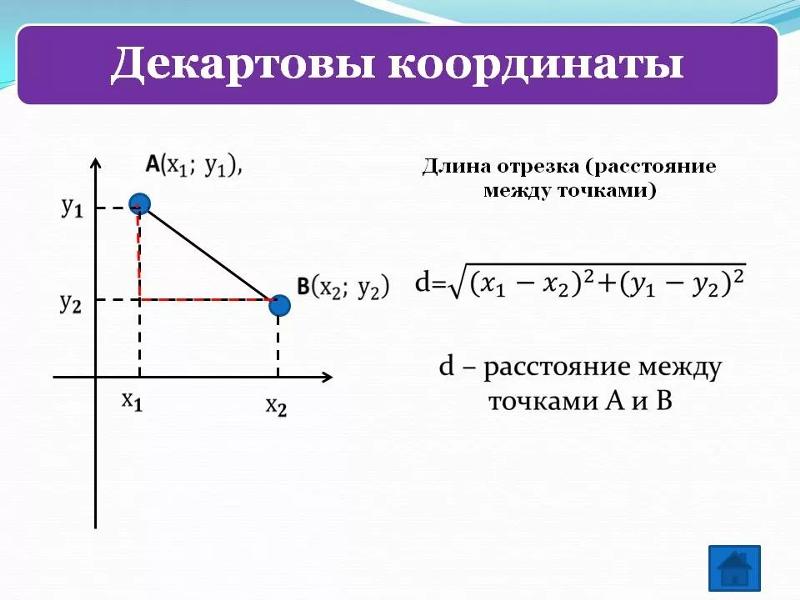
Пусть заданы на оси OX точки A с координатой xa и B с координатой xb (Рис.1). Найдем расстояние между точками A и B.
Расстояние между точками A и В равно:
| \( \small AB=OB-OA. \) | (1) |
Поскольку расстояние от O до В равна xb, а расстояние от O до A равна xa, получим:
| \( \small AB=x_b-x_a . \) | (2) |
На рисунке 2 точки A и В находятся по разные стороны начала координат O. B этом случае рассояние между точками A и B равно:
| \( \small AB=OB+OA. \) | (3) |
Поскольку координата точки A отрицательна а координата точки
| \( \small AB=x_b+|x_a|=x_b-x_a . \) | (4) |
На рисунке 3 точки A и В находятся c левой стороны начала координат O.
B этом случае рассояние между точками A и B равно:
| \( \small AB=OA-OB. \) | (5) |
Координаты точек A и B отрицательны. Тогда , то (5) можно записать так:
| \( \small AB=|x_a|-|x_b|=x_b-x_a . \) | (6) |
Из формул (2),(4),(6) следует, что независимо от расположения точек отностительно начала координат рассояние этих точек равна разности координат этих точек, причем от большего значения вычитается меньшее (так как расстояние не может быть отрицательным числом).
Формулы (2),(4),(6) можно записать и так:
| \( \small AB=|x_b-x_a|= |x_a-x_b| . \) | (7) |
Пример 1. на оси Ox заданы точки \( \small A(x_a)=A(-4) \) и \( \small B(x_b)=B(7) \) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (7):
\( \small AB=|x_b-x_a|= |7-(-4)|=11 .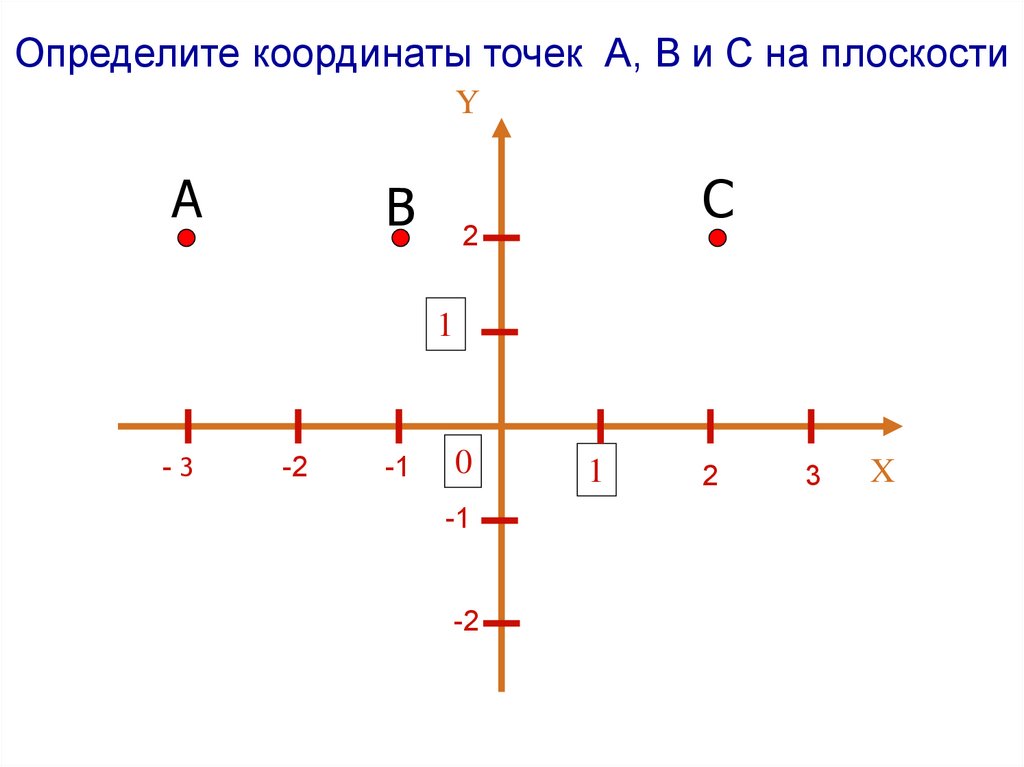 2}. \) | (9) |
Пример 2. На плоскости, в декартовой прямоугольной системе координат XOY заданы точки \( \small A(x_a; \ y_a)=A(-6;3) \) и \( \small B(x_b, \ y_b)=B(11,-4). \) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (9). Подставляя координаты точек
Ответ: .
Расстояние между двумя точками в пространстве
Рассмотрим в пространстве, в декартовой прямоугольной системе координат точки A и B, где A имеет координаты (xa,ya,za), а B имеет координаты (xb,yb,zb) (Рис.5).
AB является диагональю параллелепипеда, грани которго параллельны координатным плоскостьям и проходят через точки A и B. Но AB является гипотенузой прямоугольного треугольника AMB, а AM и BM являются катетами этого прямоугольного треугольника.
2}. \)
Пример 3. В пространстве задана декартова прямоугольная система координат XOY и точки \( \small A(x_a; \ y_a ;\ z_a)=A(5;1;0) \) и \( \small B(x_b, \ y_b, \ z_b)=B(-8,-4;21). \) Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (12). Подставляя координаты точек A и B в формулу (12), получим:
Ответ: .
Вычисление расстояния и начального азимута между двумя точками на сфере
Эта страница опубликована в основном списке статей сайта
по адресу http://gis-lab.info/qa/great-circles.html
Измерение расстояния и начального азимута между точками без проекционных преобразований
Содержание
|
5 Реализация на языке PythonДлина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения. Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.
Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется.
Начальный азимут [angles-rhumb.html отличен от постоянного], следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не
большой круг
Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или pi*R, где R – радиус сферы.
расстояние большого круга
На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии.
На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.
Маршрут Нью-Йорк — Пекин
Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.
Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.
Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.
Существует три способа расчета сферического расстояния большого круга (подробнее).
[править] Сферическая теорема косинусов
В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением. Графическое изображение формул здесь и далее — из Википедии.
— широта и долгота двух точек в радианах
— разница координат по долготе
— угловая разница
Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).
[править] Формула гаверсинусов
Используется, чтобы избежать проблем с небольшими расстояниями.
[править] Модификация для антиподов
Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.
[править] Реализация на Avenue
На языке Avenue, используя последнюю формулу для вычисления расстояния большого круга между двумя точками, можно использовать следующий код. Точки для вычисления передаются другим скриптом, либо добавляются в начало данного в виде pnt = point.make(long, lat) (скачать скрипт):
'pnt1, pnt2 - точки между которыми вычисляются расстояния 'pi - число pi, rad - радиус сферы (Земли), num - количество знаков после запятой pi = 3.14159265358979 rad = 6372795 num = 7 'получение координат точек в радианах lat1 = pnt1.getY*pi/180 lat2 = pnt2.getY*pi/180 long1 = pnt1.getX*pi/180 long2 = pnt2.getX*pi/180 'косинусы и синусы широт и разниц долгот cl1 = lat1.cos cl2 = lat2.0.5 p4 = sl1*sl2 p5 = cl1*cl2*cdelta p6 = p4 + p5 p7 = p3/p6 anglerad = (p7.atan).SetFormatPrecision (num)
dist = anglerad*rad
'вычисление начального азимута
x = (cl1*sl2) - (sl1*cl2*cdelta)
y = sdelta*cl2
z = (-y/x).ATan.AsDegrees
if (x < 0) then z = z+180 end
z = -(z + 180 mod 360 - 180).AsRadians
anglerad2 = z - ((2*pi)*((z/(2*pi)).floor)) angledeg = (anglerad2*180)/pi'возврат значений длины большого круга и начального азимута
distlist = {dist, angledeg}
return distlist
0.5
p4 = sl1*sl2
p5 = cl1*cl2*cdelta
p6 = p4 + p5
p7 = p3/p6
anglerad = (p7.atan).SetFormatPrecision (num)Для вызова процедуры расчета длин приведенной выше, можно также воспользоваться следующим скриптом, результатом его работы будет расчет длин между точкой testpont до всех точек активной темы вида и запись результата в поле Newdist атрибутивной таблицы этой темы:
atheme = av.getactivedoc.getactivethemes.get(0)
aftab = atheme.getftab
f_shape = aftab.findfield("Shape")
f_dist = aftab.findfield("dist")
f_ang = aftab.findfield("ang")
'testpoint - точка отсчета
testpoint = point. make(25.85, 55.15)
aftab.seteditable(true)
'для каждой точки темы до которых считают расстояния от точки отсчета
for each rec in aftab
pnts = {}
apoint = aftab.returnvalue(f_shape, rec)
pnts.add(apoint.getx)
pnts.add(testpoint.getx)
pnts.add(apoint.gety)
pnts.add(testpoint.gety)
'Вызов процедуры расчета расстояний
'"Calc-distance" - название скрипта с процедурой в проекте
param = av.run("Calc-distance", pnts)
aftab.setvalue(f_dist, rec, param.get(0))
aftab.setvalue(f_ang, rec, param.get(1))
end
aftab.seteditable(false)
make(25.85, 55.15)
aftab.seteditable(true)
'для каждой точки темы до которых считают расстояния от точки отсчета
for each rec in aftab
pnts = {}
apoint = aftab.returnvalue(f_shape, rec)
pnts.add(apoint.getx)
pnts.add(testpoint.getx)
pnts.add(apoint.gety)
pnts.add(testpoint.gety)
'Вызов процедуры расчета расстояний
'"Calc-distance" - название скрипта с процедурой в проекте
param = av.run("Calc-distance", pnts)
aftab.setvalue(f_dist, rec, param.get(0))
aftab.setvalue(f_ang, rec, param.get(1))
end
aftab.seteditable(false)
[править] Реализация на языке Python
Реализует полный вариант расчета через atan2(), более универсальнее, чем вариант для Avenue. (скачать скрипт)
import math #pi - число pi, rad - радиус сферы (Земли) rad = 6372795 #координаты двух точек llat1 = 77.1539 llong1 = -120.398 llat2 = 77.1804 llong2 = 129.55 #в радианах lat1 = llat1*math.pi/180. lat2 = llat2*math.pi/180. long1 = llong1*math.pi/180. long2 = llong2*math.pi/180.
#косинусы и синусы широт и разницы долгот
cl1 = math.cos(lat1)
cl2 = math.cos(lat2)
sl1 = math.sin(lat1)
sl2 = math.sin(lat2)
delta = long2 - long1
cdelta = math.cos(delta)
sdelta = math.sin(delta)
#вычисления длины большого круга
y = math.sqrt(math.pow(cl2*sdelta,2)+math.pow(cl1*sl2-sl1*cl2*cdelta,2))
x = sl1*sl2+cl1*cl2*cdelta
ad = math.atan2(y,x)
dist = ad*rad
#вычисление начального азимута
x = (cl1*sl2) - (sl1*cl2*cdelta)
y = sdelta*cl2
z = math.degrees(math.atan(-y/x))
if (x < 0):
z = z+180.
z2 = (z+180.) % 360. - 180.
z2 = - math.radians(z2)
anglerad2 = z2 - ((2*math.pi)*math.floor((z2/(2*math.pi))) )
angledeg = (anglerad2*180.)/math.pi
print 'Distance >> %.0f' % dist, ' [meters]'
print 'Initial bearing >> ', angledeg, '[degrees]'
[править] Реализация в Excel
Скачать пример расчета расстояния большого круга и начального азимута в Excel. Демонстрирует расчеты через закон косинусов, гаверсинус, полное уравнение и полное уравнение через atan2().
0.5) * 6372795
End With
End Function
[править] Проверочный набор данных
Если все считается правильно, должны быть получены следующие результаты (координаты точек даны как широта/долгота, расстояние в метрах, начальный угол в десятичных градусах):
| # | Точка 1 | Точка 2 | Расстояние | Угол |
| 1 | 77.1539/-139.398 | -77.1804/-139.55 | 17166029 | 180.077867811 |
| 2 | 77.1539/120.398 | 77.1804/129.55 | 225883 | 84.7925159033 |
| 3 | 77.1539/-120.398 | 77.1804/129.55 | 2332669 | 324.384112704 |
[править] Ссылки по теме
- Вычисление азимута из одной точки на другую и угла образованного тремя точками на сфере
- Вычисление постоянного азимута и длины линии румба между двумя точками для геодезических координат
- Сравнение разных способов вычисления длин и азимутов
Расстояние между точками координатной прямой.
Вычислить расстояние между точками.- Альфашкола
- Статьи
- Расстояние между точками на координатной прямой
Расстояние между двумя точками является длиной отрезка, между этими точками. Как найти расстояние между двумя заданными точками?
Для того чтобы найти длину отрезка на координатной прямой надо из координаты ее конца вычесть координату начала по модулю.
Пример . Найдите расстояние между точками:
- \(A(-15)\) и \(B(3)\)
- \(C(3,2)\) и \(D(7,8)\)
- \(E(5)\) и \(K(-17)\)
Для понимания важно знать какая из точек находится правее, а какая левее.
Хотя это не важно, так как мы берем расстояние по модулю, то есть отрицательным значение не может быть.
Решение:
\(|AB|=b-a\)
1) \(|AB| = 3-(-15)=|18|=18\)
2) \(|CD| = (3;2)-(7;8)=|(-4;-6)|=(4;6)-\) это означает на рисунке выше по оси x расстояние равно четырем единицам и по оси y 6 единицам длины.
3) \(|EK| = 5-(-17)=|22|=22\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Анна Казимировна Пятчиц
Репетитор по математике
Стаж (лет)
Образование:
Барановичский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку для 1-4 классов и по математике для 1-5 классов.
Доброжелательна, позитивно настроена, всегда в хорошем настроении с улыбкой на лице. На занятии учитываю психотип ребёнка и его «язык» коммуникаций. Встречаю учеников с хорошим и доброжелательным настроением, настраиваю ребят на отличную тренировку. Проявляю интерес к увлечениям учеников, поддерживаю их достижения. Использую юмор, задания на внимание, игры на скорость. Имею опыт взаимодействия с группами детей разных возрастов. Опыт с детьми более 20 лет
Андрей Андреевич Лаптик
Репетитор по математике
Стаж (лет)
Образование:
Мозырский государственный педагогический университет им. И.П. Шамякина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 1-7 классов и по информатике для 1-7 классов.
Применяю индивидуальный подход в обучении каждого ученика. Могу заинтересовать учащихся изучением своего предмета, поддерживая корректные и уважительные отношения. Младшие классы — программирование в Scratch, 5-7 классы — программирование в чертежнике/PascalABC
Виктория Григорьевна Рагузина
Репетитор по математике
Стаж (лет)
Образование:
Самарская государственная академия. / Столичный учебный центр
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 2-9 классов, подготавливаю к ОГЭ.
Математика есть прообраз красоты мира! Люблю математику и люблю учить так, чтобы был результат. С терпением отношусь к тем, кому математика дается не просто. Как репетитор использую новые методики, разные учебники и пособия, предлагаю дополнительные материалы и компьютерные технологии
Похожие статьи
- Задачи на движение
- Стадии подготовки к экзамену по математике
- Центральный угол окружности
- Как легко умножить на 0,5
- НИУ ВШЭ: вступительные испытания и проходные баллы
- ЕГЭ по математике, базовый уровень. Задачи на координатной решетке
- Профессиональное выгорание: как вернуть энергию?
- «Неблагодарный!»: что делать, если родители манипулируют?
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Расстояние между двумя точками — формула, расчет, примеры
Расстояние между двумя точками — это длина отрезка, соединяющего две заданные точки.
Расстояние между двумя точками в координатной геометрии можно рассчитать, найдя длину отрезка, соединяющего заданные координаты. Давайте поймем формулу, чтобы найти расстояние между двумя точками в двумерной и трехмерной плоскости.
| 1. | Какое расстояние между двумя точками? |
| 2. | Расстояние между двумя точками Формула |
| 3. | Вывод формулы для расстояния между двумя точками |
| 4. | Как найти расстояние между двумя точками? |
| 5. | Расстояние между двумя точками на комплексной плоскости |
| 6. | Часто задаваемые вопросы о расстоянии между двумя точками |
Какое расстояние между двумя точками?
Расстояние между любыми двумя точками — это длина отрезка, соединяющего точки. Через две точки проходит только одна прямая.
Итак, расстояние между двумя точками можно рассчитать, найдя длину этого отрезка, соединяющего две точки. Например, если A и B — две точки и \(\overline{AB}=10\) см, это означает, что расстояние между A и B равно 10 см.
Расстояние между двумя точками равно длине соединяющего их отрезка (но это НЕ МОЖЕТ быть длиной соединяющей их кривой). Обратите внимание, что расстояние между двумя точками всегда положительно.
Расстояние между двумя точками Формула
Расстояние между двумя точками с заданными координатами можно рассчитать, применив формулу расстояния. Для любой точки, заданной на двумерной плоскости, мы можем применить формулу двумерного расстояния или формулу евклидова расстояния, заданную как
Формула для расстояния между двумя точками:
Формула для расстояния \(d\) между двумя точками с координатами \((x_1, y_1)\) и \((x_2, y_2\)) выглядит следующим образом:
d = √[(\(x_2\) − \(x_1\)) 2 + (\(y_2\) − \(y_1\)) 2 ]
Это называется формулой расстояния .
Чтобы найти расстояние между двумя точками, заданными в трехмерной плоскости, мы можем применить формулу трехмерного расстояния, заданную как
d = √[(\(x_2\) − \(x_1\)) 2 + (\(y_2\) — \(y_1\)) 2 + (\(z_2\) — \(z_1\)) 2 ]
Далее давайте узнаем, как вывести эту формулу.
Вывод формулы для расстояния между двумя точками
Чтобы вывести формулу для расчета расстояния между двумя точками на двумерной плоскости, предположим, что есть две точки с координатами, заданными как A(\(x_1, y_1\)) B(\(x_2, y_2\))
Далее предположим, что отрезок, соединяющий A и B, равен \(\overline{AB}=d\). Теперь нанесем заданные точки на координатную плоскость и соединим их линией.
Далее мы построим прямоугольный треугольник с \(\overline{AB}\) в качестве гипотенузы.
Применение теоремы Pythagoras для △ ABC:
AB 2 = AC 2 + BC 2
D 2 = (\ (x_2 \) — \ (x_1 \)) + (\(y_2\) − \(y_1\)) 2 (значения с рисунка)
Здесь вертикальное расстояние между заданными точками равно |\(y_2\) − \(y_1\)|.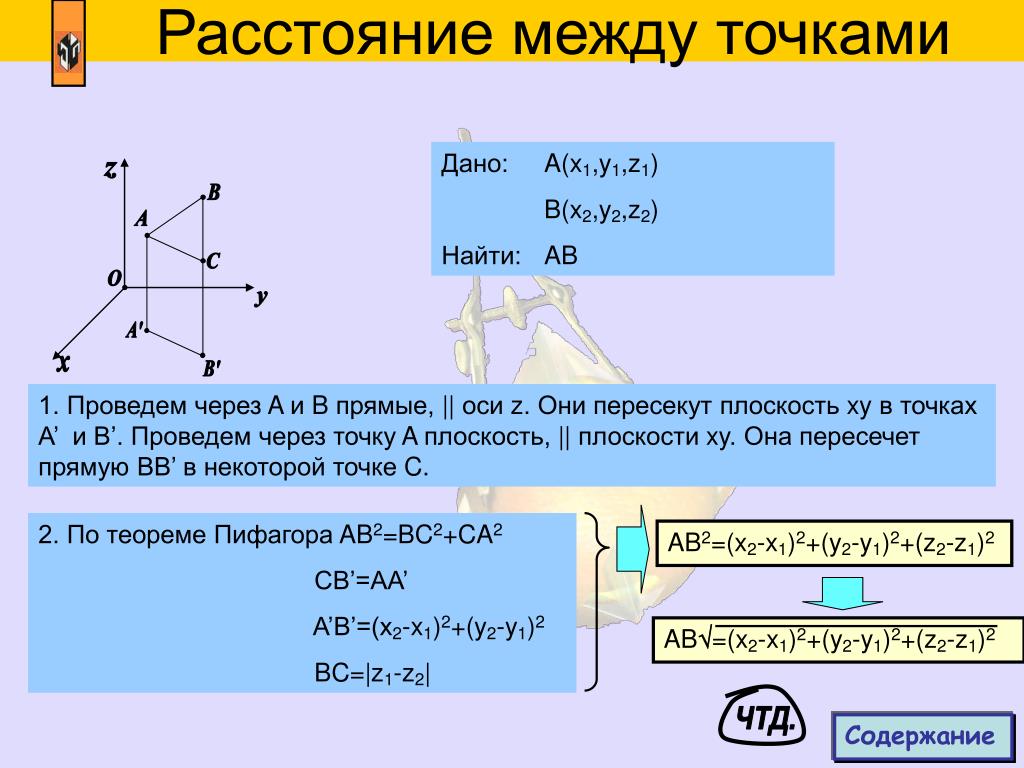
Горизонтальное расстояние между заданными точками равно |\(x_2\) − \(x_1\)|.
d = √[(\(x_2\) − \(x_1\)) 2 + (\(y_2\) − \(y_1\)) 2 ] (Извлечение квадратного корня с обеих сторон)
Таким образом, формула расстояния для нахождения расстояния между двумя точками доказана.
Примечание. Если две точки A и B находятся на оси x, т. е. координаты A и B равны (\(x_1\), 0) и (\(x_2\), 0) соответственно, то расстояние между двумя точками AB = |\(x_2\) − \(x_1\)|.
Используя аналогичные шаги и концепцию, мы также можем вывести формулу для нахождения расстояния между двумя точками, заданными в трехмерной плоскости.
Как найти расстояние между двумя точками?
Расстояние между двумя точками с заданными координатами можно рассчитать с помощью следующих шагов:
- Запишите координаты двух заданных точек на координатной плоскости как A(\(x_1, y_1\) ) и B(\(x_2, y_2\)).
- Мы можем применить формулу расстояния, чтобы найти расстояние между двумя точками, d = √[(\(x_2\) − \(x_1\)) 2 + (\(y_2\) − \(y_1\)) 2 ]
- Выразите данный ответ в единицах.
Примечание. Мы можем применить формулу трехмерного расстояния, если две точки заданы в трехмерной плоскости, d = √[(\(x_2\) − \(x_1\)) 2 + (\(y_2\) − \(y_1\)) 2 + (\(z_2\) − \(z_1\)) 2 ]
Пример: Найдите расстояние между двумя точками с координатами, заданными как, A = (1, 2) и В = (1, 5).
Решение:
Расстояние между двумя точками с помощью координат можно задать как d = √[(\(x_2\) − \(x_1\)) 2 + (\(y_2\) − \(y_1\)) 2 ], где (\(x_1, y_1\)) и (\(x_2, y_2\)) — координаты двух точек.
⇒ d = √[(1 − 1) 2 + (5 − 2) 2 ]
⇒ d = 3 единицы
данные точки одинаковы, мы можем найти расстояние между двумя точками, найдя разницу между координатами y.
Расстояние между двумя точками комплексной плоскости
Расстояние между двумя точками на комплексной плоскости или двумя комплексными числами z\(_1\) = a + ib и z\(_2\) = c + id на комплексной плоскости есть расстояние между точками (a, b) и (c, d), заданные как
|z\(_1\) − z\(_2\)| = √[(a − c) 2 + (b − d) 2 ]
Связанные темы:
- Формула Евклидова расстояния
- Геометрия
- оси x и y
Важные примечания по расстоянию между двумя точками:
- Расстояние d между двумя точками с координатами \((x_1, y_1)\) и \((x_2, y_2\)) равно: d = √[(\(x_2\) − \(x_1 \)) 2 + (\(y_2\) − \(y_1\)) 2 ]
- Расстояние точки (a, b) от:
(i) x — ось |b|.
(ii) y — ось |a|.
Мы использовали знаки абсолютного значения, потому что расстояние никогда не может быть отрицательным.
Часто задаваемые вопросы о расстоянии между двумя точками
Что понимается под расстоянием между двумя точками?
Расстояние между двумя точками определяется как длина прямой линии, соединяющей эти точки в координатной плоскости. Это расстояние никогда не может быть отрицательным, поэтому мы берем абсолютное значение при нахождении расстояния между двумя заданными точками.
Как рассчитать расстояние между двумя точками на 2D-плоскости?
Расстояние между любыми двумя точками, заданными на двумерной плоскости, можно рассчитать, используя их координаты. Расстояние между двумя точками A(\(x_1, y_1\)) и B(\(x_2, y_2\)) можно рассчитать как d = √[(\(x_2\) — \(x_1\)) 2 + (\(y_2\) − \(y_1\)) 2 ].
Как найти расстояние между двумя точками в 3D-плоскости?
Чтобы вычислить расстояние между двумя точками в трехмерной плоскости, мы можем применить формулу трехмерного расстояния, заданную как d = √[(\(x_2\) − \(x_1\)) 2 + (\( y_2\) − \(y_1\)) 2 + (\(z_2\) − \(z_1\)) 2 ], где d — расстояние между двумя точками и (\(x_1, y_1 , z_1\)), (\(x_2, y_2, z_2\)) — координаты двух точек.
Какое кратчайшее расстояние между двумя точками?
Кратчайшее расстояние между двумя точками можно рассчитать, найдя длину прямой линии, соединяющей обе точки. Мы можем применить формулу расстояния, чтобы найти это расстояние в зависимости от координат, заданных в двух- или трехмерной плоскости.
Как найти расстояние между двумя точками с помощью теоремы Пифагора?
Расстояние между двумя точками на декартовой плоскости можно рассчитать, применив теорему Пифагора. Мы можем построить прямоугольный треугольник, используя линию, соединяющую данные две точки в качестве гипотенузы. Здесь перпендикуляром и основанием будут прямые, параллельные осям x и y, с одним концом в качестве одной из заданных точек, а другим концом в качестве точки их пересечения. Используя теорему Пифагора, (гипотенуза) 2 = (основание) 2 + (перпендикуляр) 2 , мы можем найти длину гипотенузы с помощью заданных координат двух точек. Эта длина равна расстоянию между двумя точками.
Какова формула расстояния для определения расстояния между двумя точками в координатной геометрии?
В координатной геометрии формула расстояния между двумя точками задается как d = √[(\(x_2\) − \(x_1\)) 2 + (\(y_2\) − \(y_1\)) 2 ], где (\(x_1, y_1\)), (\(x_2, y_2\)) — координаты двух точек. Мы можем применить другую формулу, если заданные точки liw лежат в трехмерной плоскости, d = √[(\(x_2\) − \(x_1\)) 2 + (\(y_2\) − \(y_1\)) 2 + (\(z_2\) − \(z_1\)) 2 ], где d — расстояние между двумя точками и (\(x_1, y_1, z_1\)), (\(x_2, y_2, z_2\)) — координаты двух точек.
Как вывести формулу для нахождения расстояния между двумя точками?
Мы можем применить теорему Пифагора, чтобы вывести формулу расстояния между двумя точками. Мы можем принять линию, соединяющую две точки, как гипотенузу прямоугольного треугольника, образованного в декартовой плоскости. Длину гипотенузы можно рассчитать, используя теорему Пифагора и заданные координаты двух точек, чтобы получить формулу расстояния между двумя точками.
Как найти вертикальное расстояние между двумя точками?
Расстояние по вертикали между двумя точками можно найти, вычислив разность координат y двух точек, т. е. расстояние по вертикали между двумя точками, \(d_y\) = \(y_2 — y_1\), где (\( x_1, y_1\)), (\(x_2, y_2\)) — координаты двух точек.
Какие шаги нужно выполнить, чтобы найти евклидово расстояние между двумя точками?
Евклидово расстояние между двумя точками можно рассчитать с помощью следующих шагов:
- Запишите координаты обеих заданных точек как (\(x_1, y_1\)) и (\(x_2, y_2\)).
- Применить формулу Евклидова расстояния, расстояние, d = √[(\(x_2\) − \(x_1\)) 2 + (\(y_2\) − \(y_1\)) 2 ]
- Выразите данный ответ в единицах.
Как рассчитать расстояние между двумя точками?
Длина отрезка, соединяющего две точки, определяется как расстояние между ними. Длину отрезка, соединяющего указанные координаты, можно использовать для вычисления расстояния между двумя точками в координатной геометрии.
Давайте посмотрим на формулу расчета расстояния между двумя точками на двумерной или трехмерной плоскости.
Расстояние отрезка, соединяющего любые две точки, равно расстоянию между ними. Есть только одна линия, соединяющая две точки. В результате расстояние между двумя точками можно вычислить, определив длину отрезка, соединяющего две точки. Например, если A и B — две точки, а A B = 20 см, это означает, что расстояние между A и B равно 20 см.
Длина отрезка, соединяющего две точки, равна расстоянию между ними (но это НЕ МОЖЕТ быть длиной соединяющей их кривой). Важно отметить, что расстояние между двумя точками всегда положительно.
Формула расстояния между двумя точками Формула расстояния используется для определения расстояния между двумя точками с использованием предоставленных координат. Мы используем формулу двумерного расстояния или формулу евклидова расстояния для расчета расстояния между любыми двумя точками на двумерной плоскости.
Формула для расстояния между двумя точками
Формула для расстояния d между двумя точками с координатами (x 1 , y 1 ) и (x 2, y 2 ) равно
Это называется формулой расстояния.
Чтобы найти расстояние между двумя точками, заданными в трехмерной плоскости, мы можем применить формулу для трехмерного расстояния: вычисляя расстояние между двумя точками на двумерной плоскости, предположим, что есть две точки с координатами A (x 1 ,y 1 ) и B (x 2 ,y 2 ). После этого будем считать, что отрезок, соединяющий A и B, равен AB = d. Теперь нанесем указанные точки на координатную плоскость и соединим их линией.
Далее мы построим прямоугольный треугольник, используя AB в качестве гипотенузы.
Используя теорему Пифагора,
AB 2 = AC 2 + BC 2
d 2 = (x 2 −x 1 ) 2 + (y 2 −y 1 ) 2
Здесь вертикальное расстояние между заданными точками равно | у 2 – у 1 |
Горизонтальное расстояние между заданными точками | х 2 – х 1 |
(Извлечение квадратного корня с обеих сторон)
Таким образом, формула расстояния для нахождения расстояния между двумя точками доказана.
Используя аналогичные шаги и концепцию, мы также можем вывести формулу для нахождения расстояния между двумя точками, заданными в трехмерной плоскости.
Шаги для определения расстояния между двумя точками
Следующие шаги могут быть использованы для определения расстояния между двумя точками с использованием предоставленных координат:
- Запишите координаты двух заданных точек на координатной плоскости следующим образом: A(x 1 , y 1 ) и B(x 2 , y 2 ).
- Мы можем использовать формулу расстояния для вычисления расстояния между двумя точками,
- Выразите данный ответ в единицах.
Примечание: Мы можем применить формулу трехмерного расстояния в случае, если две точки заданы в трехмерной плоскости,
Примеры задач А(1,5) и В (2,7).
Решение:
Пусть (x 1 , y 1 ) равно (2,7) и (x 2 , y 1 , 90).
Расстояние d между точками:
Расстояние между двумя точками составляет √5 единиц.
Задача 2. Найдите расстояние между двумя точками с координатами, заданными как P (2,-6,2) и Q(7, 3, 1).
Решение:
LET (x 1 , Y 1 , Z 1 ) BE P (2, -6,2) и (x 2 , Y 2 , Z Z. 2 ) будет Q (7,3,1).
Расстояние d между точками P и Q:
Задача 3. Докажите, что вершинами прямоугольного треугольника являются точки (3, 4), (7, 4) и (3, 8).
Решение:
Расстояние между двумя точками на комплексной плоскостиПредположим, что заданы точки: , найдем каждую вершину прямоугольного треугольника по формуле расстояния.
Как мы знаем длину стороны прямоугольного треугольника, по теореме Пифагора;
AB 2 +AC 2 = BC 2
4 2 +4 2 = (4√2) 2
16 +16 = 32⟹32 = 32
16 +16 = 32⟹32.
Это доказывает, что треугольник ABC прямоугольный.Расстояние между двумя точками на комплексной плоскости или двумя комплексными числами z 1 =a+ib и z 2 =c+id в комплексной плоскости ⟹1−2k=9+4k — расстояние между точками (a, b) и (c, d), заданное as,
Задача 4. Найдите расстояние между двумя комплексными числами z 1 = 2−5i и z 2 = 7+7i
имеют два комплексных числа z 1 = 2-5i и z 2 = 7+7i.
Расстояние между этими комплексными числами равно расстоянию до двух точек на плоскости с координатами (2,-5) и (7,7).
Таким образом, расстояние между двумя точками равно
Следовательно, расстояние между двумя комплексными числами z_1=2-5i и z_2=7+7i составляет 13 единиц.
Задача 5.
Комплексное число ω на 6 единиц отличается от z 1 = -3 – i и на 6 единиц отличается от z 2 = 3 + 5i. Проверьте, является ли треугольник, образованный ω, z 1 , z 2 , прямоугольным или нет.
Решение:
Есть 3 комплексных числа ω, z 1 , z 2 .
Как мы знаем, расстояние между ω и z 1 равно 6 единицам, а расстояние между ω и z 2 равно 6 единицам.
Дано, ω, z 1 = 6 ед.
ω, z 2 = 6 ед.
По теореме Пифагора имеем;
(z 1 Z 2 ) 2 = (ωz 1 ) 2 +(ωz 2 ) 2
HEND, WE LONGUDED, WE LONGUDED, WE LONGUDED, WE LONGUDED, WE LONGUDED, WE LONGUDED, WE LONGID что данный треугольник прямоугольный. Задача 6.
Решение:
Мы знаем, что любая точка на оси x имеет координату y, равную 0. В результате мы считаем точку, равноудаленную от указанных точек, равной (k,0). т. е. расстояние между ( k, 0) и (1, -2) = расстояние между (k, 0) и (-2, -3).
\ Подразумевается -4K-2K = 9-1
С. Требуемая точка (K, 0) =
Расстояние между двумя точками
.
GENERATE WORK
сообщить об этом объявлении (x_B,y_B)` в двумерной декартовой плоскости координат и найти длину отрезка `\overline{AB}`. Для этого онлайн-инструмента геометрии требуются координаты 2 точек в двумерной декартовой координатной плоскости.
Необходимо выполнить следующие шаги:
- Введите координаты (`x_A`,`y_A`) и (`x_B`,`y_B`) двух точек `\text{A и B в поле}`. Эти значения должны быть действительными числами или параметрами;
- Нажмите кнопку » GENERATE WORK «, чтобы выполнить вычисление;
- Калькулятор расстояний выдаст длину сегмента линии `overline{AB}`.
Ввод: Две упорядоченные пары действительных чисел. Обратите внимание, что некоторые координаты могут быть переменными 92}`
Какое расстояние между двумя точками?
Для любых двух точек существует ровно один отрезок, соединяющий их. Расстояние между двумя точками — это длина отрезка, соединяющего их. Обратите внимание, что расстояние между двумя точками всегда положительно. Сегменты, имеющие одинаковую длину, называются конгруэнтными сегментами.
Расстояние между двумя точками (x A , y A ) и (x B , Y B ) Расстояние (1, 2) и (3, 4) 2,8284 (1, 3) и (-2 2,8284 (1, 3) и (-2 . ) 6.7082 (1, 2) и (5, 5) 5 (1, 2) и (7, 6) 7. (1, 1) и и (7, -7) 10 (13, 2) и (7, 10) 10 (1, 3) и (5, 0) 5 (1, 3) и (5, 6) 5 (9, 6) и (2, 2) 8.0623 (5, 7) и ( 7, 7) 2 (8, 2) и (3, 8) 7,8102 (8, -3) и (4, -7) 5,6569 (70008 5,6569 (7) 8, 2) и (6, 1) 2,2361 (-6, 8) и (-3, 9) 3,1623 (7, 11) и (-91, 91, 91, 91, 91)0008 10 (-6, 5) и (-3, 1) 5 (-6, 7) и (-1, 1) 7,8102 (5, -4) и (0, 8) 13 (5, -8) и (-3, 1) 12.0416 (-5, 4) и (2, 6) 8 7.2801
(4, 7) и (2, 2) 5.3852 (4, 2) и (8, 5) 5 (4, 6) и (3,. 1,4142 (-3, 7) и (8, 6) 11.0454 (-3, 4) и (5, 4) 8 (-3, 2, 2, 8 (-3, 2, 4) ) и (5, 8) 10 (-3, 4) и (1, 6) 4,4721 . (-2, 4) и (3, 7,0711 (-2, 4) и (4, 7) 6,7082 (-2, 5) и (5, 2) 7,6158 01, (-2, 5, 2) -1) 24.0832 (-1, 5) и (0, 4) 1,4142 (-1, 4) и (4, 1) 5,831 (0, 1) и (4, 4) 5 (0, 5) и (12, 3) 12.1655 (0, 1) и (6, 3,5) 6,5 (6, 3,5) 6,5 (6, 3,5) . 0, 8) и (4, 5) 5 (0, 0) и (3, 4) 5 (0, 0) и (1, 1) 1. (0, 1) и (4, 4) 5 (0, 5) и (12, 3) 12.1655 (2, 3) и (( 5, 7) 5 (2, 5) и (-4, 7) 6.3246 (2, 3) и (1, 7) 4.1231 (2) , 8) и (5, 3) 5,831 (3, 2) и (-1, 4) 4,4721 (3, 12) и (94, 2)0008 14.8661 (3, 7) и (6, 5) 3.6056 (3, 4) и (0, 0) 5 Как вычислять расстояние между расстоянием между расстоянием между 2 балла?
Длину сегмента обычно обозначают конечными точками без надчеркивания. Например, `\text{длина AB}` обозначается `\overline{AB}` или иногда `m\overline{AB}`. Линейка обычно используется для определения расстояния между двумя точками. Если мы поместим отметку «0» в левой конечной точке, а отметка, на которую падает другая конечная точка, будет расстоянием между двумя точками.
Расстояние также можно измерить с помощью масштаба на карте. Расстояние между двумя точками, работа с шагами, показывает полный пошаговый расчет для нахождения длины отрезка, имеющего 2 конечные точки `A` с координатами `(5,3)` и `B` с координатами `(9, 6)`. Для любых других комбинаций конечных точек просто укажите координаты 2 конечных точек и нажмите кнопку «СОЗДАТЬ РАБОТУ». Учащиеся начальной школы могут использовать этот калькулятор расстояний для создания работы, проверки результатов или эффективного решения домашних заданий.
Реальные задачи с использованием длины между двумя точками
Если мы сравниваем длины двух или более отрезков, мы используем формулу для расстояния между двумя точками. Обычно мы используем формулу расстояния для нахождения длин сторон многоугольников, если нам известны координаты их вершин. В этом случае мы можем исследовать природу полигонов. Это также может помочь нам найти площадь и периметр многоугольника.
Калькулятор расстояния между двумя точками используется практически во всех областях математики. Например, расстояние между двумя комплексными числами `z_1 = a + ib` и `z_2 = c + id` в комплексной плоскости равно расстоянию между точками `(a,b) и (c,d)`, то есть 92}`
В физике длина пути между двумя точками `A и B` при их движении называется расстоянием. На основе расстояния можно определить некоторые физические величины. Например, скорость — это расстояние, деленное на время.
Расстояние между двумя точками Практические задачи
Практическая задача 1:
Начав с одной и той же точки, Майкл и Энн шли.
Найдите точку на оси x, равноудаленную от точек (1, -2) и (-2, -3). 
2111
7)
4142
В общем, нам не нужно измерять от отметки 0. Согласно постулату линейки, расстояние между двумя точками является абсолютным значением между числами, показанными на линейке.
С другой стороны, если две точки `A и B` находятся на оси x, то есть координаты `A и B` равны `(x_A,0)` и `(x_B,0)` соответственно, то расстояние между двумя точками `AB = |x_B −x_A|`. Тот же метод можно применить, чтобы найти расстояние между двумя точками на оси Y. Формула расстояния между двумя точками в двумерной декартовой плоскости координат основана на 92}`
