16 разложить на простые множители: Разложите на простые множители число: а) 16; б) 18; в) 26; г) 35; д) 48; е) 70; ж) 144; з) 210; и) 800; к) 216; л) 343; м) 1024.

Простые множители числа 16 — Calculatio

Калькулятор «Разложение чисел на простые множители»

Какие простые множители у числа 16?

Ответ: Простые множители числа 16: 2, 2, 2, 2

или

2⁴

Объяснение разложения числа 16 на простые множители

Разложение 16 на простые множители (факторизация) — это представление числа 16 как произведения простых чисел. Другими словами, необходимо выяснить, какие простые числа нужно перемножить, чтобы получилось число 16.

Так как число 16 является составным (не простым) мы можем разложить его на простые множители.

Для того, чтобы получить список простых множителей числа 16, необходимо итеративно делить число 16 на минимально возможное простое число пока в результате не получится 1 (единица).

Ниже полное описание шагов факторизации числа 16:

Минимальное простое число на которое можно разделить 16 без остатка — это 2. Следовательно, первый этап расчета будет выглядеть следующим образом:

16 ÷ 2 = 8

Теперь необходимо повторять аналогичные действия, пока в результате не останется 1:

8 ÷ 2 = 4

4 ÷ 2 = 2

2 ÷ 2 = 1

В итоге мы получили список всех простых множителей числа 16. Это: 2, 2, 2, 2

Можно упростить выражение и записать как: 2⁴

Дерево простых множителей числа 16

Мы также можем визуализировать разложение числа 16 на простые множители в виде дерева факторизации:

Похожие расчеты

Поделитесь текущим расчетом

Печать

https://calculat.io/ru/number/prime-factors-of/16

<a href=»https://calculat.io/ru/number/prime-factors-of/16″>Простые множители числа 16 — Calculatio</a>

О калькуляторе «Разложение чисел на простые множители»

Данный калькулятор поможет разложить заданное число на простые множители. Например, он может помочь узнать какие простые множители у числа 16? Выберите начальное число (например ’16’). После чего нажмите кнопку ‘Посчитать’.

Простые множители - это положительные целые числа, имеющие только два делителя - 1 и само себя.

Калькулятор «Разложение чисел на простые множители»

Таблица разложения чисел на простые множители

Число	Простые множители
1	1
2	2
3	3
4	22
5	5
6	2, 3
7	7
8	23
9	32
10	2, 5
11	11
12	22 × 3
13	13
14	2, 7
15	3, 5
16	24
17	17
18	2 × 32
19	19
20	22 × 5
21	3, 7
22	2, 11
23	23
24	23 × 3
25	52
26	2, 13
27	33
28	22 × 7
29	29
30	2, 3, 5

Число 16

Свойства и характеристики одного числа
Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители. ..

Свойства пары чисел
Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел…

Сейчас изучают числа:

332 2011 4444444444 421 152 33322 234234 400 и 2081 54 781 768 4145 30 и 45 811 320 24481657 25814 1022102002 727 6669 1118 79957 5511 6789

Шестнадцать

Описание числа 16

Положительное рациональное двузначное число 16 является составным.

7 — сумма цифр. У числа 16 5 делителей: 1, 2, 4, 8, 16. Обратное число к 16 – это 0.0625.
Данное число представляется произведением: 2 * 2 * 2 * 2.

Число в других системах счисления: двоичная система счисления: 10000, троичная система счисления: 121, восьмеричная система счисления: 20, шестнадцатеричная система счисления: 10. Конвертация из числа байтов это 16 байтов .

Число 16 азбукой Морзе: .—- -….

Число не является числом Фибоначчи.

Синус числа: -0.2879, косинус числа: -0.9577, тангенс числа: 0.3006. Логарифм натуральный числа: 2.7726. У числа 16 есть десятичный логарифм: 1.2041. Если извлечь квадратный корень, получится 4, а если кубический — 2.5198 Число 16 в квадрате: 256.00.

Число 16 в секундах это 16 секунд . Цифра 7 — это нумерологическое значение числа 16.

• ← 15
• 17 →

Делители 16 — Найти простые факторизации/множители 16 и 16. Здесь 16 — самый большой множитель. Простые множители числа 16 — это 1, 2, 4, 8, 16, а его множители в парах — (1, 16), (2, 8) и (4, 4).

• Коэффициенты 16: 1, 2, 4, 8 и 16
• Отрицательные коэффициенты 16: -1, -2, -4, -8 и -16
• Простые множители числа 16: 2
• Факторизация числа 16: 2 × 2 × 2 × 2 = 2 ⁴
• Сумма коэффициентов 16: 31

1.	Что такое множители числа 16?
2.	Как вычислить множители числа 16?
3.	Коэффициенты 16 с помощью простой факторизации
4.	Коэффициенты 16 в парах
5.	Простые множители числа 16 по методу деления
6.	Часто задаваемые вопросы о факторах 16

Какие множители числа 16?

Число, которое делится на другое число без остатка, называется делителем этого числа. Когда мы делим 16 на 2, оно делится точно и не оставляет остатка. Следовательно, 2 является делителем 16. Точно так же 4 и 8 не оставляют остатка и, следовательно, являются делителями 16.

Обратите внимание, что 1 и число всегда являются делителями числа. Делители числа 16 равны 1, 2, 4, 8 и 16.

Как рассчитать коэффициенты числа 16?

Для нахождения множителей числа 16 можно использовать простую факторизацию или метод деления. Используя метод деления, мы можем найти числа, на которые 16 точно делится без остатка.

Делители 16 методом деления

• Чтобы найти множители 16 методом деления, мы разделим 16 путем подсчета чисел и посмотрим, какие числа точно делят 16 и дадут 0 в качестве остатка.
• Например, когда мы делим 16 на 2, 4 или 8, в остатке будет 0.
• В то же время, когда мы делим 16 на такие числа, как 3, 5 или 7, остается остаток.
• Разделим и проверим все числа.

Таким образом, все числа, у которых в остатке 0, являются делителями числа 16. Мы видим, что 1, 2, 4, 8 и 16 являются делителями числа 16

. Изучите факторы с помощью иллюстраций и интерактивных примеров:

• Множители числа 162- Множители числа 162 равны 1, 2, 3, 6, 9, 18, 27, 54, 81 и 162.
• Факторы числа 169. Делители числа 169 равны 1, 13 и 169.
• Множители числа 216. Множители числа 216 равны 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108 и 216.
• Коэффициенты 160. Коэффициенты 160 равны 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80 и 160.
• Множители числа 168. Множители числа 168 равны 1, 2, 3, 4, 6, 7, 8, 12, 14, 21, 24, 28, 42, 56, 84 и 168.

Факторизация простых чисел 16

Это делается путем деления 16 на простые числа.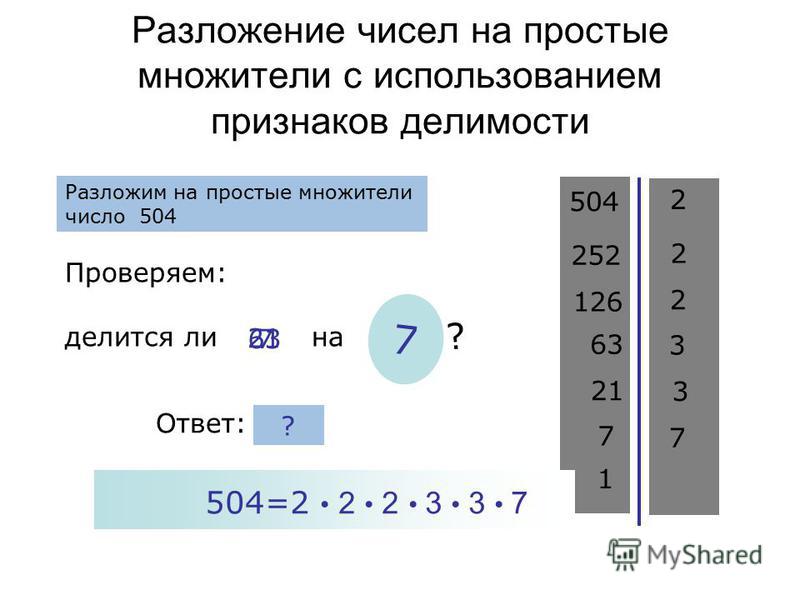 Затем мы проверим, не оставляет ли оно остатка, и продолжим деление с частным, если это составное число. Мы можем найти простые множители числа 16 методом деления или методом факторного дерева.

Разложение числа 16 на простые множители методом деления

• Шаг 1: Число 16 делится на наименьшее простое число, которое точно делится на 16.
• Шаг 2: Полученное таким образом частное затем делится на наименьшее или второе наименьшее простое число, и процесс продолжается до тех пор, пока частное нельзя разделить дальше.
• Шаг 3:
  Разделим 16 на простое число 2, т.е. 16 ÷ 2 = 8
• Шаг 4: Теперь мы делим 8 на 2 и повторяем процесс до тех пор, пока частное нельзя будет разделить дальше.

Факторизация числа 16 с помощью метода факторного дерева

Здесь мы находим простые множители числа 16, следовательно, корень нашего дерева множителей равен 16. Мы запишем пару множителей как ветвь 16.

2 — простое число. Следовательно, на этом дерево факторов заканчивается. Следовательно, простая факторизация числа 16 равна 2 × 2 × 2 × 2

Простая факторизация числа 16 методом перевернутого деления

Этот метод называется перевернутым делением, потому что символ деления переворачивается вверх ногами. Здесь мы делим 16 на наименьшее простое число 2. Если данное число нечетное, мы делим его на 3. Мы будем делить, пока не получим 1.

Из этого мы заключаем, что 16 = 2 × 2 × 2 × 2.

Аналитический центр:

• Можем ли мы записать простую факторизацию числа 16 как 2 ⁴ ?
• Какой самый большой делитель числа 16?
• Является ли 16 квадратным числом? Почему?

Пара множителей 16

Пара множителей представляет собой набор из двух чисел, при умножении которых получается число как произведение.

Факторные пары из 16:

• 1 × 16 = 16
• 2 × 8 = 16
• 4 × 4 = 16

Таким образом, парами множителей числа 16 являются (1, 16), (2, 8), и (4, 4).

Поскольку произведение двух отрицательных чисел положительно, пары отрицательных множителей числа 16 равны (-2, -8), (-4, -4), и (-1, -16) .

Простые множители числа 16 по методу деления

Для метода деления 16 следует разделить на наименьшее простое число, которое делит его точно без остатка.

• Шаг 1: Если 16 разделить на 2, то в частном будет 8, 16 ÷ 2 = 8
• Шаг 2: Число 8 не является простым; следовательно, он дополнительно разделен.
• Шаг 3: Если 8 разделить на 2, то в частном будет 4, т.е. 8 ÷ 2 = 4
• Шаг 4: Число 4 не является простым числом. Следовательно, его можно разделить как 4 ÷ 2 = 2.
• Шаг 5: 2 — простое число. Таким образом, она не может быть далее разделена.

Следовательно, делители числа 16 равны 1, 2, 4, 8 и 16, а простая факторизация числа 16 равна 16 = 2 × 2 × 2 × 2.

Важные примечания: 16 это 1, 2, 4, 8 и 16.

1 — универсальный коэффициент.

Два числа, которые умножаются, чтобы получить продукт, являются факторами продукта.

 

Коэффициенты 16 решенных примеров

1. Пример 1: Можете ли вы помочь Тому перечислить делители числа 24 и проверить, есть ли у чисел 24 и 16 общие делители?

   Решение:

   Есть восемь делителей числа 24:

   24 ÷ 1 = 24

   24 ÷ 2 = 12

   24 ÷ 3 = 8 0 3

   24002

   24 ÷ 6 = 4

   24 ÷ 8 = 3

   24 ÷ 12 = 2

   Это означает, что множители 24 равны 1, 2, 3, 4, 6, 8, 12 и 24, а множители 16 равны 1, 2, 4, 8 и 16. Следовательно, 24 и 16 имеют 1, 2, 4 и 8 как общие делители.

2. Пример 2:

   Эми хотела определить все пары положительных множителей из 16. Вы можете ей помочь?

   Решение:

   Пары множителей из 16: ), (2,8) и (4,4).

3. Пример 3: Найдите произведение всех простых множителей числа 16.

   Решение:

   Поскольку простые делители числа 16 равны 2. Следовательно, произведение простых делителей = 2 = 2.

перейти к слайдуперейти к слайдуперейти к слайду

 

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Запишитесь на бесплатный пробный урок

Часто задаваемые вопросы о факторах 16

Какие множители числа 16?

Множители числа 16 равны 1, 2, 4, 8, 16, а его отрицательные множители равны -1, -2, -4, -8, -16.

Какие числа являются простыми делителями числа 16?

Простой делитель числа 16 равен 2.

Каков наибольший общий делитель чисел 16 и 5?

Делители числа 16 равны 1, 2, 4, 8, 16, а делители числа 5 равны 1, 5. 16 и 5 имеют только один общий делитель, равный 1. Это означает, что числа 16 и 5 взаимно просты.

Следовательно, наибольший общий делитель (НОД) чисел 16 и 5 равен 1.

Чему равна сумма всех делителей числа 16?

Факторы числа 16 равны 1, 2, 4, 8, 16, а сумма всех этих факторов равна 1 + 2 + 4 + 8 + 16 = 31

Сколько факторов числа 15 также является общим для числа 16 ?

Так как делители числа 16 равны 1, 2, 4, 8, 16, а делители числа 15 равны 1, 3, 5, 15. Следовательно, числа 16 и 15 имеют только один общий делитель, равный 1. Следовательно, числа 16 и 15 являются взаимно простыми.

Факторы 16

Дата последнего обновления: 15 апреля 2023 г.

•

Всего просмотров: 312,6k

•

Просмотров сегодня: 5,82k

16 — составное число, и все его делители — целые числа, которые можно без остатка разделить на 16. Кроме того, если мы разделим 16 на один из его делителей, мы получим еще один коэффициент 16.

Например, 16 ÷ 2 = 8. Здесь 2 — это коэффициент 16, и если мы разделим 16 на 2, мы получим 8, что также является коэффициентом 16 (8 x 2 = 16). Теперь, прежде чем перейти к очевидному вопросу: «Каковы множители числа 16?» Знаем ли мы, что такое факторы? Давайте немного освежимся. Любое число может быть делителем числа, если оно делит число без остатка.

Как найти делители числа 16?

Найти коэффициент 16 проще, чем подсчитать количество людей в комнате или, может быть, алфавит английского языка. Чтобы найти множитель 16, нам просто нужно разделить 16 на все числа, начиная с 1 до 16, и посмотреть, на какое число делится 16, не оставляя остатка. Чего мы ждем? Сделаем это и найдем все делители числа 16.

16 ÷ 1 = 16

16 ÷ 2 = 8

16 ÷ 3 = 5,3

16 ÷ 4 = 4

16 ÷ 5 = 3,2

16 ÷ 6 = 2,6

16 ÷ 7 = 2,28

16 ÷ 8 = 2

16 ÷ 9 = 1,7 3 ÷ 601 6 ÷ 9003 90

16 ÷ 11 = 1,4

16 ÷ 12 = 1,3

16 ÷ 13 = 1,2

16 ÷ 14 = 1,1

16 ÷ 15 = 1,0

16 ÷ 16 = 1

903 Таким образом, мы ясно видим, что 1 6 ÷ 16 = 1

903 4, 8 и 16 — единственные делители 16. Остальные числа оставляют остаток, поскольку они дают десятичные числа и не могут быть делителями 16.

Сколько делителей на 16?

Из приведенного выше вывода мы можем вычислить, что существует 5 делителей числа 16, включая 1, и эти делители равны 1, 2, 4, 8 и 16. Все делители числа 16 составные, кроме 1 и 2. 2 — единственный простой делитель среди всех других делителей числа 16 и, согласно определению, 1 не является ни простым числом, ни составным числом. Это целые числа, которые делят 16 нацело без остатка. Мы можем выразить эти целые числа либо по отдельности, либо в виде парного множителя.

Парные множители 16

Парные множители представляют собой комбинации любых двух множителей, произведение которых при умножении дает 16. Здесь мы можем видеть все положительные парные множители числа 16.

1 × 16 = 16, следовательно, мы можем сказать, что 1 и 16 являются парными множителями числа 16.

2 × 8 = 16, следовательно, мы можем сказать, что 2 и 8 — парные множители числа 16.

4 × 4 = 16, следовательно, мы можем сказать, что 4 и 4 — парные множители числа 16.

8 × 2 = 16 Следовательно, мы можем сказать, что 8 и 2 — пара множители 16,

16 × 1 = 16 Следовательно, мы можем сказать, что 16 и 1 являются парными множителями 16.

Факторизация простых чисел

Мы можем разложить на множители набор чисел, где каждое число является простым числом, и способ сделать это называется простой факторизацией. Разложение числа 16 на простые множители можно записать как 2 x 2 x 2 x 2. 16 является составным числом, и, таким образом, в отличие от простых чисел, 16 имеет более двух разложений на множители.

Чтобы доказать утверждение, выберите крайние правые и крайние левые целые числа в 16, 8, 4, 2, 1, а затем умножьте эти целые числа, чтобы получить 16. Это будет первая факторизация. Во-вторых, мы должны выбрать второе самое правое и второе самое левое целое число, чтобы получить вторую факторизацию, которая также дает 16,9. 0003

Факторизация простых чисел, также называемая целочисленной факторизацией 16, может быть определена как определение набора простых чисел, которые, если их перемножить, дадут исходное число 16. Мы также можем назвать это простым разложением числа 16.

Факторы 16 равны 1, 2, 4, 8, 16, теперь, если мы найдем разложение 16 на простые множители, результатом будет 16 = 2 x 2 x 2 x 2, что также можно записать как 16 = 2⁴. Поскольку √16 = 4, что является целым числом, его также можно назвать полным квадратом.

Факторное дерево из 16

Почему мы называем это факторным деревом? Ну, это потому, что так же, как дерево имеет ветви, дерево факторов имеет подфакторы, которые могут быть представлены графически. Это искусственное дерево чисел, которое растет, когда мы находим множители числа, а затем находим множители числа. Процесс продолжается до тех пор, пока мы не достигнем этапа, на котором у нас будет набор простых множителей, которые также будут простой факторизацией исходного числа. Здесь мы облегчим вам понимание:

(Изображение будет загружено в ближайшее время)

Решенные примеры

Пример: Найдите следующие множители:

i) 124

ii) 72

iii) 66

3 09 3

iv) 180

vi) 52

vii) 86

viii) 120

ix) 92

x) 196

Нахождение делителей следующих чисел:

i) Делители числа 12043 68

2

124

2

62

30 9003 4 0 3 903 63

31

1

ii) Коэффициенты 72 являются:

2	72
3	2 033 36
2	18
3	9 9003	III ) Делители 66: 3 600333 3 66 2 22 11 11 1 3 9 iv) Факторы 57: 31 3 3 vii) Факторы из 86: 3 57 19 19 3 68 v) Коэффициенты 180: 3 7 2 180 3 2 0 3 90 5 45 7 1 vi) Коэффициенты 52: 2 52 2 26 3 3 9 34 2 86 43 1 viii) Коэффициенты 120: 3 2 120 2 60 2 30 3 3 90 03 9090 15 0032 5 5 1 71
2	92
2	46
23	23
3 60505

x) Коэффициенты 196:

90

2	196
	98
7	49
7	7
	1

Заключение

3 они помогают в выполнении более простых расчетов.

No related posts.