180 умножить на 8: 180 умножить на 8 столбиком

Содержание

Быстрое умножение целых чисел с использованием таблиц / Хабр

Хочу рассказать читателям о программистском трюке, с которым я познакомился в какой-то переводной книжке, содержащей подборку таких трюков, в те далёкие времена, когда ещё не изобрели не то что байт, а страшно сказать — стек, а великий Дейкстра ещё не проклял оператор GOTO (sic, in uppercase).

Трюк настолько мне понравился простотой и изяществом, что уже в этом тысячелетии я с удовольствием рассказывал о нём студентам в виде следующей задачи.

Представьте себе, что в процессе возвращения в 2030 году с Луны вы вдруг обнаружили, что ваш бортовой компьютер неправильно выполняет операции целочисленного умножения, и это непременно приведёт к аварии при посадке.

В таком сюжете нет ничего особо фантастического. Вспомним, например, какие проблемы случались когда-то с процессорами Pentium , а к моменту отправки на Луну вы ещё не достигли полного импортозамещения.

И вообще надо проверить, а не были ли процессоры просверлены специально.

Но к делу. Вам надо срочно реализовать умножение программно, чтоб работало быстро в реальном времени и укладывалось в доступный ресурс.

Из школьного курса арифметики вспоминаем, что многозначные числа умножать можно столбиком, а результат умножения отдельных цифр брать из таблицы умножения.

Вот только если цифры выбрать короткими (например 0 и 1), таблица умножения будет короткой, а столбики длинными, и их вычисление будет занимать много времени.

Если, наоборот, взять цифры длинные (например от 0 до 65535), то для 16-битной арифметики
результат берётся прямо из таблицы, а столбики отсутствуют. Однако размер классической таблицы Пифагора при этом оказывается около 17GB (4*65536*65536), если учесть симметрию относительно диагонали, то половина — около 8.5GB.

Может оказаться многовато.

Напрягаемся и вспоминаем алгебру.

(1)

(2)

Вычитаем (2) из (1)

и далее

Таким образом, имея таблицу квадратов в массиве sqr, получаем

a * b = ( sqr[a + b] — sqr[a — b]) / 4 (*)

Размер таблицы 8*(65535+65535) около 8.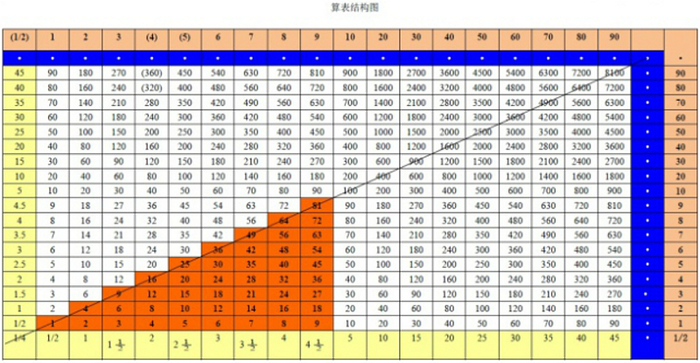 4MB, что уже может оказаться приемлемым.

Размер элемента таблицы в 8 байт связан с тем, что при максимальных a и b квадрат их суммы в 4 байта не влезает — не хватает 2-х бит.

Далее опишу некоторое улучшение, которого в книжке не было. Его я придумал сам, когда уже писал эту заметку.

Заметим, что два младших бита квадрата чётного числа всегда 00, а квадрата нечётного — всегда 01. С другой стороны для любой пары чисел их сумма и разность имеют одинаковую чётность.
Поэтому в нашей формуле (*) процесс вычитания в скобках не может иметь переносов,
связанных с двумя младшими битами. Поэтому содержимое элементов таблицы квадратов

можно заранее сдвинуть на два бита вправо и тем самым сэкономить половину памяти.

Окончательно имеем

a * b = sqr4[a + b] — sqr4[a — b] (**)

где sqr4 — модифицированная таблица квадратов.

В нашем примере её размер около 4.2 MB.

Ниже для иллюстрации этого подхода включен текст программы на языке Lua.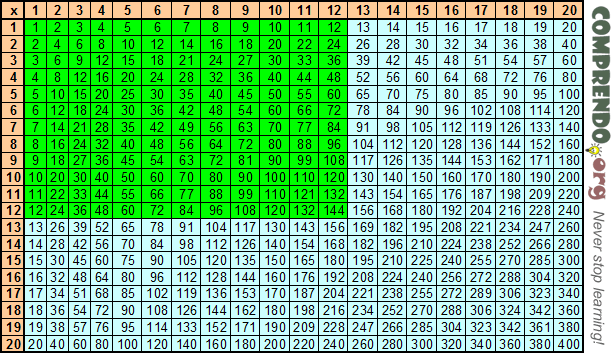

function create_multiplier(N)  -- N это число разных цифр
 local sqr4 = {}		-- создаём таблицу
 for i = 1, 2 * N - 1 do
  local temp = 0
  for j = 1, i - 1 do		-- для вычисления квадрата
   temp = temp + i - 1	-- используем многократное сложение
  end					-- т.к. умножение "неисправно"
  sqr4[i] = math.floor(temp / 4)  -- экономим 2 бита
 end
 return 			-- возвращаем мультипликатор (функцию)
  function (i, j)
   if i < j then i, j = j, i end
   return sqr4[1 + i + j] - sqr4[1 + i - j]
  end
end
N = 256
mpy = create_multiplier(N)
for i = 0, N - 1 do
 for j = 0, N - 1 do
  if i * j ~= mpy(i,j) then
   print("Ошибка", i, j, i * j, mpy(i,j))
  end
 end
end
print("Всё работает.")

Для современных процессоров представляется разумным иметь размер цифр кратным размеру байта для лёгкого доступа к ним. При цифрах размером в 1 байт, размер таблицы всего лишь 1022 байт, что может позволить использовать этот трюк в 8-битных процессорах, не имеющих аппаратного умножения.

Буду благодарен всем читателям этой заметки за исправления и замечания.

Таблица 180 — Выучить таблицу умножения на 180

LearnPracticeDownload

Таблица 180 — это таблица умножения, результатом которой является произведение последовательных натуральных чисел на число 180. Например, два раза 180 = 180 + 180 = 360, три раза 180 = 180 + 180 + 180 = 540 и так далее. На этой странице вы можете найти таблицу от 180 до 20.

Таблица 180 Диаграмма

1.	Стол из 180
2.	Таблица из 180 Скачать PDF
3.	Часто задаваемые вопросы по таблице 180

Стол из 180

Таблица 180 до 20 представлена ниже. Изучение таблицы умножения на 180 помогает детям глубже понять умножение, что полезно в долгосрочной перспективе.

Таблица от 180 до 10

180 × 1 = 180	180 × 6 = 1080
180 × 2 = 360	180 × 7 = 1260
180 × 3 = 540	180 × 8 = 1440
180 × 4 = 720	180 × 9 = 1620
180 × 5 = 900	180 × 10 = 1800

Таблица от 180 до 20

180 × 11 = 1980	180 × 16 = 2880
180 × 12 = 2160	180 × 17 = 3060
180 × 13 = 2340	180 × 18 = 3240
180 × 14 = 2520	180 × 19 = 3420
180 × 15 = 2700	180 × 20 = 3600

Вы можете распечатать или сохранить эту таблицу умножения в формате PDF, нажав на ссылку ниже.

☛ Таблица из 180 Скачать PDF

Таблица от 180 до 10 прописью

Сто восемьдесят раз Один равен ста восьмидесяти
Сто восемьдесят раз два равно тремстам шестидесяти
Сто восемьдесят раз три равно пятистам сорокам
Сто восемьдесят раз четыре равно семистам двадцати
Сто восемьдесят раз пять равно девятьсот
Сто восемьдесят раз шесть равно одной тысяче восьмидесяти
Сто восемьдесят раз семь равно одной тысяче двухсот шестидесяти
Сто восемьдесят раз восемь равно одной тысяче четыреста сороку
Сто восемьдесят раз девять равно одной тысяче шестистам двадцати
Сто восемьдесят раз десять равно одной тысяче восьмистам

☛ Также проверьте:

Таблица из 20
Стол из 15
Стол из 16
Стол из 32

Стол из 26
Стол из 17
Стол из 2

Таблицы из 180 примеров

Пример 1: Эндрю делает 6 пончиков в день. Сколько пончиков он сделал за 180 дней?
Решение:
Эндрю делает 6 пончиков в день. Следовательно, из таблицы 180 общее количество пончиков, сделанных за 180 дней, равно 6 × 180 = 1080 пончиков.
Пример 2: Клиент покупает 4 дыни каждый день. Сколько дынь покупатель купит через 180 дней?
Решение:
Клиент покупает 4 дыни в день. Следовательно, используя таблицу 180, общее количество дынь, купленных покупателем за 180 дней, равно 4 × 180 = 720 дынь.
Пример 3: Джонатан бегает трусцой по 2 мили в день. Воспользуйтесь таблицей 180 и найдите, сколько миль он пробежит за 180 дней.

Решение:
Джонатан бегает по 2 мили в день. Следовательно, общее количество миль, пройденных за 180 дней, равно 2 × 180 = 360 миль.

перейти к слайдуперейти к слайдуперейти к слайду

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем.