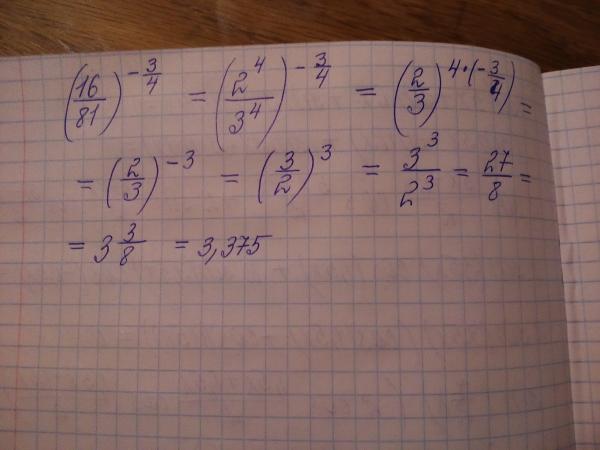Остеоартроз коленного сустава: степени, лечение, диета
Терапевт-участковый
Аблязов
Иршат Равилевич
Стаж 22 года
Терапевт-участковый высшей категории. Член Российского научного медицинского общества терапевтов.
Записаться на прием
Остеоартроз коленного сустава – следствие его хронического воспаления, которое вызывает дегенеративные изменения в тканях. Причины этого явления многочисленны и разнообразны, но все они дают одинаковый эффект – воспалительный процесс, затрагивающий хрящевую ткань, связки, мениск и т.д. В результате хрящ истончается, и кости при движении начинают тереться друг об друга, одновременно раздражая расположенные рядом нервные волокна. Возникают выраженные отеки и ощутимый болевой синдром, сустав теряет подвижность и становится более жестким. Постепенно происходит окостенение хрящевых тканей с образованием остеофитов. Современная медицина знает, как справиться с этим, и гарантирует пациентам избавление от неприятных и опасных симптомов с сохранением подвижности колена.
Причины
Большинство случаев заболевания встречается после 45 лет, но в последнее время патология уверенно «молодеет» и часто диагностируется лицам более раннего возраста, преимущественно женщин. В числе причин, вызывающих воспаление и остеоартроз коленного сустава, стоит назвать:
- возраст, вызывающий целый букет дегенеративных изменений в тканях организма;
- избыточный вес, вследствие которого нагрузка на нижние конечности и суставы резко увеличивается, и ткани быстрее изнашиваются под интенсивным механическим воздействием;
- атеросклероз;
- сахарный диабет, дающий осложнение в виде воспалительных заболеваний суставов;
- гормональные нарушения;
- генетическая предрасположенность, которая связана с особой формой нижних конечностей либо нарушениями в структуре тканей сустава;
- последствия травм и регулярных перегрузок;
- профессиональные занятия спортом, увеличивающие получение пациентом микротравм и повреждений;
- ревматоидный артрит;
- нарушения обмена веществ и т.
 д.
д.
Симптомы
Проявления заболевания зависят от пола и возраста пациента, уровня его физической активности и прочих симптомов остеоартроза коленного сустава. Обычно жалобы поступают на:
- сильную боль в коленном суставе во время активности, которая постепенно сходит на нет после длительного отдыха;
- отечность колена;
- ощущение тепла внутри сустава, что может быть вызвано воспалительным процессом и нагреванием костной ткани при трении;
- заметная жесткость коленного сустава после длительного неподвижного положения;
- сокращение диапазона подвижности сустава, которое затрудняет выполнение обычных движений: подъем по лестнице, выход из автомобиля, вставание со стула и т.д.
- посторонние звуки в коленном суставе: скрипы, хрусты и трески;
- реакция сустава на погодные условия.
Методы диагностики
Быстро и точно поставить пациенту верный диагноз позволяет изучение истории болезни и анализ жалоб на самочувствие, а также уточнение наличия такого же заболевания в семье и перечня факторов, влияющих на развитие болевого синдрома и его угасание. Кроме того, для уточнения характера патологии хирург-ортопед может выписать направление на:
Кроме того, для уточнения характера патологии хирург-ортопед может выписать направление на:
- рентгенографию, чтобы оценить состояние и тяжесть поражения костной ткани: наличие остеофитов, неправильную ось конечности, склерозирование, уменьшение хрящевой ткани;
- ультразвуковое обследование для оценки структуры сустава;
- магнитно-резонансную томографию, позволяющую точно указать причины болевых ощущений в суставе;
- анализ крови, который назначается в рамках дифференцированной диагностики для исключения ревматоиодных заболеваний, борелиоза и т.д.
Дополнительные способы диагностики назначаются по решению врача с целью уточнить нюансы развития остеоартроза коленного сустава 1, 2 или 3 степени и оценить заболевание в динамике.
Способы лечения
Еще недавно оптимальным способом лечения заболевания считалось эндопротезирование. Сегодня современная медицина готова предложить эффективные курсы консервативного лечения, позволяющие:
- справиться с болью;
- вернуть суставу подвижность;
- снизить риск прогрессирования заболевания и развития осложнений.

- меры по снижению массы тела;
- ежедневное выполнение физических упражнений;
- прием препаратов общего и местного действия;
- специальная диета при остеоартрозе коленного сустава.
В перечень препаратов для регулярного приема входят:
- анальгетики и противовоспалительные средства нестероидной группы;
- инъекции кортикостероидов;
- инъекции препаратов под ультразвуковым контролем;
- инъекции гиалуроновой кислоты, смягчающей движения костей и снижающей их взаимное трение;
- противовоспалительные мази для снятия неприятных ощущений и временного восстановления подвижности отекшего сустава;
- стабилизаторы и ортрезы колена;
- методы физиотерапии – массаж, мануальная терапия, ионофорез, ультразвук.
Оперативное лечение остеоартроза 1-3 степени
Если консервативные методы оказались малоэффективными, пациент направляется на хирургическое лечение.
- артроскопия – малоинвазивное вмешательство, позволяющая восстановить поврежденную структуру сустава, снять дискомфорт и даже на длительный срок отказаться от эндопротезирования;
- остеотомия – частичное иссечение костной ткани с существенными повреждениями, после которого пациент проходит длительный реабилитационный период;
- эндопротезирование – установка в колено части или всего сустава на место поврежденных тканей. Сравнительно сложная операция, результаты которой во многом зависят от квалификации хирурга.
При условии ранней диагностики и своевременного лечения с проблемой удастся справиться без серьезных последствий для сустава и его подвижности.
Вопросы и ответы
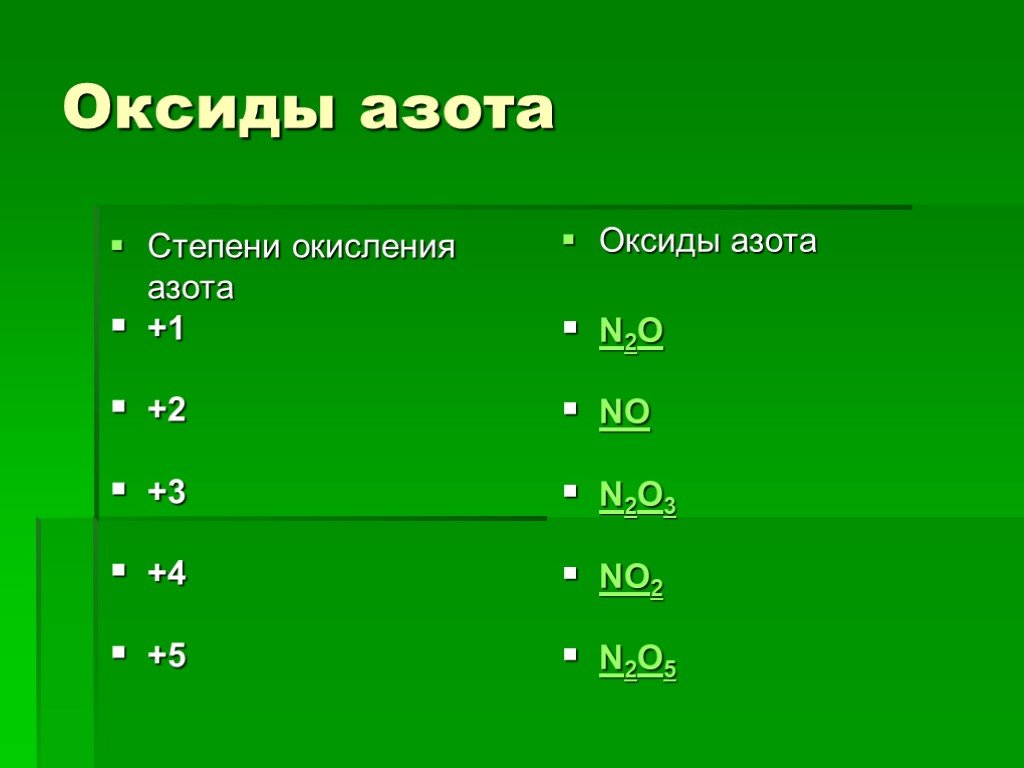
Как лечить остеоартроз коленного сустава 1 степени?
Лечение заболевания может быть консервативным или оперативным. В курс препаратов включают составы для устранения воспалительного процесса, кортикостероиды для восстановления разрушенной хрящевой ткани, составы местного действия для снятия отечности, инъекции гиалуроновой кислоты и т.д. Если прием назначенных препаратов не дал результата, или повреждения сустава значительны, принимается решение о хирургическом вмешательстве.
В курс препаратов включают составы для устранения воспалительного процесса, кортикостероиды для восстановления разрушенной хрящевой ткани, составы местного действия для снятия отечности, инъекции гиалуроновой кислоты и т.д. Если прием назначенных препаратов не дал результата, или повреждения сустава значительны, принимается решение о хирургическом вмешательстве.
Какой врач лечит остеоартроз коленного сустава
Диагностика и лечение остеоартроза – сфера компетенции хирурга-ортопеда. Он проводит осмотр пациента, назначает основные исследования для постановки точного диагноза и назначает курс лечения, ход которого контролирует с помощью снимков, дополнительных анализов и отзывов пациента. Возможно привлечение к исследованиям ревматолога, травматолога и физиотерапевта.
Возможно ли действие наследственного фактора при постановке диагноза «остеоартроз коленного сустава 2 степени»?
Наличие в анамнезе родителей остеоартроза в разы увеличивает вероятность постановки диагноза их детям. Помимо непосредственной передачи генетической склонности к заболеванию, возможно наследование неправильного положения конечности с искривлением ее оси, что вызывает деформацию сустава, его интенсивный износ и быстрое разрушение.
Помимо непосредственной передачи генетической склонности к заболеванию, возможно наследование неправильного положения конечности с искривлением ее оси, что вызывает деформацию сустава, его интенсивный износ и быстрое разрушение.
Артроз суставов: лечение, симптомы. Степени артроза.
Артроз – это хроническое дегенеративно-дистрофическое заболевание, поражающее все части сустава: хрящ, суставную оболочку, связки, капсулу, околохрящевые кости и околосуставные мышцы и связки.
По данным европейских врачей, на заболевание артрозом приходится почти 70% всех ревматологических болезней. Больше всего подвержены артрозу суставов люди в возрасте 40-60 лет. Этому способствуют как недостаток движения, так и длительные перегрузки, неправильное питание и, конечно же, травмы.
1
Рентгенография
2
Диагностика артроза суставов
3
Диагностика артроза суставов
Что же такое сустав
Обычно сустав человека состоит из 2-х и более соединяющихся костей. Все рабочие поверхности сустава имеют защитное покрытие и постоянно смазываются синовиальной жидкостью для наилучшего скольжения. Сама полость сустава герметично закрыта суставной капсулой.
Все рабочие поверхности сустава имеют защитное покрытие и постоянно смазываются синовиальной жидкостью для наилучшего скольжения. Сама полость сустава герметично закрыта суставной капсулой.
В нашем организме множество суставов, которые «отвечают» за те или иные виды движений, могут испытывать разнообразные нагрузки и имеют различный запас прочности.
Объем движения в суставах зависит от строения сустава, связочного аппарата, который ограничивает и укрепляет сустав, и различных мышц, прикрепленных к костям с помощью сухожилий.
Причины артроза суставов
Нормальная работа суставов возможна при постоянном самообновлении хрящевой ткани. В молодом возрасте скорость отмирания отживших суставных клеток равняется скорости рождения новых клеток. С годами процесс обновления клеток замедляется, и хрящевая ткань начинает истончаться. Также уменьшается выработка синовиальной жидкости. В результате этого суставной хрящ начинает истончаться и разрушаться, что приводит к артрозу.
Кроме того, существуют и другие причины артроза суставов:
- повышенная физическая нагрузка. Артроз суставов – частый спутник избыточного веса. В результате перегрузки в суставах образуются микротравмы. У спортсменов появляются повреждения суставов при увеличенных нагрузках на «непрогретые» суставы;
- травмы суставов;
- врожденные или приобретенные деформации опорно-двигательного аппарата (рахит, кифоз, сколиоз, неправильное сращивание костей после травм с появлением деформации конечностей: О-образная и Х-образная деформация ног).
Стадии артроза
В зависимости от степени разрушения хрящевой ткани, можно различать различные стадии или степени артроза.
Степени и симптомы артроза
Артроз 1 степени характеризуется периодической болью в суставах особенно при повышенной физической нагрузке. После отдыха боль, как правило, исчезает. Объем движений в суставе не ограничен, мышечная сила в поврежденной конечности не изменена. С помощью рентгена можно увидеть минимальные признаки повреждения суставов.
Объем движений в суставе не ограничен, мышечная сила в поврежденной конечности не изменена. С помощью рентгена можно увидеть минимальные признаки повреждения суставов.
Артроз 2 степени проявляется болезненными ощущениями не только при интенсивном физическом напряжении, но и при незначительных нагрузках. Даже во время отдыха болезненность в суставах может не стихать. Эта степень характеризуется скованностью в движениях, ограничением подвижности в суставах. В конечном счете это ведет к атрофии мышц. Рентгенограмма может показать деформацию сустава, уменьшение суставной щели, появление костных разрастаний рядом с этой щелью.
Артроз 3 степени — любое движение причиняет человеку большую боль. Боль в суставе присутствует даже в состоянии покоя. Поэтому человек старается как можно меньше двигаться, чтобы болезненность была минимальной. В ряде случаев передвижение требует использования костылей или каталки. Иногда происходит сращивание костей – анкилоз (как при болезни Бехтерева).
При деформирующем артрозе происходят необратимые изменения в хрящевой ткани сустава и полностью нарушаются его функции и строение. В основе деформирующего артроза суставов – появление дисфункции в образовании гиалинового хряща и синовиальной жидкости.
Диагностика артроза суставов
Основной метод диагностики суставов – это рентгенография. При артрозе можно наблюдать изменения со стороны суставов, неровную поверхность суставов и сужение суставной щели.
Какие суставы чаще страдают артрозом
Наиболее подвержены артрозу суставы конечностей: тазобедренные и коленные, плечевые, локтевые и кистей рук.
При артрозе тазобедренного сустава сначала человек может почувствовать небольшой дискомфорт в области ног после бега или ходьбы. Со временем боль усиливается, появляется ограниченность и скованность в движении. При 3 степени заболевания пациент оберегает ногу и старается по возможности на нее не наступать.
Артроз коленного сустава проявляется болезненностью в коленном суставе после сгибания и разгибания ног.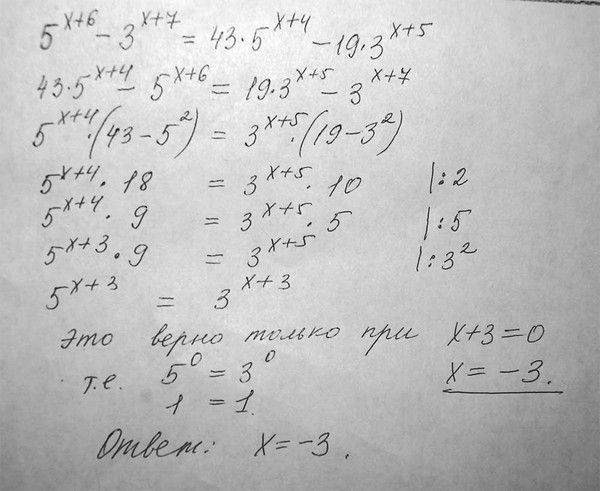 Чаще всего причиной артроза коленного сустава являются травмы, полученные в прошлом. В результате этих повреждений нарушается скольжение суставных поверхностей и происходит их быстрое изнашивание. В некоторых случаях сустав может постепенно утратить свою подвижность.
Чаще всего причиной артроза коленного сустава являются травмы, полученные в прошлом. В результате этих повреждений нарушается скольжение суставных поверхностей и происходит их быстрое изнашивание. В некоторых случаях сустав может постепенно утратить свою подвижность.
1
Диагностика артроза суставов
2
Диагностика артроза суставов
3
Рентгенография
Артроз голеностопного сустава проявляется в виде отека, боли в лодыжке ноги. Причиной артроза голеностопного сустава могут стать: деформации, переломы лодыжек и таранной кости, вывихи, плоскостопие, хронические травмы голеностопного сустава у спортсменов и балерин. У них, кстати, часто встречается и артроз стопы.
Артроз плечевого сустава и локтевого, лучезапястного суставов чаще всего появляется в результате травм, ушибов, вывихов, внутрисуставных переломов. Для артроза плечевого сустава характерны давящие, ломящие, тупые боли, которые отдают в предплечье и кисть. Боль чаще всего появляется по ночам. При артрозе рук боль сопровождается нарушением функций кисти.
Для артроза плечевого сустава характерны давящие, ломящие, тупые боли, которые отдают в предплечье и кисть. Боль чаще всего появляется по ночам. При артрозе рук боль сопровождается нарушением функций кисти.
Лечение артроза
Основные средства лечения артроза – медикаментозное лечение, использование физиотерапии и хирургическое лечение.
Медикаментозное лечение
Использование лекарственных препаратов помогает улучшить кровообращение в поврежденных суставах, восстановить свойства хряща, обладает обезболивающим и противовоспалительным действием.
Нестероидные противовоспалительные препараты
При артрозе может появиться отек сустава, сустав начинает болеть и объем движения снижается. При приеме противовоспалительных препаратов (НПВП) боль снижается, останавливается цепная воспалительная реакция и ускоряется процесс восстановления хряща.
Чаще всего используются следующие препараты: диклофенак, нимесулид, индометацин, парацетамол. Их можно применять в виде таблеток, ректальных свечей и порошка. Но помните, что самолечение недопустимо, подбор и дозу лечебного препарата от артроза осуществляет врач-ревматолог.
Но помните, что самолечение недопустимо, подбор и дозу лечебного препарата от артроза осуществляет врач-ревматолог.
Обезболивающие препараты центрального действия
Препараты опиоидного ряда снижают болевой порог чувствительности у пациента. Прием подобных препаратов возможен строго по рецепту и только под контролем врача!
Препараты-хондопротекторы
Препараты-хондопротекторы являются структурными элементами самого хряща, поэтому активно восстанавливают эту ткань и препятствуют ее дальнейшему разрушению. Лечение эффективно на начальных стадиях заболевания. Когда сустав уже полностью разрушен, вернуть первоначальную форму деформированных костей или нарастить новый хрящ, не представляется возможным.
Однако на 1- 2 стадиях артроза хондропротекторы могут принести пациенту значительное облегчение. Комбинированные препараты, в составе которых входит и глюкозамин, и хондроитин сульфат, по сравнению с однокомпонентным препаратом, дают лучший результат.
Хондроитин сульфат и глюкозамин сульфат
Данные лекарства способствуют процессу замедления воспалительной реакции в тканях, помогают уменьшить повреждение хряща и снизить болевой синдром. Чаще всего эти 2 препарата используют в лечении вместе, так как они обладают аккумулирующим действием, но принимать их надо в течение 3- 6 месяцев.
Чаще всего эти 2 препарата используют в лечении вместе, так как они обладают аккумулирующим действием, но принимать их надо в течение 3- 6 месяцев.
Гиалуроновая кислота
Обеспечивает вязкость и эластичность синовиальной жидкости. Помогает хорошему скольжению суставов. Поэтому врачи часто назначают инъекции с гиалуроновой кислотой в пораженный сустав.
Физиотерапевтические методы лечения
Среди физиотерапевтических методов лечения могут применяться:
- УВЧ-терапия;
- магнитотерапия;
- лазерное облучение низкой интенсивности;
- электрофорез с лекарственными препаратами;
- фонофорез (использование ультразвука для введения лекарственного средства в очаг воспаления).
1
Хирургическое лечение артроза
2
Хирургическое лечение артроза
3
Хирургическое лечение артроза
Хирургическое лечение
Хирургическое лечение применяется с целью восстановления и улучшения подвижности суставов, а также для того, чтобы удалить часть хряща или поврежденные мениски.
К хирургическому лечению артроза прибегают уже в крайних случаях, когда лечение медикаментами не дает результатов, при появлении сильной боли, частичной или полной неподвижности в суставах.
Во время артроскопической операции возможно удаление части пораженного артрозом хряща, его шлифовка для придания гладкой поверхности, удаление фрагментов и наростов хряща, срезание части поврежденных связок.
Протезирование коленного сустава
С помощью этой операции происходит замена суставных поверхностей коленного сустава на металлические или комбинированные протезы. Подготовленные пластины повторяют поверхность суставного хряща. Такие протезы изготавливаются из специальных сплавов, у пациентов они не вызывают реакцию отторжения, не окисляются и не травмируют окружающие ткани.
Хирургия тазобедренного сустава при артрозе
При данной операции производится частичное удаление хрящевой и костной ткани тазовой и бедренной кости. Обычно, головка бедренной кости и суставная поверхность тазовой кости удаляются и замещаются протезом из металла или металлокерамики.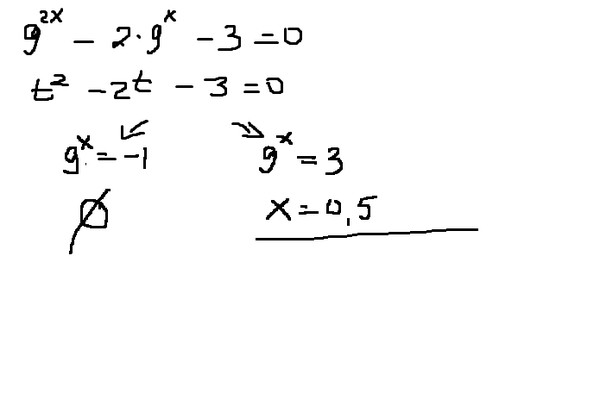
Диета при артрозе
Избыточная масса тела – большой враг ваших суставов. Большинство пациентов, страдающих от артрозов тазобедренного и коленного суставов, имеют излишек веса.
Поэтому при артрозах рекомендуется правильно подобранная диета. Считается, что при артрозе полезен холодец, приготовленный на хрящевом бульоне. В нем много коллагена и структурных компонентов хряща, помогающие восстановлению хрящевых тканей.
Полезны молочные продукты, белок и кальций. Животный белок содержится в нежирных сортах мяса и рыбы, растительный – в гречневой каше, фасоли и чечевице. Очень полезны блюда отварные, тушеные и приготовленные на пару.
Самая лучшая диета для суставов – это питание с небольшим преобладанием углеводов (желательно сложных углеводов), фруктов и овощей, достаточным количеством белка и кальция.
Профилактика артроза
Профилактика артроза, как это ни банально, заключается в здоровом образе жизни. По возможности, старайтесь бывать на свежем воздухе, двигаться, ходить босиком по песку, зеленой траве, и просто земле. Такая ходьба улучшает работу мышц и увеличивает кровообращение в стопах.
Такая ходьба улучшает работу мышц и увеличивает кровообращение в стопах.
Использование лечебной физкультуры с различными взмахами рук и ног, поворотами, наклонами даст посильную поддержку вашим суставам.
Часто пациенты спрашивают, возможно ли народное лечение артроза? Да, народные средства могут помочь на начальных стадиях заболевания, снизить боль и улучшить общее состояние больного. Но оно не заменяет выполнения предписаний вашего лечащего врача.
Многопрофильная клиника «Медиксити» — это высококвалифицированные врачи-ревматологи, обладающие богатым опытом в лечении не только артрозов, но и других ревматологических заболеваний. Мы поможем вам в борьбе с ревматизмом, полимиозитом, артритом, васкулитом, остеопорозом, подагрой, системной склеродермией и другими недугами. Главное – сделать первый шаг и записаться на прием к специалисту.
Материал подготовлен при участии специалиста:
Гуляев Сергей Викторович
Врач-ревматолог, терапевт, нефролог
Кандидат медицинских наук
1.
 3 Радикалы и рациональные показатели — Колледжская алгебра 2e
3 Радикалы и рациональные показатели — Колледжская алгебра 2eЦели обучения
В этом разделе вы:
- Вычислять квадратные корни.
- Используйте правило произведения, чтобы упростить квадратный корень.
- Используйте правило отношения для упрощения квадратных корней.
- Сложение и вычитание квадратных корней.
- Рационализировать знаменатели.
- Используйте рациональные корни.
Строительный магазин продает 16-футовые и 24-футовые лестницы. Окно расположено на высоте 12 футов над землей. Необходимо купить лестницу, которая будет доставать до окна с точки на земле в 5 футах от здания. Чтобы узнать длину необходимой лестницы, мы можем нарисовать прямоугольный треугольник, как показано на рисунке 1, и использовать теорему Пифагора.
Рисунок 1
a2+b2=c252+122=c2169=c2a2+b2=c252+122=c2169=c2
Теперь нам нужно найти длину, которая в квадрате равна 169, чтобы определить, какую лестницу выбрать. Другими словами, нам нужно найти квадратный корень. В этом разделе мы исследуем методы поиска решений таких проблем, как эта.
Другими словами, нам нужно найти квадратный корень. В этом разделе мы исследуем методы поиска решений таких проблем, как эта.
Вычисление квадратного корня
При возведении квадратного корня из числа в квадрат получается исходное число. Поскольку 42=16,42=16, квадратный корень из 1616 составляет 4,4. Функция квадратного корня является обратной функцией возведения в квадрат точно так же, как вычитание является обратной функцией сложения. Чтобы отменить возведение в квадрат, мы извлекаем квадратный корень.
В общих чертах, если aa
положительное действительное число, то квадратный корень из aa
это число, которое при умножении само на себя дает а.а.
Квадратный корень может быть положительным или отрицательным, потому что умножение двух отрицательных чисел дает положительное число. Главный квадратный корень — это неотрицательное число, которое при умножении само на себя равно a.a.a.
Квадратный корень, полученный с помощью калькулятора, является главным квадратным корнем.
Главный квадратный корень из aa записывается как а.а. Символ называется подкоренным, член под ним называется подкоренным, а все выражение называется подкоренным выражением.
Главный квадратный корень
Главный квадратный корень из aa есть неотрицательное число, которое при умножении само на себя равно а.а. Он записывается как подкоренное выражение , с символом, называемым подкоренным, над термином, называемым подкоренным: а.а.
вопросы и ответы
25=±5?25=±5?
Нет. Хотя оба числа 5252 и (−5)2(−5)2 равны 25,25, , подкоренной символ подразумевает только неотрицательный корень, главный квадратный корень. Главный квадратный корень из 25 равен 25=5,25=5.
Пример 1
Вычисление квадратных корней
Вычисление каждого выражения.
- ⓐ 100100
- ⓑ 1616
- ⓒ 25+14425+144
- ⓓ 49−8149−81
Решение
- ⓐ 100=10100=10, потому что 102=100102=100
- ⓑ 16=4=216=4=2, потому что 42=1642=16 и 22=422=4
- ⓒ 25+144=169=1325+144=169=13, потому что 132=169132=169
- ⓓ 49−81=7−9=−249−81=7−9=−2, потому что 72=4972=49 и 92=8192=81
вопросы и ответы
Для 25+144,25+144, можем ли мы найти квадратные корни перед сложением?
№ 25+144=5+12=17,25+144=5+12=17. Это не эквивалентно 25+144=13,25+144=13. Порядок операций требует, чтобы перед нахождением квадратного корня мы добавляли члены в подкоренной части.
Попытайся #1
Оценить каждое выражение.
- ⓐ 225225
- ⓑ 8181
- ⓒ 25−925−9
- ⓓ 36+12136+121
Использование правила произведения для упрощения извлечения квадратных корней
Чтобы упростить квадратный корень, мы перепишем его так, чтобы в подкоренной части не было полных квадратов. Есть несколько свойств квадратных корней, которые позволяют нам упростить сложные подкоренные выражения. Первое правило, которое мы рассмотрим, — это правило произведения для упрощения квадратных корней, , которое позволяет нам разделить квадратный корень из произведения двух чисел на произведение двух отдельных рациональных выражений. Например, мы можем переписать 1515 как 3⋅5,3⋅5. Мы также можем использовать правило произведения, чтобы выразить произведение нескольких подкоренных выражений в виде одного подкоренного выражения.
Правило произведения для упрощения квадратных корней
Если аа
и бб
неотрицательны, квадратный корень из произведения abab
равно произведению квадратных корней из aa
и б. б.
б.
аб=а⋅баб=а⋅б
Как
Имея радикальное выражение с квадратным корнем, используйте правило произведения, чтобы упростить его.
- Фактор любых полных квадратов из подкоренного числа.
- Запишите подкоренное выражение как произведение подкоренных выражений.
- Упростить.
Пример 2
Использование правила произведения для упрощения квадратных корней
Упростите подкоренное выражение.
- ⓐ 300300
- ⓑ 162a5b4162a5b4
Решение
- ⓐ
100⋅3Выразите совершенный квадрат из подкоренного и.100⋅3Запишите подкоренное выражение как произведение подкоренного выражения.103Упростите.100⋅3Выразите совершенный квадрат из подкоренного и.100⋅33Запишите подкоренное выражение как произведение подкоренного выражения.
- ⓑ
81a4b4tor -2afactor Perfect Presat от Radicand.81a4b4⋅2awrite Radical Expression как продукт радикальных экспрессии.
Попытайся #2
Упрощение 50x2y3z.50x2y3z.
Как
Получив произведение нескольких подкоренных выражений, используйте правило произведения, чтобы объединить их в одно подкоренное выражение.
- Выразите произведение нескольких радикальных выражений как одно радикальное выражение.
- Упростить.
Пример 3
Использование правила произведения для упрощения произведения кратных квадратных корней
Упростите подкоренное выражение.
12⋅312⋅3
Решение
12⋅3Выразите произведение в виде одного подкоренного выражения.36Упростите.612⋅3Выразите произведение в виде одного подкоренного выражения. 36Упростите.6
36Упростите.6
Попытайся #3
Упростить 50x⋅2x50x⋅2x предполагая, что x>0.x>0.
Использование правила отношения для упрощения квадратных корней
Точно так же, как мы можем переписать квадратный корень произведения как произведение квадратных корней, мы можем также переписать квадратный корень частного как частное квадратных корней, используя правило для упрощения квадратных корней. Может быть полезно разделить числитель и знаменатель дроби под корнем, чтобы мы могли отдельно извлекать их квадратные корни. Мы можем переписать 5252 как 52,52.
Частное правило для упрощения квадратных корней
Квадратный корень из частного abab равен частному квадратного корня из aa и b,b, где b≠0.b≠0.
аб=абаб=аб
Как
Имея подкоренное выражение, используйте правило частного, чтобы упростить его.
- Запишите подкоренное выражение как частное двух подкоренных выражений.
- Упростите числитель и знаменатель.
Пример 4
Использование правила отношения для упрощения квадратных корней
Упростите подкоренное выражение.
536536
Решение
536Запишите как частное двух подкоренных выражений.56Упростите знаменатель.536Запишите как частное двух подкоренных выражений.56Упростите знаменатель.
Попытайся #4
Упростить 2x29y4.2x29y4.
Пример 5
Использование правила отношения для упрощения выражения с двумя квадратными корнями
Упростите подкоренное выражение.
234x11y26x7y234x11y26x7y
Решение
234x11y26x7yОбъединение числителя и знаменателя в одно радикальное выражение.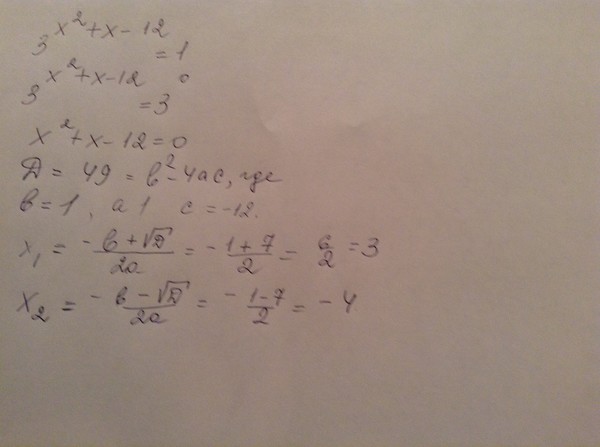 9×4Упрощение дроби.3×2 Упрощение квадратного корня.234x11y26x7yОбъединение числителя и знаменателя в одно радикальное выражение.9×4Упрощение корня повторение дроби.3×2 Упрощение квадратного корня.3×2
9×4Упрощение дроби.3×2 Упрощение квадратного корня.234x11y26x7yОбъединение числителя и знаменателя в одно радикальное выражение.9×4Упрощение корня повторение дроби.3×2 Упрощение квадратного корня.3×2
Попытайся #5
Упростить 9a5b143a4b5.9a5b143a4b5.
Сложение и вычитание квадратных корней
Мы можем складывать или вычитать подкоренные выражения, только если они имеют одинаковые подкоренные и один и тот же подкоренной тип, например, квадратные корни. Например, сумма 22 и 3232 составляет 42,42. Однако часто можно упростить радикальные выражения, и это может изменить подкоренное выражение. Радикальное выражение 1818 можно написать через 22 в подкоренном члене, как 32,32, так что 2 + 18 = 2 + 32 = 42,2 + 18 = 2 + 32 = 42.
Как
Упростите подкоренное выражение, требующее сложения или вычитания квадратных корней.
- Упростите каждое подкоренное выражение.

- Сложение или вычитание выражений с одинаковыми подкоренными числами.
Пример 6
Сложение квадратных корней
Сложение 512+23,512+23.
Решение
Мы можем переписать 512512 как 54·3,54·3. Согласно правилу произведения это становится 543,543. Квадратный корень из 44 равно 2, поэтому выражение становится 5(2)3,5(2)3, что равно 103,103. Теперь у терминов одинаковые подкоренные числа, поэтому мы можем добавить.
103+23=123103+23=123
Попытайся #6
Добавить 5+620,5+620.
Пример 7
Вычитание квадратных корней
Вычитание 2072a3b4c−148a3b4c.2072a3b4c−148a3b4c.
Решение
Умножьте первый член на 9 так, чтобы оба члена имели одинаковые подкоренные числа.
2072a3b4c=209⋅8a3b4c=2098a3b4c=20(3)8a3b4c=608a3b4c2072a3b4c=209⋅8a3b4c=2098a3b4c=20(3)8a3b4c=608a3b4c
So
2072a3b4c−148a3b4c=608a3b4c−148a3b4c=468a3b4c2072a3b4c−148a3b4c=608a3b4c− 148a3b4c=468a3b4c
Попытайся #7
Вычесть 380x−445x. 380x−445x.
380x−445x.
Рационализация знаменателей
Если выражение, включающее радикалы квадратного корня, записано в простейшей форме, оно не будет содержать радикала в знаменателе. Мы можем удалить радикалы из знаменателей дробей, используя процесс, называемый , рационализирующий знаменатель .
Мы знаем, что умножение на 1 не меняет значения выражения. Мы используем это свойство умножения, чтобы изменять выражения, содержащие радикалы в знаменателе. Чтобы удалить радикалы из знаменателей дробей, умножьте на форму 1, которая удалит радикал.
Для знаменателя, содержащего один член, умножить на радикал в знаменателе над самим собой. Другими словами, если знаменатель bc,bc, умножить на cc.cc.
Для знаменателя, содержащего сумму или разность рационального и иррационального членов, умножьте числитель и знаменатель на сопряженное значение знаменателя, которое находится путем изменения знака радикальной части знаменателя. Если знаменатель равен a+bc,a+bc, то сопряженным является a−bc.a−bc.
Если знаменатель равен a+bc,a+bc, то сопряженным является a−bc.a−bc.
Как
Дано выражение с одним корнем квадратного корня в знаменателе, рационализируйте знаменатель.
- Умножьте числитель и знаменатель на радикал в знаменателе.
- Упростить.
Пример 8
Рационализация знаменателя, содержащего один член
Запись 2331023310 в простейшей форме.
Решение
Радикал в знаменателе равен 10,10. Итак, умножьте дробь на 1010,1010. Тогда упрости.
23310⋅1010 23030 301523310⋅1010 23030 3015
Попытайся #8
Пишите 12321232 в простейшей форме.
Как
Дано выражение с подкоренным членом и константой в знаменателе, рационализируйте знаменатель.
- Найдите сопряженное число знаменателя.
- Умножить числитель и знаменатель на сопряженное.
- Используйте свойство дистрибутива.
- Упростить.
Пример 9
Рационализация знаменателя, содержащего два члена
Запись 41+541+5 в простейшей форме.
Решение
Начните с нахождения сопряжения знаменателя, написав знаменатель и изменив знак. Таким образом, сопряжение 1+51+5 составляет 1−5,1−5. Затем умножьте дробь на 1−51−5,1−51−5.
41+5⋅1-51-54-45-4Использовать свойство распределения.5-1Упростить.41+5⋅1-51-54-45-4Использовать свойство распределения.5-1Упростить.
Попытайся #9
Запись 72+372+3 в простейшей форме.
Использование Rational Roots
Хотя квадратные корни являются наиболее распространенными рациональными корнями, мы также можем найти кубические корни, корни 4-й и 5-й степени и многое другое.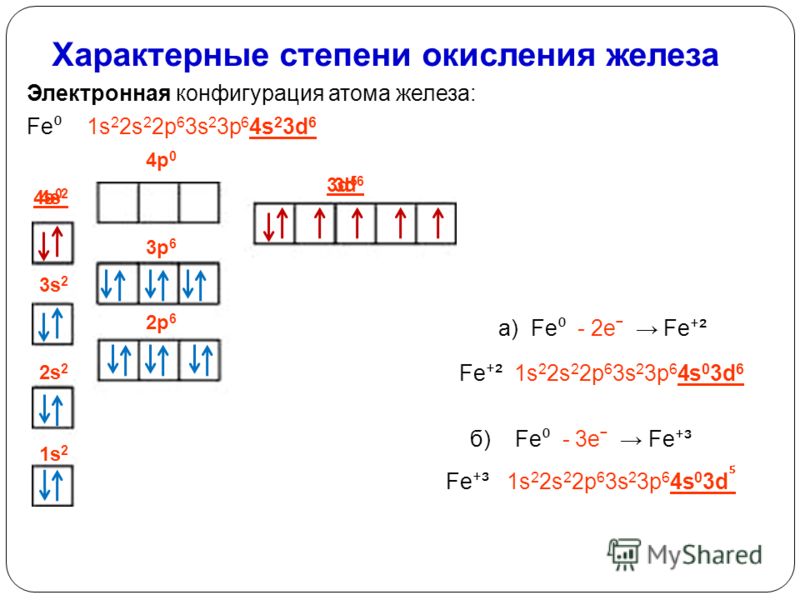 Точно так же, как функция квадратного корня является обратной функцией возведения в квадрат, эти корни являются обратными их соответствующим степенным функциям. Эти функции могут быть полезны, когда нам нужно определить число, которое при возведении в определенную степень дает определенное число.
Точно так же, как функция квадратного корня является обратной функцией возведения в квадрат, эти корни являются обратными их соответствующим степенным функциям. Эти функции могут быть полезны, когда нам нужно определить число, которое при возведении в определенную степень дает определенное число.
Понимание
n th КорниПредположим, мы знаем, что a3=8.a3=8. Мы хотим найти, какое число, возведенное в третью степень, равно 8. Поскольку 23=8,23=8, мы говорим, что 2 — это кубический корень из 8.
n корень aa
число, которое при возведении в степень n дает а.а.
Например, −3−3
корень 5-й степени из −243−243
потому что (-3)5=-243.(-3)5=-243.
Если аа
— действительное число, имеющее хотя бы один n -й корень, то главное н корень аа
число с тем же знаком, что и aa
что при возведении в степень n равно a. a.
a.
Главный n -й корень aa записывается как an,an, где nn — целое положительное число, большее или равное 2. В подкоренном выражении nn называется индексом радикала.
Главный nn-й корень
Если аа является вещественным числом, имеющим хотя бы один корень n -й степени, то главный корень n -й степени a,a, записанный как an,an, является числом с тем же знаком, что и aa что при повышении до n -я степень, равна а.о. Индекс радикала n.n.
Пример 10
Упрощение
n th КорниУпростить каждое из следующего:
- ⓐ −325−325
- ⓑ 44⋅1,024444⋅1,0244
- ⓒ −8×61253−8×61253
- ⓓ 834−484834−484
Решение
- ⓐ −325=−2−325=−2, потому что (−2)5=−32(−2)5=−32
- ⓑ Во-первых, выразите произведение как однокоренное выражение.
 4,0964=84,0964=8, потому что 84=4,09684=4,096
4,0964=84,0964=8, потому что 84=4,09684=4,096 - ⓒ -8×631253Записать как частное двух подкоренных выражений.-2×25Упростить.-8×631253Записать как частное двух подкоренных выражений.-2×25Упростить.
- ⓓ 834-234Упростить, чтобы получить равные подкоренные числа.634 Добавить.834-234Упростить, чтобы получить равные подкоренные числа.634 Добавить.
Попытайся #10
Упрощение.
- ⓐ −2163−2163
- ⓑ 380454380454
- ⓒ 69,0003+7576369,0003+75763
Использование Rational Exponents
Подкоренные выражения также можно записывать без использования подкоренного символа. Мы можем использовать рациональные (дробные) показатели. Индекс должен быть положительным целым числом. Если индекс nn четно, то aa не может быть отрицательным.
а1н=ана1н=ан
Мы также можем иметь рациональные показатели степени с числителями, отличными от 1. В этих случаях показатель степени должен быть дробью в наименьших членах.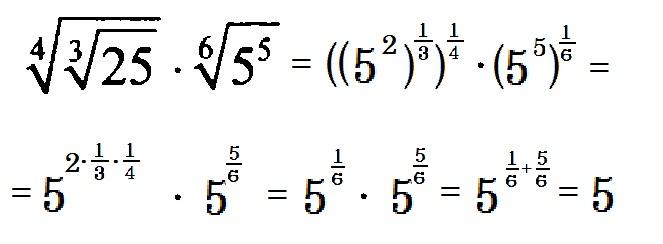 Возводим основание в степень и берем n -й корень. Числитель говорит нам степень, а знаменатель говорит нам корень.
Возводим основание в степень и берем n -й корень. Числитель говорит нам степень, а знаменатель говорит нам корень.
amn=(an)m=amnamn=(an)m=amn
Все свойства показателей, которые мы изучили для целочисленных показателей, справедливы и для рациональных показателей.
Рациональные показатели
Рациональные показатели — еще один способ выразить главные n -х корней. Общая форма преобразования подкоренного выражения с подкоренным символом в выражение с рациональным показателем степени:
amn=(an)m=amnamn=(an)m=amn
Как
Дано выражение с рациональным показателем, запишите выражение как радикал.
- Определите степень, глядя на числитель показателя степени.
- Определите корень, глядя на знаменатель показателя степени.
- Используя основание как подкоренное число, возведите подкоренное число в степень и используйте корень в качестве индекса.

Пример 11
Запись рациональных показателей в виде радикалов
Запись 3432334323 как радикал. Упрощать.
Решение
Цифра 2 указывает на мощность, а цифра 3 на корень.
34323=(3433)2=3432334323=(3433)2=34323
Мы знаем, что 3433=73433=7 потому что 73=343,73=343. Поскольку кубический корень найти легко, проще всего найти кубический корень перед возведением в квадрат этой задачи. В общем, проще сначала найти корень, а потом возводить его в степень.
34323=(3433)2=72=4934323=(3433)2=72=49
Попытайся #11
Напишите 952952 как радикал. Упрощать.
Пример 12
Написание радикалов как рациональных показателей
Пишите 4a274a27 используя рациональный показатель.
Решение
Степень равна 2, а корень равен 7, поэтому рациональный показатель степени будет равен 27,27. Получаем 4a27.4a27.
Используя свойства экспонент, получаем 4a27=4a−27.4a27=4a−27.
Получаем 4a27.4a27.
Используя свойства экспонент, получаем 4a27=4a−27.4a27=4a−27.
Попытайся #12
Запись x(5y)9x(5y)9 используя рациональный показатель.
Пример 13
Упрощение рациональных показателей
Упрощение:
- ⓐ 5(2×34)(3×15)5(2×34)(3×15)
- ⓑ (169)−12(169)−12
Решение
ⓐ
30x34x15Умножение коэффициентов.30×34+15Использование свойств показателей степени.30×1920Упрощение.30x34x15Умножение коэффициентов.30×34+15Использование свойств показателей степени.30×1920Упрощение.
ⓑ
(916). .34 Упрощение.
Попытайся №13
Упрощение (8x)13(14×65).(8x)13(14×65).
1.3 Секционные упражнения
Вербальный
1.
Что значит, когда радикал не имеет индекса? Равно ли выражение подкоренному? Объяснять.
2.
Куда придут радикалы в порядке операций? Объяснить, почему.
3.
Каждое число будет иметь два квадратных корня. Что такое главный квадратный корень?
4.
Может ли радикал с отрицательным корнем и иметь действительный квадратный корень? Почему или почему нет?
Цифровой
В следующих упражнениях упростите каждое выражение.
5.
256256
6.
256256
7.
4(9+16)4(9+16)
8.
289−121289−121
9.
196196
10.
11
11.
9898
12.
27642764
13.
815815
14.
800800
15.
169+144169+144
16.
850850
17.
1816218162
18.
192192
19.
146−624146−624
20.
155+745155+745
21.
150150
22.
9610096100
23.
(42)(30)(42)(30)
24.
123−475123−475
25.
42254225
26.
405324405324
27.
360361360361
28.
51+351+3
29.
81−1781−17
30.
164164
31.
1283+3231283+323
32.
−322435−322435
33.
1512545415125454
34.
3−4323+1633−4323+163
Алгебраический
В следующих упражнениях упростите каждое выражение.
35.
400x4400x4
36.
4y24y2
37.
49п49п
38.
(144p2q6)12(144p2q6)12
39.
м52289м52289
40.
93м2+2793м2+27
41.
3ab2-ba3ab2-ba
42.
42n16n442n16n4
43.
225x349x225x349x
44.
344z+99z344z+99z
45.
50у850у8
46.
490bc2490bc2
47.
3214d3214d
48.
q3263pq3263p
49.
81-3×81-3x
50.
20121d420121d4
51.
w3232-w3250w3232-w3250
52.
108×4+27x4108x4+27×4
53.
12×2+2312×2+23
54.
147к3147к3
55.
125n10125n10
56.
42q36q342q36q3
57.
81м361м281м361м2
58.
72с-22с72с-22с
59.
144324d2144324d2
60.
24×63+81x6324x63+81×63
61.
162x616x44162x616x44
62.
64y364y3
63.
128z33—16z33128z33—16z33
64.
1,024c1051,024c105
Реальные приложения
65.
Оттяжка подвесного моста проходит от земли по диагонали к вершине ближайшего пилона, образуя треугольник. Мы можем использовать теорему Пифагора, чтобы найти необходимую длину растяжки. Квадрат расстояния между проводом на земле и пилоном на земле составляет 90 000 футов. Квадрат высоты пилона составляет 160 000 футов.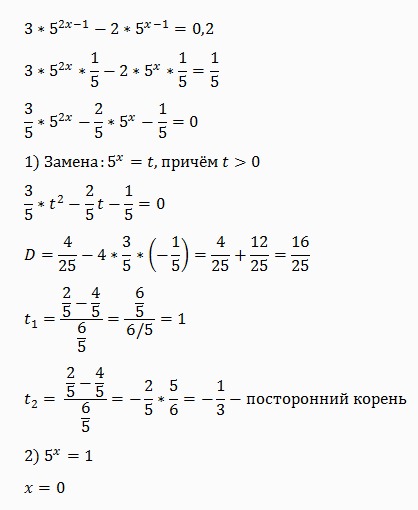

 д.
д.
 4,0964=84,0964=8, потому что 84=4,09684=4,096
4,0964=84,0964=8, потому что 84=4,09684=4,096