Презентация урока по теме: «Эллипс. Гипербола. Парабола»
Тема урока:
Эллипс. Гипербола. Парабола
Изучение нового материала
Найдите площадь треугольника по данным на чертеже.
Найдите площадь треугольника по данным на чертеже.
Найдите площадь треугольника по данным на чертеже.
Найдите площадь треугольника по данным на чертеже.
Найдите площадь треугольника по данным на чертеже.
Найдите площадь треугольника по данным на чертеже.
прямоугольный
и равнобедренный
Найдите площадь треугольника по данным на чертеже.
Повторяем уравнение окружности
1. Уравнение окружности с центром в точке и радиусом
Уравнение окружности с центром в точке и радиусом
1. Уравнение окружности с центром в точке и радиусом
А).Запишите уравнение окружности с центром в точке и радиусом, равным 3.
1. Уравнение окружности с центром в точке и радиусом
А).Запишите уравнение окружности с центром в точке и радиусом, равным 3.
Б).Запишите уравнение окружности с центром в точке и радиусом, равным 1.
1. Уравнение окружности с центром в точке и радиусом
А).Запишите уравнение окружности с центром в точке и радиусом, равным 3 .
Б). Запишите уравнение окружности с центром в точке и радиусом, равным 1.
1. Уравнение окружности с центром в точке и радиусом
В) Укажите координаты центра окружности и её радиус:
Проверка
1.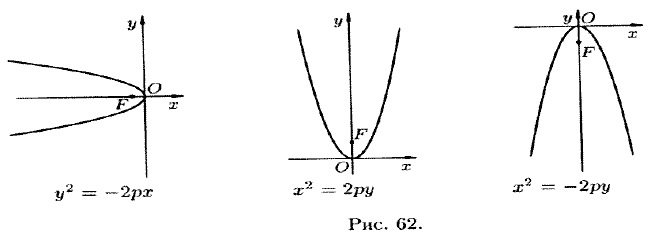 Уравнение окружности с центром в точке и радиусом
Уравнение окружности с центром в точке и радиусом
В) Укажите координаты центра окружности и её радиус:
2. Уравнение эллипса.
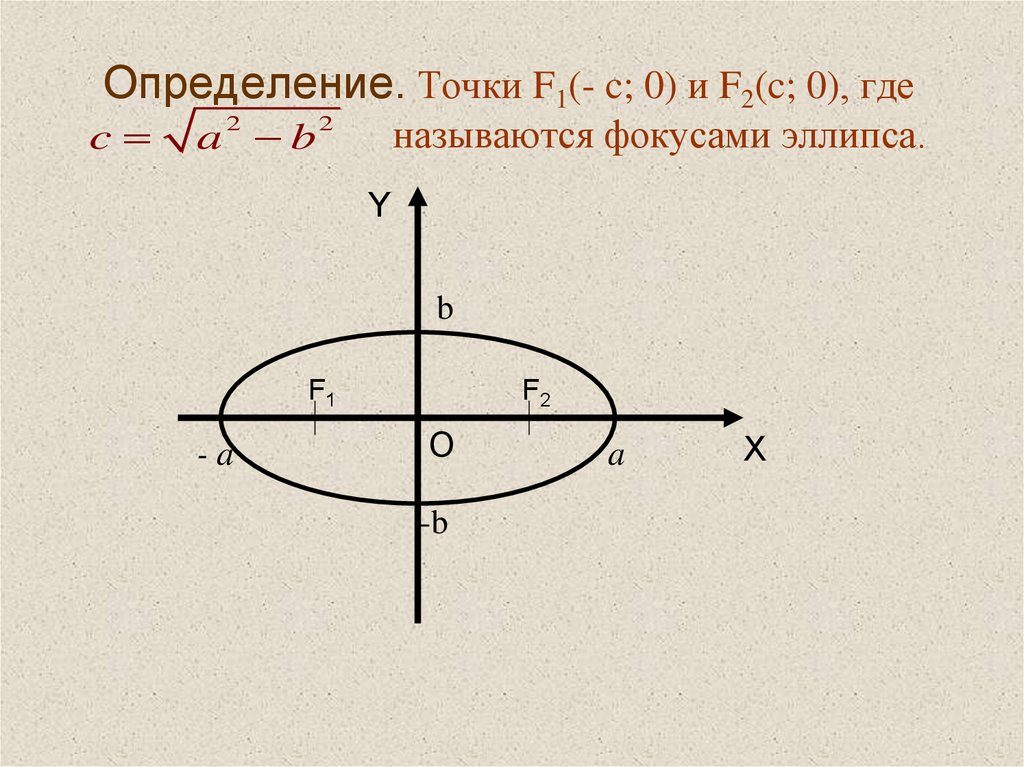
Эллипсом называется множество всех таких точек плоскости , для которых сумма расстояний до двух фиксированных точек постоянна.
Фиксированные точки называются фокусами
2.
Эллипсом называется множество всех таких точек плоскости , для которых сумма расстояний до двух фиксированных точек постоянна.
Фиксированные точки называются фокусами
Каноническое уравнение
эллипса
2. Уравнение эллипса.
Уравнение эллипса.
Каноническое уравнение
эллипса
Начертите эллипс, который
задан уравнением:
Начертите эллипс, который
задан уравнением:
Начертите эллипс, который
задан уравнением:
Напишите уравнение, которым задается эллипс
Напишите уравнение, которым задается эллипс
Работа с учебником
- Стр. 213-214 понятие директрисы эллипса и эксцентриситет эллипса
- № 863
Экспресс-опрос
Выберите верный ответ из предложенных вариантов
- Произведение отрезков одной из двух пересекающихся хорд равно
a) квадрату суммы отрезков другой хорды; b) произведению отрезков другой хорды
c) длине другой хорды.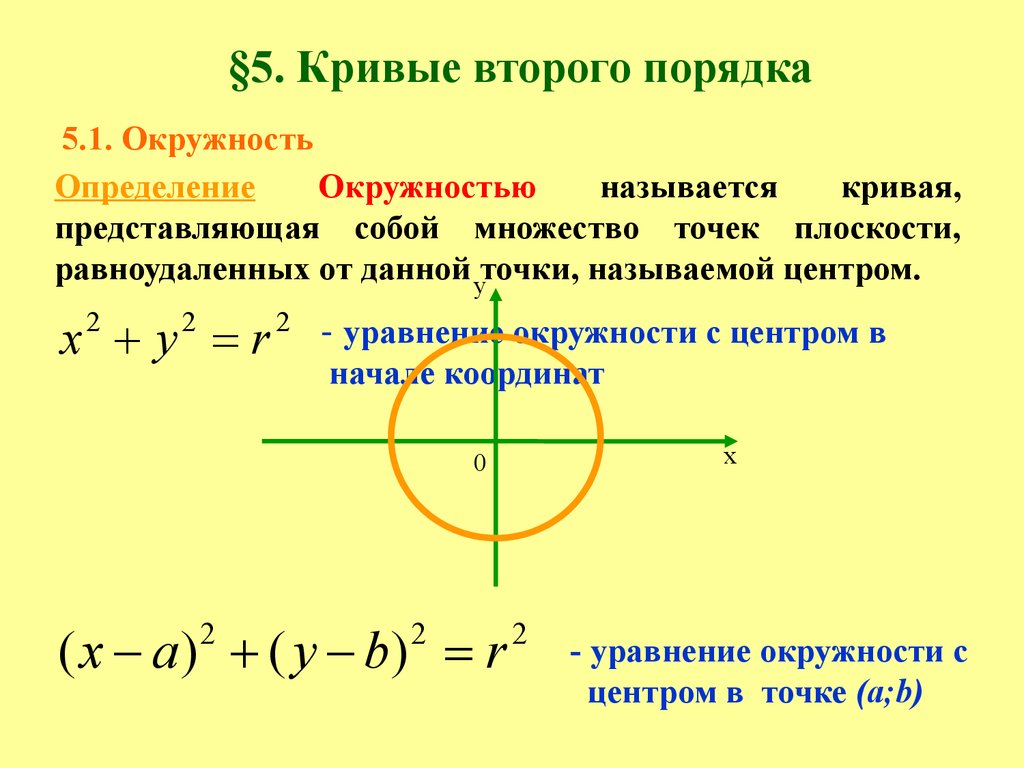
Если две хорды окружности пересекаются , то произведение отрезков одной хорды равно
К
Выберите верный ответ
2. Квадрат касательной равен
- Произведению секущей
на ее внешнюю часть;
- Произведению отрезка секущей,
заключенного внутри окружности,
на ее внешнюю часть;
- Произведению секущей на отрезок секущей, заключенный внутри
окружности.
Квадрат касательной равен произведению всей секущей, проведенной из той же точки к окружности, на её внешнюю часть.
Выберите верный ответ
5. Угол между касательной и
хордой , проходящей через точку касания, измеряется
a) Дугой, на которую он опирается;
b) Половиной заключенной в нем дуги;
c) Полуразностью заключенных
между ними дуг.
Угол между касательной и хордой , проведенной из точки касания, равен половине дуги, заключенной между ними.
Выберите верный ответ
7.
В любом вписанном четырехугольнике
a)Суммы противоположных сторон
равны;
b)Суммы односторонних углов
равны 180 ;
c)Суммы противоположных углов
равны 180 .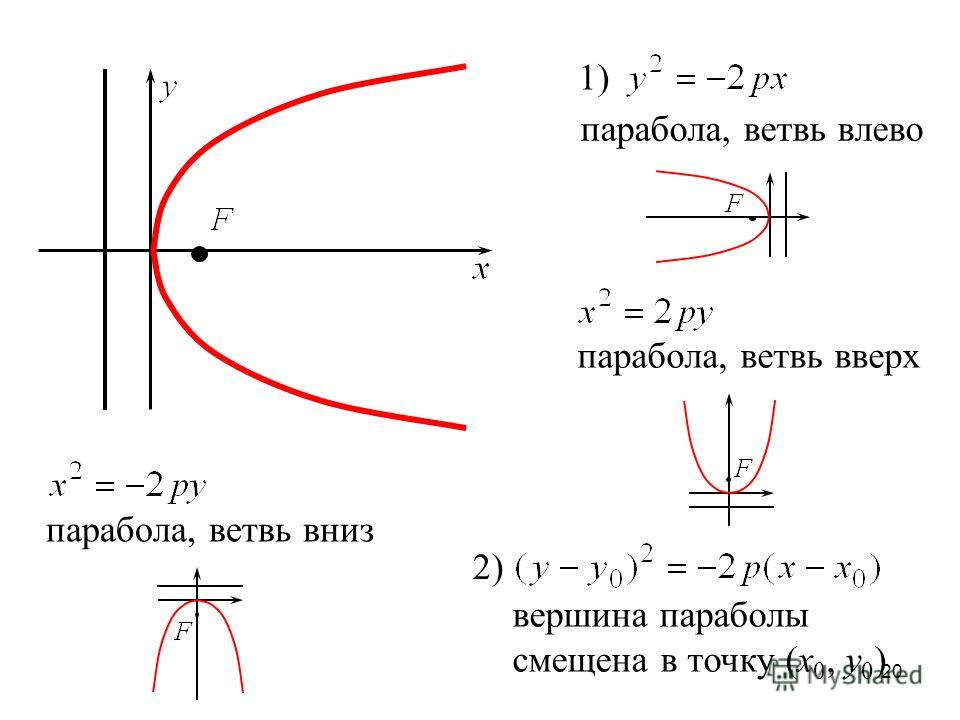
В любом вписанном четырехугольнике сумма противоположных углов
равна 180º
Выберите верный ответ
8. В выпуклый четырехугольник
можно вписать окружность, если
a)Суммы противоположных сторон
равны;
b)Суммы односторонних углов равны 180 ;
c)Суммы противоположных углов
равны 180 .
Признак описанного четырёхугольника:
Если суммы противоположных сторон четырёхугольника равны, то в него можно вписать окружность
Выберите верный ответ
9. Угол между двумя касательными,
Угол между двумя касательными,
проведенными из одной точки ,
a)Равен 180 минус величина заключенной внутри него дуги большей
полуокружности;
b)измеряется полуразностью
заключенных внутри него дуг;
c)Равен 180 минус величина заключенной внутри него дуги меньшей
полуокружности
Угол между двумя касательными , проведенными
из одной точки
Выберите верный ответ
11.Сумма квадратов диагоналей
параллелограмма равна
a)Сумме квадратов его сторон;
b)Полусумме квадратов его сторон;
c)Половине произведения его смежных
сторон.
.
Сумма квадратов диагоналей
параллелограмма равна
сумме квадратов его сторон
.
Выберите верный ответ
13. Биссектриса треугольника делит его сторону на части
- Пропорциональные двум другим
сторонам;
b) Пропорциональные двум другим
биссектрисам;
c) Пропорциональные квадратам
двух других сторон.
.
Биссектриса треугольника делит его сторону на части п ропорциональные двум другим сторонам
В
D
С
А
39
Выберите верный ответ
14. Теорема косинусов
Теорема косинусов
выражается формулой
c)сos С=
39
Выберите верный ответ
14.Теорема косинусов
выражается формулой
c)сos С=
39
Формулы для нахождения площади треугольника:
- Произвольного ( через сторону и высоту ):
- Прямоугольного:
- Равностороннего:
- Формула Герона:
- Через синусы углов треугольника:
6)Через 2 стороны и угол между ними:
- Через радиус вписанной окружности:
8) Через радиус описанной окружности:
.
39
Подводим итоги урока :
1 уровень: Вы понимали все, что предлагалось на уроке.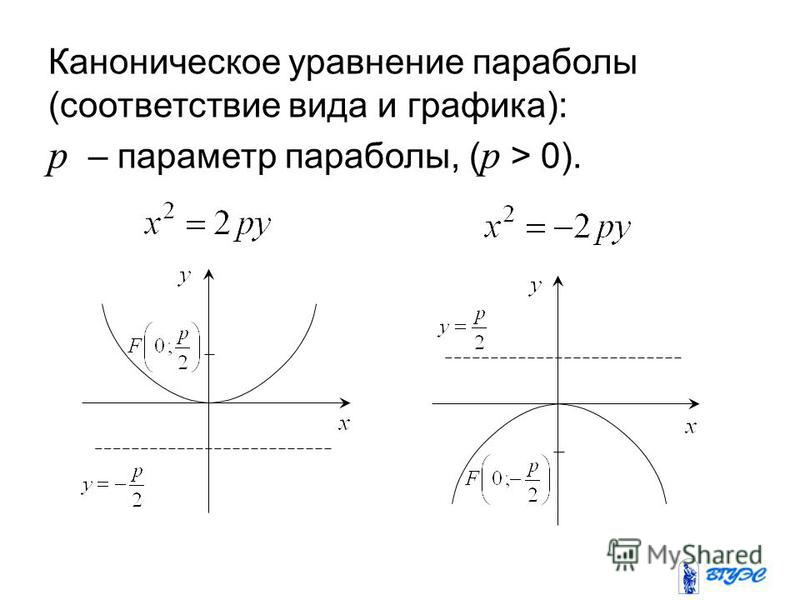 Все формулы площадей понятны, рассмотренные вопросы усвоены- отличный результат.
Все формулы площадей понятны, рассмотренные вопросы усвоены- отличный результат.
2 уровень : сегодня многие вопросы остались непонятыми. Вспоминать было трудно. С вычислениями есть проблемы. Много пробелов в раннее пройденном материале. Следует позаниматься.
Рекомендации: Материал каждого урока разбирать по конспекту урока на сайте.
39
Оцените урок и результат своей деятельности Выберите один из вариантов.
На уроке я работал Своей работой на уроке я Урок для меня показал За урок я
Материал урока мне был
активно / пассивно доволен / не доволен коротким / длинным устал / не устал
понятен / не понятен интересен / скучен
За урок я ставлю себе оценку
_________________
ДР№5 на 12 . 10.17
10.17
1. Теория. Выучить формулы площади треугольника. Проработать материал по формулам эллипса, гиперболы и параболы окружности. Учебник «Геометрия 10-11»
2.Практика . Постройте линии второго порядка:
3. Выполните домашнюю зачетную работу.
Домашняя зачетная работа №1
Домашняя зачетная работа №1
Замечательные кривые: Эллипс, гипербола, парабола
Вы можете изучить и скачать доклад-презентацию на тему Замечательные кривые: Эллипс, гипербола, парабола. Презентация на заданную тему содержит 11 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
Презентации» Математика» Замечательные кривые: Эллипс, гипербола, парабола
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Слайд 2
Описание слайда:
Содержание
Слайд 3
Описание слайда:
Эллипс
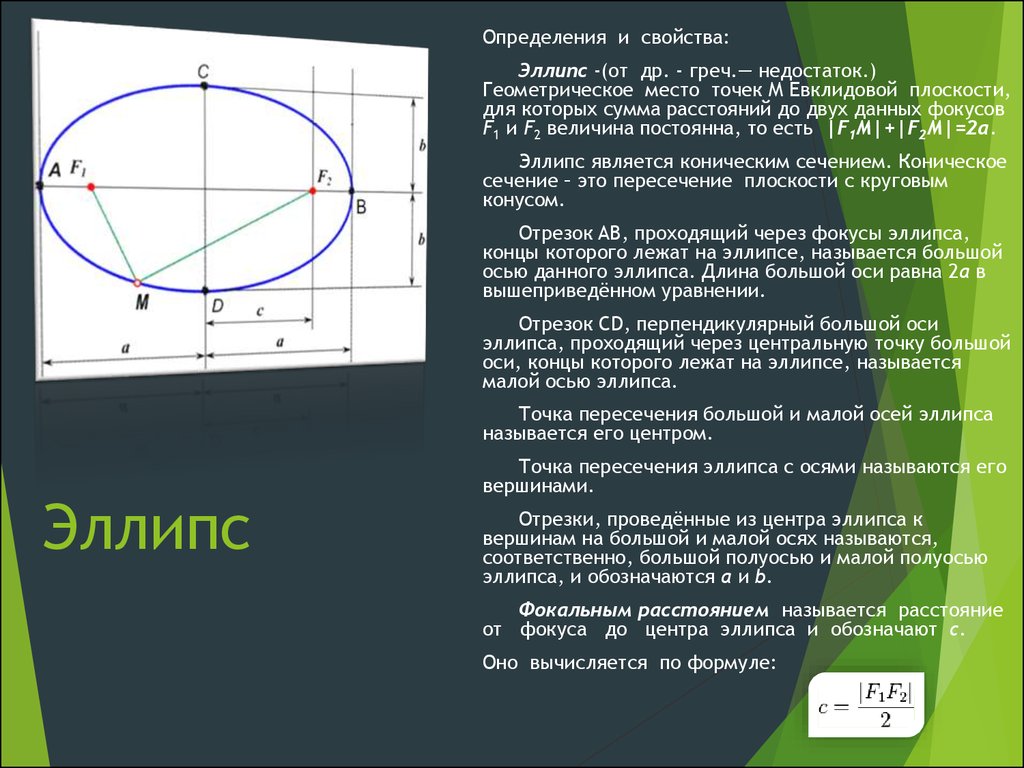
Определения и свойства:
Эллипс -(от др. — греч.— недостаток.) Геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных фокусов F1 и F2 величина постоянна, то есть |F1M|+|F2M|=2a.
Эллипс является коническим сечением. Коническое сечение – это пересечение плоскости с круговым конусом.
Отрезок AB, проходящий через фокусы эллипса, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
Точка пересечения большой и малой осей эллипса называется его центром.
Точка пересечения эллипса с осями называются его вершинами.
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
Фокальным расстоянием называется расстояние от фокуса до центра эллипса и обозначают c.
— греч.— недостаток.) Геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных фокусов F1 и F2 величина постоянна, то есть |F1M|+|F2M|=2a.
Эллипс является коническим сечением. Коническое сечение – это пересечение плоскости с круговым конусом.
Отрезок AB, проходящий через фокусы эллипса, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
Точка пересечения большой и малой осей эллипса называется его центром.
Точка пересечения эллипса с осями называются его вершинами.
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
Фокальным расстоянием называется расстояние от фокуса до центра эллипса и обозначают c. Оно вычисляется по формуле:
Оно вычисляется по формуле:
Слайд 4
Описание слайда:
Эллипс Оптические свойства эллипса: 1.Эллипс – проекция окружности на плоскость не параллельно плоскости этой окружности. 2. Если сделать зеркало в форме эллипса и поместить в один из фокусов источник света, то лучи, отразившись от зеркала, соберутся в другом фокусе. Каноническое уравнение: Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса): Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Приближённая формула для периметра: При вычислении периметра эллипса всегда есть погрешность и всегда положительная. Очень приближенная формула вычисления периметра: Площадь эллипса: Площадь эллипса вычисляется по формуле:
Слайд 5
Описание слайда:
Эллипс
Эллипсы в реальности встречаются гораздо чаще, чем, кажется. Например, планеты солнечной системы движутся по эллиптическим орбитам, кольца Сатурна также имеют эллиптическую форму.
В форме эллипса можно изготовить журнальный столик или соткать ковер.
А у садоводов свой способ применения эллипса: в землю втыкают два колышка, крепят веревку к колышкам (один конец к одному второй к другому), верёвку оттягивают в сторону и вычерчивают эллипс с помощью палки.
Например, планеты солнечной системы движутся по эллиптическим орбитам, кольца Сатурна также имеют эллиптическую форму.
В форме эллипса можно изготовить журнальный столик или соткать ковер.
А у садоводов свой способ применения эллипса: в землю втыкают два колышка, крепят веревку к колышкам (один конец к одному второй к другому), верёвку оттягивают в сторону и вычерчивают эллипс с помощью палки.
Слайд 6
Описание слайда:
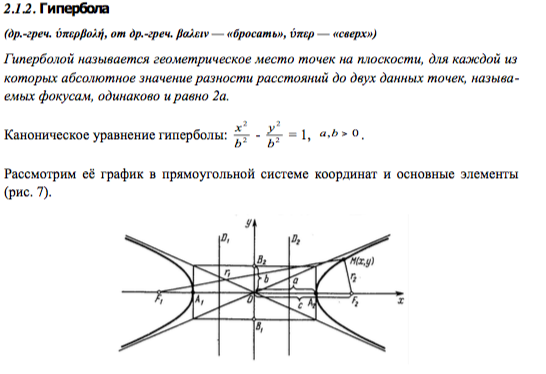
Гипербола
Определение и свойства:
Гипербола (от др. — греч. бол— «бросать», гипер— «сверх». Термин «гипербола» был введён Аполлонием Пергским.) —геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух данных фокусов F1 и F2 постоянно, то есть
||F1M|−|F2M|| =C
Гипербола является коническим сечением.
Осью гиперболы называется прямая, соединяющая её фокусы.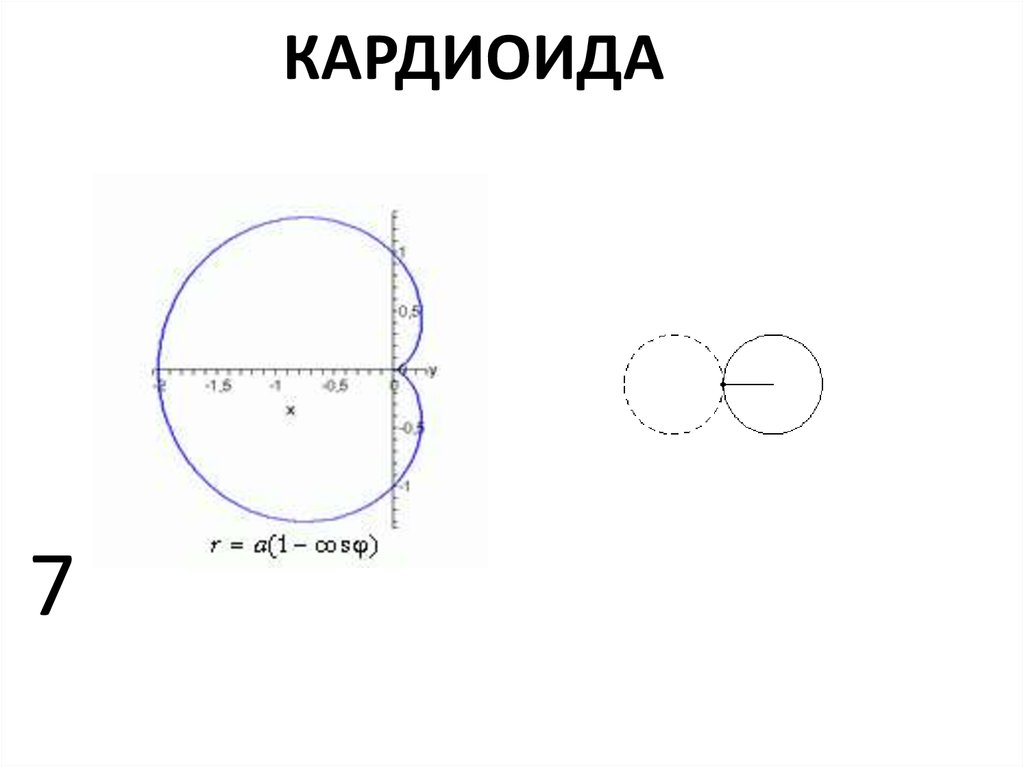 Расстояние от начала координат до одного из фокусов гиперболы называют фокусным расстоянием гиперболы и обозначают с.
Каждая гипербола имеет пару асимптот: Асимптота кривой – это прямая к которой стремится ветвь кривой неограниченно приближаясь, но никогда не пересекая её.
Расстояние от начала координат до одной из вершин гиперболы называется большой или вещественной полуосью гиперболы и обозначается a.
Расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат называется малой или мнимой полуосью гиперболы и обозначается b.
Расстояние от начала координат до одного из фокусов гиперболы называют фокусным расстоянием гиперболы и обозначают с.
Каждая гипербола имеет пару асимптот: Асимптота кривой – это прямая к которой стремится ветвь кривой неограниченно приближаясь, но никогда не пересекая её.
Расстояние от начала координат до одной из вершин гиперболы называется большой или вещественной полуосью гиперболы и обозначается a.
Расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат называется малой или мнимой полуосью гиперболы и обозначается b.
Слайд 7
Описание слайда:
Гипербола
Оптические свойства:
Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе. Каноническое уравнение:
Для любой гиперболы можно найти декартову систему координат такую, что гипербола будет описываться уравнением:
Равнобочная гипербола:
Гиперболу, у которой a = b, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением:
X*Y = a2/2
Каноническое уравнение:
Для любой гиперболы можно найти декартову систему координат такую, что гипербола будет описываться уравнением:
Равнобочная гипербола:
Гиперболу, у которой a = b, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением:
X*Y = a2/2
Слайд 8
Описание слайда:
ГИПЕРБОЛА Гиперболу можно встретить везде, даже в космосе: Траектории некоторых космических тел, проходящих вблизи звезды или другого массивного объекта на достаточно большой скорости могут имеют форму гиперболы. С помощью гиперболы военные определяют, как нужно направить орудие, чтобы поразить неподвижную звучащую цель, например, стреляющее орудие противника.
Слайд 9
Описание слайда:
Парабола
Определение и свойства:
Парабола — (от греч. — приложение) —геометрическое место точек M равноудалённых от данной прямой(называемой директрисой параболы) и данного фокуса.
Рассмотрим такие точки M на плоскости, которые равноудалены от фокуса F и от директрисы PQ (Это значит, что длина отрезка FM равна длине перпендикуляра, опущенного из точки M на директрису PQ)
Парабола является коническим сечением.
Начало координат O — середина отрезка CF.
Парабола имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе.
Все параболы подобны, а расстояние между фокусом и директрисой определяет масштаб.
— приложение) —геометрическое место точек M равноудалённых от данной прямой(называемой директрисой параболы) и данного фокуса.
Рассмотрим такие точки M на плоскости, которые равноудалены от фокуса F и от директрисы PQ (Это значит, что длина отрезка FM равна длине перпендикуляра, опущенного из точки M на директрису PQ)
Парабола является коническим сечением.
Начало координат O — середина отрезка CF.
Парабола имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе.
Все параболы подобны, а расстояние между фокусом и директрисой определяет масштаб.
Слайд 10
Описание слайда:
Парабола
Оптические свойства:
1.Пучок лучей параллельных оси, отражаясь в параболе, собирается в её фокусе.2.При вращении параболы вокруг оси симметрии получается эллиптический параболоид. Каноническое уравнение:
Каноническое уравнение параболы в прямоугольной системе координат:
Где p является расстоянием от фокуса до директрисы.
Каноническое уравнение:
Каноническое уравнение параболы в прямоугольной системе координат:
Где p является расстоянием от фокуса до директрисы.
Слайд 11
Описание слайда:
Парабола частое явление в повседневной жизни. Например, хорошо знакомый падающий мяч футболисты даже не подозревают, что после каждого удара они имеют дело с параболой. Ведь траектория материальной точки, брошенной в наклонном или горизонтальном направлении и падающей под действием силы притяжения Земли, имеет форму параболы.
Свойство параболы о фокусировании параллельного пучка прямых используется в конструкции прожекторов, фонарей, фар, в конструкции антенн необходимых для передачи данных на большие расстояния, солнечных электростанций и т.д.
Применение замечательных кривых широко распространенно, их применяют в производстве, строительстве, военном деле и т. д.
Замечательные кривые поистине замечательны своими свойствами, трудно себе представить мир без этих кривых, хоть они так не заметны для нашего повседневного взора.
д.
Замечательные кривые поистине замечательны своими свойствами, трудно себе представить мир без этих кривых, хоть они так не заметны для нашего повседневного взора.
Tags Замечательные кривые: Эллипс, гипербола, парабола
Похожие презентации
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
Эксцентриситет – формула для окружности, параболы и гиперболы
Давайте обсудим определение эксцентриситета, формулу эксцентриситета, эксцентриситет окружности, эксцентриситет параболы, эксцентриситет эллипса и эксцентриситет гиперболы
насколько коническое сечение (круг, эллипс, парабола или гипербола) на самом деле отличается от круглого.
Эксцентриситет окружности равен нулю, поэтому эксцентриситет показывает, насколько некруглой является данная кривая.
 Большие эксцентриситеты менее изогнуты.
Большие эксцентриситеты менее изогнуты.
Формула эксцентриситета
В математике для любого конического сечения существует геометрическое место точки, в которой расстояния до точки (фокуса) и линии (известной как направляющая) находятся в постоянном соотношении. Это отношение называется эксцентриситетом и обозначается символом «е».
Формула для определения эксцентриситета любого конического сечения может быть определена как центр к фокусу 92 + Dx + Ey + F\] и это уравнение равно нулю.
Теперь давайте подробно обсудим эксцентриситет различных конических сечений, а именно параболы, эллипса и гиперболы.
Эксцентриситет окружности
Окружность может быть определена как набор точек на плоскости, которые равноудалены от фиксированной точки на плоскости, известной как «центр».
Теперь вы можете подумать о том, что такое радиус.
 Термин «радиус» используется для определения расстояния от центра и точки на окружности.
Термин «радиус» используется для определения расстояния от центра и точки на окружности.Если центр круга находится в начале координат, становится легко вывести уравнение круга.
Мы можем вывести уравнение Круга, используя приведенные ниже условия.
В данной окружности, если «r» равно радиусу, а C (h, k) равно центру окружности, то по определению окружности и эксцентриситета мы получаем
| КП | = радиус(r)
Мы знаем, что формула для нахождения расстояния: 92\]
Кроме того, e = 0 для круга.
Эксцентриситет параболы
Парабола в математике определяется как множество точек P, в которых расстояния от фиксированной точки F (Фокус) на плоскости равны их расстояниям от фиксированной линии l (направляющая ) в плоскости.
Другими словами, мы можем сказать, что расстояние от фиксированной точки на плоскости имеет постоянный коэффициент, равный расстоянию от фиксированной линии на плоскости.

Следовательно, эксцентриситет параболы всегда равен 1 (e=1)
Общее уравнение параболы можно записать как x2 = 4ay, а эксцентриситет всегда равен 1.
Забавный факт: всякий раз, когда снаряд запущен, он проходит параболический путь. Это связано с тем, что наряду с горизонтальной составляющей ему также сопутствует вертикальная составляющая. Снаряд преодолевает самое длинное горизонтальное расстояние, когда он брошен под углом 45 градусов. Поэтому в следующий раз, когда вы будете бросать мяч и хотите произвести впечатление на своих друзей, убедитесь, что вы запускаете снаряд под углом 45 градусов и видите перед глазами параболическое движение!
Эксцентриситет эллипса
Эллипс можно определить как набор точек на плоскости, в которых сумма расстояний от двух фиксированных точек постоянна.
Проще говоря, расстояние от фиксированной точки на плоскости имеет постоянный коэффициент меньше, чем расстояние от фиксированной линии на плоскости.
 2}}{ а} \]
2}}{ а} \]Для эллипса значения a и b — это длины большой и малой полуосей соответственно.
Забавный факт: вам может быть интересно узнать, что Эллипс и связанные с ним понятия имеют очень широкое применение в области космических наук. Потому что большинство небесных тел, таких как планеты, спутники, кометы, искусственные спутники и т. д., имеют тенденцию двигаться по эллиптическим орбитам. Помимо концепции эксцентриситета, другие концепции, такие как апогей и перигей, входят в картину при понимании положения этих тел. Это делает изучение эллипсов и связанных с ними понятий еще более интересным.
Эксцентриситет гиперболы
Гипербола определяется как множество всех точек на плоскости, где разница расстояний от двух фиксированных точек постоянна.
Проще говоря, расстояние от фиксированной точки на плоскости имеет постоянный коэффициент, больший, чем расстояние от фиксированной линии на плоскости.
 2}} {а} \]
2}} {а} \]Для любой гиперболы значения a и b являются длинами большой и малой полуосей соответственно.
Забавный факт: ученые используют понятия, связанные с гиперболой, для определения местоположения радиостанций. Это обеспечивает оптимизацию области, охватываемой сигналами станции. Это позволяет людям находить объекты на большой площади. Это приложение сыграло важную роль во Второй мировой войне.
Различные значения эксцентриситета создают разные кривые:
при эксцентричности, равном 0
Мы получаем круг
для 0
.
Для значения Эксцентриситета = 1
Получаем Параболу.
Для значения эксцентриситета > 1
Получаем гиперболу.

Для значения Эксцентриситета =∞
Получаем прямую.
Эксцентриситет часто обозначается буквой (имейте в виду, что вы не путаете это с числом Эйлера E, они разные).
Расчет значения эксцентриситета (формула эксцентриситета):
Эксцентриситет окружности:
2}}{a} \]
Перечислите формулы для расчета эксцентриситета параболы и окружности.
Ответ: для параболы значение эксцентриситета равно 1
для окружности значение эксцентриситета = 0. Поскольку для окружности a=b
малая полуось для данного эллипса в вопросе
Эксцентриситет с веб-сайта Vedantu
Весь контент, связанный с эксцентриситетами параболы, окружности, гиперболы и эллипса на этом веб-сайте, подготовлен экспертами Веданту в данной области.
 Эти специалисты имеют многолетний опыт работы в области математики. На протяжении многих лет они внимательно следили за прошлыми экзаменационными листами для различных экзаменов, таких как класс 11, класс 12, экзамены IIT-JEE, государственные экзамены CET и т. Д., И только после тщательного исследования и анализа содержание на этой странице было сделано. доступны для вас.
Эти специалисты имеют многолетний опыт работы в области математики. На протяжении многих лет они внимательно следили за прошлыми экзаменационными листами для различных экзаменов, таких как класс 11, класс 12, экзамены IIT-JEE, государственные экзамены CET и т. Д., И только после тщательного исследования и анализа содержание на этой странице было сделано. доступны для вас.Чтобы использовать эти усилия, предпринимаемые от вашего имени экспертами Веданту, вы должны ссылаться на концепцию Эксцентриситета только с веб-сайта Веданту. Это гарантирует, что вы получите преимущество перед другими и очень хорошо сдадите все экзамены, где задаются вопросы, связанные с этой темой.
Другие понятия, объясненные Веданту
Помимо Эксцентрика, Веданту объяснил многие другие математические понятия на своем веб-сайте. Это может помочь учащимся сделать математику легкой и увлекательной. Все концепции объясняются только экспертами Веданту. Другие связанные темы, которые могут вас заинтересовать, следующие:
Algebra Symbols
Area of Hemisphere
Circumference of Circle
Semi-Circle
Parabola graph
Equation of a Парабола
Площадь эллипса
Формула эллипса
Фокусы эллипса
Equations of Ellipse
Hyperbola
Hyperbola formulas
Hyperbolic Functions
Hyperbolic Function Foumlas
Area segment Circle
Secant of a Круг
Уравнение круга
Круги
Эти понятия цвета вместе с понятием эксцентриситета помогут вам укрепить ваши представления о геометрии и полетах.

Применение коников в реальной жизни
Содержание
1. Введение 2. Что такое коническое сечение 3. Парабола в реальной жизни 4. Эллипсы в реальной жизни 5. Гиперболы в реальной жизни 6. Резюме 7. Часто задаваемые вопросы 27 октября 2020 г.
Время чтения: 8 минут
ВведениеКоники или конические сечения изучались греческими математиками, а Аполлоний Пергосский работал над их свойствами около 200 г. до н.э.
Конические сечения представляют собой плоскости, вырезанные из конуса под разными углами. Формы различаются в зависимости от угла, под которым он срезан с конуса.

Поскольку они нарезаны из конусов, их называют Кони. Кроме того, у них есть некоторые общие свойства, поскольку все они принадлежат конусам. Эти изогнутые участки относятся к .
Читайте также:
Геометрия сложная?
Коники в реальной жизниВот PDF-файл, который расскажет нам больше о кониках в реальной жизни. Они могут думать об этом. Нажмите на кнопку загрузки, чтобы изучить их.
Что такое коническое сечение?Коническое сечение – это кривая, полученная пересечением поверхности конуса с плоскостью.
В аналитической геометрии коника определяется как плоская алгебраическая кривая степени 2. То есть она состоит из множества точек, удовлетворяющих квадратному уравнению с двумя переменными. Это квадратное уравнение можно записать в матричной форме. Благодаря этому некоторые геометрические свойства можно изучать как алгебраические условия.

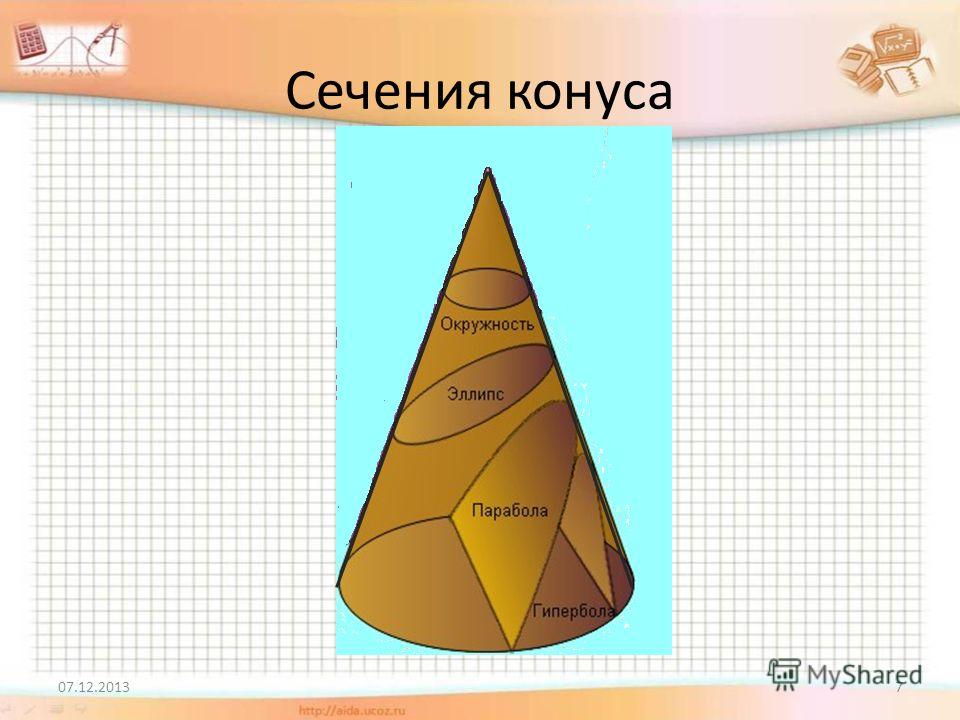
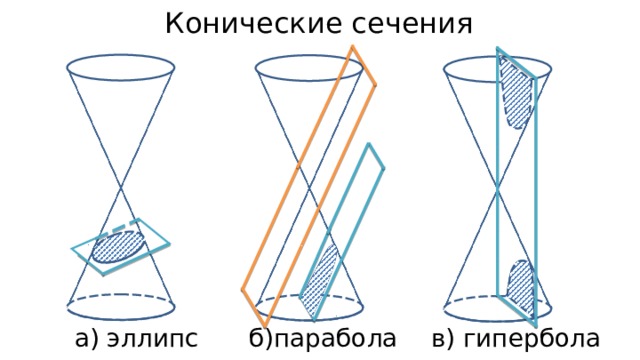
Таким образом, разрезая и беря разные срезы (плоскости) под разными углами к краю конуса, мы можем создать круг, эллипс, параболу или гиперболу, как показано ниже
Окружность является разновидностью эллипса, остальные части не являются круглыми. Итак, круг четвертого типа.
Фокус, директриса и эксцентриситет
Кривая также определяется с помощью точки (фокуса) и прямой линии (директрисы).
Если мы измерим и примем
а — перпендикулярное расстояние от фокуса до точки P на кривой,
и b — расстояние от директрисы до точки P,
, то а: b всегда будет постоянным .
\(a: b < 1\) для эллипса
\(a: b= 1\) для параболы как \(a= b\)
и \(a: b> 1\) для гиперболы.
Эксцентриситет: Приведенное выше соотношение a:b представляет собой эксцентриситет.
Таким образом, на любом коническом сечении есть все точки, расстояние между которыми до фокуса равно эксцентриситету, умноженному на эксцентриситет директрисы.

Таким образом, если эксцентриситет \(<1\), то это эллипс.
если эксцентриситет \(=1\), то это парабола.
и если эксцентриситет \(=1\), то это гипербола.
Для круга эксцентриситет равен нулю. Чем выше эксцентриситет, тем меньше кривизна конической части.
Широкая прямая кишкаЛиния, параллельная директрисе и проходящая через фокус, называется широкой прямой кишкой.
Длина прямой кишки в 4 раза больше фокусного расстояния 92\) по оси х – у.
Эту формулу вывел математик Менехм.
Парабола встречается в природе и в произведениях человека.
Вода из фонтана падает на землю по параболе.
Мяч, брошенный высоко, летит по параболе.
Американские горки идут по пути подъема и спуска по параболической дорожке моря.

Архитектурное сооружение, построенное и названное Парабола в Лондоне в 1962 году, имеет медную крышу с параболическими и гиперболическими обшивками.
Мост Золотые Ворота в Сан-Франциско в Калифорнии знаменит параболическими пролетами с обеих сторон.
В маяках предусмотрены параболические лампы, обеспечивающие хорошую фокусировку луча, чтобы моряки могли видеть их на расстоянии.
Автомобильные фары также параболического типа.
Вытянутая дуга запуска ракеты параболическая.
Спутниковая антенна представляет собой параболическую конструкцию, облегчающую фокусировку и отражение радиоволн.
Эллипсы в реальной жизниЭлектроны в атоме движутся вокруг ядра по эллиптической орбите.

Свойство Эллипса отражать звук и свет используется для измельчения камней в почках. Больного укладывают в эллиптическую емкость с водой. Камни в почках, находящиеся в другом очаге, концентрируются и измельчаются.
Собор Святого Павла представляет собой сооружение эллиптической формы для облегчения разговора на одном конце слышимым на другом конце благодаря свойству эллипса.
Перед Белым домом в Вашингтоне есть парк в форме эллипса.
При наклоне стакана с водой видна эллиптическая поверхность воды.
Продукты питания морковь, огурец, срезанные под углом к главной оси, придают им эллиптическую форму и элегантный внешний вид.
Шепчущие галереи в статутной столице США и Соборе Святого Павла в Лондоне демонстрируют свойство эллипса, состоящее в том, что шепот из одного фокуса может быть услышан в другом фокусе только тем человеком, которому он направлен
>Эллиптические тренажеры позволяют бегать или ходить без нагрузки на сердце.

Гиперболы в реальной жизниГитара является примером гиперболы, поскольку ее стороны образуют гиперболу.
Аэропорт Даллес имеет гиперболическую параболическую конструкцию. Он имеет одно поперечное сечение гиперболы, а другое параболы.
Зубчатая передача с парой гиперболических шестерен. Он имеет перекошенные оси и форму песочных часов, придающую форму гиперболе. Гиперболические передачи передают движение на наклонную ось.
Башня порта Кобе имеет форму песочных часов, что означает наличие двух гипербол. Вещи, видимые из точки с одной стороны, будут такими же, если смотреть из той же точки с другой стороны.
Спутниковые системы, Радиосистемы используют гиперболические функции.

Обратная зависимость связана с гиперболой. Давление и объем газа находятся в обратной зависимости. Это можно описать гиперболой.
Линзы, мониторы и оптические стекла имеют форму гиперболы.
РезюмеКонические или конические формы представляют собой плоскости, вырезанные через конус. В зависимости от угла пересечения получаются разные коники. Парабола, эллипс и гипербола являются кониками. Окружность является специальной коникой. Конические формы двумерны, показаны на оси x, y. Конические формы широко распространены в природе и в рукотворных произведениях и сооружениях. Они успешно используются в электронике, архитектуре, пищевой и хлебопекарной, автомобильной и медицинской областях.
Источник: google content
Часто задаваемые вопросы (FAQ) Какие существуют 4 типа конических сечений?В зависимости от угла пересечения плоскости и конуса получаются четыре различных конических сечения.
 Это парабола, эллипс, гипербола и окружность. Они двухмерны по оси x-y.
Это парабола, эллипс, гипербола и окружность. Они двухмерны по оси x-y.
Как получить конические сечения?Коническое сечение включает секущую плоскость, поверхность двойного конуса в форме песочных часов и пересечение конуса плоскостью. В зависимости от угла резания, то есть светового угла, параллельного краю и глубокого угла, получаются эллипс, парабола и гипербола соответственно. Окружность также коническая и вырезана параллельно круглой нижней грани конуса.
Как найти площадь эллипса?Площадь эллипса равна \((a \times b \times π)\) квадратных единиц.
Источник: i.pinimg.comгде a = длина большой оси эллипса
b = длина малой оси эллипса.
Каковы некоторые реальные приложения коников?Планеты движутся вокруг Солнца по эллиптическим траекториям в одном фокусе.


 Большие эксцентриситеты менее изогнуты.
Большие эксцентриситеты менее изогнуты. Термин «радиус» используется для определения расстояния от центра и точки на окружности.
Термин «радиус» используется для определения расстояния от центра и точки на окружности.
 2}}{ а} \]
2}}{ а} \] 2}} {а} \]
2}} {а} \]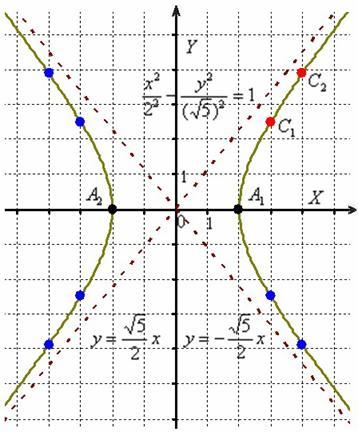
 Эти специалисты имеют многолетний опыт работы в области математики. На протяжении многих лет они внимательно следили за прошлыми экзаменационными листами для различных экзаменов, таких как класс 11, класс 12, экзамены IIT-JEE, государственные экзамены CET и т. Д., И только после тщательного исследования и анализа содержание на этой странице было сделано. доступны для вас.
Эти специалисты имеют многолетний опыт работы в области математики. На протяжении многих лет они внимательно следили за прошлыми экзаменационными листами для различных экзаменов, таких как класс 11, класс 12, экзамены IIT-JEE, государственные экзамены CET и т. Д., И только после тщательного исследования и анализа содержание на этой странице было сделано. доступны для вас.


 Это парабола, эллипс, гипербола и окружность. Они двухмерны по оси x-y.
Это парабола, эллипс, гипербола и окружность. Они двухмерны по оси x-y. 