20 число четное или нечетное число: Определить чётное или нечётное число онлайн

Как объяснить 5-ти летке что такое четные числа?

1. Форум
2. Архив
3. Детская психология и развитие

Педагоги, воспитатели, пожалуйста, подскажите, как корректно объяснить ребенку что такое четное число? Ребенку 5.5, складывать и вычитать может до 20, но вот деление пока не знает. Т.е. объяснить на уровне «делится пополам поровну» я не могу (( Пытаюсь говорить о том, что четное — если можно распределить это число ушей по зайцам, и не останется лишних ушей, но это явное не то… Как бы Вы объяснили? Или все-таки вначале деление на 2, а потом четное/нечетное проходить?

Да именно так, четное число можно поделить на 2, на две равных части. Хватило одного раза, чтобы ребенок понял. Сейчас может сразу про любое число в пределах первой сотни сказать четное оно или не четное. Сыну 5,3.
А вашего объяснения про зайцев даже я не поняла

Объясните на уровне «делится на 2 одинаковые кучки» и поделите-таки конфеты, например В принципе мы научились делить на 2 кучки числа до 10ти включительно.

Я своей 4-летке объясняла, что чётное количество можно распределить группами по 2 штуки без остатка. Нарисовала, к примеру, 5 точек, две обвела кругом, ещё 2 обвела кругом, осталась одна без пары — значит, 5 — нечётное число. Дочь поняла сразу.
Ещё очень помогла таблица сотни, дочка сообразила, что чётные и нечётные чередуются, и что весь столбик под числом 1 ( 21, 31 и т.д.) — нечётные, так как заканчиваются на 1. То же самое со всеми остальными числами.

+1 так же объясняла. Ребенок все понял.

Если можно все разделить на двоих так, чтобы получилось у обоих одинаковое количество. Лучше всего объяснять на конфетах

А зачем это знать 5-летке???. ..числа до 20 но не знает деления…

Зачем гнать если в 7лет можно рассказать за пару минут и ребенок сразу все поймет?

Которые кончаются на 0,2,4,6,8.

А зачем вам это объяснять???? В школе научат. Господи, не отнимайте у ребенка детство….

Зачем???

Потому что когда есть желание учиться и бесконечное любопытство — надо его удовлетворять. И если моих педагогических способностей не хватает чтобы объяснить, надо лезть в Инет, и разбираться, как такие вещи доносят до детей.

Я бы объяснила так (хоть и не педагог) ,четные числа -это то количество(допустим яблок) которое всегда можно поделить поровну с другом(допустим)

как объяснить маме пятилетки не бежать впереди паровоза?!

оно делится на 2

в свое время объясняла дочке, что четные числа те, корорые можно «разделить поровну» разделить на 2 маленькому ребенку не понятно, а поровну понятно.

Четное количество предметов можно «постоить» по парам.

Т.е. все книжки, где упоминаются четные/нечетные — забрать (или страницы, где про ЭТО есть, вырезать?), и на вопросы не отвечать?

Разумеется. Дать пирамидку, сказку про репку и пусть с ними до школы сидит. Остальному научат без Вас…

разложите на примере на кучки пополам.

Почему отнимать детство?Если ребенок сам интересуется?Мою было от математики не оторвать в 5 лет.

вот у нас такая есть одна девочка со сказкой про репкусамая тупая в школе в 1 нашем классе.Единственная,что пришла и ничего не знала, включая чтение.Учитель ругает на каждом уроке.Моя вон сколько всего выучила, а и то тяжеловато, такие у нас нагрузки.Учитель так и сказала на собрании, что «официально до школы учить не надо- а на деле, сами видите, как кому что дается.Так что выбирайте»

Напишите в топике плз., зачем ему эта информация. Интересно и понять хочется

А Вам зачем этот навык? … В данный момент операции с числами это один из видов развлечений наряду скучей других

У меня тоже есть дети 6 и 4 года — вот и интересно как и зачем может ребенок в этом возрасте использовать такие знания. Мне кажется, что для того чтобы усвоить эту информацию ребенок должен свободно делить и умножать, а потом уже обратить его внимание на четность и нечетность чисел. Так ему легче будет понять и усвоить. Но эта задача явно не для пятилетнего ребенка, тем более в качестве развлечения. В этом возрасте физиология мозга не готова адекватно принимать такую информацию. Хотя, конечно, есть исключения, но их мало. Если ребенок хорошо усваивает новый материал, получает удовольствие от подобных занятий — тогда конечно такие развлечения и интересны, и полезны для малыша. Это мое мнение. Если Вам не сложно, дайте ссылочку где можно посмотреть эти упражнения\задания. Хочу попробовать с сыном 6,5 лет полистать.

Согласна про физиологию мозга Не дам. Сами на ходу придумываются.

Понятно.

Моему 5-и летке это просто интересно, ему интересны разные операции с цифрами интересно считать туда и обратно, интересно счет через единицу, как раз сначала считает все нечетные, затем четные цифры , считает десятками, любит писать большие (4,5,6,7 и т.д. значные числа) Напишет потом выясняет, что он написал, любимая игрушка калькулятор. Всерьез интересуется таблицей умножения. Почему его это интересует я не знаю, с пеленок ребенка цифрами никто не грузил, просто, как только научился говорить, стал задавать вопросы. И кстати, он не только цифрами интересуется, ребенку интересно в принципе все, он с удовольствием изучает анатомические атласы, выращивает кристаллы, собирает из наборов молекулы разнообразных веществ, знает строение атома ну и многое другое. И я могу сказать, что у меня самый обычный ребенок, которому просто предоставлена возможность удовлетворить потребность в информации.

а за что ругает??? за то, что научить не может??? в сад таких учителей, которые могут «учить» только тех, кто уже все знает!

Да-да, а вес класс будет сидеть, деградировать и ждать когда там эту единственную девочку читать научат и дотянут до уровня остальных детей.

Умница Ваш малыш. А он умеет умножать и делить? И как он понимает четные и нечетные числа? Вот если его спросить: Какие ты знаешь четные\нечетные числа? Почему они четные\нечетные? Ведь для того, чтобы ответить на этот вопрос он должен хорошо знать умножение\деление.

Нет, умножать делить пока не учили, хотя он и интересуется таблицей умножения, если найду хорошее пособие обучающее, при случае куплю ему.
Четные числа это те, которые можно разделить на 2, на 2-е равные части, не четные соответственно нельзя. Про то, что может быть остаток у числа мы не разбирали, разбирали только числовую прямую -1, 0, 1 объясняли про бесконечность (ребенок задался этим вопросом после взгляда на уличный градусник), ну и на уроках в школе они уже разбирают такие понятия как отрезок, линия, ломаная линия, луч это, кстати, из Патерсона для 5-6 леток.

а так весь класс получает ценнейшие знания, пока учтель ругает девочку.

Ну а пойдет он в школу — все это знает и умеет. Ему там станет скучно и не интересно.
Мир безграничен — зачем обязательно изучать школьную программу?

Занимаемся по книжкам изд-ва Стрекоза (серия с Дружком, 6+, Математика, Считаем до 20 и пр.) — и там есть это понятие. Ответ «тебе рано про это знать, зайка» ребенка не удовлетворяет Вообще книжки улетные — когда деть болеет, это мое спасение. Пока занята — готовлю, убираюсь, дела делаю, ребенка не видно и не слышно — сидит сам разбирается. Правда хватает ненадолго — одна книжка 3-4 занятия максимум.

Собственно, вопрос как объяснить, а не зачем изучать.

Вот мы зайцам уши и пририсовывали, чтобы построить по парам. Только уж больно муторно, «отоварить» десяток зайцев ))

Будем пробовать с конфетами, спасибо

на конфетах или машинках покажите, через что им нравится они быстро понимают.

Ну просто знаете, некоторые пятилетки интересуются такими вещами. Что, не отвечать?

Открыть тему в окнах

Знаменитости в тренде

Счастливая мама важнее! Почему не стоит проводить с малышом все время, забывая о себе

Ко Дню учителя! Топ-8 вдохновляющих фильмов о наставниках и их учениках

Стала известна сумма гонорара Вина Дизеля за участие в фильме «Аватар-2»

5 класс.

Делимость натуральных чисел

Признаки делимости

Доказываем

616. Докажите, что произведение чётного числа и любого натурального числа есть число чётное.

Так как чётное число делится на 2, то произведение его и любого натурального числа делится на 2 (по свойству 1: если один из множителей делится на некоторое число, то и произведение делится на это число), то есть произведение — число чётное, что и требовалось доказать.

617. Докажите, что сумма двух чётных чисел является чётным числом.

Так как каждое из двух чисел делится на 2, то их сумма делится на 2 (по свойству 3: если каждое из двух чисел делится на некоторое число, то их сумма и разность делится на это число), то есть их сумма — число чётное, что и требовалось доказать.

618. Покажите, что нечётные числа 7, 9, 5, 13 можно записать в виде 2 • k + 1, где k — некоторое натуральное число.

7 = 2 • 3 + 1;
9 = 2 • 4 + 1;
5 = 2 • 2 + 1;
13 = 2 • 6 + 1.

Доказываем

619. Докажите, что сумма двух нечетных чисел является четным числом.

Представим нечетное число в виде: 2 • k + 1, где k — некоторое натуральное число (либо чётное, либо нечётное).
Сложим это число само с собой: (2 • k + 1) + (2 • k + 1) = 2 • k + 1 + 2 • k + 1 = 2 • k + 2 • k + 2 = 2 • (k + k + 1) = 2 • (2 • k + 1)
По свойству 1: если один из множителей делится на некоторое число, то и произведение делится на это число — получается, что один из множителей произведения 2 • (2 • k + 1) делится на 2 (2 : 2 = 1), следовательно, сумма двух нечётных чисел делится на 2, что и требовалось доказать.

620. Определите, делится ли число 111 111 111 111 111:
а) на 3; б) на 9.

а) 1) 1 • 15 = 15 — сумма цифр числа 111 111 111 111 111;
2) 15 : 3 = 5 — значит число 111 111 111 111 111 делится на 3;

б) 1) 1 • 15 = 15 — сумма цифр числа 111 111 111 111 111;
2) 15 : 9 = 1 (ост. 6) — не делится на 9 нацело, значит число 111 111 111 111 111 не делится на 9.

621. Какую цифру нужно поставить вместо звездочки, чтобы полученное число делилось на 9:
а) 4∗;   б) 5∗;   в) 85∗;    г) 738∗;
д) 6∗7; е) 7∗2; ж) 24∗0; з) 2090∗?

Разложим числа на разрядные слагаемые.

а) 4(0) + ∗ = 9
∗ = 9 – 4
∗ = 5
Ответ: 45

б) 5(0) + ∗ = 9
∗ = 9 – 5
∗ = 4
Ответ: 54

в) 8(00) + 5(0) + ∗ = 18
∗ = 18 − 8 – 5
∗ = 5
Ответ: 855

г) 7(000) + 3(00) + 8(0) + ∗ = 18
∗ = 18 − 7 − 3 – 8
∗ = 0
Ответ: 7380

д) 6(00) + ∗(0) + 7 = 18
∗ = 18 − 6 – 7
∗ = 5
Ответ: 657

е) 7(00) + ∗(0) + 2 = 9
∗ = 9 − 7 – 2
∗ = 0
Ответ: 702

ж) 2(000) + 4(00) + ∗(0) + 0 = 9
∗ = 9 − 2 – 4
∗ = 3
Ответ: 2430

з) 2(0000) + 0(000) + 9(00) + 0(0) + ∗ = 18
∗ = 18 − 2 – 9
∗ = 7
Ответ: 20907

622. Ученик выполнил сложение:

Учитель, не проверяя вычислений, определил, что в обоих примерах допущена ошибка. Как он обнаружил ошибку?

а) Все слагаемые в примере — чётные числа. Это значит, что их сумма — чётное число, а на доске в решении записано нечётное число.
б) Два слагаемых — чётные числа, это значит, что их сумма тоже чётное число. Если к чётному числу прибавить нечётное (третье слагаемое), то получится нечётное число, а на доске в решении записано чётное число.

623. Назовите наибольшее и наименьшее шестизначное число, которое делится на: а) 2; б) 3; в) 5; г) 9; д) 10.

а) наибольшее число: 999998, наименьшее число: 100000;
б) наибольшее число: 999999, наименьшее число: 100002;
в) наибольшее число: 999995, наименьшее число: 100000;
г) наибольшее число: 999999, наименьшее число: 100008;
д) наибольшее число: 999990, наименьшее число: 100000.

624. Саша купил в магазине 20 тетрадей, 2 альбома для рисования, авторучку за 6 р., несколько карандашей по 60 к. и несколько обложек для книг по 1 р. 20 к. Продавец сказал, что нужно заплатить в кассу 34 р. 25 к. Саша попросил пересчитать стоимость покупки, и ошибка была исправлена. Как он определил, что продавец ошибся в подсчётах?

Тетрадей и альбомов куплено чётное число, следовательно, независимо от цены (чётное или нечётное число) их стоимость будет чётным числом. Цена карандаша и обложки — чётное число, и, независимо от того, какое их количество купили (чётное или нечётное), их стоимость будет чётным числом. Поэтому и сумма стоимостей всех покупок должна быть чётным числом. А продавец сказал, что нужно уплатить нечётную сумму. Эту ошибку и определил Саша.

Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.

Математика. 5 класс

30 четное число или нет. Чётные и нечётные числа. Умножение четных и нечетных чисел

212. Какое число получится: чётное или нечётное, если нечётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи три примера, подтверждающих твоё предположение.

При делении нечётного числа на нечётное число результат всегда будет нечётным числом.
45 : 5 = 9 55 : 11 = 5 63 : 7 = 9

213. Какое число получится: чётное или нечётное, если чётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи несколько примеров, подтверждающих твоё предположение. Обсуди результат с соседом по парте.

При делении чётного числа на нечётное число результат всегда будет чётным числом.

214. Можешь ли ты привести пример такого случая деления, когда нечётное число делится нацело на чётное число? Почему? Вспомни, как можно получить делимое из делителя и значения частного.

Делимое можно получить, умножив делитель на значение частного. По условию делитель является чётным числом. Мы знаем, что если чётное число умножить на чётное или нечётное число, то результатом будет всегда чётное число. В нашем же случае делимое должно быть нечётным числом. Это означает, что никакое значение частного в этом случае подобрать нельзя и привести пример такого случая деления невозможно.

215. Представь число 2873 в виде суммы круглых десятков и однозначного числа. Чётным или нечётным числом является каждое из слагаемых? Чётным или нечётным числом будет значение их суммы? На какую цифру может оканчиваться запись чётного числа? А нечётного?

2873 = 2870 + 3
Первое слагаемое – чётное число, второе слагаемое – нечётное число.
2873 – нечётное число.
Нечётное число 2873 заканчивается на нечётную цифру 3, запись чётного числа 2870 — на чётную цифру 0.
Запись чётного числа может оканчиваться чётными цифрами (0, 2, 4, 6, 8), а запись нечётного числа — нечётными числами (1, 3, 5, 7, 9).

216. Выпиши чётные числа в один столбик, а нечётные — в другой.

2844 57893
67586 9231
10050 9929

217. Сколько существует чётных двузначных натуральных чисел? А сколько таких же нечётных чисел?

Самое маленькое двузначное чётное число 10, а самое большое – нечётное число 99. Всего их 99 – 10 + 1 = 90. Чётные и нечётные числа в натуральном ряду чередуются, поэтому чётных двузначных чисел столько же сколько и нечётных, то есть 45, поскольку 90 : 2 = 45.

218. Запиши самое большле чётное шестизначное число.

Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.

Например: -24, 0, 6, 38 — все это четные числа.

m = 2k — общая формула написания четных чисел, где k — целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.

Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.

Пример нечетных чисел: 3, 1, 7 и 35.

n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k — целое число.

Сложение и вычитание четных и нечетных чисел

В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.

Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.

Умножение четных и нечетных чисел

При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.

А теперь рассмотрим дробные числа.

Десятичная запись числа

Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.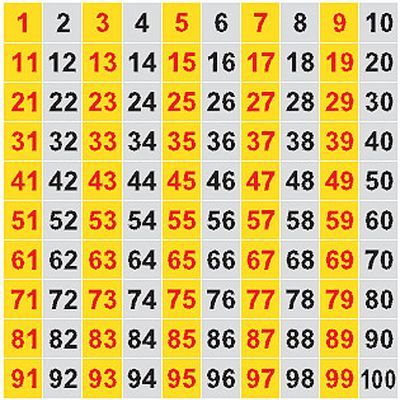

Например: 3,14; 5,1; 6,789 — это все

С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.

Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.

Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.

А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом — дробную.

Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.

Определения

• Чётное число — целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
• Нечётное число — целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …

В соответствии с этим определением нуль является чётным числом.

Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .

В разных странах существуют связанные с количеством даримых цветов традиции.

В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.

Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов , у которых они, в принципе, не подсчитываются.
Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.

Примечания

Wikimedia Foundation . 2010 .

Смотреть что такое «Чётные и нечётные числа» в других словарях:

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа. Но со времён Пифагора,… … Википедия

Целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …

Целые (0, 1, 2,…) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы.… … Большая советская энциклопедия

Книги

• Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна. В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…

Что означают чётные и нечётные числа в духовной нумерологии. В изучении это очень важная тема! Чем по своей СУТИ чётные числа отличаются от нечётных чисел?

Чётные числа

Общеизвестно, что чётные числа — те, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.

А что означают чётные числа относительно ? Какова нумерологическая суть деления на два? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.

У несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».

А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.

Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?

Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.

Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.

Нечётные числа

Нечётные числа — те, которые не делятся на два: числа 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и так далее. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.

Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное… Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?

Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел , никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.

Возьмём для примера — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.

Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!

Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…

Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.

Чётные и нечётные числа в нумерологии

Подведём итоги. В чём главное отличие чётных чисел от нечётных?

Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…

Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь…

Обратите внимание!

В магазины уже поступила моя книга под названием «Духовная нумерология. Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел. Подробнее об этом, а также для заказа книги пройдите по следующей ссылке: ««

———————————————————————————————

Программа Python для вывода всех нечетных чисел в диапазоне

Задав начальную и конечную точки, напишите программу Python для вывода всех нечетных чисел в заданном диапазоне.

Пример:

  Ввод:  начало = 4, конец = 15
  Выход:  5, 7, 9, 11, 13, 15
  Ввод:  начало = 3, конец = 11
  Вывод:  3, 5, 7, 9, 11 

Пример №1: Вывести все нечетные числа из заданного списка, используя цикл for

1. Определить начальный и конечный пределы диапазона.
2. Выполнить итерацию от начала до диапазона в списке, используя цикл for и 
3. проверить, если num % 2 != 0. 
4. Если условие выполнено, то вывести только число.

Python3

Output:

 5 7 9 11 13 15 17 19 

  Пример 2: Ограничение диапазона от пользовательского ввода

Python3

Выход:

Пример №3: Получение ограничения диапазона от пользовательского ввода или статических вводов для сокращения времени выполнения кода и повышения производительности кода.

Python3

Выход

 5 7 9 11 13 15 19 

Пример № 4: .0002  

start = int ( input ( "Enter the start of range: " ))

end = int ( Вход ( «Введите конец диапазона:» ))

ровный0042 % 2 :: 2 ]

for num in even_list:

     print (num, end = " " )

 Введите начало диапазона: 3
Введите конец диапазона: 11
3 5 7 9 11 

Метод: использование лямбда-функции

Python3

 5 7 9 11 13 15  

 5 9 
 
 .  

 [5, 7 , 9, 11, 13, 15] 

 5 7 9 11 13 15 

 5 7 9 13 15 919
 0017 
 Видео-урок: Определение нечетных и четных чисел: пропуск счета 
 Стенограмма видео 
 Определение нечетных и четных чисел:
 Пропустить счет
 В этом видео мы научимся
 как определить, является ли число до 20 нечетным или четным. И мы собираемся сделать это, пропустив
 считая двойками. Давайте начнем с практики нашего пропуска
 навыки счета. Мы знаем, что когда мы пропускаем счет, мы
 назовите число, затем пропустите несколько, затем произнесите другое число, пропустите еще несколько и так далее.
 на. И в этом видео мы собираемся
 пропустить счет двойками.
 Давайте построим из них башню
 ледяные кирпичи. Чтобы помочь нам пропустить счет двойками,
 мы будем класть по два кирпича за раз. Какие числа мы скажем? ну там кирпичей нету
 начать с, так что мы можем начать считать с нуля, а затем два, четыре, шесть, восемь, 10,
 12. Что вы заметили в
 числа, которые мы сказали? Если мы начнем с нуля и пропустим счет
 в двойках все числа, которые мы произносим, ​​будут четными: два, четыре, шесть, восемь,
 10, 12. Продолжим считать в
 двоек, так что мы произносим все остальные четные числа до 20. После 12 идут 14, 16, 18 и
 20. Возможно, вы также заметили, что
 все эти четные числа являются числами в таблице умножения на два. Один раз два два, две двойки
 четыре, трижды два — шесть и так далее. И поэтому мы можем сказать, что все четные числа
 кратны двум.
 А как насчет чисел в
 между? Мы все еще могли бы сказать эти числа по
 пропустим счет двойками, но нам придется начинать с единицы, а не с нуля. Это будет немного похоже на
 положить один ледяной кирпич для начала, а затем считать по два, как
 до. Мы бы закончили тем, что сказали бы цифры один,
 три, пять. Кстати, вы можете посмотреть, что
 происходит с нашей башней каждый раз? Всегда остается один кирпич
 на вершине. Семь, девять, 11. Мы называем эти числа нечетными
 числа. Начнем с последнего нечетного числа
 что мы сказали, 11, и давайте продолжим считать двойками, чтобы мы сказали все
 нечетные числа до 20,
 Итак, у нас есть 11, а затем 13, 15,
 17 и 19. Посмотрите, как каждое из наших нечетных чисел
 на единицу больше, чем четное число. Три на один больше, чем два, пять на
 на единицу больше четырех, семь на единицу больше шести. Вот почему, когда мы пытаемся сделать нашу
 башня, это выглядело так интересно. Всегда был еще один кирпич
 осталось сверху. Итак, теперь, когда мы попробовали
 считая ледяные кирпичи по двое. Давайте попробуем ввести
 вопрос, где мы должны посчитать другой тип объекта двойками. Посмотрим, сможем ли мы справиться
 является ли число нечетным или четным.
 Майкл считает своих медведей в
 двойки. Он доходит до 12 и затем видит, что он
 осталось сосчитать только одного медведя. У него четное или нечетное число
 медведей?
 Похоже, у Майкла довольно
 коллекция игрушечных медведей здесь, не так ли? И нам говорят в первую
 предложение этой задачи, что он их считает. Но он не считает их в
 таким же образом, как, может быть, мы могли бы обычно считать группу предметов, один, два, три и т. д.
 на. Нам говорят, что он их считает
 в двойках. И, подсчитав их по группам
 два, как это, это гораздо более быстрый способ подсчета. Мы называем это пропуском счета, потому что мы
 не обязательно говорить каждое число. Некоторые цифры пропускаем. Чтобы понять, что сделал Майкл
 вот и попробуем сами.
 Итак, вот наша коллекция медведей. Начнем считать двойками. Два, четыре, шесть, восемь, 10, 12. Но подождите минутку. Мы больше не можем считать двойками. Остался только один медведь. Давайте поставим ее с
 другие. Теперь, делая это для себя, мы
 может понять, что говорит нам следующее предложение в нашей задаче. Нам говорят, что Майкл доходит до 12 лет.
 а потом видит, что ему осталось сосчитать только одного медведя. Теперь вы можете подумать, что это
 Теперь нас спросят, сколько медведей у ​​Майкла? И чтобы найти ответ, нам нужно
 думать о том, что один больше, чем 12. Но нас об этом не спрашивают. Нам не нужно считать, сколько
 медведи у Майкла есть вообще. Вместо этого нам нужно сказать, является ли он
 имеет четное или нечетное количество медведей.
 Теперь, когда Майкл пересчитал свои
 медведи, он начал без медведей. Пометим ноль, просто чтобы показать, что он
 начал считать отсюда. Теперь мы знаем, что если мы начнем с
 ноль, и мы пропускаем счет двойками, каждое число, которое мы произносим, ​​будет четным
 количество. Итак, если бы у Майкла было только два медведя,
 у него будет четное количество медведей, или четыре медведя, или шесть, восемь, 10 или 12. Это все четные числа.
 Но мы знаем, что Майкл не был
 способен считать своих медведей по двое. Он дошел до числа 12, но
 потом у него остался один. У Майкла нет четного числа
 медведей. У него нечетное количество медведей. Если мы пропустим счет двойками от нуля
 но у нас остался один, у нас нечетное число. Другой способ сказать то же самое
 Дело в том, что на единицу больше, чем четное число, является нечетным числом. Количество медведей, которое Майкл
 имеет странное.
 Ты помнишь наш номерной трек
 которые мы раскрасили, чтобы показать нечетные и четные числа? Ну, давайте нарежем его на квадраты и
 мы сложим все нечетные числа вместе и все четные числа вместе. Итак, у нас есть нечетные числа: один,
 три, пять, семь, девять, 11, 13, 15, 17, 19. И у нас есть четные числа:
 два, четыре, шесть, восемь, 10, 12, 14, 16, 18, 20. Теперь вы заметили что-нибудь о
 эти группы чисел теперь, когда мы собрали их все вместе? Давайте поиграем в игру, которая может помочь
 ты что-то замечаешь.
 Этот медведь держит двузначный
 карты, и они составляют число. Но является ли это загадочное число четным или
 странный? А теперь приходит вызов. Чтобы найти ответ, вам нужно всего лишь
 разрешено перевернуть одну из карт. Что это будет? Во-первых, мы знаем, что наша
 номер состоит из двух цифр. Но если мы перевернем цифру на
 левые здесь, это на самом деле не поможет нам. Представьте, что мы посмотрели на это, и это
 показал цифру один. Ну там много нечетных чисел
 с единицей в разряде десятков: 11, 13, 15 и так далее. Но есть и четные числа
 с единицей в разряде десятков: 12, 14, 16.
 В этом разряде десятков есть
 много нечетных и четных чисел, сидящих рядом. Итак, чтобы решить нашу задачу, один
 карта, на которую нам нужно взглянуть, находится справа. Это цифра единиц. И цифра единиц - ноль. Теперь мы не знаем, что другое
 цифра есть, но нам это не нужно знать. Это может быть один, делая
 число 10, или это может быть двойка, что дает число 20. На самом деле это не имеет значения. И причина, почему это не так
 все дело в схеме, которую мы можем видеть в цифрах. Если мы начнем с рассмотрения нашего
 четные числа, мы можем видеть, что они всегда заканчиваются одним и тем же набором цифр. Это может быть цифра два, как в
 числа два или 12, четыре, как в числах четыре или 14, шесть, восемь или ноль.
 Теперь мы знаем, потому что решили
 посмотрите на эту вторую карту, число, которое показывает нам медведь, заканчивается нулем. Это должно быть даже. И хотя любое число, оканчивающееся на
 два, четыре, шесть, восемь или ноль четны, мы можем сказать, что любое число, оканчивающееся на
 один, три, пять, семь или девять — нечетное число. Итак, если бы наш друг медведь
 перевернул свою карточку, а на ней была семерка вместо нуля, мы бы знали
 что его номер был бы нечетным.
 И, знаете ли, знание закономерностей и
 подобные последовательности могут помочь нам расширить наши знания о нечетных и четных числах за пределы
 20. 28 оканчивается цифрой восемь. Это должно быть четное число. Мы знаем, что один странный
 цифра. Поэтому любое число, оканчивающееся на единицу
 также должно быть нечетным. тогда 31 нечетное число, как и
 21. Давайте сейчас ответим на несколько вопросов
 где мы должны применить на практике эти два факта, которые мы только что узнали. Четные числа всегда заканчиваются на ноль,
 два, четыре, шесть или восемь. А нечетные числа всегда заканчиваются на
 один, три, пять, семь или девять.
 Запишите следующие два нечетных числа:
 семь, девять, 11, 13, что, что.
 В этом вопросе нам дается
 последовательность нечетных чисел. Мы знаем, что один из способов подсчета
 нечетные числа, чтобы начать с нечетного числа и пропустить счет по двое. Итак, если мы начнем с семи, наш следующий
 нечетное число девять, затем 11, и 13. И вы можете видеть, пропуская счет в
 двойки, мы пропускаем четные числа между восьмерками, 10 и 12? Итак, какие следующие два странных
 числа в нашей последовательности? Какое нечетное число идет после
 13? Ну, если мы продолжим пропускать счет
 по двойке от 13 доходим до числа 15 и затем до числа 17. Мы знаем, что нечетные числа по порядку
 всегда следуйте шаблону. Последняя цифра единица, затем
 три, пять, семь и девять.
 Хотя мы начали с цифры
 семь, мы можем продолжить этот шаблон и просто проверить правильность нашего ответа. Итак, у нас есть семь, девять, а затем
 снова к началу, раз, три, пять, семь. Мы пропускаем счет по двое, чтобы найти
 следующие два нечетных числа в нашей последовательности. Полная последовательность: семь, девять,
 11, 13, а затем два недостающих числа, 15, 17.
 Найдите большее нечетное число
 чем 93 и меньше 97.
 В этом вопросе мы на охоте
 для нечетного числа. И нам дают две подсказки о нашем
 количество. Нам говорят, что это больше, чем
 93, а также меньше 97. Если сказать по-другому, то
 нужно найти нечетное число между 93 и 97. Теперь в
 между 93 и 97, но только одно нечетное число. Чтобы узнать, что это такое, мы можем использовать
 наше знание некоторых моделей, которые мы можем видеть в четных и нечетных числах. Как мы могли определить даже
 номер, если мы видели один? Мы могли бы сказать, просто
 глядя на последнюю цифру, потому что четные числа всегда заканчиваются на ноль, два, четыре, шесть,
 или восемь.
 Так что же это говорит нам о нечетных
 числа? Ну, они всегда заканчиваются цифрами
 между. Нечетные числа всегда заканчиваются на
 цифры один, три, пять, семь или девять. Итак, если мы посмотрим на два нечетных
 числа, которые нам дали в нашем вопросе, 93 оканчивается на тройку, 97 оканчивается на
 Семь. Вот откуда мы знаем, что они странные. Знаешь, может быть полезно
 обозначьте цифру три и цифру семь в нашем списке здесь, потому что если мы посмотрим
 в наших нечетных цифрах по порядку мы можем увидеть цифру между ними. Между тремя и семью
 пять. Итак, нечетное число между 93
 а 97 равно 95.
 Если мы знаем, какая последняя цифра в
 число, мы всегда можем сказать, четное оно или нечетное. Четные числа всегда заканчиваются на ноль,
 два, четыре, шесть или восемь. И нечетные числа всегда заканчиваются на единицу,
 три, пять, семь или девять. И вот как мы знаем нечетное
 число больше 93 и меньше 97 равно 95.
 Что мы узнали из этого
 видео? Мы научились решать,
 число является нечетным или четным при пропуске счета двойками.
 Как учить четные и нечетные числа 
 Поделись с друзьями!
 0
акции
 Поделиться
 Твит
 Четные и нечетные числа являются основным математическим понятием. Так как же научить их весело и запоминающимся образом? У нас есть методы для любого стиля обучения!
 Обучение детей четным и нечетным числам 
 Целые числа можно разделить на две категории: четные и нечетные. Признание разницы может помочь вам в делении и умножении, поэтому важно, чтобы вы знали, как их различать.
 Обычно вы знакомите ребенка с этим понятием в первом или втором классе, а затем повторяете его в более поздних начальных классах. Чтобы понимать четные и нечетные числа, ребенок должен знать свои числа и уметь считать до 100.
 Решая, как учить четные и нечетные числа, изучите варианты! Вот несколько способов преподавания этой концепции.
 Как ввести четные и нечетные числа 
 Чтобы представить понятие четных и нечетных чисел, используйте маленькие счетчики. Съедобные жетоны, такие как M&Ms, особенно интересны!
 Для юных учеников можно поставить две фигурки (это могут быть куклы, фигурки, мягкие игрушки и т. д.). Скажите: «Тебе когда-нибудь приходилось делиться с братом или сестрой? Вы хотите, чтобы обмен был справедливым; вы оба хотите одну и ту же сумму. Вот что происходит здесь с Фредом и Джинджер. Их родители оставили им немного M&Ms (или печенье, игрушки и т. д.) и сказали им поделиться».
 Пройдите через различные числа 1-10. Могут ли они поровну разделить 1 M&M? Не без разреза. Могут ли они разделить 2? Разделите их на 2 стопки, по одной перед каждой фигуркой. Да, 2 можно разделить поровну. Напишите цифру 2 на доске или листе бумаги.
 В конце концов, у вас будет такой список чисел: 2, 4, 6, 8, 10.  Объясните, что эти числа называются четными, потому что их можно разделить нацело, не разрезая на части. Остальные числа нечетные; они нечетные: 1, 3, 5, 7, 9.  (Технически 0 также является четным числом, но не будем его рассматривать в этом базовом введении).
 Как учить четные и нечетные числа с помощью цветов 
 Мы устроены так, чтобы замечать закономерности, и дети не исключение. Помогите детям выучить нечетные и четные числа, используя цвет.
 Вы можете использовать трехмерные цифры двух цветов или сделать свой собственный набор с маркерами на каталожных карточках (или использовать цифры, вырезанные из картона).
 Выберите один цвет для нечетных чисел (красный) и один для четных (синий). Это особенно эффективный метод для визуалов.
 Выложите на стол цифры от 0 до 10. Спросите: «Вы видите закономерность?» Они заметят, что цвета чередуются между красным и синим.
 Назовите четные числа, а затем нечетные.
 Повторите их (это особенно важный шаг для аудиалов).
 Затем составьте двузначные нечетные и четные числа, ориентируясь на их последнюю цифру. «Это четное число, потому что оно заканчивается на 2».
 Как обучать четным и нечетным числам с помощью счетчиков 
 Этот метод обучения нечетным и четным числам особенно хорошо работает с кинестетиками. Вам понадобятся объемные буквы и фишки. Выстройте числа 1-10.
 Под номером 2 положите две жетоны рядом. Скажите: «Видишь, у этого счетчика есть партнер? Мы называем номера, у которых есть партнеры, «четными номерами». 
 Теперь поместите одну фишку под номером 1, выровняв ее по левому краю, чтобы показать, где может стоять отсутствующая фишка. «У этого счетчика нет партнера. Это все в одиночку. Мы называем номера, в которых последний счетчик отсутствует партнером, «нечетными номерами».  
 Повторите этот процесс для номера 3.  Поместите пару счетчиков непосредственно под номером 3 и один счетчик под этой парой. «Посмотрите на последний счетчик. Есть ли у него партнер? Нет? Тогда это нечетное число».
 Повторите процесс с цифрой 4, поместите две пары жетонов под цифрой. Затем сделайте то же самое для 5, 6, 7 и т. д.
 Как учить четные и нечетные числа с помощью числовой строки 
 Старшие школьники могут визуализировать нечетные и четные числа с помощью числовой строки. Начните с числа 0. Объясните, что это четное начальное число. Теперь перепрыгните через 1, чтобы приземлиться на 2. 
 «Когда я прыгаю на 2 единицы, я приземляюсь на четное число».
 Используя этот метод, вы можете отображать как положительные, так и отрицательные четные числа. Числа, которые вы пропускаете, являются нечетными числами!
 Как учить с помощью числовой таблицы 
 Этот метод снова показывает взаимосвязь шаблонов, которые могут кристаллизовать понимание для некоторых учащихся (особенно тех, кто учится визуально и мыслит логически).
No related posts.