Sin (pi — alpha) соs (пи/2 -альфа) __________________… -reshimne.ru
Новые вопросы
упростите выражение
пожалуйстааа
Ответы
Решение задания смотри на фотографии
Похожие вопросы
Помогите пожалуйста упростить выражение…
КАРТОФЕЛЬ МАССОЙ 70.8Г ИМЕЕТ ОБЪЕМ 60СМ3 ОПРЕДЕЛИТЬ ПЛОТНОСТЬ КАРТОФЕЛЯ…
4•. Кут при основі рівнобедреного трикутника дорівнює 58°. Знайдіть кут при вершині цього трикутника….
Дано: найдите НОД:72 и 96 мы разложили на простые множители 72:2;2;2;3;3;,,,96:2;2;2;2;2;3; после это как нам узнать что НОД равен 24? и почему мы умножаем на 2*2*2*3?. ..
..
1. -4x³(x²-3x+2)
2. (1-x)(2y+x)
3. (5c-4)²…
РЕШИТЕ ПОЖАЛУЙСТА 1 ЗАДАНИЕ С РЕШЕНИЕМ…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский языкХимия
Физика
Биология
Другие предметы
История
Обществознание
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
sin(pi*x)^2=1
 2 – 4 * (1) * (-1) = 4
2 – 4 * (1) * (-1) = 4Т.к. D > 0, то уравнение имеет два корня.
w1 = (-b + sqrt(D)) / (2*a)
w2 = (-b – sqrt(D)) / (2*a)
или
$$w_{1} = 1$$
$$w_{2} = -1$$
делаем обратную замену
$$sin{left (pi x right )} = w$$
Дано уравнение
$$sin{left (pi x right )} = w$$
– это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$pi x = 2 pi n + {asin}{left (w right )}$$
$$pi x = 2 pi n – {asin}{left (w right )} + pi$$
Или
$$pi x = 2 pi n + {asin}{left (w right )}$$
$$pi x = 2 pi n – {asin}{left (w right )} + pi$$
, где n – любое целое число
Разделим обе части полученного ур-ния на
подставляем w:
$$x_{1} = frac{1}{pi} left(2 pi n + {asin}{left (w_{1} right )}right)$$
$$x_{1} = frac{1}{pi} left(2 pi n + {asin}{left (1 right )}right)$$
$$x_{1} = frac{1}{pi} left(2 pi n + frac{pi}{2}right)$$
$$x_{2} = frac{1}{pi} left(2 pi n + {asin}{left (w_{2} right )}right)$$
$$x_{2} = frac{1}{pi} left(2 pi n + {asin}{left (-1 right )}right)$$
$$x_{2} = frac{1}{pi} left(2 pi n – frac{pi}{2}right)$$
$$x_{3} = frac{1}{pi} left(2 pi n – {asin}{left (w_{1} right )} + piright)$$
$$x_{3} = frac{1}{pi} left(2 pi n – {asin}{left (1 right )} + piright)$$
$$x_{3} = frac{1}{pi} left(2 pi n + frac{pi}{2}right)$$
$$x_{4} = frac{1}{pi} left(2 pi n – {asin}{left (w_{2} right )} + piright)$$
$$x_{4} = frac{1}{pi} left(2 pi n – {asin}{left (-1 right )} + piright)$$
$$x_{4} = frac{1}{pi} left(2 pi n + frac{3 pi}{2}right)$$
Ответ
$$x_{1} = – frac{1}{2}$$
x2 = 1/2
x3 = 3/2
$$x_{3} = frac{3}{2}$$
Численный ответ
x1 = -51.
5000000000000
x2 = -71.5000000000000
x3 = -23.5000000000000
x4 = 88.5000000000000
x5 = 64.5000000000000
x6 = -55.5000000000000
x7 = 4.50000000000000
x8 = 86.5000000000000
x9 = 66.5000000000000
x10 = -25.5000000000000
x11 = 58.5000000000000
x12 = 34.5000000000000
x13 = 82.5000000000000
x14 = 50.5000000000000
x15 = -35.5000000000000
x16 = 96.5000000000000
x17 = -49.5000000000000
x18 = -87.5000000000000
x19 = -47.5000000000000
x20 = 14.
5000000000000
x21 = -65.5000000000000
x22 = -11.5000000000000
x23 = 8.50000000000000
x24 = -57.5000000000000
x25 = -37.5000000000000
x26 = -61.5000000000000
x27 = 10.5000000000000
x28 = -95.5000000000000
x29 = 46.5000000000000
x30 = 98.5000000000000
x31 = 72.5000000000000
x32 = -5.50000000000000
x33 = 90.5000000000000
x34 = -93.5000000000000
x35 = 22.5000000000000
x36 = 74.5000000000000
x37 = 60.5000000000000
x38 = 26.5000000000000
x39 = 52.
5000000000000
x40 = -97.5000000000000
x41 = -41.5000000000000
x42 = 70.5000000000000
x43 = -7.50000000000000
x44 = 30.5000000000000
x45 = -9.50000000000000
x46 = -75.5000000000000
x47 = 20.5000000000000
x48 = -69.5000000000000
x49 = -21.5000000000000
x50 = 12.5000000000000
x51 = -19.5000000000000
x52 = -77.5000000000000
x53 = 32.5000000000000
x54 = -29.5000000000000
x55 = -99.5000000000000
x56 = -81.5000000000000
x57 = 68.5000000000000
x58 = 84.
5000000000000
x59 = -79.5000000000000
x60 = -89.5000000000000
x61 = 100.500000000000
x62 = 6.50000000000000
x63 = 78.5000000000000
x64 = 28.5000000000000
x65 = -33.5000000000000
x66 = -3.50000000000000
x67 = -27.5000000000000
x68 = -39.5000000000000
x69 = 18.5000000000000
x70 = 56.5000000000000
x71 = -53.5000000000000
x72 = 2.50000000000000
x73 = 80.5000000000000
x74 = 42.5000000000000
x75 = 92.5000000000000
x76 = -1.50000000000000
x77 = 40.
5000000000000
x78 = 76.5000000000000
x79 = 24.5000000000000
x80 = 54.5000000000000
x81 = -73.5000000000000
x82 = -45.5000000000000
x83 = -59.5000000000000
x84 = 0.500000000000000
x85 = 48.5000000000000
x86 = -43.5000000000000
x87 = -15.5000000000000
x88 = -85.5000000000000
x89 = -67.5000000000000
x90 = 38.5000000000000
x91 = -13.5000000000000
x92 = -63.5000000000000
x93 = -31.5000000000000
x94 = -83.5000000000000
x95 = 36.5000000000000
x96 = 44.
5000000000000
x97 = -91.5000000000000
x98 = -17.5000000000000
x99 = 16.5000000000000
x100 = 62.5000000000000
x101 = 94.5000000000000
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
Другие ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Боря купил 4 книги. Все книги без первой стоят 42 р., без второй — 40 р., без третьей — 38 р., без четвёртой — 36 р. Сколько стоит каждая книга?
Все книги без первой стоят 42 р., без второй — 40 р., без третьей — 38 р., без четвёртой — 36 р. Сколько стоит каждая книга?
Лестница соединяет точки A и B и состоит из 25 ступеней. Высота каждой ступени равна 14 см, а длина – 48 см. Найдите расстояние между точками A и B (в метрах).
Решено
пол комнаты имеющий форму прямоугольника со сторнами 5 м и 6 м требуется покрыть пакретом из прямоугольных дощечек со сторонами 10см и 40см .сколько потребуется таких дощечек
на карте с масштабом 1:8000000…
Решено
высота над землёй подброшенного вверх мяча меняется по закону h(t)=1.8+13t-5t2 h высота т время в секундах прошедшее с момента броска. сколько секунд мяч будет находиться на высоте не менее 9м?
Пользуйтесь нашим приложением
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
тригонометрия — Нахождение греха с помощью Pi
Задавать вопрос
Спросил
Изменено 6 лет, 5 месяцев назад
Просмотрено 2к раз
$\begingroup$
Нахождение греха с помощью пи
Я возился с вычислением числа пи, находя периметр многоугольника со многими сторонами и разделив его на диаметр (как это сделал Архимед). Уравнение, которое я нашел, было
Уравнение, которое я нашел, было n(sin(180/n))=pi , где n — количество сторон многоугольника. Мне было интересно, есть ли способ обратить это уравнение, сделав так, чтобы вы могли найти синус, используя число пи.
Вот что я пробовал:
(Примечание: это все в градусах, потому что я плохо знаю радианы)
Это то, что я начал с n(sin(180/n))=pi
Разделить обе части на n
(sin(180/n))=pi/n
Подставить a для 180/n , чтобы получить (sin(a))=pi/n .
Это означает 180/n=a
Затем я умножил обе части этого числа на n , чтобы получить 180=a*n
И разделил обе части на a, чтобы получить 180/a=n
Теперь я Я решил это уравнение для n , поэтому я могу подставить его обратно в исходное уравнение
вместо n , чтобы получить (sin(a))=pi/(180/a) , что может быть
упрощено до sin(a)=pi*a/180 . Это говорит о том, что
Это говорит о том, что sin(a) равно
pi*a/180 , что определенно неверно. Одна интересная вещь в этом уравнении
заключается в том, что это уравнение для преобразования градусов в радианы. Кроме того, если вы нарисуете это уравнение, вы будете очень близки к синусоидальной волне примерно до 25.
(Если вы рисуете это уравнение, убедитесь, что вы используете градусы, а не радианы) некоторые исследования и обнаружили, что нет простого способа вычислить синус. Тем не менее, я все еще хотел бы знать, что не так с математикой, которую я сделал, чтобы упростить это.
Спасибо.
Мне 13 лет, и это мой первый вопрос, который я задал, так что извините за возможные ошибки.
- тригонометрия
- пи
$\endgroup$
4
$\begingroup$
Оказывается, «уравнение» $n \sin(180/n))=\pi$ неверно.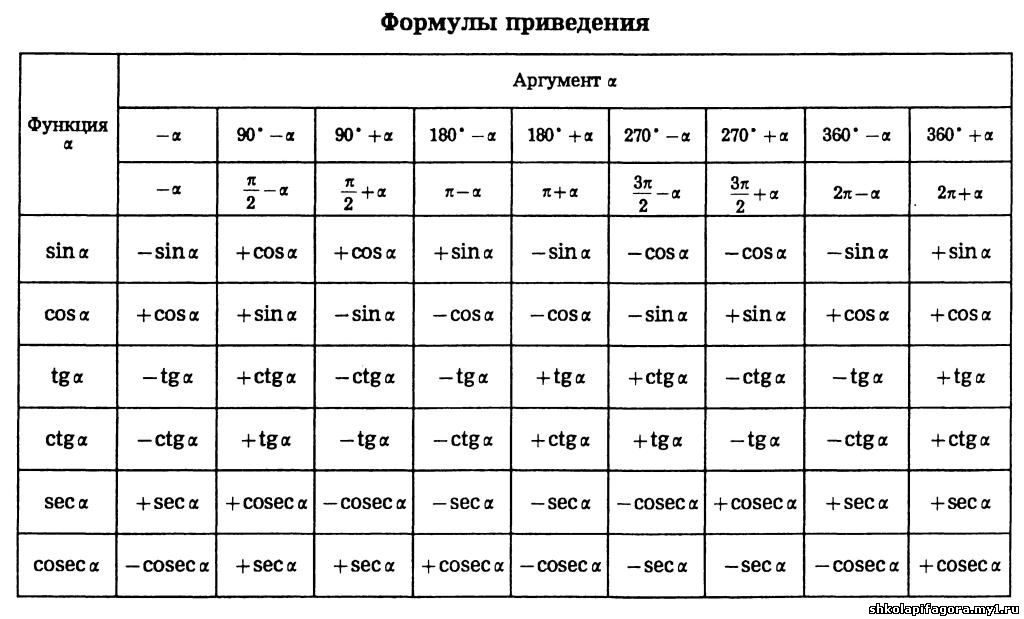 \circ$ и так далее.
\circ$ и так далее.
$\endgroup$
4
$\begingroup$
Давайте разберем задачу по частям.
Во-первых: sin(x) — это функция, обратная ей функция arcsin. См. Обратные тригонометрические функции для определений и свойств.
Секунды: 180 градусов = пи радианы. Равенство, которое вы написали, оказывается пределом:
lim [n -> oo] n * sin(pi/n) = pi
Другими словами: когда n растет до бесконечности, n * sin(pi/n) приближается Пи. См. Ограничение для формального определения предела. Предполагая достаточно большое n, это почти равенство:
n * sin(pi/n) = pi
sin(pi/n) = pi/n
pi/n = arcsin(pi/n)
Больше никаких упрощений не требуется.
Связано: lim [x -> 0] (sin(x) / x) = 1. Это можно доказать, набросок см. в Теореме сжатия.
$\endgroup$
$\begingroup$
У нас есть $\sin \pi/4=\cos \pi /4=1/\sqrt 2. $ И $\sin \pi /6=1/2$ и $\cos \pi /6=\sqrt 3 /2.$
$ И $\sin \pi /6=1/2$ и $\cos \pi /6=\sqrt 3 /2.$
Вы можете перейти от случая $n$ к случаю $2 n$ с $|\sin x/2|=\sqrt {(1-\cos x)/2}$ и $|\cos x /2|=\sqrt {(1+\cos x)/2}.$
Имеем $n \sin \pi /n<\pi
Существует также простой геометрический способ явного получения $\sin\pi/5$ и $\cos\pi/5.$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Калькулятор — sin(pi) — Solumaths
Грех, онлайн-исчисление
Резюме:
Тригонометрическая функция sin для вычисления синуса угла в радианах,
градусов или градианов.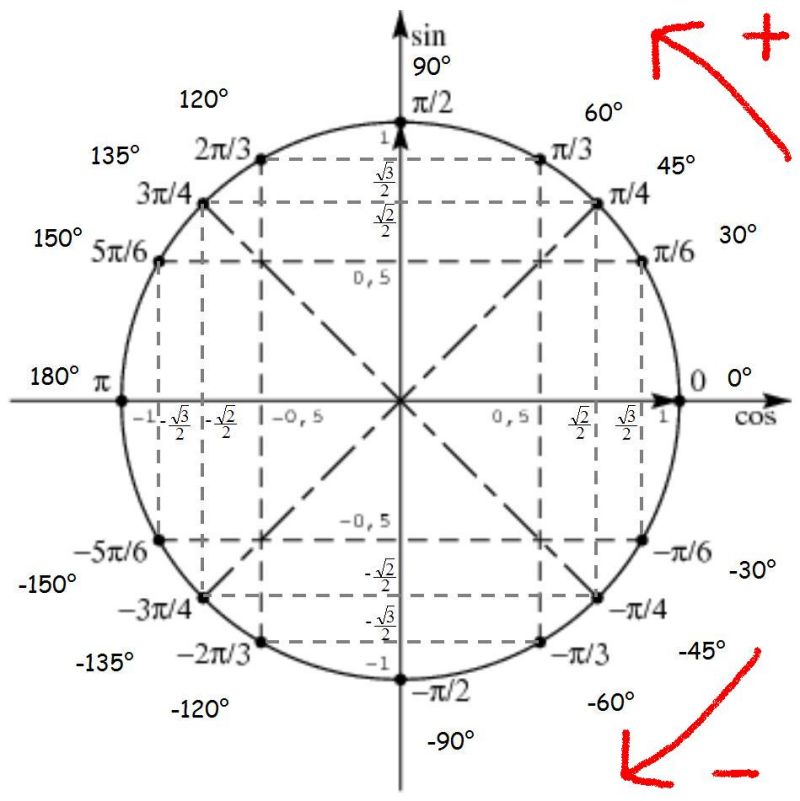
sin online
Описание:
Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить синус , косинус и касательная угла через одноименные функции.
Тригонометрическая функция синус отметил синус , позволяет вычислить синус угла онлайн , можно использовать разные угловые единицы: градус, градус и радианы, которые по умолчанию являются угловыми единицами.
- Расчет синуса
- Таблица специальных синусоидальных значений
- Основные свойства
- `sin(-x)= -sin(x)`
- `sin(x+2*k*pi)=sin(x)`
- `sin(pi-x)=sin(x) `
- `sin(pi+x)=-sin(x)`
- `sin(pi/2-x)=cos(x)`
- `sin(pi/2+x)=cos(x) `
- Производная синуса
- Первообразная синуса
- Свойства функции синуса
- Уравнение с синусом
- Арккосинус: арккосинус.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс : косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.

Синус вычисляет угол в радианах
Калькулятор синуса позволяет с помощью функции sin вычислить онлайн синус синус угла в радианах, вы должны сначала
выберите нужную единицу, нажав на кнопку параметров расчетного модуля.
После этого можно приступать к расчетам.
Чтобы вычислить синус онлайн от `pi/6`, введите sin(`pi/6`), после вычисления результат `1/2` возвращается.
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить синус угла в градусах
Чтобы рассчитать синус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Для вычисления синуса 90, введите sin(90), после вычисления результат 1 возвращается.
Вычислить синус угла в градусах
Чтобы вычислить синус угла в градианах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить синус 50, введите sin(50), после вычисления
возвращается результат `sqrt(2)/2`.
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
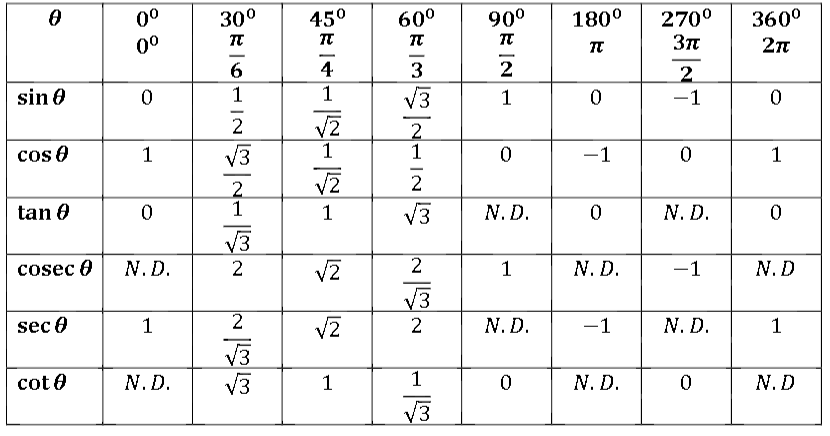
Синус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот таблица значений общего синуса :
| sin(`2*pi`) | `0` | |||||||||||
| sin(`pi`) | `0` | |||||||||||
| sin(`pi/2`) | `1` | |||||||||||
| sin(`pi/4`) | `sqrt(2)/2` 03 03 | 5 90(0) `pi/3`) | `sqrt(3)/2` | |||||||||
| sin(`pi/6`) | `1/2` | |||||||||||
| sin(`2*pi/3`) | `sqrt(3)/2` | |||||||||||
| sin(`3*pi/4`) | `sqrt(2)/2` | |||||||||||
| sin(`5*pi/6`) | ` 1/2` | |||||||||||
| sin(`0`) | `0` | |||||||||||
| sin(`-2*pi`) | `0` | |||||||||||
| sin(`-pi`) | `0` | |||||||||||
| `2` 1` | |||
| sin(`-pi/4`) | `-sqrt(2)/2` | ||
| sin(`-pi/3`) | `-sqrt(3)/2` | ||
| sin(`-pi/6`) | `-1/2` | ||
| sin(`-2*pi/3`) | `-sqrt(3)/2` | sin(`-3*pi/4`) | `-sqrt(2)/2` |
| sin(`-5*pi/6`) | `-1/2` |
`AA x в RR, k в ZZ`,
Производная синуса равна cos(x).
Первообразная синуса равна -cos(x).
Функция sine является нечетной функцией, для каждого действительного x `sin(-x)=-sin(x)`. Следствием для кривой, представляющей синусоидальную функцию, является то, что она допускает начало отсчета как точку симметрии.
Калькулятор имеет решатель, который позволяет решать уравнение с синусом формы cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `грех(х)=1/2` или же `2*sin(x)=sqrt(2)` с этапами расчета.
Синтаксис:
sin(x), где x — мера угла в градусах, радианах или градах.
Примеры:
sin(`0`), возвращает 0
Производный синус:
Чтобы дифференцировать функцию синуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции синуса
производная sin(x) является производной(`sin(x)`)=`cos(x)`
Первообразная синуса :
Калькулятор первообразной позволяет вычислить первообразную функции синуса.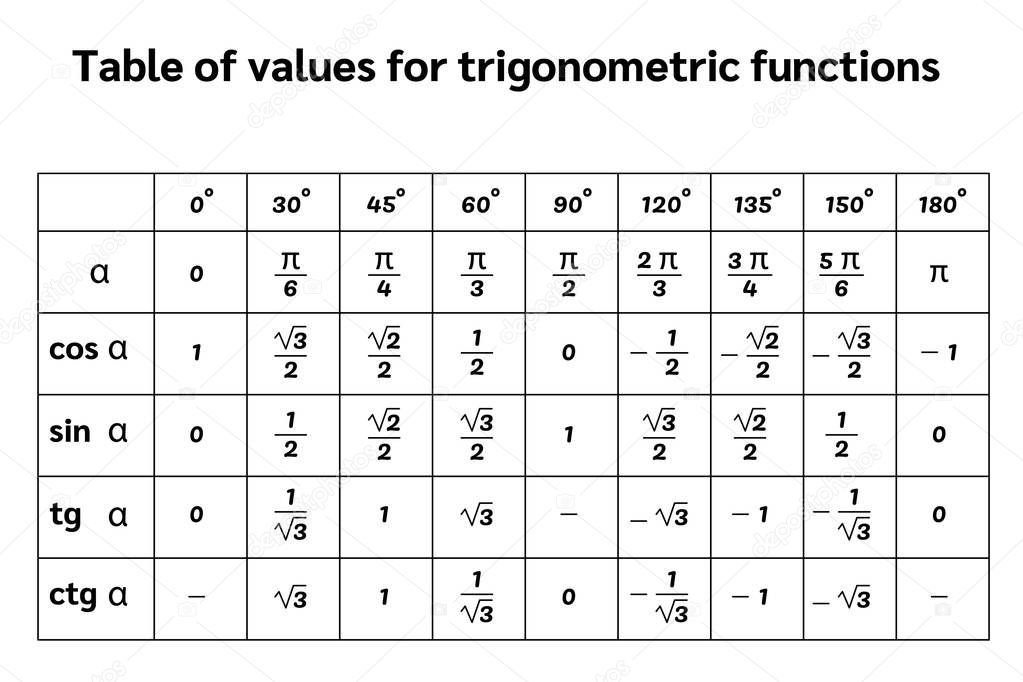
Первообразная sin(x) является первообразной(`sin(x)`)=`-cos(x)`
Предельный синус :
Калькулятор пределов позволяет вычислять пределы синусоидальной функции.
предел sin(x) is limit(`sin(x)`)
Обратная функция синуса :
обратная функция синуса есть функция арксинуса, отмеченная как arcsin.
График синуса :
Графический калькулятор может отображать синусоидальную функцию в заданном интервале.
Свойство функции синуса:
Функция синуса является нечетной функцией.
Расчет онлайн с синусом
См. также
Список связанных калькуляторов:

 5000000000000
5000000000000 5000000000000
5000000000000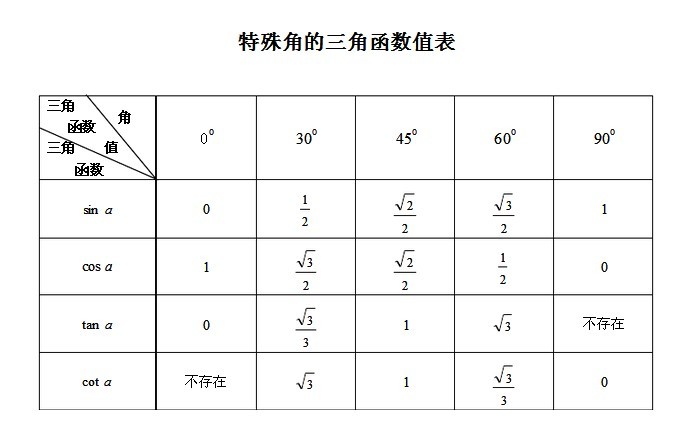 5000000000000
5000000000000 5000000000000
5000000000000 5000000000000
5000000000000 5000000000000
5000000000000 11.14
11.14 11.14
11.14 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.