Решение уравнений с десятичными дробями
1. «Решение уравнений с десятичными дробями» 5 класс
2. Реши уравнение:
К. 4х = 0,22+0,26;Т. 5х = 8,17+2,48;
З. 6х = 3,9*8;
Х. 7х-4х = 0,96;
А. х+2х = 21,42;
С. 2х+5х = 42,7;
Н. 12х-3х = 41,4.
0,12
7,14
5,2
7,14
0,32
6,1
2,13
7,14
4,6
3. Прогулка в лес
Вы бывали летом в лесу?Прогулка по лесу – это так приятно,
а наблюдательному человеку ещё и
интересно!
4. «На опушке леса»
5. Сформулируйте правила нахождения неизвестных компонентов в уравнении.
Как найти неизвестноеслагаемое?
Как умножить десятичную
дробь на 0,1; 0,01; 0,001?
8. Сформулируйте правило умножения десятичных дробей.
Что надо сделать приумножении на десятичную
дробь, если в произведении
меньше цифр, чем надо
отделить запятой?
«Собери грибы в лукошко»
Лес – это кладовая, щедро отдающая свои дары.
11.
Поставьте запятые в произведении2,31 ∙ 5,4 = 12474;,
2,31 ∙ 0,54 = 12474;
,
23,1 ∙ 5,4 = 12474;
,
0,231 ∙ 54 = 12474;
,
0,231 ∙ 0,54 =0, 12474.
проверить
12. «Молчанка»
6,7 ∙ 8,4 + 6,7 ∙ 1,643,2
12,37 ∙ 4,185 – 12,37 ∙ 3,185
67
6,1 ∙ 3,4 + 6,1 ∙ 2,6
36,6
9,1 ∙ 0,387 – 9,1 ∙ 0,287
12,37
0,5 ∙ 43,2 ∙ 2
6,2711
1,25 ∙ 3,27 ∙ 8
4,516
62,711 : 10
0,91
451,6 ∙ 0,01
32,7
13. «В гостях у Старичка – лесовичка»
-А у меня для вас задание припасено.Если выполните его, то смело заходите
в глубь леса!
14. «Привал»
0,3 · 2,253,03 ∙ 0,01
1,05 ∙ 5,27
2,8 ∙ 6,28
4,2 ∙ 6,3
7,3 ∙ 4
17,3 · 12,25
1,103 · 2,65
20,3 · 0,2
0,0003 ∙ 1,2
10,5 ∙ 4,2
3 · 2,2
15. «На лесной полянке» Лес – это источник радости и здоровья.
Хвоя сосныВы можете
158,6
Зверобой
16,362
Земляника
лесная
Медуница
лекарственная
2,08
Крапива
0,74
Подорожник
1,44
1,08
Узнай, какое растение леса — клад витаминов.
Для этого найди корень уравнения:
(х + 2,4) : 0,8 = 5,6
Узнай, какое растение леса — клад витаминов.
Для этого найди корень уравнения:
(х + 2,4) : 0,8 = 5,6
Плоды растения издревле употребляются человеком
в пищу. Водный настой листьев земляники лесной
применяются в качестве мочегонного средства при
мочекаменной и желчнокаменной болезнях. Их
употребление также назначается при диабете и
малокровии. Плоды применяют как витаминное
средство.
О каком растении говорится в загадке?
Это зелье ты не тронь:
Жжется больно, как огонь.
Ответь на вопрос, решив уравнение.
(3,5 — х) : 2,3 = 1,2
19. О каком растении говорится в загадке? Это зелье ты не тронь: Жжется больно, как огонь. Ответь на вопрос, решив уравнение.
(3,5 — х) : 2,3 = 1,2Крапива используется в народной медицине для
лечения многих болезней, применяется при
различных кровотечениях, почечнокаменной,
желчекаменной болезни, удушье, болезнях печени и
желчных путей, отеках, заболеваниях сердца,
туберкулезе, бронхиальной астме,
бронхитах, аллергиях.
Наружно крапивуиспользуют при открытых ранах,
кровотечениях, кожных заболеваниях, для
укрепления и роста волос.
Если ты порезал ногу, не рыдай и не реви.
Вот растенье на подмогу. Ты скорей его зови!
Что это за растение? Правильное решение уравнения
поможет ответить на этот вопрос.
х : 4,8 + 3,6 = 3,9
21. Если ты порезал ногу, не рыдай и не реви. Вот растенье на подмогу. Ты скорей его зови! Что это за растение? Правильное решение
уравненияпоможет ответить на этот вопрос.
х : 4,8 + 3,6 = 3,9
Настой из листьев подорожника обладает
отхаркивающим свойством, благодаря чему и
используется при лечении бронхитов, бронхиальной
астмы, туберкулеза легких. Сок свежих листьев
подорожника эффективен в лечении язвенной
болезни желудка и двенадцатиперстной кишки,
хронических гастритов. А водный настой
свежих листьев способствует быстрому
очищению и лечению ран, порезов,
кожных язв, нарывов и фурункулов.
Назови растение, имеющее репутацию лекарства от
100 болезней.
Реши уравнение и узнай ответ.
х : 2,7 — 5,16 = 0,9
Назови растение, имеющее репутацию лекарства от
100 болезней.
Реши уравнение и узнай ответ.
х : 2,7 — 5,16 = 0,9
Зверобой применяют для лечения многих
недугов: в качестве антисептического средства,
для смазывания десен и полосканий, при
заболеваниях дыхательных путей, гипертонии,
анемии, при лечении пролежней, аллергии, ран,
язв, сыпи, при болезнях мочевого пузыря,
желудочно-кишечного тракта, болезнях почек,
гриппе, слабости сердца, простудных
заболеваниях, туберкулезе, для лечения мастита,
желтухи, кашля, желудочных и легочных
заболеваний, мигрени, при язве желудка,
головной боли, нервных болезнях, повышенной
кислотности желудочного сока.
24. «Заветная тропинка»
Чтобы выйти из леса и вернутьсядомой, вы должны проявить
самостоятельность, показать волю и
упорство.
25. Итог урока
Домашнее задание:1 уровень: № 1476, № 1482,
2 уровень: № 1475, № 1513;
Решить сложное уравнение онлайн.
Решение простых линейных уравнений. Дроби бывают правильными и неправильнымиКвадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть.
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
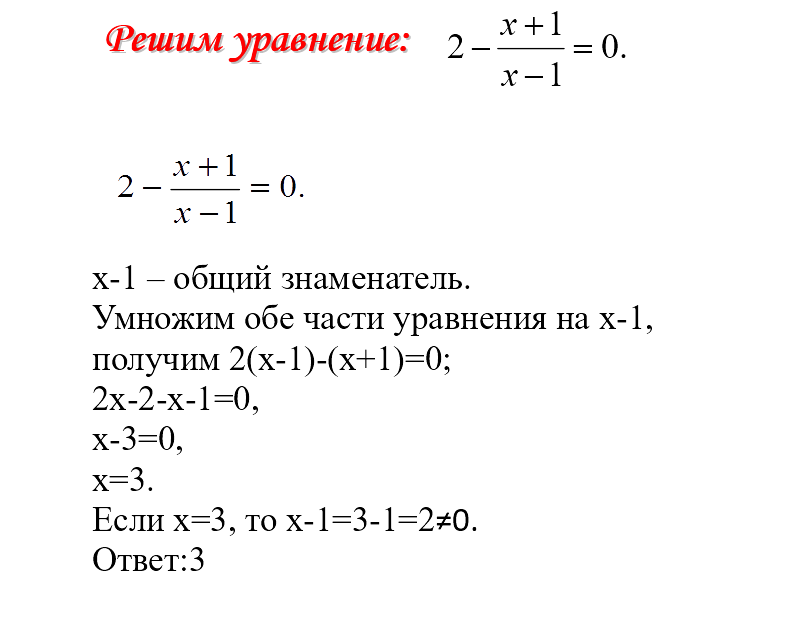
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении.
Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax
2 + c
= 0 выполнено неравенство (−c
/a
) ≥ 0, корней будет два.
Формула дана выше; - Если же (−c /a )
Формула дана выше;Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобку
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x
2 − 7x
= 0 ⇒ x
· (x
− 7) = 0 ⇒ x
1 = 0; x
2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн
, трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн .
Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме 
Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.Инструкция
Примечание: π записывается как pi; корень квадратный как sqrt().
Шаг 1. Введите заданный пример, состоящий из дробей.
Шаг 2. Нажмите кнопку “Решить”.
Шаг 3. Получите подробный результат.
Чтобы калькулятор посчитал дроби правильно, вводите дробь через знак: “/”. Например: . Калькулятор посчитает уравнение и даже покажет на графике, почему получился такой результат.
Что такое уравнение с дробями
Уравнение с дробями – это уравнение, в котором коэффициенты являются дробными числами. Линейные уравнения с дробями решается по стандартной схеме: неизвестные переносятся в одну сторону, а известные – в другую.
Рассмотрим на примере:
Дроби с неизвестными переносятся влево, а остальные дроби – вправо. Когда переносятся числа за знак равенства, тогда у чисел знак меняется на противоположный:
Теперь нужно выполнить только действия обеих частей равенства:
Получилось обыкновенное линейное уравнение. Теперь нужно поделить левую и правую части на коэффициент при переменной.
Решить уравнение с дробями онлайн обновлено: 7 октября, 2018 автором: Научные Статьи.Ру
Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид
aх + b = 0 , где a и b произвольные числа, называется линейным уравнением с одним неизвестным.
Cегодня разберёмся, как эти линейные уравнения решать.
Например, все уравнения:
2х + 3= 7 – 0,5х; 0,3х = 0; x/2 + 3 = 1/2 (х – 2) — линейные.
Значение неизвестного, обращающее уравнение в верное равенство называется решением или корнем уравнения .
Например, если в уравнении 3х + 7 = 13 вместо неизвестного х подставить число 2 , то получим верное равенство 3· 2 +7 = 13. Значит, значение х = 2 есть решение или корень уравнения.
А значение х = 3 не обращает уравнение 3х + 7 = 13 в верное равенство, так как 3· 2 +7 ≠ 13. Значит, значение х = 3 не является решением или корнем уравнения.
Решение любых линейных уравнений сводится к решению уравнений вида
aх + b = 0.
Перенесем свободный член из левой части уравнения в правую, изменив при этом знак перед b на противоположный, получим
Если a ≠ 0, то х = ‒ b/a .
Пример 1. Решите уравнение 3х + 2 =11.
Перенесем 2 из левой части уравнения в правую, изменив при этом знак перед 2 на противоположный, получим
3х = 11 – 2.
Выполним вычитание, тогда
3х = 9.
Чтобы найти х надо разделить произведение на известный множитель, то есть
х = 9: 3.
Значит, значение х = 3 является решением или корнем уравнения.
Ответ: х = 3 .
Если а = 0 и b = 0 , то получим уравнение 0х = 0. Это уравнение имеет бесконечно много решений, так как при умножении любого числа на 0 мы получаем 0,но b тоже равно 0. Решением этого уравнения является любое число.
Пример 2. Решите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.
Раскроем скобки:
5х – 15 + 2 = 3х – 12 + 2х ‒ 1.
5х – 3х ‒ 2х = – 12 ‒ 1 + 15 ‒ 2.
Приведем подобные члены:
0х = 0.
Ответ: х — любое число .
Если а = 0 и b ≠ 0 , то получим уравнение 0х = — b. Это уравнение решений не имеет, так как при умножении любого числа на 0 мы получаем 0, но b ≠ 0 .
Пример 3. Решите уравнение х + 8 = х + 5.
Сгруппируем в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
х – х = 5 ‒ 8.
Приведем подобные члены:
0х = ‒ 3.
Ответ: нет решений.
На рисунке 1 изображена схема решения линейного уравнения
Составим общую схему решения уравнений с одной переменной. Рассмотрим решение примера 4.
Пример 4. Пусть надо решить уравнение
1) Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.
2) После сокращения получим
4 (х – 4) + 3·2 (х + 1) ‒ 12 = 6·5 (х – 3) + 24х – 2 (11х + 43)
3) Чтобы отделить члены, содержащие неизвестные и свободные члены, раскроем скобки:
4х – 16 + 6х + 6 – 12 = 30х – 90 + 24х – 22х – 86 .
4) Сгруппируем в одной части члены, содержащие неизвестные, а в другой – свободные члены:
4х + 6х – 30х – 24х + 22х = ‒ 90 – 86 + 16 – 6 + 12.
5) Приведем подобные члены:
‒ 22х = ‒ 154.
6) Разделим на – 22 , Получим
х = 7.
Как видим, корень уравнения равен семи.
Вообще такие уравнения можно решать по следующей схеме :
а) привести уравнение к целому виду;
б) раскрыть скобки;
в) сгруппировать члены, содержащие неизвестное, в одной части уравнения, а свободные члены ‒ в другой;
г) привести подобные члены;
д) решить уравнение вида aх = b,которое получили после приведения подобных членов.
Однако эта схема не обязательна для всякого уравнения. При решении многих более простых уравнений приходится начинать не с первого, а со второго (Пример. 2 ), третьего (Пример. 1, 3 ) и даже с пятого этапа, как в примере 5.
Пример 5. Решите уравнение 2х = 1/4.
Находим неизвестное х = 1/4: 2,
х = 1/8 .
Рассмотрим решение некоторых линейных уравнений, встречающихся на основном государственном экзамене.
Пример 6. Решите уравнение 2 (х + 3) = 5 – 6х.
2х + 6 = 5 – 6х
2х + 6х = 5 – 6
Ответ: ‒ 0, 125
Пример 7. Решите уравнение – 6 (5 – 3х) = 8х – 7.
– 30 + 18х = 8х – 7
18х – 8х = – 7 +30
Ответ: 2,3
Пример 8. Решите уравнение
3(3х – 4) = 4 · 7х + 24
9х – 12 = 28х + 24
9х – 28х = 24 + 12
Пример 9. Найдите f(6), если f (x + 2) = 3 7-х
Решение
Так как надо найти f(6), а нам известно f (x + 2),
то х + 2 = 6.
Решаем линейное уравнение х + 2 = 6,
получаем х = 6 – 2, х = 4.
Если х = 4, тогда
f(6) = 3 7-4 = 3 3 = 27
Ответ: 27.
Если у Вас остались вопросы, есть желание разобраться с решением уравнений более основательно, записывайтесь на мои уроки в РАСПИСАНИИ . Буду рада Вам помочь!
Также TutorOnline советует посмотреть новый видеоурок от нашего репетитора Ольги Александровны, который поможет разобраться как с линейными уравнениями, так и с другими.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Период десятичной дроби. Онлайн калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Онлайн калькулятор нахождения периода десятичной дроби может вычислить период дроби, числителем и знаменателем которой могут быть как целые числа, так и десятичные дроби.
Для записи десятичной дроби используйте точку либо запятую (например, 1.12 или 1,12). Обратите внимание, что калькулятор вычисления периода десятичной дроби находит период в пределах 30000 чисел, так как длина периода может достигать сотен тысяч символов и вычисления займут большое количество времени.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Математические уравнения – Справочный центр Notion
В этой статьеНа любой странице Notion вы можете отображать красиво отформатированные, понятные математические символы, выражения и уравнения. Это удобно для ведения заметок, технической документации, домашних заданий или везде, где вам нужно использовать дроби и уравнения
Содержание Редактировать встроенное уравнение
Notion использует библиотеку KaTeX для отображения математических уравнений, которая поддерживает большое подмножество функций LaTeX.
Нажмите
+, которая появляется слева при наведении указателя мыши на новую строку. Прокрутите вниз и выберитеУравнение блокав раскрывающемся списке. Либо введите/mathи нажмите клавишу ввода.Разместив новый блок уравнений, щелкните внутри него, чтобы ввести или вставить уравнение, или используйте
cmd/ctrl+ввод/возврат.
Точно так же, как вы можете отформатировать текст в Notion как полужирный , зачеркнутый или кодовое обозначение , вы также можете отформатировать текст как математическое уравнение, например эту квадратную формулу:
Существует несколько различных способов добавить встроенные математические уравнения, и все они удобны для клавиатуры.
С текстовыми сочетаниями клавиш:
С вводом уравнения:
Чтобы открыть ввод уравнения, используйте сочетание клавиш
ctrl/cmd+shift+E.Введите уравнение в поле ввода и нажмите
введите.
В меню форматирования:
Выделите уравнение в абзаце.
Нажмите кнопку
√xв появившемся меню форматирования или используйте сочетание клавишctrl/cmd+shift+E. Ваш выбранный текст должен превратиться в уравнение.
Редактирование встроенного уравнения
Вы можете редактировать существующее уравнение, щелкнув по нему. Это откроет ввод уравнения, и любые изменения, внесенные вами в уравнение, будут отображаться на вашей странице.
Для перехода к уравнению также можно использовать клавиши со стрелками на клавиатуре. Ввод уравнения откроется, когда ваш курсор пройдет над уравнением, и ввод уравнения закроется, если вы продолжите нажимать клавишу со стрелкой в том же направлении.
Notion поддерживает весь спектр символов и операций языка \KaTeX.
Полный список поддерживаемых функций можно найти по ссылкам ниже:
Поддерживаемые функции · KaTeX
Таблица поддержки · KaTeX
Примечание: KaTeX охватывает большинство, но не все математические обозначения, поддерживаемые LaTeX. Если ваше уравнение не отображается правильно в Notion, перейдите по ссылкам выше, чтобы узнать, поддерживается ли эта функция.
Часто задаваемые вопросы
Я не знаю LaTeX, но хочу использовать уравнения Notion. Как мне начать?
Легко начать использовать LaTeX для выполнения домашних заданий, конспектов занятий или лабораторных отчетов. Базовая арифметика и имена переменных уже допустимы в LaTeX.
Если вам просто нужно найти определенные символы, Detexify — отличный ресурс, который позволяет вам нарисовать символ и найти соответствующий код LaTeX.
Чтобы изучить более мощный LaTeX, документация Overleaf — отличное место для изучения основ:
Mathematical expressions
Subscripts and superscripts
Brackets and Parentheses
Matrices
Fractions and Binomials
Aligning Equations
Operators
Spacing in math режим
Интегралы, суммы и пределы
Стиль отображения в математическом режиме
Список греческих букв и математических символов
Математические шрифты
Обратите внимание, что Overleaf является полнофункциональным редактором LaTeX, поэтому не все в документации поддерживается в Notion.
Если у вас есть сомнения, вы всегда можете проверить этот список поддерживаемых функций или таблицу поддержки в алфавитном порядке, чтобы определить, какие функции поддерживаются.
Почему я не могу отобразить конкретное уравнение? Какие формулы/библиотеки вы поддерживаете? Можете ли вы добавить поддержку формулы или библиотеки, которую я хочу использовать?
Notion использует библиотеку KaTeX для отображения уравнений. KaTeX поддерживает большое подмножество LaTeX, задокументированное в их списке поддерживаемых функций и расположенное в алфавитном порядке в этой таблице поддержки. Чтобы запросить поддержку новых функций или сред, вы можете открыть вопрос в проекте KaTeX GitHub.
Я пытаюсь использовать среду выравнивания, но она не работает!
На странице общих проблем документации KaTeX:
«KaTeX не поддерживает среду align , поскольку LaTeX не поддерживает 9{rd}
Что происходит, когда я копирую/вставляю встроенный LaTeX?
Это даст вам исходный код.
Как использовать Notion для химии?
Notion поддерживает макросы химических уравнений \\ce и \\pu из расширения mhchem. Эти ярлыки позволяют быстро и легко набирать красивые химические и математические уравнения.
Как преобразовать встроенные уравнения в блочные?
Если у вас есть блок, содержащий встроенное уравнение, вы можете использовать меню «Превратить в», чтобы сделать его блоковым уравнением.
Остались вопросы? Поддержка сообщенийДроби с обеих сторон Уравнения
Источник изображения: http://www.blogspot.com
В этом уроке мы рассмотрим, как решать уравнения с дробями с обеих сторон.
Прежде чем приступить к этому уроку, вам необходимо научиться решать уравнения с буквами и/или скобками с обеих сторон.
Если вам нужно узнать, как делать уравнения с переменными буквами в обеих сторонах, то пройдите наш предыдущий урок на эту тему по следующей ссылке:
Решение букв переменной с обеих сторон Урок
Метод «Дробей с обеих сторон» в основном такой же, как и решение уравнений с буквами с обеих сторон, за исключением того, что нам нужно выполнить дополнительный шаг перекрестного умножения в начале.
Прежде чем приступить к уроку «Дроби с обеих сторон»:
Мы также рекомендуем вам проверить, хорошо ли вы усвоили материал из следующих предыдущих уроков:
Уравнения перекрестного умножения, урок
Раскрытие скобок с помощью правила распределения Урок
Уравнение двух сторон дробей
Вот типичное уравнение «Дроби обеих сторон».
Image Copyright 2013 by Passy’s World of Mathematics
Эти типы уравнений выполняются так же, как уравнения «Переменная буква с обеих сторон», но у нас есть один дополнительный начальный шаг в начале.
Дроби Двусторонняя отработка Этапы
Image Copyright 2013 by Passy’s World of Mathematics
Крестное умножение такое же, как и для коэффициентов.
Напр. Уравнение отношения 3/4 = 6/8, умноженное на крест, дает
8×3 = 6×4, что является истинным уравнением,
, и поэтому метод перекрестного умножения является законным.
Дроби с обеих сторон – Пример 1
Вот как мы выполняем этап перекрестного умножения для типичного уравнения «Дроби с обеих сторон»:
Image Copyright 2013 by Passy’s World of Mathematics
Обратите внимание, что нам нужно использовать скобки, чтобы убедиться, что ВСЕ члены в верхней строке «числитель» умножаются.
После того, как мы завершили перекрестное умножение, нам осталось решить обычное уравнение «Переменная буква с обеих сторон».
Решаем это следующим образом:
Image Copyright 2013 by Passy’s World of Mathematics
Если вы не знаете, как найти переменную букву с обеих сторон, то посмотрите наш предыдущий урок на эту тему по следующей ссылке:
Решение буквы переменной с обеих сторон Урок
Дроби с обеих сторон – пример второй
В этом примере дробь есть только на одной стороне.
Мы проделываем небольшой «трюк», который заключается в том, чтобы представить не дробную часть как дробь, которая равна / 1
Затем мы можем выполнить шаг перекрестного умножения.
Вот пример, показывающий шаг перекрестного умножения
Изображение Copyright 2013 by Passy’s World of Mathematics
Вот оставшиеся шаги, необходимые для получения окончательного ответа:
Image Copyright 2013 by Passy’s World of Mathematics
Видео о дробях Обе стороны Уравнения
Эти два видео показывают, как использовать пропорции Метод перекрестного умножения для решения уравнений.
А вот и второе видео, которое нужно посмотреть.
Связанные позиции
Решение уравнений с переменной буквой на обеих сторонах
Раскрытие скобок с использованием распределительного правила
Как преобразовать текстовые задачи в уравнения
Решение одношаговых уравнений на сложение
Решение одношаговых уравнений на вычитание
Решение одношаговых уравнений — все типы
Двухшаговые уравнения с использованием блок-схем и обратное отслеживание
Двухшаговые уравнения с использованием обратных операций
Трехшаговые уравнения с использованием блок-схем и обратного отслеживания
Уравнения балансира
Решение уравнений с использованием методов луковой шелухи
Эквивалентные уравнения
Уравнения фракций
Решение уравнений Проблемы слов
Транспозиция и перестройка Уравнения формулы
Решенные с использованием уравнений алгебры
Microsoft Matematic Уравнения Solver
.
этот урок, почему бы не получить бесплатную подписку на наш сайт.
После этого вы сможете получать уведомления о новых страницах прямо на свой адрес электронной почты.
Перейдите в область подписки на правой боковой панели, введите свой адрес электронной почты и нажмите кнопку «Подписаться».
Чтобы точно узнать, как работает бесплатная подписка, нажмите на следующую ссылку:
Как работает бесплатная подписка
Если вы хотите предложить идею для статьи или стать приглашенным автором на нашем веб-сайте, напишите нам по адресу адрес горячей почты, показанный в правой части этой страницы.
Если вы являетесь подписчиком Passy’s World of Mathematics и хотели бы получить бесплатную версию этого урока в PowerPoint, которая на 100 % бесплатна для вас как подписчика, напишите нам по следующему адресу:
Пожалуйста, укажите в своем электронном письме, что вы хотите получить бесплатную подписную копию «Дробей в уравнениях обеих сторон» Powerpoint.
Не стесняйтесь размещать ссылки на любые наши уроки, делиться ими в социальных сетях или использовать их в системах управления обучением в школах.
Нравится нам на Facebook
На нашей странице Facebook есть много дополнительных элементов, которые не размещены на этом сайте.
Сюда входят предметы, представляющие математический интерес, забавные математические картинки и мультфильмы, а также случайные зарисовки из личной жизни «Пасси».
Проверьте это по следующей ссылке:
https://www.facebook.com/PassysWorldOfMathematics
Пока вы там, ставьте лайк странице, чтобы вы могли получать наши обновления FB в своей ленте новостей Facebook.
Помогите Passy’s World расти
Каждый день Passy’s World предоставляет сотням людей бесплатные уроки математики.
Помогите нам поддерживать этот бесплатный сервис и поддерживать его рост.
Пожертвуйте любую сумму от $2 и выше через PayPal, щелкнув изображение PayPal ниже.
Благодарю вас!
PayPal принимает кредитные карты, но вам нужно будет указать адрес электронной почты и пароль, чтобы PayPal мог создать для вас учетную запись PayPal для обработки транзакции. За это действие с вас не будет взиматься плата за обработку, так как PayPal вычитает комиссию из вашего пожертвования до того, как оно попадет в Passy’s World.
Enjoy,
Passy
Эта запись была размещена в Алгебра, Уравнения и отмечена скобками с обеих сторон. как сделать дробь с обеих сторон, уравнения со скобками, раскрывающиеся скобки, дробь с обеих сторон, дроби с обеих сторон уравнения, рабочий лист дробей с обеих сторон, как сделать скобки с обеих сторон, как решать уравнения, многошаговые уравнения, луковая шелуха метод уравнений, решение уравнений, решение уравнений с дробями с обеих сторон, решение уравнений с отношениями с обеих сторон, переменные с обеих сторон, видео. Добавьте постоянную ссылку в закладки.
Бесплатные онлайн-калькуляторы дробей
Наши пользователи: Спасибо, что очень быстро ответили на мой вопрос, я буду рекомендовать вас во всем мире. Этот продукт является величайшей вещью. Я всегда ходил к своим друзьям, чтобы использовать ее, пока мне не удавалось убедить родителей купить ее для меня. Ненавижу это говорить, но мне действительно нужна была помощь с алгеброй, и теперь я ее получил! Если бы не Алгебратор, я бы никогда не был достаточно уверен в себе, чтобы сдать SAT, не говоря уже о таких хороших результатах в математическом разделе (особенно в алгебре). У меня есть шанс поступить в колледж, чего никто в моей семье никогда не делал. После поддержки и любви моей матери и отца я думаю, что мы все согласимся, что остальным своим успехом в качестве студента я обязан вашему программному обеспечению. Это действительно замечательно! Этот продукт великолепен. Я студент по математике с отличием, и мои родители купили вашу программу по алгебре, чтобы помочь мне. Я не думал, что буду использовать его так часто, как сейчас, но пошаговые инструкции пригодились. Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение спасает им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?Поисковые фразы, использованные 06.08.2011:
|
