Четные и нечетные числа для дошкольников
Цифры, числа…. Знакомиться с ними малыш начинает уже в дошкольном возрасте, и сначала они ему кажутся непонятными знаками в виде крючков и загогулин. Постепенно ребёнок осваивает не только цифры и счёт в пределах двадцати, но и простейшие навыки сложения и вычитания. Пришла пора познакомить его с таким понятием, как чётные и нечётные числа.
Но как сделать, чтобы процесс обучения не превратился в скучное занятие? Да и как вообще разобраться и запомнить все эти определения и свойства? Ответ прост: учиться лучше через игру и занимательные упражнения.
Что такое четные и нечетные числа?
Прежде чем приступать к знакомству с четными и нечетными числами, следует убедиться в том, что малыш хорошо знает последовательность цифр. Используйте для проверки игровой формат «Мои и твои цифры». У игры очень простые правила: вы называете цифру 1, ребёнок называет следующую. Затем снова ваша очередь (цифра 3), а потом очередь ребенка (цифра 4) и так далее до десяти или до двадцати. На следующем этапе можно поменять последовательность: числовой ряд начинает ребенок, а вы его продолжаете. Это хорошая тренировка для памяти и внимательности.
На следующем этапе можно поменять последовательность: числовой ряд начинает ребенок, а вы его продолжаете. Это хорошая тренировка для памяти и внимательности.
Теперь можно объяснить ребёнку, что такое чётные и нечётные числа. Итак, четные числа – это те, которые делятся на два без остатка. Нечетные разделить пополам нельзя. Малышу будет проще понять этот принцип на наглядном примере:
Возьмём три апельсина и попробуем разделить их поровну между тобой и другом. Как это сделать и сколько апельсинов достанется каждому из вас?
Наверняка ребёнок придёт к выводу, что разделить фрукты ровно пополам не получится. Кому-то достанется больше, а кому-то – меньше. Или же один апельсин придётся разрезать, то есть каждому достанется по одному целому фрукту и ещё по половинке.
А если вам дали четыре апельсина? Вы с другом сможете поделить их поровну?
В этом случае ребенок разделит витаминный запас так, чтобы никому не было обидно: каждому достанется по два апельсина.
Также следует объяснить ребенку, что четные и нечетные числа в последовательном ряду чередуются друг с другом:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
И ещё несколько правил, которые необходимо запомнить:
Все числа, оканчивающиеся на 0, 2, 4, 6, 8, являются четными.
Числа, оканчивающиеся на 1, 3, 5, 7, 9 – нечетные.
Эти правила применяются как к простым однозначным числам, так и к двузначным. Понимание сути поможет ребенку в дальнейшем справляться со сложными математическими задачами.
Четные и нечетные числа на практических примерах
Главная цель любого образовательного процесса – активизировать мыслительную деятельность. Не нужно концентрироваться только на том, чтобы давать ребёнку уже готовые знания. Любая информация гораздо лучше запоминается, если осваивать её на практических примерах.
Сначала попросите кроху сосчитать количество конфет в вазе или цветов в букете и определить, какое это число – четное или нечетное?
Подобные приёмы можно использовать не только во время занятий, но и в обычной жизни: на прогулке, во время поездки на дачу, при посещении кафе. Пусть малыш считает все попадающиеся на вид предметы – машины, пирожные, дорожные знаки, столовые приборы, игрушки. Если он правильно выполняет задания, можно приступать к более сложным понятиям: свойствам четных и нечетных чисел.
Пусть малыш считает все попадающиеся на вид предметы – машины, пирожные, дорожные знаки, столовые приборы, игрушки. Если он правильно выполняет задания, можно приступать к более сложным понятиям: свойствам четных и нечетных чисел.
Свойства четных и нечетных чисел
Свойства четных и нечетных чисел пригодятся при выполнении всех математических действий: сложения, вычитания, умножения, деления. Есть несколько основных свойств, и начнём мы с самых простых:
При сложении двух четных чисел в сумме всегда получается четное число.
2 + 4 = 6;
8 + 2 = 10.
При сложении четного и нечетного числа получается нечетное число.
7 + 2 = 9;
4 + 5 = 9.
При сложении двух нечетных чисел в сумме получается четное число.
3 + 7 = 10;
5 + 1 = 6.
Тот же принцип используется и при вычитании:
6 – 2 = 4;
9 – 7 = 2;
10 – 3 = 7.
Если ребенок хорошо усвоил сложение и вычитание однозначных чисел, можно потренироваться на примерах с двузначными. И не забудьте напомнить юному математику о тех же свойствах сложения и вычитания.
Сложение двузначных чисел:
12 + 24 = 36;
28 + 17 = 45;
11 + 19 = 30;
Вычитание двузначных чисел:
24 – 12 = 12;
39 – 15 = 24;
48 – 25 = 23.
С умножение и делением всё немного сложнее. Здесь понадобится не только умение запомнить свойства, но и понимание смысла математических действий.
Свойства при умножении:
При умножении четного на четное всегда получается четное.
2 х 8 = 16.
При умножении четного на нечетное получается четное.
3 х 4 = 12.
При умножении нечетного на нечетное получается нечетное.
5 х 3 = 15.
Свойства при делении:
При делении двух четных чисел результат может быть и четным, и нечетным:
12 : 4 = 3;
16 : 4 = 4.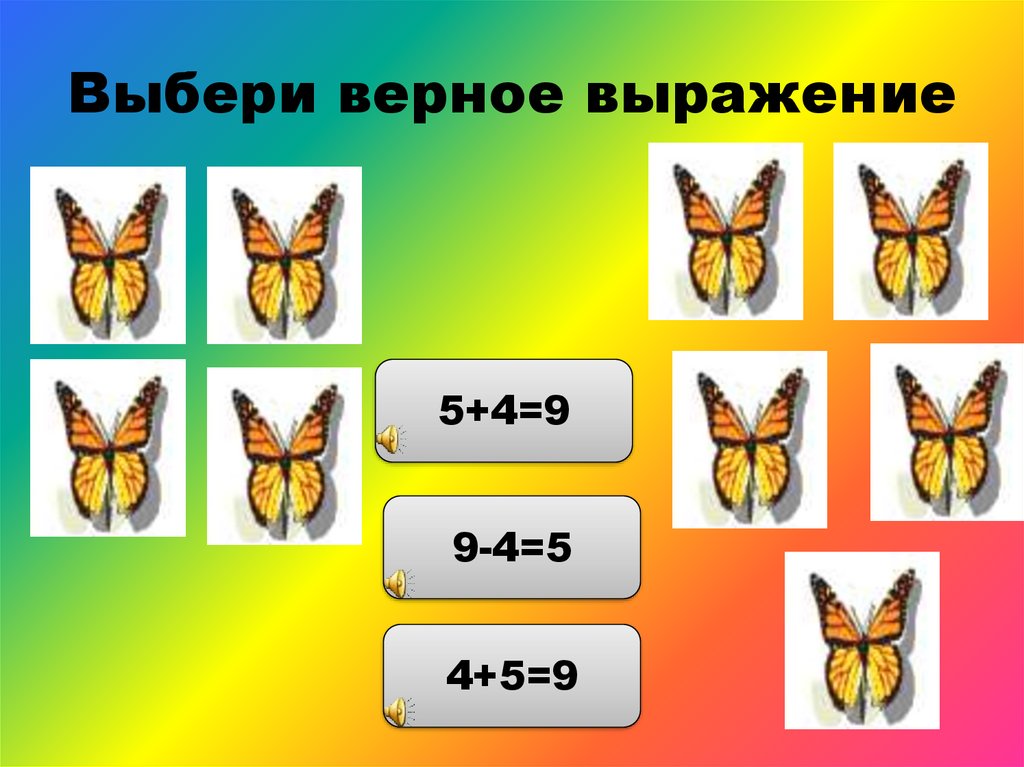
Если четное разделить на нечетное, то получится четное.
12 : 3 = 4.
Разделив нечетное на нечетное, получим нечетное.
21 : 3 = 7.
При делении нечетного на четное нельзя получить целое число, поэтому определить его четность или нечетность невозможно.
О числе ноль
Как уже было отмечено выше, ноль является четным числом. К сожалению, многих взрослых вопрос о принадлежности нуля к конкретной группе поставит в тупик. Что уж говорить о детях, которым этот странный кружок, похожий на букву «о», до определённого момента и вовсе остаётся загадкой.
Чтобы было проще определиться с четностью и нечетностью, нужно вспомнить определение: четные числа делятся на два без остатка, нечетные не делятся. Но тут в отношении ноля возникает ещё одна сложность: далеко не каждый ребенок вообще может понять, что значит разделить ноль на какое-либо число. И вот как раз в этом случае лучше просто запомнить несколько правил:
Ноль – это четное число, оно стоит первым в числовом ряду.
При делении ноля на любое число – четное или нечетное – всегда в результате получается ноль. То есть все то же четное число.
Тренируйте навыки определения четности и нечетности чисел при любом удобном случае. Если ребенок ещё только освоил простейшие действия в пределах двадцати, то используйте задачки с простыми числами. И уже затем, по мере изучения материала, можно воспользоваться более сложными примерами.
Как объяснить ребенку четное и нечетное. Глава «Математика и логика» из книги «Поверь в своё дитя. Соедини числа по правилу
В этом материале дети узнают, что такое четные и нечетные числа от 1 до 20 и научатся различать их, выполняя различные задания в картинках. Дети дошкольного возраста еще не умеют делить числа, поэтому основное правило четных чисел (т.е. четное — это число, которое делится на 2) им будет очень сложно понять. Чтобы решить эту проблему, воспользуйтесь нашими рекомендациями и заданиями, которые предназначены для первого ознакомления с этим математическим понятием.
Прежде чем выполнять задания, ребенок должен понять, что такое четные и нечетные числа от 1 до 20. Для этого можете распечатать и показать ему самое первое правило, которое он должен запомнить (можно прикрепить его к стене на время обучения). Объясните ребенку, что все числа, заканчивающиеся на 0, 2, 4, 6 и 8 — четные. Руководствуясь этим правилом, пусть ребенок ответит, на какие цифры должны заканчиваться нечетные числа (т.е. на 1, 3, 5, 7, 9).
Затем объясните ребенку, что все четные числа делятся на 2, а нечетные — не делятся на 2. Распечатайте второе правило:
Распечатайте Лист задания №1 и предложите ребенку обвести все четные числа, затем все нечетные числа.
Лист задание №1
Можете пояснить ребенку, что деление числа на 2 означает, что число делится пополам. Попросите его поделить пополам некоторые числа. Если ребенок затрудняется с ответами, то делить поровну нужно не числа, а предметы. Разложите перед ним несколько конфет, карандашей или других мелких предметов. Попросите его, например, поделить поровну 6 карандашей. Когда ребенок разделит карандаши, скажите ему, что он только что разделил число 6 на 2. Значит, 6 — это четное число. Попросите поделить поровну 5 карандашей. Когда ребенок поймет, что 5 невозможно поделить на одинаковое количество — скажите, что это и есть НЕчетное число, его невозможно разделить на 2.
Попросите его, например, поделить поровну 6 карандашей. Когда ребенок разделит карандаши, скажите ему, что он только что разделил число 6 на 2. Значит, 6 — это четное число. Попросите поделить поровну 5 карандашей. Когда ребенок поймет, что 5 невозможно поделить на одинаковое количество — скажите, что это и есть НЕчетное число, его невозможно разделить на 2.
Соедини числа по правилу — четное, нечетное
После того, как ребенок разобрался с понятием четных и нечетных чисел, предложите ему выполнить наши веселые задания в картинках. В первом задании обаятельного волка из всеми известного мультика «Ну погоди!» нужно привести к зайцу. Волк в этом задании настроен очень дружелюбно и совершенно не хочет конфликтовать с зайцем, поэтому идет к нему с цветами. Чтобы волк смог дойти, ему нужно проложить путь с помощью кружочков с числами. Но соединять эти числа между собой нужно определенным образом. Пусть ребенок возьмет цветной карандаш и, начиная с самой маленькой цифры, начнет проводить путь только через кружки с четными числами, и самое главное — по порядку счета! Второе задание выполняется аналогично — только теперь путь прокладывается через кружки с нечетными числами.
Скачать задание «Соедини четные и нечетные числа» вы можете внизу страницы.
Посчитай и найди четные или нечетные числа
Еще одна проверка знаний четных и нечетных чисел для детей представлена в следующем упражнении. В первом задании ребенок должен сказать, какие продукты зайчики поделили поровну между собой. Чтобы узнать это, ребенку необходимо посчитать количество продуктов в каждой группе и сказать, четное оно или нечетное. Если четное — продукты поделятся поровну, если нечетное — то нет. Во втором задании нужно посчитать, сколько на картинке: солнечных лучиков, тучек, яблок, грибов, птичек, зверят, деревьев, цветов. А затем ответить, чего или кого получилось четное количество?
Скачать задания по нахождению четных и нечетных чисел вы можете во вложениях внизу страницы.
Вам могут быть полезны и другие материалы по обучению счету для распечатки:
Здесь вы можете состав числа до 20 распечатать в виде числовой таблицы и дать ребенку для заполнения.
В этих занимательных задачках мы учимся считать до 20 вместе с героями мультиков и сказок. Дети дошкольного возраста совершенно не любят однообразие и скуку.
Здесь мы считаем до 20, используя карточки с числами. На каждом листе-карточке расположено число от 1 до 20 и различные предметы, количество которых равняется данному числу.
Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках.
Чтобы дети могли быстро и с интересом освоить счет в пределах 10, мы подготовили для вас веселые раскраски с заданиями.
Здесь вы можете скачать прописи цифры, распечатать их на принтере и использовать в домашнем обучении для подготовки детей к школе
А также потренируйтесь в математических играх от лисенка Бибуши:
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания.
 Все материалы проверены антивирусной программой.
Все материалы проверены антивирусной программой.Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 1 класса
Электронное учебное пособие к учебнику Моро М.И.
Электронное учебное пособие к учебнику Петерсон Л.Г.
Определение четных и нечетных чисел от 1 до 10 с картинками.
1. Сколько собачек на картинке? Это число четное или не четное?
2. Сколько клоунов на картинке? Это число четное или не четное?
3. Сколько стульев на картинке? Это число четное или не четное?
4. Сколько ламп на картинке? Это число четное или не четное?
5. Сколько мужчин на картинке? Это число четное или не четное?
6. Сколько морковок на картинке? Это число четное или не четное?
7. Сколько девочек на картинке? Это число четное или не четное?
Четные и нечетные числа до 10
1. Обведите все нечетные числа.
10, 8, 7, 9, 5, 6, 4, 1, 3
2. Обведи все четные числа.
9, 7, 3, 4, 8, 5, 2, 1, 10,
3. Выбери наибольшее четное число из числового ряда.
2, 3, 6, 5, 1
4. Выбери наименьшее четное число из числового ряда.
1, 7, 9, 6, 5
5. Выбери наибольшее нечетное число из числового ряда.
5, 4, 2, 6, 7
6. Выбери наименьшее нечетное число из числового ряда.
8, 4, 1, 8, 6
Сложи или вычти числа от 1 до 10. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.
2 + 2 = _____ четное/нечетное 4 + 5 = _____ четное/нечетное 3 + 5 = _____ четное/нечетное 4 + 2 = _____ четное/нечетное 3 + 1 = _____ четное/нечетное 8 + 2 = _____ четное/нечетное 7 + 3 = _____ четное/нечетное 8 + 2 = _____ четное/нечетное 3 + 3 = _____ четное/нечетное 8 + 1 = _____ четное/нечетное 7 + 2 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 6 + 4 = _____ четное/нечетное 4 + 2 = _____ четное/нечетное 4 + 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 + 1 = _____ четное/нечетное 9 + 1 = _____ четное/нечетное 2 + 1 = _____ четное/нечетное 3 — 3 = _____ четное/нечетное 8 — 1 = _____ четное/нечетное 7 — 2 = _____ четное/нечетное 1 — 3 = _____ четное/нечетное 6 — 3 = _____ четное/нечетное 4 — 2 = _____ четное/нечетное 4 — 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 — 1 = _____ четное/нечетное 9 — 1 = _____ четное/нечетное 2 — 1 = _____ четное/нечетное 4 — 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 — 1 = _____ четное/нечетное 9 — 1 = _____ четное/нечетное 2 — 1 = _____ четное/нечетное
Определение четных и нечетных чисел о 1 до 20 с картинками.

1. Количество головок чеснока четное или нечетное? _______
2. Количество очков четное или нечетное? _______
3. Количество зонтов четное или нечетное? _______
4. Количество туфель четное или нечетное? _______
5. Количество мальчиков четное или нечетное? _______
Четные и нечетные числа до 20
1. Обведи все нечетные числа.
7, 10, 11, 14, 1, 1, 2, 12, 11, 10
2. Обведи все четные числа.
12, 4, 8, 7, 14, 7, 20, 17, 15, 8
3. Обведи все нечетные числа.
15, 19, 14, 4, 15, 11, 1, 10, 15, 9
4. Обведи все четные числа.
15, 9, 1, 7, 5, 9, 14, 8, 3, 15
5. Подчеркни все нечетные числа.
9, 18, 20, 13, 12, 10, 6, 20, 10, 2
6. Подчеркни все четные числа.
7, 17, 3, 3, 15, 10, 8, 14, 17, 1
7. Выбери наибольшее четное число из заданной числовой последовательности.
5, 5, 15, 7, 15, 4, 17, 19, 17, 11
8. Выбери наименьшее четное число из заданной числовой последовательности.
11, 16, 8, 8, 19, 10, 15, 15, 15, 9
3, 9, 6, 7, 13, 11, 11, 13, 6, 3
10. Выбери наименьшее нечетное число из заданной числовой последовательности.
20, 20, 8, 12, 8, 1, 18, 2, 2, 17
11. Выбери наибольшее четное число из заданной числовой последовательности.
8, 7, 15, 15, 8, 2, 5, 19, 15, 5
12. Выбери наибольшее нечетное число из заданной числовой последовательности.
20, 11, 2, 13, 3, 1, 14, 5, 19, 2
13. Выбери наименьшее четное число из заданной числовой последовательности.
4, 11, 20, 9, 15, 14, 16, 9, 17, 13
14. Выбери наименьшее нечетное число из заданной числовой последовательности.
15, 20, 8, 18, 16, 17, 9, 5, 12, 8
Сложи или вычти числа от 1 до 20. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.
2 + 4 = _____ четное/нечетное 16 — 5 = _____ четное/нечетное 5 + 13 = _____ четное/нечетное 14 + 4 = _____ четное/нечетное 7 + 9 = _____ четное/нечетное 16 — 16 = _____ четное/нечетное 7 + 10 = _____ четное/нечетное 2 + 18 = _____ четное/нечетное 18 — 6 = _____ четное/нечетное 9 — 6 = _____ четное/нечетное 3 + 7 = _____ четное/нечетное 5 + 11 = _____ четное/нечетное 15 — 2 = _____ четное/нечетное 18 — 6 = _____ четное/нечетное 20 — 18 = _____ четное/нечетное 2 + 5 = _____ четное/нечетное 19 — 5 = _____ четное/нечетное 4 + 9 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 14 — 11 = _____ четное/нечетное 3 + 7 = _____ четное/нечетное 5 + 8 = _____ четное/нечетное 15 + 2 = _____ четное/нечетное 18 — 6 = _____ четное/нечетное 20 — 18 = _____ четное/нечетное 2 + 5 = _____ четное/нечетное 19 — 5 = _____ четное/нечетное 4 + 9 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 14 — 11 = _____ четное/нечетное
Четные и нечетные числа до 50
1. Обведи все нечетные числа.
Обведи все нечетные числа.
6, 36, 22, 25, 19, 24, 10, 39, 48, 37, 26, 50, 8, 35, 7, 3, 40, 47, 11, 9, 38, 28, 43, 41, 18, 23, 21, 1, 46, 30
2. Обведи все нечетные числа.
18, 31, 12, 28, 29, 35, 10, 4, 40, 39, 20, 6, 45, 30, 14, 36, 16, 48, 25, 24, 47, 37, 34, 11, 46, 32, 42, 2, 27, 41
3. Обведи все нечетные числа.
28, 35, 32, 47, 37, 43, 22, 14, 45, 24, 39, 29, 21, 42, 8, 41, 17, 36, 20, 9, 38, 46, 1, 23, 15, 27, 4, 12, 34, 26
4. Обведи все четные числа.
17, 36, 48, 12, 29, 49, 20, 9, 47, 27, 28, 6, 37, 4, 16, 25, 7, 34, 41, 18, 42, 32, 5, 23, 40, 2, 39, 45, 26, 14
5. Обведи все четные числа.
13, 47, 18, 50, 6, 5, 34, 48, 45, 33, 15, 3, 42, 26, 17, 22, 39, 25, 2, 30, 29, 4, 38, 8, 16, 35, 40, 31, 20, 23
30, 39, 46, 40, 2, 17, 50, 16, 19, 31, 50, 9, 20, 2, 12
7. Выбери наибольшее четное число из заданной числовой последовательности.
15, 37, 38, 45, 46, 26, 49, 25, 35, 22, 33, 42, 13, 8, 31
39, 28, 50, 14, 32, 11, 8, 40, 18, 34, 6, 45, 21, 37, 43
9.
24, 41, 49, 35, 21, 37, 20, 10, 1, 36, 8, 25, 4, 12, 40
2, 21, 10, 45, 36, 48, 40, 14, 38, 13, 25, 28, 30, 42, 8
39, 6, 26, 11, 50, 17, 7, 30, 10, 24, 19, 33, 1, 25, 31
28, 42, 21, 36, 39, 10, 2, 37, 13, 20, 38, 11, 17, 18, 40
Сложи или вычти числа от 1 до 50. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.
21 + 18 = _____ четное/нечетное 42 + 3 = _____ четное/нечетное 10 + 40 = _____ четное/нечетное 12 + 14 = _____ четное/нечетное 7 + 29 = _____ четное/нечетное 15 — 3 = _____ четное/нечетное 5 + 12 = _____ четное/нечетное 47 — 1 = _____ четное/нечетное 46 — 46 = _____ четное/нечетное 47 — 26 = _____ четное/нечетное 38 — 41 = _____ четное/нечетное 23 + 25 = _____ четное/нечетное 24 + 13 = _____ четное/нечетное 7 + 40 = _____ четное/нечетное 19 + 2 = _____ четное/нечетное 26 + 8 = _____ четное/нечетное 8 + 36 = _____ четное/нечетное 19 + 28 = _____ четное/нечетное 40 + 9 = _____ четное/нечетное 25 + 15 = _____ четное/нечетное 22 + 14 = _____ четное/нечетное 19 + 24 = _____ четное/нечетное 46 — 48 = _____ четное/нечетное 13 + 23 = _____ четное/нечетное 21 + 21 = _____ четное/нечетное 36 + 2 = _____ четное/нечетное 20 — 19 = _____ четное/нечетное 14 + 13 = _____ четное/нечетное 35 — 23 = _____ четное/нечетное 39 — 34 = _____ четное/нечетное 43 + 4 = _____ четное/нечетное 6 + 10 = _____ четное/нечетное 20 + 26 = _____ четное/нечетное 2 + 43 = _____ четное/нечетное 17 + 23 = _____ четное/нечетное 37 + 5 = _____ четное/нечетное 16 + 15 = _____ четное/нечетное 22 + 15 = _____ четное/нечетное 33 + 6 = _____ четное/нечетное
Четные и нечетные числа до 100.

1. Обведи все нечетные числа.
25, 72, 53, 47, 14, 92, 91, 45, 73, 27, 31, 7, 19, 28, 26, 82, 66, 65, 32, 69, 90, 13, 40, 77, 88, 86, 12, 16, 38, 59
2. Обведи все нечетные числа.
8, 16, 42, 62, 36, 64, 45, 35, 51, 98, 99, 81, 83, 65, 77, 82, 43, 4, 10, 33, 68, 27, 13, 34, 48, 21, 49, 90, 11, 25
3. Обведи все нечетные числа.
4. Обведи все четные числа.
49, 74, 2, 1, 100, 32, 54, 7, 51, 82, 33, 47, 96, 46, 78, 65, 36, 69, 75, 19, 31, 77, 35, 64, 97, 84, 37, 98, 85, 30
5. Обведи все четные числа.
22, 77, 90, 33, 10, 41, 23, 49, 53, 40, 84, 32, 13, 8, 60, 85, 89, 31, 30, 42, 96, 28, 62, 27, 45, 65, 66, 26, 55, 56
6. Выбери наибольшее четное число из заданной числовой последовательности.
9, 20, 55, 7, 100, 37, 52, 65, 19, 28, 47, 61, 32, 57, 93
7. Выбери наибольшее четное число из заданной числовой последовательности.
62, 90, 12, 34, 74, 37, 75, 91, 97, 53, 33, 60, 45, 16, 61
8. Выбери наибольшее нечетное число из заданной числовой последовательности.
81, 12, 49, 3, 52, 33, 34, 64, 41, 94, 93, 83, 80, 23, 24
9. Выбери наибольшее нечетное число из заданной числовой последовательности.
56, 4, 67, 34, 60, 88, 76, 85, 99, 33, 17, 79, 61, 7, 10
10. Выбери наименьшее четное число из заданной числовой последовательности.
94, 95, 25, 80, 71, 32, 99, 24, 8, 44, 69, 93, 38, 4, 68
11. Выбери наименьшее нечетное число из заданной числовой последовательности.
20, 12, 5, 68, 32, 54, 57, 13, 64, 82, 35, 38, 52, 92, 46
12. Выбери наименьшее четное число из заданной числовой последовательности.
2, 70, 82, 87, 27, 38, 55, 73, 84, 37, 60, 23, 63, 4, 86
Сложи или вычти числа от 1 до 100. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.
9 + 18 = _____ четное/нечетное 46 + 28 = _____ четное/нечетное 43 + 52 = _____ четное/нечетное 76 — 43 = _____ четное/нечетное 84 — 42 = _____ четное/нечетное 12 + 84 = _____ четное/нечетное 95 — 87 = _____ четное/нечетное 38 + 6 = _____ четное/нечетное 84 — 48 = _____ четное/нечетное 94 — 53 = _____ четное/нечетное 69 — 48 = _____ четное/нечетное 96 — 39 = _____ четное/нечетное 27 + 62 = _____ четное/нечетное 48 — 26 = _____ четное/нечетное 44 + 32 = _____ четное/нечетное 26 + 52 = _____ четное/нечетное 37 + 48 = _____ четное/нечетное 97 — 43 = _____ четное/нечетное 74 — 36 = _____ четное/нечетное 30 + 3 = _____ четное/нечетное 69 + 2 = _____ четное/нечетное 37 + 44 = _____ четное/нечетное 34 + 55 = _____ четное/нечетное 44 + 38 = _____ четное/нечетное 25 + 26 = _____ четное/нечетное 55 + 43 = _____ четное/нечетное 33 + 92 = _____ четное/нечетное 44 + 35 = _____ четное/нечетное 64 + 34 = _____ четное/нечетное 5 + 46 = _____ четное/нечетное 67 + 2 = _____ четное/нечетное 73 + 42 = _____ четное/нечетное 51 — 33 = _____ четное/нечетное 9 + 23 = _____ четное/нечетное 48 — 34 = _____ четное/нечетное 34 + 35 = _____ четное/нечетное 21 — 6 = _____ четное/нечетное 42 — 20 = _____ четное/нечетное 71 — 50 = _____ четное/нечетное 4 + 94 = _____ четное/нечетное 36 + 53 = _____ четное/нечетное 39 + 48 = _____ четное/нечетное 99 — 33 = _____ четное/нечетное 83 — 34 = _____ четное/нечетное 87 — 83 = _____ четное/нечетное 42 + 4 = _____ четное/нечетное 8 + 15 = _____ четное/нечетное 24 + 50 = _____ четное/нечетное 39 + 46 = _____ четное/нечетное 81 — 30 = _____ четное/нечетное
Поочередный счет. Когда малыш хорошо выучит названия чисел, поиграйте с ним в поочередный счет: вы говорите 1, он говорит 2, вы говорите 3, он говорит 4 и т.д. Вначале он захочет называть ваши числа; объясните ему, что это запрещено правилами игры. В следующий раз начинать должен он: он говорит 1, вы говорите 2 и т.д. Когда ребенок будет легко справляться с подобным заданием, привлеките к игре кого-нибудь еще (скажем, другого ребенка, ему это тоже понравится!) и поиграйте втроем, потом вчетвером, и т.д. Теперь, когда он быстро разберется, что к чему, продолжайте играть только в том случае, если он проявляет интерес.
Когда малыш хорошо выучит названия чисел, поиграйте с ним в поочередный счет: вы говорите 1, он говорит 2, вы говорите 3, он говорит 4 и т.д. Вначале он захочет называть ваши числа; объясните ему, что это запрещено правилами игры. В следующий раз начинать должен он: он говорит 1, вы говорите 2 и т.д. Когда ребенок будет легко справляться с подобным заданием, привлеките к игре кого-нибудь еще (скажем, другого ребенка, ему это тоже понравится!) и поиграйте втроем, потом вчетвером, и т.д. Теперь, когда он быстро разберется, что к чему, продолжайте играть только в том случае, если он проявляет интерес.
Четные и нечетные числа. Чтобы объяснить ребенку это понятие, возьмите две тарелки и горсть фасолин:
Это твоя тарелка, а это — моя. Вот две фасолины. Можешь ли ты положить столько же фасолин в мою тарелку, сколько и в свою? Да, конечно! Ты можешь положить одну фасолину в свою тарелку и одну — в мою. Теперь вот тебе три фасолины, посмотри, можно ли сделать с ними то же самое?. . Нет! В одной тарелке оказывается две фасолины, а в другой — одна. Видишь, оказывается, число 2 можно разделить на две равные части (такое число называется четным), а число 3 нельзя разделить на две равные части (его называют нечетным). Посмотрим теперь, как ведет себя 4…
. Нет! В одной тарелке оказывается две фасолины, а в другой — одна. Видишь, оказывается, число 2 можно разделить на две равные части (такое число называется четным), а число 3 нельзя разделить на две равные части (его называют нечетным). Посмотрим теперь, как ведет себя 4…
Когда малыш поймет разницу между четным и нечетным числом, поиграйте с ним в поочередный счет, при этом один из вас будет называть нечетные числа, а второй — четные.
Цифры в их графической форме. Прежде чем показать ребенку абстрактные символы, обозначающие числа, нужно, чтобы он научился хорошо считать. В противном случае он уподобится большинству из нас (а это нежелательно!): счет будет означать для него лишь игру абстрактными символами. Представьте себе человека, для которого слова «банан», «стул», «ботинок» ассоциируются исключительно с их письменной формой, а не с конкретными предметами. Такой человек в действительности ничего не знал бы об окружающем его мире, и его знакомство с языком было бы поверхностным и бесполезным. Как он напоминает всех тех, кто в ужасе замирает при слове «математика». Такие люди знают символы, но не поняли по-настоящему, зачем они нужны и что символизируют!
Как он напоминает всех тех, кто в ужасе замирает при слове «математика». Такие люди знают символы, но не поняли по-настоящему, зачем они нужны и что символизируют!
Как и в случае с алфавитом, есть дети, которых очень увлекает процедура придания имени абстрактному символу. Они моментально выучивают цифры, достаточно их несколько раз им показать. Но есть и другие дети, которые, умея хорошо считать, не могут запомнить, какая цифра соответствует какому числу. Потому что это им неинтересно! Вот игра, которая должна им понравиться.
Сначала покажите малышу рисунок с тремя первыми цифрами. Когда он их выучит, вознаградите его, включив в игру четвертый персонаж. По-прежнему используйте только вопросительную форму. Только в этом случае число будет называть он, а не вы. Когда ребенок выучит цифры с маленькими рисунками, покажите ему те же. цифры, но без рисунков. Напомните малышу текст, если он его забудет. Таким способом даже самый упрямый ребенок быстро выучит цифры. НО ПЕРЕХОДИТЕ К ЦИФРАМ ТОЛЬКО ТОГДА, КОГДА ОН НАУЧИТСЯ НАЗЫВАТЬ ЧИСЛА И СЧИТАТЬ!
С. Лупан. Поверь в свое дитя. «Дельта»,Спб. — 494 с
Лупан. Поверь в свое дитя. «Дельта»,Спб. — 494 с
А в жизни где используются знания чётных и нечетных чисел? Во-первых, любое чётное число чего-либо делится пополам. Во-вторых, это важная информация, если нужно разыскать какой-либо адрес. Если идти от начала улицы, то дома с чётными номерами будут справа, а с нечётными слева. Ещё в поездах номера спальных мест: нижние «нечетные», а верхние « четные». Расписание приёма врачей или рабочих дней у других специалистов бывает по чётным дням или по нечётным. Есть и дорожный знак с запретом или разрешением на парковку: по чётным или нечётным дням месяца.
Посчитайте чётными двойками до ста! Это умение пригодится ребятам в изучении таблицы умножения на 2, 4.
карточная игра
Математическая сказка
Однажды в королевстве Математика произошла удивительная история. Числа, которые жили в этом королевстве, были очень дружные. Они часто ходили в гости друг к другу, собирались вместе и придумывали различные игры. Один раз они решили поиграть в такую игру: каждое число должно было разделиться на 2. Но в итоге все числа переругались и даже стали жить на разных сторонах улиц.
Один раз они решили поиграть в такую игру: каждое число должно было разделиться на 2. Но в итоге все числа переругались и даже стали жить на разных сторонах улиц.
– Как вы думаете, что же произошло? (Не все числа делятся на 2)
– Верно, с тех пор, те числа, которые смогли разделиться на 2, стали жить на одной стороне улицы, а те, что не смогли разделиться на 2, стали жить на другой стороне.
– Давайте вместе попробуем расселить наши числа.
(На доске дома, дети разносят карточки с числами по улицам.)
2, 4, 6, 8, 10
1, 3, 5, 7, 9
– Улица, на которой живут числа 2, 4, 6, 8, 10, которые смогли разделиться на 2, стала называться – ЧЁТНАЯ, а числа – чётными.
– Улица, на которой живут числа 1, 3, 5, 7, 9, которые не смогли разделиться на 2, стала называться – НЕЧЁТНАЯ, а числа – нечётными.
– И в наше время для удобства нумерацию домов располагают в определённом порядке: чётные числа — на одной стороне улицы, а нечётные –на другой.
Цветные домики с номерами
цветные конверты с номерами для игры в почту
Можно скачать шаблоны домиков, дверей и номеров:
theteacherwife. com com |
Игра «Чёт или нечёт?»
В моем кулаке несколько пуговиц. Угадай, чет или нет?
(Если игрок угадал, ведущий отдает ему пуговицы из кулака. Если не угадал, меняет количество пуговиц и снова обращается к одному из зрителей. Таким способом ведущий набирает несколько игроков.)
Каждому игроку добавляют еще по 5 штук пуговиц. Игрок берет и зажимает в кулаке несколько пуговиц, вытягивает его в направлении другого игрока и спрашивает: «Чет или нечет?» Другой игрок отвечает, если угадал — забирает себе, если не угадал – отдает свои, столько же, сколько было зажато в руке у первого игрока. Играем до тех пор, пока один из ребят не накопит 10 пуговиц.
Игра на пальцах «Чёт-нечёт» по типу «Камень, ножницы, бумага». Дети в паре хором считают «раз, два, три!» и показывают произвольное число пальцев на обеих руках. Один из них- «чёт» и всегда показывает только чётное количество пальцев(кулак- ноль в том числе). Другой- «нечёт». Дети считают сумму пальцев и отмечают сумму на листе бумаге в графе чёт или нечёт. Победитель тот, в чьей графе больше отметок-сумм.
Победитель тот, в чьей графе больше отметок-сумм.
Игры, которые можно распечатать и играть , заменив английские слова на русские «чётные и нечётные»:
«Привидения»
домики чисел на состав числа специально обозначены по-разному: с облачком- чётные, с солнышком- нечётные
Конспект НОД по ФЭМП «Клуб юных знатоков».
Образовательная область: познание.
Интеграция образовательных областей: коммуникация, социализация, кругозор, здоровье, чтение художественной литературы.
Тип: интегрированное.
Форма непосредственной образовательной деятельности: путешествие
Форма организации: групповая.
Цель: Познакомить детей с «четных» и «нечетных» числами.
Задачи:
Закрепить умение составлять арифметические задачи и записывать их решение с помощью цифр: выделять в задаче условия, вопрос, ответ
Упражнять в ориентировке на листе бумаги в клетку;
Развивать бинокулярное зрение.
Воспитывать интерес к математическим занятиям, взаимопомощь, взаимоконтроль.
Предварительная работа: составление и решение задач, решение примеров, отгадывание загадок.
Оборудование и материалы: картинки яблок, мудрой совы, набор цифр, картинки геометрических фигур, медальки.
Ход занятия: Ребята, сегодня у нас в гостях Мудрая Сова. Если вы смотрите программу «Что? Где? Когда?», то знаете, что она является талисманом этой игры. И если она появилась у нас, значит, не просто так. Оказывается, она давно за нами наблюдает, и вы ей очень понравились, т.к. очень серьезно относитесь к математике. Вот она и решила открыть у нас «Клуб юных Знатоков». Членом клуба может стать только тот, кто докажет, что он самый умный, сообразительный, достойный. Сегодня у нас будет проходить отборочный турнир в несколько этапов. Мудрая Сова приготовила нам интересные задания. А в конце турнира она будет вручать членские билеты «Юных Знатоков». Кто хочет участвовать в турнире, подойдите, пожалуйста, ко мне, встаньте в кружок.
1 этап «Четные — нечетные».
Мудрая Сова приготовила для нас 1 задание.
Послушайте правила. Я бросаю мячик и называю число. Ребенок поймавший мяч продолжает считать т. е называйте два числа до названного, т. е четное. А вы знаете какие числа называются четными, а какие нечетными? Хотите узнать? Слушайте! Четными называются числа, которые делятся на две равные группы предметов. Например, число 2 можно разделить пополам, чтобы предметов в двух группах было поровну. Вот 2 яблока. Можно разделить их между двумя детьми поровну? Как? (1 и 1). Значит это число четное. А число 3 можно разделить на две равные группы предметов? (Нет). Верно, число 3 не делится поровну, значит оно нечетное. Ребята теперь я вам предлагаю разложить в ряд цифры по порядку от 1 до 10. Выдвиньте числа четные (2, 4, 6, 8, 10). Ребята а какие это числа? Это четные числа. А назовите невыдвинутые числа, они у вас в нижнем ряду 1, 3, 5, 7, 9. Какие это числа? Это нечетные числа. Отлично, все справились с заданием. Давайте посмотрим, что же нам еще приготовила Мудрая Сова.
Давайте посмотрим, что же нам еще приготовила Мудрая Сова.
2 этап «Заяви о себе»
И так мудрая Сова приготовила для нас второе задание. Тот кого я спрошу должен ответить на вопрос.
Сосчитай порядковым счетом до 20…
Сосчитай обратным счетом от 20 до 1 …
Назови «четные» числа до 10 …
Назови «нечетные» числа до 10…
Назови дни недели …
Назови времена года …
Назови месяцы года…
Отлично! Все справились и все проходят на следующий этап.
Физминутка «Чётные и нечётные числа»
Ребята, физминутка у нас будет необычной. У нас пройдут соревнования. Нужно встать в шеренгу, рассчитаться по номерам от 1 до 10: затем чётные числа образуют 1 команду, а нечётные – 2 команду. А задание будет такое:
Каждому ребенку я раздаю карточку с изображением геометрических фигур, задание – рассказать про свою геометрическую фигуру и попробовать нарисовать ее глазами. Круг — круговые движения глаз. Квадрат – вправо, вниз, влево, вверх. Треугольник – вниз, влево, вверх. Молодцы. Присаживайтесь.
Треугольник – вниз, влево, вверх. Молодцы. Присаживайтесь.
3 этап: «Нарисуй фигуру»
Следующее задание будет таким. Возьмите лист в клетку и карандаш. Под мою диктовку вы должны нарисовать изображение. Будьте внимательны, не переспрашивайте, я буду повторять 2 раза.
Начали:
Я довольна вами. И последний завершающий этап, который все решит: быть ли всем членами клуба или кому-то не повезет.
4 этап «Задачки»
Нам предстоит составлять и решать задачи по схемам. Давайте вспомним, из каких частей состоит задача?
(Условие, вопрос, решение, ответ)
Что такое условие к задаче? (это то, что нам известно, в условие должно быть не менее двух чисел).
Что такое вопрос к задаче? (это то, что нам надо узнать).
Ну вот, вспомнили, теперь можем начинать.
Составьте задачу по данной схеме:
5+4=
На клумбе распустилось 5 тюльпанов, на следующий день еще 4. Сколько всего тюльпанов распустилось на клумбе?
5+4=9 На клумбе всего распустилось 9 тюльпанов.
Следующая схема вот такая:
10-2=
В порту стояло 10 кораблей, 2 из них уплыло. Сколько кораблей осталось в порту?
10-2=8 В порту осталось 8 кораблей.
И последняя схема, вот какая:
4+3=
Для салата взяли 4 огурца и 3 помидоры. Сколько всего овощей взяли для салата?
4+3=7 Для салата взяли всего 7 овощей.
Итог занятия
Ребята, наконец, мы выполнили все задания Мудрой Совы. Давайте, послушаем ее мнение.
Сова: Ребята, я не думала, что вы так легко справитесь с заданиями. Я уверена, что вы все заслужили звание участника «Клуба Знатоков». Поэтому я всем вручаю членские билеты. Спасибо, до новых встреч!
факты о числах — Ни о какой безапелляционности в моих высказываниях не может быть и речи! — ЖЖ
?
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Гадание по часам онлайн. На что обращать внимание. Четные и нечетные числа
Чтобы гадание правдиво рассказало о будущем, необходимо соблюдать несколько несложных правил:
- Предсказание лучшего всего проводить на старинных часах по циферблату с наличием часовой и минутной стрелок.
 Однако в современном мире люди чаще пользуются электронными ходиками. Они также подойдут для гадания.
Однако в современном мире люди чаще пользуются электронными ходиками. Они также подойдут для гадания. - Если человеку важно узнать ближайшие перспективы будущего, важно обратить внимание на день недели. Лучше всего проводить предсказание во вторник и субботу. Гадание в эти дни будет наиболее точным.
- Нельзя специально стараться подгадать нужное время. В таком случае полученная информация не будет иметь никакого смысла и силы. Лучше просто присматриваться и стараться запоминать комбинации цифр, которые чаще всего попадаются на глаза.
Кроме дня недели, следует обращать внимание на то, в какое время суток встречаются комбинации, так как значения гадания могут совершенно отличаться друг от друга:
- С утра – подсказывает о нежелательных в этот день действиях.
- Днем гадание по часам подскажет о необходимых изменениях в отношениях с родными людьми, хорошими друзьями, коллегами во избежание возможных конфликтов.
- Вечером предсказание поможет узнать о личной жизни, есть ли будущее у этих отношений.

Ночью люди могут узнать информацию о возможных путях достижения успеха в профессиональном плане.
Значение цифр в нашей жизни преуменьшать не стоит. Наука нумерология по времени рождения может предсказать характер человека и основные моменты его будущей жизни. И в повседневности числа сопровождают нас всегда — от появления на свет до самой смерти.
Нумерологи утверждают, что когда человек видит на часах похожие цифры (они могут быть двойными, повторяющимися или парными) — это неспроста. Таким образом он получает послания от своего ангела-хранителя. И пренебрегать информацией, идущей к нам из тонкого мира, по меньшей мере неразумно. Нумерология времени способна открыть каждому из нас глаза на неочевидные, но от того не менее важные вещи.
На что обращать внимание
Следует внимательно приглядеться ко всем встречающимся на нашем пути повторам цифр — на табло часов или экране монитора, на номерных знаках встречных машин или на рекламных стендах. Нумерология по дате времени дает возможность читать послания наших невидимых защитников — ангелов-хранителей, которые беспокоятся о нас и норовят предупредить о надвигающихся неприятностях. Или же наоборот — оповестить о грядущем радостном событии, настроить на нужный лад, подсказать правильное решение в сложной ситуации.
Нумерология по дате времени дает возможность читать послания наших невидимых защитников — ангелов-хранителей, которые беспокоятся о нас и норовят предупредить о надвигающихся неприятностях. Или же наоборот — оповестить о грядущем радостном событии, настроить на нужный лад, подсказать правильное решение в сложной ситуации.
Наш невидимый защитник
Считается, что каждый из нас обладает своим собственным ангелом-хранителем. Он дается нам при рождении, и задача его — сопровождать и охранять нас на протяжении всей жизни. Ангел-хранитель незримо стоит за плечом, отгоняет напасти, а порой и призывает на помощь силы, более влиятельные.
Каждый день наш защитник пытается «подбросить» нам какую-то немаловажную информацию. Чаще всего мы не слышим этих подсказок, но порой они звучат вполне явственно и прорываются к нам в виде вещих снов, интуитивных озарений, внезапных звонков знакомых людей, кстати мелькнувшей строчки в газете или услышанной фразы.
Это правда работает?
Люди с развитой интуицией научились считывать эти подсказки и достаточно верно интерпретировать их. Другие же, сугубые материалисты, упрямо отрицают наличие во всём этом смысла, не считают нужным прислушаться к внутреннему голосу и списывают всё на случайное совпадение. А зря! Ведь задача ангела-хранителя — помогать нам. Когда мы просим вашего небесного защитника о защите и поддержке, чаще всего результат бывает налицо.
Другие же, сугубые материалисты, упрямо отрицают наличие во всём этом смысла, не считают нужным прислушаться к внутреннему голосу и списывают всё на случайное совпадение. А зря! Ведь задача ангела-хранителя — помогать нам. Когда мы просим вашего небесного защитника о защите и поддержке, чаще всего результат бывает налицо.
Конечно, если речь не идет о плохом деле. Причинять зло другому человеку, наносить вред, делать прочие нехорошие вещи упрашивать ангела-хранителя не стоит — тут он вам не помощник. Но в «мирных целях» или о помощи в безвыходной ситуации следует просить его от души, с чистым сердцем, и тогда желаемое почти наверняка исполнится.
Чего можно ожидать
Не следует рассчитывать на моментальное исполнение желания — нашему небесному защитнику всегда виднее, в какой момент оно должно сбыться. Запаситесь терпением — и в конечном итоге всё сложится, как надо.
Чтобы заручиться поддержкой и расположением своего хранителя, следует общаться к нему почаще и всегда произносить слова благодарности за оказанную помощь. Это можно делать и не вслух, довольно мысленно проговаривать то, что, по вашему мнению, следует донести. Приступая к важному делу, попросите ангела не покидать вас и направлять в нужное русло.
Это можно делать и не вслух, довольно мысленно проговаривать то, что, по вашему мнению, следует донести. Приступая к важному делу, попросите ангела не покидать вас и направлять в нужное русло.
Как нам общаться с ними?
Ангелы — нежные существа, они не выносят скверного поведения подопечного, грубости, нецензурщины, дурных привычек, запаха алкоголя. Все эти негативные проявления человека заставляют его болеть и страдать от отрицательной энергетики.
Каким же образом ангел-хранитель может стараться передать нам информацию из тонкого мира? Очень часто для этого используются самые обычные цифры, которые мы ежедневно видим вокруг себя. А точнее, их комбинации. Нумерология по времени на часах способна делать далеко идущие выводы. Если при взгляде на циферблат вы регулярно замечаете одно и то же сочетание, например, три или четыре одинаковые цифры подряд, парные либо симметричные, то следует понять: случайных совпадений не бывает.
Когда цифры выстроились в ряд.
 ..
..Попробуйте выяснить, что всё это означает. О чём вас хотят предупредить? Какое событие из будущего скрывается за данным сочетанием?
Рассмотрим вначале, как нумерология времени интерпретирует повторяющиеся цифры. При этом следует знать, что чем длиннее ряд одинаковых цифр (две подряд, три или четыре), тем важнее послание, и тем настойчивее ангел-хранитель пытается донести до вас определённую информацию. Итак, о чем скажут нам конкретные цифры?
Ангельская нумерология времени — от единицы до девятки
Если в вашей жизни часто повторяется цифра 1, это прямой намек на то, что пора уделить внимание собственному внутреннему миру, заняться саморазвитием. Повторяющиеся двойки говорят о различиях в характерах между вами и вашим избранником. Следует попытаться подкорректировать отношения или при необходимости найти разумный компромисс.
Цифра 3 говорит о том, что у вас проблемы с самоопределением. Пора вспомнить случившиеся в прошлом события, разобраться с текущим моментом и утвердить планы на будущее. Важно настроиться на четкую цель, чтобы не допустить тех ошибок, от которых ваш небесный защитник пытается предостеречь.
Важно настроиться на четкую цель, чтобы не допустить тех ошибок, от которых ваш небесный защитник пытается предостеречь.
Когда речь идёт о четверке, это намек на чрезмерную погруженность в сферу карьеры и работы. Разумеется, трудолюбие — замечательное качество, но следует уделять внимание и прочим сторонам собственной жизни. Возможно, вам требуется отдых и забота о здоровье.
Регулярно попадающиеся на глаза пятёрки говорят о зачастую необоснованной жажде риска и приключений. Похоже, настала пора воспринимать жизнь более серьезно.
Шестерка символизирует гармонию и существование в мире с себе подобными. Вам следует упорядочить отношения с окружающими.
Семерка почти у всех народов несет в себе мистических колорит. Нумерология времени утверждает: тот, кто часто сталкивается с этой цифрой, возможно, обладает способностью к ясновидению и очень развитой интуицией. Такой человек в состоянии постичь многие тайны вселенной и серьезно влиять на окружающих.
Восьмерка — символ бесконечности. Эта цифра скажет о том, что нельзя терять время, его потом не вернешь. Уже сейчас следует предпринять конкретные шаги для того, чтобы будущее стало спокойным и счастливым.
Эта цифра скажет о том, что нельзя терять время, его потом не вернешь. Уже сейчас следует предпринять конкретные шаги для того, чтобы будущее стало спокойным и счастливым.
Если же часы часто показывают нам цифру 9, следует набраться твердости, перестать бросать незавершённые дела и огорчаться из-за пустяков.
Сигналом личного ангела-хранителя может быть такое время на циферблате часов, как 11:11 или 12:12
Что означают определенные сочетания цифр?
Ангельская нумерология: время на часах
00.00 — если желание загадывалось с чистым сердцем, ему суждено сбыться.
01.01 — вас ожидает хорошее известие со стороны мужчины.
01.10 — к сожалению, затеянное вами кончится ничем.
01.11 — не спешите в этот день отвергать любые предложения.
02.02 — вас могут пригласить в ресторан или в гости.
02.20 — следите за речью, не поддавайтесь раздражению.
02.22 — небеса приоткроют вам какую-то тайну.
03.03 — вас ожидает новая любовь.
03. 30 — ваши чувства не взаимны.
30 — ваши чувства не взаимны.
03.33 — впереди — удача и счастье.
04.04 — попробуйте взглянуть на текущие дела с другой точки зрения.
04.40 — удача отвернулась от вас — похоже, это не ваш день.
04.44 — на работе навлечете гнев начальника.
05.05 — против вас плетутся интриги, враги затеяли нечестную игру.
05.50 — бойтесь огненной стихии, а также воды.
05.55 — скоро вам повезет встретить мудрого человека.
06.06 — впереди — женитьба или замужество.
07.07 — остерегайтесь человека в военной форме.
08.08 — можно ожидать карьерного взлета.
09.09 —берегитесь кражи, позаботьтесь о собственном кошельке или сумочке.
10.01 — вы познакомитесь со значительным человеком (мужчиной), обладающим серьезным влиянием.
10.10 — время приходит.
11.11 — вам грозит зависимость от кого-либо (или чего-либо).
12.12 — ждите удачу в делах сердечных.
12.21 — встреча с незнакомцем, новые отношения.
13.13 — соперники могут напакостить.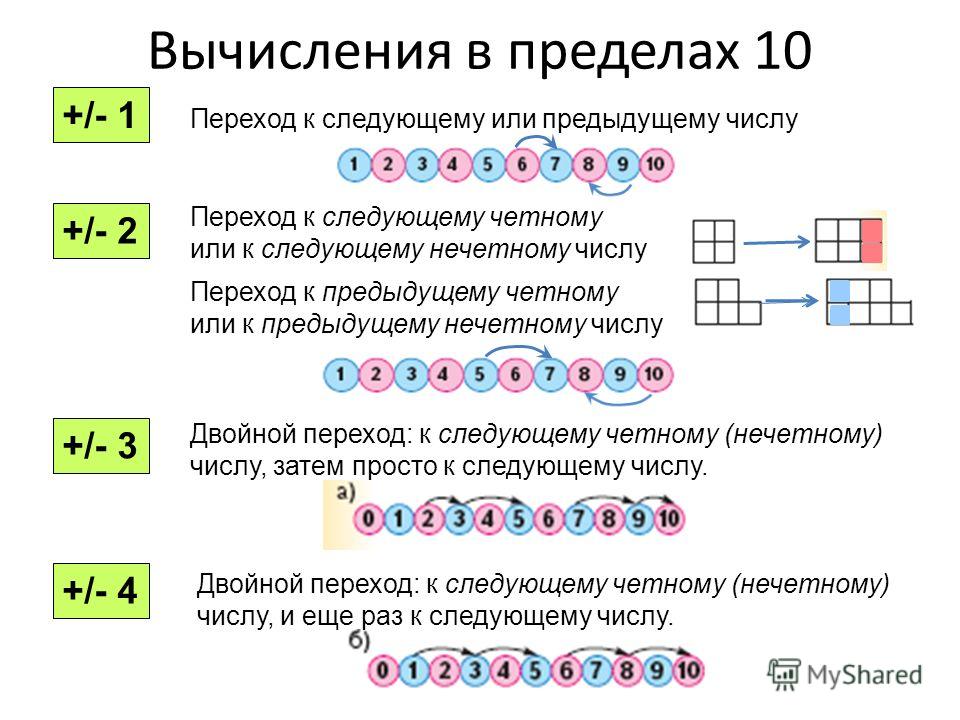
13.31 — наконец-то добьетесь желаемого.
14.14 — любовь захватит вас целиком.
14.41 — возможна крайне неприятная ситуация.
15.15 — мудрый человек даст совет, которому стоит последовать.
15.51 — вас ожидает короткий и яркий роман.
16.16 — берегите себя в пути.
17.17 — угроза от уличных хулиганов.
18.18 — в дороге соблюдайте осторожность.
19.19 — в делах можно рассчитывать на успех.
20.02 — поссоритесь с близким вам человеком.
20.20 — в семье возможны скандалы.
21.12 — в скором будущем вас ожидает новый проект или рождение малыша.
21.21 — яркое романтическое увлечение.
22.22 — вероятность нового знакомства, встречи.
23.23 — речь идет об опасной связи.
23.32 — поберегите здоровье, возможны проблемы.
Возможно, вы считаете, что нумерология времени — типичная лженаука, что-то вроде несерьезного развлечения для скучающих домохозяек. Но попробуйте все же приглядеться к якобы «случайным» совпадениям и проанализировать последующие за этим события. Быть может, вашему мнению суждено измениться!
Быть может, вашему мнению суждено измениться!
С очень древних времен люди всматриваются в свое будущее и анализируют прошлое, его связь с настоящим и с различными событиями, в надежде найти закономерность, связь, которая поможет ориентироваться в будущем и менять свою судьбу по желанию. Как говорится: информирован – значит вооружен, соответственно человек, знающий своё будущее – готов к нему, так или иначе он его ждет, и оно не станет для него роковой неожиданностью.
Из покон веков люди обращаются за информацией о себе и будущем к специалистам в этой области – колдунам магам и звездочетам, за любой имеющейся информацией, любой ниточкой, что укажет в будущее как путеводная звезда.
Порой нам не нужно обращаться к гадалкам или мы просто не можем физически к ним попасть, но ответ на важный вопрос необходим! В таком случае можно просто присмотреться к мелочам – , сны или же время на часах. Сегодня мы поговорим о последнем случае – гаданию по часам. Разные мастера своего дела предлагают различные способы гадания, мы собрали лучшие из них и представили Вам.
Внимание! Для наиболее точного результата стоит точно соблюдать последовательность действий, иначе результат может быть непредсказуем.
Гадание по часам – прекрасная возможность узнать о своем будущем, она появилась на свет ровно тогда же, когда и первые часы, но сегодня это проверенный годами метод, который заслуживает большого внимания.
Гадание на часах — одинаковые цифры
Гадание по часам предполагает трактовку одинаковых цифр, но магическое значение также имеют еще некоторые комбинации. Просто посмотрите на часы и узнайте, что сулит увиденная комбинация (конечно, если это сочетание чисел имеет магическое значение).
Гадание по часам – штука простая и многим привычная, и большинство людей даже как-то неосознанно, интуитивно загадывают желание, если видят на часах красивое число или одинаковые цифры. К примеру, 20:02, или 12:21. И правильно делают!
На самом деле, это не простое совпадение, это – очень тонкий момент, когда у человека действительно может всего на несколько мгновений установиться связь с высшими силами, а желание может осуществиться.
Особенно у того, кто в гадание по часам верит!
К таким «совпадениям» нужно относиться внимательнее, чем к счастливым комбинациям, ведь в предостережении может содержаться и руководство к действию, рекомендации, позволяющие выйти из любого сложного положения. В любом случае, если вы посмотрели на часы и увидели повторяющуюся четную комбинацию, вам нужно задуматься: о чем именно высшие силы хотят вас предупредить, о каком испытании и каких трудностях говорят вам часы.
Но смысл кроется не только в совпадении чисел, но и в любой другой комбинации. В некоторых случаях, значение имеет какое-то одно число, которое постоянно попадается вам на глаза. Если вы постараетесь, то обязательно сможете вспомнить, хотя бы один момент из жизни, когда несколько раз подряд, глядя на часы, вы видели одну и туже цифру.
К примеру, вы несколько раз за день увидели минутную стрелку на отметке «12», вы можете не обратить на это никакого внимания, но если вам известны значения чисел, то вы сразу поймете, что высшие силы говорят вам о том, что в скором времени вам предстоит знакомство с интересным человеком, которое способно коренным образом изменить всю вашу жизнь.
Особое значение имеют также зеркальные отражение чисел, к примеру, если вы увидели на часах значение: 10:01, то это явный знак, и не стоит пропускать его, ведь зная о своем будущем, вы сможете упростить свою жизнь и не пропустить свой счастливый шанс.
Именно поэтому многие эзотерики крайне серьезно относятся к часам и гаданию по этому механизму.
Который час? Что сбудется?
Существует гадание по времени на часах, помимо простого загадывания желаний при виде одинаковых циферок. Есть особенные комбинации чисел, которые не только очень красивы и гармоничны, но и имеют особое магическое значение.
Это гадание получится на любых часах с электронным циферблатом – не только на наручных, но даже на мониторе компьютера. Узнайте, что вас ждет!
- 00:00 – если вы взглянули и увидели эти цифры, ровно в полночь, высшие силы предостерегают вас – день будет не самым удачным для новых начинаний. Не планируйте на этот день никаких новых проектов или смелых действий, если возможно, отложите это.
Постарайтесь провести день спокойно и тихо.
- 3:33 – эта красивая комбинация троек очень удачна для того, кто ее увидел. Тройки говорят о том, что сегодня начатые вами дела непременно завершатся очень удачным образом, или же будут правильно и удачно развиваться.Сегодня можно начинать новые дела, строить смелые планы и делать решительные шаги. Это ваш день!
- 10:01 – комбинация, которую сложно не заметить. Если вы увидели на часиках 10:01, будьте уверены, сегодняшний день будет очень удачным во всем.Таким образом, высшие силы как бы подбадривают вас и подталкивают к смелым действиям – стройте свою судьбу, ничего не бойтесь, у вас все получится! Сегодня удача стоит на вашей стороне.
- 10:10 – еще одно счастливое утреннее совпадение. Эти цифры на часах указывают на удачу в рабочей и деловой сфере, так что, если вы увидели их, будьте смелее и решительнее! Все проекты будут развиваться отлично, а переговоры пройдут в вашу пользу.
- 11:11 – сегодня вам предстоит получать подарки от судьбы.
Кстати, о материальных подарках со стороны близких людей тоже идет речь, потому что сегодня такое время, когда вам предстоит получить сюрпризы и приятные неожиданности. Вы будете приятно удивлены не один раз!
- 12:12 – это необычная комбинация, и нечасто именно ее приходится заметить. Если вам повезло, и на циферблате часов вы обнаружили 12:12, радуйтесь! Сегодня абсолютно все, за что вы ни возьметесь, будет идти наилучшим образом, все получится, никакие трудности вам мне помешают.
- 12:21 – тоже красивая комбинация из единиц и двоек, ее трудно пропустить, ведь что-то она должна означать! Разумеется, как и другие необычные и редкие комбинации, 12:21 – особенная.Это знак, что сегодня вам предстоит влюбиться, или же вы целый день проведете в романтический мыслях о ком-то. Возможно, сегодня вас ожидает очень романтичный сюрприз от любимого человека, свидание или приятное предложение.
- 14:41 – это удачная комбинация, которая может иметь несколько значений.
К примеру, для молодых людей и незамужних девушек 14:41 означает любовные приключения, новые знакомства, флирт и все самое приятное, связанное с романтической сферой.Для людей же семейных и взрослых, цифры 14:41 сулят приятное общение, отдых, примирение в семье, гармоничный и спокойный день, полный радости.
- 15:15 – не самое удачное сочетание цифр. Это гадание говорит, что если на часах вы увидели 15:15, будьте осторожны сегодня – не рискуйте и не начинайте новых дел. Может случиться неприятный сюрприз или нежеланная встреча, старайтесь ко всему относиться максимально спокойно и мудро.
- 15:51 – напротив, хорошее сочетание. Комбинация 15:51 сулит вам приятный сюрприз и хороший вечер. Даже если этот день трудный и полный разных нежеланных событий, стрессов и неудач, знайте, что к вечеру все изменится в лучшую сторону.
- 20:02 – необычное число. Это не предсказание, а совет вам, если вы увидели 20:02 на часах, то будьте сдержаннее в этот вечер.
Комбинация 20:02 состоит из двоек и нолей, и может сулить ссору с любимым или близким человеком. Держите эмоции под контролем, умейте промолчать.
- 21:12 – будет для вас успешным и принесет новую радость.
- 21:21 – предупреждение, будьте осторожны и взвешивайте свои поступки. Возможно, вы уже совершили ошибку, о которой придется жалеть – обдумайте это.
- 23:23 – Завтра вас ждет большая удача и радость. Засыпайте с хорошими мыслями!
Гадания по часам и цифрам – это то, что поможет вам ориентироваться в своей реальности, не забывать о том, что жить и действовать надо по совести, и избегать ошибок.
Дополнительные значения
Некоторые народы уверены, что счастливой комбинацией совпадение чисел на часах будет лишь та, в которой присутствуют только нечетные числа. Однако люди, проживающие на Востоке, полагали, что стоит опасаться чисел, в которых присутствует цифра 9, ведь она говорит о скорых изменениях в жизни.
Но никто не может точно сказать, положительными они будут или отрицательными.
Также некоторые народы считают, что если в комбинации повторяется много четных, это говорит о том, что человек находится в опасной ситуации.
Четные цифры пытаются предупредить человека, что у них есть недоброжелатели, которые могут в скором будущем нанести урон. Это говорит о том, что стоит оградить себя от потенциальных врагов и на время «залечь на дно».
Правила проведения гадания с часами
В любых гаданиях, на бумаге, с монетами, на палочках, на картах Таро, есть свои правила, которых необходимо придерживаться для того, чтобы получить точный результат. Это — не исключение.
Помните, точный результат можно получить только во вторник и в четверг. Другие дни недели не несут особую ценность и любые совпадения чисел, которые вы увидели не в указанные дни, не несут логического значения.
Также не следует специально подбирать нужное время. Это будет всего лишь искусственное совпадение и не будет иметь никакой реальной силы.
Гадание по количеству часов в доме
Помимо распространенного ритуала, который позволяет узнать ваше будущее по одинаковым цифрам на электронных часах, есть еще это, менее распространенное гадание. Узнать энергетику дома и хозяина можно по тому, сколько в помещении находится часов.
- Одни — дом наполнен любовью, пониманием, благополучием.
- Двое — помещение сохраняет положительную энергетику, хозяева находятся в гармонии с собой.
- Трое — хозяин дома очень прагматичный человек, реалист, который любит отстаивать свою правоту.
- Четверо — в этом помещении мало тепла и любви.
- Пять — хозяин дома любит гостей, он всегда дружелюбен, рад новым встречам и знакомствам.
- Шесть — в этом доме тяжело расслабиться, везде спешка и суета, хозяин помещения возможно очень занятой и скандальный человек.
- Семь — в помещении нет энергетики спокойствия и благополучия, хозяину дома необходимо наладить отношения со своими близкими людьми.
- Восемь — также говорит об отсутствие энергетики комфорта и уюта. Хозяева дома обеспокоены мелкими хлопотами, мало времени уделяет друг другу.
- Девять — в помещении царит атмосфера спокойствия и благополучия, здесь любой гость может чувствовать себя как дома.
Если в помещении более 9 часов, то для получения результата необходимо сложить цифры например: 14 = 1+4 = 5.
Если вы решили провести любое гадание, заранее настройтесь на положительный результат. Потому что, даже если цифры предупредят о чем-то негативном, это всего лишь руководство к тому, чтобы быть более осторожными, но не гарантия того, что случится что-либо плохое.
grimuar.ru/gadanie/gadanie-na-chasah.html
Гадание на электронных часах
Гадания сегодня разные и много примет, некоторые гадания пришли к нам с древности, некоторые мы сами приобрели в современном мире. Часы и время – это вечное, которое было всегда, возможно изначально и не было у людей часов, но так они определяли время по солнцу, но все равно множество гаданий и примет связано с часами.
Но так как мы с вами живем в современном мире, то рассмотрим гадание по электронным часам, которые мы можем наблюдать не только в офисе или дома, но и в магазинах, на вокзалах, на улицах, в метро и т.д.
Очень много примет уже связано с цифрами и на электронных часах оно то и дело меняются, и каждый человек интуитивно смотри на время и видит разные цифры не случайно.
Доказано, что какие – то высшие силы пытаются донести до человека что-то важное, подсказать или предупредить его с помощью цифр. А электронные часы – это именно тот предмет, где цифры есть постоянно и постоянно они несут разную информацию.
Какие вы для себя делаете выводы, когда смотрите на электронные часы несколько раз в день и не обязательно на одни и те же и цифры попадают на глаза все время 12 или 48 ? Скорее всего, вы ответите на этот вопрос так: я вообще не замечаю этого, не придаю значения или не акцентирую на этом внимание.
А ведь напрасно это высшие силы пытаются вам что-то подсказать и предупредить.
К примеру, те же 12 все время перед вашими глазами не просто говорят вам, а «кричат» о том, что вас ждет новое интересное знакомство, а цифра 48 – это уже предвещает бурный роман.
Но магическое значение по многим мнениям магов и экспертов имеют цифры зеркально отражающие т.е. это, к примеру, такие 12,21 или те которые повторяются 13:13, которые и напоминают электронные часы даже когда записаны. Поэтому гадание по электронным часам есть смысл изучать и применять каждый день для того чтобы знать что в ближайшем будущем нас ждет.
Единственное вам нужно учитывать два всего лишь простых правила, для того, чтобы гадания были правдивыми и действительно исполнялись. Если их не учитывать, то гадания не будут правдивыми и вы вскоре скажите, что гадание по электронным часам – это ерунда, поэтому соблюдайте правила и убедитесь сами на личном опыте, что гадание действительно правдивое и действительно говорит нам правду.
- Итак, правило номер один. Вы можете прибегать к помощи электронных часов и их цифр только два раза в неделю – это вторник и четверг, когда цифры более всего настроен на то, чтобы говорить правду.
- Правило номер два. Не нужно специально подгадывать время или мухлевать, так как врятли специально что-то получиться и часы вам скажут правду, только случайно увиденные цифры парные или одинаковые могут правду на будущее время тебе напророчить.
Когда увидели те самые цифры, смотрите интерпретацию на нашем сайте и открывайте для себя завесу будущего.
Но не забывайте два заветных правила, только интуитивный взгляд может сказать вам правду и посоветовать, то чего нужно опасаться или наоборот что хорошее вас ждет.
Интерпретация значений цифр, гадания по электронным часам.
- 00.00 — если ваше желание идет от чистого сердце без злых помыслов оно обязательно сбудется
- 01.01 — ожидай хорошей новости от мужчины
- 01.10 — к сожаленью, то дело, которое ты начала не принесет желаемого результата
- 01.11 — звезды советую не отказываться ни от каких-либо предложений сегодня
- 02.
02 — тебя ждет приглашение или в клуб или просто в гости
- 02.20 — предостережение для тебя: следи за тем, что ты говоришь, не раздражайся
- 02.22 — тебе откроется секрет или тайна
- 03.03 — к тебе спешит любовь на своих крыльях, открой ей двери
- 03.30 — к сожалению, если твое желание связано с переменами в жизни, оно на данный момент не исполниться
- 03.33 — счастье и удача у тебя на пороге
- 04.04 — попытайся посмотреть на сложившуюся ситуацию с другой стороны
- 04.40 — это не твой день. Фортуна не на твоей стороне
- 04.44 — от начальства тебе попадет
- 05.05 — враги что-то замыслили против тебя
- 05.50 — бойся воды и огня
- 05.55 — скоро ждет тебя встреча с умным человеком
- 06.06 — скоро свадьба
- 07.07 — относись осторожно к людям в военной форме
- 08.08 — карьерный взлет
- 09.09 — береги деньги и сумочку
- 10.01 — тебя ждет знакомство с мужчиной очень влиятельным
- 10.
10 — твое время наступает
- 11.11 — будешь зависима от кого-то или же чего-то
- 12.12 — тебя ждет большой успех в любви.
- 12.21 — тебя ждет знакомство с красивой девушкой
- 13.13 -соперники будь осторожней
- 13.31 — наконец то ты получишь, то чего долго хотела
- 14.14 — балом твоим правит любовь
- 14.41 — тебя ждет неприятная ситуация
- 15.15 — послушай совет умного человека
- 15.51 — тебя ждет короткий но бурный роман
- 16.16 — осторожней на дороге
- 17.17 — осторожней на улице могут быть хулиганы
- 18.18 — на дороге осторожней
- 19.19 -в делах тебя ждет успех
- 20.02 — ссора с человеком, который тебе дорог
- 20.20 — в твоей семье ссора
- 21.12 — у тебя родиться в голове новый проект или же эти цифры предвещают рождение ребенка
- 21.21 — роман бурный страстей
- 22.22 — новое знакомство.
- 23.23 — у тебя может быть опасная связь.
- 23.32 — со здоровьем могут возникнуть проблемы.
Как только люди создали настенные и наручные циферблаты, гадание по цифрам на часах стало пользоваться популярностью. Самой большой магической силой наделены одинаковые и зеркальные числа. Каждая комбинация является маленьким предсказанием.
Суть ворожбы
Узнать будущее можно не только благодаря картам Таро и . Вы можете заниматься ворожбой, не привязываясь к лунному циклу.
Цифры, которые вы видите на циферблатах часов, являются не только констатацией реального времени, но и подсказкой судьбы.
Относясь к необычным цифровым значениям как к совпадению, вы не разгадаете послание . Современное гадание на циферблате отличается высокой информативностью и не требует от вас сложной подготовки.
Вы можете проигнорировать часто повторяющуюся комбинацию чисел и , но с помощью гадания вы узнаете: такое сочетание сулит вам знакомство с харизматичным и богатым поклонником.
Увидев одинаковые значения чисел () на часовой и минутной стрелке, вы должны внимательно проанализировать собственную жизнь. В вашу судьбу стучатся важные открытия или перемены.
В вашу судьбу стучатся важные открытия или перемены.
Проводя гадание по наручным часам, помните, что значение одинаковых чисел может быть таким:
- вам предстоит разочароваться в своем супруге или в ком-то из близких друзей, но это событие освободит вас от возможных потерь и потрясений в будущем;
- наступает удачное время для поиска своей половинки;
- ваши таланты раскроются на полную силу;
- благодаря счастливому совпадению, вы получите престижную должность;
- удвоение чисел и «10» сообщает, что вам необходимо проявить упорство, чтобы выйти на благоприятную полосу жизни.
Зеркальные комбинации цифровых значений ( :41) нередко указывают, что вы неправильно видите ситуацию. Они сообщают о невозможности решить проблему привычным для вас способом.
Правила гадания по часам
Есть два вида гадания по часам.
- Спонтанная ворожба. Посмотрев на часы, вы случайно увидели одинаковые значения на часовой и минутной стрелке.

- Запланированное гадание. В начале дня сформулируйте вопрос, который больше всего вас тревожит. Вы можете спросить: «Будем ли мы с (таким-то парнем) встречаться?». В течение дня смотрите на часы как обычно. Заметив зеркальные цифры или одинаковую числовую комбинацию, смотрите в толкование.
Правила ворожбы:
- наиболее удачные дни для гадания по времени — вторник и четверг;
- незамужние барышни и одинокие дамы могут заниматься ворожбой в пятницу;
- если вы доверили электронным часикам миссию прорицателя, позаботьтесь, чтобы они выглядели презентабельно — наличие царапин на циферблате недопустимо;
- не стоит навязывать свою волю и специально смотреть на циферблат по несколько раз, чтобы получить нужное значение, в таком случае правдивых предсказаний можете не ждать;
- откажитесь от идеи гадать, когда вы расстроены или пьяны;
- не рассказывайте никому о магических таинствах.
Ворожба на разных часах
Не имеет значения, по каким часам вы будете гадать: по электронным или по механическим. Главное, чтобы техника была исправной. Гадание по электронным часам удобно для путешественников. Где бы вы ни находились, вы сможете уделить несколько секунд, чтобы посмотреть на циферблат.
Главное, чтобы техника была исправной. Гадание по электронным часам удобно для путешественников. Где бы вы ни находились, вы сможете уделить несколько секунд, чтобы посмотреть на циферблат.
Еще один нюанс: благодаря светящемуся циферблату электронные часы больше подходят для ночной ворожбы, чем механические. Желая знать, что ожидает вас в пункте назначения, воспользуйтесь таким вариантом гадания. Когда вы будете ехать в поезде или лететь на самолете, среди ночи посмотрите, что показывают часы.
Числа и на минутной стрелке предостерегают: вам предстоит встреча с хитрыми людьми. Не исключено, что вас попытаются втянуть в нечестную сделку. Хорошим знаком являются числа и 41. Ваша поездка будет благополучной, и вы вернетесь домой с ценным приобретением.
Если верить примете, для гадания можно использовать только собственные часы, которые никто, кроме вас, не носил.
Существует старинный способ узнать ближайшее будущее своей семьи. Лучший период для ворожбы — первые 20 дней после Нового года. В четверг посмотрите время на настенных часах. Увидев на минутной стрелке число 55, 15 или 31, готовьтесь к позитивным событиям: рождению ребенка, улучшению жилищных условий. Если вам встретится повторяющееся число , вам стоит приложить усилия для реализации в профессиональной сфере.
В четверг посмотрите время на настенных часах. Увидев на минутной стрелке число 55, 15 или 31, готовьтесь к позитивным событиям: рождению ребенка, улучшению жилищных условий. Если вам встретится повторяющееся число , вам стоит приложить усилия для реализации в профессиональной сфере.
Значения распространенных комбинаций
Колоссальным магическим смыслом наделены 5 комбинаций.
00:00. Сочетание говорит, что вскоре может исполниться ваша заветная мечта. Чтобы осуществиться, ваше желание должно быть добрым. Если вы захотите причинить вред своим коллегам или сопернице, двойное сочетание сыграет против вас. Все попытки повысить свою значимость за счет других, обернутся проигрышем.
11:11. Тревожное предзнаменование. Не относитесь к появлению 4 единиц на циферблате, как к совпадению. Такая комбинация предупреждает: в будущем вы попадете в зависимость от влиятельных людей (богатых родственников, начальника или непорядочного возлюбленного). Не позволяйте втянуть себя в финансовые авантюры. Второй вариант толкования: вас ожидает болезнь. Иногда двукратное повторение цифры «11» показывает, что гадающая особа попала в плен своих пагубных пристрастий (игромании, курения).
Второй вариант толкования: вас ожидает болезнь. Иногда двукратное повторение цифры «11» показывает, что гадающая особа попала в плен своих пагубных пристрастий (игромании, курения).
Благоприятный знак. Одиноким парням и девушкам он предвещает встречу с половинкой. Супругам, чьи отношения проходят проверку бытовыми проблемами, повторение числа 12 сулит возрождение любви и страсти. Родителям, которые переживают за детей-подростков, эта комбинация обещает: все трудности и недоразумения унесет река времени. Главное, не навязывать младшему поколению свои взгляды на жизнь.
14:14. Судьба приготовила гадающей особе щедрый подарок — любовь. Если в этот момент избранник не отвечает вам взаимностью, вскоре в его сердце вспыхнет влюбленность. Одно из значений цифры «14» — стабильность, устойчивость. Чтобы новая любовь приносила вам радость, не спешите менять себя в угоду страсти.
22:22. Увидев эти значения, ждите встречи с необычной и яркой личностью, которая изменит вашу жизнь. На вашем пути повстречается человек, который поможет вам построить головокружительную карьеру. Вместе с влиятельным другом (коллегой) вам суждено сделать важные открытия.
На вашем пути повстречается человек, который поможет вам построить головокружительную карьеру. Вместе с влиятельным другом (коллегой) вам суждено сделать важные открытия.
Другие цифровые сочетания
Выполняя гадание по любым часам, по одинаковым цифрам можно узнать многое, но будьте готовы к неожиданностям. Ответ Высших Сил покажется вам неправильным или слишком запутанным. Все, что вам необходимо делать — принять к сведению информацию, полученную в результате гадания. В этих цифровых комбинациях скрывается точное предсказание:
- 01:01 — девушкам и женщинам эта комбинация обещает головокружительный роман, для представителей сильного пола в этом значении закодирован иной смысл — приятель или бывший сослуживец, живущий в другом городе или за границей, предложит вам прибыльный проект;
- 02:02 — если вы увидели это сочетание чисел, ждите выгодного предложения — оно может поступить от вашего руководства или от старого друга;
- 10:10 — эта комбинация чисел призывает вас мобилизовать свои силы, если вы хотите добиться успехов в работе, проявите настойчивость и смекалку;
- 13:13 — вскоре у вас появится соперник;
- 17:17 — проявите осторожность, вам предстоит провести некоторое время в обществе завистливых или агрессивных людей — чтобы не навлечь на себя беду, оградите себя от злобного окружения;
- 18:18 — если вы гадаете по часам, эта комбинация вас не обрадует, она предупреждает вас о возможной автокатастрофе — постарайтесь реже пользоваться личным автомобилем и общественным транспортом;
- 19:19 — вам суждено стать любимцем Фортуны, во всех начинаниях вас ожидает успех;
- 21:21 — судьба предсказывает вам начало новой любви, у вашего романа будет много шансов перерасти в счастливый брак;
- 23:23 — знак, что вам необходимо пересмотреть свой круг общения, среди ваших знакомых есть злобный и коварный тип, не исключено, что он попытается навредить вашей репутации.

Приступать к повторному гаданию по часам можно через неделю после первого сеанса ворожбы.
Четные и нечетные числа
В славянской магической традиции нечетным числам приписывалась роль удачливых символов. Числа , считались символами достатка, радости и любви. Повторение нечетного числа (55) сулит крупный выигрыш или новую денежную работу.
Единица символизирует активность, напор, здоровый риск. В сложных цифровых комбинациях (2121) нечетное число обещает избавление от проблем. Числа 51 и 31 можно назвать символами семейного счастья.
Увидеть четные числа на циферблате считалось дурным предзнаменованием. Некоторые люди уверены: цифры 2 и 4 зазывают беду в дом.
В наши дни отношение к числам изменилось. Четное может приносить удачу. Главное — в какой комбинации оно вам встретилось: число 23 предупреждает вас об опасности, а его зеркальное отражение (число 32) символизирует освобождение от проблем.
Неоднозначные толкования вызывает цифра . Во многих культурах она предсказывает бесповоротные изменения, жертвы ради достижения цели. Увидеть 9 или 19 на часах — значит, получить предсказание, что вскоре вам придется порвать с прежними привычками и связями и начать новую жизнь.
Во многих культурах она предсказывает бесповоротные изменения, жертвы ради достижения цели. Увидеть 9 или 19 на часах — значит, получить предсказание, что вскоре вам придется порвать с прежними привычками и связями и начать новую жизнь.
Подсказки для гадания Гадая по электронным часам, не забывайте записывать результаты в блокнот. Если в течение месяца вам несколько раз попалась на глаза одна и та же комбинация чисел, будьте внимательны. Гадание по часам сообщает о ваших дремлющих талантах или о скрытых проблемах.
В одном из увиденных вами цифровых значений может скрываться число или месяц вашего рождения. Если вы родились на свет 1 мая, это число на часах — послание вашего ангела. Вы слишком увлеклись достижением чужих целей и забыли о собственных планах.
Каждая единица времени несет в себе большое значение, но ворожба не является окончательным решением. Если вас не устраивает предсказание, не впадайте в уныние. Получив предупреждение о возможных опасностях, вы сможете повернуть ситуацию в свою пользу.
Самый простой и безопасный способ узнать будущее — гадание по времени на часах. Ориентируясь по числам, которые попадаются вам на глаза, вы можете избежать опасности и получить подсказку в интересующем вас вопросе.
Некоторые привычки детства остаются на всю жизнь. Мы можем быть трижды взрослыми и серьёзными, со своими семьями, карьерами и важными жизненными устремлениями… И при этом так же торопиться загадать желание, оказавшись между двумя тёзками. Или встретив на улице машину с приметным номером 777. Или увидев на табло электронных часов необычную комбинацию цифр. Впрочем, к чему стесняться? Это так замечательно и мило — сохранить в себе хоть кроху детской веры в чудеса! И потом, кто сказал, что она вредна? Если всей душой ждать от «удачных» циферок добра, они действительно работают!
Что означают одни и те же цифры или зеркальные числа на часахПостоянно сменяя друг друга, спеша вперёд, светящиеся циферки наших электронных часов то и дело складываются в разнообразные комбинации. Чаще всего они ничем не примечательны. В самом деле, кого удивишь, например, указанным на табло временем 16:15? Но порой цифры складываются весьма интересным образом — 05:05, 12:12, 13:31. Ещё поразительнее, если они начинают попадаться на глаза не разово, а день за днём, словно пытаются обратить на себя внимание! Человек, далёкий от суеверий, и тот почувствует себя сбитым с толку. А любитель примет обязательно увидит в этом событии прямой намёк на грядущее и тут же попытается разгадать: чего ждать, как себя вести и как использовать обстоятельства себе на пользу.
Чаще всего они ничем не примечательны. В самом деле, кого удивишь, например, указанным на табло временем 16:15? Но порой цифры складываются весьма интересным образом — 05:05, 12:12, 13:31. Ещё поразительнее, если они начинают попадаться на глаза не разово, а день за днём, словно пытаются обратить на себя внимание! Человек, далёкий от суеверий, и тот почувствует себя сбитым с толку. А любитель примет обязательно увидит в этом событии прямой намёк на грядущее и тут же попытается разгадать: чего ждать, как себя вести и как использовать обстоятельства себе на пользу.
00:00 — время загадывать любые желания, планировать перемены и начинать сначала то, что когда-то не получилось. Лишь бы вы действовали с чистым сердцем и поменьше думали о корысти.
Впрочем, есть прямо противоположная точка зрения, убеждающая: если на часах мелькнули четыре нуля, лучше в этот день ничего не планировать и новых проектов не начинать. Какому из толкований верить, решайте сами.
01:01 — появление этих цифр сулит хорошие новости и оставляет надежду на исполнение заветной мечты. Правда, считается, что эта комбинация отличается меньшей силой, чем предыдущая.
Правда, считается, что эта комбинация отличается меньшей силой, чем предыдущая.
01:10 — к сожалению, «зеркальные» цифры не принесут удачи. Начатое дело либо захиреет, либо зайдёт в тупик, поэтому лучше немного повременить с ним.
01:11 — три единицы подряд обещают интересное предложение, которое вскоре вам поступит. Не оставляйте его без внимания!
02:02 — богатая на предсказания комбинация. Первое: судьба усиленно посылает вам знаки, которые нужно научиться видеть. Внимательнее смотрите по сторонам. Второе: если получите приглашение в гости или просьбу о помощи, не отказывайте. Результат будет неожиданным и приятным. Третье: не оставляйте без внимания здоровье, с ним возможны проблемы.
02:20 — воспользуйтесь зеркальным временем, чтобы взглянуть на себя со стороны. Кажется, вы слишком бурно реагируете на обстоятельства и людей, позволяя себе неоправданные вспышки гнева.
02:22 — три двойки подряд символизируют тайну, которая вам сегодня приоткроется.
Тройка — знак удачи
03:03 — Судьба ведёт вас самым прямым путём к счастью и любви. Если в данный момент вы заняты каким-то важным проектом, тройки обещают его успешное завершение и неплохие дивиденды в итоге.
Если в данный момент вы заняты каким-то важным проектом, тройки обещают его успешное завершение и неплохие дивиденды в итоге.
03:30 – «зеркальная» пара из тройки и нуля, увы, не сулит удачу. В жизни намечается период застоя, а в чувствах — охлаждение.
03:33 — зато три тройки очень приятный знак, сулящий успехи, радостные события и настоящее счастье.
04:04 — если вам кажется, что вы зашли в тупик, просто оглядитесь по сторонам. Выход рядом, нужно лишь посмотреть на него под другим углом. Возможно, обстоятельства заставят вас изменить своё мнение по какому-либо вопросу. Не сопротивляйтесь и доверьтесь судьбе, она выведет вас на верный путь.
04:40 — зеркальный день, по традиции не обещает золотых гор. Ведите себя осторожнее, не планируйте серьёзных перемен в жизни. Но можете осмелиться на знакомство с симпатичным представителем противоположного пола, если представится возможность.
04:44 — появление трёх четвёрок предупреждает о конфликте с человеком, занимающим более высокое положение. Возможно, предстоит визит на ковёр к начальнику?
Возможно, предстоит визит на ковёр к начальнику?
05:05 — недруги придут в движение, плетя заговоры против вас. Не волнуйтесь, их интриги не увенчаются успехом, так как день обещает быть благоприятным. Тем же, кто пока одинок, он может подарить встречу со своей будущей половинкой.
05:50 — опасайтесь несчастных случаев, связанных с водой и огнём.
05:55 — судьба пошлёт вам мудрого советчика, не отмахнитесь о него.
06:06 — в большинстве случаев эта цифра намекает на то, что вы уделяете слишком много внимания материальному, забывая о душе. Но некоторым две шестёрки рядышком предсказывают скорую свадьбу.
07:07 — круговорот событий захватит вас с головой. Если поблизости окажутся верные друзья, сообща вы горы свернёте и осуществите все мечты. Окружите себя недостойными людьми — увы, добра не ждите. И постарайтесь избежать столкновений с теми, кто носит форму, это может плохо кончиться.
08:08 — день располагает к трудовым подвигам, получению прибыли и продвижению вверх по карьерной лестнице. Но только если вы сумеете не поддаться на провокации злопыхателей и не ввяжетесь в конфликт.
Но только если вы сумеете не поддаться на провокации злопыхателей и не ввяжетесь в конфликт.
09:09 — сочетание девяток и нулей предупреждает о потерях. Что бы это ни было — кошелёк, который ловко вытащит из вашей сумочки воришка, или завершившиеся разрывом отношения — примите случившееся спокойно. Всё, что вам действительно нужно, останется при вас.
Кто-то умудряется строить свою жизнь по показаниям часов!
10:01 — ждите знакомства с влиятельным человеком, вероятнее всего, мужчиной.
10:10 — удача и новые возможности у вас на пороге. Самое время для реализации давно вынашиваемых идей и планов.
11:11 — подсчитывая подарки судьбы, которые вам сегодня обещаны, не теряйте головы. Велик риск угодить в зависимость от нечистоплотного в моральном плане субъекта.
12:12 — удачный час и удачный день. Звёзды собираются устроить вам встречу с родственным по духу человеком! Не упустите шанс обрести друга, с которым можно будет разделить свои взгляды и убеждения. Впрочем, отчего только друга? Счастливая комбинация цифр предсказывает вам сегодня колоссальный успех у противоположного пола.
Впрочем, отчего только друга? Счастливая комбинация цифр предсказывает вам сегодня колоссальный успех у противоположного пола.
12:21 — знакомство с обаятельной женщиной. Дамы обретут интересную собеседницу, мужчины — надежду на увлекательный роман.
13:13 — если научитесь действовать рассудительно и держать эмоции под контролем, сумеете осуществить потаённое желание. Вы движетесь в верном направлении, но не забывайте о соперниках, которые не упустят случая подставить вам подножку. Будьте осмотрительнее.
13:31 — зеркальная комбинация тройки и единицы означает избавление от преград и конец периода застоя. Вы наконец-то обретёте то, что так жаждете получить.
14:14 — прагматичная четвёрка в компании единицы изменяет своим обычным принципам и советует вам поддаться новому романтичному чувству. Лёгкая влюблённость, огненная страсть или крепкий брачный союз — когда на часах эта удачная комбинация, возможно всё.
14:41 — следует вести себя осмотрительней, вам грозит несчастный случай, болезнь или другие неприятности.
15:15 — из неловкой ситуации поможет выбраться дельный совет опытного человека, возможно, родственника.
15:51 — готовьтесь потерять голову от любви.
16:16 — судьба постоянно подбрасывает вам возможности изменить то, чем вы недовольны в своей жизни. Но научиться видеть их вы сможете, лишь поработав над своими моральными качествами. Слегка приструните эгоизм, научитесь видеть проблемы других людей, и удача не обойдёт вас стороной. Тем, кто в этот день находится в пути, следует поберечься: возможны травмы или встреча с грабителями.
17:17 — ваш девиз на сегодня «Кто не рискует, тот не пьёт шампанского!» Однако не забывайте, что мудрый человек просчитывает все возможные варианты развития событий и успевает подстелить соломку в самых опасных местах. Рискуя, не забывайте о здравомыслии.
18:18 — две восьмёрки символизируют значительную финансовую поддержку или рост доходов. Но вместе с тем вы можете лишиться хорошего друга или пострадать в путешествии.
Что бы ни сулили часы, верьте в удачу
19:19 — двойственная комбинация. Одни толкователи считают тандем девятки и единицы несомненным знаком полосы везения в жизни, другие, наоборот, советуют собрать силы в кулак и стойко переждать неудачный период. Чтобы мрачные прогнозы гарантированно не сбылись, действуйте обдуманно. А лучше постарайтесь взять несколько дней отдыха от забот.
20:02 — зеркальные цифры предсказывает разлад с близкими…
20:20 — …да и прямая комбинация прогнозами не радует: вам грозят ссоры, дрязги и бурное выяснение отношений. Не идите на поводу у эмоций, даже если очень захочется!
21:12 — время обновления: новый образ, новое мировоззрение, новые интересные идеи в голове. Нацеленные на карьеру граждане начнут выдавать одну креативную мысль за другой, а занятые семьёй имеют все шансы на появление желанного малыша.
21:21 — удержать себя в разумных рамках будет сложно, ибо звёзды заготовили для вас незабываемое любовное приключение. Но придётся придерживать сердце в узде и почаще обращаться к разуму, иначе очень скоро вы будете горько сожалеть о своих действиях.
Но придётся придерживать сердце в узде и почаще обращаться к разуму, иначе очень скоро вы будете горько сожалеть о своих действиях.
22:22 — осторожность, осторожность и ещё раз осторожность. Ведите себя осмотрительно, но не отказывайтесь от общения с новыми людьми. Именно в это непростое время вам дано заводить выгодные знакомства и находить настоящих друзей.
23:23 — отношения, недавно появившиеся в вашей жизни, несут с собой опасность. Обдумайте как следует, всё ли вас в них устраивает, а заодно поразмыслите над своими ошибками в общем. Чем скорее вы поймёте, в чём были неправы, тем быстрее начнёте двигаться к намеченным целям.
23:32 — следите за здоровьем.
Девичьи приметы: что обозначает одинаковое время для дам
Помимо всего перечисленного есть ещё одно, чисто женское поверье. Увидели на часах одинаковые цифры? Назовите имя мужчины, который вам нравится, и он перед вами не устоит. Даже если «магия чисел» подкачает, подействует ваше женское обаяние, подкреплённое верой в добрую примету. Как выглядит девушка, уверенная в своей неотразимости для желанного мужчины? Блеск в глазах, улыбка победительницы на губах, шаг летучий и чуть-чуть кошачий… Как говорила Верочка из «Служебного романа», мужчины такую женщину не пропускают! Кто знает, вдруг и сердце любимого пронзит стрела Амура?
Как выглядит девушка, уверенная в своей неотразимости для желанного мужчины? Блеск в глазах, улыбка победительницы на губах, шаг летучий и чуть-чуть кошачий… Как говорила Верочка из «Служебного романа», мужчины такую женщину не пропускают! Кто знает, вдруг и сердце любимого пронзит стрела Амура?
Знатоки человеческой психики считают, что в появлении на часах одних и тех же необычных цифр виноваты мы сами. Подметив их раз, мы подсознательно начинаем бросать взгляды в сторону табло в нужное время и не очень-то отмечаем в памяти цифры, которые не «вписываются» в примету. Чистая психология и никакой мистики! А может быть, дело обстоит иначе. К примеру, для вас сочетание двойки и нуля означает что-то своё, не отмеченное традиционным толкованием. Если подсознание привлекло внимание именно к этому числу, не торопитесь шуршать листиками таблички в поисках ответа. Обратитесь к собственным ощущениям и интуиции. Что они говорят вам? О чём предупреждают? Ответ может оказаться очень ясным и очень неожиданным!
Введение в математическую логику
2.
 1Высказывания
1Высказывания2.1.1Примеры высказываний
Вероятно, в главе с таким названием читатель ожидает наконец увидеть аккуратные определения всем вводимым понятиям. Но нет.
Как бы определение 1. Высказывание — это утверждение с чётко определенным смыслом, которое может быть истинным или ложным.
Как обычно, проще привести несколько примеров.
Пример.
- «2+2=5» — пример высказывания. Оно ложно.
- «3>2» — ещё один пример высказывания. Оно истинно.
- «5 — простое число» — ещё одно истинное высказывание.
- «Множество простых чисел конечно» — это ложное высказывание.
- «Если целое число простое и оно больше двух, оно нечётно» — истинное высказывание.
- «Каждое чётное число, большее двух, можно представить в виде суммы двух простых чисел» — это высказывание, истинность которого в настоящий момент неизвестна (это так называемая бинарная проблема Гольдбаха).
- «n — чётное число» — это не высказывание, потому что непонятно,
чему равно n (здесь, конечно, под n подразумевается не
собственно буква, а переменная, которая может принимать разные
значения), и поэтому это утверждение не является ни ложным, ни
истинным.
 С такого типа утверждениями (они называются предикатами)
мы познакомимся чуть позже.
С такого типа утверждениями (они называются предикатами)
мы познакомимся чуть позже.
Вместо «истинно» или «ложно» используются и другие синонимичные выражения: верно (неверно), корректно (некорректно) и т.д.
2.1.2Операции с высказываниями
Из существующих высказываний можно делать новые высказывания с помощью логических операций (которые также называются операциями булевой алгебры). Пусть даны какие-то высказывания A и B.
Определение 1. Высказывание «верно по крайней мере одно из двух высказываний A или B (или оба)», называется дизъюнкцией высказываний A и B. Оно обозначается A∨B. Другой термин для дизъюнкции — логическое «ИЛИ».
Определение 2. Высказывание «верны оба высказывания A и B» называется конъюнкцией высказываний A и B. Оно обозначается A∧B. Другой термин для конъюнкции — логическое «И».
Определение 3. Высказывание «высказывание A неверно» называется отрицанием A.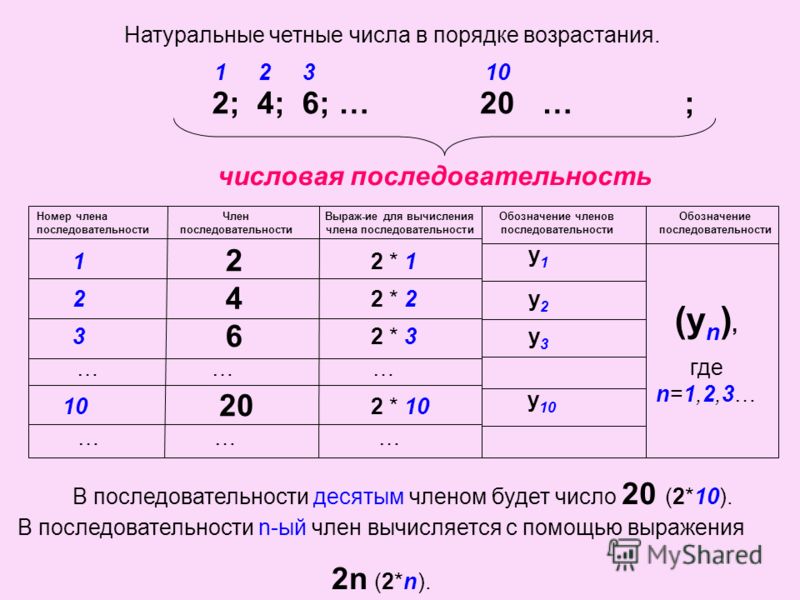 Обозначается ¬A. Другой термин — логическое «НЕ».
Обозначается ¬A. Другой термин — логическое «НЕ».
Если про каждое из высказываний A и B известно, является оно истинным или ложным, легко установить истинность их конъюнкции, дизъюнкции и отрицания. Например, если A истинно, то ¬A ложно. Если A и B оба истинны, то A∧B истинно, иначе оно ложно. И так далее. Эту информацию удобно записывать в виде табличек, которые называются таблицами истинности.
Таблица истинности для отрицания выглядит так:
A¬AИЛЛИ
Таблицы истинности для конъюнкции и дизъюнкции:
ABA∨BA∧BИИИИИЛИЛЛИИЛЛЛЛЛ
В дальнейшем нам понадобится ещё одна важная логическая операция, но пока остановимся на этих.
2.1.3Раскрытие скобок с отрицанием
Пусть A и B — какие-то высказывания. Рассмотрим высказывание ¬(A∨B), то есть отрицание высказывания A∨B. В каком случае оно истинно?
Только в том случае, когда оба высказывания A и B ложны. Действительно, если
хотя бы одно из них истинно, тогда их дизъюнкция (логическое ИЛИ) истинна и
значит её отрицание ложно. Записывая это соображение в виде формулы, получаем
такое равенство:
Действительно, если
хотя бы одно из них истинно, тогда их дизъюнкция (логическое ИЛИ) истинна и
значит её отрицание ложно. Записывая это соображение в виде формулы, получаем
такое равенство:
¬(A∨B)=(¬A)∧(¬B)=¬A∧¬B
¬(A∨B)=(¬A)∧(¬B)==¬A∧¬B
Второе равенство верно, поскольку операция отрицания имеет приоритет перед конъюнкцией, то есть в формуле ¬A∧¬B сначала выполняются отрицания, а потом конъюнкция, так что скобки вокруг ¬A и ¬B можно не писать.
Аналогично можно рассмотреть высказывание ¬(A∧B). Чтобы оно стало истинным, достаточно, чтобы хотя бы одно из высказываний A или B было ложным: тогда их конъюнкция (логическое И) ложна и её отрицание истинно. Таким образом:
¬(A∧B)=(¬A)∨(¬B)=¬A∨¬B.
¬(A∧B)=(¬A)∨(¬B)==¬A∨¬B.
Можно сказать, что при раскрытии скобок, перед которыми стоит отрицание, знак ∨ меняется на ∧ и наоборот.
Эти правила преобразования формул в алгебре логики называются законами де
Моргана.
2.1.4Логические операции в программировании
В распространённых языках программирования высказываниям соответствуют
выражения, имеющие значения типа «булевская величина» (например, в Python это bool), то есть принимающие значения «истина» или «ложь» (True и False). Например, 2 + 3 == 4 имеет значение False, а 3 > 2 — True. К булевским значениям можно применять логические операторы and, or и not. Например, 2 * 0 == 1 or 3 > 2 имеет значение True.
2.2Предикаты и кванторы
2.2.1Примеры предикатов
Выше фигурировал пример утверждения «n — чётное число». Если задать вопрос,
является оно истинным или ложным, вы скорее всего скажете, что вопрос не имеет
смысла: как можно на него ответить, если не знаешь, чему равно n? Это пример
утверждения, не являющегося высказыванием. Утверждения такого типа называются предикатами.
Утверждения такого типа называются предикатами.
Как бы определение 2. Грубо говоря, предикат — это такое утверждение, которое зависит от одной или нескольких переменных, и становится высказыванием, если задать значения этих переменных.
Пример 1. Рассмотрим предикат «n — чётное число». Его можно обозначить какой-нибудь буквой, аналогично обозначению функций — например, E(n). При подстановке конкретного n предикат становится высказыванием, которое является истинным или ложным. Например, E(2) истинно, а E(17) — ложно. Подобно функциям, у предикатов есть «область определения» — множество значений, которые могут принимать переменные. Например, давайте считать, что областью определения для E(n) является множество натуральных чисел, n∈N (но можно было бы определить аналогичный предикат и для множества всех целых чисел).
Пример 2. Определим предикат D(k,n) — «n делится на k». Этот
предикат зависит от двух переменных. Будем считать, что n∈N и k∈N. Например, D(2,3) — ложь, а D(2,4) — истина.
Пример 3. Ещё нам понадобится предикат S(x,y):=«x2=y», определенный для вещественных x и y. Он проверяет, что x2 равняется y.
Одни предикаты можно определять через другие. Например, если бы у нас был готовый предикат D, проверяющий делимость, и нам нужно было изготовить из него предикат E, проверяющий число на чётность, его легко можно было бы задать таким образом:
E(n):=D(2,n).
В следующем разделе мы познакомимся с ещё одним способом создания новых предикатов из существующих.
2.2.2Квантор всеобщности
Давайте рассмотрим предикат T(n):=D(1,n). Он проверяет, что натуральное число n делится на 1. Но все натуральные числа делятся на 1! Это можно сформулировать следующим образом: «для всех значений n предикат T(n) имеет значение „истина”». Есть специальный короткий способ записывать такого типа утверждения:
∀n T(n).
Знак ∀ (перевёрнутая буква A, от all) называется квантором
всеобщности. Он читается «для всякого».
Он читается «для всякого».
Вопрос 1. Рассмотрим утверждение ∀n E(n), где E(n) — предикат, проверяющий, что натуральное число n является чётным. Что вы можете сказать про построенное таким образом утверждение?
Оно истинно.
Неверный ответ. Вы уверены? В этом утверждении сказано: «для любого натурального n верно, что n чётно». Иными словами, это утверждение можно переписать так: «все натуральные числа — чётны».
Оно ложно.
Верный ответ. Да, потому что бывают нечётные числа. Например, E(3) — ложно.
Невозможно определить его истинность, зависит от значения n.
Неверный ответ.
Нет! В этом утверждении сказано: «для любого натурального n
верно, что n чётно». Иными словами, это утверждение можно
переписать так: «все натуральные числа — чётны». Это утверждение
попросту неверно.
2.2.3Квантор существования
Совершенными числами называются натуральные числа, которые равны сумме всех своих положительных делителей, отличных от самого числа (так называемых «собственных делителей»).
Рассмотрим предикат R(n), проверяющий, является ли натуральное число n совершенным. (Иными словами, R(n) соответствует утверждению «n — совершенное число».)
Если взять какое-то конкретное n, очень легко проверить, является ли оно совершенным. Например, число 10 имеет три собственных делителя, 5, 2 и 1, но 5+2+1=8≠10 — значит, оно не совершенное. Но существуют ли вообще совершенные числа? Иными словами, верно ли утверждение: «существует такое n, что R(n) имеет значение „истина”»?
Для формулирования таких утверждений также есть специальное короткое обозначение:
∃n R(n).
Знак ∃ (перевернутая буква E, от exists) называется квантором существования. Читается просто «существует [такое]».
Читается просто «существует [такое]».
Аналогично квантору всеобщности (см. замечание 3), квантор существования «связывает» соответствующую переменную. Утверждение ∃n R(n), хотя в нём фигурирует переменная n, не является предикатом, зависящим от n. Это просто высказывание, которое является истинным (если совершенные числа существуют), или ложным (если их нет).
Кстати, совершенные числа существуют. Например, число 6 совершенно. Это доказывает, что утверждение ∃n R(n) является истинным.
2.2.4Кванторы и отрицание
Есть обобщение законов де Моргана на формулы с кванторами. Рассмотрим какой-нибудь предикат P(x). (Например, x принадлежит множеству всех крокодилов, а P(x) проверяет, что крокодил x является красным.)
Рассмотрим высказывание ∀x P(x) («все крокодилы красные»). Чтобы его опровергнуть (то есть доказать его отрицание), достаточно предъявить какого-нибудь крокодила, который бы не был красным. Иными словами, верно равенство:
¬(∀x P(x))=(∃x ¬P(x))(2. 1)
1)
Аналогично, можно рассмотреть утверждение ∃x P(x) («существует по крайней мере один красный крокодил»). Чтобы его опровергнуть, нужно перебрать всех крокодилов, и проверить, что каждый из них не является красным. Иными словами, верно такое равенство:
¬(∃x P(x))=(∀x ¬P(x))(2.2)
Можно сказать, что при переносе знака отрицания через квантор он меняется на обратный: существование на всеобщность и наоборот.
2.3Кванторы и предикаты с несколькими переменными
2.3.1Связывание одной переменной
Рассмотрим предикат S(x,y):=«x2=y», определённый для вещественных x и y. Рассмотрим такое утверждение: ∃x S(x,y). Что это за объект?
Если задать конкретное значение y, например, y=4, получается такая штука: ∃x S(x,4), или попросту
∃x(x2=4).
Иными словами, получается высказывание о том, что существует квадратный корень
из числа 4. Это высказывание ни от чего не зависит и является верным, чтобы
его доказать, достаточно предъявить x=2.
Это высказывание ни от чего не зависит и является верным, чтобы
его доказать, достаточно предъявить x=2.
Однако, можно выбрать другое значение y, например, положить y=−1. Тогда получается утверждение
∃x(x2=−1).
Это утверждение неверно: мы знаем, что квадраты вещественных чисел неотрицательны, и значит не существует такого x, что его квадрат равен −1.
Вернёмся теперь к утверждению ∃x S(x,y). Мы видим, что в это утверждение вместо y можно подставлять различные числа и получать разные высказывания — верные и неверные. Значит, перед нами предикат, зависящий от y. Обозначим его через Q(y). Можно записать:
Q(y):=(∃x S(x,y))
Таким образом, из предиката с двумя переменными S мы получили предикат с одной
переменной y, поскольку переменную x «связали» с помощью квантора. В
высказывании ∃x S(x,y) переменная y называется «свободной»
(мы можем задавать её значения как хотим и получать разные высказывания), а
переменная x — «связанной».
2.3.2Последовательное применение кванторов
Рассмотрим предикат G(n,m):=«n>m», определенный на множестве натуральных чисел. Он проверяет, что n больше m. Введём новый предикат:
Z(m):=(∃n G(n,m))=(∃n(n>m)).
Теперь можно рассмотреть высказывание ∀m Z(m). Его можно записать так:
∀m (∃n(n>m)).(2.3)
Скобки вокруг предиката (∃n (n>m)) можно убрать, и получится такая запись:
∀m ∃n(n>m).(2.4)
Читается: «для всякого m существует такое n, что n>m».
Во-первых, нужно заметить, что получившееся утверждение не является предикатом — мы последовательно связали обе переменные и то, что получилось, уже ни от чего не зависит, это просто высказывание, которое может быть истинным или ложным.
Является ли оно истинным? Да, является. Действительно, возьмём любое m.
Заметим, что для него предикат Z(m) верен, поскольку существует такое n
(например, можно взять n=m+1), для которого n>m. (Действительно, m+1>m,
каким бы ни было m.)
(Действительно, m+1>m,
каким бы ни было m.)
Словами это высказывание можно было бы записать так: «для всякого натурального числа найдётся большее его число». Эта формулировка с точки зрения привычного нам языка выглядит немножко неестественно и может возникнуть искушение сделать её более привычной, переформулировав таким образом: «найдется натуральное число, большее любого другого натурального числа». Однако, то, что в результате получилось — не переформулировка исходного утверждения, а совсем другое высказывание. Оно формально записывается так:
∃n ∀m(n>m)(2.5)
Как видно, эта формулировка отличается от (2.4) только
порядком следования кванторов. Однако, её смысл совсем иной. При доказательстве
высказывания (2.4) мы для каждого конкретного m могли
выбирать своё n, так, чтобы сделать предикат n>m справедливым. В
высказывании (2.5) мы должны задать одно-единственное n,
такое, что для него предикат n>m был бы верен для всех возможных m. Нетрудно
видеть, что среди натуральных чисел такого n нет. Действительно, каким бы мы
ни взяли n, можно положить m=n (или m=n+1, или m=n+2 и т.д.), и предикат
n>m не будет верным. Видно, что порядок следования кванторов очень важен: он
определяет порядок, в котором соответствующие переменные могут выбираться. В
данном случае при изменении порядка кванторов получились разные результаты:
утверждение с одним порядок истинное, а с другим ложное. Так бывает не всегда
(придумайте пример, когда это не так), но важно понимать, что изменение порядка
следования кванторов создаёт другое утверждение.
Нетрудно
видеть, что среди натуральных чисел такого n нет. Действительно, каким бы мы
ни взяли n, можно положить m=n (или m=n+1, или m=n+2 и т.д.), и предикат
n>m не будет верным. Видно, что порядок следования кванторов очень важен: он
определяет порядок, в котором соответствующие переменные могут выбираться. В
данном случае при изменении порядка кванторов получились разные результаты:
утверждение с одним порядок истинное, а с другим ложное. Так бывает не всегда
(придумайте пример, когда это не так), но важно понимать, что изменение порядка
следования кванторов создаёт другое утверждение.
2.3.3Отрицание и серия кванторов
Мы уже опровергли утверждение (2.5), но давайте ещё раз более
подробно поговорим, как мы это сделали. Чтобы опровергнуть утверждение с
кванторами обычно проще всего записать к нему отрицание, а потом доказать это
отрицание.
Воспользуемся формулами из раздела 2.2.4. Обозначим предикат
∀m (n>m) через W(n). Утверждение (2. 5) можно
переписать в виде:
5) можно
переписать в виде:
¬(∃nW(n)).
Применим к нему равенство (2.2):
¬(∃nW(n))=∀n(¬W(n))=∀n(¬(∀m(n>m)))=…(2.6)
¬(∃nW(n))=∀n(¬W(n))==∀n(¬(∀m(n>m)))=…(2.6)
Теперь можно к выражению ¬(∀m (n>m)) применить формулу (2.1) и подставить результат в (2.6):
…=(∀n ∃m¬(n>m))=(∀n ∃m(n⩽m)).
Мы как бы последовательно перекинули знак отрицания сначала через первый квантор, а потом через второй. Каждый раз квантор менялся на противоположный. Наконец, отрицание оказалось записано перед предикатом n>m, но мы знаем, что отрицание к утверждение n>m — это утверждение, что n⩽m. Итак, отрицанием к высказыванию (2.5) является высказывание
∀n ∃m(n⩽m).
Докажем его. Для этого нужно научиться для всякого n предъявлять такое m,
что n⩽m. Это просто: достаточно взять, например, m=n. С тем же
успехом можно было бы взять m=n+1 или m=n+100.
2.4Импликация
Давайте рассмотрим такое утверждение: «если натуральное число делится на 4, то оно делится на 2» (обозначим его за A). Как мы знаем, это верное утверждение. Как его сформулировать на языке кванторов и предикатов? Давайте введём предикат Q(n), проверяющий, что n делится на 4. Раньше мы вводили предикат E(n), проверяющий чётность n. Поскольку речь про все натуральные числа, следует начать с квантора ∀n. Очевидно, дальше нужно написать какое-то утверждение с предикатами Q(n) и E(n), но какое?
Вероятно, здесь проще начать с отрицания. Что нам нужно было бы сделать, чтобы опровергнуть утверждение A? Нужно придумать такое n, чтобы оно делилось на 4, но при этом не делилось на 2. Именно такой контрпример, если бы он был построен, опроверг бы наше утверждение. Иными словами, нам нужно было бы предъявить такое n, что Q(n) выполняется, а E(n) нет, то есть верно утверждение Q(n)∧¬E(n). Итак, отрицание к A выглядит так:
¬A=(∃n(Q(n)∧¬E(n))).
Взяв отрицание от этой формулы, получим формулировку для исходного утверждения:
A=(∀n(¬Q(n)∨E(n))).(2.7)
Иными словами, мы утверждаем, что для всякого n выполняется следующее. Либо оно не делится на 4 (тогда ¬Q(n) является истинным: про числа, которые не делятся на 4, мы ничего не утверждаем, а если мы ничего не утверждаем, то нечему быть неверным), либо, если оно делится на 4 (то есть ¬Q(n) ложно), оно обязано делиться на 2 (чтобы вся дизъюнкция была истинной, если второй её аргумент ложный, то первый — в данном случае, E(n) — должен быть истинным).
Это ровно то, что мы хотим сказать.
Вопрос 2. Зачем городить такой огород? Почему нельзя было просто написать
∀n(E(n)∧Q(n))?(2.8)
Можно было так и написать, формулы (2.8) и (2.7) эквивалентны.
Неверный ответ.
А вот и нет. Например, утверждение A и формула
(2. 7) являются истинными, а утверждение в формуле
(2.8) ложно. Действительно, возьмём, например,
n=6. Оно не делится на 4, значит, Q(6) ложно, и значит для
этого значения n конъюнкция ложна, а раз такое n нашлось, то
и всё утверждение ложно. Проверьте, что этот пример не
опровергает утверждение (2.7).
7) являются истинными, а утверждение в формуле
(2.8) ложно. Действительно, возьмём, например,
n=6. Оно не делится на 4, значит, Q(6) ложно, и значит для
этого значения n конъюнкция ложна, а раз такое n нашлось, то
и всё утверждение ложно. Проверьте, что этот пример не
опровергает утверждение (2.7).
Потому что это совсем другое утверждение, оно не эквивалентно A.
Верный ответ. Так и есть. Например, утверждение A и формула (2.7) являются истинными, а утверждение в формуле (2.8) ложно. Действительно, возьмём, например, n=6. Оно не делится на 4, значит, Q(6) ложно, и значит для этого значения n конъюнкция ложна, а раз такое n нашлось, то и всё утверждение ложно. Проверьте, что этот пример не опровергает утверждение (2.7).
В общем виде это формулируется так. Пусть есть два высказывания, A и B.
Утверждения «из A следует B» или «A влечёт B» или «если A
истинно, то B тоже истинно», формально записываются как ¬A∨B. Иными словами, говоря «если A истинно, то B тоже истинно», мы
говорим, что A может и не быть истинным, но нас этот случай, не интересует, мы
про него никаких выводов не делаем (а значит, и ошибаться не можем), но если уж
A истинно, то B обязано быть истинным.
Иными словами, говоря «если A истинно, то B тоже истинно», мы
говорим, что A может и не быть истинным, но нас этот случай, не интересует, мы
про него никаких выводов не делаем (а значит, и ошибаться не можем), но если уж
A истинно, то B обязано быть истинным.
Эта операция с высказываниями A и B настолько важна, что хотя она и выражается через конъюнкцию, дизъюнкцию и отрицание, у него есть специальное название — импликация (ср. с английским словом imply, влечёт), и специальное обозначение: A⇒B. Утверждение A называется посылкой, а утверждение B — заключением.
Давайте построим таблицу истинности для A⇒B (то есть ¬A∨B).
ABA⇒BИИИИЛЛЛИИЛЛИ
Эта таблица, и особенно её третья строчка, обычно ставит в тупик всех, кто её в
первый раз видит. «Из лжи следует истина!» — как такое может быть? Дело в том,
что если вы делаете утверждение A⇒B («Если A истинно, то B
тоже истинно»), и A оказалось ложным, то это просто означает, что вы
находитесь в ситуации, про которую вы ничего не утверждали. А раз ничего не
утверждали, то не могли и ошибиться. И значит вы правы (ваше утверждение
истинно), вне зависимости от того, является ли B истинным или ложным.
А раз ничего не
утверждали, то не могли и ошибиться. И значит вы правы (ваше утверждение
истинно), вне зависимости от того, является ли B истинным или ложным.
Возвращаясь к примеру, который мы разбирали раньше: «если число n делится на 4, то оно чётное». Рассмотрим число n=6. Для него посылка оказалась ложной (оно не делится на 4), и хотя заключение оказалось истинным (оно чётно), это никак не противоречит нашей импликации: она остаётся верна и в этом случае.
В дальнейшем мы будем постоянно пользоваться импликацией в доказательствах. Начнём прямо со следующей лекции.
2.5Применение языка матлогики в этой книге
2.5.1Формальный и естественный язык
Обозначения математической логики, которые мы ввели выше, позволяют записывать
утверждения и даже их доказательства в виде длинных формул, состоящих из
кванторов и предикатов. Они хороши своей чёткостью и однозначностью:
после того, как утверждение записано на этом формальном языке, прочитать его можно
единственным образом, а доказательство может проверить (или, в некоторых
случаях, даже придумать) и компьютер, пользуясь чисто формальными правилами,
описывающими допустимые преобразования одних строчек символов в другие.
Когда я учился на первом курсе и только познакомился с этим языком, я был им очарован: какое-то время мне казалось, что достаточно записать любое утверждение «в кванторах», и дальше станет понятно, как его доказывать. Однако очень быстро я обнаружил, что это не так: формальная запись иногда упрощает некоторые логические переходы, и она часто необходима, чтобы убедиться в правильности доказательства, но чтобы придумать доказательство, нужно проникнуть в суть утверждения, а не просто манипулировать строчками с кванторами.
При этом «суть», то есть идеи, стоящие за математическими рассуждениями, как
правило проще передавать, пользуясь преимущественно естественным языком, а не
формальным. В конце концов, профессиональные математики пишут научные статьи
именно на естественном языке, используя формальный лишь там, где это
действительно необходимо. Что уж говорить об учебнике, читатели которого видят
все эти кванторы впервые в жизни! Так что пусть вас не пугает обилие новых
обозначений и понятий в этой главе: мы будем ими пользоваться и их нужно
освоить, но все утверждения, сформулированные формально, мы будем подробно
комментировать «по-человечески».
2.5.2Сокращённые обозначения
Чтобы немножко упростить обозначения в формулах с кванторами и приблизить их к естественному языку, я разрешу себе чуть-чуть отступить от правил формального языка, введённого выше. Во-первых, часто после серии кванторов я буду ставить двоеточие — например, вместо
∀x ∃y(x<y)
буду писать
∀x ∃y:x<y.
Двоеточие тут не несёт никакой содержательной нагрузки и служит просто для визуального отделения предиката, на который навешиваются кванторы. Оно также будет заменять скобки — например, в высказывании
∀x ∃y:x≠0⇒xy=1(2.9)
кванторы навешиваются целиком на предикат (x≠0⇒xy=1), а не только на часть x≠0. Иными словами, эта запись эквивалентна такой:
∀x ∃y(x≠0⇒xy=1).
Во-вторых, я буду зачастую писать условие, которому должно удовлетворять
значение переменной, сразу после квантора. Например, утверждение (2.9)
можно записать так:
Например, утверждение (2.9)
можно записать так:
∀x≠0 ∃y:xy=1.
Аналогично я часто буду указывать, из каких множеств допустимо брать значения переменных. Например, если бы я хотел сказать, что для любого натурального числа найдётся такое рациональное число, что их произведение больше 9, то записал бы это так:
∀x∈N ∃y∈Q:xy>9.
Формально более аккуратная, но громоздкая запись этого же утверждения звучит следующим образом:
∀x ∃y(x∈N⇒(y∈Q∧xy>9)).(2.10)
Вопрос 3. Останется ли это утверждение верным, если заменить условие x∈N на условие x∈Z?
Да.
Неверный ответ. Прямо-таки для любого целого числа вы можете найти рациональное, чтобы их произведение было больше 9? Гм… А какие ненатуральные целые числа вы знаете? Приведите пару примеров.
Нет.
Верный ответ. Конечно, достаточно взять x=0
Конечно, достаточно взять x=0
Вопрос 4. Останется ли это это утверждение верным, если заменить условие y∈Q на условие y<0?
Да.
Неверный ответ. Какой знак имеет произведение натурального числа и отрицательного?
Нет.
Верный ответ. Конечно, произведение натурального числа и отрицательного всегда отрицательно и не может быть больше 9.
Условия, записываемые после квантора существования, в более подробной записи приписываются к предикату через конъюнкцию (потому что нам нужно, чтобы существовало значение переменной, удовлетворяющей условию, и предикат был бы верен), а те, что идут после квантора всеобщности — через импликацию (потому что мы утверждаем, что предикат верен для всех значения переменной, удовлетворяющей условию, а для тех, кто не удовлетворяют, ничего не утверждаем).
Упражнение 1. Запишите отрицание к утверждению (2.10), пользуясь правилами переноса
отрицания через кванторы и законами де Моргана. Запишите получившееся
утверждение в краткой форме, размещая условия сразу после кванторов. Что
происходит с этими условиями при переносе через них отрицания — меняются ли
они?
Запишите отрицание к утверждению (2.10), пользуясь правилами переноса
отрицания через кванторы и законами де Моргана. Запишите получившееся
утверждение в краткой форме, размещая условия сразу после кванторов. Что
происходит с этими условиями при переносе через них отрицания — меняются ли
они?
2.6Заключение
Теперь у нас есть математический аппарат, своего рода язык, который позволяет аккуратно записывать и даже в какой-то мере автоматически анализировать довольно сложные утверждения. Мы рассматривали самые простые примеры, чтобы было понятно, как работает «механика» математической логики. Совсем скоро мы будем использовать её в условиях реальных математических задач.
← Предыдущая глава Следующая глава →
Знать определение, список, свойства, нечетные простые числа
Нечетные числа противоположны четным числам. Определение четных и нечетных чисел является важным навыком для молодежи, чтобы лучше понять нашу систему счисления и подготовиться к операциям с целыми числами. Это также поможет детям в изучении деления, простых чисел и квадратных корней. В этой статье мы изучим, что такое нечетное число, определение нечетного числа, список нечетных чисел, нечетные числа от 1 до 100, нечетные и четные числа, сумму нечетных чисел, сумму первых n нечетных чисел, все ли простые числа нечетные, что нечетное простое число, Свойства нечетного числа, Решенные примеры с нечетными числами и часто задаваемые вопросы
Это также поможет детям в изучении деления, простых чисел и квадратных корней. В этой статье мы изучим, что такое нечетное число, определение нечетного числа, список нечетных чисел, нечетные числа от 1 до 100, нечетные и четные числа, сумму нечетных чисел, сумму первых n нечетных чисел, все ли простые числа нечетные, что нечетное простое число, Свойства нечетного числа, Решенные примеры с нечетными числами и часто задаваемые вопросы
Нечетные числа
Числа, которые нельзя разделить на пары поровну, называются нечетными. Когда вы делите нечетные целые числа на два, вы получаете остаток от единицы. Вместо единиц в нечетных числах стоят цифры 1, 3, 5, 7 или 9. Нечетные числа — это целые числа, которые при делении на два всегда оставляют остаток. Это целые числа типа n = 2k + 1, где k — натуральное число. К нечетным числам относятся такие числа, как 51, 733, 55, 97 и так далее.
Определение нечетных чисел
Нечетные числа являются частью системы счисления. Понимание нечетных чисел является базовой математикой и важной темой алгебры. Нечетные числа определяются как числа, которые не делятся точно на два. Или, другими словами, нечетное число — это число, которое не является четным и не делится на два.
Понимание нечетных чисел является базовой математикой и важной темой алгебры. Нечетные числа определяются как числа, которые не делятся точно на два. Или, другими словами, нечетное число — это число, которое не является четным и не делится на два.
Например, 13 не делится точно на два, так как при делении на два остается единица. В результате 13 — необычное число.
Нечетные числа не являются двузначными кратными.
Например, умножение 2 на любое другое число не даст 1, 3, 5, 7, 9, 11, 13, 15,……, 51, 53,…… и так далее. Это нечетное число. Таким образом, нечетные числа оканчиваются на 1, 3, 5, 7 и 9.
Список нечетных чисел
Мы можем легко идентифицировать нечетные числа от 1 до 10, от 1 до 20, от 1 до 50 и от 1 до 100. Знание нечетных чисел между этими диапазонами поможет вам решить многие математические задачи. Вы можете легко решать такие задачи, как GCD, LCM, факторизация и т. д.
Список нечетных чисел от 1 до 10
Пять нечетных чисел от 1 до 10. Список четных чисел от 1 до 10: 1, 3, 5, 7 и 9.
Список четных чисел от 1 до 10: 1, 3, 5, 7 и 9.
Список нечетных номеров между 1 до 200023
Списки. числа от 1 до 20: 1, 3, 5, 7, 9, 11, 13, 15, 17, and 19.
| Odd Numbers from 1-20 | |
| 1 | 11 |
| 3 | 13 |
| 5 | 15 |
| 7 | 17 |
| 19 | |
Список нечетных чисел между 1-50 2
. 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47 и 49.
| Нечетные числа from 1-50 | ||||
| 1 | 11 | 21 | 31 | 41 |
| 3 | 13 | 23 | 33 | 43 |
| 5 | 15 | 25 | 35 | 45 |
| 7 | 17 | 27 | 37 | 47 |
| 19 | 29 | 39 | 49 | |
СПИСОК ОДНА.
 до 100: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97 и 99.
до 100: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97 и 99.| Odd Numbers from 1-100 | ||||
| 1 | 21 | 41 | 61 | 81 |
| 3 | 23 | 43 | 63 | 83 |
| 5 | 25 | 45 | 65 | 85 |
| 7 | 27 | 47 | 67 | 87 |
| 9 | 29 | 49 | 69 | 89 |
| 11 | 31 | 51 | 71 | 91 |
| 13 | 33 | 53 | 73 | 93 |
| 15 | 35 | 55 | 75 | 95 |
| 17 | 37 | 57 | 77 | 97 |
| 19 | 39 | 59 | 79 | 99 |
Properties of Odd Numbers
Некоторые из важных свойств нечетных чисел приведены ниже:
- Свойство сложения двух нечетных чисел гласит, что когда мы складываем два нечетных числа, результатом всегда является четное число.
 Например: 7 + 3 = 10
Например: 7 + 3 = 10 - Свойство вычитания двух нечетных чисел гласит, что при вычитании двух нечетных чисел результатом всегда будет четное число. Например: 7 – 3 = 4
- Свойство сложения одного нечетного и одного четного числа гласит, что когда мы складываем четное число и нечетное число, результат всегда будет нечетным. Например: 9 + 4 = 13
- Свойство вычитания одного нечетного и одного четного числа гласит, что w когда мы вычитаем четное число и нечетное число, результат всегда будет нечетным. Например: 9 – 4 = 5
- Свойство сложения двух четных чисел гласит, что при сложении двух четных чисел результатом всегда будет четное число. Например: 10 + 4 = 14
- Свойство вычитания двух четных чисел гласит, что при вычитании двух четных чисел результатом всегда будет четное число. Например: 10 – 4 = 6
- Свойство умножения двух нечетных чисел гласит, что при умножении двух нечетных чисел результатом всегда будет нечетное число.
 Например: 7 × 5 = 35
Например: 7 × 5 = 35 - Свойство умножения одного нечетного и одного четного числа гласит, что когда мы умножаем четное число на нечетное число, результатом всегда будет четное число. Например: 7 × 6 = 42
- Свойство умножения двух четных чисел гласит, что при умножении двух четных чисел всегда получается четное число. Например: 10 × 4 = 40
Разница между нечетными и четными числами
Разница между нечетным числом и четным числом составляет следующее:
| нечетные числа | даже числа | .
| Целое число, которое нельзя разделить на 2, является нечетным числом | Целое число, которое можно разделить на 2, является четным числом. |
| При делении на нечетное число остается напоминание 1 | При делении на четное число остается напоминание 0 |
Все числа, оканчивающиеся на 1, 3, 5, 7 и 9, являются нечетными. | Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными. |
| Нечетные числа не могут быть сгруппированы в пары. | Четные числа можно объединять в пары. |
| Если последняя цифра заданного числа нечетная, число нечетное. | Если последняя цифра заданного числа четная, то число четное. |
Решенные примеры с нечетными числами
Теперь давайте посмотрим на некоторые решенные примеры с нечетными числами, которые часто задают на многих экзаменах.
Решено Пример: Как проверить, является ли число четным или нечетным?
Решение:
Есть два способа определить, является число четным или нечетным. Они следующие:
1. В месте нахождения единицы проверьте цифру числа:
Чтобы определить, является ли число нечетным или четным, мы должны проверить его на позиции «единицы» или «единицы» или последнюю цифру числа. число.
число.
Нечетные числа — это те, которые заканчиваются цифрами 1,3,5,7 и 9.
7,11,283,5735,9859 и так далее.
Данное число является нечетным, поскольку число 2835 оканчивается цифрой 5 (нечетное число).
Кроме того, четными считаются числа, оканчивающиеся цифрами 0, 2, 4, 6 и 8.
Данное число является четным, так как число 2838 оканчивается цифрой 8 (четное число)
2. По группировке:
Всего на этом рисунке 11 точек. Все точки не связаны. На картинке не хватает одной точки.
Нечетные числа — это числа, которые нельзя поставить вместе парами.
Нечетные числа — это любые числа, которые не делятся точно на два.
Теперь 12 точек. Поскольку все точки парные и не осталось ни одной непарной точки, мы можем заключить, что 12 — четное число.
Мы можем сделать вывод, что четные числа — это все те, которые можно разделить на пары.
Решено Пример: Найдите четыре последовательных нечетных числа, сумма которых равна 152.
Решение:
Если мы начнем с нечетного числа и каждое число в последовательности на 2 больше предыдущего, то мы получат последовательные нечетные целые числа. Пусть первое нечетное число равно n. Следующие три последовательных нечетных числа: (n + 2), (n + 4) и (n + 6) 9.0003
Следовательно,
n + (n + 2) + (n + 4) + (n + 6) = 152
n + n + 2 + n + 4 + n + 6 = 152
4n + 12 = 152
4n = 140
n = 35.
Остальные числа
(n + 2) = 35 + 2 = 37
(n + 4) = 35 + 4 = 39
3 и (9 n + 6) = 35 + 6 = 41
Следовательно, последовательные нечетные числа равны 35, 37, 39 и 41.
Решено Пример: Длины сторон треугольника являются последовательными нечетными числами. Какова длина наибольшей стороны, если периметр равен 45?
Решение: Будучи последовательным нечетным числом, нам нужно добавить 2 к предыдущему числу. Пусть первое нечетное число будет х. Следующие два последовательных нечетных числа равны (x + 2) и (x + 4).
Следующие два последовательных нечетных числа равны (x + 2) и (x + 4).
Периметр треугольника = сумма трех сторон
45 = x + x + 2 + x + 4
45 = 3x + 6
3x = 45 – 6
3x = 39
x = 13
Длина самого длинного = 13 + 4 = 17
Надеюсь, что эта статья о нечетных числах была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о нечетных числах
В.1 Как вы решаете нечетные числа?
Ответ 1 Чтобы определить, является ли число нечетным или четным, мы должны проверить его на позиции «единицы» или «единицы» или последнюю цифру числа. Нечетные числа — это числа, оканчивающиеся на цифры 1,3,5,7 и 9.. 7,11,283,5735,9859 и так далее. Предоставленное число является нечетным, так как число 2835 заканчивается цифрой 5 (нечетное число). Кроме того, четные числа — это те, которые заканчиваются цифрами 0, 2, 4, 6 и 8. Предоставленное число является четным числом, поскольку число 2838 заканчивается цифрой 8 (четное число).
Предоставленное число является четным числом, поскольку число 2838 заканчивается цифрой 8 (четное число).
Q.2 Что такое нечетные числа с примерами?
Ответ 2 Нечетные числа определяются как числа, которые не делятся точно на два. Или, другими словами, нечетное число — это число, которое не является четным и не делится на два. Например, 13 точно не делится на два, так как при делении на два остается один. В результате 13 — необычное число. Нечетные числа не являются двузначными кратными. Например, умножение 2 на любое другое число не даст 1, 3, 5, 7, 9., 11, 13,
Q.3 Что такое нечетное число, приведите 10 примеров?
Ответ 3 1, 3, 5, 7, 9, 11, 13, 15, 17 и 19. Числа, которые нельзя разделить на пары поровну, называются нечетными. Когда вы делите нечетные целые числа на два, вы получаете остаток от единицы. Вместо единиц в нечетных числах стоят цифры 1, 3, 5, 7 или 9. Нечетные числа — это целые числа, которые при делении на два всегда оставляют остаток. Это целые числа типа n = 2k + 1, где k — натуральное число. Нечетное число включает такие числа, как 51, 733, 55, 9.7 и так далее.
Это целые числа типа n = 2k + 1, где k — натуральное число. Нечетное число включает такие числа, как 51, 733, 55, 9.7 и так далее.
В.4 Все ли простые числа нечетные?
Ответ 4 Простые числа — это положительное целое число, которое не делится без остатка ни на какое целое число, кроме самого себя и 1. Простое число нельзя разделить ни на какое другое число без остатка. За исключением числа 2, все простые числа нечетные, так как четное число делится на 2, что делает его составным. Следовательно, расстояние между любыми двумя простыми числами в строке не меньше 2,9.0003
В.5 Четное или нечетное число?
Ответ 5 Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными числами. Например, такие числа, как 14, 26, 32, 40 и 88, являются четными числами. Если мы разделим число на две группы с равным количеством элементов в каждой, то число будет четным числом. В начальной школе детей учат понятию четного числа, чтобы различать четное и нечетное число. С другой стороны, нечетные числа — это целые числа, которые не делятся на 2 или оканчиваются на 1, 3, 5, 7 и 9..
С другой стороны, нечетные числа — это целые числа, которые не делятся на 2 или оканчиваются на 1, 3, 5, 7 и 9..
| Четные числа: определение, список четных чисел, свойства на примерах! |
| Простые числа с определением, взаимно простые, нечетные и четные простые числа |
| Производная от arcsinx с доказательством и формулой Коэффициент корреляции: свойства и решенный пример |
Нечетные и четные числа — Числа | Термин 3 Глава 1
Числа, которые можно полностью составить по двое, называются четными. Предметы, которые нельзя полностью расположить по двое, называются нечетными числами.
ЕДИНИЦА 1
Numbers
Odd and Even numbers
Проезд через
Пары
Некоторые объекты
которые доступны парами, приведены ниже.
Ключевые слова: Пара, Нечетный, Четный объекты с одинаковыми свойствами. Например, набор из двух ножных браслетов, набор из двух браслеты.
Номера числа, которые можно полностью расположить по двое, называются четными числами.
Здесь 6 птиц составляют 3 пары по двое. Итак, 6 есть четное число.
Объекты числа, которые нельзя полностью разложить по два, называются нечетными числами.
Здесь из 5 птиц можно сделать 2 сета по двое. Но осталась 1 птица.
Следовательно, 5 — нечетное число.
Практика
Группа объекты по двое и найти, являются ли они четными или странный. Один сделан для вас.
Ответ:
10 даже
7 ODD
8 даже
13 ODD
Learn
Дайте нам
разложите данные семена попарно в соответствии с номером и проверьте,
являются нечетными или четными.
Откуда приведенной выше таблицы, можно сделать вывод, что числа 1,3,5,7,9,11,13,15,17,19 и т. д. имеют один набор семян, которые не могут быть расположены по два, и они называются нечетными числами.
числа 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 имеют все семена, расположенные по двое, и поэтому они называются четными числами.
Посмотреть нечетные числа, указанные выше. Эти числа имеют любое из чисел 1,3,5,7 и 9 на своем месте.
Посмотреть четные числа, указанные выше. Эти числа имеют любое из чисел 2,4,6,8 и 0 на их месте.
Кроме того, мы можем заметить, что нечетные и четные числа приезжайте как вариант.
Игра
* В эту игру играют два игрока, используя семена тамаринда. Сначала семена тамаринда делят на две равные группы. Позволять игрок 1 берет горсть семян из одной из групп, а игрок 2 угадывает является ли количество семян в его руке четным или нечетным.
* Как только игрок 2 дает ответ как нечетный или
даже. Игрок 1 раскладывает семена, находящиеся у него в руках, попарно, чтобы проверить
отвечать.
Игрок 1 раскладывает семена, находящиеся у него в руках, попарно, чтобы проверить
отвечать.
* Если предположение игрока 2 верно, игрок 1 отдает все семена в своей руке игроку 2 и дает возможность сыграть переходит к игроку 2.
* Если предположение, сделанное игроком 2 неверно, игрок 2 должен дать равное количество семян игроку 1 и следующий шанс игра будет предоставлена игроку 1.
* Игра продолжается таким образом, и игрок с большим количеством семян выигрывает игру.
Практика
I. Обведите/подчеркните нечетное число и отметьте четное число.
i) 71 , 64 ✔, 45 , 82 ✔
ii) 9 , 7 , 11 , 8✔
iii) 10✔, 17 , 27 , 16✔
IV) 94✔, 37 , 26✔, 69
В) 25 , 52✔, 81 , 18✔
Vi) 16✔, 81 , 18✔
Vi) 16✔, , 18✔
Vi) 16✔, 81 , 18✔
Vi) 16✔, 81 , 18✔
Vi) 16✔, 81 , 18✔
Vi) 16. 0608 21 , 33 , 30✔
0608 21 , 33 , 30✔
VII) 88✔, 74✔, 11 , 53
VIII) 13 , 92✔, 74✔, 6663
) 18✔, 83 , 86✔
х) 96✔, 69 , 72✔, 27
II. Запишите следующие пять четных чисел.
i) 24, 26, 28, 30, 32, 34, 36
ii) 40, 42, 44, 46, 48, 50, 52 9, iii) , iii)0608 92, 94, 96, 98, 100
iv) 8, 10, 12, 14, 16, 18, 20
v) 66, 68, 70, 72, 76, 74, 74 78
III. Запишите следующие пять нечетных чисел.
i) 7, 9, 11, 13, 15, 17, 19, 21
ii) 21, 23, 25, 27, 29, 31, 33 5 09, 8, iii 87, 89, 91, 93, 95
iv) 49, 51, 53, 55, 57, 59, 61
v) 71, 73, 75, 77, 79, 81, 83
Попробуйте
Рамья
хочет составить все возможные двузначные числа, используя только нечетных чисел. Помогите ей составить двузначные числа, используя
1,3,5,7,9.
Помогите ей составить двузначные числа, используя
1,3,5,7,9.
11,13,15,17,19,31,33,35,37,39,51,53,55,57,59,71,73,75,77,79,91,73,75,77 ,79
Есть 25 количество нечетных двузначных чисел.
Кавита хочет составить все возможные двузначные числа, используя только даже номеров. Помогите ей составить двузначные числа, используя 0,2,4,6,8.
20,22,24,26,28,40,42,44,46,48,60,62,64,66,68,80,82,84,86,88
Есть 20 число даже двузначных чисел.
Время удовольствия
Числовая таблица 1-99
Изучите числовую таблицу и ответьте на следующие вопросы. вопросы.
i) Напишите все нечетные числа от 30 до 60.
31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59
ii) Напишите все четные числа от 70 до 99.
72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98
iii) Запишите все
нечетные числа от 1 до 40.
3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39,
iv) Начиная с 10, раскрасьте числа, пропуская счет десятками. Что можно сказать об этих цифрах.
10, 20, 30, 40, 50, 60, 70, 80, 90 Четное число
v) Закрасьте нечетное цифры на диаграмме синим цветом. Обратите внимание на неокрашенные числа. Что вы можете сказать о них.
Четный номера
Попробуйте
Использование данные цифры, образуют все возможные двузначные нечетные числа без повторения цифры.
1) 3,6 63
2) 8,1 8 1
3) 5,2 25
4) 9,4 49
5) 0,7 нет ответ
6) 5,1 15
Среди
пары цифр, приведенной выше, существует ли какая-либо пара чисел, с которой вы не можете
образовать двузначное нечетное число? Напишите такую пару цифр. Ответ: 0,7
Ответ: 0,7
Теги : Числа | Срок 3 Глава 1 | 2-й курс математики, 2-й курс математики: семестр 3, раздел 1: Числа
Учебный материал, конспекты лекций, задание, справочник, описание вики, краткое описание
2-й курс математики: семестр 3, раздел 1: Числа: нечетные и четные числа | Числа | Срок 3 Глава 1 | 2-я математика
Обучение математике: четные и нечетные числа
Скрыть все ответы Скрыть все ответы Просмотреть все ответы Просмотреть все ответы Распечатать Попробуйте викторину
| Введите ответы в поля ввода. |
1. Сколько существует трехзначных нечетных чисел?
Ответ: Ответ: 450
Существует 900 трехзначных чисел, начинающихся со 100 и заканчивающихся на 999. Половина из них — нечетные числа, а половина — четные числа.
2. Какое наибольшее трехзначное нечетное число можно составить из цифр 6, 8 и 9 только один раз?
Ответ: Ответ: 869
Чтобы число было нечетным, оно должно оканчиваться на 9. Если расположить остальные две цифры в порядке убывания, то наибольшее трехзначное нечетное число окажется равным 869.
Если расположить остальные две цифры в порядке убывания, то наибольшее трехзначное нечетное число окажется равным 869.
3. Сколько существует двузначных четных чисел?
Ответ: Ответ: 45
Существует 90 двузначных чисел, начинающихся с 10 и заканчивающихся на 99. Половина из них — четные числа, а половина — четные числа.
4. Какое наименьшее четырехзначное четное число можно составить из цифр 6, 7, 8 и 9 только один раз?
Ответ: Ответ: 6798
При расположении цифр в порядке возрастания наименьшее число, которое можно получить, равно 6789 (это нечетное число). При замене двух последних цифр следующим числом будет 6798.
5. Какое из следующих чисел является наименьшим нечетным числом: 989, 567, 456, 322?
Ответ: Ответ: 567
Четные числа 322 и 456. Нечетные числа 567 и 989. Итак, наименьшее нечетное число 567.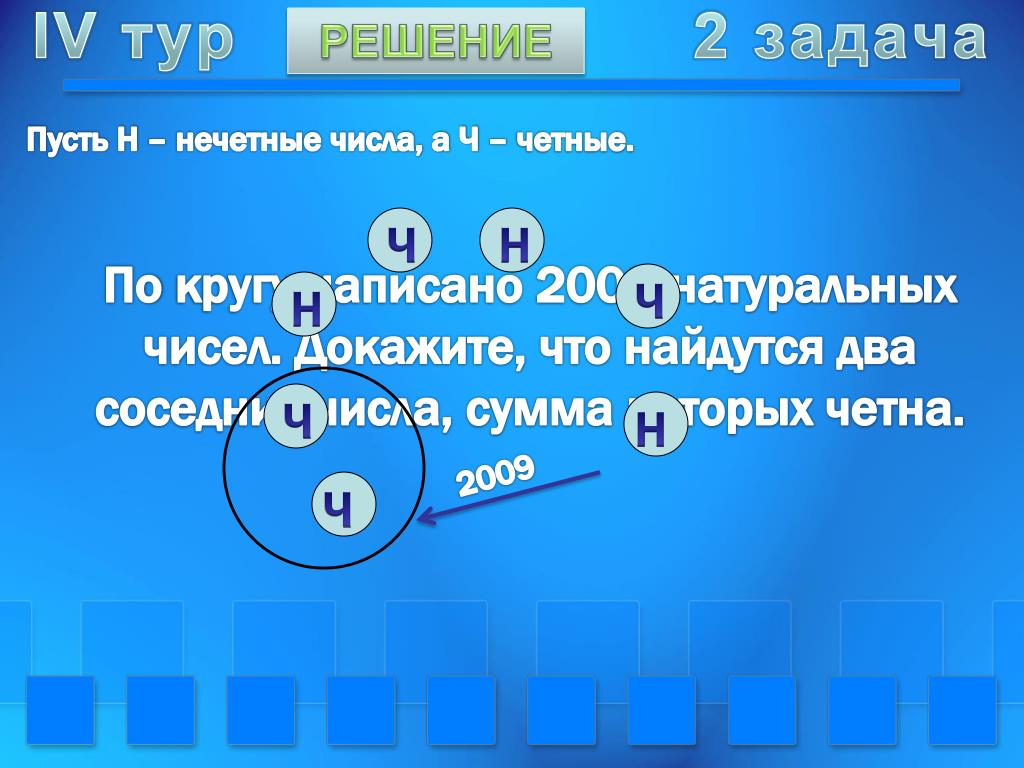
6. Какое из следующих чисел является наибольшим четным числом: 678, 786, 768, 867?
Ответ: Ответ: 786
Из четных чисел (678, 768, 786) наибольшее число равно 786.
7. Какое из следующих чисел является наибольшим четным: 2604?
Ответ: Ответ: 2640
2640 > 2604 > 2406 > 2046.
8. Какое 13-е четное число после 89?
Ответ: Ответ: 114
Следующее четное число после 89 — 90. 12-е четное число после 90 будет 90 + (12 × 2) = 114.
9. Сколькими способами можно выразить 48 как произведение двух четных чисел?
Ответ: Ответ: 3
3 способа выразить 48 в виде произведения двух четных чисел: 2 × 24, 4 × 12, 6 × 8. Четвертый способ — 3 × 16, но 3 — нечетное число.
10. Какое 103-е четное число после 118?
Ответ: Ответ: 324
103-е четное число после 118 будет 118 + (103 × 2) = 324.
11. Какое 14-е нечетное число после 192?
Ответ: Ответ: 219
Следующее нечетное число после 192 — 193. 13-е нечетное число после 193 будет 193 + (13 × 2) = 219.
12. Какое 106-е нечетное число после 292 ?
Ответ: Ответ: 503
Следующее нечетное число после 292 — 293. 105-е нечетное число после 293 будет 293 + (105 × 2) = 503.
13. Какое из следующих чисел при умножении на 5 дает нечетное число: 88 , 76, 97, 66?
Ответ: Ответ: 97
Когда число умножается на 5, получается число с 0 или 5 в разряде единиц. Только нечетное число при умножении на 5 дает нечетное число с 5 на месте единиц.
14. Какое из следующих чисел при делении на 2 оставляет в остатке 1: 5626, 6233, 7568, 8970?
Ответ: Ответ: 6233
Только нечетное число при делении на 2 оставляет 1 в остатке.
15. Если сумму двух нечетных чисел разделить на 2, какой будет остаток?
Ответ: Ответ: 0
Сумма двух нечетных чисел всегда будет четным числом. Если четное число разделить на 2, то в остатке будет 0.
16. Что нужно прибавить к 197, чтобы получить последовательно после него третье нечетное число?
Ответ: Ответ: 6
Третье нечетное число после 197 — это 203. Обратите внимание, что 197 + 6 = 203.
17. Что нужно добавить к 198, чтобы получить четвертое нечетное число после него?
Ответ: Ответ: 7
Четвертое нечетное число после 198 — это 205. Обратите внимание, что 198 + 7 = 205.
18. В каком из следующих чисел сумма цифр является четным числом: 9574 , 8313, 7685, 6924?
Ответ: Ответ: 7685
9 + 5 + 7 + 4 = 25. с с с 8 + 3 + 1 + 3 = 15,
7 + 6 + 8 + 5 = 26. s s s 6 + 9 + 2 + 4 = 21.
s s s 6 + 9 + 2 + 4 = 21.
Сумма цифр в числе 7685 равна 26 (четное число).
19. Какова сумма нечетных чисел от 30 до 40?
Ответ: Ответ: 175
Нечетные числа от 30 до 40 равны 31, 33, 35, 37, 39. Их сумма равна (30 × 5) + (1 + 3 + 5 + 7 + 9) = 150 + 25 = 175. Обратите внимание, что 175 просто в 5 раз больше среднего числа (т. е. 5 × 35 = 175).
20. Какова сумма четных чисел от 41 до 51?
Ответ: Ответ: 230
Четные числа между 41 и 51 — это 42, 44, 46, 48, 50. Их сумма равна (40 × 5) + (2 + 4 + 6 + 8 + 10) = 200 + 30 = 230. Обратите внимание, что 230 просто в 5 раз больше среднего числа (т. е. 5 × 46 = 230).
21. Чему равна сумма шестого, седьмого и восьмого четных чисел после 70?
Ответ: Ответ: 252
Шестое, седьмое и восьмое четные числа после 70 равны 82, 84, 86. Их сумма равна (80 × 3) + (2 + 4 + 6) = 240 + 12 = 252.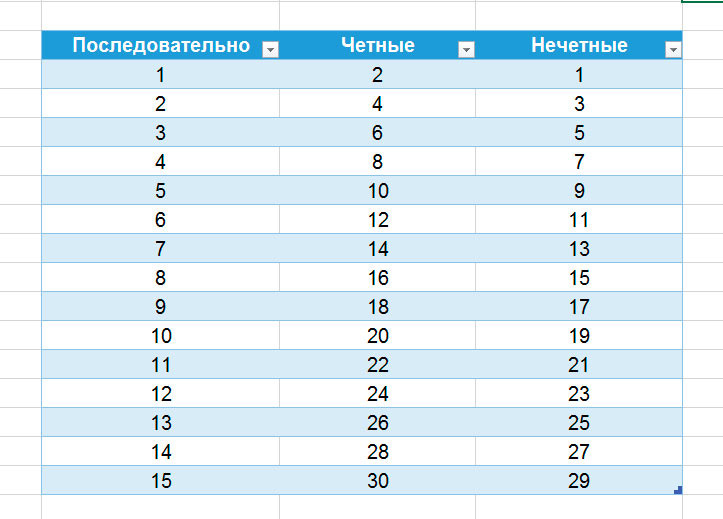
22. Чему равна сумма шестого, седьмого, восьмого и девятого нечетных чисел после 30?
Ответ: Ответ: 176
Шестое, седьмое, восьмое и девятое нечетные числа после 30 равны 41, 43, 45, 47. Их сумма равна (40 × 4) + (1 + 3 + 5 + 7) = 160 + 16 = 176.
23. В чем разница между 23-м и 26-м нечетными числами после 25?
Ответ: Ответ: 6
Разница между последовательными нечетными числами равна 2. Следовательно, разница между 23-м и 26-м нечетными числами будет 2 × (26 − 23) = 6,
24. В чем разница между 17-м и 21-м четными числами после 250?
Ответ: Ответ: 8
Разница между последовательными четными числами равна 2. Следовательно, разница между 17-м и 21-м четными числами будет 2 × (21 − 17) = 8.
25. Что такое разница между суммой четных чисел и суммой нечетных чисел между 20 и 31?
Ответ: Ответ: 5
Четные числа 22, 24, 26, 28, 30. Нечетные числа 21, 23, 25, 27, 29. Таким образом, ответ равен
Нечетные числа 21, 23, 25, 27, 29. Таким образом, ответ равен
(22 + 24 + 26 + 28 + 30) − (21 + 23 + 25 + 27 + 29)
= (22 − 21) + (24 − 23) + (26 − 25) + ( 28 − 27) + (30 − 29)
= 1 + 1 + 1 + 1 + 1 = 5.
26. Какова сумма наибольшего четырехзначного нечетного числа и наибольшего трехзначного четного числа ?
Ответ: Ответ: 10997
Наибольшее четырехзначное нечетное число 9999. Наибольшее трехзначное четное число равно 998. Их сумма равна 10997.
27. Чем отличается наибольшее четырехзначное число четное число и наименьшее четырехзначное нечетное число?
Ответ: Ответ: 8997
Самое большое четырехзначное четное число 9998. Наименьшее четырехзначное нечетное число 1001. Их разница 8997.
28. Чему равна сумма 30-го и 50-го четных числа после 26?
Ответ: Ответ: 212
30-е четное число после 26 равно 26 + (2 × 30). 50-е четное число после 26 равно 26 + (2 × 50). Их сумма дает
50-е четное число после 26 равно 26 + (2 × 50). Их сумма дает
(2 × 26) + (2 × 30) + (2 × 50)
= 2 (26 + 30 + 50) = 2 × 106 = 212.
29. Используя каждую из цифр 0, 5, 7 только один раз, сколько трехзначных нечетных чисел можно составить?
Ответ: Ответ: 2
Можно составить 2 трехзначных нечетных числа: 507 и 705. числа можно составить?
Ответ: Ответ: 4
Можно составить 4 трехзначных четных числа: 236, 326, 362 и 632.
Попробуйте пройти викторину : Изучение математики: четные и нечетные числа
Свойства чисел — четные и нечетные | Prime
Здравствуйте, читатель,
Мы видим, что вы хотите знать основы и свойства чисел.
Вы приземлились как раз в нужном месте.
Цель статьи:
В этой статье
- Вы получите более глубокое представление о поведении чисел и их операциях
- Вы также узнаете несколько фактов о свойствах чисел.

Итак, приступим непосредственно к статье.
Четные числа
- Любое целое число, кратное 2, является четным числом.
- Итак, любое целое число в форме 2k, где k — целое число, является четным числом
- Итак, все целые числа, оканчивающиеся на 0, 2, 4, 6 или 8, являются четными числами
Пример : 4, 56, 98, 200 — все четные числа
Нечетные числа
- Любое целое число, не являющееся четным, является нечетным числом
- Или, другими словами, целое число, равное , а не , кратное 2, является нечетным числом
- Итак, любое целое число в форме 2k ± 1, где k — целое число, является нечетным числом
- Итак, все целые числа, оканчивающиеся на 1, 3, 5, 7 или 9, являются нечетными числами
Пример : 7, 31, 75, 499 — все нечетные числа
Примечание: Между каждыми двумя последовательными четными числами есть нечетное число.
В соответствии с определениями, данными выше, является ли 0 четным или нечетным числом?
Свойства чисел: свойства четных и нечетных чисел
Теперь, когда мы знаем, что такое четные и нечетные числа, давайте посмотрим на их свойства.
[три_четвертый]
| Номер 1 | Эксплуатация | Номер 2 | Результат | E примеры | |
| Четный | ± | Четный | = | Четный | · 4 + 2 = 4 · 4 – 2 = 2 |
| Четный | ± | Нечетный | = | Нечетный | · 4 + 1 = 5 · 4 – 1 = 3 |
| Нечетный | ± | Четный | = | Нечетный | · 5 + 2 = 7 · 5 – 2 = 3 |
| Нечетный | ± | Нечетный | = | Четный | · 5 + 3 = 8 · 5 – 3 = 2 |
| Четный | × | Четный | = | Четный | · 2 × 4 = 8 |
| Четный | × | Нечетный | = | Четный | · 2 × 3 = 6 |
| Нечетный | × | Четный | = | Четный | · 3 × 2 = 6 |
| Нечетный | × | Нечетный | = | Нечетный | · 3 × 5 = 15 |
| Четный | ÷ | Четный | = | Может быть или не быть целым числом | · 4 ÷ 2 = 2 · 2 ÷ 4 = 0,5 |
| Четный | ÷ | Нечетный | = | Может быть или не быть целым числом | · 4 ÷ 1 = 4 · 4 ÷ 3 = 1,33 |
| Нечетный | ÷ | Четный | = | Не целое число | · 3 ÷ 2 = 1,5 |
| Нечетный | ÷ | Нечетный | = | Может быть или не быть целым числом | · 3 ÷ 1 = 3 · 1 ÷ 3 = 0,33 |
[/three_fourth]
[one_fourth_last][/one_fourth_last]
Свойства чисел: простые числа простое число
Пример : 2, 3, 5, 7, 11……….
Примечание: 2 — единственное простое число, которое является четным, потому что все остальные четные числа будут делиться как минимум на три числа: 1, 2 и само число.
- Каждое натуральное число может быть представлено как произведение одного или нескольких простых чисел
Пример : 55 = 5 * 11, где 5 и 11 — два простых числа
Исходя из приведенного выше определения, является ли 1 простым числом?
Итак, мы знаем, что такое простое число, но как проверить, является ли данное число простым или нет?
Как проверить, является ли заданное число простым?
Легко проверить, является ли однозначное или двузначное число простым или нет, но что, если нам дано трехзначное или более число.
- Допустим, число 123. Можем ли мы быстро определить, является ли число 123 простым или нет?
Для этого давайте изучим пятиэтапный подход к проверке, является ли заданное число простым или нет?
Шаг 1 : Найдите квадратный корень из заданного числа
- Квадратный корень из 123 приблизительно равен 11 как 11 2 = 121
Шаг 2 : Округлите до ближайшего целого числа
- Ближайшее целое число равно 11.

Шаг 3 : Перечислите все простые числа, которые меньше или равны этому целому числу
- Простые числа, меньшие или равные 11, это 2, 3, 5, 7 и 11.
Шаг 4 : Проверить, может ли любое из этих простых чисел делиться на данное число или нет
- 123 не делится на 2.
- Но 123 делится на 3.
- Нам не нужно проверять другие простые числа
Шаг 5 : Если да, то данное число не является простым, иначе это простое число
- 123 делится на 3. Следовательно, это не простое число.
Популярная викторина: является ли 157 простым числом?
Факторизация простых чисел
Мы уже знаем, что любое натуральное число может быть представлено как произведение одного или нескольких простых чисел. Такое представление любого числа называется простой факторизацией.
Например, :
420 = 2 × 210 = 2 × 2 × 105 = 2 × 2 × 3 × 35 = 2 × 2 × 3 × 5 × 7 = 2 2 × 3 × 5 × 7
Теперь давайте изучим еще несколько свойств чисел, к которым мы применяем простую факторизацию.
Свойства чисел: наименьшее общее кратное (НОК)
Прежде чем мы узнаем, что такое НОК, давайте поймем значение кратного.
Несколько: Если остаток при делении числа «N» на другое число «n» равен нулю, , то говорят, что N кратно n .
И LCM — это наименьшее общее кратное любых двух или более данных положительных целых чисел.
Например, : LCM 4 и 6 равно 12, поскольку 12 является наименьшим числом, которое кратно и 4, и 6
Свойства чисел: наибольший общий делитель или наибольший общий делитель (HCF/GCD)
Давайте сначала узнаем, что такое множитель или делитель, а затем мы можем узнать о GCD или HCF.
Множитель/делитель: Если остаток при делении числа «N» на другое число «n» равен нулю, то говорят, что n является множителем или делителем числа N .
И, HCF или GCD — это наибольший общий множитель/делитель любых двух или более заданных положительных целых чисел.
Например: НОД 24 и 30 равен 6, поскольку 6 — наибольшее число, являющееся делителем 24 и 30.
Метод нахождения НОК и НОД любых двух заданных положительных целых чисел
Теперь, когда мы знаем, что такое НОК и НОД, давайте изучим метод нахождения НОК и НОД любых двух данных положительных целых чисел.
Как найти LCM?
Рассмотрим два натуральных числа 72 и 300
Шаг 1 : Представим два заданных числа в их простой факторизации
- 72 = 2 2 0 90 9000 × 9 3 9169
- 300 = 2 2 × 3 × 5 2
Шаг 2 : Перечислите все различные простые множители обоих чисел
- Простые множители 72 = 2 и 3
- Простые множители 300 = 2, 3 и 5
- Таким образом, различные простые множители из обеих сумм равны 2, 3 и 5
Шаг 3 : Найдите степень каждого из этих простых множителей, которая является наибольшей между обоими числами.
- Степень 2 в 72 = 3 и степень 2 в 300 = 2,
- Итак, степень 2 в НОК 72 и 300 = 3, так как степень 2 наибольшая в 72
- Точно так же мы получаем степени 3 и 5 как 2 и 2 соответственно
Шаг 4 : Умножьте все эти члены, чтобы получить НОК
- Следовательно, НОК 72 и 300 = 2 3 × 3 2 90 700 х 5 99
Как найти GCD/HCF?
Рассмотрим два одинаковых натуральных числа, 72 и 300
Шаг 1 : Представим два заданных числа в их простой факторизации
- 72 = 2 3 0 7 9 1 6 9 9 3
- 300 = 2 2 × 3 × 5 2
Шаг 2 : Перечислите все общие простые делители
- Простые делители числа 72 = 2 и 3
- Простые множители 300 = 2, 3 и 5
- Таким образом, общие простые делители 2 и 3
Шаг 3 : Найдите мощность каждого из этих простых множителей, которая является наименьшей между
- Степень 2 в 72 = 3 и степень 2 в 300 = 2,
- Итак, степень 2 в НОД 72 и 300 = 2, так как степень 2 наименьшая в 300
- Точно так же мы получаем степени 3 и 5 как 1 и 0 соответственно
Шаг 4 : Умножьте все эти члены, чтобы получить НОД
- Следовательно, НОД 72 и 300 = 2 2 × 3 = 12
Примечание: Произведение НОК и НОД любых двух заданных натуральных чисел равно произведению двух заданных целых чисел.
- LCM × HCF = Произведение целых чисел
Что такое НОД и НОД двух простых чисел? Если вам понравилась эта статья, вот еще пара статей о свойствах чисел:
- 3 Наиболее распространенные ошибки в вопросах GMAT по четным и нечетным
- 3 Наиболее распространенные ошибки в вопросах GMAT LCM/GCD
Свойства чисел: тест по применению
Вопрос 1
Каков четный/нечетный характер выражения, 2k 2 + 14k + 7, где k — натуральное число?
- Четный
- Нечетный
- Невозможно определить
Решение
Дано
- Выражение, 2k 2 + 14k + 7, где k — натуральное число
Найти
- Четность/нечетность данного выражения
Подход и отработка
- Мы умеем писать, 2k 2 + 14k + 7 = 2k 2 + 14k + 6 + 1
Теперь, если мы видим, в данном выражении
- Член 2k 2 всегда четен для любого значения k
- Так как четное * любое целое число = четное
- Член 14k всегда четен для любого значения k
- Так как четное * любое целое число = четное
- Член 6 тоже четный, а 1 нечетный
Итак, 2к 2 + 14к + 7 = 2к 2 + 14к + 6 + 1 = чет + чет + чет + чет + нечет = нечет
Следовательно, данное выражение всегда нечетно при любом значении k
Следовательно, правильный ответ Вариант B .
Тест по свойствам чисел: вопрос 2
НОК двух натуральных чисел, p и q, равен 42, а HCF равен 1. Если p — четное простое число, то каково значение q?
- 6
- 7
- 14
- 21
- 42
Решение
Дано
- Два положительных целых числа p и q
- p — четное простое число
- LCM pf p и q = 42
- HCF p и q = 1
Найти
- Значение q
Подход и разработка
Значение p = 2, поскольку 2 — единственное четное простое число
И мы знаем, что
- LCM × HCF = произведение двух целых чисел
- 42 × 1 = 2 × q
Следовательно, значение q = 42/2 = 21,
Следовательно, правильный ответ Опция D .
Ретроградное движение Солнца и нарушение правила четно-нечетного цикла активности солнечных пятен | Ежемесячные уведомления Королевского астрономического общества
Журнальная статья
Дж. Джаварая
Джаварая
Дж. Джаварайя ⋆
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
ОБЪЯВЛЕНИЯ
Примечания автора
Ежемесячные уведомления Королевского астрономического общества , том 362, выпуск 4, октябрь 2005 г., страницы 1311–1318, https://doi.org/10.1111/j.1365-2966.2005.09403.x
3.x
.xОпубликовано:
01 октября 2005 г.
История статьи
Получено:
02 июля 2005 г.
Принято:
04 июля 2005 г.
Опубликовано:
01 октября 2005 г.
Фильтр поиска панели навигации Ежемесячные уведомления Королевского астрономического обществаЭтот выпускЖурналы РАНАстрономия и астрофизикаКнигиЖурналыOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Ежемесячные уведомления Королевского астрономического обществаЭтот выпускЖурналы РАНАстрономия и астрофизикаКнигиЖурналыOxford Academic Термин поиска на микросайте
Advanced Search
Abstract
Сумма чисел солнечных пятен за нечетный 11-летний цикл солнечных пятен превышает сумму предшествующего четного цикла, и это хорошо известно как правило Гневышева и Оля (или правило Г–О). ) по именам авторов, открывших его в 1948 году. Правило G – O можно использовать для предсказания суммы количества солнечных пятен в предстоящем нечетном цикле по количеству солнечных пятен в предыдущем четном цикле. Однако это не всегда возможно, поскольку иногда нарушается правило G–O. До сих пор не известна правдоподобная причина ни правила G-O, ни нарушения этого правила. Здесь мы показываем, что эпохи нарушения правила Г–О близки к эпохам обратного орбитального движения Солнца вокруг центра масс Солнечной системы (т.е. к эпохам, когда орбитальный угловой момент Солнца слабо отрицательный). Используя этот результат, легко заранее предсказать эпохи нарушения правила G–O. Мы также показываем, что скорость вращения экватора Солнца, определенная по данным о группах солнечных пятен за период 1879 г.–2004 коррелирует/антикоррелирует с орбитальным моментом Солнца до/после 1945 г. Мы обнаружили наличие статистически значимой ∼17-летней периодичности в скорости вращения Солнца на экваторе. Обсуждаются последствия этих открытий для понимания механизма солнечного цикла и солнечно-земных отношений.
) по именам авторов, открывших его в 1948 году. Правило G – O можно использовать для предсказания суммы количества солнечных пятен в предстоящем нечетном цикле по количеству солнечных пятен в предыдущем четном цикле. Однако это не всегда возможно, поскольку иногда нарушается правило G–O. До сих пор не известна правдоподобная причина ни правила G-O, ни нарушения этого правила. Здесь мы показываем, что эпохи нарушения правила Г–О близки к эпохам обратного орбитального движения Солнца вокруг центра масс Солнечной системы (т.е. к эпохам, когда орбитальный угловой момент Солнца слабо отрицательный). Используя этот результат, легко заранее предсказать эпохи нарушения правила G–O. Мы также показываем, что скорость вращения экватора Солнца, определенная по данным о группах солнечных пятен за период 1879 г.–2004 коррелирует/антикоррелирует с орбитальным моментом Солнца до/после 1945 г. Мы обнаружили наличие статистически значимой ∼17-летней периодичности в скорости вращения Солнца на экваторе. Обсуждаются последствия этих открытий для понимания механизма солнечного цикла и солнечно-земных отношений.
Солнце: магнитные поля, Солнце: вращение, солнечные пятна, Солнечная система: общие сведения
1 Введение
Солнечная активность изменяется во многих временных масштабах. Это может повлиять на климат и околоземную космическую среду (например, Hoyt & Schatten 1997; Хэтэуэй, Уилсон и Райхманн, 1999 г .; Розелот 2001; Хиремат и Манди, 2004 г .; Георгиева и др. 2005). Поэтому предсказание амплитуд колебаний солнечной активности очень поможет обществу. Солнечные пятна — это самое раннее наблюдаемое явление солнечной активности. Циклы солнечных пятен нумеруются от цикла, начавшегося в 1755 году (цикл 1). Текущий цикл солнечных пятен, начавшийся в 1996 году, является циклом с нечетным номером (цикл 23). Хорошо известное правило Гневышева-Оля или правило Г-О (Gnevyshev & Ohl 1948) утверждает, что сумма чисел солнечных пятен ( R сумма ) за нечетный цикл солнечных пятен превышает сумму предшествующего четного цикла солнечных пятен. Используя правило G-O, можно предсказать сумму R цикла с нечетным номером по сумме предшествующего цикла с четным номером с разумной точностью (Wilson 1988). Однако некоторые пары четно-нечетных циклов нарушали правило G–O, т. е. в таких парах R сумма нечетного цикла меньше суммы предшествующего ему четного цикла (например, пары циклов 4, 5 и 22, 23). До сих пор не известно правдоподобной причины ни правила G-O, ни его нарушения. Чтобы предсказать амплитуду нечетного цикла с помощью правила G-O, необходимо и важно заранее знать, будет ли пара циклов с четными и нечетными номерами удовлетворять правилу G-O или нет. Однако не существует метода прогнозирования нарушения правила G-O. Прогнозы на основе метода предвестников, правила G–O и статистического анализа предшествующих циклов указывали на высокую R Сумма для текущего 23-го цикла аналогична или больше, чем в 22-м цикле (Joselyn et al. 1997). Прогноз нарушения правила G–O парой циклов 22, 23, основанный на многолетних трендах пятнистой активности (Шове, 1955; Комитов, Бонев, 2001; Джаварая, 2003b), кажется верным.
Используя правило G-O, можно предсказать сумму R цикла с нечетным номером по сумме предшествующего цикла с четным номером с разумной точностью (Wilson 1988). Однако некоторые пары четно-нечетных циклов нарушали правило G–O, т. е. в таких парах R сумма нечетного цикла меньше суммы предшествующего ему четного цикла (например, пары циклов 4, 5 и 22, 23). До сих пор не известно правдоподобной причины ни правила G-O, ни его нарушения. Чтобы предсказать амплитуду нечетного цикла с помощью правила G-O, необходимо и важно заранее знать, будет ли пара циклов с четными и нечетными номерами удовлетворять правилу G-O или нет. Однако не существует метода прогнозирования нарушения правила G-O. Прогнозы на основе метода предвестников, правила G–O и статистического анализа предшествующих циклов указывали на высокую R Сумма для текущего 23-го цикла аналогична или больше, чем в 22-м цикле (Joselyn et al. 1997). Прогноз нарушения правила G–O парой циклов 22, 23, основанный на многолетних трендах пятнистой активности (Шове, 1955; Комитов, Бонев, 2001; Джаварая, 2003b), кажется верным. Однако эпоха следующего нарушения правила G–O еще не предсказана, и имеющихся данных о солнечных пятнах может быть недостаточно для использования этого метода.
Однако эпоха следующего нарушения правила G–O еще не предсказана, и имеющихся данных о солнечных пятнах может быть недостаточно для использования этого метода.
Существует два основных подхода к объяснению механизма солнечного цикла: один основан на турбулентном динамо, действующем внутри или непосредственно под оболочкой солнечной конвекции, а другой — на крупномасштабных колебаниях, наложенных на ископаемое магнитное поле в радиационное ядро. Согласно теории турбулентного динамо, дифференциальное вращение Солнца создает тороидальное поле (составляющая восток-запад) путем непрерывной намотки полоидального поля (составляющая север-юг), индукционный эффект циклонической турбулентности регенерирует полоидальное поле, а избыточное полоидальное и тороидальные поля устраняются усилением диффузии за счет конвективной турбулентности. Достаточно подробная и реалистичная модель динамо-процесса, чтобы учесть все различные аспекты солнечного магнетизма, пока недоступна. Имеющиеся модели турбулентного динамо имеют несколько трудностей. Например, в этих моделях неясна роль дифференциального вращения в циклическом изменении солнечной активности; причина межцикловых модуляций солнечной активности еще не найдена и не имеет предсказательной силы. Основная идея моделей магнитных осцилляторов состоит в том, чтобы рассматривать наблюдаемое колеблющееся крупномасштабное солнечное магнитное поле как эффект периодического усиления первичных полей из-за колебаний дифференциальной скорости вращения недр Солнца. Основная трудность в моделях осцилляторов связана с энергетикой. Ни одна из моделей осцилляторов не предлагает средств поддержания колебаний против рассеяния скорости и магнитных полей (см. обзоры Рознера и Вайса 19).92; Оссендерейвер 2003). В связи с этим, возможно, стоит исследовать, может ли динамика Солнечной системы влиять на внутреннюю динамику Солнца (Gokhale & Javaraiah 1995).
Например, в этих моделях неясна роль дифференциального вращения в циклическом изменении солнечной активности; причина межцикловых модуляций солнечной активности еще не найдена и не имеет предсказательной силы. Основная идея моделей магнитных осцилляторов состоит в том, чтобы рассматривать наблюдаемое колеблющееся крупномасштабное солнечное магнитное поле как эффект периодического усиления первичных полей из-за колебаний дифференциальной скорости вращения недр Солнца. Основная трудность в моделях осцилляторов связана с энергетикой. Ни одна из моделей осцилляторов не предлагает средств поддержания колебаний против рассеяния скорости и магнитных полей (см. обзоры Рознера и Вайса 19).92; Оссендерейвер 2003). В связи с этим, возможно, стоит исследовать, может ли динамика Солнечной системы влиять на внутреннюю динамику Солнца (Gokhale & Javaraiah 1995).
Идея о том, что гравитация планет может быть причиной солнечного цикла, восходит, по крайней мере, к Кэррингтону (Brown 1900). Впоследствии многие ученые предполагали, что приливные силы, вызванные планетами, или скорость изменения орбитального углового момента Солнца относительно центра масс Солнечной системы (барицентра) играют роль в механизме солнечной активности. Такое представление о роли динамики Солнечной системы подвергалось сомнению, поскольку (см. Ferris 1969): (i) энергия приливной силы от планет мала по сравнению с гравитацией на поверхности Солнца; и (ii) центр масс Солнца находится в свободном падении в суммарном гравитационном поле всех планет. Тем не менее, гипотеза о связи между движением Солнца вокруг барицентра и солнечной активностью подтверждается растущим числом исследований, указывающих на то, что что-то должно быть верным в «планетарной гипотезе» (Jose 1965; Wood & Wood 1965; Blizard 1983, 1989; Фэйрбридж и Ширли 1987; Спербер и Фэйрбридж, 1990; Гокхале 1996; Закарашвили 1997; Ландшейдт 1999; Харватова 2000; Джакетт 2000, 2003).
Такое представление о роли динамики Солнечной системы подвергалось сомнению, поскольку (см. Ferris 1969): (i) энергия приливной силы от планет мала по сравнению с гравитацией на поверхности Солнца; и (ii) центр масс Солнца находится в свободном падении в суммарном гравитационном поле всех планет. Тем не менее, гипотеза о связи между движением Солнца вокруг барицентра и солнечной активностью подтверждается растущим числом исследований, указывающих на то, что что-то должно быть верным в «планетарной гипотезе» (Jose 1965; Wood & Wood 1965; Blizard 1983, 1989; Фэйрбридж и Ширли 1987; Спербер и Фэйрбридж, 1990; Гокхале 1996; Закарашвили 1997; Ландшейдт 1999; Харватова 2000; Джакетт 2000, 2003).
Солнце колеблется вокруг барицентра Солнечной системы на расстоянии, в два раза превышающем его радиус. Вращение Солнца составляет 1–2 процента от общего углового момента Солнечной системы. Хосе (1965) показал наличие связи между циклом Хейла и изменениями углового момента при движении Солнца вокруг барицентра. Недавно Закарашвили (1997) и Juckett (2000) обнаружили, что движение Солнца вокруг барицентра играет роль даже в причине дифференциального вращения Солнца. Конфигурации и направления выравнивания больших планет значительно различаются во время четных и нечетных циклов (Mörth & Schlamminger 1979). Дифференциальный анализ вращения, проведенный Джаварайей и Гокхейлом (1995) и Джаварайей (1996, 2003а), выявил частоты, совместимые с частотами конкретных выравниваний двух или более планет. Существование зависимости, аналогичной правилу G-O в активности солнечных пятен, также обнаружено между различиями в дифференциальном вращении во время нечетных и четных циклов (Javaraiah, Bertello & Ulrich, 2005a). Следовательно, можно было бы разумно ожидать, что нарушение правила G – O и вариации дифференциального вращения, вероятно, связаны с движением Солнца вокруг барицентра. Мы исследовали это в настоящей статье.
Недавно Закарашвили (1997) и Juckett (2000) обнаружили, что движение Солнца вокруг барицентра играет роль даже в причине дифференциального вращения Солнца. Конфигурации и направления выравнивания больших планет значительно различаются во время четных и нечетных циклов (Mörth & Schlamminger 1979). Дифференциальный анализ вращения, проведенный Джаварайей и Гокхейлом (1995) и Джаварайей (1996, 2003а), выявил частоты, совместимые с частотами конкретных выравниваний двух или более планет. Существование зависимости, аналогичной правилу G-O в активности солнечных пятен, также обнаружено между различиями в дифференциальном вращении во время нечетных и четных циклов (Javaraiah, Bertello & Ulrich, 2005a). Следовательно, можно было бы разумно ожидать, что нарушение правила G – O и вариации дифференциального вращения, вероятно, связаны с движением Солнца вокруг барицентра. Мы исследовали это в настоящей статье.
В разделе 2 мы описываем данные и анализ. В разделе 3 мы показываем наличие связи между нарушением правила G–O в активности солнечных пятен и попятным движением Солнца вокруг центра масс Солнечной системы. В разделе 4 мы показываем наличие связи во вращении Солнца и орбитальном движении. В разделе 5 мы обсуждаем значение этих результатов для понимания долговременных вариаций солнечной активности (включая минимум Маундера) и солнечно-земных отношений.
В разделе 4 мы показываем наличие связи во вращении Солнца и орбитальном движении. В разделе 5 мы обсуждаем значение этих результатов для понимания долговременных вариаций солнечной активности (включая минимум Маундера) и солнечно-земных отношений.
2 Данные и анализ
Доктор Ференц Варади любезно предоставил нам значения расстояния ( R ) центра Солнца от барицентра Солнечной системы, орбитальную скорость Солнца ( V ), орбитальный угловой момент Солнца ( L ) и скорость изменения орбитального углового момента (орбитальный момент d L /d t ) для каждого интервала продолжительностью 10 дней в период 16:00–2099. Он определил эти значения, используя последние эфемериды DE405 Лаборатории реактивного движения (JPL) (Seidelmann 1992; Standish 1998) за период 1600–2100 гг.
Дифференциальное вращение Солнца может быть определено из данных полной скорости диска с использованием стандартного полиномиального разложения (Howard & Harvey 1970),
, в то время как для данных о солнечных пятнах достаточно использовать только первые два члена разложения (Newton & Nunn 1951), т. е.
е.
, где ω(φ) — звездная угловая скорость Солнца на широте φ, коэффициенты A представляют экваториальную скорость вращения и B и C измеряют широтный градиент скорости вращения, при этом B представляет в основном низкие широты, а C — в основном более высокие широты ( C слишком мал, чтобы его можно было определить по данным о солнечных пятнах). (Обратите внимание, что приведенные выше уравнения не имеют теоретической основы, но очень хорошо согласуются с соответствующими данными, указанными выше.) б). Мы использовали гринвичские данные о группах солнечных пятен за период 1879 г.–1976 г. и данные о группах пятен из Solar Optical Observing Network (SOON) за период 1977–2004 гг. (доступно на ftp://ftp.science.mfsc.nasa.gov/ssl/pad/solar/greenwich.htm). Данные состоят из времени наблюдения, гелиографической широты и долготы, расстояния до центрального меридиана (CMD) и т. д. для каждой группы точек в каждый день ее наблюдения. Звездные скорости вращения (ω) рассчитаны для каждой пары последовательных дней жизни каждой группы пятен с использованием их продольных и временных разностей между этими днями. Мы не использовали данные, соответствующие |CMD| > 75° в любой день жизни группы пятен и смещения более 3° по долготе или 2° по широте в сутки. Определены годовые вариации коэффициентов A и B путем подгонки данных групп точек за каждый год к уравнению (2).
Звездные скорости вращения (ω) рассчитаны для каждой пары последовательных дней жизни каждой группы пятен с использованием их продольных и временных разностей между этими днями. Мы не использовали данные, соответствующие |CMD| > 75° в любой день жизни группы пятен и смещения более 3° по долготе или 2° по широте в сутки. Определены годовые вариации коэффициентов A и B путем подгонки данных групп точек за каждый год к уравнению (2).
3 Нарушение правила G–O
На рис. 1 показаны вариации R , V , L и d L /d t , определенные для каждого планетарного 10 д, в период 1600–2099 гг. На этом рисунке мы также показываем вариации среднегодовых значений числа солнечных пятен в период 1600–2004 гг. (нижняя панель). Эпохи 1632, 1811 и 19 гг.90, когда движение Солнца вокруг барицентра было ретроградным (т. е. когда L изменилось с положительного на слабо отрицательное; Хосе, 1965), показаны пунктирными вертикальными линиями. Две другие эпохи больших падений в L приходятся на 1672 и 1851 годы, а ожидаемая следующая эпоха такого большого падения в L будет в 2030 году. Все они обозначены пунктирными вертикальными линиями. По понятным причинам возле каждой из больших капель в L находится большая капля d л /д т . Мы привели в табл. 1 значения R , L , V и d L /d t , а также значения эклиптических долготных положений планет-гигантов в эти шесть эпох. Фаза d L /d t опережает фазу L примерно на 4 года у пунктирных линий и примерно на 5 лет у пунктирных линий. Этого и следовало ожидать, потому что первое — это сила, а второе — движение, и оба имеют основной период 190,86 года, период соединения Юпитера и Сатурна. В эпохи, когда крутые спады L показаны пунктирными вертикальными линиями, спад R более крутой, чем спад V . В случае эпох, отмеченных пунктирными вертикальными линиями, все наоборот.
Две другие эпохи больших падений в L приходятся на 1672 и 1851 годы, а ожидаемая следующая эпоха такого большого падения в L будет в 2030 году. Все они обозначены пунктирными вертикальными линиями. По понятным причинам возле каждой из больших капель в L находится большая капля d л /д т . Мы привели в табл. 1 значения R , L , V и d L /d t , а также значения эклиптических долготных положений планет-гигантов в эти шесть эпох. Фаза d L /d t опережает фазу L примерно на 4 года у пунктирных линий и примерно на 5 лет у пунктирных линий. Этого и следовало ожидать, потому что первое — это сила, а второе — движение, и оба имеют основной период 190,86 года, период соединения Юпитера и Сатурна. В эпохи, когда крутые спады L показаны пунктирными вертикальными линиями, спад R более крутой, чем спад V . В случае эпох, отмеченных пунктирными вертикальными линиями, все наоборот. Промежуток между последовательными пунктирными линиями, а также между последовательными штриховыми линиями составляет около 179 лет, т.е. период известного 179-летнего цикла в движении Солнца, связанного с барицентром Солнечной системы. Это также период интервала между выравниваниями всех внешних планет в одной конфигурации и в одном и том же направлении в пространстве. Он примерно равен девяти периодам соединения Юпитера и Сатурна (Хосе 1965). Промежуток между пунктирной линией и соседней пунктирной линией составляет около 43 лет, период соединения Сатурна и Урана.
Промежуток между последовательными пунктирными линиями, а также между последовательными штриховыми линиями составляет около 179 лет, т.е. период известного 179-летнего цикла в движении Солнца, связанного с барицентром Солнечной системы. Это также период интервала между выравниваниями всех внешних планет в одной конфигурации и в одном и том же направлении в пространстве. Он примерно равен девяти периодам соединения Юпитера и Сатурна (Хосе 1965). Промежуток между пунктирной линией и соседней пунктирной линией составляет около 43 лет, период соединения Сатурна и Урана.
Рис. 1.
Открыть в новой вкладкеСкачать слайд
Значения R , V , L и d L /d /d в период 90 t в каждом интервале 90–01 90–01 среднегодовое количество солнечных пятен за период 1600–2004 гг. Агрегаты Р , В , Л и д Л /D T — AU, AU D -1 , M ⊙ × (AU) 2 D -1 и M ⊙ × (AU)
2 D D D 9199. 1999999 2 D 9199.19.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169. соответственно, где M ⊙ — масса Солнца, а а.е. — астрономическая единица. Рядом с пиком каждого цикла солнечных пятен отмечен соответствующий номер цикла солнечных пятен Вальдмейра. Эпохи 1632, 1811 и 1990 гг., когда орбитальное движение Солнца было ретроградным, обозначены пунктирными вертикальными линиями. Остальные три эпохи, 1672, 1851 и 2030 гг., где L круто уменьшаются, отмечены пунктирными вертикальными линиями. Горизонтальные линии представляют средние значения.
1999999 2 D 9199.19.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169.169. соответственно, где M ⊙ — масса Солнца, а а.е. — астрономическая единица. Рядом с пиком каждого цикла солнечных пятен отмечен соответствующий номер цикла солнечных пятен Вальдмейра. Эпохи 1632, 1811 и 1990 гг., когда орбитальное движение Солнца было ретроградным, обозначены пунктирными вертикальными линиями. Остальные три эпохи, 1672, 1851 и 2030 гг., где L круто уменьшаются, отмечены пунктирными вертикальными линиями. Горизонтальные линии представляют средние значения.
Таблица 1.
Открыть в новой вкладкеСкачать слайд
Значения d L /d t , L , R , V — Юпитер (J), Сатурн (S), Уран (U) и Нептун (N) — в эпохи, для которых значения L даны и отмечены на рис. 1 пунктирной и штриховой вертикальными линиями. из R , V , L и D L /D T — AU, AU D -1 , M ⊙ × (AU) 9199 2 D D D D D 2 2 2 2 2 2 2 2 2 2 2 2 ⊙ × (A) , M ⊙ × (A) , M ⊙ × (A) ⊙ × (а. е.) 2 d −2 соответственно, где M ⊙ — масса Солнца, а «а.е.» — астрономическая единица.
е.) 2 d −2 соответственно, где M ⊙ — масса Солнца, а «а.е.» — астрономическая единица.
Правило G–O было нарушено парой циклов солнечных пятен 4, 5 в начале минимума Дальтона, и, скорее всего, оно будет нарушено парой циклов 22, 23 (например, Javaraiah 2003b). Похоже, что ближе к концу цикла, который был всего за один цикл до цикла в начале минимума Маундера, правило G – O было нарушено (скажем, парой циклов -12, -11). (Бир и др. 1990 показали существование циклического поведения во время минимума Маундера.) Интересно, что каждая из этих пар циклов близка к эпохе, когда орбитальное движение Солнца является ретроградным, что показано (рис. 1) пунктирными вертикальными линиями. Пиковое значение цикла солнечных пятен 8 выше, чем у цикла 9. В силу этого различия пара циклов 8, 9 нарушила правило G–O. Временное поведение L и d L /d t предполагает, что такая ситуация могла иметь место в 1672 г., а следующая такая ситуация может произойти около 2030 г. (однако в эту эпоху падение л будет относительно небольшим; см. рис. 1 и табл. 1). Эти данные указывают на существование связи между нарушением правила G-O и обратным движением Солнца относительно центра масс Солнечной системы. Из таблицы 1 видно, что эпохи, в которые L резко уменьшались, Сатурн располагался примерно в оппозиции к Юпитеру, а Уран и Нептун были ближе к Сатурну (т.е. Юпитер опережает примерно на 180° относительно другого три планеты-гиганта). Очевидно, такие конфигурации больших планет ответственны за ретроградное движение Солнца вокруг барицентра, что, в свою очередь, кажется ответственным за нарушение правила G-O. Поскольку конфигурации планет и ретроградное движение Солнца можно рассчитать заранее, можно заранее знать эпохи нарушений правила G – O. Следовательно, ожидается, что правило G – O будет нарушено циклом Хейла, который будет включать (или заканчиваться) 2169 год., то есть только после промежутка примерно в восемь циклов Хейла после текущего цикла Хейла 11 (содержит пару циклов 22, 23).
(однако в эту эпоху падение л будет относительно небольшим; см. рис. 1 и табл. 1). Эти данные указывают на существование связи между нарушением правила G-O и обратным движением Солнца относительно центра масс Солнечной системы. Из таблицы 1 видно, что эпохи, в которые L резко уменьшались, Сатурн располагался примерно в оппозиции к Юпитеру, а Уран и Нептун были ближе к Сатурну (т.е. Юпитер опережает примерно на 180° относительно другого три планеты-гиганта). Очевидно, такие конфигурации больших планет ответственны за ретроградное движение Солнца вокруг барицентра, что, в свою очередь, кажется ответственным за нарушение правила G-O. Поскольку конфигурации планет и ретроградное движение Солнца можно рассчитать заранее, можно заранее знать эпохи нарушений правила G – O. Следовательно, ожидается, что правило G – O будет нарушено циклом Хейла, который будет включать (или заканчиваться) 2169 год., то есть только после промежутка примерно в восемь циклов Хейла после текущего цикла Хейла 11 (содержит пару циклов 22, 23). Однако нарушение в силу разности высот пиков циклов — подобно паре циклов 8, 9 около 1851 г. — ожидается около 2030 г., т. е. парой циклов 26, 27.
Однако нарушение в силу разности высот пиков циклов — подобно паре циклов 8, 9 около 1851 г. — ожидается около 2030 г., т. е. парой циклов 26, 27.
4 Спин-орбитальная связь Солнца
На рис. 2 показаны вариации среднегодовых значений R , V , L , d L /d t и значения параметров дифференциального вращения A и B , определенные по годовым данным групп солнечных пятен за период 1879–2004 гг. Планки погрешностей представляют собой значения ± 1σ (стандартное отклонение). Из-за уменьшенного количества групп солнечных пятен значения имеют большие ошибки в минимумах циклов. Мы скорректировали временные ряды A и B , заменив значения с ошибкой, превышающей трехкратную медианную ошибку, значениями, смоделированными на основе линейной аппроксимации [аналогичная коррекция была применена в более ранней статье Джаварайи и Комма (19).99)]. На рис. 2 сплошные кривые на двух нижних панелях соединяют точки скорректированных данных, а пунктирные кривые соединяют нескорректированные данные. На этом рисунке вариации скорости вращения экватора Солнца A кажутся во многом похожими на вариации d L / d t . После 1945 г. вариации как A , так и d L /d t имеют несколько большую амплитуду. В это время средний уровень активности также относительно велик (см. рис. 1). Эпоха, 1990–1991, когда орбитальное движение Солнца ретроградно, значение A мало, а d L /d t почти равно нулю. Корреляция между A и d L / d t положительна примерно до 1945 г. и отрицательна после этого времени (коэффициент корреляции r = 40 и -50 в интервалах примерно 50 лет до и после 1945 г. соответственно) . Эти результаты указывают на существование связи между A и d L /d т . Орбитальный угловой момент мог быть передан вращательному импульсу примерно за 50 лет до 1945 г.
2 сплошные кривые на двух нижних панелях соединяют точки скорректированных данных, а пунктирные кривые соединяют нескорректированные данные. На этом рисунке вариации скорости вращения экватора Солнца A кажутся во многом похожими на вариации d L / d t . После 1945 г. вариации как A , так и d L /d t имеют несколько большую амплитуду. В это время средний уровень активности также относительно велик (см. рис. 1). Эпоха, 1990–1991, когда орбитальное движение Солнца ретроградно, значение A мало, а d L /d t почти равно нулю. Корреляция между A и d L / d t положительна примерно до 1945 г. и отрицательна после этого времени (коэффициент корреляции r = 40 и -50 в интервалах примерно 50 лет до и после 1945 г. соответственно) . Эти результаты указывают на существование связи между A и d L /d т . Орбитальный угловой момент мог быть передан вращательному импульсу примерно за 50 лет до 1945 г. , а в последние 50 лет мог произойти обратный процесс (Джакетт, 2000).
, а в последние 50 лет мог произойти обратный процесс (Джакетт, 2000).
Figure 2.
Open in new tabDownload slide
Variations in the yearly mean values of R , V , L , d L /d t , A and B . Агрегаты Р , В , Л и д L /d t такие же, как на рис. 1 и в таблице 1. В случае A и B сплошная и штриховая кривые представляют скорректированные и нескорректированные данные соответственно, а планки ошибок являются значениями 1σ. Эпоха 1990 г., когда орбитальное движение Солнца было ретроградным, обозначена пунктирной вертикальной линией. Горизонтальные линии представляют средние значения.
Корреляция между широтным градиентом вращения ( B ) и d L /d t слаб. Знаки корреляций ( r ≈ −20 до +25) между ( B ) и d L /d t оказываются противоположными в указанные эпохи положительных и отрицательных корреляций между A и d L /d t .
Джаварая и Гокхале (1995) и Javaraiah & Komm (1999) обнаружили ∼18,3-летнюю, ∼8-летнюю и несколько других коротких периодов в B . На рис. 3 показаны спектры быстрого преобразования Фурье (БПФ) годовых вариаций d L /d t , A и B . Из этого рисунка видно, что оба спектра A и B имеют доминирующие пики на частоте 1/18 года -1 , которые значимы на уровнях 3,6σ и 5,5σ соответственно. Соответствующие периодичности в A и B примерно совпадают с основной периодичностью в d L / d t (пик в 1/21 года −1 , 6.6σ). Мы повторили анализ БПФ, расширив временной ряд от исходных 126 точек данных до 1024 точек данных, дополнив временной ряд нулями. Значения указанных выше основных периодичностей в A , B и d L /d t составляют 17,1, 18,29 и 19,69 лет соответственно.
Рис. 3.
Открыть в новой вкладке Загрузить слайд
Спектры мощности БПФ d L /d t (штриховая кривая), A (пунктирная кривая) и B (сплошная кривая).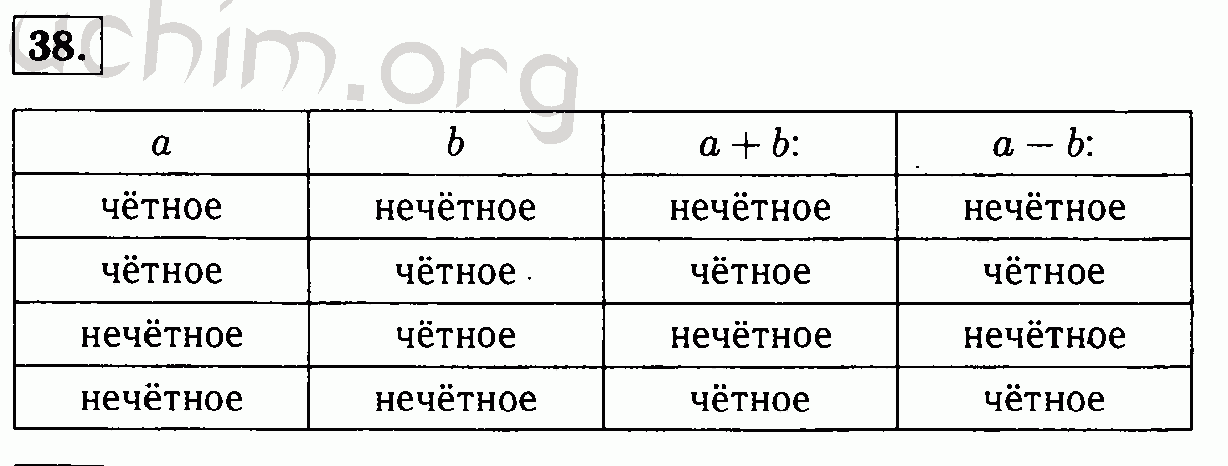 Значения мощности нормированы на единицу. Вблизи вершин доминирующих пиков, значимых на >3σ (особенно у A и B ), показаны значения соответствующих периодов.
Значения мощности нормированы на единицу. Вблизи вершин доминирующих пиков, значимых на >3σ (особенно у A и B ), показаны значения соответствующих периодов.
Обратите внимание, что существует разница примерно в 1 год между вышеупомянутыми основными периодами А и В . Это можно объяснить следующим образом. Считается, что магнитные структуры активных областей зарождаются вблизи основания конвективной зоны (около 200 000 км ниже поверхности), а магнитная плавучесть заставляет их подниматься через конвективную зону и выходить на поверхность. Скорость вращения групп пятен зависит от их продолжительности жизни и возраста. Это можно интерпретировать как изменение скорости вращения магнитных структур групп пятен по мере изменения глубины их закрепления в течение их жизни (Javaraiah & Gokhale 19).97; Гокхале и Джаварая, 2002 г .; Хиремат 2002; Сивараман и др. 2003). На рис. 4 представлены спектры БПФ A и B , определенные по первым 2-дневным данным (молодые группы) групп пятен с продолжительностью жизни 7–12 сут.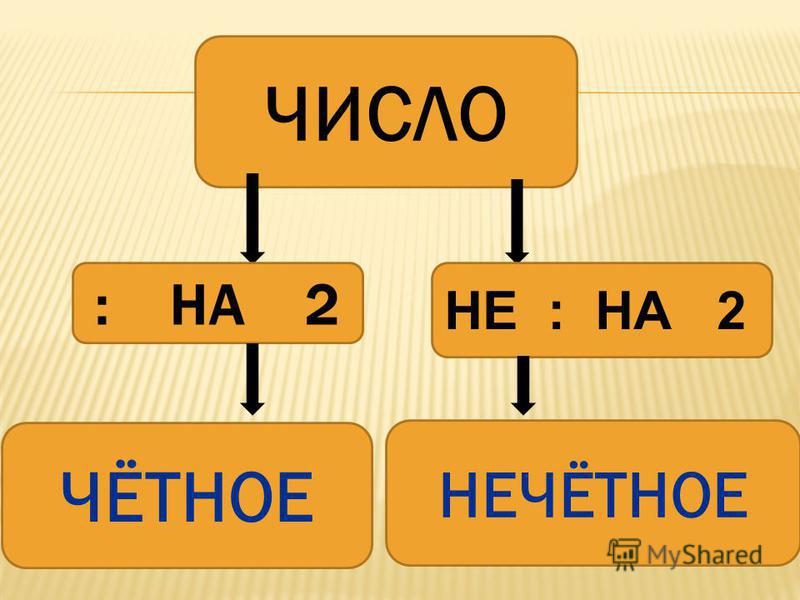 Чтобы получить адекватные данные, мы использовали скользящие временные интервалы величиной 5 лет (такие же, как в Javaraiah & Gokhale 1995; Javaraiah 1998). На рис. 4 мы также показали спектр БПФ, определенный из 5-летнего сглаженного временного ряда d L /d t . На этом рисунке видно, что доминирующие пики в спектрах A и B хорошо совпали. Мы также повторили анализ БПФ для этих сглаженных временных рядов, расширив их, как описано выше. Установлено, что доминирующие пики в спектрах расширенных временных рядов как A , так и B приходится на 1/17,4 года −1 . Это указывает на то, что 18,3-летняя периодичность, обнаруженная у B и полученная по объединенным данным (с преобладанием малых и короткоживущих групп) групп пятен разной продолжительности жизни и возраста, может соответствовать немного более мелким слоям. 17,1-летняя периодичность может соответствовать несколько более глубоким слоям (см. также Джаварайя 19).
Чтобы получить адекватные данные, мы использовали скользящие временные интервалы величиной 5 лет (такие же, как в Javaraiah & Gokhale 1995; Javaraiah 1998). На рис. 4 мы также показали спектр БПФ, определенный из 5-летнего сглаженного временного ряда d L /d t . На этом рисунке видно, что доминирующие пики в спектрах A и B хорошо совпали. Мы также повторили анализ БПФ для этих сглаженных временных рядов, расширив их, как описано выше. Установлено, что доминирующие пики в спектрах расширенных временных рядов как A , так и B приходится на 1/17,4 года −1 . Это указывает на то, что 18,3-летняя периодичность, обнаруженная у B и полученная по объединенным данным (с преобладанием малых и короткоживущих групп) групп пятен разной продолжительности жизни и возраста, может соответствовать немного более мелким слоям. 17,1-летняя периодичность может соответствовать несколько более глубоким слоям (см. также Джаварайя 19). 98).
98).
Рис. 4.
Открыть в новой вкладкеСкачать слайд
То же, что и на рис. 3, но А и В определяются только по первым 2-м (молодые группы) данным групп пятен ПЖ 7– 12 д. Для получения адекватных данных о группе точек используются 5-летние скользящие временные интервалы. В случае d L /d t используется 5-летний сглаженный временной ряд.
17,1-летняя периодичность как A , так и B близко совпадает с 17,5-летним периодом, обнаруженным при смешивании низкочастотных компонентов L и мгновенный вектор проекции спина (Джакетт, 2000). Кроме того, по-видимому, существует хорошее соответствие между амплитудами вариаций вращения Солнца и орбитальных угловых моментов, особенно в общие эпохи крутых спадов как L , так и A . В эти эпохи L уменьшается на величину, примерно равную ее среднему значению. Например, в эпоху 1990.97 г. величина резкого уменьшения л составляет около -2,1 × 10 47 г см 2 с -1 . В эту эпоху величина падения в A составляет около 1 процента, а соответствующий вращательный момент равен примерно -1,1 × 10 47 г см 2 с -1 . (Среднее годовое значение A составляет 14,505 ± 0,008° d −1 . Неопределенность, значение 1σ, в этом среднем значении предполагает, что средняя амплитуда годового изменения скорости вращения экватора Солнца в течение периода 1879 г.–2004 составляет всего около 0,056%. В целом между средними скоростями экваториального вращения во время четных и нечетных циклов обнаруживается разница около 0,1%; Javaraiah 2003a.)
В эту эпоху величина падения в A составляет около 1 процента, а соответствующий вращательный момент равен примерно -1,1 × 10 47 г см 2 с -1 . (Среднее годовое значение A составляет 14,505 ± 0,008° d −1 . Неопределенность, значение 1σ, в этом среднем значении предполагает, что средняя амплитуда годового изменения скорости вращения экватора Солнца в течение периода 1879 г.–2004 составляет всего около 0,056%. В целом между средними скоростями экваториального вращения во время четных и нечетных циклов обнаруживается разница около 0,1%; Javaraiah 2003a.)
Приведенные выше результаты обеспечивают прямую наблюдательную поддержку моделей спин-орбитальной связи сплюснутого Солнца (например, Juckett 2000). Результаты также указывают на то, что возмущения, необходимые для поддержания колебаний дифференциального вращения Солнца и солнечного магнитного поля как участников механизма солнечного цикла, исходят от динамики Солнечной системы.
5 Обсуждение
Усоскин, Мурсула и Ковальцов (2001) утверждали, что между циклами солнечных пятен 4 и 5 данные редки и ненадежны, и интерпретировали очень длинный цикл 4 как состоящий из двух коротких циклов. Если эта интерпретация верна, то кажется, что правило Г-О не было нарушено циклом Хейла 2. Сравнивая наблюдения солнечных пятен в указанный период с наблюдениями в другое время, а также анализируя другие показатели солнечной активности, Кривова, Solanki & Beer (2002) показали, что в конце 18 века не было пропущено ни одного цикла, а официальная нумерация и параметры цикла солнечных пятен верны. Усоскин, Мурсула и Ковальцов (2003) утверждали, что статистический анализ, проведенный в статье Кривовой и соавт. (2002) не был подтвержден количественными тестами и даже содержит несколько ошибок. Следовательно, было ли нарушено правило G–O во время цикла Хейла 2 или был дополнительный слабый цикл в 1790s, еще не подтверждено. Результат, полученный в разделе 3, в значительной степени свидетельствует о том, что правило G–O действительно было нарушено циклом Хейла 2. солнце. Это видно на рис. 1, т.е. уровень активности относительно низок в течение, по крайней мере, нескольких циклов, следующих за пунктирными вертикальными линиями. (Примерно в 1730 и 1900 годах уровень активности был значительно ниже, тогда как размеры капель в L и R были невелики, но в V были значительно большие падения. В 1900 г. произошло выравнивание всех других больших планет с Нептуном в оппозиции примерно на 25°.) Как уже упоминалось в разделе 3, за ожидаемым нарушением правила G–O вблизи пунктирной вертикальной линии в 1632 г. следует Маундеровское минимум, а за нарушением правила G – O рядом с пунктирной вертикальной линией в 1811 следует минимум Дальтона. Таким образом, нарушение правила G–O вблизи пунктирной вертикальной линии на 19Ожидается также, что за 90 последует минимум активности, подобный Маундеру/Дальтону.
Результат, полученный в разделе 3, в значительной степени свидетельствует о том, что правило G–O действительно было нарушено циклом Хейла 2. солнце. Это видно на рис. 1, т.е. уровень активности относительно низок в течение, по крайней мере, нескольких циклов, следующих за пунктирными вертикальными линиями. (Примерно в 1730 и 1900 годах уровень активности был значительно ниже, тогда как размеры капель в L и R были невелики, но в V были значительно большие падения. В 1900 г. произошло выравнивание всех других больших планет с Нептуном в оппозиции примерно на 25°.) Как уже упоминалось в разделе 3, за ожидаемым нарушением правила G–O вблизи пунктирной вертикальной линии в 1632 г. следует Маундеровское минимум, а за нарушением правила G – O рядом с пунктирной вертикальной линией в 1811 следует минимум Дальтона. Таким образом, нарушение правила G–O вблизи пунктирной вертикальной линии на 19Ожидается также, что за 90 последует минимум активности, подобный Маундеру/Дальтону. То есть нынешняя тенденция относительно низкого уровня активности солнечных пятен в текущем 23-м цикле, который следует за пунктирной вертикальной линией в 1990 г., может сохраниться еще в течение нескольких циклов солнечных пятен. Такое указание также обнаружено в недавних исследованиях долговременных изменений активности солнечных пятен (например, Бонев, Пенев и Селло, 2004; Хэтэуэй и Уилсон, 2005) и скорости вращения Солнца на экваторе (Джаварайя, 2003b; Джаварайя, Бертелло и Ульрих, 2005b). Кроме того, ряд авторов предсказал слабую активность во время следующего цикла 24, используя большое количество методик (например, Кейн 19).99; Эчер и др. 2004 г.; Свальгаард, Кливер и Камиде, 2005 г.). Таким образом, нарушение правила G-O может свидетельствовать о начале Маундерово-Дальтоновского минимума активности. Все эти результаты, по-видимому, согласуются с выводом Хосе (1965) о существовании связи когерентности 179-летнего цикла между солнечной магнитной активностью и динамикой Солнечной системы.
То есть нынешняя тенденция относительно низкого уровня активности солнечных пятен в текущем 23-м цикле, который следует за пунктирной вертикальной линией в 1990 г., может сохраниться еще в течение нескольких циклов солнечных пятен. Такое указание также обнаружено в недавних исследованиях долговременных изменений активности солнечных пятен (например, Бонев, Пенев и Селло, 2004; Хэтэуэй и Уилсон, 2005) и скорости вращения Солнца на экваторе (Джаварайя, 2003b; Джаварайя, Бертелло и Ульрих, 2005b). Кроме того, ряд авторов предсказал слабую активность во время следующего цикла 24, используя большое количество методик (например, Кейн 19).99; Эчер и др. 2004 г.; Свальгаард, Кливер и Камиде, 2005 г.). Таким образом, нарушение правила G-O может свидетельствовать о начале Маундерово-Дальтоновского минимума активности. Все эти результаты, по-видимому, согласуются с выводом Хосе (1965) о существовании связи когерентности 179-летнего цикла между солнечной магнитной активностью и динамикой Солнечной системы. Если учесть, что последние три последовательных 179-летних цикла активности солнечных пятен начались примерно в 1632, 1811 и 1990 годах, первая половина (может представлять цикл Глейсберга) каждого из первых двух циклов слабее, чем соответствующая вторая половина, предполагая, что текущий полупериод (включает около 80 процентов текущего столетия) будет слабее, чем его вторая половина. В течение этой половины 179годового цикла средняя активность в течение первой половины (двойной цикл Хейла, включающий циклы 22–25) может быть слабее, чем во второй половине (Javaraiah 2003b). [Обратите внимание, что два основных падения L происходят в течение первой четверти 179-летнего цикла, во временном промежутке около 43 лет. На самом деле, текущая эпоха активности солнечных пятен, по-видимому, приходится на фазу спада цикла Глейсберга, минимум которого ожидается ближе к концу 25-го цикла (Javaraiah et al. 2005b).]
Если учесть, что последние три последовательных 179-летних цикла активности солнечных пятен начались примерно в 1632, 1811 и 1990 годах, первая половина (может представлять цикл Глейсберга) каждого из первых двух циклов слабее, чем соответствующая вторая половина, предполагая, что текущий полупериод (включает около 80 процентов текущего столетия) будет слабее, чем его вторая половина. В течение этой половины 179годового цикла средняя активность в течение первой половины (двойной цикл Хейла, включающий циклы 22–25) может быть слабее, чем во второй половине (Javaraiah 2003b). [Обратите внимание, что два основных падения L происходят в течение первой четверти 179-летнего цикла, во временном промежутке около 43 лет. На самом деле, текущая эпоха активности солнечных пятен, по-видимому, приходится на фазу спада цикла Глейсберга, минимум которого ожидается ближе к концу 25-го цикла (Javaraiah et al. 2005b).]
Минимум Маундера (1645–1715) и другие подобные эпохи низкой активности также объяснялись на основе изменений в движении Солнца вокруг центра масс Солнечной системы (Fairbridge & Shirley 1987; Charvátová 2000; Juckett 2000). Одна из часто цитируемых причин отказа от роли динамики Солнечной системы в механизме солнечной активности заключается в том, что активность солнечных пятен отсутствовала во время минимума Маундера, но присутствовали планетарные конфигурации (например, Смайт и Эдди 19).77). Этот аргумент кажется неверным, поскольку интервал между выравниваниями всех внешних планет в одной и той же конфигурации и в одном и том же направлении в пространстве составляет около 179 лет, и ни одно выравнивание больших планет не повторяется в точности (Хосе, 1965, а также см. Таблицу 1). Имеется значительный объем информации о скорости вращения Солнца во время минимума Маундера. Эдди, Гилман и Троттер (1976) проанализировали рисунки солнечных пятен, сделанные Дж. Гевелием в период 1662–1664 гг., т. е. как раз перед началом минимума Маундера, и обнаружили, что скорость экваториального вращения была примерно на 4 % выше, чем значение в современное время. Абарбанелл и Вёль (1981) проанализировал те же данные и обнаружил, что в период 1662–1664 годов скорость вращения экватора была такой же, как и в наше время.
Одна из часто цитируемых причин отказа от роли динамики Солнечной системы в механизме солнечной активности заключается в том, что активность солнечных пятен отсутствовала во время минимума Маундера, но присутствовали планетарные конфигурации (например, Смайт и Эдди 19).77). Этот аргумент кажется неверным, поскольку интервал между выравниваниями всех внешних планет в одной и той же конфигурации и в одном и том же направлении в пространстве составляет около 179 лет, и ни одно выравнивание больших планет не повторяется в точности (Хосе, 1965, а также см. Таблицу 1). Имеется значительный объем информации о скорости вращения Солнца во время минимума Маундера. Эдди, Гилман и Троттер (1976) проанализировали рисунки солнечных пятен, сделанные Дж. Гевелием в период 1662–1664 гг., т. е. как раз перед началом минимума Маундера, и обнаружили, что скорость экваториального вращения была примерно на 4 % выше, чем значение в современное время. Абарбанелл и Вёль (1981) проанализировал те же данные и обнаружил, что в период 1662–1664 годов скорость вращения экватора была такой же, как и в наше время. Ribes & Nesme-Ribes (1993) проанализировали уникальную коллекцию наблюдений за солнечными пятнами, зарегистрированных в Парижской обсерватории с 1660 по 1719 год, и обнаружили, что экваториальное вращение было примерно на 2 процента ниже, чем в наше время. Недавно Vaquero, Sánchez-Bajo & Gallego (2002) проанализировали наблюдения солнечного пятна, проведенные Флемстидом (1684) с 25 апреля 1684 года по май 1684 года, и обнаружили, что во время глубокого минимума Маундера (1666–1700) скорость вращения около экватор был примерно на 5 процентов ниже, чем в наше время. В целом эти результаты предполагают наличие большого падения скорости экваториального вращения во время глубокого минимума Маундера. Большое падение скорости экваториального вращения во время глубокого минимума Маундера может быть связано с резким уменьшением скорости L в 16:32 и 1671 (см. рис. 1), и, очевидно, к конфигурациям больших планет в эти эпохи (см. табл. 1). Эффект большого падения A вблизи этих эпох мог сохраняться на протяжении всего минимума Маундера и вызывать почти полное отсутствие активности (Javaraiah 2003b).
Ribes & Nesme-Ribes (1993) проанализировали уникальную коллекцию наблюдений за солнечными пятнами, зарегистрированных в Парижской обсерватории с 1660 по 1719 год, и обнаружили, что экваториальное вращение было примерно на 2 процента ниже, чем в наше время. Недавно Vaquero, Sánchez-Bajo & Gallego (2002) проанализировали наблюдения солнечного пятна, проведенные Флемстидом (1684) с 25 апреля 1684 года по май 1684 года, и обнаружили, что во время глубокого минимума Маундера (1666–1700) скорость вращения около экватор был примерно на 5 процентов ниже, чем в наше время. В целом эти результаты предполагают наличие большого падения скорости экваториального вращения во время глубокого минимума Маундера. Большое падение скорости экваториального вращения во время глубокого минимума Маундера может быть связано с резким уменьшением скорости L в 16:32 и 1671 (см. рис. 1), и, очевидно, к конфигурациям больших планет в эти эпохи (см. табл. 1). Эффект большого падения A вблизи этих эпох мог сохраняться на протяжении всего минимума Маундера и вызывать почти полное отсутствие активности (Javaraiah 2003b). Интересно отметить, что начало известного минимума Шпёрера (1450–1550 гг.) было примерно около 179 лет назад с 1632 года. Следовательно, причина минимума Шпёрера может быть такой же, как и причина минимума Маундера, как было предложено выше.
Интересно отметить, что начало известного минимума Шпёрера (1450–1550 гг.) было примерно около 179 лет назад с 1632 года. Следовательно, причина минимума Шпёрера может быть такой же, как и причина минимума Маундера, как было предложено выше.
Мы использовали здесь данные только о планетах-гигантах. Однако внутренние планеты также могут быть важны из-за их близости к Солнцу. Их приливные силы на Солнце больше, чем у внешних планет (кроме Юпитера). Поэтому, когда они близко выровнены с Юпитером, комбинированный эффект может вызвать «рывки» (скорость изменения ускорения) в орбитальном движении Солнца (Вуд и Вуд, 1965). Есть некоторые всплески в вариациях A и B . В частности, в некоторые минимальные годы значения B почти равны нулю или даже положительны (см. рис. 2). Многие из этих всплесков могут быть результатом того, что размеры данных групп пятен в эти годы малы. Всплески вариации B в 1887, 1962 и 1996 годах оказывают значительное влияние на уровни значимости полученных периодичностей B (Javaraiah & Komm 1999). Однако в эти годы статистика достаточно хороша, а значения имеют погрешность менее чем в три раза превышающую медианную ошибку. Более того, мы обнаружили аналогичные аномалии в значениях B в течение 1962 г. по данным обсерватории Маунт-Вильсон и Кодайканалской обсерватории (доступно на сайте ). Мы подтвердили аномальное поведение B в течение 1996 года, используя данные рисунков солнечных пятен обсерватории Маунт-Вилсон (доступны по адресу ). Kambry & Nishikawa (1990) также получили аналогичное значение B в течение 1962 года на основе данных о группе пятен, измеренных в Национальной астрономической обсерватории Японии. Следовательно, вышеупомянутое аномальное поведение B год кажется реальным свойством вращения солнечных пятен в указанные годы. Между прочим, 5 февраля 1962 года пять видимых невооруженным глазом планет плюс Солнце и Луна выровнялись в пределах 15,8°, и в это же время произошло солнечное затмение (Мозли, 1996).
Однако в эти годы статистика достаточно хороша, а значения имеют погрешность менее чем в три раза превышающую медианную ошибку. Более того, мы обнаружили аналогичные аномалии в значениях B в течение 1962 г. по данным обсерватории Маунт-Вильсон и Кодайканалской обсерватории (доступно на сайте ). Мы подтвердили аномальное поведение B в течение 1996 года, используя данные рисунков солнечных пятен обсерватории Маунт-Вилсон (доступны по адресу ). Kambry & Nishikawa (1990) также получили аналогичное значение B в течение 1962 года на основе данных о группе пятен, измеренных в Национальной астрономической обсерватории Японии. Следовательно, вышеупомянутое аномальное поведение B год кажется реальным свойством вращения солнечных пятен в указанные годы. Между прочим, 5 февраля 1962 года пять видимых невооруженным глазом планет плюс Солнце и Луна выровнялись в пределах 15,8°, и в это же время произошло солнечное затмение (Мозли, 1996).
Принимая во внимание наличие статистически значимой периодичности ∼18,3 в B , интересно отметить, что самые сильные засухи в мире (Hoyt & Schatten 1997) и даже сильные землетрясения в Калифорнии (), по-видимому, происходили с перерывами около 18 лет. Подобная периодичность может существовать и во вращении Земли (Киров, Георгиева и Джаварая, 2002). Период прецессии Луны также равен 18,6 года. Кроме того, были сильные засухи в 1886/1887, 1962/1963 и 1995/1996 (Foweler & Kilsby 2000), когда значения коэффициента B являются аномальными. Поэтому, принимая во внимание результаты разделов 3 и 4, может быть целесообразно исследовать, все ли изменения во внутренней динамике Солнца и Земли, а также земные явления определяются динамикой Солнечной системы. Однако здесь следует отметить, что до сих пор не найдено убедительных доказательств влияния планетарной динамики на земные явления, климат, динамику Земли и/или землетрясений. Гриббин и Плагеманн (1974) описал выравнивание всех девяти планет в 1982 году как суперсоединение, при котором все они находились на одной стороне от Солнца. Они предсказали, что такое выравнивание вызовет сильное землетрясение в 1982 году и крупную катастрофу в Лос-Анджелесе. К счастью, это предсказание не сбылось.
Подобная периодичность может существовать и во вращении Земли (Киров, Георгиева и Джаварая, 2002). Период прецессии Луны также равен 18,6 года. Кроме того, были сильные засухи в 1886/1887, 1962/1963 и 1995/1996 (Foweler & Kilsby 2000), когда значения коэффициента B являются аномальными. Поэтому, принимая во внимание результаты разделов 3 и 4, может быть целесообразно исследовать, все ли изменения во внутренней динамике Солнца и Земли, а также земные явления определяются динамикой Солнечной системы. Однако здесь следует отметить, что до сих пор не найдено убедительных доказательств влияния планетарной динамики на земные явления, климат, динамику Земли и/или землетрясений. Гриббин и Плагеманн (1974) описал выравнивание всех девяти планет в 1982 году как суперсоединение, при котором все они находились на одной стороне от Солнца. Они предсказали, что такое выравнивание вызовет сильное землетрясение в 1982 году и крупную катастрофу в Лос-Анджелесе. К счастью, это предсказание не сбылось. В выравнивании 1982 года планеты разошлись на 98° (DeYoung 1979).
В выравнивании 1982 года планеты разошлись на 98° (DeYoung 1979).
Здесь также следует отметить, что некоторые относительно краткосрочные предсказания солнечной активности, сделанные на основе гипотезы о роли динамики Солнечной системы в механизме солнечной активности, не оправдались (Миус 1991; Ли, Юн и Гу, 2001). Причиной этого может быть то, что основная физика не ясна. С другой стороны, наклоны плоскостей орбит планет и экватора Солнца к эклиптике (или к неизменной плоскости) кажутся важными (Blizard, 1983; Javaraiah, 1996, 2003a; Juckett, 2000), но они не принимались во внимание. учитываться в большинстве предыдущих исследований.
6 Подведение итогов и заключение
Мы показали, что эпохи нарушения известного правила G–O в спаривании циклов пятен близки к эпохам попятного движения Солнца по орбите вокруг центра масс Солнечной системы. система. Из этого результата легко заранее узнать эпохи нарушения правила G–O. Ожидается, что правило G – O будет нарушено циклом Хейла, который будет включать (или заканчиваться) 2169 год., т.е. только после разрыва примерно в восемь циклов Хейла после текущего цикла Хейла 11. Однако нарушение правила G–O в силу различия значений пиков пары циклов — как и пары циклов 8, 9 около 1851 г. — ожидается, что произойдет около 2030 г., т. е. по паре циклов 26, 27. Мы также показали, что скорость экваториального вращения Солнца, определенная по данным о группе солнечных пятен за период 1879–2004 гг., коррелирует к орбитальному крутящему моменту Солнца, положительно до 1945 и отрицательно после этого времени. Экваториальное вращение имеет доминирующую периодичность около 17 лет. Эти результаты хорошо согласуются с результатами модели спин-орбитального взаимодействия сплюснутого Солнца Джакетта (2000) и могут служить прямым наблюдательным подтверждением гипотезы о роли солнечной динамики во внутренней динамике Солнца. и в вариациях солнечной активности.
Ожидается, что правило G – O будет нарушено циклом Хейла, который будет включать (или заканчиваться) 2169 год., т.е. только после разрыва примерно в восемь циклов Хейла после текущего цикла Хейла 11. Однако нарушение правила G–O в силу различия значений пиков пары циклов — как и пары циклов 8, 9 около 1851 г. — ожидается, что произойдет около 2030 г., т. е. по паре циклов 26, 27. Мы также показали, что скорость экваториального вращения Солнца, определенная по данным о группе солнечных пятен за период 1879–2004 гг., коррелирует к орбитальному крутящему моменту Солнца, положительно до 1945 и отрицательно после этого времени. Экваториальное вращение имеет доминирующую периодичность около 17 лет. Эти результаты хорошо согласуются с результатами модели спин-орбитального взаимодействия сплюснутого Солнца Джакетта (2000) и могут служить прямым наблюдательным подтверждением гипотезы о роли солнечной динамики во внутренней динамике Солнца. и в вариациях солнечной активности.
Благодарности
Автор выражает благодарность д-ру Ференцу Варади за предоставление полных планетарных данных, использованных здесь, и за плодотворное обсуждение результатов. Автор также благодарит профессора Роджера К. Ульриха за комментарии и анонимного рецензента за полезные предложения. В настоящее время автор работает над проектом оцифровки архива Маунт-Вилсон в Калифорнийском университете в Лос-Анджелесе, финансируемом грантом NSF ATM-0236682.
Автор также благодарит профессора Роджера К. Ульриха за комментарии и анонимного рецензента за полезные предложения. В настоящее время автор работает над проектом оцифровки архива Маунт-Вилсон в Калифорнийском университете в Лос-Анджелесе, финансируемом грантом NSF ATM-0236682.
Ссылки
Abarbanell
C.
Wöhl
H.
,
1981
,
3 Sol. физ.
,
70
,
197
Beer
J.
Blinov
A.
Bonani
G.
Hofmann
H. J.
Finkel
R. C.
,
1990
,
Нац
,
347
,
164
Blizard
J. B.
B.
,
1983
,
BAAS
,
15
,
906
Blizard
J. B.
,
1989
,
PASP
,
101
,
890
Bonev
B. P.
Penev
K. M.
Sello
0003S.
,
2004
,
ApJ
,
605
,
L81
Brown
E. W.
,
1900
,
MNRAS
,
60
,
599
Харватова
I.
,
2000
,
Анн. Геофиз. 18
,
399
де Янг
D. B.
,
1979
, Impact No. 72 (только онлайн-справка), http://www.icr.org/pubs/imp/imp-072.htm
Echer
E.
3
RigozoN. R.
Nordemann
D. J. R.
Vieira
L. E. A.
,
2004 , 9108 Геофиз. 22
,
2239
Эдди
Дж. А.
Гилман
P. A.
Trotter
D. E.
,
1976
,
Sol. физ.
,
46
,
3
Fairbridge
R. W.
W.
Shirley
J. H.
,
1987
,
Sol. физ.
,
110
,
191
Феррис
Г. А. Дж.
,
1963
03
Дж.Бр. Астрон. доц. 79
,
385
Флэмстид
Дж.
,
1684
,
2 . Транс. 14
,
535
Fowler
H. J.
Kilsby
C. G.
,
2002
,
J. Hydrol.
,
262
,
177
(http://www.staff. ncl.ac.uk/h.j.fowler/histdrought.htm)
ncl.ac.uk/h.j.fowler/histdrought.htm)
Georgivea
K.
Kirov
B.
Javaraiah
J.
Krasteva
R.
,
2005
,
. Космические науки.
,
53
,
197
Gnevyshev
M. N.
Ohl
A. I.
,
1948
,
AZh
,
25
,
18
Гокхале
М. Х.
,
1996
,
Bull. Астрон. соц. Индия
,
24
,
121
Gokhale
M. H.
H.
Javaraiah
J.
,
1995
,
. физ.
,
156
,
157
Гокхале
М. Х.
Джаварая
J
, eds,
2002
,
Вращение Солнца
.
Nova Science Publishers, Inc.
,
Нью-Йорк
, с.
109
Gribbin
J.
Plagemann
S.
,
1974
,
Эффект Jupiter
.
Walker & Co.
,
Нью-Йорк
, с.
261
Hathaway
D. H.
Wilson
R. M.
,
2005
,
Sol. физ.
,
224
,
5
Hathaway
D. H.
Wilson
R. M.
REICHMANN
E. J.
,
1999
,
,
1999
,
. Рез.
,
104
,
22375
Hiremath
K. M.
,
2002
,
A&A
,
386
,
674
Hiremath
K. M.
M.
Mandi
P. I.
,
2004
,
Newa
,
,
651
Howard
R.
Harvey
J.
,
1970
,
.0003
Сол. физ.
,
12
,
23
Hoyt
D. V.
Schatten
K. H.
,
1997
,
Роль из Climate Change
.
Оксфорд Юниверсити Пресс, Инк. Астрон. соц. Индия
,
24
,
351
Javaraiah
J.
,
1998
, in
Korzennik
S. G.
G.
Wilson
A.
, eds,
Structure and Динамика недр Солнца и солнцеподобных звезд
, ESA SP-418.
ESA Publications Division
,
Noordwijk
, p.
809
Джаварая
Дж.
,
2003
,
Сол. физ.
,
212
,
23
Javaraiah
J.
,
2003
,
A&A
,
401
,
L9
Javaraiah
J.
Гокхале
М. Х.
,
1995
,
Сол. физ.
физ.
,
158
,
173
Javaraiah
J.
Gokhale
M. H.
,
1997
,
A & A
,
,
A & A
,
.
Дж.
Комм
Р. В.
,
1999
,
Сол. физ.
,
184
,
41
Джаварая
J.
Bertello
L.
ULRICH
R. K.
,
2005
,
,
626
,
,
626
. Бертелло
Бертелло
Л.
Ульрих
Р. К.
,
2005
,
Сол. физ.
, в печати
Хосе
ПД
,
1965
,
AJ
,
70
,
193
Joselyn
J.
3 et al. ,
1997
,
ЭОС. Транс. амер. Геофиз. Union
,
78
,
211
Juckett
D. A.
,
2000
,
Sol. физ.
,
191
,
201
Джакетт
D. A.
A.
,
2003
,
A&A
,
399
,
731
Kambry
M. A.
Nishikawa
J.
,
1990
,
Сол. физ.
,
126
,
89
Kane
R. P.
,
1999
,
Sol Phys.
,
189
,
217
Kirov
B.
Georgieva
K.
Javaraiah
J.
,
, в
,
, в
,
, в
,
, в
,
. ,
,
Солнечная изменчивость: от ядра до внешних границ
, ESA SP-506.
ESA Publications Division
,
Noordwijk
, p.
149
Комитов
Б.
Bonev
B.
,
2001
,
ApJ
,
554
,
L119
Krivova
N. A.
Solanki
S. K.
Beer
J.
,
2002
,
A & A
,
396
,
235
Landscheidt
T.
,
T.
,
T.
,
T.
,
T.
,
1081 ,Сол. физ.
,
150
,
359
Li
K. J.
Yun
H. S.
Gu
X. M.
,
2001
,
A&A
,
368
,
285
Меус
Дж.
,
1991
,
Дж.Бр. Астрон. доц. 101
,
115
Mosely
J.
,
1996
,
Planetarian, 256
(http://www. griffithobs.org/SkyAlignments.html)
griffithobs.org/SkyAlignments.html)
Mörth
H. T.
Schlamminger
L.
,
1979
, в
McCormac
B. M.
Seliga
T. A.
, Eds,
Solar-Cerrestrevial Iffectials на погоду и клима
, Eds,
Солневые0003
.
Reidel
,
Дордрехт
, с.
183
Newton
H. W.
Nunn
M. L.
,
1951
,
MNRAS
,
111
,
413
Ossenderijver
M.
,
2003
,
АиАР
,
11
,
287
Ribes
J. C.
C.
Nesme-Ribes
E.
,
1993
,
A&A
,
276
,
549
Rosner
R.
Вайс
Н.О.
,
1992
, в
Харви
К.Л.
, изд.,
АСП сер. Том. 27, Солнечный цикл. Астрон. соц. пакет
,
Сан-Франциско
, с.
511
Розелот
J. P.
,
2001
,
J. Atmos. Соль.-Терр. Phys
,
63
,
375
Schove
D. J.
,
1955
,
J. Geophys. Рез. 60
,
127
Seidelmann
P. K.
,
1992
,
Пояснительное приложение к Астрономическому альманаху
, исправленное издание.
University Science Books
,
Mill Valley, CA, USA
Sivaraman
K. R.
Sivaraman
H.
Gupta
S. S.
Howard
R. F.
,
2003
,
Сол. физ.
,
214
,
65
Smythe
C. M.
Eddy
J. A.
,
1977
,
Nat
,
266
,
434
Sperber
K. R.
R.
Fairbridge
R. W.
,
1990
,
Сол. физ.
,
127
,
379
Стэндиш
Э. М.
,
1998
,
Лаборатория реактивного движения Планетарные и лунные эфемериды, DE405/LE405, Межведомственная записка. 312.F-98-048
.
Jet Propulsion Laboratory
,
Pasadena, CA
(ftp://navigator.jpl.nasa.gov/ephem/export/de405.iom)
Svalgaard
L.
Cliver
E. W.
Камиде
Ю.
,
2005
,
Геофиз. Рез. лат.
,
32
,
L01104
Usoskin
I. G.
G.
Mursula
K.
Kovaltsov
G. A.
,
2001
,
A&A
,
370
,
L31
USOSKIN
I. G.
Mursula
K.
Kovaltsov
G. A.
,
2003
,
A & A
,
,
A & A
,
,
A & A
,
,
A & A
,
,
A & A
,
,
A & A
,
,
A & A
,
403
,
743
Vaquero
J. M.
M.
Sánchez-Bajo
F.
Gallego
M. C.
,
2002
,
Sol. физ.
,
207
,
219
Wilson
R. M.
,
1988
,
Sol. физ.
,
117
,
269
Древесина
R. M.
Wood
K. D.
,
1965
,
Nat
,
208
,
129
Zaqarashvili
T. V.
,
1997
,
ApJ
,
487
,
930
Примечания автора
†.
Постоянный адрес: Индийский институт астрофизики, Бангалор-560 034, Индия (Электронная почта: [email protected])
© 2005 РАН
© 2005 РАН
Раздел выпуска:
Статьи
Скачать все слайды
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Оповещение о текущей проблеме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Система астрофизических данных
Резюме объявленийСсылки на статьи по номеру
Последний
Самые читаемые
Самые цитируемые
Эксперимент кластерных возрастов (CASE) – IX.

 n.
n.
 1 — известная гипотеза Триппербаха, доказанная совсем недавно японским математиком Хацукаки в 300-страничной работе. Международное матемематическое сообщество всё ещё не пришло к общему мнению, можно ли представленный текст считать доказательством. Три айнзатц-группы разбирают доказательстви, проверяя его в мельчайших деталях. Если ошибок не будет найдено, то на следующем конгрессе ММО автор несомненно будет удостоен Филдсовской медали.
1 — известная гипотеза Триппербаха, доказанная совсем недавно японским математиком Хацукаки в 300-страничной работе. Международное матемематическое сообщество всё ещё не пришло к общему мнению, можно ли представленный текст считать доказательством. Три айнзатц-группы разбирают доказательстви, проверяя его в мельчайших деталях. Если ошибок не будет найдено, то на следующем конгрессе ММО автор несомненно будет удостоен Филдсовской медали. c.
c.
 Однако в современном мире люди чаще пользуются электронными ходиками. Они также подойдут для гадания.
Однако в современном мире люди чаще пользуются электронными ходиками. Они также подойдут для гадания.
 Особенно у того, кто в гадание по часам верит!
Особенно у того, кто в гадание по часам верит!
 Постарайтесь провести день спокойно и тихо.
Постарайтесь провести день спокойно и тихо. Кстати, о материальных подарках со стороны близких людей тоже идет речь, потому что сегодня такое время, когда вам предстоит получить сюрпризы и приятные неожиданности. Вы будете приятно удивлены не один раз!
Кстати, о материальных подарках со стороны близких людей тоже идет речь, потому что сегодня такое время, когда вам предстоит получить сюрпризы и приятные неожиданности. Вы будете приятно удивлены не один раз! К примеру, для молодых людей и незамужних девушек 14:41 означает любовные приключения, новые знакомства, флирт и все самое приятное, связанное с романтической сферой.Для людей же семейных и взрослых, цифры 14:41 сулят приятное общение, отдых, примирение в семье, гармоничный и спокойный день, полный радости.
К примеру, для молодых людей и незамужних девушек 14:41 означает любовные приключения, новые знакомства, флирт и все самое приятное, связанное с романтической сферой.Для людей же семейных и взрослых, цифры 14:41 сулят приятное общение, отдых, примирение в семье, гармоничный и спокойный день, полный радости. Комбинация 20:02 состоит из двоек и нолей, и может сулить ссору с любимым или близким человеком. Держите эмоции под контролем, умейте промолчать.
Комбинация 20:02 состоит из двоек и нолей, и может сулить ссору с любимым или близким человеком. Держите эмоции под контролем, умейте промолчать. Но никто не может точно сказать, положительными они будут или отрицательными.
Но никто не может точно сказать, положительными они будут или отрицательными.

 Но так как мы с вами живем в современном мире, то рассмотрим гадание по электронным часам, которые мы можем наблюдать не только в офисе или дома, но и в магазинах, на вокзалах, на улицах, в метро и т.д.
Но так как мы с вами живем в современном мире, то рассмотрим гадание по электронным часам, которые мы можем наблюдать не только в офисе или дома, но и в магазинах, на вокзалах, на улицах, в метро и т.д. К примеру, те же 12 все время перед вашими глазами не просто говорят вам, а «кричат» о том, что вас ждет новое интересное знакомство, а цифра 48 – это уже предвещает бурный роман.
К примеру, те же 12 все время перед вашими глазами не просто говорят вам, а «кричат» о том, что вас ждет новое интересное знакомство, а цифра 48 – это уже предвещает бурный роман.
 02 — тебя ждет приглашение или в клуб или просто в гости
02 — тебя ждет приглашение или в клуб или просто в гости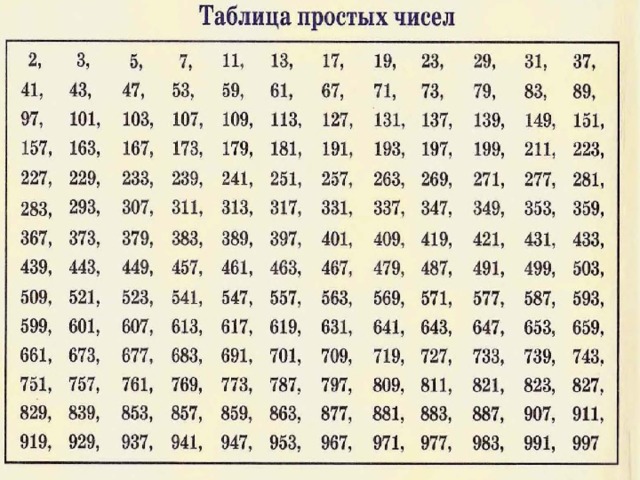 10 — твое время наступает
10 — твое время наступает


 С такого типа утверждениями (они называются предикатами)
мы познакомимся чуть позже.
С такого типа утверждениями (они называются предикатами)
мы познакомимся чуть позже. Например: 7 + 3 = 10
Например: 7 + 3 = 10 Например: 7 × 5 = 35
Например: 7 × 5 = 35

 Джаварая, Ретроградное движение Солнца и нарушение правила четно-нечетного цикла активности солнечных пятен, Ежемесячные уведомления Королевского астрономического общества , том 362, выпуск 4, октябрь 2005 г., страницы 1311–1318, https://doi.org/10.1111/j.1365-2966.2005.09403.x
Джаварая, Ретроградное движение Солнца и нарушение правила четно-нечетного цикла активности солнечных пятен, Ежемесячные уведомления Королевского астрономического общества , том 362, выпуск 4, октябрь 2005 г., страницы 1311–1318, https://doi.org/10.1111/j.1365-2966.2005.09403.x