Доказательство неравенств методом математической индукции.
Доказательство методом математической индукции основано на следующей аксиоме: если предложение, в формулировку которого входит натуральное число п, истинно при п=1 и из его истинности при n=k ( где ) следует, что оно истинно и при , то оно истинно при всех натуральных значениях п.
Таким образом, доказательство по методу математической индукции проводится следующим образом:
1) доказываемое утверждение проверяется при п =1;
2) предполагая справедливость утверждения при n=k, доказывается справедливость утверждения для n=k+1.
Некоторые утверждения справедливы не для всех натуральных п, а для п, начиная с некоторого числа р. В таком случае первый шаг доказательства – это проверка справедливости утверждения для п=р .
П р и м е р. Доказать, что если , то
Доказательство. При n=3 неравенство верно: . Предположим, что неравенство выполняется при n=k (k>3), т.е. предположим, что , и докажем, что тогда неравенство выполняется и при n=k+1, т. е. докажем, что
Предположим, что неравенство выполняется при n=k (k>3), т.е. предположим, что , и докажем, что тогда неравенство выполняется и при n=k+1, т. е. докажем, что
В самом деле, имеем: . Итак, .
Но при любом натуральном значении k. Следовательно, тем более .
Согласно методу математической индукции можно сделать вывод о том, что доказываемое неравенство справедливо при всех .
Доказательство неравенств методом полной индукции.
Полная индукция – это метод рассуждений, при котором вывод делается на основании рассмотрения всех случаев, возможных по условию задачи.
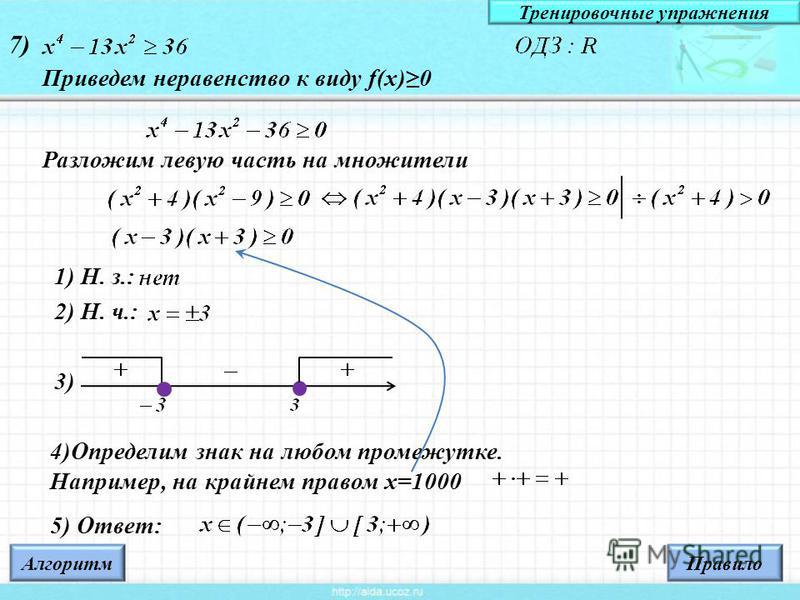
П р и м е р. Доказать, что если .
Доказательство. Рассмотрим случаи:
1) . Получаем
, т.к.
Неравенство верно.
2) , т.е. .
Тогда . Неравенство справедливо.
3) т.е. .
Тогда . Неравенство справедливо.
Мы рассмотрели все возможные случаи. Значит неравенство верно для .
6. Доказательство неравенств с помощью методов математического анализа.
В этом случае доказательство неравенств сводят к исследованию соответствующих функций с помощью производных.
П р и м е р. Доказать неравенство
Доказательство. Перепишем неравенство в виде: .
Рассмотрим функцию .
Найдём производную . При , . Это значит, что при возрастает, причём . Поэтому при .
Литература
1. В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М, 1999
2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000
Тема: Иррациональные уравнения и неравенства.
План
1. Иррациональные уравнения, основные методы их решения.
2. Иррациональные неравенства.
Иррациональные уравнения.
Иррациональными называются уравнения и неравенства, содержащие переменную под знаком корня или под знаком возведения в дробную степень.
Все корни чётной степени, входящие в уравнение, являются арифметическими, т.е. если подкоренное выражение отрицательно, то корень лишён смысла; если подкоренное выражение равно нулю, то корень также равен нулю; если подкоренное выражение положительно, то значение корня положительно.
Все корни нечётной степени, входящие в уравнение, определены при любом действительном значении подкоренного выражения и в зависимости от знака подкоренного выражения могут принимать как неотрицательные, так и отрицательные значения.
Основные методы решения иррациональных уравнений:
1. возведение обеих частей уравнения в одну и ту же степень;
2. замена переменной;
3. умножение обеих частей уравнения на одну и ту же функцию;
4. применение свойств функций, входящих в уравнение.
Следует помнить, что ряд преобразований, которые применяются при реализации указанных методов, например возведение обеих частей уравнения в чётную степень, приводят к уравнению-следствию. Оно, наряду с корнями исходного уравнения содержит и другие корни, которые называют посторонними. Поэтому после решения уравнения-следствия необходимо найти способ отсеять посторонние корни. Обычно это можно сделать при помощи проверки, которая в данном случае рассматривается как один из этапов решения.
Оно, наряду с корнями исходного уравнения содержит и другие корни, которые называют посторонними. Поэтому после решения уравнения-следствия необходимо найти способ отсеять посторонние корни. Обычно это можно сделать при помощи проверки, которая в данном случае рассматривается как один из этапов решения.
Возможен и другой путь реализации некоторых методов решения иррациональных уравнений – переход к равносильным системам, в которых учитывается область определения уравнения и требование неотрицательности обеих частей уравнения, возводимых в чётную степень.
Рассмотрим несколько примеров.
Пример 1. Решим уравнение .
Решение. Возводим обе части уравнения в квадрат, получаем:
Проверка показывает, что только является корнем исходного уравнения.
Ответ: -4.
Пример 2. Решим уравнение
Решение. Выполним замену. Обозначим: заметим, что .
Тогда и .
Исходное уравнение принимает вид:
Полученное уравнение равносильно системе:
Из получившейся системы, имеем: .
Возвращаемся к подстановке, получаем:
Ответ: 1; .
Пример 3. Решим уравнение .
Решение: Пусть
Тогда имеем:
Откуда последовательно получаем:
Возвращаясь к первоначальным подстановкам, получим:
Откуда
С помощью проверки убеждаемся, что оба корня являются корнями исходного уравнения.
Ответ: 1; -15.
Пример 4. Решим уравнение .
Решение: Рассмотрим функцию .
Исходное уравнение принимает вид: .
. Функция монотонно возрастает на всей области определения. Поэтому уравнение может иметь не более одного корня. Легко видеть, что является корнем уравнения.
Ответ: 5.
Иррациональные неравенства.
Основным методом решения иррациональных неравенств является метод сведения исходного неравенства к равносильной системе рациональных неравенств или совокупности таких систем. При этом используются те же приёмы, что и при решении иррациональных уравнений: возведение обеих частей неравенства в одну и ту же степень, введение новых переменных, использование свойств функций, входящих в обе части неравенства и т. д.
д.
Рассмотрим некоторые виды иррациональных неравенств и подходы к их решению:
1) Неравенство вида равносильно системе
2) Неравенство вида равносильно неравенству .
3) Неравенство вида равносильно совокупности систем
4) Неравенство вида равносильно системе
Пример 5. Решим неравенство .
Решение. Введём новую переменную . Тогда исходное неравенство принимает вид:
.
Решая это неравенство и возвращаясь к исходным переменным, получаем: .
Ответ: .
Пример 6. Решим неравенство .
Решение: Перепишем неравенство в виде: .
Это неравенство равносильно системе неравенств:
Откуда получаем .
Пример 6. Решим неравенство .
Решение: Рассмотрим функцию . Область определения этой функции . Функция возрастает на всей области определения, причём . Значит, неравенство решений не имеет.
Ответ: нет решений.
Литература
1. В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М, 1999
2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000
Текстовые задачи
План
Метод математической индукции презентация, доклад
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
СОДЕРЖАНИЕ
Полная и неполная индукция
Принцип математической индукции
Метод математической индукции
Применение метода математической индукции к суммированию рядов
Метод математической индукции в решении задач на делимость
Доказательство тождеств с помощью математической индукции
Доказательство неравенств с помощью математической индукции
Решение геометрических задач с помощью математической индукции
ПОЛНАЯ И НЕПОЛНАЯ ИНДУКЦИЯ
По своему первоначальному смыслу слово “индукция” применяется к рассуждениям, при помощи которых получают общие выводы, опираясь на ряд частных утверждений.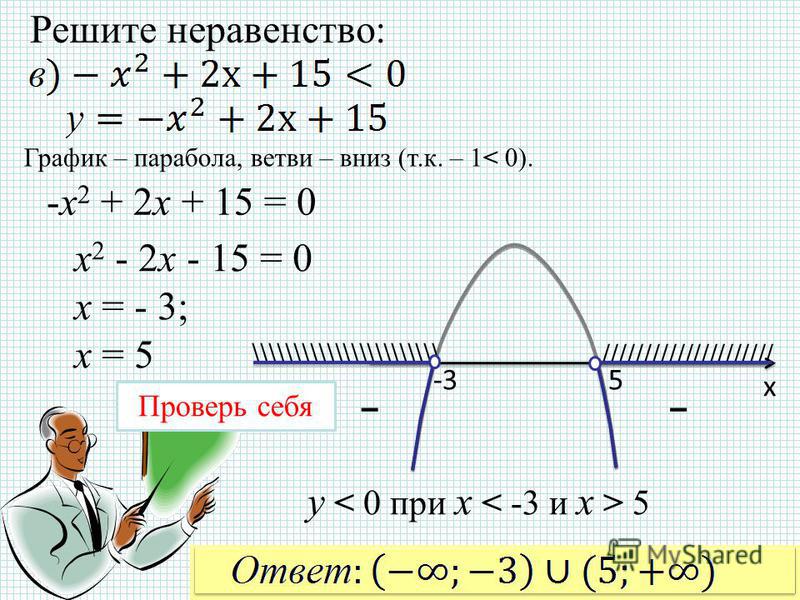 Простейшим методом рассуждений такого рода является полная индукция.
Простейшим методом рассуждений такого рода является полная индукция.
пример
ПОЛНАЯ И НЕПОЛНАЯ ИНДУКЦИЯ
Пусть требуется установить, что каждое натуральное чётное число n в пределах 44=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5;
14=7+7; 16=11+5; 18=13+5; 20=13+7.
Эти девять равенств показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.
Таким образом, полная индукция заключается в том, что общее утверждение доказывается по отдельности в каждом из конечного числа возможных случаев.
ПОЛНАЯ И НЕПОЛНАЯ ИНДУКЦИЯ
Иногда общий результат удаётся предугадать после рассмотрения не всех, а достаточно большого числа частных случаев (так называемая неполная индукция). Результат, полученный неполной индукцией, остается, однако, лишь гипотезой, пока он не доказан точным математическим рассуждением, охватывающим все частные случаи.
пример
ПОЛНАЯ И НЕПОЛНАЯ ИНДУКЦИЯ
Пусть, например, требуется найти сумму первых n последовательных нечётных чисел. Рассмотрим частные случаи:
1=1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
Разумеется, сделанное наблюдение ещё не может служить доказательством справедливости приведённой формулы.
После рассмотрения этих нескольких частных случаев напрашивается следующий общий вывод:
1+3+5+…+(2n-1)=n2
т.е. сумма n первых последовательных нечётных чисел равна n2
ПОЛНАЯ И НЕПОЛНАЯ ИНДУКЦИЯ
Полная индукция имеет в математике лишь ограниченное применение. Многие интересные математические утверждения охватывают бесконечное число частных случаев, а провести проверку для бесконечного числа случаев мы не в состоянии.
ПРИНЦИП МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Предложение А(n) считается истинным для всех натуральных значений переменной, если выполнены следующие два условия:
Предложение А(n) истинно для n=1.
Из предположения, что А(n) истинно для n=k (где k – любое натуральное число), следует, что оно истинно и для следующего значения n=k+1.
ПРИНЦИП МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Обычно он выбирается в качестве одной из аксиом, определяющих натуральный ряд чисел, и, следовательно, принимается без доказательства.
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Под методом математической индукции понимают следующий способ доказательства.
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Если требуется доказать истинность предложения А(n) для всех натуральных n, то, во-первых, следует проверить истинность высказывания А(1) и, во-вторых, предположив истинность высказывания А(k), попытаться доказать, что высказывание А(k+1) истинно. Если это удается доказать, причем доказательство остается справедливым для каждого натурального значения k, то в соответствии с принципом математической индукции предложение А(n) признается истинным для всех значений n.
Если это удается доказать, причем доказательство остается справедливым для каждого натурального значения k, то в соответствии с принципом математической индукции предложение А(n) признается истинным для всех значений n.
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
ПРОВЕРИМ истинность утверждения при n=1
ДОКАЖЕМ истинность утверждения при n=k+1
СДЕЛАЕМ ВЫВОД
пример
ПРИМЕНЕНИЕ МЕТОДА МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ К
СУММИРОВАНИЮ РЯДОВ
ПРИМЕНЕНИЕ МЕТОДА МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ К
СУММИРОВАНИЮ РЯДОВ
Пример 1. Доказать формулу
n – натуральное число.
Решение.
При n=1 обе части равенства обращаются в единицу и, следовательно, первое условие принципа математической индукции выполнено.
Предположим, что формула верна при n=k, т.е.
.
Прибавим к обеим частям этого равенства и преобразуем правую часть. Тогда получим
Таким образом, из того, что формула верна при n=k, следует, что она верна и при n=k+1. Это утверждение справедливо при любом натуральном значении k. Итак, второе условие принципа математической индукции тоже выполнено. Формула доказана.
ПРИМЕНЕНИЕ МЕТОДА МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ К
СУММИРОВАНИЮ РЯДОВ
Доказать, что
ПРИМЕНЕНИЕ МЕТОДА МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ К
СУММИРОВАНИЮ РЯДОВ
Решение.
при n=1
Если
то
ПРИМЕНЕНИЕ МЕТОДА МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ К
СУММИРОВАНИЮ РЯДОВ
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ В РЕШЕНИИ ЗАДАЧ НА ДЕЛИМОСТЬ
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ В РЕШЕНИИ ЗАДАЧ НА ДЕЛИМОСТЬ
С помощью метода математической индукции можно доказывать различные утверждения, касающиеся делимости натуральных чисел.
пример
Если n – натуральное число, то число n2-n — четное.
проверим истинность утверждения при n=1, наше утверждение истинно:12-1=0 — четное число
предположим истинность утверждения при n=k, где k>1 (или k>m) , k2-k — четное число
докажем истинность утверждения при n=k+1 (k+1)2-(k+1)-(k2-k)=2k, a 2k – четное число, то и четное (k+1)2-(k+1).
Вывод Итак, четность n2-n доказана при n=1, из k2-k четности выведена четность (k+1)2-(k+1) .Значит, n2-n четно при всех натуральных значениях n.
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ В РЕШЕНИИ ЗАДАЧ НА ДЕЛИМОСТЬ
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ В РЕШЕНИИ ЗАДАЧ НА ДЕЛИМОСТЬ
проверим истинность утверждения при n=1 высказывание А(1)={число 5*2-32 кратно 19} истинно.
предположим истинность утверждения при n=k, где k>1 (или k>m)? А(k)={число 5*23k-2-33k-1 кратно 19} истинно
докажем истинность утверждения при n=k+1 тогда А(k+1)={число 5*23(k+1)-2-33(k+1)-1 =8*5*23k+2+27*33k-1 =8(5*23k-2+ 33k-1)+19* 33k-1 кратно 19} т.
 к 5*23k-2+ 33k-1 кратно 19 из предположения, а 19 кратно 19.
к 5*23k-2+ 33k-1 кратно 19 из предположения, а 19 кратно 19.Вывод Оба условия принципа математической индукции выполнены, следовательно, предложение A(n) истинно при всех значениях n.
Решите сами
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ В РЕШЕНИИ ЗАДАЧ НА ДЕЛИМОСТЬ
(4n+1 +15n+32) кратно 3 для любого n
ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Доказать, что при любом натуральном n>1
.
ДОКАЗАТЕЛЬСТВО
ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Обозначим левую часть неравенства через Sn .
проверим истинность утверждения при n=2, следовательно, при n=2 неравенство справедливо.
предположим истинность утверждения при n=k, где k>1 (или k>m) Пусть
докажем истинность утверждения при n=k+1 тогда
Имеем
и
Сравнивая Sk и Sk +1
Т.е
ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
При любом натуральном k правая часть последнего равенства положительна.
Поэтому .
Но , значит,
и .
Значит и
Верно при любом натуральном n>1
ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Найти ошибку в рассуждении
Утверждение. При любом натуральном n справедливо неравенство .
ДОКАЗАТЕЛЬСТВО
ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Пусть неравенство справедливо при n=k, где k – некоторое натуральное число, т.е.
(1)
Докажем, что тогда неравенство справедливо и при n=k+1, т. е.
е.
Действительно, не меньше 2 при любом натуральном k. Прибавим к левой части неравенства (1) , а к правой 2. Получим справедливое неравенство ,
Утверждение доказано.
.
РЕШИТЕ САМИ
ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
2n >n для n N
2n >2n+1 n>=3
ДОКАЗАТЕЛЬСТВО ТОЖДЕСТВ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
ДОКАЗАТЕЛЬСТВО ТОЖДЕСТВ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Доказать тождество, что для любого n принадлежащий множеству N.
12 + 22 +…+ n2 = (n*(n+1)*(2n+1))/6
ДОКАЗАТЕЛЬСТВО
ДОКАЗАТЕЛЬСТВО ТОЖДЕСТВ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
ПРОВЕРИМ истинность утверждения при n=1 12 = (1*2*3)/6 (верно)
ПРЕДПОЛОЖИМ истинность утверждения при n=k, где k>1 (или k>m)
12 + 22 +…+ k2 = (k*(k+1)*(2k+1))/6
k- слагаемое
ДОКАЖЕМ истинность утверждения при n=k+1
12 + 22 +…+ k2 +(k+1)2 =((k+1)*(k+2)*(2k+3))/6
12 + 22 +…+ k2 +(k+1)2 =(k*(k+1)*(2k+1))/6+(k+1)2= =(k*(k+1)*(2k+1) +6(k+1) 2) /6 =((k+1)*(k*(2k+1) +6(k+1) ) /6= =((k+1)*(2k2+k+6k+6))/6=((k+1)*(2k+3)*(k+2))/6
Вывод: равенство верно для любого n
РЕШИ САМ
ДОКАЗАТЕЛЬСТВО ТОЖДЕСТВ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Доказать, что 1+3+5+…+(2n-1)=n2.
Решение: 1) Имеем n=1=12. Следовательно, утверждение верно при n=1, т.е. А(1) истинно.
2) Докажем, что А(k)Þ A(k+1).
Пусть k-любое натуральное число и пусть утверж-дение справедливо для n=k, т.е.
1+3+5+…+(2k-1)=k2.
Докажем, что тогда утверждение справедливо и для следующего натурального числа n=k+1, т.е. что
1+3+5+…+(2k+1)=(k+1)2.
В самом деле,
1+3+5+…+(2k-1)+(2k+1)=k2+2k+1=(k+1)2.
Итак, А(k)Þ А(k+1). На основании принципа математической индукции заключаем, что предпо-ложение А(n) истинно для любого nÎ N.
ДОКАЗАТЕЛЬСТВО ТОЖДЕСТВ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Доказать , что при всех допустимых значениях x имеет место тождество:
ПРОВЕРОЧКА
РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Вычислить сторону a2n правильного — 2n угольника, вписанного в круг радиуса R.
ДОКАЗАТЕЛЬСТВО
РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
При n=2 правильный 2n – угольник есть квадрат; его сторона . Далее, согласно формуле удвоения.
находим, что сторона правильного
восьмиугольника
РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
сторона правильного шестнадцатиугольника
сторона правильного тридцатидвухугольника
Можно предположить поэтому, что сторона правильного вписанного 2n – угольника при любом n>= равна
(1)
РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Допустим, что сторона правильного вписанного 2n — угольника выражается формулой (1). В таком случае по формуле удвоения
откуда следует, что формула (1) справедлива при всех n.
КОНЕЦ
Скачать презентацию
2. Использование метода математической индукции для нахождения сумм конечного числа слагаемых
Этот метод можно эффективно использовать для нахождения формул вычисления сумм, когда число слагаемых зависит от n, доказательства тождеств, доказательства неравенств, у которых одна или обе части зависят от n.
Пример 1. Пусть дана последовательность (n) натуральных чисел. Найдем формулу вычисления суммы первых n чисел:
S(n)=l+2 + 3 + … + n.
Решение. Рассмотрим S(1), S(2), S(3), S(4). Мы имеем:
S(l)=l,
S(2)=1+2 = 3,
S(3)=1+2 + 3 = 6,
S(4)=1+2 + 3 + 4=10.
Заметив, что полученные числа можно записать в виде
естественно сделать предположение, что
(1)
Применим
теперь метод математической индукции
для доказательства
полученной формулы (1).
При n = 1: S(1) = 12/2=1.
Формула верна при n = 1. Предположим, что формула верна при n = k > 1:
Тогда
‘Значит, из справедливости формулы для n = k вытекает ее справедливость для n = k + 1 По принципу математической индукции отсюда вытекает справедливость формулы (1) для всех натуральных значений n.
В некоторых случаях для доказательства тождества Р(n) = Q (n) можем сначала убедиться, что Р (1) = Q (1), и, предполагая справедливость равенства P(k)=Q(k), k>1, доказать тождество P(k + 1) = Q(k + 1). Тогда из истинности равенства P(k) = Q(k) будет следовать истинность равенства P(k + 1) = Q(k + 1)и по принципу математической индукции будет следовать истинность тождества P(n)=Q(n) для всех n.
Пример 2. Рассмотрим последовательность (n2) квадратов натуральных чисел. Докажем справедливость формулы для вычисления суммы первых n членов этой последовательности:
(2)
Обозначим
l2 + 22 + 32 + . .. + n2 = S
(n) и
.. + n2 = S
(n) и
При n = 1: S(1) = 1, Т.е. S(1) = P(1).
Предполагаем теперь, что равенство верно для n = k, k > 1, т. е. S(k) = P(k).
Рассмотрим разности:
Итак, мы доказали, что S(1) = P(1) и S(k+l) — S (k) = = P (k+1) — P (k). Тогда по принципу математической индукции тождество (2) справедливо для всех n.
Ранее доказанные формулы могут служить источником получения новых формул.
Пример 3. Пусть дана последовательность (n3) кубов натуральных чисел. Выведем формулу для вычисления суммы первых n членов этой последовательности:
S(n)=l3 + 23 + 33 + … + n3.
Как и в примере 1, рассмотрим суммы S(1), S (2), S (3), S (4). Здесь мы имеем:
S(l)=l,
S(2)=l3 + 23 = 9,
S(3)=l3 + 23 + 33 = 36,
S
(4)= 13 + 23 + 33 + 43=
100.
Поскольку мы предполагали, что S(k) = P(k), то отсюда следует равенство S (k+ 1) = P (k + 1). Следовательно, по принципу математической индукции формула (3) справедлива для всех n.
3. Использование метода математической индукции для доказательства неравенств и делимости выражений, зависящих от n на некоторое число
Метод математической индукции успешно применяется и при доказательстве различных неравенств, при этом используются свойства неравенств. В качестве примера рассмотрим доказательство неравенства, называемое неравенством Бернулли, которое имеет следующий вид:
(4)
при всех натуральных значениях n и для всех х> — 1.
При n = 1 это неравенство справедливо, так как 1 + х = 1 + x.
Предположим, что оно справедливо при n = k>1, т. е. справедливо
Докажем, что оно верно и для n = k+1: умножим обе части равенства на 1 + х:
Учитывая,
что kx2
0 и, следовательно, 1 + kx
+ x
+ kx2
1 + kx
+ x
= 1+ x(k
+ 1). Тогда имеем:
Тогда имеем:
(1 + x)k+1 1 + (k + 1)x.
Таким образом, мы показали, что неравенство (4) верно для n =1, и в предположении, что оно верно для n = k, доказали его справедливость для n = k+1 Значит, по принципу математической индукции неравенство Бернулли справедливо для всех натуральных значений n.
Пример 4. Используя неравенство Бернулли доказать справедливость неравенства
При n = 1:
Пусть при n = k неравенство верно, т.е.
Докажем справедливость при n = k+1, т.е.
Левую часть представим в виде Используя неравенство Бернулли, имеем
Где
Но
Значит неравенство верно при любом n.
Пример 4. Доказать, что n3 – n делится на 3 при любом n.
При n = 1: 1 – 1 = 0 , 0 делится на 3.
Пусть при n = k : k3 – k делится на 3.
Докажем делимость при n = k + 1:
(k + 1)3 – (k + 1) = k3 + 3k2 + 3k + 1 – k – 1 = k3 + 3(k2 + k) – k = k3 – k + 3(k2 + k).
Т.к. k3 – k делится на 3 (по индуктивному предположению), 3(k2 + k) делится на 3, то и их сумма делится на 3.
Пример 5. Доказать, что сумма кубов трех последовательных натуральных чисел делится на 9.
Т.е. необходимо доказать, что n3 +(n + 1)3 + (n + 2)3 делится на 9.
При n = 1: 1+ 8 + 27 = 36 – делится на 9.
Пусть при n = k : k3 +(k + 1)3 + (k + 2)3 делится на 9.
Докажем, что делимость на 9 имеет место при n = k + 1:
(k+1)3+(k+2)3+(k+3)3 = (k+2)3 + k3 +3k2 +3k +1 +k3 + 9k2 +27k+27 = (k+2)2+k3+(k+1)3 +9(k2 +3k + 3), где
(k+2)2+k3+(k+1)3 делится на 9 по индуктивному предположению,
9(k2 +3k
+ 3) делится на 9.
Следовательно, их сумма делится на 9.
Открытый урок по алгебре и началам анализа в 10-м классе по теме «Метод математической индукции»
Цели:
Дидактические:
- обеспечить в ходе урока усвоение метода математической индукции;
- сформировать умение применять этот метод для доказательства тождеств, неравенств, задач на делимость, логических задач.
Воспитательные:
- формирование научного мировоззрения;
- формирование интереса к исследовательской деятельности;
- формирование культуры речи;
- формирование умения корректно высказывать точку зрения.
Развивающие:
- развитие у школьников умение выделять главное, существенное в изучаемом материале;
- умение сравнивать, обобщать, логически излагать свои мысли;
- формирование интеллектуальных чувств (новизны,
интереса, удивления).

Форма обучения:
Урок лекция, беседа. Объяснение нового материала
Материально-техническое обеспечение:
Мультимедийное оборудование, опорный конспект урока (Приложение 2). Презентация по данной теме (Приложение 1).
Ход урока
I. Актуализация знаний
При изучении явлений в любой области знаний – будь, то математика или история, физика или медицина, астрономия или экономика всюду и всегда основным этапом является установление определенных закономерностей связывающих отдельные элементы изучаемого явления. Мы подмечаем определенную связь между элементами изучаемого явления справедливого для многих частных случаев, затем распространяем на все случае вообще, устанавливая тем самым общий закон, раскрывающий сущность данного явления.
Все утверждения можно разделить на
общие и частные. Например, утверждение “Во
всяком параллелограмме диагонали делятся в
точке пересечения пополам”, является общим, так
как относится ко всему множеству
параллелограммов. В то же время утверждение “В
параллелограмме ABCD диагонали делятся в точке
пересечения пополам”, является частным, так как
относится к конкретному параллелограмму ABCD.
Например, утверждение “Во
всяком параллелограмме диагонали делятся в
точке пересечения пополам”, является общим, так
как относится ко всему множеству
параллелограммов. В то же время утверждение “В
параллелограмме ABCD диагонали делятся в точке
пересечения пополам”, является частным, так как
относится к конкретному параллелограмму ABCD.
На основе частных утверждений делают некоторые предположения (гипотезы) о справедливости какого либо утверждения. Иногда эти предположения оказываются верными, иногда ошибочными.
Многие свойства чисел сначала были открыты путем наблюдений, задолго до того как истинность была строго доказана.
II. Основная часть урока
Переход от частных утверждений к общим
называют индукцией (от латинского слова inductio –
наведение). Например, знаменитый математик XVII в. П.Ферма, проверив, что числа
П.Ферма, проверив, что числа
, , , , простые, сделал по индукции предположение, что для всех n=1,2,3,… числа вида , простые. Однако это предположение оказалось неверным, так как в XVIII веке Л. Эйлер нашел, что — составное число. Как видим, индукция не является методом доказательства, а лишь помогает сформулировать неизвестный результат в виде некоторой гипотезы, справедливость которой надо потом доказать.
В случае когда утверждение касается конечного числа объектов, его можно доказать, проверяя для каждого объекта.
В чем же заключается суть исследования которое позволяет доказать или опровергнуть математическое утверждение? Ответ мы найдем при разборе следующей задачи.
Задача
Перед нами последовательность нечетных чисел натурального ряда.
1,3,5,7,9,11,13…
Чему равна сумма n первых членов этой последовательности?
Решение
Составим суммы одного, двух, трех, и т. д.
первых членов данной последовательности:
д.
первых членов данной последовательности:
S1=1;
S2=1+3=4;
S3=1+3+5=9;
S4=1+3+5+7=16;
S5=1+3+5+7+9=25;
Заметим, что
S1=12;
S2=4=22;
S3=9=32;
S4=16=42;
S5=25=52;
На основе этих наблюдений мы можем высказать предположение, что
Sn=1+3+5+7+…+(2n-1)=n2 (1)
Верно ли это предположение при любом целом положительном n?
Приняв наше предположение за закон, не уподобимся ли мы тем зоологам, которые до открытия Австралии утверждали, что все лебеди на земле белые?
Лучше пойдем по иному пути в поисках
общего доказательства высказанного нами
утверждения.
Предположим, что формула (1) верна для n=k, где kN, то есть
1+3+5+7+…+(2k-1)=k2 (2)
Докажем ее справедливость и для числа, непосредственно следующего за k, для числа n=k+1.
Sk+1=1+3+5+7+…+(2k-1)+(2k+1)=(k+1)2 (3)
Заменим на основе равенства (2) Sk=1+3+5+7+…+(2k-1) на k2.
Sk+1= Sk +(2k+1)= k2 +(2k+1)= (k+1)2 (3)
Мы пришли к очень важному выводу:
Если наше предположение верно для некоторого натурального k, то оно непременно остается верным для следующего целого числа k+1.
Мы уверены, что предположение верно,
для n=1,2,3,4,5. Будучи верным, для 5 оно на основе
полученного вывода оно должно быть верным и для
следующего целого числа 6, будучи верным, для 6 оно
должно быть верным и для 7 и так далее. Предположение верно для всех натуральных чисел.
Предположение верно для всех натуральных чисел.
Данное решение может быть укорочено. При переходе, от какого либо произвольного натурального числа k к следующему за ним натуральному числу k+1 нужно ли проверять наше предположение для n=5,4,3,2. Достаточно быть уверенным в том, что оно справедливо для n=1. И тогда мы скажем: если предположение верно для n=1, то оно на основе доказанного верно и для n=2, если оно верно при n=2, то оно верно и для n=3 и так далее.
Решая эту задачу, мы познакомились с очень важным методом доказательства. Такой можно было бы назвать “переходом от k к k+1”, но обычно его называют методом математической или полной индукции.
В основе этого метода лежит принцип математической индукции, который заключается в следующем.
Утверждение P(n) справедливо для всякого натурального n, если:
- Оно справедливо для n=1 или для наименьшего из
натуральных чисел при котором закономерность
имеет смысл.

- Из справедливости утверждения, для какого либо произвольного натурально n=k, следует его справедливость для n=k+1.
Само доказательство методом математической индукции состоит из следующих частей.
- Проверяют справедливость гипотезы для наименьшего из натуральных чисел при котором гипотеза имеет смысл (базис).
- Сделав предположение, что гипотеза верна для некоторого значения k, стремятся доказать справедливость ее для k+1.
- Если такое доказательство удалось довести до конца, то, на основе принципа математической индукции можно утверждать, что высказанная гипотеза справедлива для любого натурального числа n.
III. Закрепление материала
Применим метод математической
индукции к решению следующей задачи.
Задача
Доказать, что , при n2.
Решение
- Гипотеза имеет смысл при n2. Проверим верность утверждения при n=2
- Предположим, что при n=k>2, . Докажем, что .
- На основе принципа математической индукции можно утверждать, что высказанная гипотеза справедлива для любого натурального числа n2.
, 57=19? 3
Гипотеза оказалось справедливой и при n=k+1
При доказательстве гипотезы методом математической индукции очень важно выполнение всех его составляющих.
Рассмотрим следующие примеры.
- При отсутствии первого шага можно “доказать”, что числа вида 2n-1 являются четными при nN.
- В поисках формулы дающий только простые числа Л. Эйлер подверг испытанию трехчлен
Пусть при n=k утверждение верно, то есть
2k-1 четное число.
Проверим верность утверждения при n=k+1
2(k+1)-1=2k+2-1=(2k-1)+2
По предположению индукции 2k-1 четное число,
следовательно число (2k-1)+2 тоже четное.
Отсутствие первого шага приводит к ошибке.
P(n)=n2+n+41
Этот трехчлен давал простые числа при всех
значениях n от 1 до 39:
P(1)=12+1+41=43;
P(2)=22+2+41=47;
P(3)=32+3+41=53;
…
P(39)=392+39+41=1601;
P(40)=402+40+41=1641=412.
Обратите внимание, что отсутствие второго шага приводит к неверному результату
Метод математической индукции можно
эффективно использовать для формул вычисления
сумм, когда число слагаемых зависит от n, для
доказательство тождеств и неравенств, задач на
делимость, логических задач.
Задача
Каждый человек в мире пожал какое-то количество рук. Докажите, что число людей пожавших нечетное число рук – четно.
Решение
Пронумеруем все рукопожатия в мире от первого (его не обязательно должны были совершить Адам и Ева) до произвольного натурального n. Очевидно, что при n=1 утверждение задачи справедливо. Предположим, что оно верно при каком-то n=k, то есть количество людей участвовавших в рукопожатиях с номерами от 1 до k и сделавших нечетное количество рукопожатий, четно.
Докажем справедливость этого утверждения для n=k+1, возможны три варианта осуществления k+1 рукопожатия: друг другу пожимают руки:
- два особых человека;
- два неособых человека;
- один особый и один неособый человек.
В каждом из этих трех случаев количество особых людей либо уменьшается на два, либо увеличивается на два, либо неизменяется.
Утверждение доказано.
IV. Итоги урока
Вывод
Метод математической индукции не дает ни каких указаний, как построить гипотезу. Вопрос о том, как возникает гипотеза, принадлежит к той области, в которой нет никаких общих правил, здесь делает свое дело эксперимент, аналогия, конструктивная индукция.
Без индукции было бы невозможно творчество ни в математике, ни в физике, ни в любой иной области науки.
“Понимание и умение правильно применять принцип математической индукции, является хорошим критерием логической зрелости, которая совершенно необходима математику” А.Н. Колмогоров
Домашнее задание
- Доказать неравенство , где x-1, x0, nN, n>1.
- Доказать, что сумма квадратов чисел натурального ряда от 1 до n, равна , то есть 12+22+32+…+n2=
Это неравенство называется
неравенством Бернулли.
доказательства / Вопрос про использование метода математической индукции / Математика
|
Интересует следующий вопрос про метод математической индукции — при каких условиях он работает? Вопрос вызван тем, что многие учебные задания на применение этого метода решаются как по маслу и может сложиться впечатление, что так оно всегда и будет. Однако, кажется сомнительным, что любое верное утверждение вида $%A(n), n \geqslant n_0$% можно доказать с использованием математической индукции. Честно говоря, сходу в голову ничего не приходит, но уверен такие утверждения есть. Интересно было бы узнать природу таких утверждений, а именно — с чем связано то, что их нельзя доказать данным методом (несмотря на то, что они верные). индукция доказательства задан 16 Ноя ’15 0:40 marcin63 |
старыеновыеценные
|
С помощью только матиндукции и аксиом Пеано (которые содержат матиндукцию) нельзя доказать любое недоказуемое в рамках формальной арифметики утверждение. Не доказано. Скорее всего, это ложное утверждение. Само понятие «доказать с использованием матиндукции» нуждается в строгом уточнении, которого пока даже близко не видно. Как раз это утверждение легко доказывается с помощью матиндукции — достаточно подобрать удобный для сравнения телескопический ряд.
тоже не сформулировано толком и не доказано. Если имеется ввиду действительно «нечеткое свойство», то оно лежит вне математики и вопрос не имеет смысла (это то же самое, что утверждать, что по индукции нельзя доказать, что Обама — президент). Если же имеется ввиду утверждение типа теории вероятностей о вероятности события, то тогда ответ неочевиден.
это какой-то унылый софизм
тоже не сформулировано толком и не доказано и неверно. Можно сконструировать формально истинное доказательство, использующее матиндукцию: если $%n=ab$%, то $%a,b<n$%, и так как $%a,b$% разложимы на простые множители, то $%n=ab$% тоже разложимо (объединяем разложения). А ежели $%n\neq ab$%, то $%n$% — простое, значит уже разложено на простые множители. (здесь напоминаю, что $%P(1)\wedge … \wedge P(n-1)\Rightarrow P(n)$% — тоже матиндукция) В общем, без наличия маломальской приличной теории нет смысла даже пытаться высказываться подобным образом. ссылка отвечен 16 Ноя ’15 9:42 {n+1}}$%. Как и выше, совершенно очевидно, что из этого равенства и неравенства $%b_n < 1$% не следует неравенство $%b_{n+1} < 1$% (подразумевается, что от определения последовательности мы взяли только рекуррентное равенство, а остальное «забыли»).Но этот пример отличается от предыдущего, потому что здесь имеется простое арифметическое доказательство на основе другой «аксиомы». А именно, можно заметить, что $%1+b_n=2b_{n+1}$%. Принимая такую «аксиому», мы мгновенно выводим неравенство $%b_{n+1} < 1$% из предположения $%b_n < 1$%. Из всего сказанного я хотел бы сделать такой общий вывод. Когда ставятся вопросы, можно ли доказать то-то и то-то, надо чётко указывать, какими средствами разрешено пользоваться, после чего вопрос приобретает точный смысл. Понятно, что если пользоваться можно «всем», никак себя в средствах не ограничивая, то и доказать в результате можно будет всё, что в принципе доказуемо. ссылка отвечен 27 Ноя ’15 15:50 org/Person»>falcao279k●9●37●51 |
|
Топикстартер интересовался какими-то «естественными» объяснениями, почему иногда индукция работает, а иногда нет. Ну что ж. Давайте, раз уж речь идет о доказательстве неравенств, будем рассматривать доказательство неравенства $%P(n) < Q(n)$% по индукции. Как это обычно делается?
Либо из «нового» неравенства вычитают старое, либо (если все величины положительны) делят новое на старое. Иначе говоря, в первом случае фактически доказывается разностное неравенство $%P(n+1)-P(n) < Q(n+1)-Q(n)$%, а во втором — аналогичное неравенство где вместо P и Q стоят функции ln(P) и ln(Q). Если для первых разностей неравенство очевидно, то вот уже в лоб работает индукционный переход. ссылка отвечен 28 Ноя ’15 2:01 knop |
Ваш ответ
Если вы не нашли ответ, задайте вопрос.
7.3.3: Индукция и неравенства — K12 LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14793
Индукция и неравенства
Это третий урок из серии математических доказательств. В этом уроке мы продолжаем фокусироваться в основном на доказательство по индукции , на этот раз неравенств и других видов доказательств, таких как доказательство по геометрии.
Induction and Inequalities
The Transitive Property of Inequality
Below, we will prove several statements about inequalities that rely on the transitive property of inequality:
If a < b and б < в , тогда a < c .
Обратите внимание, что мы могли бы также сделать такое утверждение, изменив отношения (т. е. используя утверждения «больше чем») или сделав включающие утверждения, такие как a ≥ b .
Также важно отметить, что это свойство целых чисел является постулатом или утверждением, которое мы предполагаем истинным. Это означает, что нам не нужно доказывать транзитивность неравенства.
Вы столкнулись с другими полезными свойствами неравенства на более ранних курсах алгебры:
Дополнение. + c .
Свойство умножения: если a > b и c > 0, то ac 9{n}\) for \(\ n \geq 4\)
Решение
Шаг 1) Базовый случай: n = 4:4! = 24, 2 4 = 16. 24 ≥ 16, поэтому базовый случай верен.
Шаг 2) Предположим, что k ! ≥ 2 k для некоторого значения k такого, что k ≥ 4
Шаг 3) Покажите, что ( k +1 )! ≥ 2 k+1
| ( к +1)! = к !( к +1) | Переписать ( к +1)! в пересчете на к ! |
|---|---|
| ≥ 2 к ( к +1) | Используйте шаг 2 и свойство умножения. |
| ≥ 2 к (2) | к +1 ≥ 5 >2, поэтому мы снова можем использовать свойство умножения. |
| = 2 к+1 |
Поэтому n ! ≥ 2 n for n ≥ 4.
Example 2
For what values of x is the inequality x > x 2 true?
Решение
Неравенство верно, если 9Пример 3
Решение
| 1. Базовый вариант: | Если n = 1, 9 n — 1 = 9-1 = 8 = 8(1) |
|---|---|
| 2. Индуктивная гипотеза: | Предположим, что 9 k — 1 делится на 8. |
| 3. Индуктивный шаг: | Покажите, что 9 k+1 — 1 делится на 8. |
| 9 k — 1 divisible by 8 ⇒ 8 W = (9 k -1) for some integer W | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 k+1 — 1 = 9(9 k — 1) + 8 = 9(8W) + 8, которое делится на 8 9{n}\) для \(\ n=7,8,9, \ldots\) Завершите следующие доказательства геометрической индукции.
Обзор (ответы) Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 7. Словарь
Эта страница под названием 7.3.3: Индукция и неравенства распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу. ПОД ЛИЦЕНЗИЕЙ
Доказательство и математическая индукция: шаги и примерыДоказательство — очень важный элемент математики. Как математики, мы не можем поверить в факт, если он не был полностью подтвержден другими известными нам фактами. Есть несколько ключевых типов доказательств, которые мы кратко рассмотрим. Это:
Затем мы перейдем к более сложным элементам доказательства, специальному доказательству, называемому математической индукцией. Эти доказательства относительно просты и методичны, однако мы рассмотрим несколько приемов, которые можно использовать для ускорения процесса. Что такое доказательство контрпримером? Доказательство контрпримером, вероятно, является одним из основных доказательств, которые мы рассмотрим. В значительной степени это то, что он утверждает и включает в себя доказательство чего-либо путем поиска контрпримера. Шаги следующие.
Гипотеза: Заявление о том, что мы пытаемся доказать или опровергнуть. Давайте рассмотрим короткий пример, который поможет нам понять, что происходит. Докажите контрпримером, что все значения нечетны, ибо. РЕШЕНИЕ: Если допустить, то 4 нельзя записать как, с. Так что 4 не нечетное. Мы нашли контрпример, чтобы опровергнуть гипотезу. Что такое доказательство исчерпыванием? Доказательство исчерпыванием включает в себя проверку всех релевантных примеров и проверку того, что все они удовлетворяют гипотезе.
Давайте рассмотрим на коротком примере, как это работает. Докажите методом исчерпывания, что последовательные положительные четные числа меньше 10 составляют сумму четных чисел. РЕШЕНИЕ: Мы хотим убедиться, что сумма двух последовательных положительных четных чисел до 10 четна. Следовательно, мы будем использовать числа 2, 4, 6 и 8. 6, 10 и 14 — все четные числа, поскольку все они кратны 2: Следовательно, все эти суммы четные. числа. Итак, наша гипотеза подтвердилась. Есть несколько полезных символов, которые мы можем использовать во время и после завершения доказательства. Это может сделать наше доказательство более привлекательным. Это:
Что такое доказательство от противного?Доказательство от противного — это процесс, в котором мы пытаемся доказать противоположное тому, о чем нас просят. Затем поймите, что в нашем перечисленном доказательстве есть противоречие. На самом деле нет списка шагов для этого. мы просто начинаем с попытки доказать обратное, а затем используем алгебраические манипуляции, чтобы в конечном итоге показать, что это неправильно. Давайте посмотрим на ключевой пример этого, который должен иметь достаточно смысла. Докажите, что это иррационально. РЕШЕНИЕ: Во-первых, давайте разберем, о чем нас спрашивают. Мы хотим показать, что это нельзя записать в виде дроби. Попробуем доказать, что это дробь, и найти противоречие. Пусть, где дробь в ее простейшей форме. Тогда, если возвести в квадрат обе стороны: должно быть четным, потому что оно четное, а квадратный корень из четного числа четный. Лет,
Это означает, что четно. Следовательно, это означает, что это даже. Если и то, и другое четное, это означает, что оно не в простейшей форме. Это противоречие, как мы первоначально предполагали, было в его простейшей форме. Следовательно, не рационально и иррационально. Итак, в этом примере мы использовали алгебраические манипуляции и основные математические факты, чтобы перемещать некоторые термины и показывать, что что-то иррационально. Поэтому всякий раз, когда мы получаем такой вопрос, все, что мы делаем, это используем алгебру и факты о числах, чтобы показать, что у нас есть противоречие. На латыни это известно как reductio ad absurdum, что по существу переводится как доказательство абсурдом, то есть предположение чего-то неправильного и обнаружение противоречия. Что такое математическая индукция? Математическая индукция — это процесс, в котором мы используем предыдущие значения для поиска новых значений. Докажите, что « гипотеза» верно для всех значений н≥м.
Давайте рассмотрим два примера, один из которых является более общим, а другой — специфичным для рядов и последовательностей. Докажите с помощью математической индукции, что все делятся на 4. РЕШЕНИЕ: Шаг 1 : Сначала нам нужно проверить, это дает. Таким образом, это число кратно 4. Шаг 2 : Предположим, что когда утверждение верно. Если мы запишем это в математической нотации, то получим, где m — положительное число. Шаг 3 : Теперь давайте используем тот факт, что это правда, чтобы доказать это для: 9Шаг 4 а для некоторых это правда для некоторых. Следовательно, гипотеза доказана. Давайте рассмотрим еще один пример, относящийся к сериям и последовательностям. Докажите с помощью математической индукции, что для всех. РЕШЕНИЕ: Шаг 1 : Сначала нам нужно проверить случай, когда. Шаг 2 : Предположим, что случай правильный. Шаг 3 , если вернуться к тому, что Этап 4 : Следовательно, это было доказано для того времени и для кого-то, для кого оно было доказано. Поэтому верно для всех. Итак, мы видим, что с помощью алгебраических манипуляций и использования некоторых правил о рядах мы можем доказать гипотезы для всех значений. Доказательство и математическая индукция. Ключевые выводы
Как доказывать неравенства. Методы, помогающие доказать, чтоФото Антуана Дотри на UnsplashМетоды, помогающие доказать, что a< bКогда вы проявите интерес к математике и начнете работать с материалом, который серьезно относится к доказательствам, рано или поздно вы будете пытаться найти доказательства неравенств. Доказать, что равно чему-то другому, обычно несколько проще. Вы манипулируете обеими сторонами одинаково, пока не придете к рассматриваемому уравнению. Возможно, вам придется сделать некоторые умные замены, но вы можете сделать очень много вещей. Неравенства могут быть немного сложнее из-за транзитивности. Если вы хотите показать для некоторых Давайте рассмотрим примеры обоих случаев, мы начнем с «простого» случая, для которого нам не нужно изобретать промежуточные звенья. Все числа в примерах действительны. Имея действительные числа Развитие интуиции Давайте сначала найдем время, чтобы развить интуицию для того, что она говорит. Давайте выберем несколько чисел для 1/2 < 2/3 < 3/4 < 9/10 < 99/100 Хорошо, понятно. Я могу с этим согласиться. Как теперь доказать, что это всегда верно? Расширение до того же знаменателя Чтобы сравнивать дроби, полезно расширить их, чтобы они имели одинаковые знаменатели. Давайте сделаем это и посмотрим, где мы находимся. Теперь, когда знаменатели равны, оказывается, от них можно избавиться. Мы знаем, что Нам не нужно менять направление неравенства, поскольку известно, что число, на которое мы умножаем, положительное. Я бы сказал, что это прогресс. Давай сделаем это. У нас осталось: Упростим суммы в скобках Умножая суммы, мы получаем, что мы получаем общий член с обеих сторон: Поменяйте шаги в обратном порядке, чтобы обеспечить простое доказательство. Чтобы представить формальное доказательство, мы просто поменяем наши исследовательские шаги на противоположные, чтобы рассуждения имели смысл, если читать их сверху вниз. Наше доказательство, каждый шаг, оправданный данными, является обратным нашим исследовательским шагамДоказательство было простым — в некотором смысле — потому что оно не требовало от нас творчества с какими-либо промежуточными выражениями. Мы могли бы обрабатывать доказательство очень похоже на доказательство равенства. Давайте перейдем к чему-то более сложному. Имея любые два действительных числа Развитие интуиции О боже. Тот выглядит немного более требовательным. Во-первых, давайте интуитивно поймем, что он говорит. Выберем 4/5 <= 2/3 + 2/3 Хорошо, попробуем другую пару: -1 /2 <= 2/3 + 3/4 ОК, похоже, мы всегда будем оставаться ниже 1 с левой стороны, даже ниже 0. Обратите внимание, что когда мы выбираем Хорошо, у нас есть немного интуиции насчет того, что происходит. Посмотрим, сможем ли мы это доказать. Развернуть до того же знаменателя В правой части стоит сумма дробей. Мы можем попробовать сформировать сумму, чтобы увидеть, как она соотносится с левой частью. Нам нужно расширить левый член на Хорошо. Вот как это выглядит, когда мы суммируем правую часть. Неравенство, которое необходимо доказать, принимает следующий вид: Найдите известные неравенства При доказательстве неравенств вам часто приходится вводить одно или несколько дополнительных условий, которые находятся между двумя уже рассмотренными. Всегда проверяйте учебник на наличие неравенств, которые вы должны знать, и смотрите, не покажется ли какое-нибудь из них полезным. Упражнения часто будут основываться друг на друге. Иногда результат упражнения а) является ключевым в упражнении б). Так что не «забываете» о своих предыдущих результатах. В нашем случае мы видим, что обе стороны похожи на знакомый нам шаблон Давайте посмотрим, что нужно, чтобы обе стороны согласились с нашим доказанным неравенством, чтобы мы могли его использовать. Выращивание левой стороныДавайте посмотрим на нашу левую сторону. Если взять абсолютное значение Итак, у нас есть: Похоже, с левой стороны мы закончили. Уменьшение правой стороныДавайте посмотрим на нашу правую сторону. Что нам нужно сделать, чтобы получить желаемую форму Если мы заменим Следовательно, у нас есть: И мы получили желаемую форму числа 9.1006 s/(1+s) Выстраивание наших уток в ряд Мы преобразовали обе стороны в формы Если мы можем показать, что r/(r+1) < s/(s+1) Мы подставили Отлично! Мы знаем Мы сделали это! Наши исходные левые и правые члены было трудно сравнивать напрямую. Но мы могли бы поместить между ними некоторые термины, которые мы знали, как сравнивать, образуя таким образом цепочку, доказывающую наше исходное утверждение. При доказательстве неравенств полезно искать способы контролируемого уменьшения или увеличения членов, чтобы они соответствовали известным неравенствам и образовывали транзитивные цепочки. Если вы чувствуете, что у вас это не получается, почему бы не проверить себя и не попробовать доказать оба неравенства с нуля? Вы только что прочитали решения, так что… насколько это может быть сложно? Вот они снова. Первое неравенство: Второе неравенство: Вот это! Математическая индукция | Примечания к курсуПринцип математической индукции формулируется следующим образом: Если данное утверждение S n относительно натурального числа n верно для n = 1, и если истинность S n для n = k, где k является положительным целым числом, подразумевает, что S n истинно для n = k + 1, тогда S n истинно для каждого положительного целого числа n. Посылка, лежащая в основе этого принципа, интуитивно понятна. Если конкретное утверждение S n (обычно математическое уравнение или неравенство, включающее переменную n) верно для n = 1, и также можно доказать, что S n истинность означает, что S n + 1 также истинно, тогда утверждение S n истинно для n = 1 + 1 = 2. Следует отметить, что принцип математической индукции можно распространить на целые числа, просто доказав, что S n истинно для Принцип математической индукции очень полезен при доказательстве многих утверждений о положительных целых числах. В соответствии с этим принципом можно показать, что математическое утверждение, включающее переменную n, истинно для любого положительного целого числа n, доказав следующие два утверждения: (1) Утверждение верно для n = 1,9.1268 (2) Если утверждение верно для любого положительного целого числа k, то оно также Следующие примеры должны прояснить использование этого принципа: Пример 1: Используйте математическую индукцию, чтобы доказать, что 1 + 3 + 5 + .... + (2n - 1) = n² верно для каждого положительного целого числа n. Решение: используйте два описанных выше шага математической индукции. Шаг 1. Замена n на 1 в приведенном выше уравнении дает 2 (1) - 1 = 1 = 1², поэтому n = 1 удовлетворяет уравнению. Шаг 2 Предположим, что уравнение верно для n = k. Тогда 1 + 3 + 5 + .... + (2k - 1) = k² Окончательное равенство доказывает, что уравнение верно для n = k + 1, если это верно для n = k. Доказательство приведенного выше равенства по математической индукции завершено. Пример 2. Используйте математическую индукцию, чтобы доказать, что 0 + 1 + 2 + .... + n = n (n+1)/2 верно для любого целого числа n. Решение: Примените два шага математической индукции, но докажите, что равенство верно для n = 0, так как утверждение должно быть верным для всех целых чисел (включая ноль). Шаг 1 Подставив n = 0, мы получим 0 = 0 (0+1) / 2 = 0, поэтому n = 0 удовлетворяет уравнению. Шаг 2 Предположим, что уравнение верно для n = k. Тогда 0 + 1 + 2 + .... + k = k (k+1) / 2 Последнее равенство доказывает, что n = k, удовлетворяющее приведенному выше уравнению, означает, что n = k + 1 также удовлетворяет ему. Таким образом, указанное выше равенство выполняется для n = 0, а также n = 0 + 1 = 1, n = 1 + 1 = 2 и т. д. для всех натуральных чисел; это верно для всех целых чисел. Следующий пример иллюстрирует полезный метод формулировки необходимых доказательств на шаге 2. В этом примере рассматриваемое математическое утверждение явно выписывается для n = k и n = k + 1. Пример 3. Используйте математическую индукцию, чтобы показать, что n² < 2 n для всех положительных целых чисел n > 4 Решение. процесс решения. Поскольку уравнение должно быть верным для всех целых чисел больше 4, отправной точкой должно быть n = 5 вместо n = 1. Кроме того, тот факт, что n > 4, следует использовать на шаге 2. Шаг 1. Использование п = 5, у нас есть
Шаг 2 Предположим, что неравенство верно при n = k, где k > 4. Тогда
Чтобы показать, что n = k + 1 удовлетворяет неравенству, мы должны показать, что (k+1) 2 < 2 k + 1 , где k > 4. Так как k > 4, k - 1 > 3 > 2. Поскольку k + 1 > k, Так как и (k + 1) 2 < 2k 2 < 2k 2 и k+1 < 2 k+2 , поэтому n = k + 1 удовлетворяет приведенному выше неравенству всякий раз, когда n = k удовлетворяет. На этом доказательство завершено. Индукционные неравенства. Дополнение 2 по математике. 12-й классДомашняя страницаУказатель курсовСоздать викторинуПодпискиэлектронные книгиКурсыNSW Y12 Математический стандарт 1 NSW Y12 Математический стандарт 2 Новый Южный Уэльс, 12 лет, математика для продвинутого уровня Новый Южный Уэльс, Y12, математика, расширение 1 NSW Y12 Расширение по математике 2ТемыКомплексные числа Доказательство Дальнейшая работа с векторами Интеграция МеханикаИндукционные неравенства Тесты на повторение Расширенные ответы Прошлые экзаменационные работы Видео Как купитьУчебный план Назад к теме (пруф) Доказательства ПодтемыЩелкните поля ниже для перехода между подтемами Язык доказательства Методы доказательства Доказательство неравенства Индукционная серия Индукционная делимость Индукционные неравенства Индукция Другое индукционный рекурсивный Ресурсы по индукционным неравенствам Чтобы найти ресурсы по подтемам по индукционным неравенствам, выберите подтему выше. Тесты по теме ← Нажмите здесь, чтобы задать вопросы по Индукционные неравенства с полностью разработанными решениями. Вопросы прошлых экзаменов ← Нажмите здесь, чтобы просмотреть вопросы прошлых экзаменов на неравенств индукции с полностью разработанными решениями. Видео ← Щелкните здесь, чтобы просмотреть выбранные видео по Индукционным неравенствам Вернуться к теме (пруф) Проверка знанийЭти викторины на повторение вопросов по теме Индукция: Неравенства . *Если вы хотите пройти онлайн-викторину, создайте бесплатную учетную запись и пройдите онлайн-тест, чтобы получить мгновенные результаты. Проверьте свои ответы бесплатно онлайн после прохождения теста. Используйте QR-код или тестовый код, который находится в верхней части викторины по теме. Следующие тесты по теме являются частью темы Индукционные неравенства . Каждая тематическая викторина содержит 4-6 вопросов. Как использовать:
Вернуться к теме (пруф) Вопросы с расширенными ответами Дополнительные вопросы по всем Индукция: Неравенства подтем. Вернуться к теме (пруф) Наши прошлые экзаменационные работы сгруппированы по подтемам ниже: Прошлые экзаменационные работыПрошлые экзаменационные вопросы, которые включали Введение: неравенства . Вернуться к теме (пруф) ВидеоВидео по теме Индукция: Неравенства .
Подписка на занятия по математикеПодписка для студентовПодписка для учителей и репетиторовСправочник по учебной программе9N {\ dfrac {1} {{(2n + 1) (2n - 1)}} = \ dfrac {N} {{2N + 1}}} \)Принцип математической индукции 2022 Индуктивное рассуждение — это рассуждение, в котором на основании ряда отдельных случаев мы делаем вывод об общем правиле. Математическая индукция — это метод доказательства, который используется для демонстрации различных свойств натуральных чисел. Принцип математической индукции. Если известно, что какое-то утверждение верно для $n=1$ и если из предположения, что оно верно для некоторого натурального числа $n$, следует, что оно верно для следующего натурального числа $n+1$, то утверждение верно для любого натурального числа $n$. Математическая индукция дана как аксиома, то есть это одна из аксиом Пеано, данная в следующей форме; Если $M \subseteq \mathbb{N}$ такое, что: 1.) (B) $1 \in M$ 2.) (I) $n \in M \Rightarrow n + 1 \in M$ , то $M = \mathbb{N}$, , то есть множество $M$ равно множеству натуральных чисел. Шаг (B) называется базисом , а (I) называется индуктивным шагом, , то есть доказательство, которое мы приводим в два этапа. Пример 1. Докажите формулу суммы первых $n$ натуральных чисел, используя принцип математической индукции: $$ 1 + 2 + 3 + \ldots + n = \frac{n(n+) 1)}{2}, \quad \forall n \in \mathbb{N}.$$ Решение : Нам нужно доказать, верно ли данное утверждение для $n=1$: $ $1 = \frac{1(1+1)}{2} = 1.$$ Следовательно, утверждение верно для $n=1$. Предположим , что утверждение верно для некоторого $n \in \mathbb{N}$ , то есть что для некоторого $n \in \mathbb{N}$ верно следующее: $$ 1 + 2 + 3 + \ldots + n = \frac{n(n+1)}{2}$$ Теперь мы должны доказать, что утверждение верно и для $n+1 \in \ mathbb{N}$, то есть для $n+1 \in \mathbb{N}$ справедливо следующее: $$ 1 + 2 + 3 + \ldots + n+n+1 = \frac{ (n+1)((n+1)+1)}{2} = \frac{(n+1)(n+2)}{2}. Используя предположение, мы имеем: $$\underbrace{ 1 + 2 + 3 + \ldots + n}_{ = \frac{n(n+1)}{2}} + n+1 = \frac{n(n+1)}{ 2} + n + 1 = \frac{n(n+1)+ 2(n+1)}{2} = \frac{(n+1)(n+2)}{2}.$$ Следовательно, утверждение верно для $n+1 \in \mathbb{N}$. По аксиоме математической индукции утверждение верно для любого натурального числа $n$. Пример 2 . Докажите, что $\forall n \in \mathbb{N}$ верно: $$\frac{1}{1 \cdot 3} + \frac{1}{3 \cdot 5} + \cdots + \frac{1}{(2n-1)(2n+1)} = \frac{n}{2n+1}.$$ Решение : Для $n=1$ $$ \ frac{1}{1 \cdot 3} = \frac{1}{2\cdot 1 +1}$$ $$\frac{1}{3} = \frac{1}{3}$$ утверждение верно. Предположим, что для некоторого $n \in \mathbb{N}$ утверждение верно, то есть что для некоторого $n \in \mathbb{N}$ верно: $$\frac{1}{ 1 \cdot 3} + \frac{1}{3 \cdot 5} + \cdots + \frac{1}{(2n-1)(2n+1)} = \frac{n}{2n+1}. $$ Мы должны доказать, что утверждение верно и для $n+1 \in \mathbb{N}$: $$\frac{1}{1 \cdot 3} + \frac{1}{3 \cdot 5} + \cdots + \frac{1}{(2n-1)(2n+1)}+ \frac{1}{(2(n+1)-1)(2(n+1)+ 1)} = \frac{n+1}{2(n+1)+1},$$ 92 + 3n +1}{(2n+1)(2n+3)} $$ $$= \frac{(2n+1) (n+1)}{(2n+1)(2n+3) } $$ $$= \frac{n+1}{2n+3}.
Следовательно, утверждение верно для $n+1 \in \mathbb{N}$. По аксиоме математической индукции утверждение верно для любого натурального числа $n$. Принцип математической индукции применим во многих случаях и для доказательства различных неравенств и делимости чисел. Пример 3 . Докажите, что для всех натуральных чисел таких, что $n \ge 3$ верно: 9{2n+3},$$ , поэтому утверждение верно для $n+1 \in \mathbb{N}$. По аксиоме математической индукции утверждение верно для $\forall n \in \mathbb{N}$. Пример 5 . Докажите, что $\для всех n \in \mathbb{N}$ , $n>2$ справедливо следующее неравенство: $$\frac{1}{n} + \frac{1}{n+1 } + \frac{1}{n+2} + \cdots + \frac{1}{2n} < 1.$$ Решение : Левую часть неравенства обозначим как $A_n$ , это $$A_n = \frac{1}{n} + \frac{1}{n+1} + \frac{1}{n+2} + \cdots + \frac{1}{2n}.$ $ Нам нужно доказать, что верно утверждение $\forall n \in \mathbb{N}, n >2$, поэтому в базисе имеем $n=3$. Для $n=3$ имеем $$A_3 = \frac{1}{3} + \frac{1}{4} + \frac{1}{5} < 1,$$ , поэтому утверждение верно для $n=3$. Предположим, что утверждение верно для некоторого $n \in \mathbb{N}$. Нам нужно доказать, что утверждение верно и для $n+1 \in \mathbb{N}$, то есть $$A_{n+1} < 1.$$ Наблюдаем разницу между двумя последовательными соседними элементами: $$A_n = \frac{1}{n} + \frac{1}{n +1} + \frac{1}{n+2} + \cdots + \frac{1}{2n},$$ $$A_{n+1} =\frac{1}{n} + \ frac{1}{n+1} + \frac{1}{n+2} + \cdots + \frac{1}{2n} + \frac{1}{2n +1} + \frac{1}{ 2n+2} .$$ Отсюда следует $$A_{n+1} – A_{n} = \frac{1}{2n+1} + \frac{1}{2n+2} – \ frac{1}{n} \cdot \frac{2}{2} $$ $$= \frac{1}{2n+1} + \frac{1}{2n+2} – \frac{1 {2n} – \frac{1}{2n} $$ $$=\underbrace{\left( \frac{1}{2n+1} – \frac{1}{2n} \right)}_{<0} + \ underbrace{\left( \frac{1 }{2n+2} – \frac{1}{2n} \right)}_{<0} < 0. $$
Получаем, что $ A_{n+1}+ A_{n} < 0 $, то есть $A_{n+1} < A_{n}$. |



 Может есть какая-то характеризация всех таких утверждений? Ещё интересует, как это дело связано с выбором системы аксиом (в частности, с аксиоматикой Пеано)?
Может есть какая-то характеризация всех таких утверждений? Ещё интересует, как это дело связано с выбором системы аксиом (в частности, с аксиоматикой Пеано)? 2}<2$%.
2}<2$%. Будем продолжать процесс до тех пор, пока лист не станет полностью чёрным. При этом ни на одном из шагов человек не заменит смены цвета листа, то есть будет считать его белым.
Будем продолжать процесс до тех пор, пока лист не станет полностью чёрным. При этом ни на одном из шагов человек не заменит смены цвета листа, то есть будет считать его белым. 2}=a_{n+1} — a_n \le \frac1n — \frac1{n+1}$%. Ну а это уже очевидно и в лоб, индукционного доказательства дальше раскручивать не требует.
2}=a_{n+1} — a_n \le \frac1n — \frac1{n+1}$%. Ну а это уже очевидно и в лоб, индукционного доказательства дальше раскручивать не требует. 8.
8.
 ck12.org/c/analysis
ck12.org/c/analysis
 Это, так как используется, когда есть ограниченные случаи, поэтому тестирование всех соответствующих примеров не займет много времени. Давайте рассмотрим, как мы это делаем, в виде последовательности шагов:
Это, так как используется, когда есть ограниченные случаи, поэтому тестирование всех соответствующих примеров не займет много времени. Давайте рассмотрим, как мы это делаем, в виде последовательности шагов:
 е. а=2 ∴ а+2=4.
е. а=2 ∴ а+2=4. 
 Поэтому мы используем его, когда пытаемся доказать, что что-то верно для всех значений. Итак, вот список шагов для ответа на общий вопрос:
Поэтому мы используем его, когда пытаемся доказать, что что-то верно для всех значений. Итак, вот список шагов для ответа на общий вопрос:


 Если не представляется очевидного решения, может оказаться необходимым найти некоторое число
Если не представляется очевидного решения, может оказаться необходимым найти некоторое число  Нам пришлось бы расширить левую сторону с помощью
Нам пришлось бы расширить левую сторону с помощью  Правая сторона может вырасти выше 1 и никогда не опустится ниже 0 потому что отдельные термины никогда не станут отрицательными.
Правая сторона может вырасти выше 1 и никогда не опустится ниже 0 потому что отдельные термины никогда не станут отрицательными. Часто это означает что-то убрать или добавить, например, добавить третий термин.
Часто это означает что-то убрать или добавить, например, добавить третий термин. Абсолютное значение
Абсолютное значение  Это термины, которые мы хотим вставить между нашей начальной левой и правой сторонами.
Это термины, которые мы хотим вставить между нашей начальной левой и правой сторонами.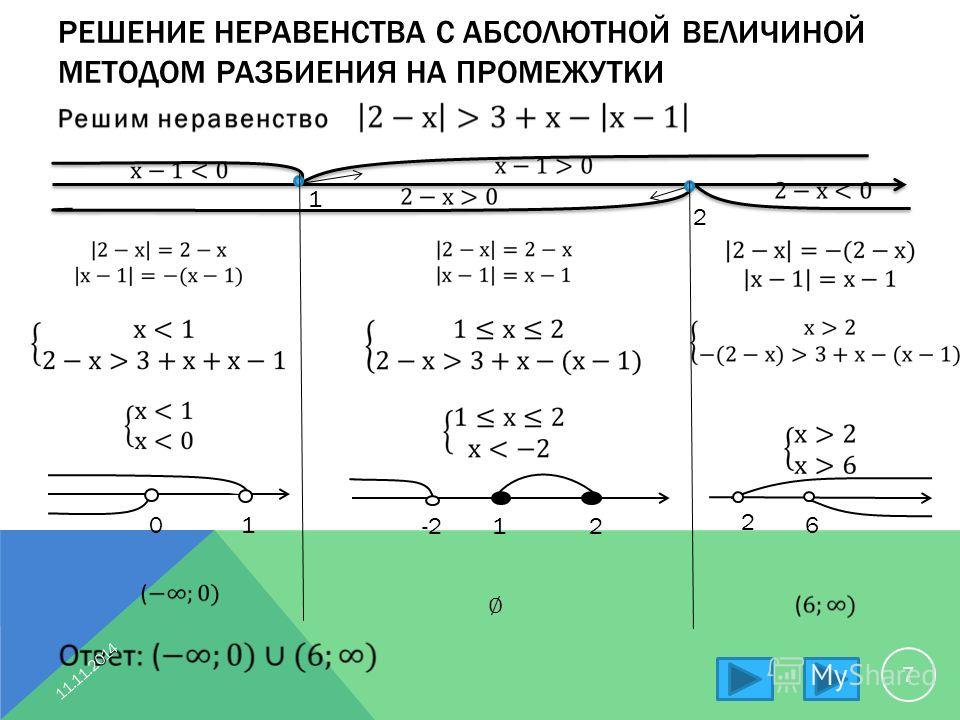
 Аналогично, S n истинно для n = 2 + 1 = 3, n = 3 + 1 = 4 и так далее для всех натуральных чисел.
Аналогично, S n истинно для n = 2 + 1 = 3, n = 3 + 1 = 4 и так далее для всех натуральных чисел.
 Затем делается попытка вывести последнее утверждение из первого с использованием аксиом и ранее доказанных теорем. Эта процедура может облегчить мыслительный процесс, необходимый для установления соответствующих доказательств, как в данном случае.
Затем делается попытка вывести последнее утверждение из первого с использованием аксиом и ранее доказанных теорем. Эта процедура может облегчить мыслительный процесс, необходимый для установления соответствующих доказательств, как в данном случае. Если можно доказать, что (k+1) 2 < 2k 2 , тогда (k+1) 2 < 2 k+1 по транзитивности.
Если можно доказать, что (k+1) 2 < 2k 2 , тогда (k+1) 2 < 2 k+1 по транзитивности.


 Однако этот вывод не обязательно должен быть правильным. Поэтому его также называют неполной индукцией.
Однако этот вывод не обязательно должен быть правильным. Поэтому его также называют неполной индукцией. В базисе мы доказываем, что некоторое утверждение верно для $n=1$, а на индукционном шаге от предположения, что утверждение верно для некоторого $n \in \mathbb{N}$, мы доказываем, что утверждение верно и для следующего натуральное число $ n + 1$.
В базисе мы доказываем, что некоторое утверждение верно для $n=1$, а на индукционном шаге от предположения, что утверждение верно для некоторого $n \in \mathbb{N}$, мы доказываем, что утверждение верно и для следующего натуральное число $ n + 1$. $$
$$ $$
$$
