Замена формулы на ее результат
Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Вы можете преобразовать содержимое ячейки, содержаной формулу, чтобы вычисляемая ячейка заменила ее. Если вы хотите зависать только часть формулы, можно заменить только ту часть формулы, которые не нужно пересчитыть. Замена формулы ее результатом может быть полезной, если в книге много или сложных формул, и вы хотите повысить производительность путем создания статических данных.
Формулы можно преобразовывать в значения по ячейкам или сразу во всем диапазоне.
Важно: Проверьте влияние замены формулы ее результатами, особенно если формулы ссылаются на другие ячейки, содержащие формулы. Перед заменой формулы ее результатом рекомендуется создать резервную копию книги.
В этой статье не говорится о параметрах и методах вычислений. Чтобы узнать, как включить или отключить автоматический пересчет на нем, см.
Замена формул вычисляемой величиной
При замене формул их значениями Excel окончательно удаляет их. Если вы случайно заменяете формулу значением и хотите ее восстановить, нажмите кнопку Отменить сразу после ввода или вжатия значения.
-
Вы можете выбрать ячейку или диапазон ячеек, которые содержат формулы.
Если формула является формула массива, выделите диапазон ячеек, содержащих формулу массива.
Как выбрать диапазон, содержащий формулу массива
-
Щелкните ячейку в формуле массива.
-
На вкладке Главная в группе Редактирование нажмите кнопку Найти и выделить, а затем выберите команду Перейти.
-
Нажмите кнопку Дополнительный.
Щелкните Текущий массив.
Нажмите кнопку Копировать .
Нажмите кнопку В .
Щелкните стрелку рядом с кнопкой Параметры в и выберите только значения.
В следующем примере показана формула в ячейке D2, которая умножает ячейки A2, B2 и скидку из ячейки C2 для расчета суммы счета для продажи. Чтобы скопировать фактическое значение вместо формулы из ячейки на другой книгу или на другой, можно преобразовать формулу в ячейку в ее значение, выстроив следующее:
- org/ListItem»>
-
Нажмите F9, а затем ввод.
Нажмите F2, чтобы изменить ячейку.
После преобразования ячейки из формулы в значение в области формул отображается значение 1932,322. Обратите внимание, что 1932,322 — фактическое вычисляемого значения, а 1932,32 — значение, отображаемого в ячейке в валютном формате.
Совет: При редактировании ячейки с формулой можно нажать F9, чтобы окончательно заменить формулу ее вычисляемой величиной.
Замена части формулы значением, полученным при ее вычислении
Иногда требуется заменить только часть формулы ее вычисляемой величиной. Например, вы хотите заблокировать значение, которое используется в качестве аванса по кредиту на автомобиль. Этот первый взнос вычислялся на основе процента от годового дохода компании. В настоящее время сумма дохода не изменится, поэтому вы хотите заблокировать первый взнос в формуле, которая вычисляет платеж на основе различных сумм ссуды.
Например, вы хотите заблокировать значение, которое используется в качестве аванса по кредиту на автомобиль. Этот первый взнос вычислялся на основе процента от годового дохода компании. В настоящее время сумма дохода не изменится, поэтому вы хотите заблокировать первый взнос в формуле, которая вычисляет платеж на основе различных сумм ссуды.
При замене части формулы ее значением ее часть восстановить невозможно.
-
Щелкните ячейку с формулой.
-
В строка формул выберите часть формулы, которую нужно заменить ее вычисляемой величиной. При выборе части формулы, которую вы хотите заменить, убедитесь, что вы включили все операнд.
 Например, при выборе функции необходимо выбрать имя функции целиком, открываемую скобки, аргументы и закрываюю скобки.
Например, при выборе функции необходимо выбрать имя функции целиком, открываемую скобки, аргументы и закрываюю скобки. -
Чтобы вычислить выбранную часть, нажмите F9.
-
Чтобы заменить выбранную часть формулы ее вычисляемой величиной, нажмите ввод.
В Excel в Интернете результаты уже отображаются в ячейке книги, а формула отображается только в .
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Показывать и печатать формулы в Excel для Mac
Excel для Microsoft 365 для Mac Excel 2021 for Mac Excel 2019 для Mac Excel 2016 для Mac Excel для Mac 2011 Еще.
Результаты вычисления формулы отображаются в ячейках на листе, а сами формулы отображаются только в строке формул, что препятствует их выведению на печать. Отображение формул в ячейках упрощает поиск ячеек, содержащих формулы, проверку на ошибки или печать с отображением формул.
С помощью быстрого сочетания клавиш вы можете вместо результатов отобразить на листе формулы.
Отображение всех формул во всех ячейках
Чтобы отобразить формулы в ячейках, нажмите сочетание клавиш CTRL+` (маленький значок — это значок тупого ударения). Когда формулы отобразятся, распечатайте лист обычным способом.
Чтобы вернуться к отображению результатов в ячейках, снова нажмите CTRL+`.
Совет: Подсказка на случай, если вам не удастся найти клавишу значка тупого ударения (`): обычно (но не всегда) она располагается в верхнем левом углу клавиатуры.
Отображение формулы только для одной ячейки
Описанная выше процедура не подходит для одной или нескольких ячеек. Она действует для всего листа. Чтобы обойти это ограничение, некоторые пользователи вводят один апостроф перед формулой в ячейке. Например, ‘=СУММ(1+2+3)
Формулы все равно не отображаются?
Иногда строка формул бывает отключена. Кроме того, показ формул на листе может быть заблокирован. Ниже описана процедура, которой можно воспользоваться в этих ситуациях.
- org/ListItem»>
-
Если вышеуказанное не работает, убедитесь, что на листе включены формулы. Для этого:
В меню Excel выберите пункт Параметры.
-
В области «Авторство»нажмите кнопку .

-
В области Показать в книге,выберите формулы.
Этот параметр применяется только к листу, который вы просматриваете в данный момент.
-
Если формулы в ячейках по-прежнему не отображаются, попытайтесь снять защиту с листа или всей книги.
На вкладке Рецензирование нажмите кнопку Снять защиту листа или Снять защиту книги. При необходимости введите пароль.
Чтобы отобразить строку формул, откройте вкладку Вид и установите флажок Строка формул.
Совет: Чтобы развернуть строку и отображать на ней несколько формул, нажмите клавиши CONTROL+SHIFT+U.
- org/ListItem»>
-
В области «Авторство»нажмите кнопку .
-
В области Параметрыокна выберите параметр Показывать формулы и нажмите кнопку ОК.
Этот параметр применяется только к листу, который вы просматриваете в данный момент.
Примечание: Если включен параметр отображения формул, вы можете переключаться между просмотром значений и формулами, которые их создают, нажав control+’ (ударение).
org/ListItem»>
В меню Excel выберите пункт Параметры.
Если формулы в ячейках по-прежнему не отображаются, попытайтесь снять защиту с листа или всей книги.
На вкладке Рецензия в области Защитанажмите кнопку Книга. При необходимости введите пароль.
Дополнительные сведения
Печать примечаний
Блокировка ячеек для их защиты (2016)
Защита книги
Создание математических формул онлайн
|
|
|
|||||||||||||||||||||||||
Как выразить переменную из формулы с дробью
Серия
Как работать с формулой, чтобы выразить из нее указанную переменную
1. а) Если формула содержит дроби, то сначала нужно избавиться от них, умножив обе части формулы на общий знаменатель;
б) если формула содержит корень, то нужно избавиться от него, возведя обе части формулы в квадрат;
в) если формула содержит дроби и корень, то нужно выполнить действия а) и б) в удобной последовательности.
2. Слагаемое (слагаемые), содержащие переменную, которую нужно выразить, перенести в левую часть, если они не находятся там. Иногда для этого достаточно просто поменять местами левую и правую части формулы.
3. Привести левую часть к виду, в котором нужная переменная будет являться одним из множителей. Иногда для этого нужно будет сгруппировать слагаемые, то есть выполнить разложение на множители левой части формулы.
4. Разделить обе части формулы на лишние множители, находящиеся в левой части, чтобы произошло сокращение, и нужная переменная осталась в левой части одна-единственная.
5. Если полученная таким образом переменная находится в степени, то нужно извлечь из обеих частей формулы корни этой же степени.
При разборе примеров, объясняйте себе каждый шаг!!
Серия
Как работать с формулой, чтобы выразить из нее указанную переменную
1. а) Если формула содержит дроби, то сначала нужно избавиться от них, умножив обе части формулы на общий знаменатель;
б) если формула содержит корень, то нужно избавиться от него, возведя обе части формулы в квадрат;
в) если формула содержит дроби и корень, то нужно выполнить действия а) и б) в удобной последовательности.
2. Слагаемое (слагаемые), содержащие переменную, которую нужно выразить, перенести в левую часть, если они не находятся там. Иногда для этого достаточно просто поменять местами левую и правую части формулы.
3. Привести левую часть к виду, в котором нужная переменная будет являться одним из множителей. Иногда для этого нужно будет сгруппировать слагаемые, то есть выполнить разложение на множители левой части формулы.
4. Разделить обе части формулы на лишние множители, находящиеся в левой части, чтобы произошло сокращение, и нужная переменная осталась в левой части одна-единственная.
5. Если полученная таким образом переменная находится в степени, то нужно извлечь из обеих частей формулы корни этой же степени.
При разборе примеров, объясняйте себе каждый шаг!!
Этот урок – полезное дополнение к предыдущей теме » Тождественные преобразования уравнений «.
Умение делать такие вещи – штука не просто полезная, она – необходимая. Во всех разделах математики, от школьной до высшей. Да и в физике тоже. Именно по этой причине задания подобного рода обязательно присутствуют и в ЕГЭ и в ОГЭ. Во всех уровнях – как базовом, так и профильном.
Во всех разделах математики, от школьной до высшей. Да и в физике тоже. Именно по этой причине задания подобного рода обязательно присутствуют и в ЕГЭ и в ОГЭ. Во всех уровнях – как базовом, так и профильном.
Собственно, вся теоретическая часть подобных заданий представляет собой одну единственную фразу. Универсальную и простую до безобразия.
Удивляемся, но запоминаем:
Любое равенство с буквами, любая формула – это ТОЖЕ УРАВНЕНИЕ!
А где уравнение, там автоматически и тождественные преобразования уравнений . Вот и применяем их в удобном нам порядке и – готово дело.) Читали предыдущий урок? Нет? Однако… Тогда эта ссылочка – для вас.
Ах, вы в курсе? Отлично! Тогда применяем теоретические знания на практике.
Начнём с простого.
Как выразить одну переменную через другую?
Такая задача постоянно возникает при решении систем уравнений. Например, имеется равенство:
Здесь две переменные – икс и игрек.
Что означает это задание? Оно означает, что мы должны получить некоторое равенство, где слева стоит чистый икс. В гордом одиночестве, безо всяких соседей и коэффициентов. А справа – что уж получится.
И как же нам получить такое равенство? Очень просто! С помощью всё тех же старых добрых тождественных преобразований! Вот и применяем их в удобном нам порядке, шаг за шагом добираясь до чистого икса.
Анализируем левую часть уравнения:
Здесь нам мешаются тройка перед иксом и —2y. Начнём с —2у, это попроще будет.
Перекидываем —2у из левой части в правую. Меняя минус на плюс, разумеется. Т.е. применяем первое тождественное преобразование:
Полдела сделано. Осталась тройка перед иксом. Как от неё избавиться? Разделить обе части на эту самую тройку! Т.е. задействовать второе тождественное преобразование.
Вот и всё. Мы выразили икс через игрек. Слева – чистый икс, а справа – что уж получилось в результате «очищения» икса.
Можно было бы сначала поделить обе части на тройку, а затем – переносить. Но это привело бы к появлению дробей в процессе преобразований, что не очень удобно. А так, дробь появилась лишь в самом конце.
Напоминаю, что порядок преобразований никакой роли не играет. Как нам удобно, так и делаем. Самое главное – не порядок применения тождественных преобразований, а их правильность!
А можно из этого же равенства
А почему – нет? Можно! Всё то же самое, только на этот раз нас интересует слева чистый игрек. Вот и очищаем игрек от всего лишнего.
Первым делом избавляемся от выражения 3х. Перебрасываем его в правую часть:
Осталась двойка с минусом. Делим обе части на (-2):
И все дела.) Мы выразили y через х. Переходим к более серьёзным заданиям.
Как выразить переменную из формулы?
Не проблема! Точно так же! Если понимать, что любая формула – тоже уравнение.
Например, такое задание:
выразить переменную с.
Формула – тоже уравнение! Задание означает, что через преобразования из предложенной формулы нам надо получить какую-то новую формулу. В которой слева будет стоять чистая с, а справа – что уж получится, то и получится…
Однако… Как нам эту самую с вытаскивать-то?
Как-как… По шагам! Ясное дело, что выделить чистую с сразу невозможно: она в дроби сидит. А дробь умножается на r… Значит, первым делом очищаем выражение с буквой с, т.е. всю дробь целиком. Здесь можно поделить обе части формулы на r.
Следующим шагом надо вытащить с из числителя дроби. Как? Легко! Избавимся от дроби. Нету дроби – нету и числителя.) Умножаем обе части формулы на 2:
Осталась элементарщина. Обеспечим справа букве с гордое одиночество. Для этого переменные a и b переносим влево:
Вот и всё, можно сказать. Осталось переписать равенство в привычном виде, слева направо и – ответ готов:
Осталось переписать равенство в привычном виде, слева направо и – ответ готов:
Это было несложное задание. А теперь задание на основе реального варианта ЕГЭ:
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость погружения батискафа вычисляется по формуле
где с = 1500 м/с – скорость звука в воде,
f – частота отражённого от дна сигнала, регистрируемая приёмником (в МГц).
Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 2 м/с.
«Многа букафф», да… Но буквы – это лирика, а общая суть всё равно та же самая. Первым делом надо выразить эту самую частоту отражённого сигнала (т.е. букву f) из предложенной нам формулы. Вот этим и займёмся. Смотрим на формулу:
Напрямую, естественно, букву f никак не выдернешь, она снова в дробь запрятана. Причём и в числитель и в знаменатель. Поэтому самым логичным шагом будет избавиться от дроби. А там – видно будет. Для этого применяем второе преобразование – умножаем обе части на знаменатель.
Поэтому самым логичным шагом будет избавиться от дроби. А там – видно будет. Для этого применяем второе преобразование – умножаем обе части на знаменатель.
А вот тут – очередные грабли. Прошу обратить внимание на скобки обеих частях! Частенько именно в этих самых скобочках и кроются ошибки в подобных заданиях. Точнее, не в самих скобочках, а в их отсутствии.)
Скобки слева означают, что буква v умножается на весь знаменатель целиком. А не на его отдельные кусочки…
Справа же, после умножения, дробь исчезла и остался одинокий числитель. Который, опять же, весь целиком умножается на буковку с. Что и выражается скобками в правой части.)
А вот теперь скобки и раскрыть можно:
Дальше дело нехитрое. Всё что с f собираем слева, а всё что без f – справа. Займёмся переносом:
Отлично. Процесс идёт.) Теперь буковка f слева стала общим множителем.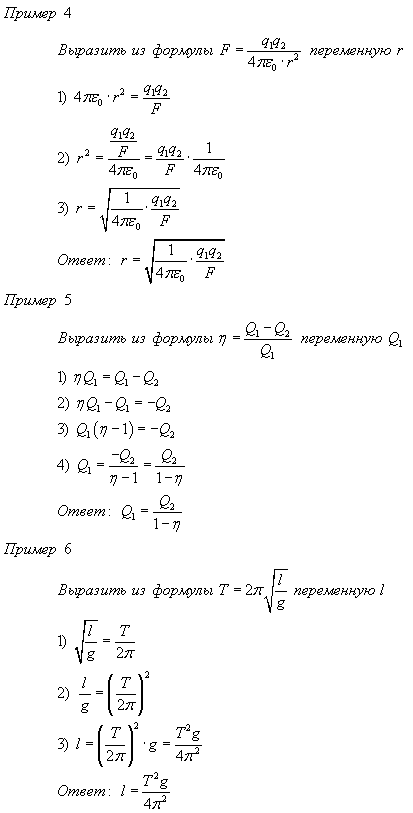 Выносим её за скобки:
Выносим её за скобки:
Осталось всего ничего. Делим обе части на скобку (v—c) и – дело в шляпе!
В принципе, всё готово. Переменная f уже выражена. Но можно дополнительно «причесать» полученное выражение – вынести f за скобку в числителе и сократить всю дробь на (-1), тем самым избавившись от лишних минусов:
Вот такое выражение. А вот теперь и числовые данные подставить можно. Получим:
Вот и всё. Надеюсь, общая идея понятна.
Делаем элементарные тождественные преобразования с целью уединить интересующую нас переменную. Главное здесь — не последовательность действий (она может быть любой), а их правильность.
В этих двух уроках рассматриваются лишь два базовых тождественных преобразования уравнений. Они работают всегда. На то они и базовые. Помимо этой парочки, существует ещё множество других преобразований, которые тоже будут тождественными, но не всегда, а лишь при определённых условиях.
Например, возведение обеих частей уравнения (или формулы) в квадрат (или наоборот, извлечение корня из обеих частей) будет тождественным преобразованием, если обе части уравнения заведомо неотрицательны.
Или, скажем, логарифмирование обеих частей уравнения будет тождественным преобразованием, если обе части заведомо положительны. И так далее…
Подобные преобразования будут рассматриваться в соответствующих темах.
А здесь и сейчас — примеры для тренировки по элементарным базовым преобразованиям.
Средняя скорость лыжника (в км/ч) на дистанции в два круга рассчитывается по формуле:
где V1 и V2 – средние скорости (в км/ч) на первом и втором кругах соответственно. Какова была средняя скорость лыжника на втором круге, если известно, что первый круг лыжник пробежал со скоростью 15 км/ч, а средняя скорость на всей дистанции оказалась равной 12 км/ч?
Задача на основе реального варианта ОГЭ:
Центростремительное ускорение при движении по окружности (в м/с 2 ) можно вычислить по формуле a=ω 2 R, где ω – угловая скорость (в с -1 ), а R – радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с -1 , а центростремительное ускорение равно 289 м/с 2 .
Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с -1 , а центростремительное ускорение равно 289 м/с 2 .
Задача на основе реального варианта профильного ЕГЭ:
К источнику с ЭДС ε=155 В и внутренним сопротивлением r=0,5 Ом хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой:
При каком сопротивлении нагрузки напряжение на ней будет 150 В? Ответ выразите в омах.
Ответы (в беспорядке): 4; 15; 2; 10.
А уж где числа, километры в час, метры, омы – это как-нибудь сами…)
Привлекайте внимание посетителей к Вашему магазину, публикуя новости о Вашей компании и товарах!
Привлекайте внимание посетителей к Вашему магазину, публикуя новости о Вашей компании и товарах!
Привлекайте внимание посетителей к Вашему магазину, публикуя новости о Вашей компании и товарах!
Идёт приём заявок
Подать заявку
Для учеников 1-11 классов и дошкольников
Описание презентации по отдельным слайдам:
Выразить переменную из формулы Дудников Ю. А. МБОУ Качалинская СОШ 2017
А. МБОУ Качалинская СОШ 2017
1. В той части формулы, где содержится переменная, которую нужно выразить, расставьте порядок действий. В одночленах и многочленах, не содержащих искомую величину, порядок действий не расставляем. 2. Найдите в выражении последнее действие, и перенести одночлен или многочлен, исполняющий это действие через знак равенства первым, но уже с противоположным действием. Таким образом, перенесите из одной части равенства в другую все известные величины. В заключение перепишите формулу так, чтобы неизвестная переменная стояла слева. Порядок выражения переменной
1 2 1 2 3 S a t 2 = 1 2 2 S a t 2 = 2 S a t 2 =
a = 1 1 2 1 0 — t υ υ 0 t a = + υ υ t a = + 0 υ υ t a — = 0 υ υ
1 2 1 2 3 1 1 2 b + S = a h h = + 2 ) ( a b ( ) h b a 2 S + = h a b 2 S — = h b a a b
1 2 1 1 a = υ υ 0 — t Заново расставляем порядок действий, так как нужная переменная оказалась в другой части формулы. t — t = υ 0 a υ
1 2 1 2 3 1 1 2 υ + S = υ 0 t t = + 2 0 ) ( υ υ ( ) t 0 υ υ 2 S + = t 0 υ υ 2 S — = t 0 υ υ υ υ
1 2 1 ( ) c 0 t t к c 0 t t к c 0 t t к Q m + = c 0 t t к
3 1 2 1 2 1 υ υ 1 2 S 2 = 0 2 — a υ — 2 S a 2 = υ 2 0 2 S a 2 = + 2 0 υ υ 2 S a = 2 + 0 υ υ 2 2 S a = + 0 υ υ
1 3 2 2 3 3 g ℓ = T 2 π g ℓ = T 2 π 2 2 g ℓ = T 4 π 2 2 g ℓ T 4 π = g
3 2 1 1 4 3 2 1 1 2 ν h = + ν кр h m 2 2 υ ν h — = ν кр h m 2 2 υ 2 ν h — = ν кр h m 2 υ ( ) 2 ν h — = ν кр h m 2 υ ( ) ν h — = ν кр h m 2 υ ( ) ν h — = ν кр h m 2 υ ( )
1 = T T х — Т η н н = T T х — Т η н н — T T х = Т η н н — — T х = Т η н — ( 1 ) — 1 = T T х — н η 1 = T T х — н η
— k d = — C 2 d — k d = C 2 d ( ) — — k d = C 2 d — C + k d = C 2 d + C ( ) + k 1 = C 2 d + C + k 1 = C 2 d + C
1 1 1 2 1 2 2 + S = υ 0 t 3 t = + 2 0 ) ( υ υ υ ( ) t 0 υ υ 2 S + = t 0 υ υ 2 S — = t 0 υ υ υ υ
2 2 3 5 1 4 x a + t k + b = 1 x a — t k + b = 1 2 2 3 1 4 ( x a — t k + b = 1 2 2 3 1 ) 2 ( x a — t k + b = 1 2 ) 2 ) ( 1 ( x a — t k + b = 1 ) 2 ) ( (
1 2 1 4 3 1 3 2 2 4 1 3 2 1 1 S = ) + K 2 E m a x — b ( + K E m ) 2 a x — b ( = S + K E m 2 a x — b = S 2 a x + K E m + b = S m + K E + b = S S 2 a x + K E + b = S S m x a + K E + b = S S m
h + g R G = ) 2 M ( h + g R G = ) 2 M ( h + g R G = ) 2 M ( h + g R G = M h — g R G = M
1 1 2 Приведем к общему знаменателю левую часть формулы Если дроби равны, то обратные им дроби тоже равны. Перевернем дроби, для того чтобы неизвестная переменная оказалась в числителе. F 1 1 = + f 1 d F 1 1 = — f 1 d F d 1 = — f F d F d 1 = — f F d F d = — f F d
Перевернем дроби, для того чтобы неизвестная переменная оказалась в числителе. F 1 1 = + f 1 d F 1 1 = — f 1 d F d 1 = — f F d F d 1 = — f F d F d = — f F d
1 1 2 1 Приведем к общему знаменателю левую часть формулы Переворачиваем дробь. k 1 2 = + f 3 d k 1 2 = — f 3 d k d = — f k d 2 3 — k d 2 = f k d 3 1 k d 2 = — f k d 3 1
X A + = ( ) ω φ t s i n r c r c X A — = a ω t s i n r c ω 1
U U X β = 2 l o g 0 δ U U X β = 2 l o g 0 δ U U X β = 0 δ 2 U U X β = 0 δ 2
f 0 f 1 = — c υ ( f 0 f 1 = — c υ ) ( )
В каждой задаче по физике требуется из формулы выразить неизвестную, следующим шагом подставить численные значения и получить ответ, в некоторых случаях необходимо только выразить неизвестную величину. Способов выведения неизвестной из формулы много. Если посмотреть страницы Интернета, то мы увидим множество рекомендаций по этому поводу. Это говорит о том, что единого подхода к решению этой проблемы научное сообщество еще не выработало, а те способы, которые используются, как показывает опыт работы в школе – все они малоэффективны. До 90% учащихся выпускных классов не умеют правильно выразить неизвестное. Те же, кто умеют это делать – выполняют громоздкие преобразования. Очень странно, но физики, математики, химики имеют разные подходы, объясняя методы переноса параметров через знак равенства (предлагают правила треугольника, креста или пропорций др.) Можно сказать, что имеют разную культуру работы с формулами. Можно представить, что происходит с большинством учеников, которые встречается с разными трактовками решения данной проблемы, последовательно посещая уроки этих предметов. Эту ситуацию описывает типичный диалог в сети:
До 90% учащихся выпускных классов не умеют правильно выразить неизвестное. Те же, кто умеют это делать – выполняют громоздкие преобразования. Очень странно, но физики, математики, химики имеют разные подходы, объясняя методы переноса параметров через знак равенства (предлагают правила треугольника, креста или пропорций др.) Можно сказать, что имеют разную культуру работы с формулами. Можно представить, что происходит с большинством учеников, которые встречается с разными трактовками решения данной проблемы, последовательно посещая уроки этих предметов. Эту ситуацию описывает типичный диалог в сети:
Научите выражать из формул величины. 10 класс, мне стыдно не знать, как из одной формулы делать другую.
Да не переживай — это проблема многих моих одноклассников, хоть я и в 9 кл. Учителя показывают это чаще всего методом треугольника, но мне кажется, что это неудобно, да и запутаться легко. Покажу наиболее простой способ, которым я пользуюсь.
Допустим, дана формула:
Ну более простая. тебе из этой формулы нужно найти время. Ты берешь и в эту формулу подставляешь числа только разные, исходя из алгебры. Допустим:
тебе из этой формулы нужно найти время. Ты берешь и в эту формулу подставляешь числа только разные, исходя из алгебры. Допустим:
и тебе наверное хорошо видно, что чтобы найти время в алгебраическом выражении 5 нужно 45/9 т.е переходим к физике: t=s/v
У большинства учащихся формируется психологический блок. Часто учащиеся отмечают, что при чтении учебника трудности в первую очередь вызывают те фрагменты текста, в которых много формул, что «длинные выводы все равно не понять», но при этом возникает чувство неполноценности, неверия в свои силы.
Я, предлагаю следующее решение данной проблемы – большинство учащихся все — таки могут решать примеры и, следовательно, расставлять порядок действий. Используем это их умение.
1. В той части формулы, где содержится переменная, которую нужно выразить, надо расставь порядок действий, причем в одночленах, не содержащих искомую величину этого делать не будем.
2. Затем в обратной последовательности вычислений перенесите элементы формулы в другую часть формулы ( через знак равенства) с противоположным действием ( « минус» — «плюс», «разделить» — « умножить», « возведение в квадрат» – «извлечение корня квадратного»).
То есть найдем в выражении последнее действие и перенесем одночлен или многочлен, исполняющий это действие, через знак равенства первым, но уже с противоположным действием. Таким образом, последовательно, находя последнее действие в выражении, перенесите из одной части равенства в другую все известные величины. В заключение перепишем формулу так, чтобы неизвестная переменная стояла слева.
Получаем четкий алгоритм работы, точно знаем, сколько преобразований необходимо выполнить. Можем для тренировки использовать уже известные формулы, можем выдумывать свои. Для начала работы над усвоением данного алгоритма была создана презентация.
Опыт работы с учащимися показывает, что данный способ хорошо воспринимается ими. Реакция учителей на мое выступление на фестивале «Учитель профильной школы» также говорит о положительном зерне, заложенном в этой работе.
Глава 7. Вращательное движение. Кинематика и динамика
Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
(7.1) |
В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения
(7. |
Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.
Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим
(7.3) |
Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.
Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т. е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
(7.4) |
Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах
(7.5) |
Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
(7. |
Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.
Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.
Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).
Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7. 5). Имеем
5). Имеем
(правильный ответ – 2).
Применяя определение угловой скорости к колесу (задача 7.1.3), получаем
(правильный ответ 1).
Из формулы (7.2) имеем
(задача 7.1.4 – правильный ответ 4).
Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска
А теперь по формуле (7.5) для второй точки получаем
(ответ 2).
Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7. 4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).
4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).
Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно
(ответ 4).
Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).
Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с2, получим для равнодействующей =2 Н (ответ 2).
Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1
(ответ 1).
Для сравнения центростремительных ускорений материальных точек в задаче 7.2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
(ответ 3).
Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим
(7.5) |
Поэтому
(ответ 1).
Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)
где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем
(ответ 2).
Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения
Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
(ответ 4).
В задаче 7.2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
(ответ 3).
В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает
(1) |
На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем
Подставляя в эту формулу силу из формулы (1), находим (ответ 2).
В задаче 7.2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
(ответ 3).
Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):
где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно
(задача 7. 2.9 – ответ 1).
2.9 – ответ 1).
Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).
Кинематика — Физика — Теория, тесты, формулы и задачи
Оглавление:
- Основные теоретические сведения
- Система СИ
- Путь и перемещение
- Средняя скорость
- Равноускоренное прямолинейное движение
- Свободное падение по вертикали
- Горизонтальный бросок
- Бросок под углом к горизонту (с земли на землю)
- Сложение скоростей
- Равномерное движение по окружности
Система СИ
К оглавлению…
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины — метр (1 м),
- времени — секунда (1 с),
- массы — килограмм (1 кг),
- количества вещества — моль (1 моль),
- температуры — кельвин (1 К),
- силы электрического тока — ампер (1 А),
- Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).

При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
К оглавлению…
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
К оглавлению…
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
К оглавлению. ..
..
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:
Свободное падение по вертикали
К оглавлению…
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
К оглавлению…
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:
Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
К оглавлению…
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
К оглавлению…
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
К оглавлению…
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:
Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω:
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:
Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
Вывод сложных процентов
Показывая, как работают формулы, с примерами!
С помощью сложного процента мы вычисляем проценты за первый период, прибавляем их к итогу, и затем вычисляем проценты за следующий период и так далее…, вот так:
Составим формулу
Давайте начнем с первого года:
1000,00 долл. США + (1000,00 долл. США × 10%) = 1100,00 долл. США
США + (1000,00 долл. США × 10%) = 1100,00 долл. США
Мы можем изменить его следующим образом:
Таким образом, прибавление 10 % равносильно умножению на 1,10
(Примечание: процентная ставка была преобразована в десятичную дробь путем деления на 100: узнайте больше.)
И эта формула работает для любого года:
- Мы могли бы сделать следующий год следующим образом: 1100 долл. США × 1,10 = 1210 долл. США
- Затем перейдите к следующему году: 1 210 долл. США × 1,10 = 1 331 долл. США
- и т.д…
Таким образом, он работает так:
Фактически, мы могли бы перейти прямо с начала до 5 -го года, если мы
умножьте 5 раза :$ 1000 × 1,10 × 1,10 × 1,10 × 1,10 × 1,107 $ 1,610,51
Но легче записать серию умножений, используя Экспоненты (или Степени) следующим образом:
Формула
Мы использовали реальный пример, но давайте сделаем его более общим на , используя буквы вместо цифры , например:
(Сравните это с приведенным выше расчетом: PV = 1000 долларов, r = 0,10, n = 5 и FV = 1610,51 доллара)
- Если процентная ставка годовая, то
число лет
- Если процентная ставка месячная, то n количество месяцев
- и так далее
Примеры
Как насчет некоторых примеров. ..
..
… а если кредит ушел на 15 лет ? … просто измените значение «n»:
… а что, если кредит был на 5 лет, но процентная ставка была всего 6%? Здесь:
(Обратите внимание, что это 1,06 , а не 1,6)
Четыре формулы
Итак, основная формула сложных процентов:
FV = PV (1+r)
7 n
С учетом этого мы можем рассчитать будущую стоимость FV , когда мы знаем текущую стоимость PV , процентную ставку r и количество периодов n
И мы можем изменить эту формулу, чтобы найти FV , процентная ставка или количество периодов, когда мы знаем остальные три.
Вот все четыре фурмулы:
| FV = PV (1+r) n | Найдите будущую стоимость , когда мы знаем текущую стоимость, процентную ставку и количество периодов. | |
| PV = FV / (1+r) n | Найдите текущую стоимость , когда мы знаем будущую стоимость, процентную ставку и количество периодов. | |
| r = ( FV / PV ) 1/n — 1 | Найдите Процентную ставку , зная текущую стоимость, будущую стоимость и количество периодов. | |
| н = Лн(ФВ/ПВ) пер(1+р) | Найдите количество периодов , когда мы знаем текущую стоимость, будущую стоимость и процентную ставку |
Как мы получили эти три другие формулы? Читать дальше!
Расчет приведенной стоимости
Пример: Сэм хочет заработать 2000 долларов за 5 лет под 10% годовых.
 С какого количества должен начать Сэм?
С какого количества должен начать Сэм?Другими словами, мы знаем будущую стоимость, и хотим знать текущую стоимость .
Мы можем просто изменить формулу, чтобы она подходила … разделив обе части на (1+r) n , чтобы получить:
Начнем с: FV = PV (1+r) n
Поменять местами: PV (1+r) n = FV
Разделить обе стороны на (1+r) n :PV = ФВ (1+R) N
Так теперь мы можем рассчитать ответ:
Пример (продолжение):
PV = 2000 долл. США / (1+0,10) 5 = 2000 долл.
Итак, Сэм должен начать с 1 241,84 доллара
Это работает следующим образом:
Другой пример: Сколько вам нужно инвестировать сейчас, чтобы получить 10 000 долларов через 10 лет при процентной ставке 8%? PV = 10 000 долл. США / (1+0,08) 10 = 10 000 долл. США / 2,1589 = $ 4 631,93
США / 2,1589 = $ 4 631,93
Таким образом, долл. США 4,631,93 инвестировали на 8% на 10 лет. : У Сэма всего 1000 долларов, и он хочет, чтобы через 5 лет они выросли до 2000 долларов. Какую процентную ставку следует искать Сэму?
Нам нужно изменить первую формулу, чтобы получить ее:
Начать с: FV = PV (1+r) n
Поменять местами стороны: PV (1+r) n = FV
Разделить с обеих сторон PV:(1+r) n = ФВ PV
Взять корень n-й степени из обеих сторон:1+r = ( ФВ ПВ ) 1/n
Вычесть 1 с обеих сторон:r = ( ФВ ФВ ) 1/n − 1
(Примечание: чтобы понять шаг «извлечь корень n-й степени», пожалуйста, прочитайте дробные показатели)
Результат:
r = ( FV / PV ) 1/n − 1
Теперь у нас есть формула, нужно просто «подставить» значения, чтобы получить результат:
Пример (продолжение):
r = (2000 долл. США / 1000 долл. США) 1/5 − 1
США / 1000 долл. США) 1/5 − 1
= ( 2 ) 0,2 — 1
= 1,1487 — 1
= 0,1487
И 0,1487 в процентах равно 14,87%
Итак, Сэму нужно 14,87% , чтобы превратить 1000 долларов в 2000 долларов за 5 лет.
Другой пример: Какая процентная ставка вам нужна, чтобы превратить 1000 долларов в 5000 долларов за 20 лет?R = (5000 долл. США / 1000 долл. США) 1/20 — 1 = (5) 0,05 — 1 = 1,0838 — 1 = 0,0838
и 0,0838. Процент 8.38% . Таким образом, 8,38% превратят 1000 долларов в 5000 долларов за 20 лет.
Расчет количества периодов
Пример: Сэм может получить только 10% процентную ставку. Через сколько лет Сэм получит 2000 долларов?
Если мы хотим узнать, сколько периодов потребуется, чтобы превратить 1000 долларов в 2000 долларов под 10% годовых, мы можем изменить основную формулу.
Но для этого нам нужно использовать функцию натурального логарифма ln() .
Начать с: FV = PV (1+r) n
Поменять стороны: PV (1+r) n = FV
Разделить обе части на PV:(1+r) n = FV / PV
Использовать логарифмы: ln(1+r) × n = ln( FV / PV )
Разделить 90 обе стороны на ln(1+r):n = лин( ФВ/ПВ) ln(1+r)
(Примечание: чтобы понять шаг «использовать логарифмы», пожалуйста, прочитайте «Работа с экспонентами и логарифмами»).
Теперь подставим значения:
Пример (продолжение):
n = ln(2000 долл. США / 1000 долл. США) / ln(1 + 0,10) = ln(2)/ln(1,10) = 0,69315/0,09531 = 7,27
Магия! Потребуется 7,27 лет , чтобы превратить 1000 долларов в 2000 долларов под 10% годовых.
Бедному Сэму придется ждать более 7 лет.
Другой пример: Сколько лет потребуется, чтобы превратить 1000 долларов в 10000 долларов под 5% годовых?
n = ln(10 000 долл.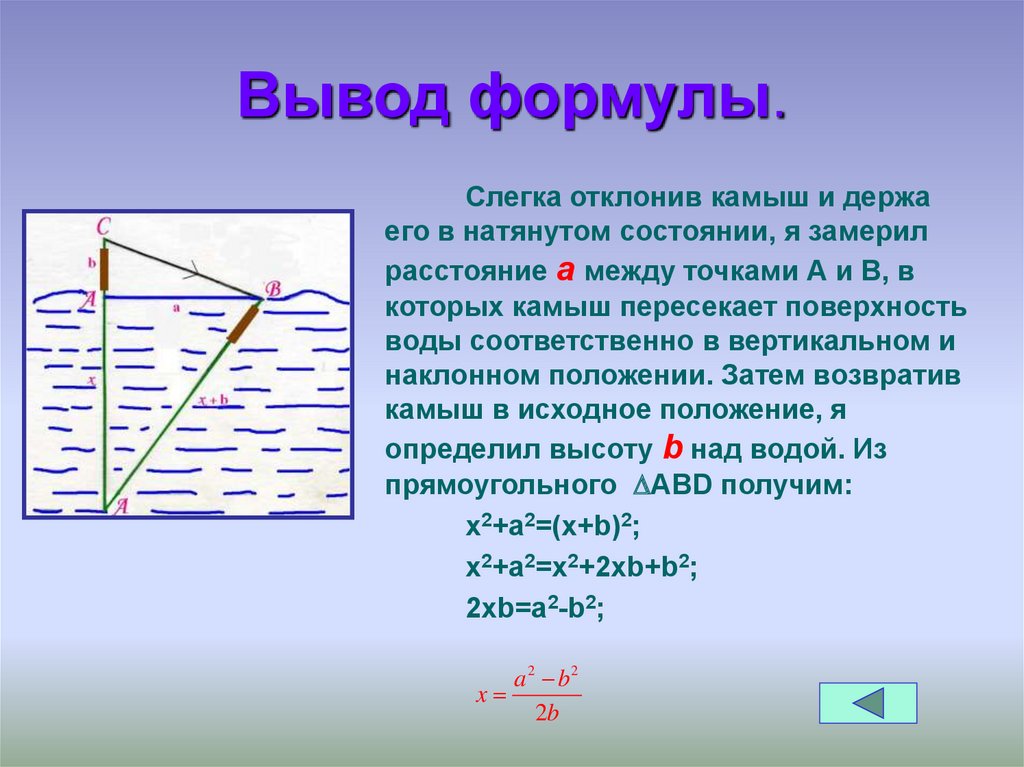 США / 1000 долл. США) / ln(1 + 0,05) = ln(10)/ln(1,05) = 2,3026/0,04879 = 47,19
США / 1000 долл. США) / ln(1 + 0,05) = ln(10)/ln(1,05) = 2,3026/0,04879 = 47,19
47 лет! Но речь идет о 10-кратном увеличении, всего под 5% годовых.
Заключение
Знание того, как получаются и используются формулы, облегчает их запоминание и использование в различных ситуациях.
Калькулятор текущей стоимости
Использование калькулятора
Найдите текущую стоимость будущей денежной суммы. Калькулятор текущей стоимости отвечает на вопрос: «Что мне нужно инвестировать сегодня, чтобы иметь определенную сумму денег в будущем?»
Текущую стоимость можно представить как сумму, которую необходимо отложить сейчас, чтобы иметь определенную сумму денег в будущем. Формула текущей стоимости применяет скидку к вашей будущей стоимости, вычитая заработанные проценты, чтобы найти текущую стоимость в сегодняшних деньгах.
Формула текущей стоимости и калькулятор
Формула текущей стоимости: PV=FV/(1+i) n , где вы делите будущую стоимость FV на коэффициент 1 + i для каждого периода между настоящим и будущим. даты.
даты.
Введите эти числа в калькулятор текущей стоимости для расчета PV:
- Сумма будущей стоимости FV
- Количество периодов времени (лет) t , что равно n в формуле
- Процентная ставка Р , что равно i в формуле
- Частота компаундирования
- Выплаты денежных потоков
- Темп роста ренты
Текущая стоимость денежной суммы будет выше в будущем, когда она будет инвестирована и принесет проценты.
Приведенная стоимость — это сумма, которую вам необходимо инвестировать сейчас при известном проценте и процентной ставке, чтобы у вас была определенная сумма денег в определенный момент в будущем.
Вы можете ввести 0 для любой переменной, которую хотите исключить при использовании этого калькулятора. Наш другой
Калькуляторы текущей стоимости предлагают более специализированные расчеты текущей стоимости.
Что входит в расчет текущей стоимости
Калькулятор текущей стоимости использует следующее для определения текущей стоимости PV будущей суммы плюс проценты минус выплаты денежных потоков:
- Будущая стоимость FV
- Будущая стоимость денежной суммы
- Количество периодов времени t
- • Периоды времени обычно составляют несколько лет.
• Убедитесь, что все ваши входные данные используют одну и ту же единицу измерения периода времени (годы, месяцы и т. д.).
• Введите p или perpetuity для бессрочной ренты - Процентная ставка Р
- Номинальная процентная ставка или заявленная ставка в процентах
- Компаундирование м
- • Количество начислений сложных процентов за период
• Введите 1 для ежегодного начисления сложных процентов, то есть один раз в год.
• Введите 4 для ежеквартального начисления процентов
• Введите 12 для ежемесячного начисления сложных процентов.
• Введите 365 для ежедневного начисления процентов.
• Введите c или Continuous для непрерывного компаундирования - Выплаты аннуитета денежного потока PMT
- Сумма платежа за каждый период
- Скорость роста G
- Темп роста аннуитетных платежей за период вводится в процентах
- Количество платежей q за период
- • Частота платежей
• Введите 1 для ежегодных платежей, то есть один раз в год.
• Введите 4 для ежеквартальных платежей
• Введите 12 для ежемесячных платежей
• Введите 365 для ежедневных платежей - Когда происходят аннуитетные платежи T
- • Выберите и , который представляет собой обычный аннуитет для платежей в конце периода.

• Выберите начало для платежей в начале периода - Приведенная стоимость ФВ
- Результатом расчета PV является текущая стоимость любой суммы будущей стоимости плюс будущие денежные потоки или аннуитетные платежи
В следующих разделах показано, как вывести формулы приведенной стоимости. Список формул, представленных здесь, см. на нашей странице «Формулы приведенной стоимости».
Вывод формулы текущей стоимости
Будущая стоимость ( FV ) суммы текущей стоимости ( PV ), которая накапливает проценты по ставке i за один период времени, представляет собой текущую стоимость плюс проценты, полученные на эту сумму. Математическое уравнение 9n}\tag{1b} \)
Уравнения, которые у нас есть (1a)
будущая стоимость настоящей суммы и (1b)
текущая стоимость будущей суммы при периодической процентной ставке i, где n — количество периодов в будущем. n}\right]\tag{2.1} \) 9n\right](1+iT)\tag{3} \)
n}\right]\tag{2.1} \) 9n\right](1+iT)\tag{3} \)
Текущая стоимость растущей ренты (g = i)
Если g = i, вы заметите, что члены (1 + g) сокращаются в уравнении ( 3а) и получаем
\( PV=\dfrac{PMT}{(1+i)}+\dfrac{PMT}{(1+i)}+\dfrac{PMT}{(1+i)}+ …+\dfrac{PMT}{(1+i)} \)
, так как теперь у нас есть n экземпляров PMT /(1+i) мы можем сократить уравнение. Также учитывая причитающуюся ренту или обычную ренту, умножаем на (1 + iT), и получаем
\( PV=\dfrac{PMTn}{(1+i)}(1+iT)\tag{4} \)
Текущая стоимость вечности (t → ∞ и n = mt → ∞)
Для бессрочная рента, вечная рента, время и количество периодов стремится к бесконечности, поэтому n стремится к бесконечности. По мере увеличения n член 1/(1 + i) n в формуле (2) стремится к 0, оставляя
\( PV=\dfrac{PMT}{i}(1+iT)\tag{5} \)
Текущая стоимость растущей вечности (g
< i) (t → ∞ и n = mt → ∞) Аналогично для возрастающей вечности, где мы должны иметь g
\( PV=\dfrac{PMT}{(i-g)}(1+iT)\tag{6} \)
Текущая стоимость растущей вечности (g = i) (t → ∞ и n = mt → ∞)
Поскольку n также стремится к бесконечности (n → ∞), когда t стремится к бесконечности (t → ∞), мы видим, что Текущая стоимость с растущим аннуитетом (g = i) также стремится к бесконечности
\( PV=\dfrac{PMTn}{(1+i)}(1+iT)\rightarrow\infty\tag{7} \) 9{mt}}\right](1+(\frac{r}{m})T)\tag{11} \)
, где n = mt и \(i = \frac{r}{m}\) . t — количество периодов, m — интервалы начисления процентов за период, r — ставка за период t. (это легко понять, если применить t в годах, r — номинальную ставку в год и m — интервалы начисления процентов в год). При записи в виде i и n i — это ставка за интервал начисления процентов, а n — общее количество интервалов начисления процентов, хотя это все еще можно сформулировать как «i — это ставка за период, а n — количество периодов», где период = интервал начисления процентов. «Период» может быть широким термином.
t — количество периодов, m — интервалы начисления процентов за период, r — ставка за период t. (это легко понять, если применить t в годах, r — номинальную ставку в год и m — интервалы начисления процентов в год). При записи в виде i и n i — это ставка за интервал начисления процентов, а n — общее количество интервалов начисления процентов, хотя это все еще можно сформулировать как «i — это ставка за период, а n — количество периодов», где период = интервал начисления процентов. «Период» может быть широким термином.
Относительно входных данных калькулятора, r = R/100 и g = G/100. Если в этих расчетах частоты начисления сложных процентов (m) и выплат (q) не совпадают, r преобразуется в эквивалентной ставки, чтобы она совпадала с платежами, то n и i пересчитываются через периодичность платежей, q. Первая часть уравнения – это текущая стоимость будущей суммы, а вторая часть Текущая стоимость аннуитета.
Приведенная стоимость бессрочной лицензии (t → ∞ и n = mt → ∞)
Для бессрочной, бессрочной ренты число периодов t стремится к бесконечности, поэтому n стремится к бесконечности. Член FV в уравнении (11) становится равным 0, и 1/(1 + i) n во втором члене также становится равным 0, оставляя только формулу (5)
Член FV в уравнении (11) становится равным 0, и 1/(1 + i) n во втором члене также становится равным 0, оставляя только формулу (5)
\( PV=\dfrac{PMT}{i}(1+iT)\tag{5} \)
Текущая стоимость растущей вечности (g
< i) (t → ∞ и n = mt → ∞) Аналогично для возрастающей вечности, где мы должны иметь g
\( PV=\dfrac{PMT}{(i-g)}(1+iT)\tag{6} \)
Текущая стоимость растущей вечности (g = i) (t → ∞ и n = mt → ∞)
Поскольку n также стремится к бесконечности (n → ∞), когда t стремится к бесконечности (t → ∞), мы видим, что Приведенная стоимость с растущим аннуитетом (g = i) (10) стремится к бесконечности, и мы снова возвращаемся к уравнению (7)
9{mt}}\right](1+(\frac{r}{m})T)\tag{11} \) Эффективная ставка равна i eff = (1 + (r/m)) m — 1 для ставки r, начисляемой m раз за период. Математически можно доказать, что при m → ∞ i eff (эффективная ставка r при непрерывном начислении процентов) достигает верхнего предела, равного e r — 1.
Математически можно доказать, что при m → ∞ i eff (эффективная ставка r при непрерывном начислении процентов) достигает верхнего предела, равного e r — 1.
Приведенная стоимость с непрерывным начислением процентов (m → ∞)
Удаление m и изменение r на эффективную ставку r, e 9р-1)Т)\стрелка вправо\infty\тег{17} \)
Формула Герона. Калькулятор | Formula
Автор: Hanna Pamuła, PhD доказательство
Если вам интересно, как вычислить площадь треугольника, зная его три стороны, вы попали в нужное место — этот калькулятор формулы Герона может сделать это в кратчайшие сроки. Просто введите заданные значения — например. стороны треугольника — и наш инструмент покажет вам ответ. Если вам интересно узнать о формуле площади Герона, вы прочтете о ней ниже. Кроме того, там можно найти доказательства формулы Герона, так что продолжайте прокручивать, чтобы узнать больше об этой полезной, но не очень известной формуле.
Формула площади Герона: уравнение площади треугольника с тремя сторонами по данным
Формула Герона, также известная как формула Герона, представляет собой формулу для расчета площади треугольника по трем сторонам треугольника. Впервые он упоминается в книге Герона Metrica , написанной ок. 60 г. н.э., который представлял собой сборник формул для вычисления поверхностей и объемов различных объектов. Основная формула:
площадь = √(s * (s - a) * (s - b) * (s - c))
, где
s — это полупериметр — половина периметра треугольника:
s = (a + b + c) / 2
Однако существуют и другие формы этой формулы — если вы не хотите вычислять полупериметр по стороны, вы можете использовать формулу только с длинами сторон:
площадь = 0,25 * √((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))
Доказательство формулы Герона
Есть много способов доказать формулу площади Герона, но вам нужно знать некоторые основы геометрии. Вы можете использовать:
Вы можете использовать:
- Алгебра и теорема Пифагора;
- Тригонометрия и закон косинусов.
Существуют и другие доказательства, но они более сложны или используют менее популярные законы (например, тригонометрическое доказательство с использованием закона котангенсов).
- Алгебраическое доказательство
В этом доказательстве нам нужно использовать формулу площади треугольника:
площадь = (c * h) / 2
Все значения в формуле должны быть выражены через стороны треугольника: c — это сторона, поэтому она соответствует условию, но мы мало знаем о своем росте. Итак, чтобы получить доказательство формулы Герона, нам нужно найти ч с точки зрения сторон.
Из теоремы Пифагора мы знаем, что:
h² + (c - d)² = a²иh² + d² = b², согласно рисунку вышеВычитание этих двух уравнений дает нам:
c² - 2 * c * d = a² - b²из чего можно вывести формулу дляdв пересчете на стороны треугольника:d = (-a² + b² + c²) / (2 * c)Следующим шагом будет определение высоты относительно сторон треугольника.
 Снова используйте теорему Пифагора:
Снова используйте теорему Пифагора:h² = b² - d²h² = b² - ((-a² + b² + c²) / (2 * c))²— это уже в терминах сторон, но попробуем привести к более красивому виду, применяя тождество разности квадратов:h² = ((2 * b * c) - a² + b² + c²) * ((2 * b * c) - a² + b² + c²) / (4 * c⁴)h² = ((b + c)² - a²) * (a² - (b - c)²) / (4 * c²)h² = (b + c - a) * (b + c + a) * (a + b - c) * (a - b + c) / (4 * c²)Примените эту формулу к первому уравнению для площади треугольника:
площадь = (c * h) / 2 = 0,5 * c * hплощадь = 0,5 * c * √((b + c - a) * (b + c + a) * (a + b - c) * (a - b + c) / (4 * c²))площадь = 0,25 * √((b + c - a) * (b + c + a) * (a + b - c) * (a - b + c)
Вот ты где! Это доказательство площади Герона. Преобразование окончательного уравнения в форму с использованием полупериметра является тривиальной задачей.
- Тригонометрическое доказательство
Посмотрите на рисунок — a, b, c — стороны треугольника, а α, β, γ — углы, противолежащие этим сторонам. Чтобы найти доказательство формулы Герона с помощью тригонометрии, нам нужно использовать другую формулу площади треугольника — учитывая две стороны и угол между ними:
площадь = 0,5 * a * b * sin(γ)
Чтобы получить доказательство формулы Герона в этом случае, нам нужно выразить синус угла через стороны треугольника. Мы можем использовать закон косинусов:
c² = a² + b² - 2 * a * b * cos(γ)Благодаря этому закону мы получаем косинус, зависящий от стороны. Но как найти формулу синуса? Это легко, просто используйте основное соотношение между функциями синуса и косинуса — тригонометрическое тождество Пифагора:
sin²(γ) + cos²(γ) = 1, поэтому формула для косинуса равнаsin(γ) = √(1 - cos²(γ)) = (√(4 * a² * b² - (a² + b² -c²)²)) / (2 * a * b)Теперь можно подставить синус в формулу площади треугольника:
площадь = 0,5 * a * b * sin(γ)площадь = 0,25 * √(4 * a² * b² - (a² + b² - c²)²))площадь = 0,25 * √(2 * a * b - (a² + b² - c²) * (2 * a * b + (a² + b² - c²))площадь = 0,25 * √(c² - (a - b)²) * (- c² + (a + b)²)площадь = 0,25 * √(c - a + b) * (c + a - b) * (- c + a + b) * (c + a + b)
что и должно было доказать.
Отлично! Теперь вы понимаете, почему эта формула действительна, поэтому не ждите больше и попробуйте калькулятор формулы Герона!
Как использовать калькулятор формул Герона?
Это очень просто! Просто выполните эти два простых шага:
- Введите данные значения в соответствующие поля . Предположим, что a = 12 дюймов, b = 5 дюймов и c = 13 дюймов.
- Неизвестное значение появляется мгновенно! В нашем примере площадь треугольника — это недостающее значение, которое мы хотим найти. Калькулятор формулы Герона выяснил, что площадь такого треугольника равна 30 дм².
Помните, что почти в каждом калькуляторе вы можете изменить единицы измерения простым нажатием на название единицы измерения. Также вы можете воспользоваться нашим инструментом, чтобы узнать недостающую сторону треугольника, зная две стороны и площадь. Однако существуют два таких треугольника, которые удовлетворяют условию, поэтому мы показываем только одно решение — например, треугольники со сторонами 12, 13, 5 и 12, 13, 24,515 будут иметь одинаковую площадь, равную 30.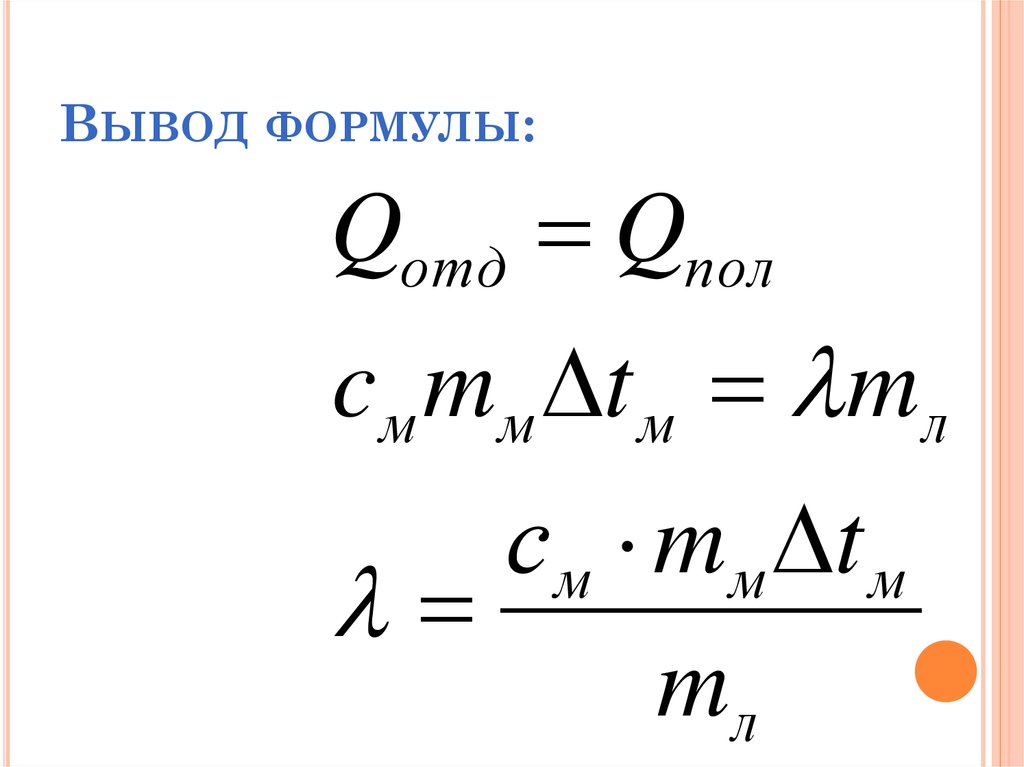
Hanna Pamuła, кандидат в PhD
Сторона A
Стоя B
Сторона C
Периметр
Проверьте 18 аналогичных кальляторов треугольных
Калькулятор физических уравнений и формул
Калькулятор проектирования цепей переменного тока
Решение задач, связанных с электричеством переменного тока, индуктивным сопротивлением, емкостной индуктивностью, емкостью, частотой и индуктивностью.
Калькулятор конструкции конденсатора
Решение задач, связанных с емкостью, плоскопараллельными конденсаторами, накопленной энергией, цилиндрическими конденсаторами, диэлектрической проницаемостью, площадью, разделительным расстоянием, проводниками, длиной, диаметром, электрическим зарядом, разностью потенциалов, манометром, вольтом, запасом энергии, кулонов и фарада.
Калькулятор кругового движения
Решение задач, связанных с центростремительным ускорением, скоростью, радиусом, периодом, орбитами и спутниками.
Калькулятор движения с постоянным ускорением
Онлайн-программа для расчета различных уравнений, связанных с движением с постоянным ускорением. Калькулятор включает в себя решения для начальной и конечной скорости, ускорения, расстояния перемещения и времени. Уравнения можно использовать для одно-, двух- и трехмерного пространства.
Калькулятор уравнений плотности
Решите уравнение плотности для любой переменной. Переменные включают плотность, массу и объем.
Калькулятор уравнений трения
Решение для кинетического трения, статического трения, нормальной силы, коэффициента, максимальной силы трения.
Калькулятор уравнения силы
Решение задач, связанных с силой, массой и ускорением.
Калькулятор гравитационных уравнений
Решает задачи, связанные с законом всемирного тяготения Ньютона, универсальной гравитационной постоянной, массой, силой, периодом обращения спутника, массой планеты, средним радиусом орбиты спутника, ускорением, критической скоростью, скоростью убегания, радиусом от центра планеты и коэффициентом Кеплера. третий закон.
третий закон.
Калькулятор закона Гука
Решения для силы, постоянной силы пружины, расстояния от точки равновесия, потенциальной энергии, длины растяжения пружины и положения равновесия пружины.
Калькулятор закона идеального газа
Решите любую переменную в уравнении закона идеального или идеального газа. Переменные включают моль, температуру, объем и давление.
Калькулятор уравнений для импульса и количества движения
Решите для импульса, импульса, массы, изменения скорости, силы и времени.
Калькулятор конструкции индуктора
Решение задач, связанных с индукторами, числом витков катушки, проницаемостью материала катушки, площадью катушки, средней длиной катушки и индуктивностью.
Калькулятор кинетической энергии
Выполнение вычислений, связанных с кинетической энергией, массой и скоростью.
Калькулятор уравнения момента
Решает задачи, связанные с моментом, силой и длиной плеча рычага.
Калькулятор уравнений второго закона Ньютона
Решите для любой переменной уравнение второго закона Ньютона. Переменные включают результирующую силу, массу и ускорение.
Переменные включают результирующую силу, массу и ускорение.
Калькулятор закона Ома
Решает любую переменную в уравнении закона Ома. Включает расчеты электрического сопротивления (Ом), мощности (Вт), тока (Ампер) и напряжения (Вольт).
Калькулятор формул маятника
Решает задачи, связанные с простыми и физическими маятниками, периодом, временем, центром масс, моментом инерции, расстоянием, осью вращения, ускорением свободного падения и длиной.
Калькулятор потенциальной энергии
Решает задачи, связанные с потенциальной энергией, массой, ускорением свободного падения и высотой.
Калькулятор мощности
Расчет переменных, связанных с мощностью, силой, временем, перемещением и скоростью.
Калькулятор давления
Решите для различных переменных, связанных с силой, площадью, объемным модулем, сжимаемостью, изменением объема, верхним и нижним давлением столба жидкости, плотностью, ускорением свободного падения, глубиной, высотой, абсолютным, атмосферным и манометрическим давлением.
Калькулятор движения снаряда
Решает задачи, связанные с движением снаряда, вертикальным смещением и скоростью, горизонтальным смещением и скоростью, дальностью полета, углом проекции, временем и ускорением свободного падения. Обратите внимание, решения для времени включают сложение и вычитание квадратного корня.
Калькулятор радиоактивных материалов
Решает решения относительно ядер, ядерных реакций, периода полураспада, константы распада, беккерелей, кюри, числа Авогадро, эквивалентной дозы облучения, повреждения, поглощенной дозы, радионуклидов, ионизирующей активности, атомного веса, добротности , рентген эквивалент человека (бэр), рад, зиверт и грей.
Калькулятор звуковых волн
Решение задач, связанных с уровнем звукового давления (SPL), интенсивностью звука точечного источника, излучаемой мощностью, частотой, длиной волны, децибелами, ваттами, наименее слышимым звуком, порогом слышимости человеческого уха, уровнем повреждения и шумового загрязнения ( НПЛ).
Калькулятор удельного веса
Решает решения, связанные с плавучестью, принципом Архимеда, удельным весом, весом воздуха, равным объемом воды, потерей веса под водой.
Калькулятор напряжения и деформации
Решает решения, связанные с напряжением, деформацией, силой, датчиками, изменением длины, исходной длиной и площадью.
Калькулятор преобразования температуры
Решает проблемы, связанные с термометрами, градусами Фаренгейта, Цельсия и Кельвина.
Калькулятор теплопроводности
Решает задачи, связанные со скоростью теплопередачи, теплопереносом, потоком, константой теплопроводности, температурным перепадом, расстоянием и длиной.
Калькулятор температуропроводности
Решает задачи, связанные с температуропроводностью, теплопроводностью, объемной и удельной теплоемкостью и плотностью.
Калькулятор теплового расширения
Решает решения, связанные с коэффициентом линейного расширения, коэффициентом объемного расширения, изменением длины и температуры.
Калькулятор крутящего момента
Решает уравнения относительно крутящего момента, силы и расстояния или длины.
Калькулятор уравнения веса
Решает задачи, связанные с весом, массой и гравитацией.
Уравнения подъемной силы крыла Калькулятор уравнений
Решите любую переменную в уравнении подъемной силы самолета или крыла самолета. Переменные включают подъемную силу аэродинамического профиля, коэффициент подъемной силы, плотность воздуха, площадь поверхности и скорость.
Калькулятор работы
Решение задач, связанных с работой, силой и расстоянием.
Графики роста младенцев — процентили младенцев Скидка в процентах — Калькулятор скидок при продаже Ипотечный калькулятор — Дополнительные платежи Конвертер зарплаты в почасовую оплату — Вакансии Калькулятор зарплаты — ставка сверхурочной работы Калькулятор повышения заработной платы Калькулятор опционов на акции Преобразователь температуры Калькулятор мощности двигателя двигателя Калькулятор возраста собаки Калькулятор коробки сабвуфера Калькулятор линейной интерполяции Калькулятор насоса — водная гидравлика Калькулятор движения снаряда Калькулятор текущей стоимости — Финансы Калькулятор плотности Калькулятор треугольника Физика движения с постоянным ускорением Калькулятор закона идеального газа Калькулятор процентных уравнений Калькулятор сравнения размеров шин Управление проектами с добавленной стоимостью Калькулятор уравнений окружности Калькулятор уравнений кинетической энергии Калькулятор ипотечного кредита — Финансы Формулы уравнений статистики
Главная: Популярные Индекс 1 Индекс 2 Индекс 3 Индекс 4 Детская диаграмма Математическая геометрия Физика Сила Гидромеханика Финансы Кредитный калькулятор Сестринская математика
Джимми Рэймонда
Веб-приложения, Интернет-приложение, Технические инструменты, Спецификации, Практические руководства, Обучение, Приложения, Примеры, Учебники, Обзоры, Ответы, Ресурсы для просмотра тестов, Анализ, Решения для домашних заданий, Справка, Данные и информация для Инженеры, техники, учителя, репетиторы, исследователи, образование K-12, учащиеся колледжей и старших классов, проекты научной ярмарки и ученые
Contact: aj@ajdesigner. com
com
Privacy Policy, Disclaimer and Terms
Copyright 2002-2015
Rearranging equations online calculator
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Формулы дискретного начисления процентов
Разовый платеж
Составная сумма
Преобразует разовый платеж (или сумму) сегодня в будущую стоимость.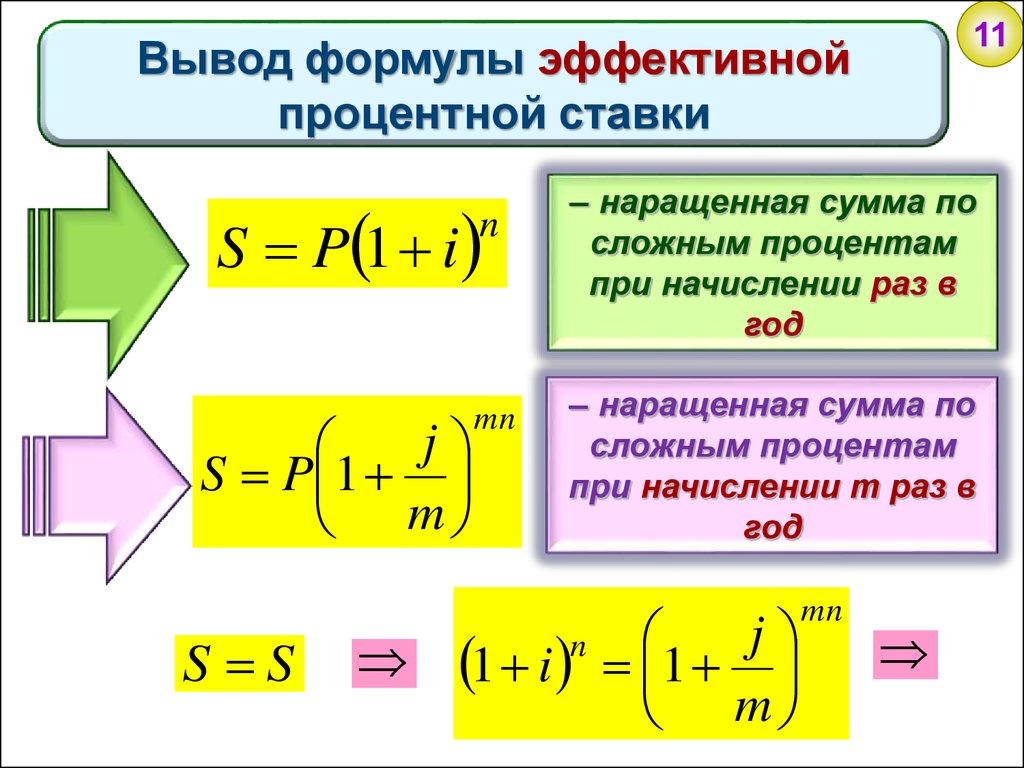
F = P [(1 + i) n ] (1)
, где
F = будущее значение
P = Одиночный платеж сегодня
I = процентная ставка за период
N = количество периодов
. распечатать График будущей стоимости настоящего платежа
Пример — Будущая стоимость первоначальной суммы, полученной сегодня
Сегодня получена сумма 5000 . Рассчитайте будущую стоимость этой суммы через 7 лет с процентной ставкой 5% .
Процентная ставка может быть рассчитана
i = (5 %) / /100 %)
= 0,05
Будущая стоимость суммы может быть рассчитана = (0) (0
F 1 + 0,05) 7 ]
= 7036
Будущая стоимость — онлайн-калькулятор
P — разовый платеж сегодня i
5 проценты0004
n — количество периодов
Обратите внимание, что процентная ставка в % используется в калькуляторе, а не в уравнении.
Текущая стоимость (или стоимость)
Преобразует будущий платеж (или стоимость) в текущую стоимость (или стоимость).
P = F [(1 + I) -N ] (2)
, где
P = Приведенное значение
F = Одно будущее платеж
i = ставка дисконтирования за период
n = количество периодов 5000 получается через 7 лет . Рассчитайте текущую стоимость (или стоимость) этого платежа с учетной ставкой 5% .
Ставка скидки может быть рассчитана
i = (5 %) / /100 %)
= 0,05
Текущая стоимость будущего платежа может быть рассчитана
F = (5000) [(1 + 0,05)
07 -7 ]= 3553
Приведенная стоимость — онлайн калькулятор
F — Одно будущее платеж
I — Ставка дисконти в % используется в калькуляторе, а не в уравнении.
Единая серия
Составная сумма — Аннуитет
Преобразует единую сумму (аннуитет) в будущую стоимость.
F = A [((1 + I) N — 1) / I] (3)
Где
F = будущее значение
A = универсальная сумма на период
i = процентная ставка
n = количество периодов
Загрузить и распечатать диаграмму Составная сумма единого аннуитета
Пример — Приведенная стоимость единообразных платежей
Единая сумма в размере 5000 выплачивается каждый год в течение 7 лет . Рассчитайте будущую стоимость этой суммы с процентной ставкой 5% .
Процентная ставка может быть рассчитана
i = (5 %) / /100 %)
= 0,05
Будущее значение аннуитета может быть рассчитано
F = 5000 [((1 + 0,05) 7 — 1) / 0,05]
= 40710
= 40710
9= 40710
9000 9000 = 40710 9.
05]
Составная сумма — онлайн-калькулятор
A — единообразная сумма за период
i — процентная ставка (%)
n — количество периодов
9000ín 9 процентная ставка % используется в калькуляторе, а не в уравнении.Амортизационный фонд
Преобразует конкретную будущую стоимость в единообразные суммы (аннуитеты) .
A = F [I / ((1 + I) N — 1)] (4)
Где
A = однородная сумма на период
F = будущее значение.
i = процентная ставка
n = количество периодов
Загрузите и распечатайте Амортизационный фонд — диаграмма унифицированной ренты к будущей стоимости
Пример — унифицированные платежи, необходимые для достижения будущей стоимости
Будущая стоимость 7-летней ренты составляет 2000 904. Рассчитайте необходимый аннуитет для достижения этого значения с процентной ставкой 5% .
Процентная ставка может быть рассчитана
i = (5 %) / /100 %)
= 0,05
Однородные платежи (аннуитет) можно рассчитать
A = 5000 [0,05 / ((1 + 0,05) 7 — 1)]
= 614
SINKKENK -Фонд — Онлайн калькулятор
F — будущая стоимость
i — процентная ставка (%)
n — количество периодов
Обратите внимание, что процентная ставка в % — не используется в уравнении .
Текущая стоимость
Преобразует единую сумму (аннуитет) в текущую стоимость .
p = a [((1 + I) N — 1) / (I (1 + I) N )] (5)
, где
P = присутствующая стоимость
A = сумма за процентный период
i = ставка дисконтирования
n = периоды дисконтирования
Загрузите и распечатайте диаграмму Текущая стоимость единого аннуитета
Пример — Текущая стоимость унифицированных сумм
Единая сумма (аннуитет), выплачиваемая по проекту 7 лет , составляет 5000 .

 Например, при выборе функции необходимо выбрать имя функции целиком, открываемую скобки, аргументы и закрываюю скобки.
Например, при выборе функции необходимо выбрать имя функции целиком, открываемую скобки, аргументы и закрываюю скобки.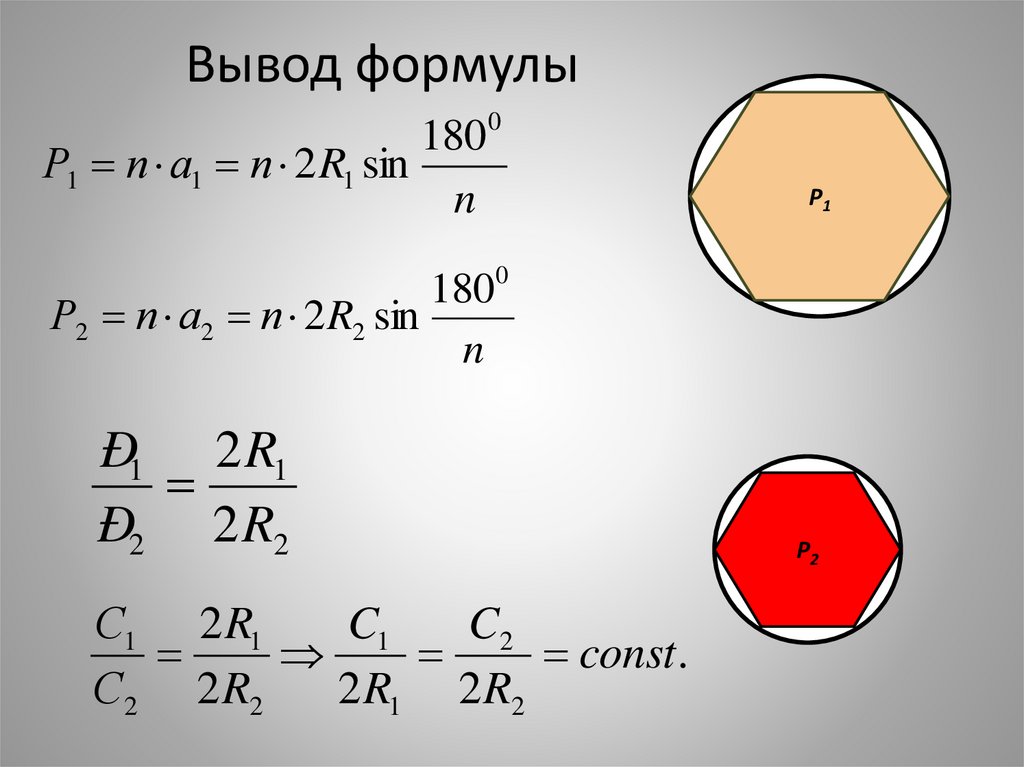
 Первые полторы тысяч разложений.
Первые полторы тысяч разложений. \prime(x)\ = \lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}
\prime(x)\ = \lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x} Настройка.
Настройка. Подробно
Подробно 2)
2) 6)
6)
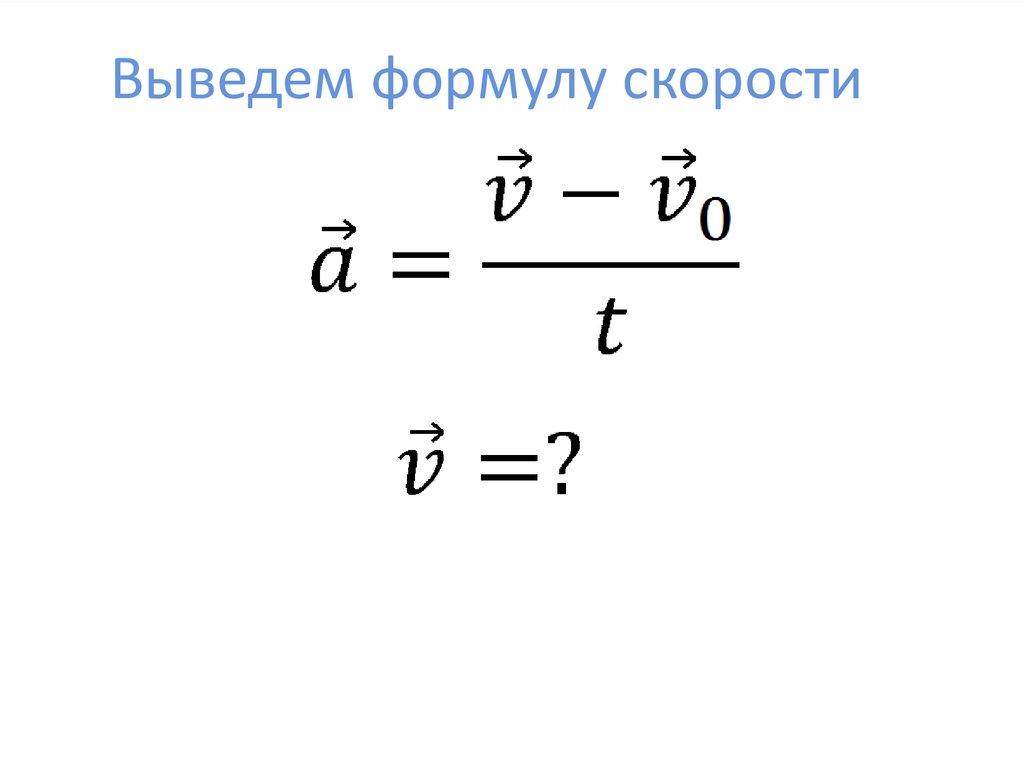

 Снова используйте теорему Пифагора:
Снова используйте теорему Пифагора:
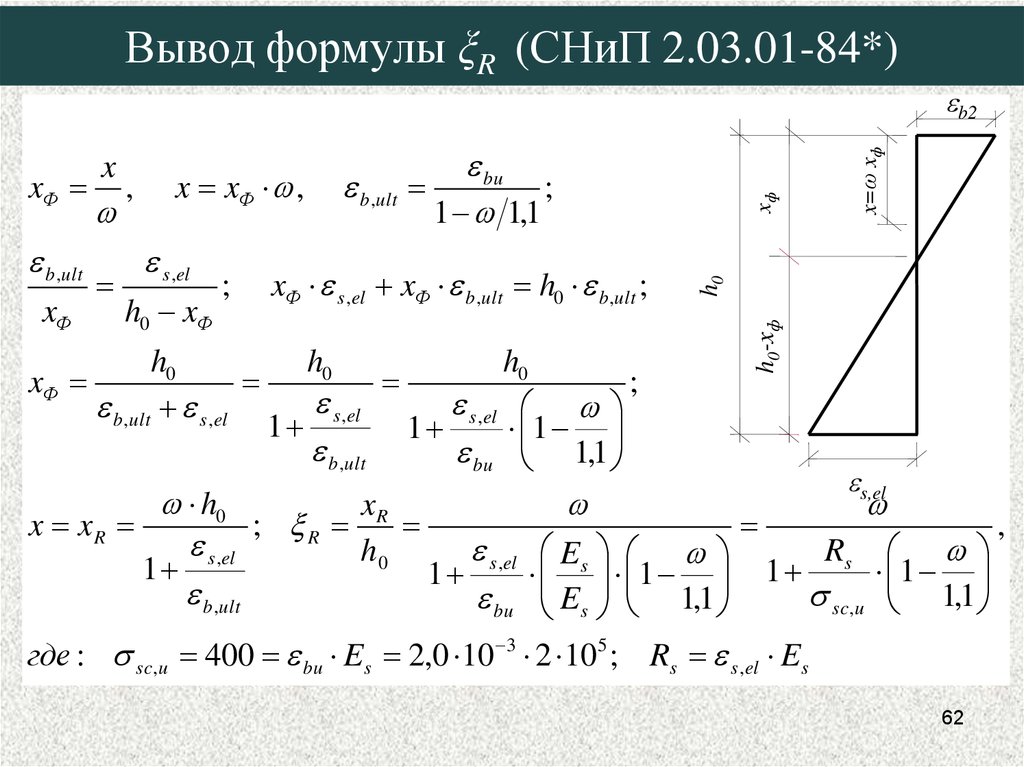 Сможете ли вы найти среди них свою?
Сможете ли вы найти среди них свою? 
 05]
05]