Таблица тангенсов углов, вычислить тангенс угла
Угол
Современные определения тригонометрических функций и их символика принадлежат Л. Эйлеру. Хотя еще в 3-м в. до н. э в трудах Архимеда, Евклида и других рассматриваются отношения сторон в прямоугольном треугольнике, что фактически и является тригонометрическими функциями. В переводе с греческого тригонометрия означает «треугольник» и «измеряю» и является разделом математики, изучающим связь между сторонами и углами треугольника. Как нам известно, в прямоугольном треугольнике 2 угла острых, а один является прямым. Стороны треугольника, прилежащие к углу, равному 90 градусов, называются катетами, с сторона напротив прямого угла является гипотенузой. Тангенс представляет собой одну из тригонометрических функций угла. Функцию тангенс для острых углов можно рассматривать как отношение двух катетов: противолежащего к прилежащему.
tg (a)=а/в
где а — катет, противолежащий углу а;
в — прилежащий катет.
Тангенс заданного угла можно определить, воспользовавшись таблицей Брадиса, где помещены тригонометрические функции всех углов. Если в задаче известна величина угла и одна из сторон треугольника, будет несложно определить остальные его стороны и углы. С помощью онлайн калькулятора ваши расчеты будут более быстрыми и правильными.
Рассчитать тангенс угла
tg (°) =
Таблица тангенсов углов от 0° до 180°
|
|
|
Таблица тангенсов углов от 180° до 360°
|
|
|
Тангенс угла онлайн. Таблица тангенсов. Формула тангенса угла.
Тангенс угла через градусы, минуты и секунды
+−
Тангенс угла через десятичную запись угла
Определение тангенса
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
tg(α) = sin(α)/cos(α)
tg(α) = 1/ctg(α)
Таблица тангенсов в радианах
tg(0°) = 0tg(π/12) = tg(15°) = 0.2679491924tg(π/6) = tg(30°) = 0.5773502692tg(π/4) = tg(45°) = 1tg(π/3) = tg(60°) = 1.732050808tg(5π/12) = tg(75°) = 3.732050808tg(π/2) = tg(90°) = ∞tg(7π/12) = tg(105°) = -3.732050808tg(2π/3) = tg(120°) = -1.732050808tg(3π/4) = tg(135°) = -1tg(5π/6) = tg(150°) = -0.5773502692tg(11π/12) = tg(165°) = -0. 2679491924tg(π) = tg(180°) = 0tg(13π/12) = tg(195°) = 0.2679491924tg(7π/6) = tg(210°) = 0.5773502692tg(5π/4) = tg(225°) = 1tg(4π/3) = tg(240°) = 1.732050808tg(17π/12) = tg(255°) = 3.732050808tg(3π/2) = tg(270°) = ∞tg(19π/12) = tg(285°) = -3.732050808tg(5π/3) = tg(300°) = -1.732050808tg(7π/4) = tg(315°) = -1tg(11π/6) = tg(330°) = -0.5773502692tg(23π/12) = tg(345°) = -0.2679491924
2679491924tg(π) = tg(180°) = 0tg(13π/12) = tg(195°) = 0.2679491924tg(7π/6) = tg(210°) = 0.5773502692tg(5π/4) = tg(225°) = 1tg(4π/3) = tg(240°) = 1.732050808tg(17π/12) = tg(255°) = 3.732050808tg(3π/2) = tg(270°) = ∞tg(19π/12) = tg(285°) = -3.732050808tg(5π/3) = tg(300°) = -1.732050808tg(7π/4) = tg(315°) = -1tg(11π/6) = tg(330°) = -0.5773502692tg(23π/12) = tg(345°) = -0.2679491924
Таблица Брадиса тангенсы
| tg(0) = 0 | tg(120) = -1.732050808 | tg(240) = 1.732050808 |
| tg(1) = 0.01745506493 | tg(121) = -1.664279482 | tg(241) = 1.804047755 |
| tg(2) = 0.03492076949 | tg(122) = -1.600334529 | tg(242) = 1.880726465 |
| tg(3) = 0.05240777928 | tg(123) = -1.539864964 | tg(243) = 1.962610506 |
| tg(4) = 0.06992681194 | tg(124) = -1.482560969 | tg(244) = 2.050303842 |
| tg(5) = 0.08748866353 | tg(125) = -1.428148007 | tg(245) = 2.144506921 |
tg(6) = 0. 1051042353 1051042353 | tg(126) = -1.37638192 | tg(246) = 2.246036774 |
| tg(7) = 0.1227845609 | tg(127) = -1.327044822 | tg(247) = 2.355852366 |
| tg(8) = 0.1405408347 | tg(128) = -1.279941632 | tg(248) = 2.475086853 |
| tg(9) = 0.1583844403 | tg(129) = -1.234897157 | tg(249) = 2.605089065 |
| tg(10) = 0.1763269807 | tg(130) = -1.191753593 | tg(250) = 2.747477419 |
| tg(11) = 0.1943803091 | tg(131) = -1.150368407 | tg(251) = 2.904210878 |
| tg(12) = 0.2125565617 | tg(132) = -1.110612515 | tg(252) = 3.077683537 |
| tg(13) = 0.2308681911 | tg(133) = -1.07236871 | tg(253) = 3.270852618 |
| tg(14) = 0.2493280028 | tg(134) = -1.035530314 | tg(254) = 3.487414444 |
| tg(15) = 0.2679491924 | tg(135) = -1 | tg(255) = 3.732050808 |
| tg(16) = 0.2867453858 | tg(136) = -0. 9656887748 9656887748 | tg(256) = 4.010780934 |
| tg(17) = 0.3057306815 | tg(137) = -0.9325150861 | tg(257) = 4.331475874 |
| tg(18) = 0.3249196962 | tg(138) = -0.9004040443 | tg(258) = 4.704630109 |
| tg(19) = 0.3443276133 | tg(139) = -0.8692867378 | tg(259) = 5.144554016 |
| tg(20) = 0.3639702343 | tg(140) = -0.8390996312 | tg(260) = 5.67128182 |
| tg(21) = 0.383864035 | tg(141) = -0.8097840332 | tg(261) = 6.313751515 |
| tg(22) = 0.4040262258 | tg(142) = -0.7812856265 | tg(262) = 7.115369722 |
| tg(23) = 0.4244748162 | tg(143) = -0.7535540501 | tg(263) = 8.144346428 |
| tg(24) = 0.4452286853 | tg(144) = -0.726542528 | tg(264) = 9.514364454 |
| tg(25) = 0.4663076582 | tg(145) = -0.7002075382 | tg(265) = 11.4300523 |
| tg(26) = 0.4877325886 | tg(146) = -0.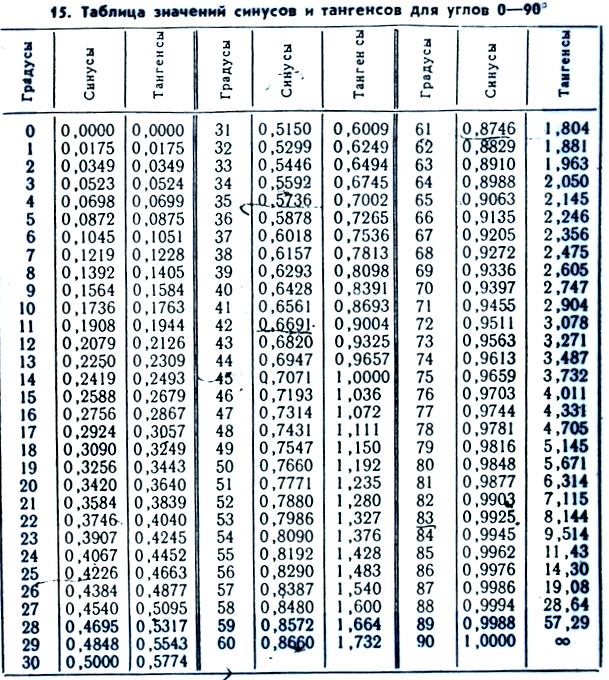 6745085168 6745085168 | tg(266) = 14.30066626 |
| tg(27) = 0.5095254495 | tg(147) = -0.6494075932 | tg(267) = 19.08113669 |
| tg(28) = 0.5317094317 | tg(148) = -0.6248693519 | tg(268) = 28.63625328 |
| tg(29) = 0.5543090515 | tg(149) = -0.600860619 | tg(269) = 57.28996163 |
| tg(30) = 0.5773502692 | tg(150) = -0.5773502692 | tg(270) = ∞ |
| tg(31) = 0.600860619 | tg(151) = -0.5543090515 | tg(271) = -57.28996163 |
| tg(32) = 0.6248693519 | tg(152) = -0.5317094317 | tg(272) = -28.63625328 |
| tg(33) = 0.6494075932 | tg(153) = -0.5095254495 | tg(273) = -19.08113669 |
| tg(34) = 0.6745085168 | tg(154) = -0.4877325886 | tg(274) = -14.30066626 |
| tg(35) = 0.7002075382 | tg(155) = -0.4663076582 | tg(275) = -11.4300523 |
| tg(36) = 0.726542528 | tg(156) = -0. 4452286853 4452286853 | tg(276) = -9.514364454 |
| tg(37) = 0.7535540501 | tg(157) = -0.4244748162 | tg(277) = -8.144346428 |
| tg(38) = 0.7812856265 | tg(158) = -0.4040262258 | tg(278) = -7.115369722 |
| tg(39) = 0.8097840332 | tg(159) = -0.383864035 | tg(279) = -6.313751515 |
| tg(40) = 0.8390996312 | tg(160) = -0.3639702343 | tg(280) = -5.67128182 |
| tg(41) = 0.8692867378 | tg(161) = -0.3443276133 | tg(281) = -5.144554016 |
| tg(42) = 0.9004040443 | tg(162) = -0.3249196962 | tg(282) = -4.704630109 |
| tg(43) = 0.9325150861 | tg(163) = -0.3057306815 | tg(283) = -4.331475874 |
| tg(44) = 0.9656887748 | tg(164) = -0.2867453858 | tg(284) = -4.010780934 |
| tg(45) = 1 | tg(165) = -0.2679491924 | tg(285) = -3.732050808 |
| tg(46) = 1.035530314 | tg(166) = -0. 2493280028 2493280028 | tg(286) = -3.487414444 |
| tg(47) = 1.07236871 | tg(167) = -0.2308681911 | tg(287) = -3.270852618 |
| tg(48) = 1.110612515 | tg(168) = -0.2125565617 | tg(288) = -3.077683537 |
| tg(49) = 1.150368407 | tg(169) = -0.1943803091 | tg(289) = -2.904210878 |
| tg(50) = 1.191753593 | tg(170) = -0.1763269807 | tg(290) = -2.747477419 |
| tg(51) = 1.234897157 | tg(171) = -0.1583844403 | tg(291) = -2.605089065 |
| tg(52) = 1.279941632 | tg(172) = -0.1405408347 | tg(292) = -2.475086853 |
| tg(53) = 1.327044822 | tg(173) = -0.1227845609 | tg(293) = -2.355852366 |
| tg(54) = 1.37638192 | tg(174) = -0.1051042353 | tg(294) = -2.246036774 |
| tg(55) = 1.428148007 | tg(175) = -0.08748866353 | tg(295) = -2.144506921 |
| tg(56) = 1.482560969 | tg(176) = -0. 06992681194 06992681194 | tg(296) = -2.050303842 |
| tg(57) = 1.539864964 | tg(177) = -0.05240777928 | tg(297) = -1.962610506 |
| tg(58) = 1.600334529 | tg(178) = -0.03492076949 | tg(298) = -1.880726465 |
| tg(59) = 1.664279482 | tg(179) = -0.01745506493 | tg(299) = -1.804047755 |
| tg(60) = 1.732050808 | tg(180) = 0 | tg(300) = -1.732050808 |
| tg(61) = 1.804047755 | tg(181) = 0.01745506493 | tg(301) = -1.664279482 |
| tg(62) = 1.880726465 | tg(182) = 0.03492076949 | tg(302) = -1.600334529 |
| tg(63) = 1.962610506 | tg(183) = 0.05240777928 | tg(303) = -1.539864964 |
| tg(64) = 2.050303842 | tg(184) = 0.06992681194 | tg(304) = -1.482560969 |
| tg(65) = 2.144506921 | tg(185) = 0.08748866353 | tg(305) = -1.428148007 |
| tg(66) = 2.246036774 | tg(186) = 0. 1051042353 1051042353 | tg(306) = -1.37638192 |
| tg(67) = 2.355852366 | tg(187) = 0.1227845609 | tg(307) = -1.327044822 |
| tg(68) = 2.475086853 | tg(188) = 0.1405408347 | tg(308) = -1.279941632 |
| tg(69) = 2.605089065 | tg(189) = 0.1583844403 | tg(309) = -1.234897157 |
| tg(70) = 2.747477419 | tg(190) = 0.1763269807 | tg(310) = -1.191753593 |
| tg(71) = 2.904210878 | tg(191) = 0.1943803091 | tg(311) = -1.150368407 |
| tg(72) = 3.077683537 | tg(192) = 0.2125565617 | tg(312) = -1.110612515 |
| tg(73) = 3.270852618 | tg(193) = 0.2308681911 | tg(313) = -1.07236871 |
| tg(74) = 3.487414444 | tg(194) = 0.2493280028 | tg(314) = -1.035530314 |
| tg(75) = 3.732050808 | tg(195) = 0.2679491924 | tg(315) = -1 |
| tg(76) = 4.010780934 | tg(196) = 0.2867453858 | tg(316) = -0. 9656887748 9656887748 |
| tg(77) = 4.331475874 | tg(197) = 0.3057306815 | tg(317) = -0.9325150861 |
| tg(78) = 4.704630109 | tg(198) = 0.3249196962 | tg(318) = -0.9004040443 |
| tg(79) = 5.144554016 | tg(199) = 0.3443276133 | tg(319) = -0.8692867378 |
| tg(80) = 5.67128182 | tg(200) = 0.3639702343 | tg(320) = -0.8390996312 |
| tg(81) = 6.313751515 | tg(201) = 0.383864035 | tg(321) = -0.8097840332 |
| tg(82) = 7.115369722 | tg(202) = 0.4040262258 | tg(322) = -0.7812856265 |
| tg(83) = 8.144346428 | tg(203) = 0.4244748162 | tg(323) = -0.7535540501 |
| tg(84) = 9.514364454 | tg(204) = 0.4452286853 | tg(324) = -0.726542528 |
| tg(85) = 11.4300523 | tg(205) = 0.4663076582 | tg(325) = -0.7002075382 |
| tg(86) = 14.30066626 | tg(206) = 0.4877325886 | tg(326) = -0. 6745085168 6745085168 |
| tg(87) = 19.08113669 | tg(207) = 0.5095254495 | tg(327) = -0.6494075932 |
| tg(88) = 28.63625328 | tg(208) = 0.5317094317 | tg(328) = -0.6248693519 |
| tg(89) = 57.28996163 | tg(209) = 0.5543090515 | tg(329) = -0.600860619 |
| tg(90) = ∞ | tg(210) = 0.5773502692 | tg(330) = -0.5773502692 |
| tg(91) = -57.28996163 | tg(211) = 0.600860619 | tg(331) = -0.5543090515 |
| tg(92) = -28.63625328 | tg(212) = 0.6248693519 | tg(332) = -0.5317094317 |
| tg(93) = -19.08113669 | tg(213) = 0.6494075932 | tg(333) = -0.5095254495 |
| tg(94) = -14.30066626 | tg(214) = 0.6745085168 | tg(334) = -0.4877325886 |
| tg(95) = -11.4300523 | tg(215) = 0.7002075382 | tg(335) = -0.4663076582 |
| tg(96) = -9.514364454 | tg(216) = 0.726542528 | tg(336) = -0. 4452286853 4452286853 |
| tg(97) = -8.144346428 | tg(217) = 0.7535540501 | tg(337) = -0.4244748162 |
| tg(98) = -7.115369722 | tg(218) = 0.7812856265 | tg(338) = -0.4040262258 |
| tg(99) = -6.313751515 | tg(219) = 0.8097840332 | tg(339) = -0.383864035 |
| tg(100) = -5.67128182 | tg(220) = 0.8390996312 | tg(340) = -0.3639702343 |
| tg(101) = -5.144554016 | tg(221) = 0.8692867378 | tg(341) = -0.3443276133 |
| tg(102) = -4.704630109 | tg(222) = 0.9004040443 | tg(342) = -0.3249196962 |
| tg(103) = -4.331475874 | tg(223) = 0.9325150861 | tg(343) = -0.3057306815 |
| tg(104) = -4.010780934 | tg(224) = 0.9656887748 | tg(344) = -0.2867453858 |
| tg(105) = -3.732050808 | tg(225) = 1 | tg(345) = -0.2679491924 |
| tg(106) = -3.487414444 | tg(226) = 1.035530314 | tg(346) = -0. 2493280028 2493280028 |
| tg(107) = -3.270852618 | tg(227) = 1.07236871 | tg(347) = -0.2308681911 |
| tg(108) = -3.077683537 | tg(228) = 1.110612515 | tg(348) = -0.2125565617 |
| tg(109) = -2.904210878 | tg(229) = 1.150368407 | tg(349) = -0.1943803091 |
| tg(110) = -2.747477419 | tg(230) = 1.191753593 | tg(350) = -0.1763269807 |
| tg(111) = -2.605089065 | tg(231) = 1.234897157 | tg(351) = -0.1583844403 |
| tg(112) = -2.475086853 | tg(232) = 1.279941632 | tg(352) = -0.1405408347 |
| tg(113) = -2.355852366 | tg(233) = 1.327044822 | tg(353) = -0.1227845609 |
| tg(114) = -2.246036774 | tg(234) = 1.37638192 | tg(354) = -0.1051042353 |
| tg(115) = -2.144506921 | tg(235) = 1.428148007 | tg(355) = -0.08748866353 |
| tg(116) = -2.050303842 | tg(236) = 1.482560969 | tg(356) = -0. 06992681194 06992681194 |
| tg(117) = -1.962610506 | tg(237) = 1.539864964 | tg(357) = -0.05240777928 |
| tg(118) = -1.880726465 | tg(238) = 1.600334529 | tg(358) = -0.03492076949 |
| tg(119) = -1.804047755 | tg(239) = 1.664279482 | tg(359) = -0.01745506493 |
Тангенс 126 градусов
Тангенс минус 32 градусов
Тангенс минус 194 градусов
Тангенс 337 градусов
Тангенс минус 56 градусов
Таблица тангенсов | umath.ru
Тангенсом угла называется отношение синуса этого угла к косинусу:
Таблица тангенсов — таблица, содержащая значения тангенсов углов. В нашей таблице вычислены тангенсы углов от 1° до 180°.
Таблицы тангенсов можно использовать при отсутствии калькулятора с тригонометрическими функциями.
См. также: таблица синусов, таблица косинусов, таблица котангенсов.
Таблица тангенсов углов 0°, 30°, 45°, 60°, 90°
Замечание: тангенс 90° не определён, так как .
Таблица тангенсов углов от 1° до 90°
| tg(1°) = 0.017455 tg(2°) = 0.034921 tg(3°) = 0.052408 tg(4°) = 0.069927 tg(5°) = 0.087489 tg(6°) = 0.105104 tg(7°) = 0.122785 tg(8°) = 0.140541 tg(9°) = 0.158384 tg(10°) = 0.176327 tg(11°) = 0.194380 tg(12°) = 0.212557 tg(13°) = 0.230868 tg(14°) = 0.249328 tg(15°) = 0.267949 tg(16°) = 0.286745 tg(17°) = 0.305731 tg(18°) = 0.324920 tg(19°) = 0.344328 tg(20°) = 0.363970 tg(21°) = 0.383864 tg(22°) = 0.404026 tg(23°) = 0.424475 tg(24°) = 0.445229 tg(25°) = 0.466308 tg(26°) = 0.487733 tg(27°) = 0.509525 tg(28°) = 0.531709 tg(29°) = 0.554309 tg(30°) = 0.577350 | tg(31°) = 0.600861 tg(32°) = 0.624869 tg(33°) = 0.649408 tg(34°) = 0.674509 tg(35°) = 0.700208 tg(36°) = 0.726543 tg(37°) = 0.753554 tg(38°) = 0.781286 tg(39°) = 0.809784 tg(40°) = 0.839100 tg(41°) = 0.  869287 869287tg(42°) = 0.900404 tg(43°) = 0.932515 tg(44°) = 0.965689 tg(45°) = 1 tg(46°) = 1.03553 tg(47°) = 1.072369 tg(48°) = 1.110613 tg(49°) = 1.150368 tg(50°) = 1.191754 tg(51°) = 1.234897 tg(52°) = 1.279942 tg(53°) = 1.327045 tg(54°) = 1.376382 tg(55°) = 1.428148 tg(56°) = 1.482561 tg(57°) = 1.539865 tg(58°) = 1.600335 tg(59°) = 1.664279 tg(60°) = 1.732051 | tg(61°) = 1.804048 tg(62°) = 1.880726 tg(63°) = 1.962611 tg(64°) = 2.050304 tg(65°) = 2.144507 tg(66°) = 2.246037 tg(67°) = 2.355852 tg(68°) = 2.475087 tg(69°) = 2.605089 tg(70°) = 2.747477 tg(71°) = 2.904211 tg(72°) = 3.077684 tg(73°) = 3.270853 tg(74°) = 3.487414 tg(75°) = 3.732051 tg(76°) = 4.010781 tg(77°) = 4.331476 tg(78°) = 4.704630 tg(79°) = 5.144554 tg(80°) = 5.671282 tg(81°) = 6.313752 tg(82°) = 7.115370 tg(83°) = 8.144346 tg(84°) = 9.514364 tg(85°) = 11.  430052 430052tg(86°) = 14.300666 tg(87°) = 19.081137 tg(88°) = 28.636253 tg(89°) = 57.289962 tg(90°) не определено |
Таблица тангенсов углов от 91° до 180°
| tg(91°) = -57.289962 tg(92°) = -28.636253 tg(93°) = -19.081137 tg(94°) = -14.300666 tg(95°) = -11.430052 tg(96°) = -9.514364 tg(97°) = -8.144346 tg(98°) = -7.115370 tg(99°) = -6.313752 tg(100°) = -5.671282 tg(101°) = -5.144554 tg(102°) = -4.704630 tg(103°) = -4.331476 tg(104°) = -4.010781 tg(105°) = -3.732051 tg(106°) = -3.487414 tg(107°) = -3.270853 tg(108°) = -3.077684 tg(109°) = -2.904211 tg(110°) = -2.747477 tg(111°) = -2.605089 tg(112°) = -2.475087 tg(113°) = -2.355852 tg(114°) = -2.246037 tg(115°) = -2.144507 tg(116°) = -2.050304 tg(117°) = -1.962611 tg(118°) = -1.880726 tg(119°) = -1.804048 tg(120°) = -1.732051 | tg(121°) = -1.664279 tg(122°) = -1.  600335 600335tg(123°) = -1.539865 tg(124°) = -1.482561 tg(125°) = -1.428148 tg(126°) = -1.376382 tg(127°) = -1.327045 tg(128°) = -1.279942 tg(129°) = -1.234897 tg(130°) = -1.191754 tg(131°) = -1.150368 tg(132°) = -1.110613 tg(133°) = -1.072369 tg(134°) = -1.035530 tg(135°) = -1 tg(136°) = -0.965689 tg(137°) = -0.932515 tg(138°) = -0.900404 tg(139°) = -0.869287 tg(140°) = -0.839100 tg(141°) = -0.809784 tg(142°) = -0.781286 tg(143°) = -0.753554 tg(144°) = -0.726543 tg(145°) = -0.700208 tg(146°) = -0.674509 tg(147°) = -0.649408 tg(148°) = -0.624869 tg(149°) = -0.600861 tg(150°) = -0.577350 | tg(151°) = -0.554309 tg(152°) = -0.531709 tg(153°) = -0.509525 tg(154°) = -0.487733 tg(155°) = -0.466308 tg(156°) = -0.445229 tg(157°) = -0.424475 tg(158°) = -0.404026 tg(159°) = -0.383864 tg(160°) = -0.363970 tg(161°) = -0.344328 tg(162°) = -0.324920 tg(163°) = -0.  305731 305731tg(164°) = -0.286745 tg(165°) = -0.267949 tg(166°) = -0.249328 tg(167°) = -0.230868 tg(168°) = -0.212557 tg(169°) = -0.194380 tg(170°) = -0.176327 tg(171°) = -0.158384 tg(172°) = -0.140541 tg(173°) = -0.122785 tg(174°) = -0.105104 tg(175°) = -0.087489 tg(176°) = -0.069927 tg(177°) = -0.052408 tg(178°) = -0.034921 tg(179°) = -0.017455 tg(180°) = 0 |
Таблица тангенсов и котангенсов. Онлайн-калькулятор
В таблице тангенсов и котангенсов приведены значения этих тригонометрических функций для углов от 0 до 360 градусов. Для расчета значений тангенсов и котангенсов для углов с минутами и секундами или отрицательных углов (например 19° 15′ 44″ или — 485° 27′ 34″ ) можно воспользоваться тригонометрическим калькулятором.
Таблица 1 — от 0 до 179 градусов
| Угол, градусы | Тангенс (tg) | Котангенс (ctg) |
|---|---|---|
| 0 | 0 | ∞ |
| 1 | 0. 01745506 01745506 | 57.28996163 |
| 2 | 0.03492077 | 28.63625328 |
| 3 | 0.05240778 | 19.08113669 |
| 4 | 0.06992681 | 14.30066626 |
| 5 | 0.08748866 | 11.4300523 |
| 6 | 0.10510424 | 9.51436445 |
| 7 | 0.12278456 | 8.14434643 |
| 8 | 0.14054083 | 7.11536972 |
| 9 | 0.15838444 | 6.31375151 |
| 10 | 0.17632698 | 5.67128182 |
| 11 | 0.19438031 | 5.14455402 |
| 12 | 0.21255656 | 4.70463011 |
| 13 | 0.23086819 | 4.33147587 |
| 14 | 0.249328 | 4.01078093 |
| 15 | 0.26794919 | 3.73205081 |
| 16 | 0.28674539 | 3.48741444 |
| 17 | 0.30573068 | 3.27085262 |
| 18 | 0.3249197 | 3.07768354 |
| 19 | 0. 34432761 34432761 | 2.90421088 |
| 20 | 0.36397023 | 2.74747742 |
| 21 | 0.38386404 | 2.60508906 |
| 22 | 0.40402623 | 2.47508685 |
| 23 | 0.42447482 | 2.35585237 |
| 24 | 0.44522869 | 2.24603677 |
| 25 | 0.46630766 | 2.14450692 |
| 26 | 0.48773259 | 2.05030384 |
| 27 | 0.50952545 | 1.96261051 |
| 28 | 0.53170943 | 1.88072647 |
| 29 | 0.55430905 | 1.80404776 |
| 30 | 0.57735027 | 1.73205081 |
| 31 | 0.60086062 | 1.66427948 |
| 32 | 0.62486935 | 1.60033453 |
| 33 | 0.64940759 | 1.53986496 |
| 34 | 0.67450852 | 1.48256097 |
| 35 | 0.70020754 | 1.42814801 |
| 36 | 0.72654253 | 1. 37638192 37638192 |
| 37 | 0.75355405 | 1.32704482 |
| 38 | 0.78128563 | 1.27994163 |
| 39 | 0.80978403 | 1.23489716 |
| 40 | 0.83909963 | 1.19175359 |
| 41 | 0.86928674 | 1.15036841 |
| 42 | 0.90040404 | 1.11061251 |
| 43 | 0.93251509 | 1.07236871 |
| 44 | 0.96568877 | 1.03553031 |
| 45 | 1 | 1 |
| 46 | 1.03553031 | 0.96568877 |
| 47 | 1.07236871 | 0.93251509 |
| 48 | 1.11061251 | 0.90040404 |
| 49 | 1.15036841 | 0.86928674 |
| 50 | 1.19175359 | 0.83909963 |
| 51 | 1.23489716 | 0.80978403 |
| 52 | 1.27994163 | 0.78128563 |
| 53 | 1.32704482 | 0.75355405 |
| 54 | 1. 37638192 37638192 | 0.72654253 |
| 55 | 1.42814801 | 0.70020754 |
| 56 | 1.48256097 | 0.67450852 |
| 57 | 1.53986496 | 0.64940759 |
| 58 | 1.60033453 | 0.62486935 |
| 59 | 1.66427948 | 0.60086062 |
| 60 | 1.73205081 | 0.57735027 |
| 61 | 1.80404776 | 0.55430905 |
| 62 | 1.88072647 | 0.53170943 |
| 63 | 1.96261051 | 0.50952545 |
| 64 | 2.05030384 | 0.48773259 |
| 65 | 2.14450692 | 0.46630766 |
| 66 | 2.24603677 | 0.44522869 |
| 67 | 2.35585237 | 0.42447482 |
| 68 | 2.47508685 | 0.40402623 |
| 69 | 2.60508906 | 0.38386404 |
| 70 | 2.74747742 | 0.36397023 |
| 71 | 2.90421088 | 0. 34432761 34432761 |
| 72 | 3.07768354 | 0.3249197 |
| 73 | 3.27085262 | 0.30573068 |
| 74 | 3.48741444 | 0.28674539 |
| 75 | 3.73205081 | 0.26794919 |
| 76 | 4.01078093 | 0.249328 |
| 77 | 4.33147587 | 0.23086819 |
| 78 | 4.70463011 | 0.21255656 |
| 79 | 5.14455402 | 0.19438031 |
| 80 | 5.67128182 | 0.17632698 |
| 81 | 6.31375151 | 0.15838444 |
| 82 | 7.11536972 | 0.14054083 |
| 83 | 8.14434643 | 0.12278456 |
| 84 | 9.51436445 | 0.10510424 |
| 85 | 11.4300523 | 0.08748866 |
| 86 | 14.30066626 | 0.06992681 |
| 87 | 19.08113669 | 0.05240778 |
| 88 | 28.63625328 | 0.03492077 |
| 89 | 57. 28996163 28996163 | 0.01745506 |
| 90 | ∞ | 0 |
| 91 | -57.28996163 | -0.01745506 |
| 92 | -28.63625328 | -0.03492077 |
| 93 | -19.08113669 | -0.05240778 |
| 94 | -14.30066626 | -0.06992681 |
| 95 | -11.4300523 | -0.08748866 |
| 96 | -9.51436445 | -0.10510424 |
| 97 | -8.14434643 | -0.12278456 |
| 98 | -7.11536972 | -0.14054083 |
| 99 | -6.31375151 | -0.15838444 |
| 100 | -5.67128182 | -0.17632698 |
| 101 | -5.14455402 | -0.19438031 |
| 102 | -4.70463011 | -0.21255656 |
| 103 | -4.33147587 | -0.23086819 |
| 104 | -4.01078093 | -0.249328 |
| 105 | -3.73205081 | -0.26794919 |
| 106 | -3. 48741444 48741444 | -0.28674539 |
| 107 | -3.27085262 | -0.30573068 |
| 108 | -3.07768354 | -0.3249197 |
| 109 | -2.90421088 | -0.34432761 |
| 110 | -2.74747742 | -0.36397023 |
| 111 | -2.60508906 | -0.38386404 |
| 112 | -2.47508685 | -0.40402623 |
| 113 | -2.35585237 | -0.42447482 |
| 114 | -2.24603677 | -0.44522869 |
| 115 | -2.14450692 | -0.46630766 |
| 116 | -2.05030384 | -0.48773259 |
| 117 | -1.96261051 | -0.50952545 |
| 118 | -1.88072647 | -0.53170943 |
| 119 | -1.80404776 | -0.55430905 |
| 120 | -1.73205081 | -0.57735027 |
| 121 | -1.66427948 | -0.60086062 |
| 122 | -1.60033453 | -0.62486935 |
| 123 | -1. 53986496 53986496 | -0.64940759 |
| 124 | -1.48256097 | -0.67450852 |
| 125 | -1.42814801 | -0.70020754 |
| 126 | -1.37638192 | -0.72654253 |
| 127 | -1.32704482 | -0.75355405 |
| 128 | -1.27994163 | -0.78128563 |
| 129 | -1.23489716 | -0.80978403 |
| 130 | -1.19175359 | -0.83909963 |
| 131 | -1.15036841 | -0.86928674 |
| 132 | -1.11061251 | -0.90040404 |
| 133 | -1.07236871 | -0.93251509 |
| 134 | -1.03553031 | -0.96568877 |
| 135 | -1 | -1 |
| 136 | -0.96568877 | -1.03553031 |
| 137 | -0.93251509 | -1.07236871 |
| 138 | -0.90040404 | -1.11061251 |
| 139 | -0.86928674 | -1.15036841 |
| 140 | -0. 83909963 83909963 | -1.19175359 |
| 141 | -0.80978403 | -1.23489716 |
| 142 | -0.78128563 | -1.27994163 |
| 143 | -0.75355405 | -1.32704482 |
| 144 | -0.72654253 | -1.37638192 |
| 145 | -0.70020754 | -1.42814801 |
| 146 | -0.67450852 | -1.48256097 |
| 147 | -0.64940759 | -1.53986496 |
| 148 | -0.62486935 | -1.60033453 |
| 149 | -0.60086062 | -1.66427948 |
| 150 | -0.57735027 | -1.73205081 |
| 151 | -0.55430905 | -1.80404776 |
| 152 | -0.53170943 | -1.88072647 |
| 153 | -0.50952545 | -1.96261051 |
| 154 | -0.48773259 | -2.05030384 |
| 155 | -0.46630766 | -2.14450692 |
| 156 | -0.44522869 | -2.24603677 |
| 157 | -0. 42447482 42447482 | -2.35585237 |
| 158 | -0.40402623 | -2.47508685 |
| 159 | -0.38386404 | -2.60508906 |
| 160 | -0.36397023 | -2.74747742 |
| 161 | -0.34432761 | -2.90421088 |
| 162 | -0.3249197 | -3.07768354 |
| 163 | -0.30573068 | -3.27085262 |
| 164 | -0.28674539 | -3.48741444 |
| 165 | -0.26794919 | -3.73205081 |
| 166 | -0.249328 | -4.01078093 |
| 167 | -0.23086819 | -4.33147587 |
| 168 | -0.21255656 | -4.70463011 |
| 169 | -0.19438031 | -5.14455402 |
| 170 | -0.17632698 | -5.67128182 |
| 171 | -0.15838444 | -6.31375151 |
| 172 | -0.14054083 | -7.11536972 |
| 173 | -0.12278456 | -8.14434643 |
| 174 | -0. 10510424 10510424 | -9.51436445 |
| 175 | -0.08748866 | -11.4300523 |
| 176 | -0.06992681 | -14.30066626 |
| 177 | -0.05240778 | -19.08113669 |
| 178 | -0.03492077 | -28.63625328 |
| 179 | -0.01745506 | -57.28996163 |
Таблица 2 — от 180 до 359 градусов
| Угол, градусы | Тангенс (tg) | Котангенс (ctg) |
|---|---|---|
| 180 | 0 | ∞ |
| 181 | 0.01745506 | 57.28996163 |
| 182 | 0.03492077 | 28.63625328 |
| 183 | 0.05240778 | 19.08113669 |
| 184 | 0.06992681 | 14.30066626 |
| 185 | 0.08748866 | 11.4300523 |
| 186 | 0.10510424 | 9.51436445 |
| 187 | 0.12278456 | 8.14434643 |
| 188 | 0. 14054083 14054083 | 7.11536972 |
| 189 | 0.15838444 | 6.31375151 |
| 190 | 0.17632698 | 5.67128182 |
| 191 | 0.19438031 | 5.14455402 |
| 192 | 0.21255656 | 4.70463011 |
| 193 | 0.23086819 | 4.33147587 |
| 194 | 0.249328 | 4.01078093 |
| 195 | 0.26794919 | 3.73205081 |
| 196 | 0.28674539 | 3.48741444 |
| 197 | 0.30573068 | 3.27085262 |
| 198 | 0.3249197 | 3.07768354 |
| 199 | 0.34432761 | 2.90421088 |
| 200 | 0.36397023 | 2.74747742 |
| 201 | 0.38386404 | 2.60508906 |
| 202 | 0.40402623 | 2.47508685 |
| 203 | 0.42447482 | 2.35585237 |
| 204 | 0.44522869 | 2.24603677 |
| 205 | 0.46630766 | 2. 14450692 14450692 |
| 206 | 0.48773259 | 2.05030384 |
| 207 | 0.50952545 | 1.96261051 |
| 208 | 0.53170943 | 1.88072647 |
| 209 | 0.55430905 | 1.80404776 |
| 210 | 0.57735027 | 1.73205081 |
| 211 | 0.60086062 | 1.66427948 |
| 212 | 0.62486935 | 1.60033453 |
| 213 | 0.64940759 | 1.53986496 |
| 214 | 0.67450852 | 1.48256097 |
| 215 | 0.70020754 | 1.42814801 |
| 216 | 0.72654253 | 1.37638192 |
| 217 | 0.75355405 | 1.32704482 |
| 218 | 0.78128563 | 1.27994163 |
| 219 | 0.80978403 | 1.23489716 |
| 220 | 0.83909963 | 1.19175359 |
| 221 | 0.86928674 | 1.15036841 |
| 222 | 0.90040404 | 1. 11061251 11061251 |
| 223 | 0.93251509 | 1.07236871 |
| 224 | 0.96568877 | 1.03553031 |
| 225 | 1 | 1 |
| 226 | 1.03553031 | 0.96568877 |
| 227 | 1.07236871 | 0.93251509 |
| 228 | 1.11061251 | 0.90040404 |
| 229 | 1.15036841 | 0.86928674 |
| 230 | 1.19175359 | 0.83909963 |
| 231 | 1.23489716 | 0.80978403 |
| 232 | 1.27994163 | 0.78128563 |
| 233 | 1.32704482 | 0.75355405 |
| 234 | 1.37638192 | 0.72654253 |
| 235 | 1.42814801 | 0.70020754 |
| 236 | 1.48256097 | 0.67450852 |
| 237 | 1.53986496 | 0.64940759 |
| 238 | 1.60033453 | 0.62486935 |
| 239 | 1.66427948 | 0.60086062 |
| 240 | 1. 73205081 73205081 | 0.57735027 |
| 241 | 1.80404776 | 0.55430905 |
| 242 | 1.88072647 | 0.53170943 |
| 243 | 1.96261051 | 0.50952545 |
| 244 | 2.05030384 | 0.48773259 |
| 245 | 2.14450692 | 0.46630766 |
| 246 | 2.24603677 | 0.44522869 |
| 247 | 2.35585237 | 0.42447482 |
| 248 | 2.47508685 | 0.40402623 |
| 249 | 2.60508906 | 0.38386404 |
| 250 | 2.74747742 | 0.36397023 |
| 251 | 2.90421088 | 0.34432761 |
| 252 | 3.07768354 | 0.3249197 |
| 253 | 3.27085262 | 0.30573068 |
| 254 | 3.48741444 | 0.28674539 |
| 255 | 3.73205081 | 0.26794919 |
| 256 | 4.01078093 | 0.249328 |
| 257 | 4.33147587 | 0. 23086819 23086819 |
| 258 | 4.70463011 | 0.21255656 |
| 259 | 5.14455402 | 0.19438031 |
| 260 | 5.67128182 | 0.17632698 |
| 261 | 6.31375151 | 0.15838444 |
| 262 | 7.11536972 | 0.14054083 |
| 263 | 8.14434643 | 0.12278456 |
| 264 | 9.51436445 | 0.10510424 |
| 265 | 11.4300523 | 0.08748866 |
| 266 | 14.30066626 | 0.06992681 |
| 267 | 19.08113669 | 0.05240778 |
| 268 | 28.63625328 | 0.03492077 |
| 269 | 57.28996163 | 0.01745506 |
| 270 | ∞ | 0 |
| 271 | -57.28996163 | -0.01745506 |
| 272 | -28.63625328 | -0.03492077 |
| 273 | -19.08113669 | -0.05240778 |
| 274 | -14.30066626 | -0. 06992681 06992681 |
| 275 | -11.4300523 | -0.08748866 |
| 276 | -9.51436445 | -0.10510424 |
| 277 | -8.14434643 | -0.12278456 |
| 278 | -7.11536972 | -0.14054083 |
| 279 | -6.31375151 | -0.15838444 |
| 280 | -5.67128182 | -0.17632698 |
| 281 | -5.14455402 | -0.19438031 |
| 282 | -4.70463011 | -0.21255656 |
| 283 | -4.33147587 | -0.23086819 |
| 284 | -4.01078093 | -0.249328 |
| 285 | -3.73205081 | -0.26794919 |
| 286 | -3.48741444 | -0.28674539 |
| 287 | -3.27085262 | -0.30573068 |
| 288 | -3.07768354 | -0.3249197 |
| 289 | -2.90421088 | -0.34432761 |
| 290 | -2.74747742 | -0.36397023 |
| 291 | -2. 60508906 60508906 | -0.38386404 |
| 292 | -2.47508685 | -0.40402623 |
| 293 | -2.35585237 | -0.42447482 |
| 294 | -2.24603677 | -0.44522869 |
| 295 | -2.14450692 | -0.46630766 |
| 296 | -2.05030384 | -0.48773259 |
| 297 | -1.96261051 | -0.50952545 |
| 298 | -1.88072647 | -0.53170943 |
| 299 | -1.80404776 | -0.55430905 |
| 300 | -1.73205081 | -0.57735027 |
| 301 | -1.66427948 | -0.60086062 |
| 302 | -1.60033453 | -0.62486935 |
| 303 | -1.53986496 | -0.64940759 |
| 304 | -1.48256097 | -0.67450852 |
| 305 | -1.42814801 | -0.70020754 |
| 306 | -1.37638192 | -0.72654253 |
| 307 | -1.32704482 | -0.75355405 |
| 308 | -1. 27994163 27994163 | -0.78128563 |
| 309 | -1.23489716 | -0.80978403 |
| 310 | -1.19175359 | -0.83909963 |
| 311 | -1.15036841 | -0.86928674 |
| 312 | -1.11061251 | -0.90040404 |
| 313 | -1.07236871 | -0.93251509 |
| 314 | -1.03553031 | -0.96568877 |
| 315 | -1 | -1 |
| 316 | -0.96568877 | -1.03553031 |
| 317 | -0.93251509 | -1.07236871 |
| 318 | -0.90040404 | -1.11061251 |
| 319 | -0.86928674 | -1.15036841 |
| 320 | -0.83909963 | -1.19175359 |
| 321 | -0.80978403 | -1.23489716 |
| 322 | -0.78128563 | -1.27994163 |
| 323 | -0.75355405 | -1.32704482 |
| 324 | -0.72654253 | -1.37638192 |
| 325 | -0. 70020754 70020754 | -1.42814801 |
| 326 | -0.67450852 | -1.48256097 |
| 327 | -0.64940759 | -1.53986496 |
| 328 | -0.62486935 | -1.60033453 |
| 329 | -0.60086062 | -1.66427948 |
| 330 | -0.57735027 | -1.73205081 |
| 331 | -0.55430905 | -1.80404776 |
| 332 | -0.53170943 | -1.88072647 |
| 333 | -0.50952545 | -1.96261051 |
| 334 | -0.48773259 | -2.05030384 |
| 335 | -0.46630766 | -2.14450692 |
| 336 | -0.44522869 | -2.24603677 |
| 337 | -0.42447482 | -2.35585237 |
| 338 | -0.40402623 | -2.47508685 |
| 339 | -0.38386404 | -2.60508906 |
| 340 | -0.36397023 | -2.74747742 |
| 341 | -0.34432761 | -2.90421088 |
| 342 | -0. 3249197 3249197 | -3.07768354 |
| 343 | -0.30573068 | -3.27085262 |
| 344 | -0.28674539 | -3.48741444 |
| 345 | -0.26794919 | -3.73205081 |
| 346 | -0.249328 | -4.01078093 |
| 347 | -0.23086819 | -4.33147587 |
| 348 | -0.21255656 | -4.70463011 |
| 349 | -0.19438031 | -5.14455402 |
| 350 | -0.17632698 | -5.67128182 |
| 351 | -0.15838444 | -6.31375151 |
| 352 | -0.14054083 | -7.11536972 |
| 353 | -0.12278456 | -8.14434643 |
| 354 | -0.10510424 | -9.51436445 |
| 355 | -0.08748866 | -11.4300523 |
| 356 | -0.06992681 | -14.30066626 |
| 357 | -0.05240778 | -19.08113669 |
| 358 | -0.03492077 | -28.63625328 |
| 359 | -0. 01745506 01745506 | -57.28996163 |
| \begin{align} \text{угол} \end{align} | \begin{align} 0 \end{align} | \begin{align} \frac{\pi}{6} \end{align} | \begin{align} \frac{\pi}{4} \end{align} | \begin{align} \frac{\pi}{3} \end{align} | \begin{align} \frac{\pi}{2} \end{align} | \begin{align} \frac{2\pi}{3} \end{align} | \begin{align} \frac{3\pi}{4} \end{align} | \begin{align} \frac{5\pi}{6} \end{align} | \begin{align} \pi \end{align} |
|---|---|---|---|---|---|---|---|---|---|
| \begin{align} \sin{x} \end{align} | \begin{align} \frac{\sqrt{0}}{2} \end{align} | \begin{align} \frac{\sqrt{1}}{2} \end{align} | \begin{align} \frac{\sqrt{2}}{2} \end{align} | \begin{align} \frac{\sqrt{3}}{2} \end{align} | \begin{align} \frac{\sqrt{4}}{2} \end{align} | \begin{align} \frac{\sqrt{3}}{2} \end{align} | \begin{align} \frac{\sqrt{2}}{2} \end{align} | \begin{align} \frac{\sqrt{1}}{2} \end{align} | \begin{align} \frac{\sqrt{0}}{2} \end{align} |
| \begin{align} \cos{x} \end{align} | \begin{align} \frac{\sqrt{4}}{2} \end{align} | \begin{align} \frac{\sqrt{3}}{2} \end{align} | \begin{align} \frac{\sqrt{2}}{2} \end{align} | \begin{align} \frac{\sqrt{1}}{2} \end{align} | \begin{align} \frac{\sqrt{0}}{2} \end{align} | \begin{align} -\frac{\sqrt{1}}{2} \end{align} | \begin{align} -\frac{\sqrt{2}}{2} \end{align} | \begin{align} -\frac{\sqrt{3}}{2} \end{align} | \begin{align} -\frac{\sqrt{4}}{2} \end{align} |
| \begin{align} \text{tg x} \end{align} | \begin{align} \sqrt{\frac{0}{4}} \end{align} | \begin{align} \sqrt{\frac{1}{3}} \end{align} | \begin{align} \sqrt{\frac{2}{2}} \end{align} | \begin{align} \sqrt{\frac{3}{1}} \end{align} | \begin{align} \varnothing \end{align} | \begin{align} -\sqrt{\frac{3}{1}} \end{align} | \begin{align} -\sqrt{\frac{2}{2}} \end{align} | \begin{align} -\sqrt{\frac{1}{3}} \end{align} | \begin{align} -\sqrt{\frac{0}{4}} \end{align} |
| \begin{align} \text{ctg x} \end{align} | \begin{align} \varnothing \end{align} | \begin{align} \sqrt{\frac{3}{1}} \end{align} | \begin{align} \sqrt{\frac{2}{2}} \end{align} | \begin{align} \sqrt{\frac{1}{3}} \end{align} | \begin{align} 0 \end{align} | \begin{align} -\sqrt{\frac{1}{3}} \end{align} | \begin{align} -\sqrt{\frac{2}{2}} \end{align} | \begin{align} -\sqrt{\frac{3}{1}} \end{align} | \begin{align} \varnothing \end{align} |
| \begin{align} \text{cosec x} \end{align} | \begin{align} \varnothing \end{align} | \begin{align} \frac{2}{\sqrt{1}} \end{align} | \begin{align} \frac{2}{\sqrt{2}} \end{align} | \begin{align} \frac{2}{\sqrt{3}} \end{align} | \begin{align} \frac{2}{\sqrt{4}} \end{align} | \begin{align} \frac{2}{\sqrt{3}} \end{align} | \begin{align} \frac{2}{\sqrt{2}} \end{align} | \begin{align} \frac{2}{\sqrt{1}} \end{align} | \begin{align} \varnothing \end{align} |
| \begin{align} \sec{x} \end{align} | \begin{align} \frac{2}{\sqrt{4}} \end{align} | \begin{align} \frac{2}{\sqrt{3}} \end{align} | \begin{align} \frac{2}{\sqrt{2}} \end{align} | \begin{align} \frac{2}{\sqrt{1}} \end{align} | \begin{align} \varnothing \end{align} | \begin{align} -\frac{2}{\sqrt{1}} \end{align} | \begin{align} -\frac{2}{\sqrt{2}} \end{align} | \begin{align} -\frac{2}{\sqrt{3}} \end{align} | \begin{align} -\frac{2}{\sqrt{4}} \end{align} |
§ 85.
 Таблица тангенсов и котангенсов . Живой учебник геометрии
Таблица тангенсов и котангенсов . Живой учебник геометрииЧтобы успешно применять на практике понятия тангенса и котангенса, необходимо уметь отыскивать в таблице тангенсы и котангенсы различных углов, а также и наоборот – подыскивать угол, если известен его тангенс или котангенс.
Пусть требуется найти в таблице tg24°. Против числа 24 левой колонки находим в графе «tg» (вверху) число 0,45; это и есть tg24° (на графы sin и cos пока не будем обращать внимания).
Так же просто отыскивать в таблице тангенсы всех углов от 1 с до 45°. Тангенсы углов от 45° до 89° находят несколько иначе. Например, tg57° ищем в графе «tg», направляясь снизу, и находим его против числа 57° правой колонки: 1,54 (в то же время 1,54 – это cotg33°, потому что 33 = 90° – 57°).
Сходным образом находим котангенсы и других углов, выражающихся целым числом градусов.
Чтобы найти tg угла, не выражающегося целым числом градусов, надо произвести маленькое дополнительное вычисление. Найдем, например, tg38°40’. Отыскиваем tg38° и tg39°.
Найдем, например, tg38°40’. Отыскиваем tg38° и tg39°.
tg38° = 0,78, tg39° = 0,81
Разница в 1° или 60’, обусловила, мы видим, увеличение тангенса на 0,03. Для небольшой разницы в углах можно считать. что разность тангенсов (и котангенсов) пропорциональна разности углов, т. е., что
Откуда:
tg38°40? – 0,78 = 0,03 ?2/3= 0,02
tg38°40? = 0,78 – 0,03 = 0,80.
Итак, мы отыскали tg нужного нам угла, хотя прямо в таблице он не помещен.
Таким же образом находим:
tg 76°24? = 4,01 + 0,32 ?24/60 = 4,14
cotg[11]21°14? = 2,61 – 0,13 ?14/60 = 2,58
Обратно: нахождение угла, которого tg или cotg известен в случае, когда данная величина tgили cotgимеется в таблице, – не требует пояснений. Например, угол, tg которого 0,27, есть 15°; угол, cotgкоторого 0,78, есть 52° и т. п. Если же данного tg или cotg в таблице нет, требуется дополнительное вычисление. Пусть, например, мы имеем угол, cotg которого =2, 19. Имеющийся в таблице cotg ближайшего меньшего[12] угла есть 2,25, отличающийся от данного на 0,06. Разность же между этим углом и ближайшим большим, имеющимся в таблице (2,14), равна 11. Подобно предыдущему, составляем пропорцию
п. Если же данного tg или cotg в таблице нет, требуется дополнительное вычисление. Пусть, например, мы имеем угол, cotg которого =2, 19. Имеющийся в таблице cotg ближайшего меньшего[12] угла есть 2,25, отличающийся от данного на 0,06. Разность же между этим углом и ближайшим большим, имеющимся в таблице (2,14), равна 11. Подобно предыдущему, составляем пропорцию
И, следовательно, неизв. угол = 66°33’ (с округлением 66°30’).
Таким же образом найдем, что угол, тангенс которого 0,86, равен 40°+ 60 ?2/3= 40°40’ и т. п.
(В виду малой точности таблиц, числа минут надо округлять до целых десятков).
Применения
Рассмотрим теперь несколько задач, при решении которых применяется таблица тангенсов и котангенсов (такие вычисления называются т р и г о н о м е т р и ч е с к и м и).
104. Найти величину острых углов треугольника, катеты которого 16 см и 23 см.
Р е ш е н и е. Тангенс меньшего из искомых углов (черт. 231)
откуда (по таблице) искомый угол x = 34°20’.
105. Телеграфный столб 8 м высоты отбрасывает тень длиною 13,5 м. Под каким углом лучи солнца встречают землю?
Р е ш е н и е сводится, очевидно, к нахождению угла, tg которого = 8/13,5 =0,52
106. Перпендикуляр, опущенный из вершины треугольника, имеет длину 62 см и делит противолежащую сторону на отрезки, длина которых 38 см и 29 см. Найти углы треугольника.
Р е ш е н и е. Сначала находим (черт. 232) величину угла A, tg которого 16/29; затем величину угла C, tg которого 16/38
(как найти третий угол?).
107. Острый угол прямоугольного треугольника 48°, прилежащий катет – 83 см. Найти другой катет.
Р е ш е н и е (черт. 231). Если угол А – 48°, а АВ – 83 см, то
BC/AB = BC/83 = tgA= tg48° = 1,11,
откуда
ВС = 83 ? 1,11 = 92.
108. Найти сторону правильного 12-угольника, описанного около круга, радиус которого 80 см.
Р е ш е н и е (черт. 233). Если сторона 12-угольника АВ, то, соединив концы ее с центром О, получаем равнобедренный треугольник, угол при вершине которого 360°/12=30°.
Проведя OD перпендикулярно к AB, имеем прямоугольный треугольник AOD, в котором катет AD = ?АВ (почему?).
Далее:
AD/OD=AD/80 = tg15°=0,26
откуда:
AD= 0,26 80 = 21,
АВ = 2AD= 42.
Итак, искомая сторона 12-угольника 42 см.
таблиц запуска тангенса-котангенса
таблиц запуска тангенса-котангенсаТаблицы тангенса и котангенса
для углов в градусах
Для тангенса прочтите первые 6 столбцов.
Для котангенса прочтите последние 6 столбцов.
| angle | angle + .0 | angle +.2 | angle +.4 | angle +.6 | angle + .8 | angle +1.0 | |||||||||||
| 0 | 0.0000 | 0.0035 | 0.0070 | 0.0105 | 0.0140 | 0.0175 | 89 | ||||||||||
| 1 | 0.0175 | 0.0209 | 0.0244 | 0.0279 | 0.0314 | 0.0349 | 88 | ||||||||||
| 2 | 0,0349 | 0,0384 | 0,0419 | 0,0454 | 0,0489 | 0,0524 | 8701|||||||||||
| 3 | 0.0524 | 0.0559 | 0.0594 | 0.0629 | 0.0664 | 0.0699 | 86 | ||||||||||
| 4 | 0.0699 | 0.0734 | 0. 0769 0769 | 0.0805 | 0.0840 | 0.0875 | 85 | ||||||||||
| 5 | 0,0875 | 0,0910 | 0,0945 | 0,0981 | 0,11010 0,110100011 | 0.1051 | 84 | ||||||||||
| 6 | 0.1051 | 0.1086 | 0.1122 | 0.1157 | 0.1192 | 0.1228 | 83 | ||||||||||
| 7 | 0.1228 | 0.1263 | 0.1299 | 0.1334 | 0,1370 | 0,1405 | 82 | ||||||||||
| 8 | 0,1405 | 0,1441 | 10 0,144110 0,14100010 0.15120.1548 | 0.1584 | 81 | ||||||||||||
| 9 | 0.1584 | 0.1620 | 0.1655 | 0.1691 | 0.1727 | 0.1763 | 80 | ||||||||||
| 10 | 0.1763 | 0. 1799 1799 | 0,1835 | 0,1871 | 0,1908 | 0,1944 | 79 | ||||||||||
| 11 | 0,1914 | 0.1980 | 0.2016 | 0.2053 | 0.2089 | 0.2126 | 78 | ||||||||||
| 12 | 0.2126 | 0.2162 | 0.2199 | 0.2235 | 0.2272 | 0.2309 | 77 | ||||||||||
| 13 | 0,2309 | 0,2345 | 0,2382 | 0,2419 | 0,2456 | 0,2493 | 76 | 14 | 0.2493 | 0.2530 | 0.2568 | 0.2605 | 0.2642 | 0.2679 | 75 | ||
| 15 | 0.2679 | 0.2717 | 0.2754 | 0.2792 | 0.2830 | 0.2867 | 74 | ||||||||||
| 16 | 0,2867 | 0,2905 | 0,2943 | 0,2981 | 0,3019 9 | 03011001173 | |||||||||||
| 17 | 0. 3057 3057 | 0.3096 | 0.3134 | 0.3172 | 0.3211 | 0.3249 | 72 | ||||||||||
| 18 | 0.3249 | 0.3288 | 0.3327 | 0.3365 | 0.3404 | 0,3443 | 71 | ||||||||||
| 19 | 0,3443 | 0,3482 | 0,3522 | 1 0,3522 | 1 0,34430011 | 0.3600 | 0.3640 | 70 | |||||||||
| 20 | 0.3640 | 0.3679 | 0.3719 | 0.3759 | 0.3799 | 0.3839 | 69 | ||||||||||
| 21 | 0.3839 | 0.3879 | 0.3919 | 0,3959 | 0,4000 | 0,4040 | 68 | ||||||||||
| 22 | 0,4040 | 1 0.0011 | 0.4122 | 0.4163 | 0.4204 | 0.4245 | 67 | ||||||||||
| 23 | 0. 4245 4245 | 0.4286 | 0.4327 | 0.4369 | 0.4411 | 0.4452 | 66 | ||||||||||
| 24 | 0.4452 | 0,4494 | 0,4536 | 0,4578 | 0,4621 | 0,4663 | 65 | ||||||||||
| 0.4663 | 0.4706 | 0.4748 | 0.4791 | 0.4834 | 0.4877 | 64 | |||||||||||
| 26 | 0.4877 | 0.4921 | 0.4964 | 0.5008 | 0.5051 | 0.5095 | 63 | ||||||||||
| 27 | 0,5095 | 0,5139 | 0,5184 | 0,5228 | 0,5272 | 0,53117 | 0010 62|||||||||||
| 28 | 0.5317 | 0.5362 | 0.5407 | 0.5452 | 0.5498 | 0.5543 | 61 | ||||||||||
| 29 | 0.5543 | 0. 5589 5589 | 0.5635 | 0.5681 | 0.5727 | 0,5774 | 60 | ||||||||||
| 30 | 0,5774 | 0,5820 | 0,5867 | 0,50114 | 0.5961 | 0.6009 | 59 | ||||||||||
| 31 | 0.6009 | 0.6056 | 0.6104 | 0.6152 | 0.6200 | 0.6249 | 58 | ||||||||||
| 32 | 0.6249 | 0.6297 | 0.6346 | 0,6395 | 0,6445 | 0,6494 | 57 | ||||||||||
| 33 | 0,6494 | 0,60144 | 0.6594 | 0.6644 | 0.6694 | 0.6745 | 56 | ||||||||||
| 34 | 0.6745 | 0.6796 | 0.6847 | 0.6899 | 0.6950 | 0.7002 | 55 | ||||||||||
| 35 | 0.7002 | 0,7054 | 0,7107 | 0,7159 | 0,7212 | 0,7265 | 54 | ||||||||||
0. 7265 7265 | 0.7319 | 0.7373 | 0.7427 | 0.7481 | 0.7536 | 53 | |||||||||||
| 37 | 0.7536 | 0.7590 | 0.7646 | 0.7701 | 0.7757 | 0.7813 | 52 | ||||||||||
| 38 | 0,7813 | 0,7869 | 0,7926 | 0,7983 | 0,8040 | 0,8098 | 0011|||||||||||
| 39 | 0.8098 | 0.8156 | 0.8214 | 0.8273 | 0.8332 | 0.8391 | 50 | ||||||||||
| 40 | 0.8391 | 0.8451 | 0.8511 | 0.8571 | 0.8632 | 0.8693 | 49 | ||||||||||
| 41 | 0,8693 | 0,8754 | 0,8816 | 0,8878 | 0 0,88780 0,8754410.9004 | 48 | |||||||||||
| 42 | 0. 9004 9004 | 0.9067 | 0.9131 | 0.9195 | 0.9260 | 0.9325 | 47 | ||||||||||
| 43 | 0.9325 | 0.9391 | 0.9457 | 0.9523 | 0,9590 | 0,9657 | 46 | ||||||||||
| 44 | 0,9657 | 0,9725 | 1 9,0793 | 0.9861 | 0.9930 | 1.0000 | 45 | ||||||||||
| 45 | 1.0000 | 1.0070 | 1.0141 | 1.0212 | 1.0283 | 1.0355 | 44 | ||||||||||
| 46 | 1.0355 | 1.0428 | 1.0501 | 1.0575 | 1.0649 | 1.0724 | 43 | ||||||||||
| 47 | 41 | 1.0799 | 1.0875 | 1.0951 | 1.1028 | 1.1106 | 42 | ||||||||||
| 48 | 1.1106 | 1.1184 | 1. 1263 1263 | 1.1343 | 1.1423 | 1.1504 | 41 | ||||||||||
| 49 | 1.1504 | 1.1585 | 1.1667 | 1.1750 | 1.1833 | 1.1918 | 110 | 110 | 0009 | 50 | 1.1918 | 1.2002 | 1.2088 | 1.2174 | 1.2261 | 1.2349 | 39 |
| 51 | 1.2349 | 1.2437 | 1.2527 | 1.2617 | 1.2708 | 1.2799 | 38 | ||||||||||
| 52 | 1.2799 | 1.2892 | 1.2985 | 1.3079 | 1.270 | 110001137 | |||||||||||
| 53 | 1.3270 | 1.3367 | 1.3465 | 1.3564 | 1.3663 | 1.3764 | 36 | ||||||||||
| 54 | 1.3764 | 1.3865 | 1.3968 | 1. 4071 4071 | 1.4176 | 1.4281 | 35 | ||||||||||
| 55 | 1.4281 | 1.4388 | 1.4496 | 0 9.00111.4715 | 1.4826 | 34 | |||||||||||
| 56 | 1.4826 | 1.4938 | 1.5051 | 1.5166 | 1.5282 | 1.5399 | 33 | ||||||||||
| 57 | 1.5399 | 1.5517 | 1.5637 | 1.5757 | 1.5880 | 1.6003 | 32 | ||||||||||
| 58 | 1.6003 | 9.0011 | 1.6255 | 1.6383 | 1.6512 | 1.6643 | 31 | ||||||||||
| 59 | 1.6643 | 1.6775 | 1.6909 | 1.7045 | 1.7182 | 1.7321 | 30 | ||||||||||
| 60 | 1.7321 | 1,7461 | 1,7603 | 1,7747 | 1,7893 | 1,8040 | 29 | ||||||||||
1. 8040 8040 | 1.8190 | 1.8341 | 1.8495 | 1.8650 | 1.8807 | 28 | |||||||||||
| 62 | 1.8807 | 1.8967 | 1.9128 | 1.9292 | 1.9458 | 1.9626 | 27 | ||||||||||
| 63 | 1,9626 | 1,9797 | 1,9970 | 2,0145 | 2,0323 | 2,01013 | 0010 26 | ||||||||||
| 64 | 2.0503 | 2.0686 | 2.0872 | 2.1060 | 2.1251 | 2.1445 | 25 | ||||||||||
| 65 | 2.1445 | 2.1642 | 2.1842 | 2.2045 | 2.2251 | 2,2460 | 24 | ||||||||||
| 66 | 2,2460 | 2,2673 | 2,2889 | 2,31109 | 2.3332 | 2.3559 | 23 | ||||||||||
| 67 | 2.3559 | 2. 3789 3789 | 2.4023 | 2.4262 | 2.4504 | 2.4751 | 22 | ||||||||||
| 68 | 2.4751 | 2.5002 | 2.5257 | 2,5517 | 2,5782 | 2,6051 | 21 | ||||||||||
| 69 | 2,6051 | 2,60115 | 2.6605 | 2.6889 | 2.7179 | 2.7475 | 20 | ||||||||||
| 70 | 2.7475 | 2.7776 | 2.8083 | 2.8397 | 2.8716 | 2.9042 | 19 | ||||||||||
| 71 | 2.9042 | 2,9375 | 2,9714 | 3,0061 | 3,0415 | 3,0777 | 18 | ||||||||||
| 3.0777 | 3.1146 | 3.1524 | 3.1910 | 3.2305 | 3.2709 | 17 | |||||||||||
| 73 | 3.2709 | 3.3122 | 3. 3544 3544 | 3.3977 | 3.4420 | 3.4874 | 16 | ||||||||||
| 74 | 3.4874 | 3.5339 | 3.5816 | 3.6305 | 3.6806 | 3.7321 | 0011 | ||||||||||
| 75 | 3.7321 | 3.7848 | 3.8391 | 3.8947 | 3.9520 | 4.0108 | 14 | ||||||||||
| 76 | 4.0108 | 4.0713 | 4.1335 | 4.1976 | 4.2635 | 4.3315 | 13 | ||||||||||
| 77 | 4.3315 | 4.4015 | 4.4737 | 4.5483 | 2 9.00114.7046 | 12 | |||||||||||
| 78 | 4.7046 | 4.7867 | 4.8716 | 4.9594 | 5.0504 | 5.1446 | 11 | ||||||||||
| 79 | 5.1446 | 5.2422 | 5.3435 | 5. 4486 4486 | 5,5578 | 5,6713 | 10 | ||||||||||
| 80 | 5,6713 | 5,7894 | 9.0011 | 6.0405 | 6.1742 | 6.3138 | 9 | ||||||||||
| 81 | 6.3138 | 6.4596 | 6.6122 | 6.7720 | 6.9395 | 7.1154 | 8 | ||||||||||
| 82 | 7.1154 | 7.3002 | 7,4947 | 7,6996 | 7,9158 | 8,1443 | 7 | ||||||||||
| 83 | 8.6427 | 8.9152 | 9.2052 | 9.5144 | 6 | ||||||||||||
| 84 | 9.5144 | 9.8448 | 10.1988 | 10.5789 | 10.9882 | 11.4301 | 5 | ||||||||||
| 85 | 11.4301 | 11.9087 | 12.4288 | 12.9962 | 13.6174 | 14. 3007 3007 | 1 4 | 0009 | 86 | 14.3007 | 15.0557 | 15.8945 | 16.8319 | 17.8863 | 19.0811 | 3 | |
| 87 | 19.0811 | 20.4465 | 22.0217 | 23.8593 | 26.0307 | 28.6363 | 2 | ||||||||||
| 88 | 28.6363 | 31.8205 | 35.8006 | 40.9174 | 47.7395 | 57.2900 | 1 | ||||||||||
| 89 | 57.2900 | 71.6151 | 95.4895 | 143.2371 | 286.4777 | infinite | 0 | ||||||||||
| 90 | infinite | ||||||||||||||||
| угол+1 | угол+.8 | угол +.6 | угол+.4 | Угол+.2 | Угол+.0 | Угол |
© 2006, Агнес Аццолино www.  mathnstuff.com/math/spoken/here/2class/330/tancott.htm mathnstuff.com/math/spoken/here/2class/330/tancott.htm |
таблица тангенсов тан тета от 1° до 89° диаграмма в формате pdf
формула слесаря 0 Комментарии градус tan thita, тан 45 градусов, тренировка слесаря, tan thita, таблица касательных pdf, таблица касательных тан тета от 1° до 45° градусов, тригонометрическая таблица, таблица тригонометрии pdf диаграмма
Пожалуйста, поделитесь постом
Таблица тангенсов tan тета диаграмма Степень 1 ° до 89 ° степень
टेन थीटा 1 डिग्री से लेक लेक के 89 डिग्री तक दिय दिया गय है औ पीडीएफ च बिल क क क क क क क क क क ोलिंग ोलिंग ोलिंग с с помощью लिंक ोलिंग डिग groving क बिल gtro सकता है
Десять тета от 1 градуса до 89 градусов дана в ней и ссылка для скачивания дана в таблице PDF и эта таблица абсолютно бесплатна может быть вам полезна для получения степени в трубопрокатке
से लेकर के 89 डिग्री तक इसमें दिया गया है
Ten Theta is given in it from 1 degree to 89 degree
1° degree = tan 0. 0174550649
0174550649
1.5° degree = tan 0.0261859216
2° degree = tan 0.034
952.5° degree = tan 0.0436609429
3° degree = tan 0.0524077793
3.5° degree = tan 0.0611626202
4° degree = tan 0.06919
4,5 ° Степень = TAN 0,0787017068
5 ° степень = TAN 0,0874886635
5,5 ° Степень = TAN 0,09628 8 6. 0,09628 8 6. 0,09628 18 6 618 209628 18 6. 0,09628 18 6.1719 6.5° degree = tan 0.11383 7° degree = tan 0.1227845609 7.5° degree = tan 0.1316524976 8° degree = tan 0.1405408347 8. 9° degree = tan 0.1583844403 9.5° degree = tan 0.1673426091 10° degree = tan 0.1763269807 10.5° degree = tan 0.18533 11° degree = tan 0.13091 11.5° degree = tan 0.2034522994 12° degree = tan 0.2125565617 12.5° degree = tan 0.22166 13° degree = tan 0.2308681911 13.5° degree = tan 0.2400787591 14° degree = tan 0.24 14.5° degree = tan 0.2586175844 15° degree = tan 0.26794 15.5° degree = tan 0.2773245441 16° degree = tan 0.2867453858 16.5° degree = tan 0. 17° degree = tan 0.3057306815 17.5° degree = tan 0,3152987889 18 ° степень = TAN 0,3152987889 18,5 ° Степень = TAN 0,3345953195 19 ° = TAN 0,3444371919 19 °.1719 20° degree = tan 0.3639702343 20.5° degree = tan 0.3738846795 21° degree = tan 0.383864035 21.5° degree = tan 0.39356 22° degree = tan 0.4040262258 22,5 ° градуал = TAN 0,4142135624 23 ° Степень = TAN 0,4244748162 23,5 ° градуса = TAN 0,4348112375 23,5 ° = TAN 0,4348112375 24.5° degree =tan 0.4557262555 25° degree = tan 0.4663076582 25. 26° degree = tan 0.4877325886 26.5° degree = tan 0.4985816081 27° degree = tan 0.5095254495 27.5° degree = tan 0.5205670506 28° degree = tan 0.53170 28.5° degree = tan 0.5429556996 29° degree =tan 0.55430 29.5° degree = tan 0.5657727782 30° degree = tan 0.5773502692 30.5° degree = tan 0.58 31° degree = tan 0.600860619 31.5° degree = tan 0.6128007881 32° degree = tan 0.62486 32.5° degree = tan 0.6370702608 33° degree = tan 0.64 33.5° degree = tan 0. 34° degree = tan 0.6745085168 34.5° degree = tan 0.6872809586 35° degree = tan 0.7002075382 35.5° degree = tan 0,7132 36 ° Степень = TAN 0,726542528 36,5 ° Степень = TAN 0,739961075 37 ° DEGE = TAN 0,75554407 37 ° DEGE = TAN 0,75554407 37 °.88 38° degree = tan 0.7812856265 38.5° degree = tan 0.7954359167 39° degree = tan 0.8097840332 39.5° degree = tan 0.8243363858 40° degree = tan 0.83 40.5° degree = tan 0.8540806855 41° degree = tan 0.86 378 41.5° degree =tan 0.8847252646 42° degree = tan 0. 42.5° degree = tan 0. 43° degree = tan 0. 43.5° degree = tan 0.45667 44° degree = tan 0.9656887748 44.5° degree = tan 0,9826972631 45 ° градуал = TAN 1 46 ° Степень = TAN 1,03553031379 46,5 ° Степень = TAN 1,053778 9000 9000 46,5 °.1719 47.5° degree = tan 1.0 48° degree = tan 1.11061251 48.5° degree = tan 1.13029438 49° degree = tan 1.15036840 49.5° degree = tan 1.17084956 50 ° Степень = TAN 1.1 59 50,5 ° Степень = TAN 1,21309700 51 ° Степень = TAN 1,23489715 9 52° degree = tan 1.279 52.5° degree = tan 1.279 53° degree = tan 1.32704482 53.5° degree = tan 1.35142243 54° degree = tan 1.37638192 54.5° degree = tan 1.4019482 55° degree = tan 1.42814800 55.5° degree = tan 1.45500902 56° degree = tan 1.48256096 56.5° degree = tan 1.51083519 57° degree = tan 1.53986496 57.5° degree = tan 1.56968557 58° degree = = tan 1.60033452 58.5° degree = TAN 1.63185168 59 ° градуал = TAN 1,66427948 59,5 ° Степень = TAN 1,69763119 60 ° DEGE = TAN 1,732080919 60 ° = TAN 1,73208080 9179 60 °. 61° degree = tan 1.80404775 61.5° degree = tan 1.841770886 62° degree = tan 1.88072646 62.5° degree = tan 1.212 63° degree = tan 1,96261050 63,5 ° степень = TAN 2,00568970 64 ° градуса = TAN 2,05030384 64,5 ° = TAN 2,096545991 64,5 °.2 65.5° degree = tan 2.173 66° degree = tan 2.24603677 66.5° degree = tan 2.2998425 67° degree = tan 2.35585236 67.5° degree = tan 2,41421356 68 ° градуал = TAN 2,47508685 68,5 ° Степень = TAN 2,53864789 69 ° Степень = TAN 2,6089069 69 °. 70° degree = tan 2.74747741 70.5° degree = tan 2.823 71° degree = tan 2. 71.5° degree = tan 2.98868496 72° degree = tan 3.07768353 72.5° degree = tan 3.17159480 73° degree = tan 3.27085261 73.5° degree = tan 3.375 74° degree = tan 3.48741444 74.5° degree = tan 3.60588350 75° degree = tan 3.73205080 75.5° degree = tan 3.86671309 76° degree = tan 4.01078093 76.5° degree =tan 4.16529977 77 ° Степень = TAN 4.33147587 77,5 ° Степень = TAN 4,51070850 79° degree = tan 5.14455401 79.5° degree = tan 5.39551717 80° degree = tan 5.671281819 80.5° degree = tan 5.97576436 81° degree = tan 6.31375151 81.5° degree = tan 6.6 82° degree = tan 7.11536972 82.5° degree = tan 7.59575411 83° degree = tan 8.14434642 83.5° degree = tan 8.77688735 84° degree = tan 9.51436445 84.5° degree = tan 10.38539708 85° degree = tan 11.43005230 85.5° degree = tan 12.70620473 86 ° Степень = TAN 14,30066625 86,5 ° Степень = TAN 16,34985547 87 ° степень = TAN 19. 88° degree = tan 28.63625328 88.5° degree = tan 38.18845929 89° degree = tan 57.28996163 89.5° degree = tan 114.58865012 Tangent table tan theta 1 ° градусов до 89° градусов Ссылка для скачивания PDF БЕСПЛАТНО 👇 (Дополнительную информацию об управлении фигурой см. в разделе Об апплете.) Но ED = tan A, AE = 1, CB = sin A, и AC = cos AB. Следовательно, мы получили фундаментальное тождество Мы будем использовать три отношения, которые у нас уже есть. Во-первых, tan A = sin A / cos A. Точка B находится там, где линия пересекает ось y . Мы можем сделать координаты B равными (0, b ), чтобы b, , называемое точкой пересечения y , указывало, насколько далеко выше x -оси B ложь. (Эти обозначения противоречат обозначению сторон треугольника a, b, и c, , поэтому не будем сейчас обозначать стороны.) Вы можете видеть, что точка на 1 единицу вправо от начала координат помечена 1, и ее координаты, конечно же, (1,0). Точка A — это место, где вертикальная линия выше 1 пересекает исходную линию. Пусть м обозначает расстояние, на котором А выше С. Тогда А имеет координаты (1, b + м ). Эта величина м называется уклоном линии. Если вы сдвинетесь вправо на одну единицу в любом месте по линии, то вы переместитесь вверх на м единиц. Теперь рассмотрим угол СВА. Назовем это углом наклона . Тангенс CA/BC = м / 1 = м. Таким образом, наклон представляет собой тангенс угла наклона. Термин «угол места» относится к углу над горизонталью от зрителя. Если вы находитесь в точке A, и AH , это горизонтальная линия, то угол возвышения точки B над горизонтом равен углу бат. Касательные часто используются для решения задач, связанных с углами возвышения и депрессии. Обратите внимание, что тангенс прямого угла указан как бесконечность. Это потому, что по мере того, как угол увеличивается до 90°, его тангенс неограниченно растет. Может быть, лучше сказать, что касательная 90 ° не определена, поскольку, используя определение окружности, луч, исходящий из начала координат под углом 90 °, никогда не пересекается с касательной. 29. 49. cos t = 2 тангенс t. Найдите значение sin t. Примечание: В следующих задачах расстояние означает расстояние по горизонтали, если не указано иное; под высотой объекта понимается его высота над горизонтальной плоскостью через точку наблюдения. Высота глаза наблюдателя не должна приниматься во внимание, если это специально не оговорено. В задачах, связанных с тенью объекта, предполагается, что тень падает на горизонтальную плоскость через основание объекта, если не указано иное. 151. Угол возвышения дерева на расстоянии 250 футов составляет 16° 13′. Найдите высоту. 152. Найти высоту колокольни на расстоянии 321 фут, угол возвышения 35° 16′. 153. С корабля угол возвышения верхней части маяка на высоте 200 футов над водой составляет 2° 20′. 154. С вершины маяка на высоте 165 футов над водой угол депрессии корабля составляет 3° 50′. Найдите расстояние. 159. Найдите высоту башни на расстоянии 186 футов, угол возвышения 40° 44′. 160. С одной стороны ручья шест высотой 50 футов имеет с противоположной точки угол возвышения 5° 33′. Найдите ширину потока. 164. От одного холма вершина другого на 128 футов выше имеет угол возвышения 2° 40′. Найдите расстояние. 165. С одного холма на вершину другого далекого 6290 футов имеет угол возвышения 4° 9′. Найдите, на сколько высота второго холма больше высоты первого. 189. Фронтон крыши имеет ширину 40 футов у основания и 26 футов от основания до конька. Под каким углом наклон стропил? 29. Так как вы знаете a и коричневый А, можно найти б. 49. Вам понадобятся два удостоверения личности. Во-первых, tan t = sin t / cos t. Во-вторых, тождество Пифагора, sin 2 t + cos 2 t = 1. Тогда вам нужно решить квадратное уравнение. 151. Помните, что тангенс угла прямоугольного треугольника равен противолежащей стороне, деленной на прилежащую сторону. Вы знаете соседнюю сторону (расстояние до дерева) и угол (угол возвышения), поэтому можете использовать касательные для нахождения высоты дерева. 152. Вы знаете угол (опять же, угол возвышения) и прилежащую сторону (расстояние до шпиля), поэтому используйте касательные, чтобы найти противоположную сторону. 153. Используя угол и противоположную сторону, используйте тангенс, чтобы найти соседнюю сторону. 154. 159. Та же подсказка, что и в 152. 160. Та же подсказка, что и в 153. 164. Та же подсказка, что и в 153. 165. Та же подсказка, что и в 152. 189. Фронтон крыши представляет собой равнобедренный треугольник. Если провести перпендикулярную линию от хребта, то получится два конгруэнтных прямоугольных треугольника. Вы знаете две стороны треугольников, поэтому можете определить угол наклона стропил с помощью арктангенса. 29. b = a /tan A = 30/2 = 15 ярдов. c = 33,5 ярда. 49. , так как COS T = 2 TAN T, Следовательно, COS T = 2 SIN T /COS T, SO COS 2 T = 2 SIN T. T., , T.0 2 T = 2 SIN 7 T. по тождеству Пифагора вы получаете 1 – sin 2 t = 2 sin t. 151. Высота = 250 tan 16°13′ = 72,7′ = 72’9″. 152. Высота = 321 tan 35°16′ = 227 футов. 153. Расстояние = 200/тангенс 2°20′ = 4908 футов, почти миля. 154. Расстояние = 165/тангенс 3°50′ = 2462 фута, почти полмили. 159. Высота = 186 tan 40°44′ = 160 футов. 160. Расстояние = 50/тангенс 5°33′ = 515 футов. 164. Расстояние = 128/тангенс 2°40′, около 2750 футов, чуть больше полумили. 165. Высота = 6290 tan 4°9′ = 456,4 фута. 189. тангенс А = 26/20, поэтому А = 52°. 2. При решении задач с использованием тригонометрических функций,
либо задан угол и должно быть найдено значение t-функции,
либо задано значение t-функции и необходимо найти угол. Эти два процесса обратны друг другу.
Таким образом, обратные обозначения используются для выражения ангела в терминах
значения t-функций. Для мгновенных затрат
a = 0,5 можно представить в виде a = cos -1 (-0,5)
или a = Arc cos (- 0,5). Два выражения
читаются как «Альфа равна «обратному косинусу (-0,5)» или Альфа равна
к Arc cos (- 0,5). Обе эти операции можно выполнить либо с помощью
калькулятор или с помощью тригонометрической таблицы. Это должно быть ясно
отметил, что и калькулятор, и таблица дают только приблизительные ответы. Успение : Различия в функциональных значениях прямо пропорциональны
Различия в мерах угла на очень маленьком интервале. Осторожно: Это не настоящий
правда ! Тем не менее, это дает лучший ответ, чем просто поиск ближайшего
значение в таблице. Иллюстрация 1 Использование линейной интерполяции Найти sin (24 0 43′), учитывая, что sin (24 0 40′) = 0,4173 и sin (24 0 50′) = 0,4200 Решение У нас есть sin (24 0 50′) = 0,4200 В связи с сделанным предположением, является ли x разностью
для искомых 3′ имеем отношение \ х = 0,3 (0,0027)
= 0,00081 » 0,0008 (округлено до 4 знаков после запятой) Иллюстрация 2 Найдите cos (64 0 26′), зная, что cos (64 0 20′) = 0,4331 и cos (64 0 30′) = 0,4305 Раствор У нас есть cos (64 0 30′) = 0,4331 \ Табличная разница
для 10′ = 0,0026 \ Требуемая разница
для 6′ =
(Если х) \ х = 0,6 (0,0026) =
0,00156 или 0,0016 (104 десятичных знака) При увеличении угла косинус угла уменьшается. = 0,4315. Иллюстрация 3 Найти тангенс (28.43) 0 , учитывая этот тангенс (28.40) 0 = 0,5407 и тангенс (28,50) 0 = 0,5430 Раствор = При увеличении угла тангенс угла также
увеличивается. Иллюстрация 4 Решение Примечание: Чтобы сэкономить время, рассмотрите
Иллюстрация 1 Иллюстрация 5 Решение Иллюстрация 6 Решение Примечание: Сохранение времени как
— (См. иллюстрацию 5) (1) Запишите угол (q) в указанном порядке
в 1-м столбце и t-коэффициенты, sin q,
cos q, тангенс q,
csc q, сек q,
кроватка д в 1-м ряду. Таким образом, у нас есть Также обратите внимание, что [следующая страница] Индекс 2.1
Тригонометрическое отношение острых углов Дополнительные задачи Глава 3 Подписаться на @Pinkmonkey_com Темы | Дом Для углов до 45° используйте левый столбец и функциональные метки синего цвета. Например, sin 5° = 0,087 sin 85° = 0,996 Темы | Дом Copyright © 2021 Лоуренс Спектор Вопросы или комментарии? Электронная почта: [email protected] Используйте онлайн-калькулятор тангенса для расчета значений тангенса для заданного угла в градусах, радианах, м радианах или пи (π) радианах. Кроме того, вы узнаете о формуле тангенса, о том, как найти тангенс, его правилах, таблице и графике и некоторых других важных терминах! Тангенс — одна из трех тригонометрических функций, сокращенно обозначаемая как «тан». В прямоугольном треугольнике тангенс угла можно определить как отношение длины противоположной стороны к длине прилежащей стороны. Наш калькулятор тангенса использует данную формулу тангенса, чтобы найти значение тангенса (x). Кроме того, тангенс угла можно определить как синус, деленный на косинус. Таким образом, формула тангенса функции тангенса определяется как \[tanx=\frac{(sinx)}{(cosx)}\] Где sin(x) — функция синуса, а cos(x) — функция косинуса . Кроме того, бесплатный онлайн-калькулятор косинуса помогает рассчитать значение косинуса заданного угла в градусах, радианах, милли-радианах и π-радианах. Закон касательной описывает отношение между касательными двух углов и длинами противоположных сторон. Затем прямоугольный треугольник ABC, в котором стороны, противоположные ∠A, ∠B и ∠C, равны a, b, и c. Итак, по закону тангенсов имеем следующее соотношение: $$\frac{a-b}{a+b} = \frac{tan(\frac{1}{2}(a-b))} {tan(\frac{1}{2}(a+b))}$$ Однако бесплатный онлайн-калькулятор Arctan позволяет вычислять функцию арктангенса в радианах, градусах и других единицах измерения. Из приведенной выше формулы мы уже знаем, что для нахождения тангенса угла нужно разделить длину противолежащего угла на длину прилежащего. Просто подставьте значения в приведенную ниже формулу, чтобы найти значение тангенса ангела: \[tan(α) = \frac{a}{b}\] Пример: Как рассчитать значение тангенса угла, когда длина противолежащей стороны угла равна 14, а прилежащей стороны равна 7? Примените уравнение тангенса и введите значения: \[tan(α) = \frac{a}{b}\] \[=\frac{7}{14}= \frac{1}{ 2} = 0,5. Тем не менее, вы можете использовать онлайн-калькулятор тангенса, чтобы мгновенно вычислить приведенное выше значение этой тригонометрической функции. Следующая таблица тангенсов может использоваться в качестве краткого справочного руководства для нахождения значения тангенса любого угла от нуля до 180 градусов соответственно. Однако, если вы хотите рассчитать значение тангенса угла, отсутствующего в таблице, используйте калькулятор тангенса. Кроме того, онлайн-калькулятор синуса определит тригонометрические значения синуса для заданного угла в градусах, радианах или π радианах. Калькулятор тангенса выполнит самые точные расчеты. Выполните следующие действия, чтобы узнать значения тангенса: Этот калькулятор покажет результаты в соответствии с формулой тангенса: Это можно упростить, указав, какой угол равен тангенсу (-1). В случае единичного круга загар (1) равен пи/4. Между тем, согласно «Тождеству шансов и четов» tan(-x) равен -tan(x). \[Tan 90° = ∞\] \[Tan π/2 = ∞\] Следовательно, \[tan-1 (∞) = π/2 или tan-1 (∞) = 90°\] Согласно определению единичного круга тангенс(тета) равен=\frac{x}{y} или тангенс(тета)=sin(тета)/cos(тета). 9000 ° 917 917 917 917 917 917 917 9000 9,5 °  5° degree = tan 0.14013
5° degree = tan 0.14013  296213495
296213495  5° degree = tan 0.4769755327
5° degree = tan 0.4769755327 16 932  6618855612
6618855612 312 
40443 1174
50861 50 
 4016
4016 
087 78 ° = TAN 4,70461010 78 ° = TAN 4,70463010 98 °.  1719
171923  08113668
08113668 9000 87 °.0376554 Касательные и уклоны
Касательные и уклоны Определение касательной
Синус и косинус — не единственные тригонометрические функции, используемые в тригонометрии. Многие другие использовались на протяжении веков, такие как гаверсины и спреды. Наиболее полезным из них является тангенс. С точки зрения диаграммы единичного круга, касательная — это длина вертикальной линии ED , касательной к окружности от точки касания E до точки D , где эта касательная пересекает луч AD , образующий угол.
Если ваш браузер поддерживает Java, вы можете перетащить точку B , чтобы увидеть, как синус, косинус и тангенс изменяются при изменении угла. Тангенс относительно синуса и косинуса
Поскольку два треугольника ADE и ABC подобны, имеем Касательные и прямоугольные треугольники
Точно так же, как синус и косинус можно найти как отношение сторон прямоугольного треугольника, можно найти и тангенс. Во-вторых, sin A = a/c. В-третьих, cos A = b/c. Разделив a/c на b/c и сократив появляющиеся c , мы заключаем, что tan A = a/b. Это означает, что касательная — это противолежащая сторона, деленная на прилежащую сторону:
Во-вторых, sin A = a/c. В-третьих, cos A = b/c. Разделив a/c на b/c и сократив появляющиеся c , мы заключаем, что tan A = a/b. Это означает, что касательная — это противолежащая сторона, деленная на прилежащую сторону: Уклоны линий
Одна из причин, по которой касательные так важны, заключается в том, что они дают наклоны прямых линий. Рассмотрим прямую линию, проведенную в координатной плоскости x-y . Пусть C будет точкой, где эта вертикальная линия пересекает горизонтальную линию через B. Тогда C имеет координаты (1, b ).
Пусть C будет точкой, где эта вертикальная линия пересекает горизонтальную линию через B. Тогда C имеет координаты (1, b ). Углы возвышения и депрессии
 Точно так же «угол депрессии» к точке C ниже горизонта составляет угол CAH.
Точно так же «угол депрессии» к точке C ниже горизонта составляет угол CAH. Опять общие углы
Мы можем расширить нашу таблицу синусов и косинусов общих углов до тангенсов. Вам не нужно запоминать всю эту информацию, если вы можете просто запомнить отношения сторон треугольника 45°-45°-90° и треугольника 30°-60°-9треугольник 0°. Отношения являются значениями триггерных функций. Угол Градусы Радианы Косинус sine tangent 90° π /2 0 1 infinity 60° π /3 1/2 √3 / 2 √3 45° π /4 √2 / 2 √2 / 2 1 30° № /6 √3/2 1/2 1/√3 0 ° 0 1 0 0 Упражнения
 В прямоугольном треугольнике a = 30 ярдов и тангенс A = 2. Найдите b и c.
В прямоугольном треугольнике a = 30 ярдов и тангенс A = 2. Найдите b и c.  Найдите расстояние.
Найдите расстояние. Советы
Общий совет для всех этих упражнений: сначала нарисуйте фигуру.  Затем можно определить c по теореме Пифагора, или с помощью синусов, или с помощью косинусов.
Затем можно определить c по теореме Пифагора, или с помощью синусов, или с помощью косинусов. Та же подсказка, что и в 153.
Та же подсказка, что и в 153. Ответы
 Получается квадратное уравнение sin 2 t + 2 sin t – 1 = 0. Решения: sin t = –1 ± √2. Из этих двух решений единственно возможным является sin t = √2 – 1.
Получается квадратное уравнение sin 2 t + 2 sin t – 1 = 0. Решения: sin t = –1 ± √2. Из этих двух решений единственно возможным является sin t = √2 – 1. PinkMonkey.com-Учебное пособие по тригонометрии — 2.4 Таблицы тригонометрических функций
 4 Таблицы тригонометрических функций
4 Таблицы тригонометрических функций  Даже в этом случае мы используем знак равенства (=), но более правильно использовать приближение
знак ( » ) приветствуется. Приблизительный
значения функций острых углов приведены в таблиц
Натуральные тригонометрические функции . Мы будем использовать тригонометрический
таблица, дающая значения до четырех знаков после запятой. Как ясно, что
Таблицы не могут перечислить все углы. Поэтому приближение должно быть
используется для нахождения значений между значениями, указанными в таблице. Этот способ
известен как Линейная интерполяция .
Даже в этом случае мы используем знак равенства (=), но более правильно использовать приближение
знак ( » ) приветствуется. Приблизительный
значения функций острых углов приведены в таблиц
Натуральные тригонометрические функции . Мы будем использовать тригонометрический
таблица, дающая значения до четырех знаков после запятой. Как ясно, что
Таблицы не могут перечислить все углы. Поэтому приближение должно быть
используется для нахождения значений между значениями, указанными в таблице. Этот способ
известен как Линейная интерполяция .
и sin (24 0 40′)= 0,4173
Разница для 10 футов = 0,0027
Таким образом, sin (24 0 40′) = sin (24 0 40′) + sin (0,3′)
угол увеличивается с приращением его синуса угла и наоборот.
Таким образом, sin (24 0 43′) = 0,4173 + 0,0008 = 0,4181
cos (64 0 20′) = 0,4305 Таким образом, cos (64 0 26′) = 0,4331 — 0,0016
Таким образом, cos (64 0 26′) = 0,4331 — 0,0016
Таким образом, тангенс (28,43) 0 = 0,5407 + 0,0007 = 0,5414
Решите прямоугольный треугольник, в котором а = 24,36.
ì А = 58 0 53′.
В прямоугольном треугольнике ABC
А + В + С = 180 0
\ 58 0 53′ + В + С = 180 0 , если C = 90 0
\ B = 90 0 — 58 0 53′
= 31 0 7′
Используя формулы для t-коэффициентов,
б/а = раскладушка А, б = раскладушка А = 24,36 (0,6036) = 14,70 (\
раскладушка А = 0,6036)
c/a = csc A, c = a csc A = 24,36 (1,1681) = 28,45
а/с = sin A, c = a / sin A = 24,36/0,8562 = 28,45
b/c = cos A, b = c cos A = 28,45 (0,5168) = 14,70
Шаг (1) грех (24 0 41′) = 0,4173, взять только 4173
(2) Найдите мысленно табличную разницу 27 между 4200 (для sin
24 0 40′) и 4173 (для sin 24 0 40′)
(3) Разница для 3′ = 0,3 (27) = 8,1 (округлено).
(4) Добавьте (начиная с синуса) к 4178, чтобы получить 4181, затем sin 24 0 31′ = 0,4181.
Найдите угол A, если sin A = 0,4234
Мы не найдем эту запись в таблице.
Однако 0,4226 = sin 25 0 0′
0,4253 = sin 25 0 10′
Табличная разница = 0,0027
Теперь 0,4226 = sin 25,0′
0,4234 = sin A
0,0008 = частичная разница
коррекция =
(ближайшая минута)
Добавление (начиная с синуса) поправки равно A = 25 0 0′ + 3′
= 25 0 3′
Найдите A, учитывая, что кроватка A = 0,6345
Имеем 0,6330 = раскладушка 57 0 40′ (из таблицы)
0,6371 = детская кроватка 57 0 30′
Табличный диф. = 0,0041
Теперь 0,6330 = детская кроватка 57 0 40′
0,6345 = детская кроватка А
Частичная диф. = 0,0015
Коррекция =
(ближайшая минута)
вычитая (начиная с кроватки), поправка равна A = 57 0 40′
— 4′ = 57 0 36′.
Шаг (1) Найдите следующую меньшую запись, 0,4226 = sin 25 0 0′. Используйте только 4226.
(2) Найдите табличную разницу. (мысленно), 27.
(3) Найдите частичную разницу. (мысленно), 8 между 4226 и 4234.
(4) Найти
(10′) = 3′ и добавьте (начиная с синуса), чтобы получить A = 25 0 3′
Запомните значения t-функций измерения углов 0 0 ,
30 0 , 45 0 , 60 0 и 90 0 как
следующим образом:
(2) Поместите 0, 1, 2, 3, 4 в столбец sin q
(см. таблицу), затем подставляем 4, 3, 2, 1, 0 в cos q
столбец (см. таблицу).
(3) Разделите на 4 каждую запись, затем найдите квадратный корень каждой записи.
Это значения отношений синуса и косинуса углов 0 0 ,
30 0 , 45 0 , 60 0 и 90 0
(4) Использовать тангенс q = q и соотношение взаимности для csc q,
sec q и кроватка q.
Нажмите здесь, чтобы увеличить
Обратите внимание, что  е. — 1£
потому что q £
1 для всех q . Они называются границами
отношений синусов и косинусов.
е. — 1£
потому что q £
1 для всех q . Они называются границами
отношений синусов и косинусов.
csc д ³
1 или csc q £
1 и сек q
³ 1 или сек q
£ 1 (численно) для допустимых значений q
.
2.2 Фундаментальное соотношение между
тригонометрические соотношения углов
2.3 Функции общих углов
Отношение или t
2.4 Таблицы тригонометрических функций Трехзначная тригонометрическая таблица
Трехзначная тригонометрическая таблица Для углов более 45° используйте правый столбец и функциональные метки красного цвета.
Для углов более 45° используйте правый столбец и функциональные метки красного цвета. θ sin θ
cos θ cos θ
sin θ коричневый θ
детская кроватка θ Детская кроватка θ
Желто-коричневый θ сек θ
csc θ csc θ
сек θ 0° . 000 1 . 000 . 000 …….. 1 . 000 …….. 90° 1° . 017 1 .  000
000 . 017 57 . 290 1 . 000 57 . 299 89° 2° . 035 . 999 . 035 28 . 636 1 . 001 28 . 654 88° 3° . 052 . 999 . 052 19 . 081 1 . 001 19 . 107 87° 4° . 070 . 998 . 070 14 . 301 1 .  002
002 14 . 336 86° 5° . 087 . 996 . 087 11 . 430 1 . 004 11 . 474 85° 6° . 105 . 995 . 105 9 . 514 1 . 006 9 . 567 84° 7° . 122 . 993 . 123 8 . 144 1 . 008 8 . 206 83° 8° .  139
139 . 990 . 141 7 . 115 1 . 010 7 . 185 82° 9° . 156 . 988 . 158 6 . 314 1 . 012 6 . 392 81° sin θ
cos θ cos θ
sin θ коричневый θ
детская кроватка θ Детская кроватка θ
Желто-коричневый θ сек θ
csc θ csc θ
сек θ 10° .  174
174 . 985 . 176 5 . 671 1 . 015 5 . 759 80° 11° . 191 . 982 . 194 5 . 145 1 . 019 5 . 241 79° 12° . 208 . 978 . 213 4 . 705 1 . 022 4 . 810 78° 13° . 225 . 974 . 231 4 .  331
331 1 . 026 4 . 445 77° 14° . 242 . 970 . 249 4 . 011 1 . 031 4 . 134 76° 15° . 259 . 966 . 268 3 . 732 1 . 035 3 . 864 75° 16° . 276 . 961 . 287 3 . 487 1 . 040 3 . 628 74° 17° .  292
292 . 956 . 306 3 . 271 1 . 046 3 . 420 73° 18° . 309 . 951 . 325 3 . 078 1 . 051 3 . 236 72° 19° . 326 . 946 . 344 2 . 904 1 . 058 3 . 072 71° sin θ
cos θ cos θ
sin θ коричневый θ
детская кроватка θ Детская кроватка θ
Желто-коричневый θ сек θ
csc θ csc θ
сек θ 20° .  342
342 . 940 . 364 2 . 747 1 . 064 2 . 924 70° 21° . 358 . 934 . 384 2 . 605 1 . 071 2 . 790 69° 22° . 375 . 927 . 404 2 . 475 1 . 079 2 . 669 68° 23° . 391 . 921 . 424 2 .  356
356 1 . 086 2 . 559 67° 24° . 407 . 914 . 445 2 . 246 1 . 095 2 . 459 66° 25° . 423 . 906 . 466 2 . 145 1 . 103 2 . 366 65° 26° . 438 . 899 . 488 2 . 050 1 . 113 2 . 281 64° 27° .  454
454 . 891 . 510 1 . 963 1 . 122 2 . 203 63° 28° . 469 . 883 . 532 1 . 881 1 . 133 2 . 130 62° 29° . 485 . 875 . 554 1 . 804 1 . 143 2 . 063 61° sin θ
cos θ cos θ
sin θ коричневый θ
детская кроватка θ Детская кроватка θ
Желто-коричневый θ сек θ
csc θ csc θ
сек θ 30° .  500
500 . 866 . 577 1 . 732 1 . 155 2 . 000 60° 31° . 515 . 857 . 601 1 . 664 1 . 167 1 . 972 59° 32° . 530 . 848 . 625 1 . 600 1 . 179 1 . 887 58° 33° . 545 . 839 . 649 1 .  540
540 1 . 192 1 . 836 57° 34° . 559 . 829 . 675 1 . 483 1 . 206 1 . 788 56° 35° . 574 . 819 . 700 1 . 428 1 . 221 1 . 743 55° 36° . 588 . 809 . 727 1 . 376 1 . 236 1 . 701 54° 37° .  602
602 . 799 . 754 1 . 327 1 . 252 1 . 662 53° 38° . 616 . 788 . 781 1 . 280 1 . 269 1 . 624 52° 39° . 629 . 777 . 810 1 . 235 1 . 287 1 . 589 51° sin θ
cos θ cos θ
sin θ коричневый θ
детская кроватка θ Детская кроватка θ
Желто-коричневый θ сек θ
csc θ csc θ
сек θ 40° .  643
643 . 766 . 839 1 . 192 1 . 305 1 . 556 50° 41° . 656 . 755 . 869 1 . 150 1 . 325 1 . 524 49° 42° . 669 . 743 . 900 1 . 111 1 . 346 1 . 494 48° 43° . 682 . 731 . 933 1 .  072
072 1 . 367 1 . 466 47° 44° . 695 . 719 . 966 1 . 036 1 . 390 1 . 440 46° 45° . 707 . 707 1 . 000 1 . 000 1 . 414 1 . 414 45° Калькулятор тангенса – Найдите угол тангенса в градусах и радианах
 Тригонометрический калькулятор загара быстро решит клубок (α) для заданной функции.
Тригонометрический калькулятор загара быстро решит клубок (α) для заданной функции.
 \]
\]
Таблица тангенсов: х (°) х (рад.) рыжевато-коричневый(х) 0° №/6 0 30° №/5 0,577350 45° №/4 1 60° №/3 1.  732051
732051 90° №/2 не определено 120° 2π/3 -1.732051 135° 3π/4 0,707107 150° 5π/6 -0,577350 180° № 0
Вывод: 
Часто задаваемые вопросы: Как решить проблему загара 1? 

 2126
2126 7265
7265 7321
7321 1443
1443 4874
4874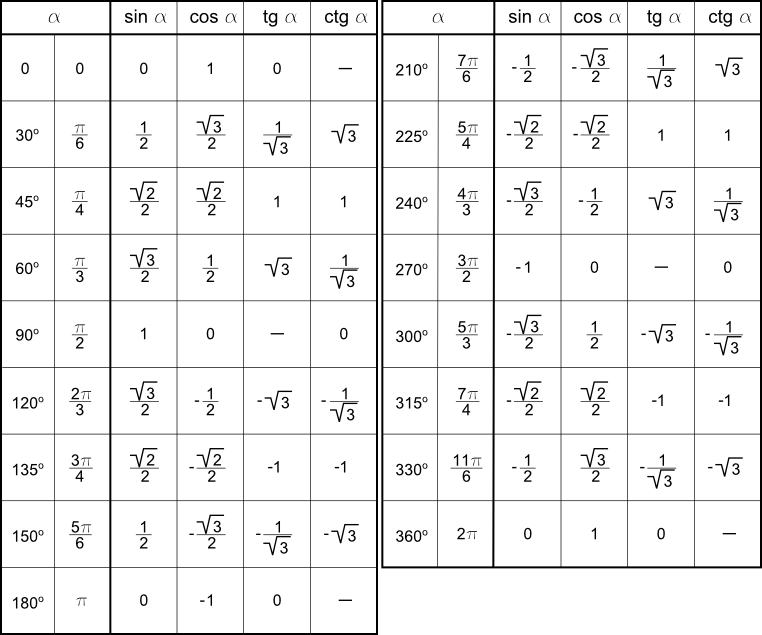 2799
2799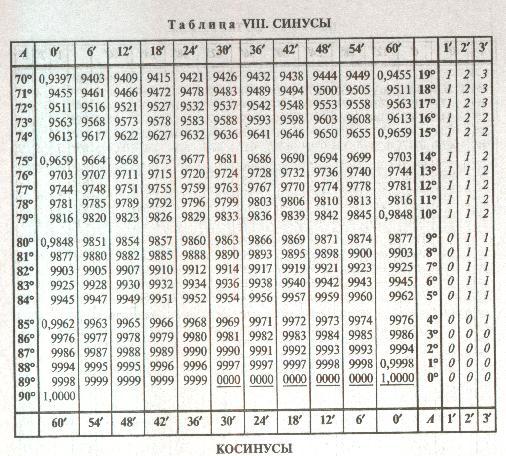 5543
5543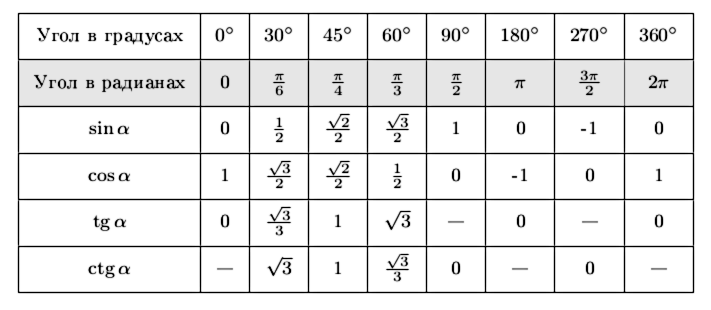 1051
1051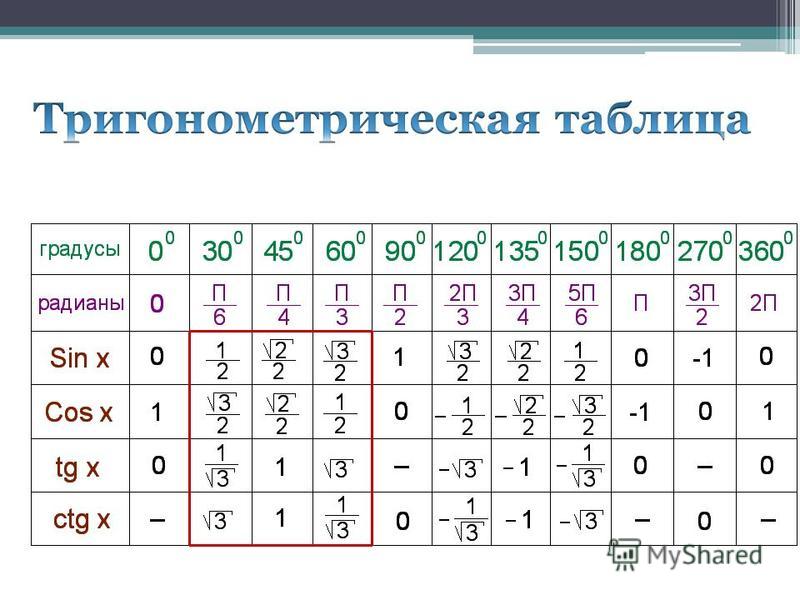 2679
2679 7813
7813 804
804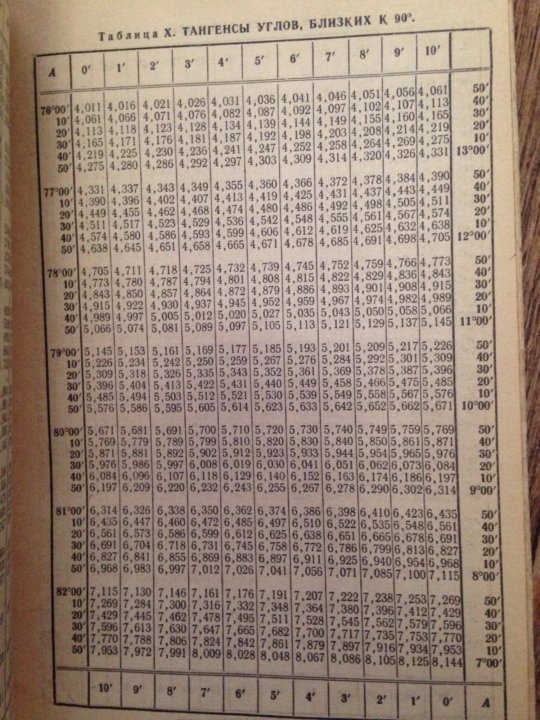 5144
5144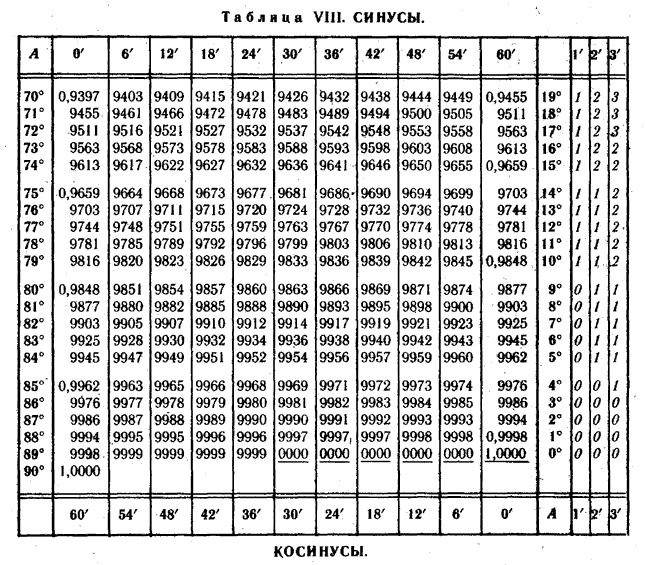 2709
2709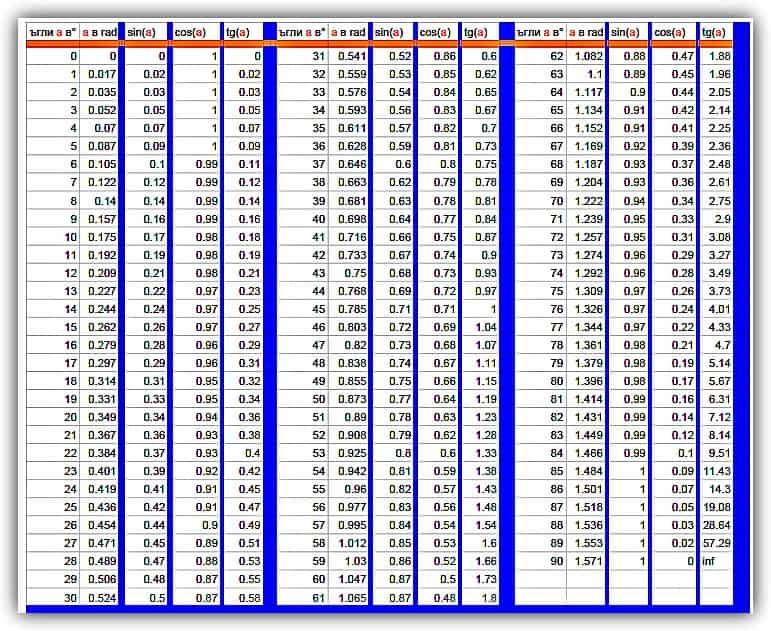 2349
2349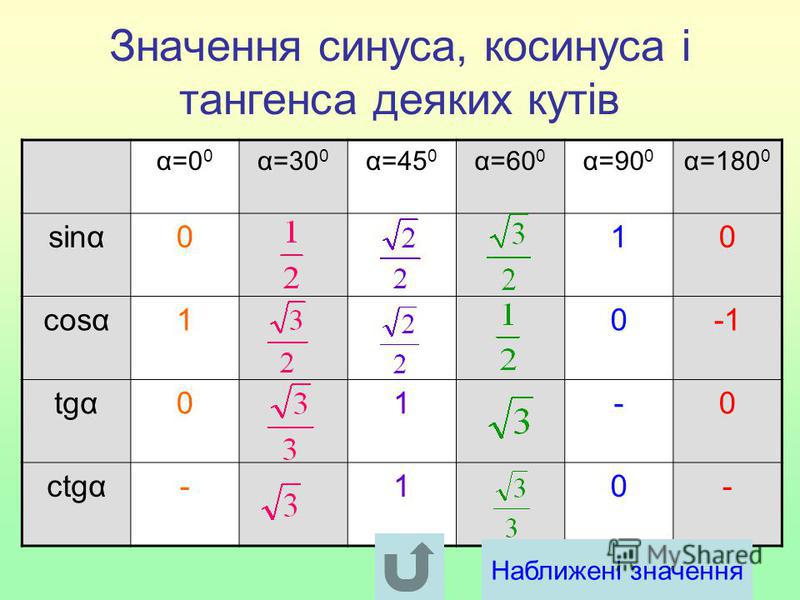 5317
5317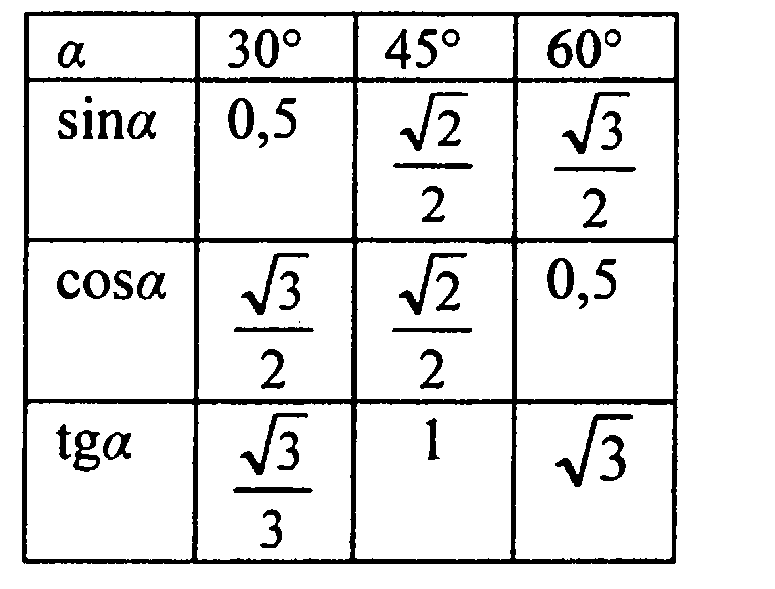 0875
0875