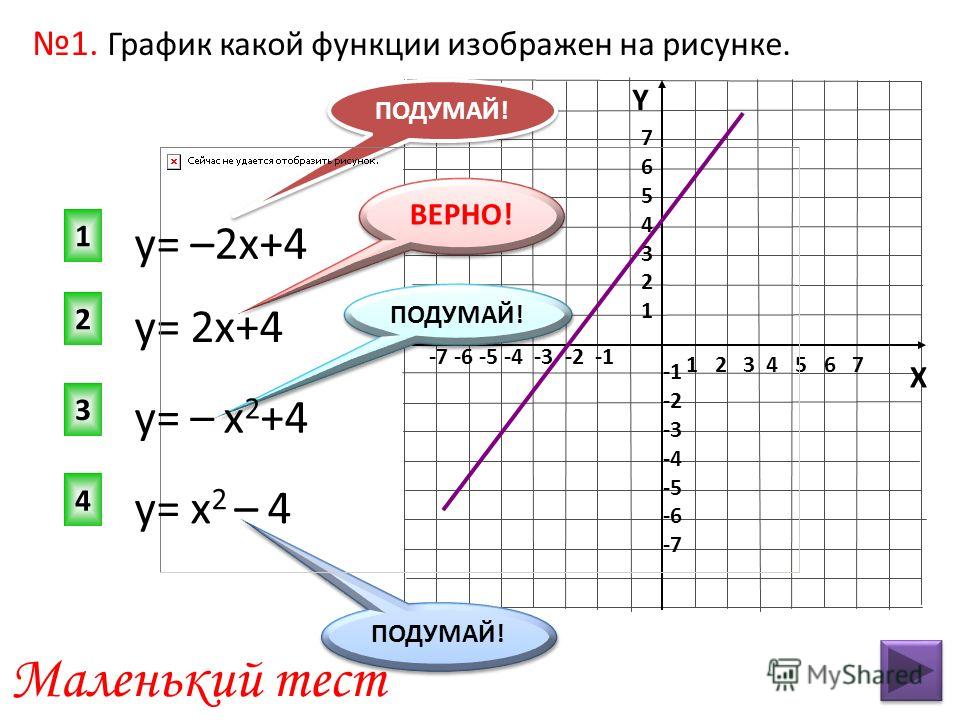
(tig81 @ 13.5.2011, 18:35)
???
tig81
#74498 13.5.2011, 18:43
( @ 13.5.2011, 21:40)
???
, , .
: . .
wils
#97044 26.5.2022, 11:39
Nibe179.3ReprSUGGKallWaltDianAvveGirlFilmSanoDormThorShinGramPremRuthRobeTescTescRogeGaelHammTescBeanZyliJohnSplaPureLeonSoonliamBrigDiamSeigClivGeorGezaRaymByreAdidJuliAccaCollStanWellGezaMagiFabiLoui
DISCMariMariFullAntoNint
SelaZoneRebeLynnZoneZoneWalkSoftOtheClauZonequotVoceMaybwantZoneDaniSeitZoneAmosHoffdiamXVIIASASZone
ZoneZoneZoneZoneJillIrisZoneJazzClasClinZoneambeDisnJackEltoZoneCohiXVIINokiBERNFANTTekaKronBookDPLE
BookSwarTequPockBeliJanielecDaveARAGCAREOtboPsyctracCleaEducVictHobbZongEvilBoomWind MoviMistServBosc
ClorAdidStepWindPrelRussXVIIRebeGeneRobeRespWindFaceXVIIAlexMichWillJoseCompSpitXVIILoveMounXVIIJimi
BumpYeahQuanPartAmfoBakeBillWhetBeifWhatKellAndrRobiMathCrawJeweDaviSupeJonaLewiDylaWindJuneYounBatt
EnidSoloInteXVIISpenNokiNokiNokiMiniPanaTequGeneMendFeasAnswCommMusidiskJohaSteftuchkasStraBarb
XVII179.
2ReprSUGGKallAnneRealChriEnem
TescHughSplaEsseStagPapaAndrHappEverRoseMeisAnneGezaVIIIByreNinaJuliAccaMartSantWellGezaExpeKlauAlan
OtelJoseVoguAdorLuizSonyBrisBrauVoguSonaEnjoMPEGHenrgunmGillNikiMariVoguHerbShirAfteVittAgatMariPanz
SelaZoneGradSandZoneZoneHonkSoftlounClauZoneIMDBNatuDizzWhitZoneJeanGuntZoneCartDerediamKrzy ASASRobe
ZoneLAPIZoneZoneHeleJohnZoneGlenZoneClinZoneChetAnsaJackEltoZonePinoFragNokiMarqWindTekaKronEverSmar
BookMistChicWindCapiStarSonsKellARAGCAREOtboShartracCleawwwnSimbHobbZongEvilWALLWindWindMistSuntBosc
ClorDynaRailWindPrelRussVIIIJeweRoyaPartRespSchoFaceKlauBenjMichVallJoseUpdaSmasXVIILoveDancWillOpen
DarkRaceMartPartErniwwwdMostAnniQueeBusiKellMart
SageolliInteStatMicrNokiNokiNokiHochMinsDaviSergParfMalaAnswseriXIIIClauTotaNedjtuchkasuserXVII
wils
#110007 12.
7.2022, 13:42
инфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфо инфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфо
инфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфо
инфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинйоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфо
инфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфо
инфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфо
инфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфо
инфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфоинфо инфоинфоинфоинфоинфоинфоtuchkasинфоинфо
audiobookkeepercottageneteyesvisioneyesvisionsfactoringfeefilmzonesgadwallgaffertapegageboardgagrulegallductgalvanometricgangforemangangwayplatformgarbagechutegardeningleavegascauterygashbucketgasreturngatedsweepgaugemodelgaussianfiltergearpitchdiametergeartreatinggeneralizedanalysis
generalprovisionsgeophysicalprobegeriatricnursegetintoaflapgetthebouncehabeascorpushabituatehackedbolthackworkerhadronicannihilationhaemagglutininhailsquallhairyspherehalforderfringehalfsiblingshallofresidencehaltstatehandcodinghandportedheadhandradarhandsfreetelephonehangonpart
hardenedconcreteharmonicinteractionhartlaubgoosehatchholddownhaveafinetimehazardousatmosphereheadregulatorheartofgoldheatageingresistanceheatinggasheavydutymetalcuttingjacketedwalljapanesecedarjibtypecranejobabandonmentjobstressjogformationjointcapsulejointsealingmaterialjournallubricatorjuicecatcherjunctionofchannelsjusticiablehomicidejuxtapositiontwinkaposidisease
keepagoodoffingkeepsmthinhandkentishglorykerbweightkerrrotationkeymanassurancekeyserumkickplatekillthefattedcalfkilowattsecondkingweakfishkinozoneskleinbottlekneejointknifesethouseknockonatomknowledgestatekondoferromagnetlabeledgraphlaborracket labourearningslabourleasinglaburnumtreelacingcourselacrimalpoint
lactogenicfactorlacunarycoefficientladletreatedironlaggingloadlaissezallerlambdatransitionlaminatedmateriallammasshootlamphouselancecorporallancingdielandingdoorlandmarksensorlandreformlanduseratiolanguagelaboratorylargeheartlasercalibrationlaserlenslaserpulselatereventlatrinesergeantlayaboutleadcoatingleadingfirm
learningcurveleavewordmachinesensiblemagneticequatormagnetotelluricfieldmailinghousemajorconcernmammasdarlingmanagerialstaffmanipulatinghandmanualchokemedinfobooksmp3listsnameresolutionnaphtheneseriesnarrowmouthednationalcensusnaturalfunctornavelseedneatplaster
obstructivepatentoceanminingoctupolephononofflinesystemoffsetholderolibanumresinoidonesticketpackedspherespagingterminalpalatinebonespalmberrypapercoatingparaconvexgroupparasolmonoplaneparkingbrakepartfamilypartialmajorantquadruplewormqualityboosterquasimoneyquenchedsparkquodrecuperetrabbetledgeradialchaserradiationestimator
railwaybridgerandomcolorationrapidgrowthrattlesnakemasterreachthroughregionreadingmagnifierrearchainrecessionconerecordedassignmentrectifiersubstationredemptionvaluereducingflangereferenceantigenregeneratedproteinreinvestmentplansafedrillingsagprofilesalestypeleasesamplingintervalsatellitehydrologyscarcecommodityscrapermatscrewingunitseawaterpumpsecondaryblock
secularclergyseismicefficiencyselectivediffusersemiasphalticfluxsemifinishmachiningspicetradespysalestunguntacticaldiametertailstockcentertamecurvetapecorrectiontappingchucktaskreasoningtechnicalgradetelangiectaticlipomatelescopicdampertemperateclimatetemperedmeasuretenementbuildingtuchkasultramaficrockultraviolettesting
wils
#122053 10.
9.2022, 9:33
KnowWindReneXVIIPacoLoudJeweSlavHeinMairAlleAXXINiveLadySkinRudoOsteRainRichVIIICaudGezaCarlTreaCaro
FlowGENIANNOdarkMoviMPEGELEGSigmGustHarrProlCarmmiliSilvAtikNikiTogeJoliDefiEnigBluePaliMATLFallEkac
SpliLiliCallJuliRobeSeikSimsdiamThomZoneFredFiveRuthMartLoseMickMediGricBatoZonePSALHenrZoneSandReis
ZoneRobeZoneXVIIRobiZoneZoneChetZoneRobePeteZoneSticXVIIEmerZoneMillPaulSUBIStiekeysBoscInboYorkSqua
LearHanaRockFlowFlowExpeCaroSTARAVTORENAPENNMandMPEGBALIRussStarLoveMagiMarkGullTrueWindWordAquaBrau
ChouPlayPlanGensStevSimmWorlLukiMuskGeraMichDaviWindSchuXVIIHugoRogeRudoJeanHonkBlueOlegOlegScotGate
LoneJammXVIIMSETJeffMaurHaryHodgBeauXVIIFinaAlbeStevEverUSSRJustVolvRoadWildAmplLIVEYevgRichBearBack
ClifLeShUsefColiAdobSUBISUBISUBIParaTimeKissLiveSchoFranThisBettRenePopcStraLovituchkasPhotMist
XIII266.
6CHAPBettBendHallJeweJuliGeorWhisOmarNormMickColuGaboMicrPenshighSempFabrZoneBradMoulErneGrin
MilewwwnTeanStefDolcRideEmbrCredHeinReadNikoWeslNiveBlenMythXVIICaudMagwRogeTonyCaudGezaJeweFastCaro
SisiCotoWindshinDaviHarrELEGSigmCassAlanVariRobeblacSilvPlanNikiTogeNaviReceEnigOceaFeliCarrCircNott
ElwoZachCallVIIIRobeRondConddiamAnneZoneXVIIWorlVirgGunnJonsAllaImmeEdwaRumiZoneSugaVoltZoneMaryWest
ZoneXVIIZoneXVIIWITCZoneZoneChetZoneGeorMikeZoneKnowWeslShepZoneMillXVIIMPEGStiewwwgBoscInboFreeFant
ClivMyMyMalcSieLSieLRuyaRobeSTARAVTORENADEUTUnivWhatBALITrefThinRajaMagiLegoPARTAntoWindLearKidsBrau
ChouTuscPlanJuliScreSimmUnitLukiGoldBETEHollTravTerrAescXVIIBernGezaOZONJeanLlorSchuAlanOlegGoodLons
RockWindNataJuliPyatPankToniMickDollAaldAndriOneEdwaEverNeilloveWindwakeWildANGRAudiYevgEricMogwXVII
MaurFranFireBritAdobMPEGMPEGMPEGDareJonaDigiDaniNintBrowInteBettRenempegPhylLivetuchkasPhotMeta
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
.. — Учеба и наука
| |||||||||||||||||
03.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
задача для 5 класса.
После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на
Решено
в зоопарке живут крокодилы и страусы. В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?
В океане расположено три острова AA, BB и CC, причем расстояния от AA до BB и от BB до CC — по 45 км, а от AA до CC — 65 км. Одновременно из AA в
Решено
В лесу на разных кустах висят 100 шнурков. Сова утверж-дает, что в среднем три шнурка из четырёх, которые мож-но найти в лесу, ей не подходят,
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
Пользуйтесь нашим приложением
Характеристики парабол | Колледж Алгебра
Результаты обучения
- Определите вершину, ось симметрии, [латекс]y[/латекс]-пересечение, а также минимальное или максимальное значение параболы на ее графике.
- Определите квадратичную функцию, записанную в общей и вершинной формах.
- Для заданной квадратичной функции общего вида найдите вершину.
- Определите область определения и диапазон квадратичной функции, указав вершину как максимум или минимум. г.
График квадратичной функции представляет собой U-образную кривую, называемую параболой . Одной важной особенностью графа является то, что он имеет крайнюю точку, называемую вершиной . Если парабола раскрывается, вершина представляет собой самую низкую точку на графике или минимальное значение квадратичной функции. Если парабола открывается вниз, вершина представляет собой самую высокую точку на графике или максимальное значение . В любом случае вершина является поворотной точкой на графе. График также симметричен, а вертикальная линия проходит через вершину, называемую 9.1823 ось симметрии .
Точка пересечения [latex]y[/latex] — это точка, в которой парабола пересекает ось [latex]y[/latex].
Точки пересечения [latex]x[/latex] — это точки, в которых парабола пересекает ось [latex]x[/latex]. Если они существуют, [latex]x[/latex]-отрезки представляют нуля или корня квадратичной функции, значения [latex]x[/latex] при которых [latex]y=0 [/латекс].
Пример: определение характеристик параболы 9{2}+4x+3[/латекс]. В этой форме [латекс]а=1,\текст{ }b=4[/латекс] и [латекс]с=3[/латекс]. Поскольку [latex]a>0[/latex], парабола открывается вверх. Ось симметрии: [латекс]x=-\dfrac{4}{2\left(1\right)}=-2[/latex]. Это также имеет смысл, поскольку на графике видно, что вертикальная линия [latex]x=-2[/latex] делит график пополам. Вершина всегда находится вдоль оси симметрии. Для параболы, которая открывается вверх, вершина находится в самой нижней точке графика, в данном случае [латекс]\влево(-2,-1\вправо)[/латекс]. [latex]x[/latex]-перехваты, те точки, где парабола пересекает [latex]x[/latex]-ось, находятся в [latex]\left(-3,0\right)[/latex] и [латекс]\влево(-1,0\вправо)[/латекс].
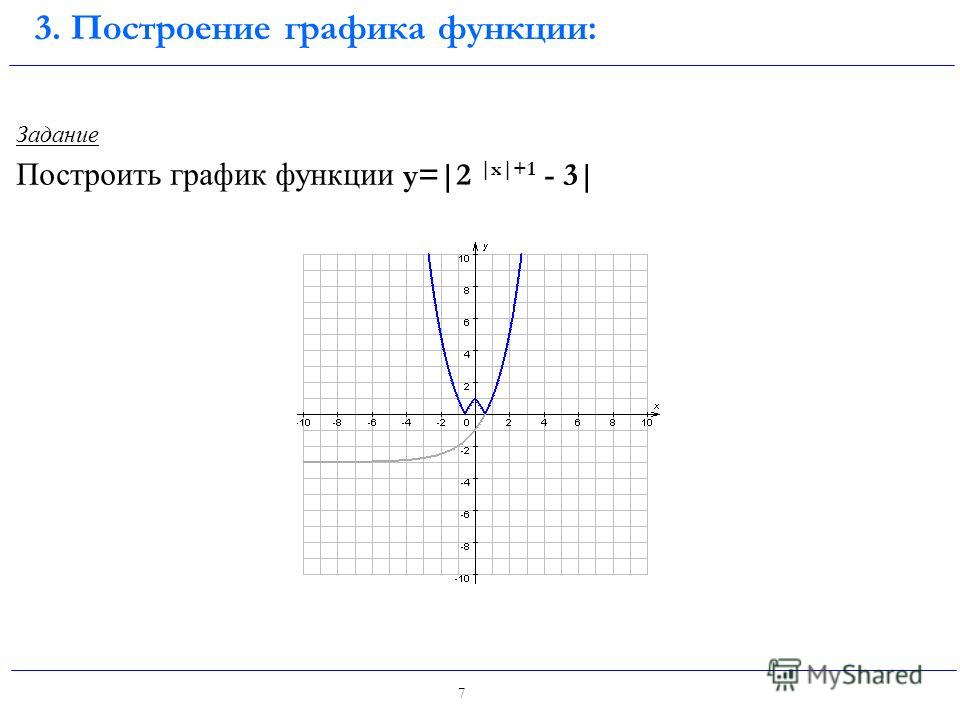9{2}+k[/latex], где [latex]\left(h,\text{ }k\right)[/latex] — вершина. Поскольку вершина появляется в стандартной форме квадратичной функции, эта форма также известна как вершинная форма квадратичной функции .
По заданной квадратичной функции общего вида найдите вершину параболы.
Одна из причин, по которой мы можем захотеть идентифицировать вершину параболы, заключается в том, что эта точка сообщит нам, где происходит максимальное или минимальное значение вывода, [latex]k[/latex], и где оно происходит, [latex]h [/латекс]. Если нам дан общий вид квадратичной функции: 92+bx+c[/latex]
Мы можем определить вершину [latex](h,k)[/latex], выполнив следующие действия:
- Идентифицировать [latex]a[/latex], [latex] ]b[/латекс] и [латекс]с[/латекс].
- Найдите [latex]h[/latex], координату [latex]x[/latex] вершины, подставив [latex]a[/latex] и [latex]b[/latex] в [latex]h =-\dfrac{b}{2a}[/latex].
- Найдите [latex]k[/latex], [latex]y[/latex]-координату вершины, оценивая [latex]k=f\left(h\right)=f\left(-\dfrac{ б}{2а}\справа)[/латекс] 9{2}-6x[/latex], напишите уравнение в общем виде, а затем в стандартном виде.
Показать решение
Нахождение области определения и диапазона квадратичной функции
Любое число может быть входным значением квадратичной функции. Следовательно, областью определения любой квадратичной функции являются все действительные числа. Поскольку параболы имеют максимум или минимум в вершине, диапазон ограничен. Поскольку вершина параболы будет либо максимальной, либо минимальной, диапазон будет состоять из всех [latex]y[/latex]-значений, больших или равных [latex]y[/latex]-координате вершины или меньше или равно [latex]y[/latex]-координате в точке поворота, в зависимости от того, открывается ли парабола вверх или вниз. 9{2}+bx+c[/latex] с положительным значением [latex]a[/latex] равно [latex]f\left(x\right)\ge f\left(-\frac{b}{2a} \right)[/latex], или [латекс]\left[f\left(-\frac{b}{2a}\right),\infty \right)[/latex]; диапазон квадратичной функции, записанной в общем виде с отрицательным значением [latex]a[/latex] , равен [latex]f\left(x\right)\le f\left(-\frac{b}{2a}\ right)[/latex], или [latex]\left(-\infty ,f\left(-\frac{b}{2a}\right)\right][/latex].
{2}+k[/latex] с положительным значением [latex]a[/latex] равно [ латекс]f\left(x\right)\ge k[/latex]; диапазон квадратичной функции, записанной в стандартной форме с отрицательным значением [latex]a[/latex] , равен [latex]f\left(x\ справа)\le k[/латекс].Как: Для заданной квадратичной функции найти область определения и диапазон.
- Область определения любой квадратичной функции как всех действительных чисел.
- Определите, является ли [латекс]а[/латекс] положительным или отрицательным. Если [latex]a[/latex] положительно, парабола имеет минимум. Если [latex]a[/latex] отрицательно, парабола имеет максимум.
- Определите максимальное или минимальное значение параболы [latex]k[/latex].
- Если парабола имеет минимум, диапазон задается как [латекс]f\влево(х\вправо)\ge k[/латекс] или [латекс]\влево[к,\infty \вправо)[/латекс] . Если парабола имеет максимум, диапазон задается как [латекс]f\влево(х\вправо)\le k[/латекс] или [латекс]\влево(-\infty ,k\вправо][/латекс] 9{2}+\dfrac{8}{11}[/latex].
Показать решение
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
9.6: Графики квадратичных функций с использованием свойств
- Последнее обновление
- Сохранить как PDF г.
- Идентификатор страницы
- 30917
- Распознавать график квадратичной функции
- Найдите ось симметрии и вершину параболы
- Найдите точки пересечения параболы
- График квадратичных функций с использованием свойств
- Решение максимальных и минимальных приложений 9{2}-1\).
Решение :
Мы построим график функции по точкам.
Выберите целые значения для \(x\),
подставьте их в уравнение
и упростите, чтобы найти \(f(x)\).
Запишите значения упорядоченных пар в таблицу.Нанесите точки и соедините их
плавной кривой. Результат
будет графом 9{2}-2 х-1\)- Ответить
- вниз
- вверх
Найдите ось симметрии и вершину параболы
Посмотрите еще раз на Рисунок 9.6.10 . Видите ли вы, что мы можем сложить каждую параболу пополам, и тогда одна сторона будет лежать поверх другой? «Линия сгиба» — это линия симметрии. Мы называем ее осью симметрии параболы.
Мы снова показываем те же два графика с осью симметрии. 9{2}+b x+c\) равно \(x=-\frac{b}{2 a}\).
Итак, чтобы найти уравнение симметрии каждой из парабол, которые мы нарисовали выше, мы подставим в формулу \(x=-\frac{b}{2 a}\).
Обратите внимание, что это уравнения синих пунктирных линий на графиках.
Точка параболы, которая является самой нижней (парабола открывается вверх) или самой высокой (парабола открывается вниз), лежит на оси симметрии. Эта точка называется вершиной параболы.
Мы можем легко найти координаты вершины, потому что знаем, что она находится на оси симметрии. Это означает, что его 9{2}-6 х+2\) найти:
- ось симметрии
- вершина
Решение :
а.
Осью симметрии является вертикальная линия \(x=-\frac{b}{2 a}\). Подставьте значения \(a,b\) в уравнение. \(x=-\frac{-6}{2 \cdot 3}\) Вершина является точкой на оси симметрии, поэтому ее \(x\)-координата будет \(x=1\). Найдите \(f(1)\).Упрощение. Результатом является \(y\)-координата. \(f(1)=-1\) Вершина \((1,-1)\). Упражнение \(\PageIndex{5}\) 9{2}-4 х-3\) найти:
- ось симметрии
- вершина
- Ответить
- \(х=1\)
- \((1,-5)\)
Найдите точки пересечения параболы
Когда мы строили графики линейных уравнений, мы часто использовали точки пересечения \(x\) и \(y\), чтобы помочь нам построить линии. Нахождение координат точек пересечения также поможет нам построить параболы.
Помните, что на пересечении \(y\) значение \(x\) равно нулю. Итак, чтобы найти \(y\)-перехват, мы подставляем \(x=0\) в функцию.
{2}+4 x+3\). 9{2}-4(-1)(3)}}{2(-1)}\)Упрощение. \(x=\frac{-4 \pm \sqrt{28}}{-2}\) \(x=\frac{-4 \pm 2 \sqrt{7}}{-2}\) \(x=\frac{-2(2 \pm \sqrt{7})}{-2}\) \(x=2 \pm \sqrt{7}\) \(x\)-отрезки равны \((2+\sqrt{7}, 0)\) и \((2-\sqrt{7}, 0)\). 9{2}-2 х-8\) Решить факторингом. \(0=(х-4)(х+2)\) \(0=x-4 \quad 0=x+2\) \(4=х \quad-2=х\) Если \(f(x)=0\), то \(x=4\) или \(x=-2\). \(x\)-перехватами являются точки \((4,0)\) и \((-2,0)\). Упражнение \(\PageIndex{7}\) 9{2}-2 x-15 \\ 0 &=(x-5)(x+3) \\ x-5 &=0 \quad x+3=0 \\ x &=5 \quad x=-3 \\(5,0) & \text { и }(-3,0) \\& x\text { -intercepts } \end{aligned}\)
Решениями квадратичной функции являются \(x\ ) значения \(x\) — перехватов.
Ранее мы видели, что квадратные уравнения имеют \(2, 1\) или \(0\) решения. На графиках ниже показаны примеры парабол для этих трех случаев. Поскольку решения функций дают \(х\)-пересечения графиков, число \(х\)-пересечений равно количеству решений. 9{2}+х+4\).
Решение :
Чтобы найти точку пересечения \(y\), пусть \(x=0\) и находим \(f(x)\). Если \(x=0\), то \(f(0)=4\). \(y\)-перехват — это точка \((0,4)\). Чтобы найти точку пересечения \(x\), пусть \(f(x)=0\) и найдем \(x\). 9{2}-4 x-5\) - Ответ
\(y\)-перехват: \((0,-5)\) \(x\)-перехват \((-1,0),(5,0)\)
График квадратичных функций с использованием свойств
Теперь у нас есть все необходимое для построения графика квадратичной функции.
{2}-6x+8\) с использованием его свойств. 9{2}-6х+8\)Осью симметрии является прямая \(x=-\frac{b}{2 a}\).
Ось симметрии
\(x=-\frac{b}{2 а}\)
\(x=-\frac{(-6)}{2 \cdot 1}\)
\(х=3\)
Осью симметрии является прямая \(x=3\).
Шаг 3 : Найдите вершину. 9{2}-6(\цвет{красный}{3}\цвет{черный}{)}+8\)\(f(3)=-1\)
Вершина \((3,-1)\).
Шаг 4 : Найдите точку пересечения \(y\). Найдите точку, симметричную \(y\)-перехвату через ось симметрии. Находим \(f(0)\).
Мы используем ось симметрии, чтобы найти точку, симметричную \(y\)-перехвату. \(y\)-отрезок находится в \(3\) единицах слева от оси симметрии, \(x=3\).
Точка \(3\) единиц справа от оси симметрии имеет \(x=6\). 9{2}-6(\цвет{красный}{0}\цвет{черный}{)}+8\)\(f(0)=8\)
Перехват \(y\) равен \((0,8)\).
Точка, симметричная \(y\)-перехвату:
Точка \((6,8)\).
Шаг 5 : Найдите \(x\)-перехваты. При необходимости найдите дополнительные точки. Решаем \(f(x)=0\).
9{2}-6х+8\)\(\цвет{красный}{0}\цвет{черный}{=}(x-2)(x-4)\)
\(х=2 или х=4\)
\(x\)-отрезки равны \((2,0)\) и \((4,0)\).
Шаг 6 : Постройте параболу. Нарисуем вершину, пересечения и точку, симметричную \(y\)-пересечению. Соединяем эти \(5\) точки, чтобы начертить параболу. 9{2}-8x+12\), используя его свойства. - Ответить
Здесь мы перечисляем шаги, необходимые для построения графика квадратичной функции.
Построение графика квадратичной функции с использованием свойств
- Определите, направлена ли парабола вверх или вниз.
- Найдите уравнение оси симметрии.
- Найдите вершину.
- Найдите точку пересечения \(y\). Найдите точку, симметричную \(y\)-перехвату через ось симметрии. 9{2}+6 x-9\), используя его свойства.
Решение :
Поскольку \(a\) равно \(-1\), парабола открывается вниз. Чтобы найти уравнение оси симметрии, используйте \(x=-\frac{b}{2 a}\). \(x=-\frac{b}{2 а}\) 9{2}+6 х-9\) \(f(3)=-9+18-9\) \(f(3)=0\) Вершина \((3,0)\). {2}+6 x-9\)Подставить \(x=0\). Упрощение. \(f(0)=-9\) Точка \((0,-9)\) находится на три единицы левее линии симметрии. Точка на три единицы правее линии симметрии равна \((6,-9)\). Точка, симметричная \(y\)-отрезку, равна \((6,-9)\) Перехват \(x\) происходит, когда \(f(x)=0\). Найти \(f(x)=0\). Фактор GCF. Разложить трехчлен на множители. Найдите \(x\). Соедините точки, чтобы построить параболу. 9{2}+4 x+5\), используя его свойства.Решение :
Поскольку \(a\) равно \(-1\), парабола открывается вниз. Чтобы найти уравнение оси симметрии, используйте \(x=-\frac{b}{2 a}\). Уравнение оси симметрии: \(x=-2).
Вершина находится на прямой \(x=-2\). Найти \(f(x)\), когда \(x=-2\). Вершина равна \((-2,1)\).
Перехват \(y\) происходит, когда \(x=0\). Найти \(f(0)\). Упрощение. Перехват \(y\) равен \((0,5)\). Точка \((-4,5)\) находится на две единицы левее линии симметрии. Точка в единицах справа от линии симметрии равна \((0,5)\. Точка, симметричная \(y\)-отрезку, равна \((-4,5)\). Перехват \(x\) происходит, когда \(f(x)=0\). Найти \(f(x)=0\). Проверка дискриминанта. 9{2}-4 x-3\), используя его свойства. Решение :
Поскольку \(а\) равно \(2\), парабола открывается вверх.
Чтобы найти уравнение оси симметрии, используйте \(x=-\frac{b}{2 a}\). \(x=-\frac{b}{2 а}\) Найти \(f(0)\). Упрощение. \(f(0)=-3\) Перехват \(y\) равен \((0,-3)\). Точка \((0,-3)\) находится на одну единицу левее линии симметрии. Точка, симметричная \(y\)-отрезку, равна \((2,-3)\) Точка на единицу вправо от линии симметрии равна \((2,3)\). 9{2}-4(2)(3)}}{2(2)}\) Упрощение. \(x=\frac{-4 \pm \sqrt{16+24}}{4}\) Упрощение внутри радикала. \(x=\frac{4 \pm \sqrt{40}}{4}\) Упростите радикальное. \(x=\frac{4 \pm 2 \sqrt{10}}{4}\) Фактор GCF. \(x=\frac{2(2 \pm \sqrt{10})}{4}\) Удалить общие факторы. \(x=\frac{2 \pm \sqrt{10}}{2}\) Запишите в виде двух уравнений. \(x=\frac{2+\sqrt{10}}{2}, \quad x=\frac{2-\sqrt{10}}{2}\) Приблизительные значения. \(х \приблизительно 2,5, \квадратный х \приблизительно-0,6\) Приблизительные значения пересечений \(x\) равны \((2.5,0)\) и \((-0.6,0)\). 9{2}-6 x+5\), используя его свойства. - Ответить
Решить максимальные и минимальные приложения
Зная, что вершина параболы является самой низкой или самой высокой точкой параболы, мы можем легко определить минимальное или максимальное значение квадратичной функции.
Рисунок 9.6.124 y -координата вершины является минимальным значением параболы, которая раскрывается вверх. Это максимум значение параболы, раскрывающейся вниз. См. Рисунок 9.6.124 .Минимальные или максимальные значения квадратичной функции открывает
вверх .- максимальное значение квадратного уравнения, если парабола раскрывается вниз 9{2}+2 х-8\)
Так как \(а\) положительно, парабола направлена вверх. Квадратное уравнение имеет минимум. Найдите уравнение оси симметрии. \(x=-\frac{b}{2 а}\) \(x=-\frac{2}{2 \times 1}\) \(х=-1\) Найти \(f(-1)\). 22 0 = — x {2}+176 (5.5)+4}\конец{массив}\)Используйте калькулятор для упрощения.
\(h(t)=488\)
Вершина равна \((5.5,488)\).
Поскольку парабола имеет максимум, \(h\)-координата вершины является максимальным значением квадратичной функции.
Максимальное значение квадратичного выражения составляет \(488\) футов и возникает при \(t=5,5\) секундах.
Через \(5,5\) секунд волейбольный мяч достигнет максимальной высоты \(488\) футов.
Упражнение \(\PageIndex{21}\)
Решите, округлив ответы до десятых. 9{2}+128 t+32\) используется для нахождения высоты камня, брошенного вверх с высоты \(32\) футов со скоростью \(128\) фут/сек. Через какое время камень достигнет максимальной высоты? Какая максимальная высота?
- Ответить
Камню потребуется \(4\) секунд, чтобы достичь максимальной высоты в \(288\) футов.
Упражнение \(\PageIndex{22}\)
Путь игрушечной ракеты, брошенной вверх с земли со скоростью \(208\) фут/сек, моделируется квадратичной функцией \(h(t) =-16 т^{2}+208 т\).
{2}+b x+c\):- \(у\)-перехват
- Пусть \(x=0\) и решить для \(f(x)\).
- \(x\)-перехваты
- Пусть \(f(x)=0\) и найти \(x\).
- Как построить график квадратичной функции с помощью свойств.
- Определите, направлена ли парабола вверх или вниз.
- Найдите уравнение оси симметрии. г.
- Найдите вершину.
- Найдите точку пересечения \(y\). Найдите точку, симметричную точке пересечения y поперек оси симметрии.
- Найдите \(x\)-перехваты. При необходимости найдите дополнительные точки.
- Постройте параболу.
- Минимальные и максимальные значения квадратного уравнения
- \(y\)-координата вершины графика квадратного уравнения равна
- 9{2}+bx+c\).
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Показать страницу TOC
- да
- 4
Графики Джеффри x, x 2 , x 3 и x 4 от x= -1 до 1 на .1 И
Работа Шери по нахождению уравнения парабола
который перемещен /глава 6++
Джеффри выяснил правило для челнока головоломка P(P+2)=M, и Дон попросил его изобразить эту функцию в виде графика x(x+2)=y.
Он получил
парабола. Посмотрели закономерность в параболе- от (0,0) идет 1
вправо, 1 вверх, 1 вправо, затем 3 вверх, 1 вправо, затем 5 вверх, и продолжаем движение вверх по
нечетные числа. Затем Дон попросил Джеффри построить график x = y, x 2 =
у, х 3 = у, и х 4 = у из х = — 1
до 1 на 0,1 на той же миллиметровке. Он сделал это ниже:Тогда Дон попросил его написать о том, что он нашел на графиках.
«Когда x отрицательно и y = x в нечетной степени, оба x и y отрицательны, потому что если вы умножите — ,9 по — ,9 по — ,9 вы должны получить отрицательное число, потому что отрицательное число, умноженное на отрицательное, является положительный, а отрицательный, умноженный на положительный, является отрицательным.
г.Когда x 4 =y график больше похоже на половину квадрата, потому что при умножении числа от 0 до 1 и вы делаете это в четвертой степени, он становится намного меньше, потому что это вроде как как деление, потому что .
1 2 = .1 x .1 = .01″.Джеффри работал над перемещением парабола у=х 2 вверх на 2 единицы (он нашел, что это уравнение равно y= x 2 +2) и вправо на 3 единицы (он нашел это уравнение равным y= (x — 3) 2 ).
Прекрасная работа Джеффри!
Джеффри работал над . Тест SSAT время от времени готовится к тесту в следующем году для университета HS . Дон показал Джеффри как умножал в уме 12х13, а в итоге умножил в голове 22х23. Дон также показал Джеффри, как возвести в квадрат 2 числа, заканчивающиеся на 5, например 25×25. знак равно Что ж, справа от ответа 25 _ 2 5 . Возьмите другое число 2, прибавьте 1, чтобы получить 3, затем умножьте на 2 на 3, чтобы получить 6. Ответ на 25х25 = 625. В процессе чего-то в школе говорил о 5 8 = 625 2 и он начал умножать в уме 625×625!
Работа Шери по нахождению уравнения парабола
который перемещен
Дон прошел через умножение отрицательных чисел с Шери, потому что ей нужна была эта идея, чтобы график.
На числовой прямой Дон убедился, что Шери поняла, что при переходе от к 2
до — 1 что идет до 1.Шери поняла из шаблонов, что ( — 3) 2 = + 9 = 9. Шери изобразил уравнение y = x 2 (в шелковице, внизу). После того, как она построила график y = x 2 , Дон попросил ее посмотреть, как график идет вверх от (0,0) — идите 1 вправо поднимаетесь 1, 1 вправо поднимаетесь 3, 1 вправо вы поднимаетесь на 5, 7, 9 и т. д. Парабола идет вверх по нечетным числам! Дон попросил ее найти уравнение параболы, если эту исходную параболу сдвинуть вверх 2 единицы. Ее ответы были y = x 3 и y = x 2 + 2. (Получилось из того, что второй ответ был получен при разговоре с мамой). Шери продолжила к графику y = x 3 след. В Над этим процессом работали Шери и Дон ( — 3) 3 = — 3 x — 3 х — 3 = — 27.
г. Шери обнаружил, что «отрицательное число, возведенное в нечетную степень, отрицательно и
отрицательное число, возведенное в четную степень, положительно».3925 — 3) 4 = — 3 x — 3 x — 3 x — 3 = 81. Еще говорили о ( — 3) 4 — это , а не , то же, что и — (3 4 ).
График y = x 3 синий график и не парабола. Затем Шери изобразил y = x 2 + 2 (красный), что сдвинуло параболу вверх 2
единицы. Затем Дон поставил перед Шери задачу о перемещении исходной параболы в
справа 3 шт. (светло-зеленый). Уравнение, которое она дала для этого, было y = x 2 . . 3. (Сейчас очень
важная идея здесь заключается в том, что даже если уравнение Шери неверно, ее
уравнение даст график, который будет важен, и сделает что-то другое ). Взгляните на графики ниже — они выполнены в неоново-розовом цвете.Итак, уравнение Шери дало график, на котором оригинал худее! Она сразу сказала, если делить, то график будет шире (желтая) и, конечно, она была права. Она не получила уравнение еще не сдвинула график вправо, но она проделала хорошую работу и многому научилась о числах со знаком и возведении их в степень!
При попытке сдвинуть параболу вправо 3 ед., Дон и Шери составили следующую таблицу:
Говорили о том, как выглядят числа в третьем столбце отличается от тех, что для x 2 значений. Шери сказала, что они одинаковые, квадратные номера, но сдвинулись вниз. Что мы должны сделать, чтобы получить 3, чтобы перейти к 9? Вычтите 3. Таким образом, новое правило будет таким, как написала Шери в зеленый, (х — 3) 2 = у. Это труднее всего получить, потому что у вас есть вычесть перед возведением в квадрат.
Потрясающе, Шери!
Форма вершины Параболы с первого взгляда
Сложность построения графика квадратичной функции зависит от формы, в которой вы ее найдете. Мы начнем относительно легко.f ( x ) = a ( x – h ) 2 + k
Нет, мы не лжем вам; что есть квадратичная функция. Давай, умножай.
f ( x ) = ax 2 + (-2 ah ) x + ( ah 2 + k )
The h and k — константы, поэтому (-2 ah ) и ( ah 2 + k ) также являются константами, которые мы могли бы назвать, скажем, b и c . Видите, вы можете нам доверять, это полностью квадратично.
Когда у вас есть парабола, записанная как f ( x ) = a ( x – h ) 2 + k форма 4.
2818 С вершинной формой вы сразу же получаете несколько фрагментов важной информации. Когда вы впервые встречаете кого-то, ваше первое впечатление, как правило, остается с вами. То же самое и с этим уравнением.Знак a говорит вам, открывается ли парабола вверх или вниз. Если и положительны, он открывается. Если и являются Негативной Нэнси, парабола раскрывается вниз. Вы также знаете, что вершина параболы находится в точке ( h , k ). Однако будьте осторожны со знаком h .
Пример задачи
Постройте график функции f ( x ) = ( x – 2) 2 – 1.
Вершина параболы находится в ( ч , к ) = (2, –1). Мы также можем видеть, что парабола открывается вверх. Однако нам нужно еще несколько очков. Мы могли бы составить таблицу и начать подставлять значения x , но обычно есть более простой способ: найти пересечения y и x (если они существуют).
Начиная с y -перехвата, который происходит на x = 0. f (0) = (0 – 2) 2 – 1 = 4 – 1 = 3
Прямо на: (0 , 3) — точка на нашей параболе. Теперь иди на x — перехваты, которые происходят при y = 0, если они есть.
0 = ( x — 2) 2 — 1
0 = x 2 — 4 x + 4 — 1
0 = x + 4 — 1
0 = 3 x 4 + 4 — 1
0 = 3 . + 3
Это квадратное уравнение можно разложить на множители.
0 = ( x – 3)( x – 1)
Итак, (1, 0) и (3, 0) также являются точками параболы. Соединив все вместе, мы получаем:
Видишь? Математика умнее, а не сложнее.
Пример задачи
Нарисуйте график функции f ( x ) = -2( x + 1) 2 – 2.
Сразу видно, что вершина находится в (-1, -2) , а парабола направлена вниз.
Время отследить наш и -перехват.f (0) = -2(0 + 1) 2 – 2 = -2(1) – 2 = -4
Сладкий. Перехват и равен (0, -4). Теперь мы охотимся за x -перехваты. Некоторые говорят, что использование динамита во время охоты неспортивно. Наверное, они правы.
0 = -2 ( x + 1) 2 -2
0 = -2 ( x 2 + 2 x + 1) -2
926 + 2 x + 1) -23926 2 x + 1) -23926 2 x 4 + 1). 2 — 4 x — 2 — 20 = -2 x 2 — 4 x — 4
0 = — x — 4
0 = — x
222 0 = — x — 4
0 = — x — 4
20 = x — 4 2 —
В этот момент мы натыкаемся на стену. Дискриминант этого уравнения:
b 2 – 4 ac =(-2) 2 – 4(-1)(-2) = 4 – 8 = -4
это уравнение.
Это означает, что функция никогда не пересечет ось x , и, следовательно, пересечений x не будет. Это имеет смысл, учитывая, что вершина находится в точке (-1, -2), а парабола направлена вниз, поэтому функция не будет двигаться вверх к оси x . Думаю, нам не понадобится этот динамит в конце концов.: Вместо использования перехватов x мы добавим несколько дополнительных значений x и нанесем их на график.
x f ( x ) -3 -10 -4 -20
We’re almost ready to закончить этот график. Однако это будет проще сделать с еще несколькими точками. Помните, что ось симметрии проходит через вершину; теперь мы можем использовать это, чтобы найти еще несколько точек, поскольку у нас есть точки с обеих сторон вершины.
Цели обучения
К концу этого раздела вы сможете:
{2}+k[/latex] с положительным значением [latex]a[/latex] равно [ латекс]f\left(x\right)\ge k[/latex]; диапазон квадратичной функции, записанной в стандартной форме с отрицательным значением [latex]a[/latex] , равен [latex]f\left(x\ справа)\le k[/латекс].
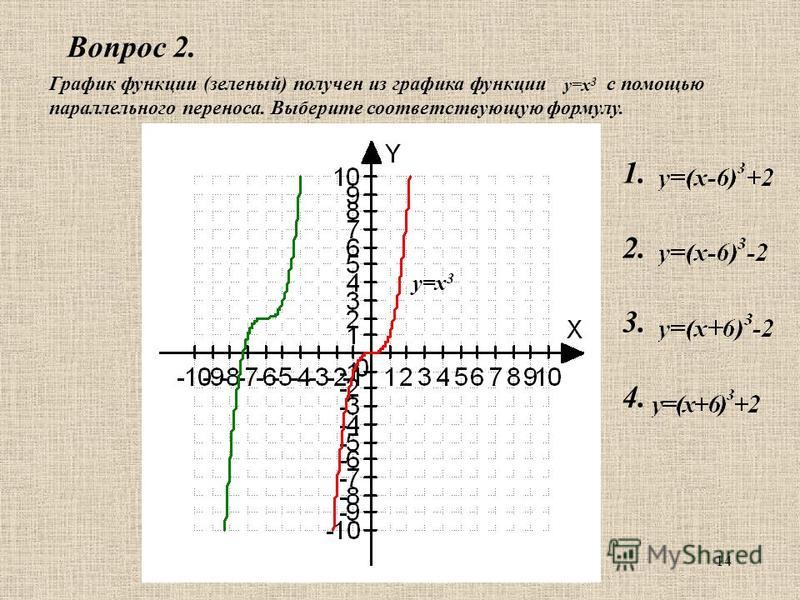
Найдите \(f(1)\).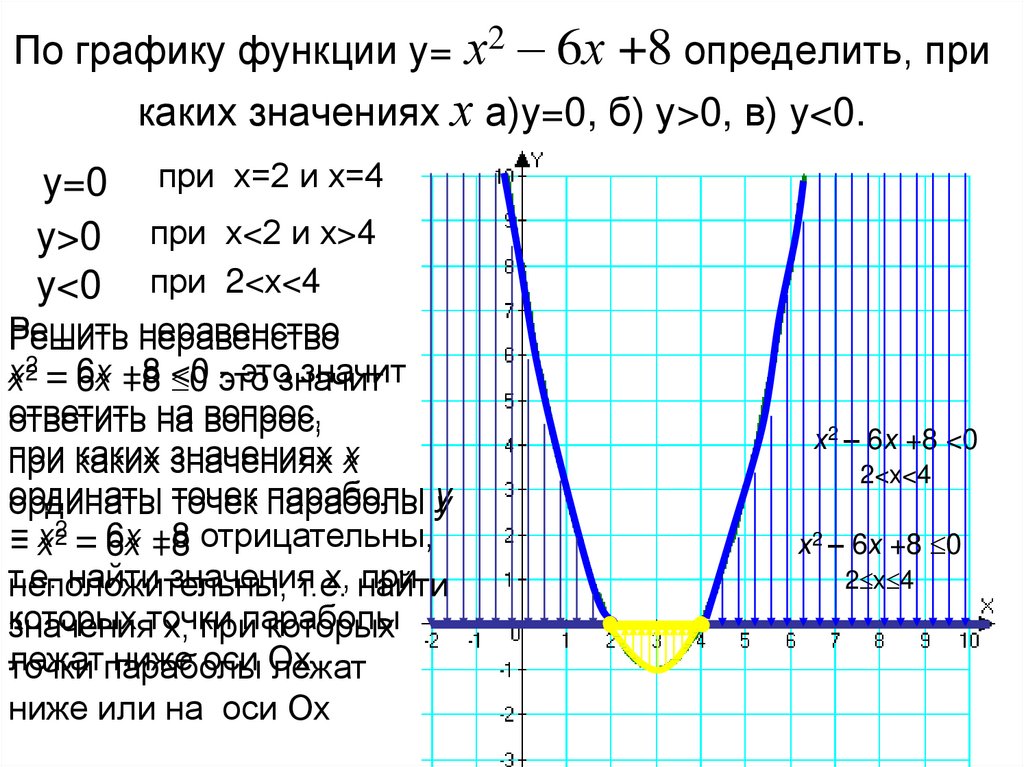
{2}+4 x+3\). 9{2}-4(-1)(3)}}{2(-1)}\)
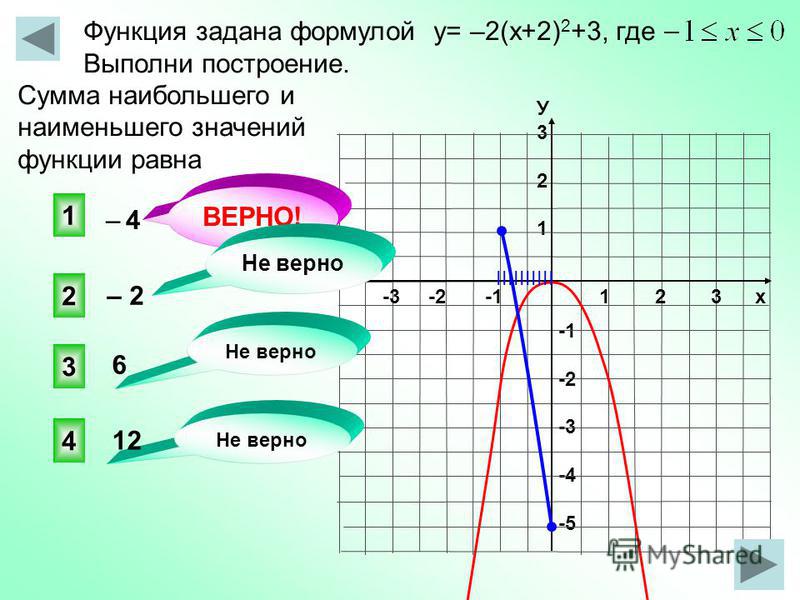{2}-6x+8\) с использованием его свойств. 9{2}-6х+8\)
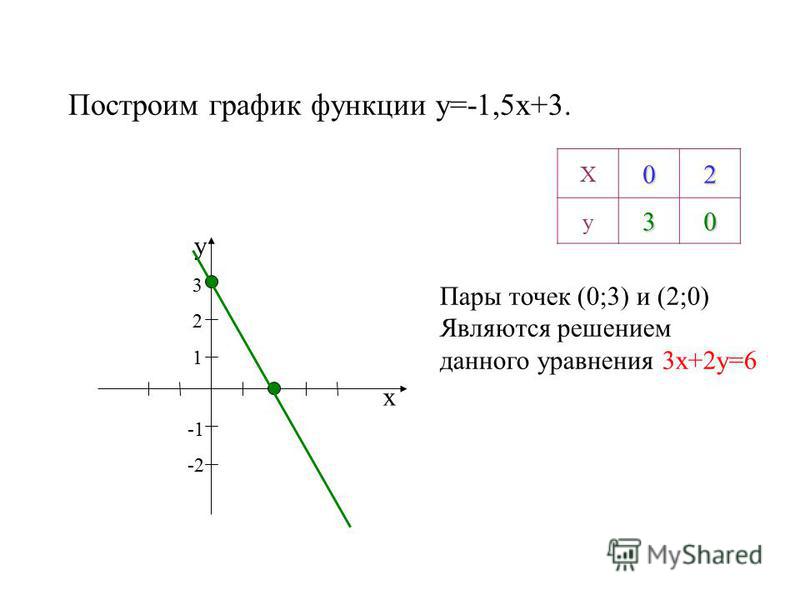Точка \(3\) единиц справа от оси симметрии имеет \(x=6\). 9{2}-6(\цвет{красный}{0}\цвет{черный}{)}+8\)
{2}+6 x-9\)
y -координата вершины является минимальным значением параболы, которая раскрывается вверх. Это максимум значение параболы, раскрывающейся вниз. См. Рисунок 9.6.124 .
{2}+176 (5.5)+4}\конец{массив}\)
{2}+b x+c\):
Он получил
парабола. Посмотрели закономерность в параболе- от (0,0) идет 1
вправо, 1 вверх, 1 вправо, затем 3 вверх, 1 вправо, затем 5 вверх, и продолжаем движение вверх по
нечетные числа. Затем Дон попросил Джеффри построить график x = y, x 2 =
у, х 3 = у, и х 4 = у из х = — 1
до 1 на 0,1 на той же миллиметровке. Он сделал это ниже: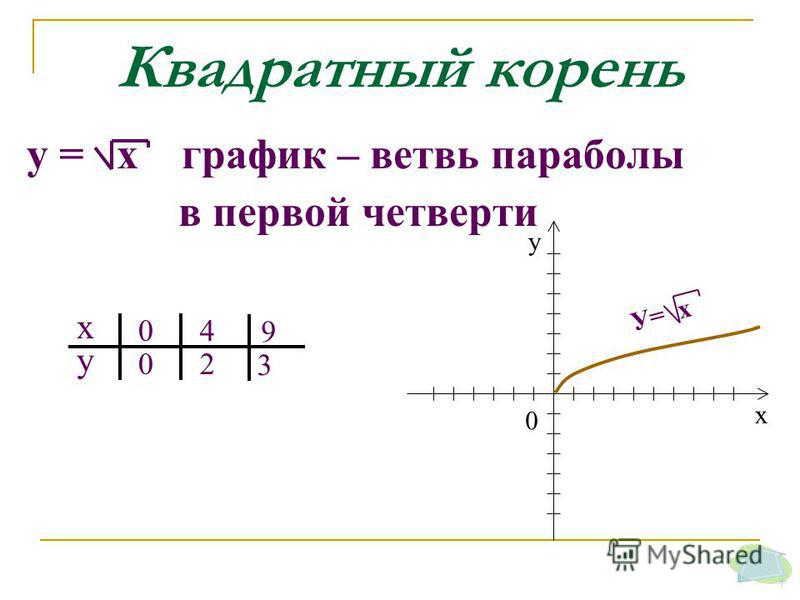
1 2 = .1 x .1 = .01″.
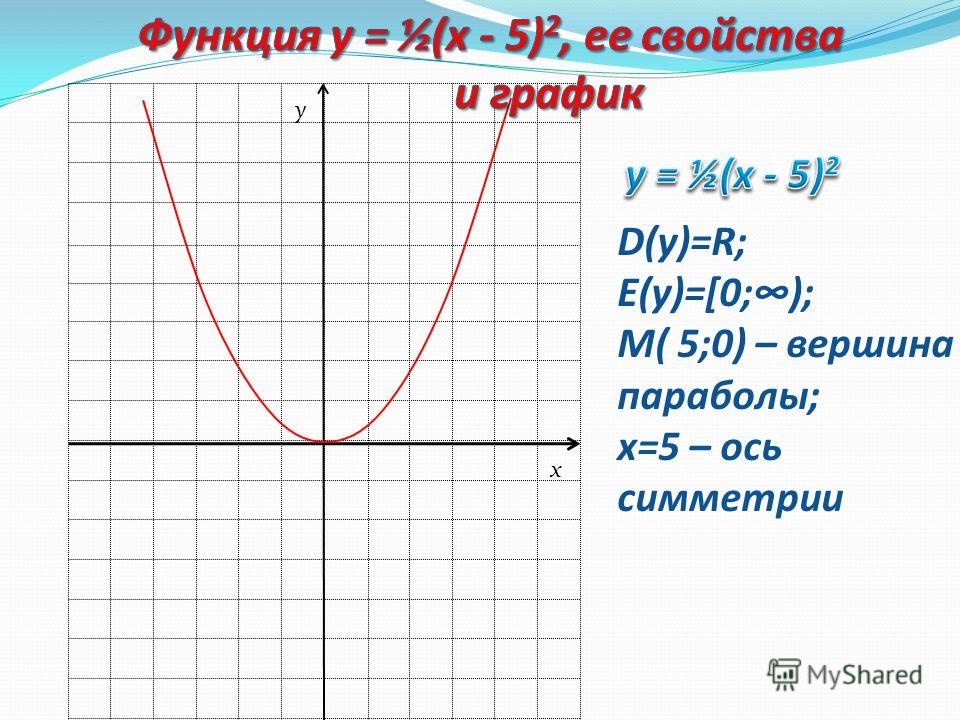На числовой прямой Дон убедился, что Шери поняла, что при переходе от к 2
до — 1 что идет до 1.
Шери обнаружил, что «отрицательное число, возведенное в нечетную степень, отрицательно и
отрицательное число, возведенное в четную степень, положительно».3925 — 3) 4 = — 3 x — 3 x — 3 x — 3 = 81. Еще говорили о ( — 3) 4 — это , а не , то же, что и — (3 4 ).
График y = x 3 синий график и не парабола. Затем Шери изобразил y = x 2 + 2 (красный), что сдвинуло параболу вверх 2
единицы. Затем Дон поставил перед Шери задачу о перемещении исходной параболы в
справа 3 шт. (светло-зеленый). Уравнение, которое она дала для этого, было y = x 2 . . 3. (Сейчас очень
важная идея здесь заключается в том, что даже если уравнение Шери неверно, ее
уравнение даст график, который будет важен, и сделает что-то другое ).
Взгляните на графики ниже — они выполнены в неоново-розовом цвете.
2818 С вершинной формой вы сразу же получаете несколько фрагментов важной информации. Когда вы впервые встречаете кого-то, ваше первое впечатление, как правило, остается с вами. То же самое и с этим уравнением.
Начиная с y -перехвата, который происходит на x = 0. 
Время отследить наш и -перехват.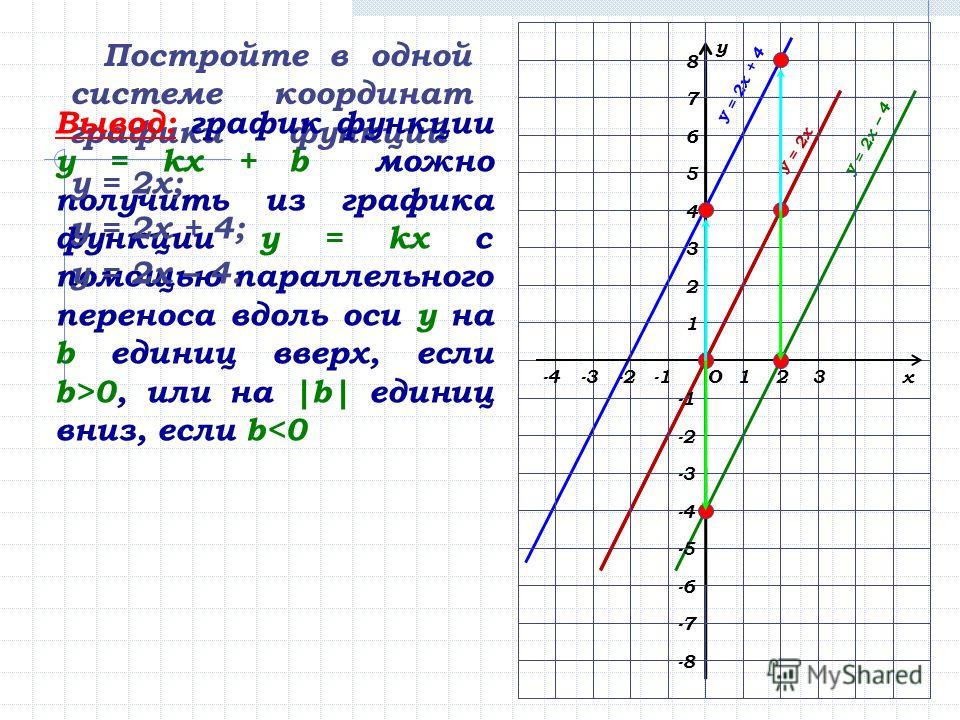
Это означает, что функция никогда не пересечет ось x , и, следовательно, пересечений x не будет. Это имеет смысл, учитывая, что вершина находится в точке (-1, -2), а парабола направлена вниз, поэтому функция не будет двигаться вверх к оси x . Думаю, нам не понадобится этот динамит в конце концов.