2N факториал разложение: Как разложить факториал? (2n)!! — Спрашивалка

Содержание

Как решить Факториал числа. Таблица, Свойства, Примеры

Поможем понять и полюбить математику

Начать учиться

200.1K

Алгебра в 9 классе полна сложных и загадочных слов. Например, факториал. Давайте разберемся, что это такое и как, что и зачем с ним собственно делать.

Факториал: определение

Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».

Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:

-3,75! 2,23! -2!

Число должно быть целое и положительное:

3! 56! 12!

Формула факториала
n!=1⋅2⋅3⋅. ..⋅(n−2)⋅(n−1)⋅n

Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.

Например:

3! = 1*2*3 = 6
4! = 1*2*3*4 = 24

5! = 1*2*3*4*5 = 120
6! = 1*2*3*4*5*6 = 720

Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Формулы и свойства факториала

Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.

Запоминаем

0! = 1

1! = 1

2! = 2

3! = 6

4! = 24

5! = 120

6! = 720

7! = 5040

8! = 40320

9! = 362880

10! = 3628800

11! = 39916800

12! = 479001600

13! = 6227020800

14! = 87178291200

15! = 1307674368000

16! = 20922789888000

17! = 355687428096000

18! = 6402373705728000

19! = 121645100408832000

20! = 2432902008176640000

21! = 51090942171709440000

22! = 1124000727777607680000

23! = 25852016738884976640000

24! = 620448401733239439360000

25! = 15511210043330985984000000

Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:

(n — 1)! = 1*2*3*4*5*…*(n — 2)(n — 1)
n! = 1*2*3*4*5*…*(n — 2)(n — 1)n
(n + 1)! = 1*2*3*4*5*…*(n — 2)(n — 1)n(n + 1)

С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.

Такая формула дает результат с небольшой погрешностью.

Пример:

Рекуррентная формула

Примеры:

5! = 5*(5 — 1)! = 5*4! = 5*24 = 120
6! = 6*(6-1)! = 6*5! = 6*120 = 720

Для решения примеров обращайтесь к таблице.

Примеры умножения факториалов:

Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800

Или раскладывайте факториалы отдельно, если хотите потренироваться:
5! = 1*2*3*4*5 = 4! * 5 =120
7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040
120 * 5040 = 604800

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Примеры решений

Давайте поупражняемся и решим пару примеров.

1. Сократите дробь:

Как решаем:

При сокращении факториалов, пользуйтесь свойством:
n! = (n — 1)! * n
100! = 99! * 100

Далее сокращаем по принципу сокращения обыкновенных дробей.

2. Вычислите значение выражения с факториалом: 8! + 5!

Как решаем:

Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.

А можно потренироваться и разложить их:

8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440

3. Вычислите значение выражения:

Как решаем:

7! = 1*2*3*4*5*6*7 = 5! * 6 *7

Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.

4. Вычислите значение выражение:

Как решаем:

Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*…..*69 = 69! * 70
49! = 1*2*3*….49! * 48

Далее сокращаем все одинаковые множители.

5. Сократите дробь:

Как решаем:

Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.

Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Анастасия Белова

К предыдущей статье

246.8K

Правильное округление чисел

К следующей статье

188.6K

Центральные и вписанные углы

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс

Формулы и уравнения рядов

Примеры решения рядов здесь.

Числовые ряды

Факториал и двойные факториалы:

— формула Стирлинга.

Геометрическая прогрессия:

|q|<1.

Основные определения и теоремы о рядах:

{u_n} — заданная бесконечная числовая последовательность,

— числовой ряд

,
u_n — члены ряда,
– частичные суммы ряда.

Сумма ряда:

сходится, S — сумма ряда.

или ряд сходится и суммы нет.

Отбрасывание конечного числа членов ряда не влияет на его сходимость (но влияет на сумму).

Свойства сходящихся рядов:

Теоремы сравнения рядов с положительными членами:

≤
Если сходится, то сходится;
если расходится, то расходится.
v_n ≠ 0, 0 < k < ∞.
Либо и , и сходятся,
либо и , и расходятся.

Достаточные признаки сходимости числовых рядов с положительными членами

u_n

Признак Даламбера
Если существует , то : сходится, если l < 1; расходится, если l > 1; признак не дает ответа, если l = 0.
Признак Коши
Если существует , то : сходится, если l < 1; расходится, если l > 1; признак не дает ответа, если l = 0.
Интегральный признак сходимости
1) u_n > 0; 2) u_n ≥ u_n+1; 3) f(x) — непрерывная невозрастающая функция, f(n) = u_n.
Либо и , и сходятся,
либо и , и расходятся.

Знакопеременные ряды

Абсолютная сходимость
Ряд сходится, откуда следует, что ряд сходится.
Условная сходимость
Ряд расходится, но ряд сходится.
Знакочередующиеся ряды
Ряды вида или где
u_n > 0.
Признак Лейбница (сходимости знакочередующегося ряда)
Если 1) u₁ > u₂ > u₃ > …, 2) то 1) ряд сходится; 2) его сумма S > 0, и 3) S < u₁.

Примеры числовых рядов

: сходится, если a > 1; расходится, если a ≤ 1.
: сходится, если a < 1; расходится, если a ≥ 1.
: сходится.
: сходятся, |q| < 1; расходятся, |q| ≥ 1.
: сходится;
: сходится, если a > 1; расходится, если a ≤ 1.
: сходится условно.
: сходится абсолютно.
: сходится абсолютно.

Функциональные ряды

Функциональный ряд – сумма вида

При из функционального ряда получается числовой ряд

Если для числовой ряд сходится, то точка называется точкой сходимости функционального ряда. Если в каждой точке числовые ряды сходятся, то функциональный ряд называется сходящимся в области . Совокупность всех точек сходимости образует область сходимости функционального ряда.

– частичные суммы ряда. Функциональный ряд сходится к функции f(x), если

Равномерная сходимость

Функциональный ряд, сходящийся для всех из области сходимости, называется равномерно сходящимся в этой области, если ∀ε > 0 существует не зависящий от x номер

N(ε), такой, что при n > N(ε) выполняется неравенство R_n(x) < ε для всех x из области сходимости, где — остаток ряда.

Геометрический смысл равномерной сходимости:

если окружить график функции y = f(x) «ε-полоской», определяемой соотношением f(x)−ε > y > f(x)+ε, то графики всех частичных сумм S_k(x), начиная с достаточно большого k, ∀x ∈ [a, b] целиком лежат в этой «ε-полоске», окружающей график предельной функции y = f(x).

— называется мажорируемым в области , если существует такой сходящийся числовой ряд u_n > 0, что для ∀x ∈ D f_n(x) ≤ u_n, n = 1, 2, …. Ряд называется мажорантой ряда

Признак Вейерштрасса (признак равномерной сходимости функционального ряда): функциональный ряд сходится равномерно в области сходимости, если он является мажорируемым в этой области.

Степенные ряды:
— степенной ряд по степеням
При – степенной ряд по степеням x.

Область сходимости степенного ряда:
Радиус сходимости, интервал сходимости R, x ∈ (-R, R):
или
При |x| < R ряд сходится, при |x| > R – расходится;
в точках x = ±R – дополнительное исследование.

На интервале сходимости ряд сходится абсолютно;
на любом отрезке из интервала сходимости он сходится равномерно.

Свойства степенных рядов

Степенной ряд сходится равномерно на [−R′, R′]
∀R′ < R, его можно почленно дифференцировать и интегрировать в интервале сходимости.
Ряды, полученные почленным дифференцированием и интегрированием, имеют тот же интервал сходимости.

Разложение элементарных функций в степенные ряды

, x ∈ (−∞; ∞).
,
x ∈ (−∞; ∞).
, x ∈ (−∞; ∞).
, x ∈ (−∞; ∞).
, x ∈ (−∞; ∞).
, x ∈ (−1; 1].
, x ∈ [−1; 1).
,
x ∈ (−1; 1).
, x ∈ [−1; 1].
, x ∈ [−1; 1].
, x ∈ (−1; 1).
, x ∈ (−1; 1).
, x ∈ (−1; 1).
, x ∈ (−1; 1).
, x ∈ (−1; 1].

Тригонометрические ряды

Ряд Фурье для периодической функции с периодом 2π

Ряд Фурье функции f(x):
Коэффициенты Фурье:

Разложение в ряд Фурье четных и нечетных функций с периодом 2π

f(-x) = f(x)
ряд Фурье содержит только косинусы кратных дуг:
f(-x) = -f(x)
ряд Фурье содержит только синусы кратных дуг:

Ряд Фурье для функции с произвольным периодом Т=2l, f(x+2l) = f(x):

где

Разложение в ряд Фурье непериодических функций, заданных на отрезке

или на отрезке

f₁(x)=f(-x), x ∈ [-l; 0] (четное продолжение)

где x ∈ [0; l] n = 0, 1, 2,…
f₁(x) = —f(−x), x ∈ [-l; 0]
(нечетное продолжение)

где x ∈ [0; l] n = 1, 2,…
На всю действительную ось ϕ(x) продолжается периодически с периодом 2l, ϕ(x) = ϕ(x + 2l). Функция ϕ(x) разлагается в ряд Фурье, причем в точках x = ±l выполняется условие: где то есть,
– левый предел f(x) в точке x = l,
– правый предел f(x) в точке x = l.

Какое будет расширение (2н)! , 2н! , (2н)!! и 2н!! ? Пожалуйста, поймите ответ подробно.

Выберите область веб-сайта для поиска

MathAllУчебные пособияПомощь по домашним заданиямПланы уроков

Искать на этом сайте

Цитата страницы Начать эссе значок-вопрос Задайте вопрос

Начать бесплатную пробную версию

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться

Укажите эту страницу следующим образом:

«Каким будет разложение (2n)!, 2n!, (2n)!! и 2n!!? Пожалуйста, поймите ответ подробно.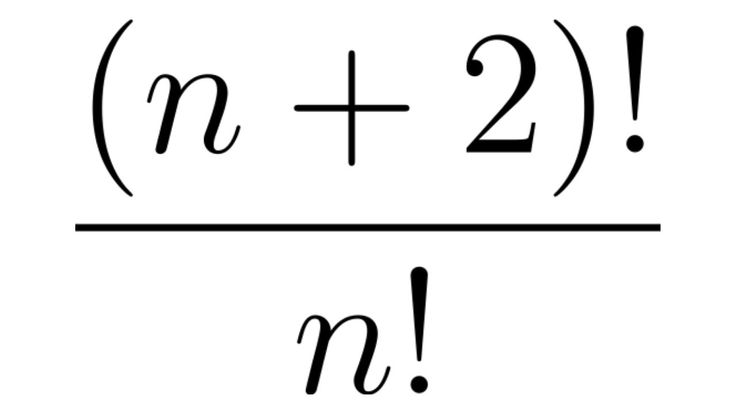 » eNotes Editorial , 8 июля 2015 г., https://www.enotes.com/homework-help/what-would-expansion-2n-2n-2n-2n-kindly-comprehend-482141. По состоянию на 20 апреля 2023 г.

Ответы экспертов

Здравствуйте!

Факториал натурального m определяется как произведение всех натуральных чисел, меньших или равных m, т. е. m! = 1*2*…*(м-1)*м. Тоже 0! определяется как 1.

Следовательно, (2n)! = 1*2*…*(2n-1)*(2n). Например, (2*0)! = 1, (2*1)! = 1*2 = 2, (2*2)! = 1*2*3*4 = 24. (2*3)! = 1*2*3*4*5*6 = 720.

2н! что я понимаю как 2*(n!) равно 2*1*2*…*(n-1)*n и почти всегда меньше (2n)!:
2*0! = 2, 2*1! = 2, 2*2! = 4, 2*3! = 12.

Теперь для (2n)!!. По определению, м!! это произведение всех натуральных чисел с той же четностью, что и m меньше или равно m:

m!! = м*(м-2)*(м-4)*…*(2 или 1).
и 0!! = 1

Для четного m существует m/2 множителя, и последний множитель равен 2. Для нечетного m существует (m+1)/2 множителя, а последний множитель равен 1.

Итак, (2n)!! = 2*4*…*(2n-2)*(2n).
0!! = 1, 2!! = 2, 4!! = 2*4 = 8, 6!! = 2*4*6 = 48, 8!! = 2*4*6*8 = 384.

2*n!! другое дело: 2*n*(n-2)*…*(2 или 1).
2*0!! = 2, 2*1!! = 2, 2*2!! = 4, 2*3!! = 6, 2*4!! = 16,

Надеюсь, это ответ на ваш вопрос.

См. eNotes без рекламы

Начните 48-часовую бесплатную пробную версию , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.

Получите 48 часов бесплатного доступа

Уже зарегистрированы? Войдите здесь.

Дополнительное чтение

https://en.wikipedia.org/wiki/Двойной_факториал
https://en.wikipedia.org/wiki/Факториал

Утверждено редакцией eNotes

Задайте вопрос

Упростите следующее факториальное выражение: $\\dfrac{{(2n + 2)!}}{{(2n)!}}$

Дата последнего обновления: 14 апреля 2023 г.

•

Всего просмотров: 250,2 тыс.

•

Просмотров сегодня: 5,20 тыс.

Ответить

Подтверждено

250,2 тыс.+ просмотров

Подсказка: Нам нужно упростить факториальное выражение, данное в дробной форме. Мы используем определение факториала $n$, которое дается формулой
$n! = n \times (n — 1) \times (n — 2) \times …… \times 3 \times 2 \times 1$ и используйте его для решения задачи.

Полное решение шаг за шагом:
Сначала запишем выражение, данное в вопросе
$\dfrac{{(2n + 2)!}}{{(2n)!}}\,{\text{ — — — — — — — — — (1)}}$
Теперь воспользуемся определением факториала, чтобы увидеть, как мы можем разложить факториалы как числителя, так и знаменателя, т. е.
$n! = n \times (n — 1) \times (n — 2) \times …… \times 3 \times 2 \times 1$
Мы видим, что факториал числа есть произведение всех целых чисел, начиная с 1 к этому числу, чтобы мы могли расширить заданные значения в нашем вопросе, например,
$
(2n + 2)! = (2n + 2) \times (2n + 1) \times (2n) \times ……. \times 2 \times 1 \\
{\text{и}}\
2н! = 2n \times (2n — 1) \times (2n — 2) \times …… \times 2 \times 1 \\
$
Теперь подставим эти значения в данное уравнение (1), чтобы увидеть, как мы можем продолжить
$\dfrac{{(2n + 2)!}}{{(2n)!}} = \dfrac{{(2n + 2) \times (2n + 1) \times (2n) \times . …… \times 2 \times 1}}{{2n \times (2n — 1) \times …… \times 2 \times 1}}$
Теперь мы видим, что оба в знаменателях у нас есть разложение $2n!$, поэтому мы записываем его как
\[\dfrac{{(2n + 2)!}}{{(2n)!}} = \dfrac{{(2n + 2) \times ( 2n + 1) \times (2n) \times ……. \times 2 \times 1}}{{2n \times (2n — 1) \times …… \times 2 \times 1 }}\left\{ {\ потому что 2n! = 2n \times (2n — 1) \times . ….. \times 2 \times 1} \right\}\]
Теперь мы можем отменить подобные условия
$
\dfrac{{(2n + 2)!}}{{(2n)!}} = \dfrac{{(2n + 2) \times (2n + 1) \ раз 2n!}}{{2n!}} \\
\Rightarrow \dfrac{{(2n + 2)!}}{{(2n)!}} = (2n + 2) \times (2n + 1) \ \
$
Итак, мы упростили дробь в этой форме.
Дополнительная информация: мы можем проверить наш ответ, поместив значение $n$ в выражение и решив его, затем мы проверяем, совпадает ли оно, когда в результирующем выражении сделана замена, т.е.
Пусть $n = 2$, поэтому мы есть
\[
\dfrac{{(2n + 2)!}}{{2n!}} = \dfrac{{(2 \times 2 + 2)!}}{{(2 \times 2)!}} \ \
= \dfrac{{6!}}{{4!}} \\
= \dfrac{{6 \times 5 \times 4!}}{{4!}} \\
= 30 \\
\ ]
А теперь поместив это же значение в RHS
$
(2n + 2)(2n + 1) = (2 \times 2 + 2) \times (2 \times 2 + 1) \\
= 6 \times 5 \
= 30 \
$
Итак, мы получили тот же ответ, подставив значение ‘n’.

Примечание: Знание свойств факториалов помогает нам в этой задаче.

2N факториал разложение: Как разложить факториал? (2n)!! — Спрашивалка

Как решить Факториал числа. Таблица, Свойства, Примеры

Факториал: определение

Формулы и свойства факториала

Примеры решений

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

Формулы и уравнения рядов

Числовые ряды

Функциональные ряды

Равномерная сходимость

Тригонометрические ряды

Какое будет расширение (2н)! , 2н! , (2н)!! и 2н!! ? Пожалуйста, поймите ответ подробно.

Укажите эту страницу следующим образом:

Ответы экспертов

См. eNotes без рекламы

Похожие вопросы

Упростите следующее факториальное выражение: $\\dfrac{{(2n + 2)!}}{{(2n)!}}$

Добавить комментарий Отменить ответ