Функция y = tg x, её график и свойства. Тригонометрия 8-11 класс смотреть онлайн видео от Математика от Баканчиковой в хорошем качестве.
12+
5 месяцев назад
Математика от Баканчиковой270 подписчиков
Тригонометрия 8-11 класс. Как построить график функции y = tg x? Что такое тангенсоида? Какие свойства есть у функции y = tg x? Сегодня мы ответим на эти вопросы. Если Вы не видели наши предыдущие уроки по теме: «Функция y=sin x, её график и свойства» и серию уроков по теме «Свойства функции», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Мы покажем, как строить график функции y = tg x. Затем по графику функции y = tg x мы подробно разберём почти все свойства этой функции: область определения, область значений, непрерывность, монотонность, наибольшее и наименьшее значения, ограниченность, выпуклость, нули функции, чётность, нечётность, периодичность, промежутки знакопостоянства. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:13 Совет Любовь Николаевны.
01:16 График функции y = tg x.
06:08 Свойства функции y = tg x.
06:12 Область определения.
07:20 Область значений.
07:28 Непрерывность.
08:20 Монотонность.
08:41 Наибольшее и наименьшее значения.
08:49 Ограниченность.
08:59 Выпуклость.
09:54 Нули функции.
10:16 Чётность, нечётность.
10:31 Периодичность.
10:43 Промежутки знакопостоянства.
11:57 На следующем уроке …
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Функция y = sin x, её график и свойства. Тригонометрия 8-11 класс. https://rutube.ru/video/a0f98530ee52e1303236e975c6a826f8/
Функция y = cos x, её график и свойства. Тригонометрия 8-11 класс. https://rutube.ru/video/79a7a2ce60eefcab7aea2ee136a00bb2/
Функция y = sin x, график функции и способы задания функции. Тригонометрия 8-11 класс. https://rutube.ru/video/f067b3cda83df006306963e40f30b5ab/
Определение синуса, косинуса, тангенса и котангенса на единичной окружности.
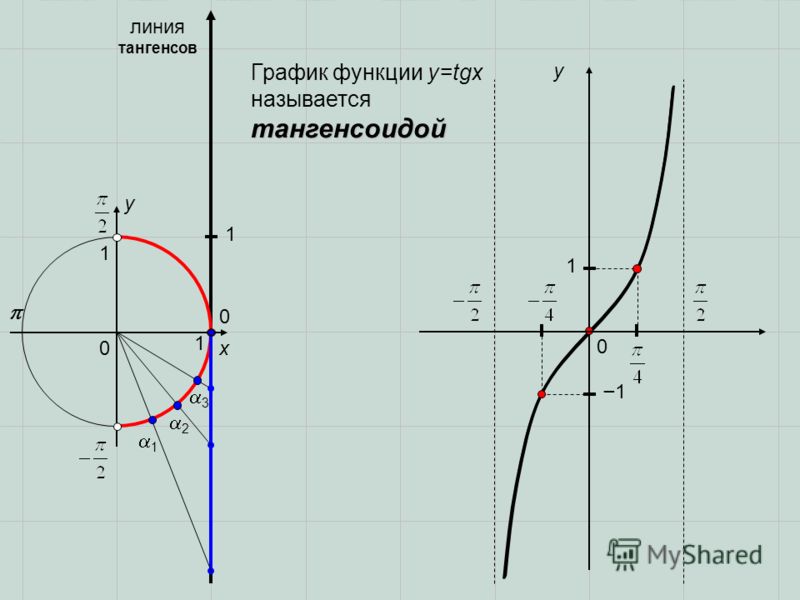
Тигонометрические функции и их графики
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас.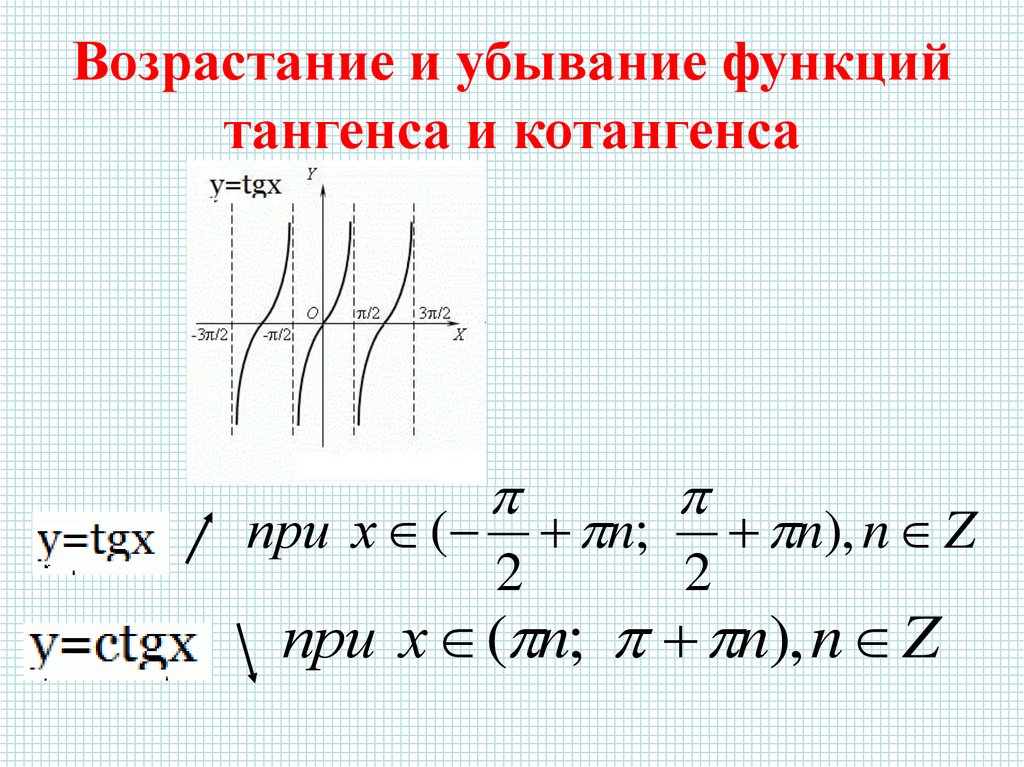
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Тригонометрические функции
и их графикиПостроение графика функции y = sinx с
применением тригонометрического круга
p — шесть клеток
О
2p
с
5p 3
ь
6
p
II
p
2
I
и
н
III
у
3
1
С
y
p
p
6
0
IY
-p
-5p
с -1
6
6 -2p
p
о-p
3
3 2
в
1
0
-p
2
-p
-5p -2p
3
6
III
p
-p
3
-p
6
IY
0
-1
p x
2
p
p
6
3
I
2p
3
5p
6
II
3.
Функция y=sin x, график и свойства.1)D(y)=2)E(y)=
3)
4)sin(-x)=-sin x
5)Возрастает на
Убывает на
6)Периодичная
4. Знаки синуса
1. Синус равен нулю при,
где n — любое целое число;
2. Синус положителен при
где n — любое целое число;
3. Синус отрицателен
при
, где n — любое
целое число.
,
5. Синусоида
у1
π
-π/2
-π
0
-1
π/2
2π
3π/2
3π
5π/2
х
6. Функция y = cos x, её свойства и график.
1)D(y)=2)E(y)=
3)
4)cos(-x)=cosx
5)Возрастает на
Убывает на
6)Периодична
7. Знаки косинуса
1.косинус равен нулю при2.косинус положителен при
3. косинус отрицателен при
где n — любое целое число.
8. y= cos x
Примерыy= cos x
у
1
π
-π/2
-π
0
-1
π/2
2π
3π/2
3π
5π/2
х
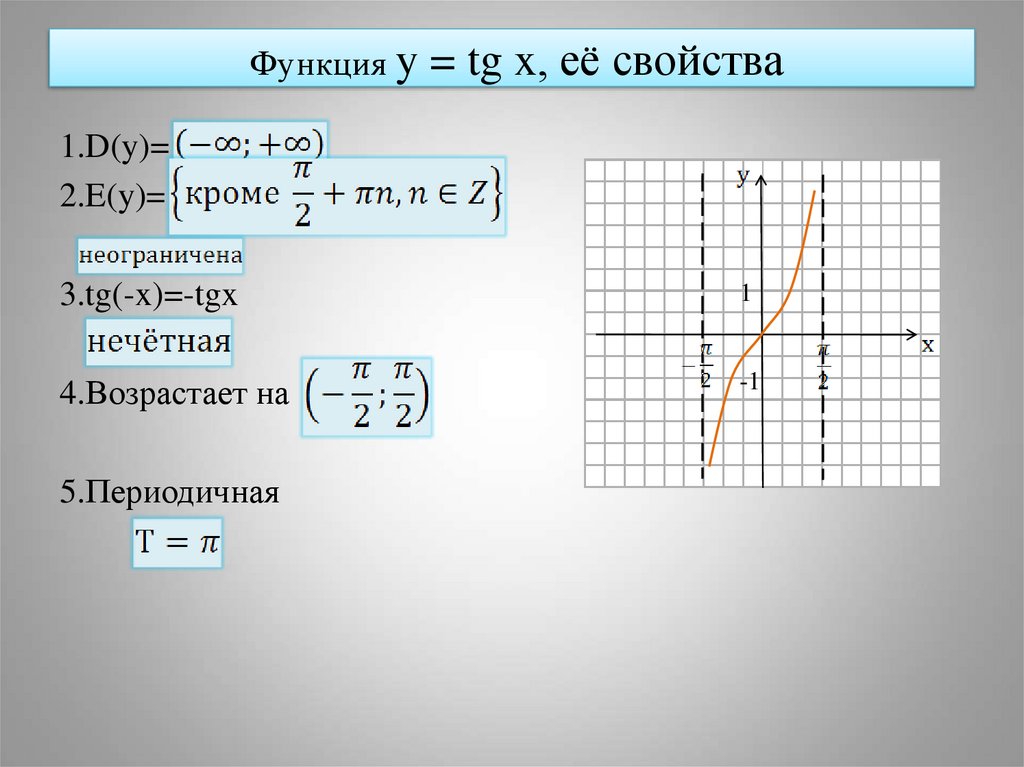
9. Функция y = tg x, её свойства и график
1.D(y)=2.E(y)=
1
3.
tg(-x)=-tgx-1
4.Возрастает на
5.Периодичная
10. Знаки тангенса
1.равен нулю, когда синус равен нулю,то есть при
, где n — любое целое число.
2.положителен, когда синус и косинус
имеют одинаковые знаки.
Это бывает только в первой и в
третьей четвертях, то есть при
где а- любое целое число.
3.отрицателен, когда синус и косинус имеют
разные знаки.
Это бывает только во второй и в
четвертой четвертях, то есть при
где а — любое целое число.
11. Тангенсоида
1-1
12. Функция y = сtg x, её свойства и график
Функция y1.D(y)=
2.E(y)=
3.ctg(-x)=-ctgx
4.Убывает на
5.Периодичная
= сtg x, её свойства и график
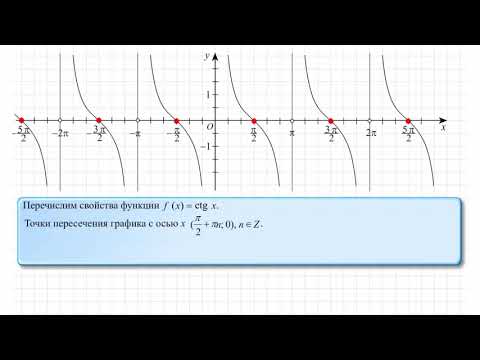
13. Знаки котангенса
1.равен нулю, когда косинус равен нулю,то есть при
2.положителен, когда синус и косинус имеют
одинаковые знаки. Это бывает только в первой и
в третьей четвертях, то есть при
3.отрицателен, когда синус и косинус имеют
разные знаки.
Это бывает только во второй и вчетвертой четвертях, то есть при
14. Домашнее задание
Колмогоров А.Н. Алгебра и начала анализа,стр.14 §1 п.2, стр. 20 № 33(а,б).
English Русский Правила
Функция тангенса и функция арктангенса
Мы знаем, что функция тангенса y = tan x используется для нахождения высот или расстояний, таких как высота здания, горы или флагштока.
Функция тангенса и функция арктангенса
Мы знаем, что функция тангенса y = tan x равна используется для нахождения высот или расстояний, таких как высота здания, горы, или флагшток. Домен y = tan x = sinx/cosx не включает значения x , которые составляют знаменатель нуль. Итак касательная функция не определено при x = …, -3π/2, -π/2, π/2, 3π/2, ….
Таким образом, область определения функции тангенса y = tan x равна , а диапазон равен (−∞, ∞) . Касательная функция y =
tan x имеет период π.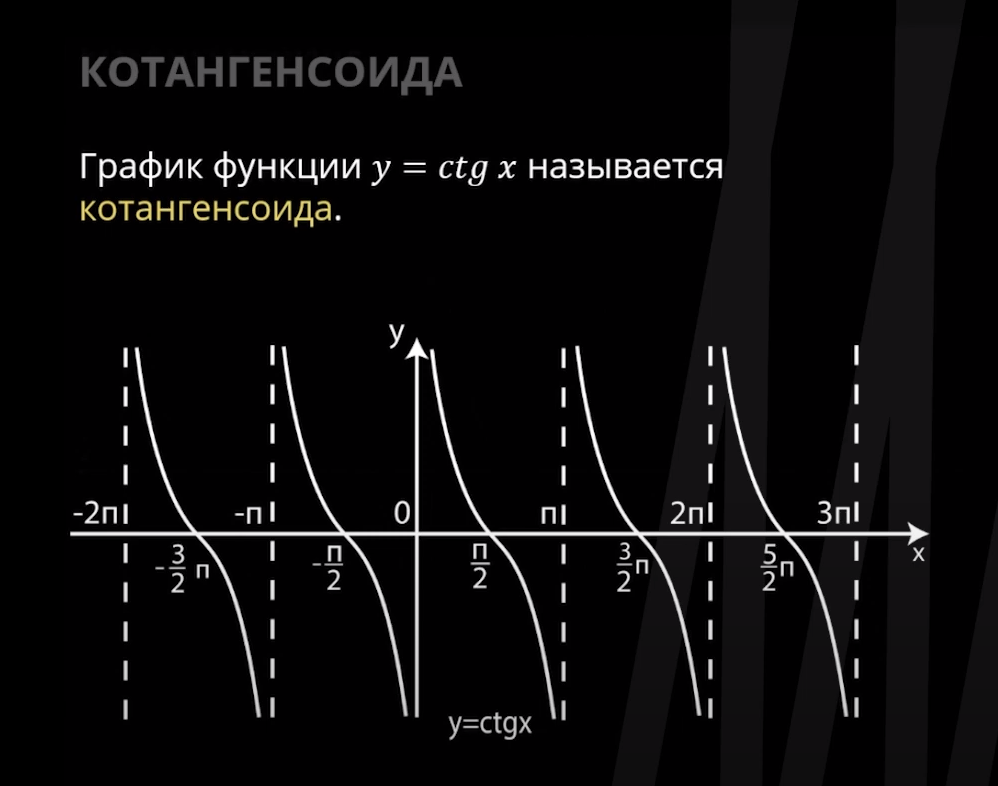
1. График функции тангенса
График функции тангенса полезен для нахождения значений функционировать в течение повторяющегося периода интервалов. Тангенс функция нечетная и следовательно, график y = tan x симметричен относительно начала координат. Поскольку период касательной функции равен π, нам нужно определить граф на некотором интервале длины π . Рассмотрим интервал (-π/2, π/2) и постройте следующую таблицу, чтобы нарисовать график y = tan x, x ∈ (-π/2, π/2).
Теперь нанесите точки и соедините их плавной кривой для частичный график y = tan x , где – π/2 ≤ x ≤ π/2. Если x близко к π/2, но остается меньше π/2, sin x будет близок к 1, а cos x будет положительным и близким к 0. Таким образом, когда x приближается к π/2, Отношение sin x/ cos x положительно и велико, поэтому приближается к ∞.
Следовательно, линия x = π/2 является вертикальной
асимптота к графику.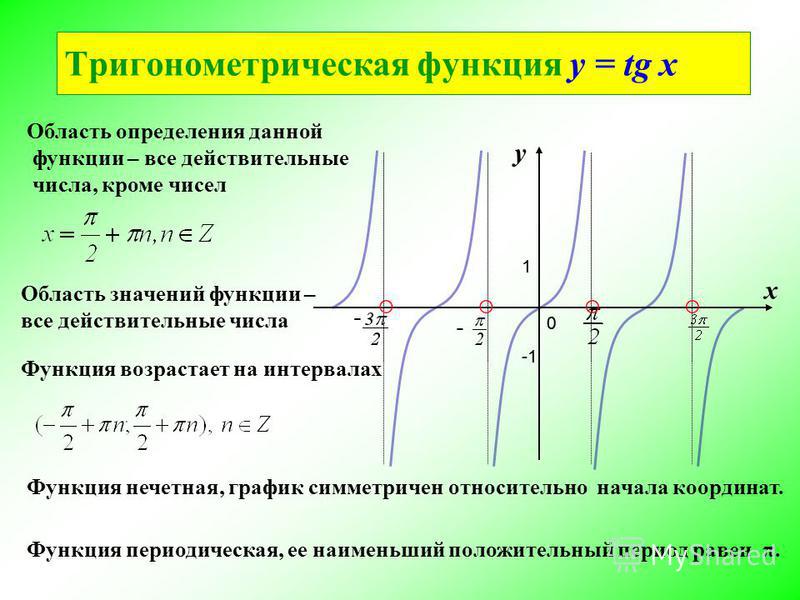
Точно так же, если x приближается к – π /2,
отношение sin x/ cos x отрицательно и велико по величине и
таким образом, приближаясь к -∞. Итак, прямая x = — π/2 есть
также вертикальная асимптота к графику. Отсюда получаем ветвь графика у = тангенс x для -π/2 < x < -π/2, как показано на рис. 4.15.
интервал (-π/2, π/2) называется главной областью из y = tan x .
Поскольку функция тангенса определена для всех действительных чисел кроме при , и возрастает , у нас есть вертикальные асимптоты .
Как ветви y = tan x симметричны с относительно x = nπ , n ∈ Z , весь граф y = tan x показано на рис. 4.16.
Примечание
Из графика видно, что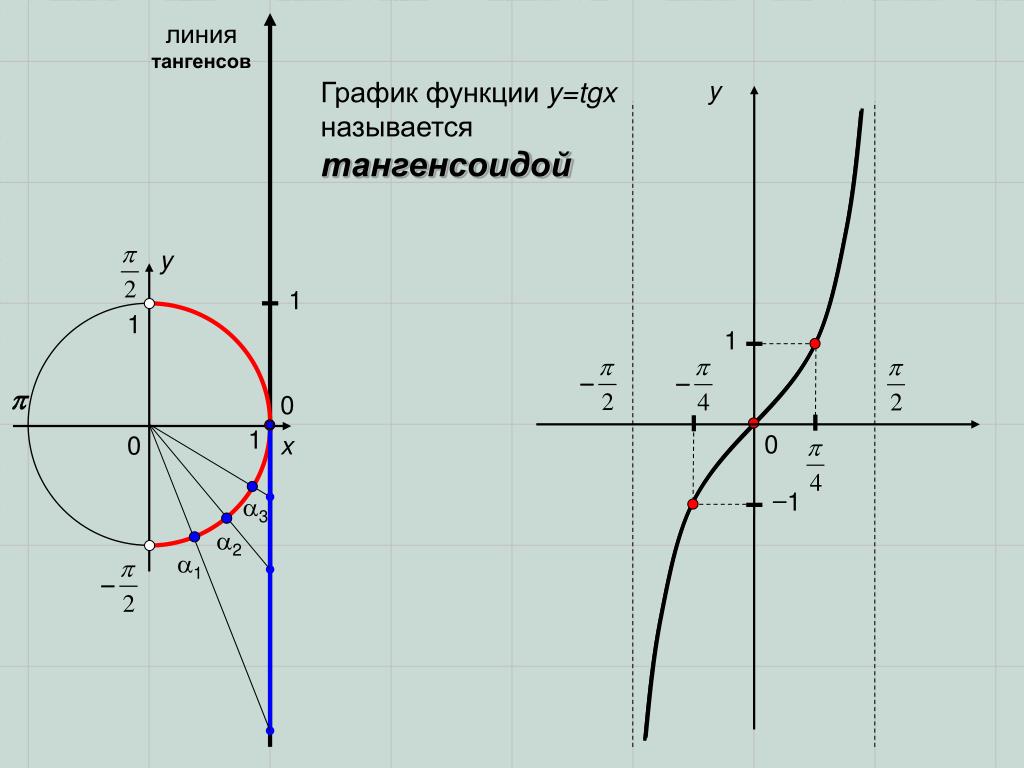 
2. Свойства функции тангенса
следующие свойства касательной функции.
(i) График не является непрерывным и имеет точки разрыва на x = (2 n +1) π/2 , n ∈ Z
(ii) Частичный граф симметричен относительно начала координат для – π/2 < x < π/2 .
(iii) Имеет бесконечно много вертикальных асимптот x = (2 n +1) π /2 , n ∈ Z
(iv) Функция тангенса не имеет ни максимума, ни минимума.
Примечание
(i) График y = a tan bx проходит через один полный цикл для
(ii) Для y = a tan bx , асимптоты линии
(iii) Поскольку функция тангенса не имеет ни максимума, ни минимума значения термин амплитуда для загара x не может быть определен.
3.
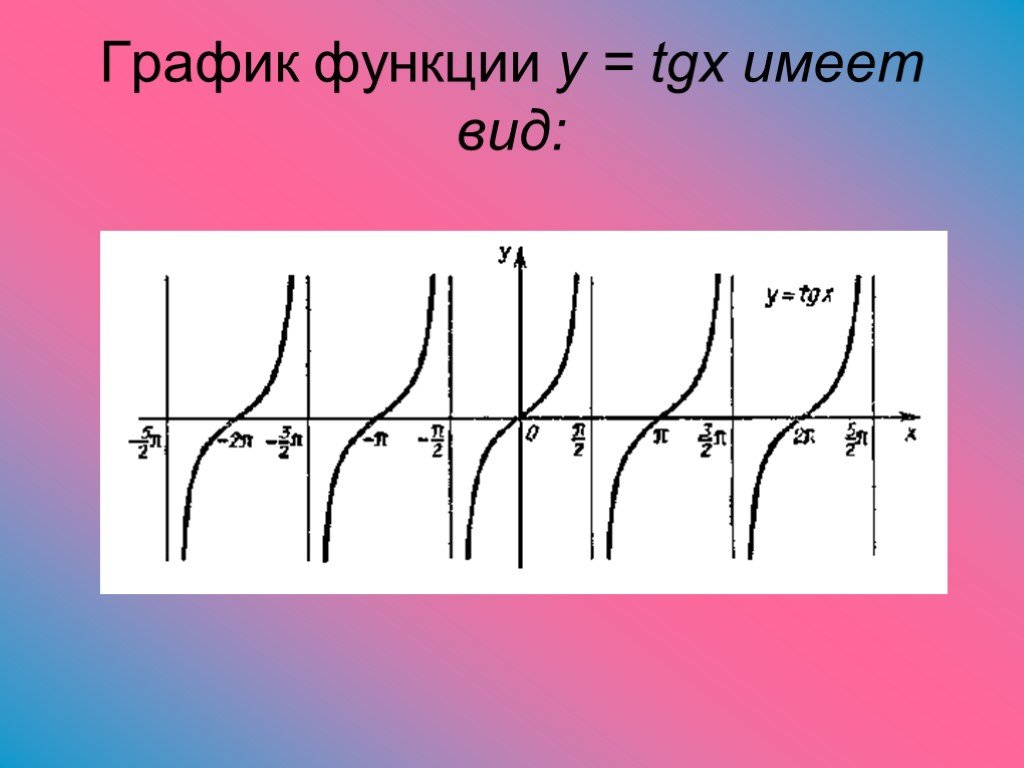Функция арктангенса и ее свойства Функция тангенса не является однозначной во всей области → R является биективным функция. Теперь мы определяем функцию арктангенса с R в качестве своего домена и (-π/2, π/2), как его диапазон.
Определение 4.5
Для любого действительного числа x определите tan -1 x как уникальный номер y в (-π/2, π/2), так что tan y = x .
Другими словами, функция арктангенса tan -1 : (∞, ∞ ) → (-π/2, π/2), определяется тангенсом -1 ( x ) = y тогда и только тогда, когда tan y = x и y ∈ (-π/2, π/2).
Из определения y = tan −1 x мы наблюдаем следующее:
(i) y = tan -1 x тогда и только тогда, когда x = tan y для x ∈ R и -π/2 < y <
π/2.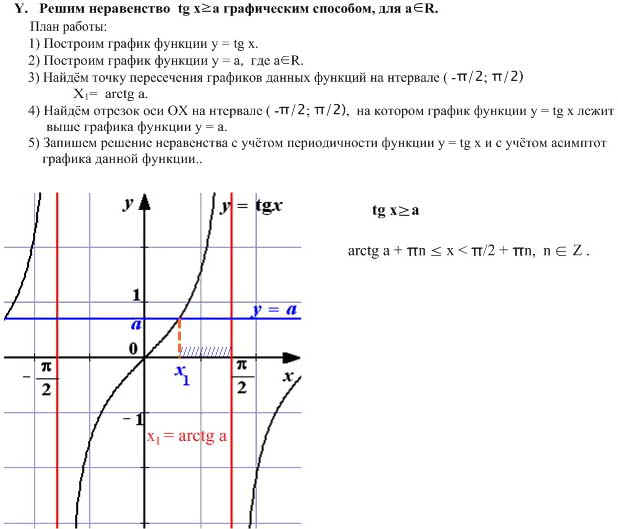
(ii) рыжевато-коричневый (рыжевато-коричневый -1 x ) = x для любого реального число x и y = тангенс -1 x является странная функция.
(iii) tan -1 (tan x ) = x тогда и только тогда, когда – π/2 < x < π/2 . Обратите внимание, что тангенс -1 (тангенс π ) = 0, а не π .
Примечание
(i) Всякий раз, когда мы говорим о функции арктангенса, мы имеем,
(ii) Ограниченный домен (- π/2 , π/2 ) позвонил директору домен из функция тангенса и значения y = tan -1 x , x ∈ R , известны как главных значений функции y = загар -1 x .
4. График функции арктангенса
y = tan -1 x is
функция со всей вещественной линией (-∞, ∞) в качестве области определения и диапазоном значений (-π/2, π/2).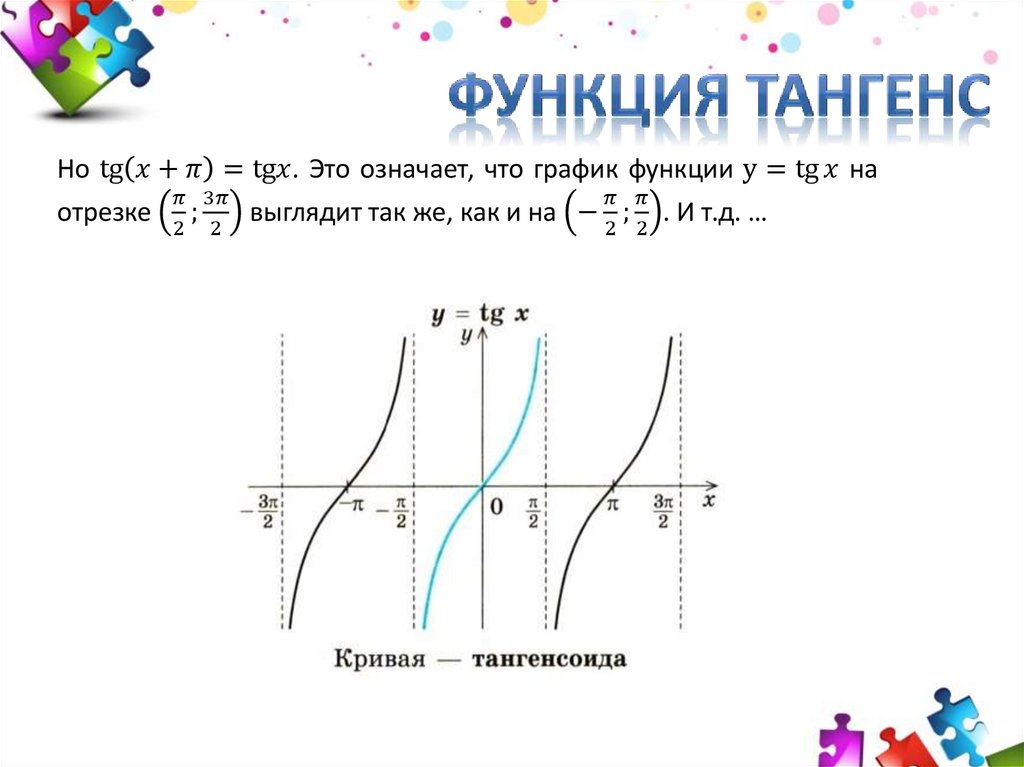
Примечание
что касательная функция не определена при – π/2 и при π/2. Итак, график y
= tan -1 x лежит строго между
две линии y = -π/2 и y = π/2 и никогда не касаются этих двух линий.
Другими словами, две строки
y=-π/2 и y = π/2 являются горизонтальными асимптотами к y = tan -1 х .
На рис. 4.17 и рис. 4.18 показаны графики y = tan x в области (- π/2 , π/2 ) и y = tan -1 x в области (-∞, ∞) соответственно.
Примечание
(i) Функция арктангенса строго возрастает и непрерывна в области (-∞, ∞) .
(ii) График y = tan -1 x проходит через источник.
(iii) Граф симметричен относительно начала координат и, следовательно, y = тангенс -1 x — нечетная функция.
Пример 4.8
Найдите основное значение TAN -1 (√3)
Решение
Let Tan- 1 (√3) = y.
Тогда тангенс у = √3.
Таким образом, y = π/3 . Поскольку π/3 ∈ (−π/2, π/2).
Таким образом, основное значение tan -1 (√3) равно π/3.
Пример 4.9Находка (I) TAN -1 (-ain (tan -1 (2019))
Решение
(iii) Так как tan (tan -1 x ) = x, x ∈ R , имеем tan (tan -1 (2019)) = 2019.
Пример 4.10
Найдите значение tan -1 (-1) + cos -1 (1/2) + sin -1 (-1/2).
РешениеПусть тангенс -1 (-1) = y . Тогда тангенс y = -1 = — тангенс π/4 = тангенс ( — π/4). Пример 4.11
0006
Если x = 0, то обе стороны равны 0. ………..(1)
Предположим, что 0 < x < 1.
Пусть θ = sin -1 x .
Тогда 0 < θ < π/2 . Теперь sin θ = x/1 дает tanθ = .
Следовательно, tan (sin -1 x ) = … (2)
Предположим, что -1 < x < 0. Тогда θ = sin – π10 9029 x 9000 /2 < θ < 0. Теперь sinθ = x/1 дает tanθ =
В этом случае также tan (sin -1 x ) = … (3)
Уравнения (1), (2) и (3) устанавливают, что tan (sin -1 x ) = -1 < x < 1.
Теги: Определение, График, Свойства, Решенные примеры задач, 12th Mathematics: UNIT 4: Обратные тригонометрические функции
Учебный материал, Лекционные заметки, Задание, Справочник, Объяснение описания Wiki, краткое описание
12th Mathematics : ГЛАВА 4 : Обратные тригонометрические функции : Функция тангенса и функция арктангенса | Определение, график, свойства, решенные примеры задач
График функций синуса, косинуса и тангенса
| 6,3 | График функций синуса, косинуса и тангенса |
| |||||||||||
| |||||||||||
| |||||||||||
|
| 9{\ circ} \ text { atau} 2 \ pi \) | ||
| (с) | \(x\)-перехватов: \(-2\пи, \ -\пи, \ 0, \ \пи, \ 2\пи \) | |
| (г) | \(y\)-перехваты: \(0\) | |
| График \(y = \text{tan } x\) для \(-2\pi \leqslant x \leqslant 2\pi\) 9{\circ}\text{ или }\pi \) | ||
| (с) | \(х\)-асимптоты: \(-\dfrac{3}{2}\pi, \ -\dfrac{1}{2}\pi, \ \dfrac{1}{2}\pi, \ \dfrac{3}{2}\ пи\) | |
| (г) | \(х\)-перехватов: \(-2\пи, \ -\пи, \ 0, \ \пи, \ 2\пи \) | |
| (д) | \(y\)-перехваты: \(0\) | |
Значения \(a\), \(b\) и \(c\) в функции \(y = a \text{ sin } bx + c\) влияют на амплитуду, период и положение график
Эффекты изменения значений \(a\), \(b\) и \(c\) на графике можно резюмировать следующим образом:
| Изменение в | Эффекты | ||||||||||||||||||
|
| ||||||||||||||||||
| |||||||||||||||||||
|
|
Пример:
| ||||||||
