3 из 5 сколько вариантов: Система 3 из 5 в ставках на спорт — как работает стратегия?

Содержание

13. Перестановки с повторениями

При перестановке букв в слове «толпа» получается P5 = 5! = 120 «слов». Если же переставлять буквы в слове «топот», то получится меньше различных «слов», потому что ни перестановка двух букв «т», ни перестановка двух букв «о» не изменяют «слова»; всего перестановок в данном случае будет . Мы имеем здесь дело с перестановками с повторениями.

Общую задачу сформулируем следующим образом.

Имеется n элементов k различных типов: n1 элементов первого типа, n2 элементов второго типа, …, nk элементов k-го типа, . Сколько можно составить различных перестановок из этих элементов?

Число перестановок c повторениями обозначают . Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют.

Точно также ничего не меняют n2! перестановок элементов во второй группе и т. д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом способами так, что она остаётся неизменной.

Число различных перестановок с повторениями, которые можно составить из данных элементов, равно

, (11.1) где .

Замечание. Отметим, что формула числа сочетаний из n элементов по k элементов совпадает с формулой для числа перестановок с повторениями из k элементов одного типа и n–k элементов другого типа:

Пример 11.1. Сколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?

Решение. Речь идет об отыскании числа перестановок с повторениями, которые можно сделать из k1=4 элементов первого типа (зеленых бус), k2=5 элементов второго типа (синих бус) и k3=6 элементов третьего типа (красных бус). По формуле (6) получаем

Пример 11.2. У мамы было 2 одинаковых яблока, 3 одинаковых груши и 4 одинаковых апельсина.

Каждый день она давала ребенку по одному фрукту. Сколькими способами она могла это сделать?

Решение. Данная задача есть задача на отыскание числа перестановок с повторениями:

Пример 11.3. Сколько различных браслетов можно сделать из пять одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?

Решение. Камни можно переставлять P(5, 6, 7) способами. При циклических перестановках и при зеркальном отражении браслет остается неизменным. В результате получаем

Пример 11.4. Сколько способами можно переставлять буквы слова «огород» так, чтобы: а) три буквы «о» не стояли рядом? б) если запрещается, чтобы две буквы «о» стояли рядом?

Решение. а) Буквы данного слова можно переставлять P(3,1,1,1) способами. Если три буквы «о» стоят рядом, то их можно считать за одну букву. Тогда буквы можно переставлять 4! Способами. Вычитая этот результат из предыдущего, получим

Б) Сначала расставляем согласные (3! способов).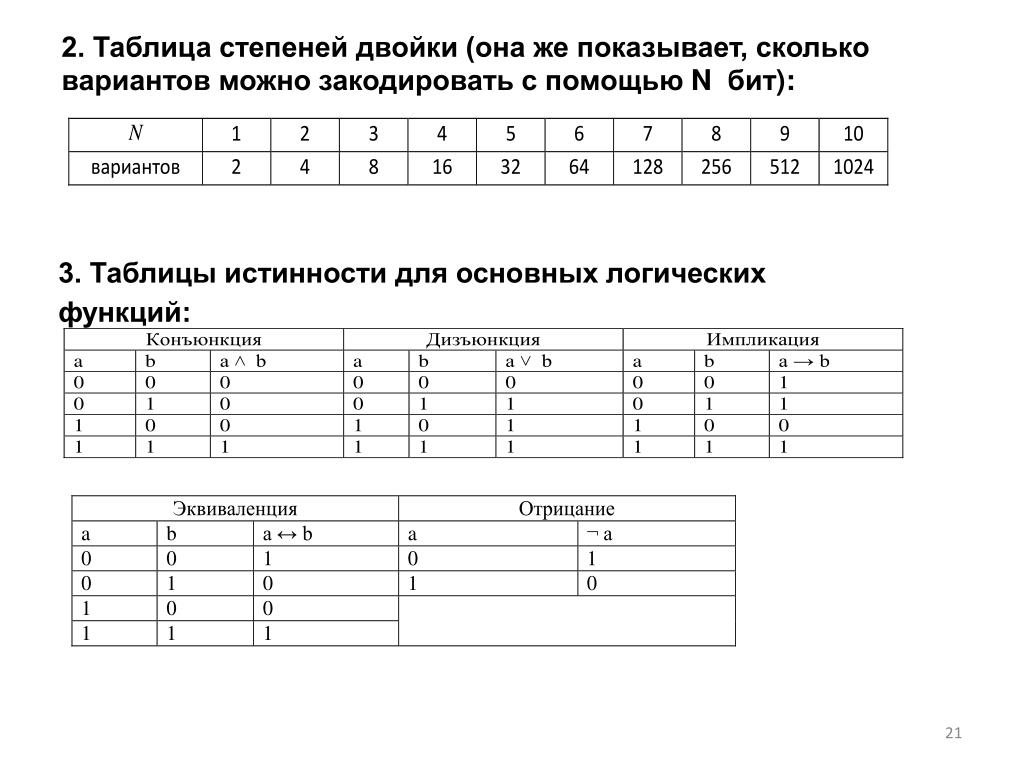 Для трёх букв «о» остаётся 4 места, и их можно расставить способами. Всего получаем способа.

Упражнения

11.1. Сколькими способами можно расположить в ряд две зелёные и четыре красные лампочки?

Ответ: .

11.2. Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами можно это сделать?

Ответ: .

11.3. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по два три, четыре книги в каждой бандероли?

Ответ: .

11.4. Группу командировочных из восьми человек требуется расселить в три комнаты, из которых две трёхместные и одна двухместная. Сколько вариантов расселения возможно?

Ответ: .

11.5. Сколько различных слов можно получить, переставляя буквы в следующих исходных словах: а) академия, б) электротехника, в) молокопродукт?

Ответ: .

11.6. Сколькими способами можно разделить 12 предметов между тремя студентами, чтобы каждому досталось ровно по четыре предмета?

Ответ: .

11.7. Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?

Ответ: .

11.8. Сколькими способами можно переставить буквы слова «обороноспособность» так, чтобы две буквы «о» не шли подряд?

Ответ: .

11.9. Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не стояли рядом?

Ответ: Гласные можно переставлять P(2,1,1)=12 способами, Аналогично, P(2,1,1)=12 способами можно расставить согласные буквы. Если согласные уже расставлены, то для гласных останется 5 мест. Поэтому места для них можно выбрать способами. Всего способов.

< Предыдущая		Следующая >

Информатика — Перемножение количеств вариантов

1. Количество слов данной длины в данном алфавите

Задача 1.1. Каждая задача в контрольной по математике имеет код, состоящий из двух символов. Первый символ – буква A, B, C или D (код группы задач), второй символ – цифра от 1 до 3 (номер задачи в группе). Сколько есть возможных кодов задач?

Решение. Достаточно подсчитать количество клеток в таблице на рис. 1. Количество решений N = 4*3 = 12.

	1	2	3
A	A1	A2	A3
B	B1	B2	B3
C	C1	C2	C3
D	D1	D2	D3

. Рис.1.

Упражнение 1.1. Реши такую же задачу, если в коде

1) 5 букв и 9 цифр;

2) 9 букв и 5 цифр;

3) 5 букв и 5 цифр;

4) 3 буквы и 7 цифр.

Чтобы проверить себя, нарисуй таблицы.

Ответы: 21, 25, 45.

Примечание. Ответы даны не в порядке номеров задач, а в порядке возрастания. Ответов три, потому, что в двух случаях ответы олинаковые.

Упражнение 1.2. Давным-давно экзамены сдавали устно. На столе лежали билеты, ученик наугад выбирал билет. При составлении билетов для экзамена по информатике каждый билет получал код, состоящий из двух символов. Каждый из символов одна из букв A, B, C, D или E. Сколько есть возможных кодов билетов?

Подсказка. Заполни таблицу на рис.2 и подсчитай, сколько в ней клеток.

	A	B	C	D	E
A
B
C
D
E

Рис. 2

Упражнение 1.3. Давным-давно экзамены сдавали устно. На столе лежали билеты, ученик наугад выбирал билет. При составлении билетов для экзамена по информатике каждый билет получал код, состоящий из двух символов. Каждый из символов одна из 8 букв A, B, C, D, E, F, G, H . Сколько есть возможных кодов билетов?

Ответы к упражнениям 1.2, 1.3: 5*5 = 5² = 25, 8*8 = 8² = 64

Задача 2.1. Каждая задача в итоговой контрольной по естествознанию имеет код, состоящий из трех символов. Первый символ – буква A, B, C или D (код группы задач). Второй символ – цифра от 1 до 3 (номер задачи в группе). Третий символ – код предмета – одна из следующих 5 букв: А (астрономия), Б (биология), Г (география), Ф (физика), Х (химия). Сколько есть возможных кодов задач?

Решение. Задача похожа на задачу 1.1, но таблицу пришлось бы делать трехмерную. Чтобы избежать этого поступим так. Каждый трехсимвольный код разобьем на две части. Первая часть – все буквы, кроме последней (т.е. две первые буквы). Вторая часть – последняя буква. Например, код B3Ф разобьется на части так: B3-Ф.

Количество вариантов для первой части мы уже знаем – их 12 (см. задачу 1.1). Значит, количество вариантов для трехсимвольного кода можно подсчитать с помощью такой таблицы:

		1	2	3	4	5
		А	Б	Г	Ф	Х
1	A1	A1А	A1Б	A1Г	A1Ф	A1Х
2	A2	A2А	A2Б	A2Г	A2Ф	A2Х
3	A3	A3А	A3Б	A3Г	A3Ф	A3Х
4	B1	B1А	B1Б	B1Г	B1Ф	B1Х
5	B2	B2А	B2Б	B2Г	B2Ф	B2Х
6	B3	B3А	B3Б	B3Г	B3Ф	B3Х
7	C1	C1А	C1Б	C1Г	C1Ф	C1Х
8	C2	C2А	C2Б	C2Г	C2Ф	C2Х
9	C3	C3А	C3Б	C3Г	C3Ф	C3Х
10	D1	D1А	D1Б	D1Г	D1Ф	D1Х
11	D2	D2А	D2Б	D2Г	D2Ф	D2Х
12	D3	D3А	D3Б	D3Г	D3Ф	D3Х

Рис. 3

Количество возможных кодов = количество клеток в таблице =

= 12*5 = (4*3)*5= 4*3*5 = 60

Ответ: 60.

Упражнение 2.1. Реши такую же задачу, если в коде

1) 5 букв, 9 цифр и 4 кода предмета;

2) 8 букв, 5 цифр и 6 кодов предмета;

3) 16 букв, 5 цифр и 3 кода предмета;

4) 10 букв, 9 цифр и 2 кода предмета;

5) 3 букв, 3 цифры и 3 кода предмета.

Чтобы проверить себя, нарисуй таблицы.

Ответы: 27, 180, 240.

Примечание. Ответы даны не в порядке номеров задач, а в порядке возрастания. Ответов три, потому, что в нескольких случаях ответы олинаковые.

Упражнение 2.2. Давным-давно экзамены сдавали устно. На столе лежали билеты, ученик наугад выбирал билет. При составлении билетов для экзамена по информатике каждый билет получал код, состоящий из трех символов. Каждый из символов одна из букв A, B, C, D или E. Сколько есть возможных кодов билетов?

Упражнение 2.3. Давным-давно экзамены сдавали устно. На столе лежали билеты, ученик наугад выбирал билет. При составлении билетов для экзамена по информатике каждый билет получал код, состоящий из трех символов. Каждый из символов одна из цифр 0, 1, 2, 3 (нули в начале кода допускаются). Сколько есть возможных кодов билетов?

Ответы к упражнениям 2.2, 2.3: 4*4*4 = 4³ = 64, 5*5*5 = 5³ = 125

Примечание. Ответы даны в порядке возрастания.

Задача 3.1. Каждая задача в итоговой контрольной по естествознанию имеет код, состоящий из 4-х символов. Первый символ – буква A, B, C или D (код группы задач). Второй символ – цифра от 1 до 3 (номер задачи в группе). Третий символ – код предмета – одна из следующих 5 букв: А (астрономия), Б (биология), Г (география), Ф (физика), Х (химия). Четвертый символ – код сложности – одна из двух букв: П (простая) или Т (трудная). Сколько есть возможных кодов задач?

Решение. Снова (как в задаче 2.1) отделим последнюю букв. Для 3-хбуквенных начал (по-научному – префиксов) ответ уже знаем – их 60 возможных вариантов. К каждому из шестидесяти можно приписать либо П, либо Т. Получаем: 60 четырехбуквенных кодов с П и 60 четырехбуквенных кодов с Т – всего

60+60 = 60*2 = 4*3*5*2 = 120

четырехбуквенных кодов.

Ответ: 120

Упражнение 3.1. Реши такую же задачу, если в коде

1) 5 букв, 9 цифр, 4 кода предмета и 5 кодов сложности;

2) 8 букв, 5 цифр, 6 кодов предмета и 2 кода сложности;

3) 16 букв, 5 цифр, 3 кода предмета и 3 кода сложности;

4) 10 букв, 9 цифр, 2 кода предмета и 2 кода сложности;

5) 3 букв, 3 цифры, 3 кода предмета и 3 кода сложности;

Ответы: 81, 360, 480, 720, 900, 1001.

Примечание. Ответы даны не в порядке номеров задач, а в порядке возрастания. Ответов 6, потому, что один лишний 🙂 .

Упражнение 3.2. Давным-давно экзамены сдавали устно. На столе лежали билеты, ученик наугад выбирал билет. При составлении билетов для экзамена по информатике каждый билет получал код, состоящий из 4-х символов. Каждый из символов одна из букв A, B, C, D или E. Сколько есть возможных кодов билетов?

Упражнение 3.3. Давным-давно экзамены сдавали устно. На столе лежали билеты, ученик наугад выбирал билет. При составлении билетов для экзамена по информатике каждый билет получал код, состоящий из 4-х символов. Каждый из символов одна из цифр 0, 1, 2, 3 (нули в начале кода допускаются). Сколько есть возможных кодов билетов?

Упражнение 3.4. Давным-давно экзамены сдавали устно. На столе лежали билеты, ученик наугад выбирал билет. При составлении билетов для экзамена по информатике каждый билет получал код, состоящий из 5-и символов. Каждый из символов одна из букв Е, Г, Э. Сколько есть возможных кодов билетов?

Ответы к упражнениям 3.2, 3.3, 3.4: 3*3*3*3*3 = 3⁵ = 243; 4*4*4*4= 4⁴ = 64*4 = 256, 5*5*5*5 = 5⁴ = 625

Примечание. Ответы даны в порядке возрастания.

AirPods (3‑го поколения) – Спецификации – Apple (RU)

Посмотрите на AirPods в дополненной реальности

Драйвер с широкой амплитудой, разработанный Apple
Особый усилитель с широким динамическим диапазоном
Пространственное аудио и функция динамического отслеживания движений головы¹
Адаптивный эквалайзер

Сдвоенные направленные микрофоны
Внутренний микрофон
Датчик контакта с кожей
Акселерометр распознавания движения
Акселерометр обнаружения голосовой активности
Датчик нажатия

Чип h2

Нажмите один раз, чтобы начать или приостановить воспроизведение либо ответить на звонок
Нажмите дважды, чтобы перейти
к следующему треку
Нажмите трижды, чтобы вернуться
к предыдущему треку
Нажмите и удерживайте, чтобы вызвать Siri²
Скажите «Привет, Siri», чтобы включить песню,
позвонить или проложить маршрут

Защита от пота и воды (IPX4)

18,26 мм

30,79 мм

Длина:
30,79 мм
Ширина: 18,26 мм
Толщина: 19,21 мм
Вес одного наушника: 4,28 г

54,40 мм

46,40 мм

21,38 мм

Высота:
46,40 мм
Ширина: 54,40 мм
Толщина: 21,38 мм
Вес: 37,91 г

Поддерживается зарядка через разъём Lightning либо с помощью зарядных устройств MagSafe или зарядных устройств стандарта Qi

AirPods без подзарядки в футляре MagSafe

До 6 часов в режиме прослушивания аудио (до 5 часов при использовании пространственного аудио)⁵
До 4 часов в режиме разговора⁶

AirPods с подзарядкой в футляре MagSafe

До 30 часов в режиме прослушивания аудио⁷
До 20 часов в режиме разговора⁸

5 минут зарядки в футляре обеспечивают примерно 1 час работы в режиме прослушивания аудио⁹ или в режиме разговора¹⁰

Bluetooth 5. 0

Наушники AirPods
Зарядный футляр MagSafe
Кабель Lightning/USB‑С
Документация

Функции универсального доступа помогают людям с особыми потребностями максимально эффективно пользоваться новыми AirPods.

Некоторые функции:

Поддержка Live‑прослушивания¹¹
Уровень звука
Адаптация наушников

Модели iPhone и iPod touch с новейшей версией iOS
Модели iPad с новейшей версией iPadOS
Модели Apple Watch с новейшей версией watchOS
Модели Mac с новейшей версией macOS
Модели Apple TV с новейшей версией tvOS

Модели iPhone

iPhone 13 mini
iPhone 13
iPhone 13 Pro
iPhone 13 Pro Max
iPhone 12 mini
iPhone 12
iPhone 12 Pro
iPhone 12 Pro Max
iPhone 11
iPhone 11 Pro
iPhone 11 Pro Max
iPhone XS
iPhone XS Max
iPhone XR
iPhone X
iPhone 8
iPhone 8 Plus
iPhone 7¹³
iPhone 7 Plus¹³
iPhone 6s¹³
iPhone 6s Plus¹³
iPhone SE (2‑го поколения)
iPhone SE (1‑го поколения)¹³

Модели iPod

iPod touch (7‑го поколения)

Модели Mac

¹³

MacBook (дисплей Retina, 12 дюймов, модели с начала 2015 по 2017 год)
MacBook Air (11 дюймов, модели с середины 2012 до начала 2015 года)
MacBook Air (13 дюймов, модели с середины 2012 по 2017 год)
MacBook Air (дисплей Retina, 13 дюймов, модели с 2018 по 2020 год)
MacBook Air (чип M1, модель 2020 года)
MacBook Pro (дисплей Retina, 13 дюймов, модели с конца 2012 до начала 2015 года)
MacBook Pro (дисплей Retina, 15 дюймов, модели с середины 2012 до середины 2015 года)
MacBook Pro (13 дюймов, модели с середины 2012 по 2020 год)
MacBook Pro (15 дюймов, модели с середины 2012 по 2019 год)
MacBook Pro 13 дюймов (модель 2020 года, 2 порта)
MacBook Pro 13 дюймов (модель 2020 года, 4 порта)
MacBook Pro 13 дюймов (чип M1, модель 2020 года)
MacBook Pro 14 дюймов (модель 2021 года)
MacBook Pro 16 дюймов (модель 2021 года)
MacBook Pro (16 дюймов, модель 2019 года)
iMac (21,5 дюйма,
модели с конца 2012 по 2017 год)
iMac (27 дюймов,
модели с конца 2012 до конца 2013 года)
iMac (дисплей Retina 4K, 21,5 дюйма, модели с конца 2015 по 2019 год)
iMac (дисплей Retina 5K, 27 дюймов, модели с конца 2014 по 2020 год)
iMac (24 дюйма, чип M1, модель 2021 года)
iMac Pro (модель 2017 года)
Mac mini (модели с конца 2012 до конца 2018 года)
Mac mini (чип M1, 2020 год)
Mac Pro (модели с конца 2013 по 2019 год)

Модели iPad

iPad Pro 12,9 дюйма (5‑го поколения)
iPad Pro 12,9 дюйма (4‑го поколения)
iPad Pro 12,9 дюйма (3‑го поколения)
iPad Pro 12,9 дюйма (2‑го поколения)
iPad Pro 12,9 дюйма (1‑го поколения)¹³
iPad Pro 11 дюймов (3‑го поколения)
iPad Pro 11 дюймов (2‑го поколения)
iPad Pro 11 дюймов (1‑го поколения)
iPad Pro 10,5 дюйма
iPad Pro 9,7 дюйма¹³
iPad (9‑го поколения)
iPad (8‑го поколения)
iPad (7‑го поколения)
iPad (6‑го поколения)
iPad (5‑го поколения)
iPad Air (4‑го поколения)
iPad Air (3‑го поколения)
iPad Air 2¹³
iPad mini (6‑го поколения)
iPad mini (5‑го поколения)
iPad mini 4¹³

Модели Apple Watch

¹³

Apple Watch Series 7
Apple Watch Series 6
Apple Watch SE
Apple Watch Series 5
Apple Watch Series 4
Apple Watch Series 3
Apple Watch Series 2
Apple Watch Series 1

Модели Apple TV

Apple TV 4K
Apple TV HD¹³

AirPods и окружающая

среда

Особенности AirPods (3‑го поколения), которые помогают снизить воздействие на окружающую среду. ¹⁴

Тщательно отобранные материалы

Все редкоземельные элементы в магнитах являются переработанными
Весь алюминий в петле зарядного футляра MagSafe является переработанным
Всё олово, используемое для пайки материнской платы зарядного футляра MagSafe, является переработанным

Химические инновации

¹⁵

Устройство не содержит ртути, бромированных огнестойких добавок, ПВХ и бериллия

Экологически чистое производство

Программа нулевого уровня отходов Apple помогает поставщикам работать без захоронения отходов
Все заводы по сборке готовых устройств переходят на использование исключительно возобновляемых источников энергии при производстве продукции Apple

Экологичная упаковка

Используемое первичное древесное волокно поступает только из рационально управляемых
лесных хозяйств
Упаковка на 90% или более состоит из древесного волокна

Apple и окружающая среда

Мы стремимся производить свои продукты без дополнительной добычи полезных ископаемых, а к 2030 году — стать полностью углеродно нейтральной компанией, включая все производственные процессы.

Ознакомьтесь с позицией Apple

sup>16 ¹⁷

Выберите свои AirPods.

AirPods 2‑го поколения

Без пространственного аудио

Без активного шумоподавления и Прозрачного режима

Без защиты от пота и воды

Зарядка: разъём Lightning

Новые

AirPods 3‑го поколения

Пространственное аудио и функция динамического отслеживания движений головы ⁴¹³¹³¹¹¹¹²¹

Без активного шумоподавления и Прозрачного режима

Защита от пота
и воды ⁵¹⁴¹⁴²³³³⁷¹¹

Зарядка: разъём Lightning, беспроводные зарядные устройства,
устройства MagSafe ⁶¹⁵¹⁵¹⁰¹⁶⁸¹⁴⁸¹²

AirPods Pro

Пространственное аудио и функция динамического отслеживания движений головы ⁴¹³¹³¹¹¹¹²¹

Активное шумоподавление
и Прозрачный режим

Защита от пота
и воды ⁵¹⁴¹⁴²³³³⁷¹¹

Зарядка: разъём Lightning, беспроводные зарядные устройства,
устройства MagSafe ⁶¹⁵¹⁵¹⁰¹⁶⁸¹⁴⁸¹²

AirPods Max

Пространственное аудио и функция динамического отслеживания движений головы ⁴¹³¹³¹¹¹¹²¹

Активное шумоподавление
и Прозрачный режим

Без защиты от пота и воды

Зарядка: разъём Lightning

Сравните все модели AirPods

комбинаций и перестановок

\(\def\d{\displaystyle} \def\курс{Математика 228} \ новая команда {\ f} [1] {\ mathfrak # 1} \ новая команда {\ s} [1] {\ mathscr # 1} \def\N{\mathbb N} \def\B{\mathbf{B}} \def\circleA{(-. {-1}} \def\nrml{\triangleleft} \ деф \ ст {:} \ деф \ ~ {\ широкая тильда} \def\rem{\mathcal R} \def\sigalg{$\sigma$-алгебра } \def\Гал{\mbox{Гал}} \def\iff{\leftrightarrow} \def\If{\Leftrightarrow} \ деф \ земля {\ клин} \def\И{\bigwedge} \защита\вход{\вход} \def\AAnd{\d\bigwedge\mkern-18mu\bigwedge} \def\Ви{\bigvee} \def\VVee{\d\Vee\mkern-18mu\Vee} \ деф \ имп {\ стрелка вправо} \def\Imp{\Rightarrow} \def\Fi{\Leftarrow} \def\var{\mbox{var}} \def\Th{\mbox{Th}} \защита\вход{\вход} \def\sat{\mbox{Sat}} \def\con{\mbox{Con}} \def\iffmodels{\bmodels\models} \def\dbland{\bigwedge \!\!\bigwedge} \def\дом{\mbox{дом}} \def\rng{\mbox{диапазон}} \def\isom{\cong} \DeclareMathOperator{\wgt}{wgt} \newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}} \ новая команда {\ va} [1] {\ vtx {выше} {# 1}} \ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}} \ новая команда {\ vr} [1] {\ vtx {право} {# 1}} \ новая команда {\ vl} [1] {\ vtx {слева} {# 1}} \renewcommand{\v}{\vtx{выше}{}} \def\circleA{(-. 5,0) круг (1)} \def\circleAlabel{(-1.5,.6) узел[выше]{$A$}} \def\circleB{(.5,0) круг (1)} \def\circleBlabel{(1.5,.6) узел[выше]{$B$}} \def\circleC{(0,-1) круг (1)} \def\circleClabel{(.5,-2) узел[справа]{$C$}} \def\twosetbox{(-2,-1.4) прямоугольник (2,1.4)} \def\threesetbox{(-2.5,-2.4) прямоугольник (2.5,1.4)} \def\ansfilename{практика-ответы} \def\shadowprops{{fill=black!50,shadow xshift=0.5ex,shadow yshift=0.5ex,path fading={круг с размытым краем 10 процентов}}} \ новая команда {\ hexbox} [3] { \def\x{-cos{30}*\r*#1+cos{30}*#2*\r*2} \def\y{-\r*#1-sin{30}*\r*#1} \рисовать (\х,\у) +(90:\r) — +(30:\r) — +(-30:\r) — +(-90:\r) — +(-150:\r) — +(150: \r) — цикл; \draw (\x,\y) узел{#3}; } \renewcommand{\bar}{\overline} \newcommand{\card}[1]{\left| #1 \справа|} \newcommand{\twoline}[2]{\begin{pmatrix}#1 \\ #2 \end{pmatrix}} \новая команда{\lt}{<} \новая команда{\gt}{>} \newcommand{\amp}{&} \)

Расследуй!8

У вас есть набор фишек пяти разных цветов: красного, синего, зеленого, фиолетового и желтого.

Сколько различных стопок по две фишки можно составить, если нижняя фишка должна быть красной или синей? Объясните свой ответ, используя как аддитивный, так и мультипликативный принцип.
Сколько различных стопок по три фишки можно составить, если нижняя фишка должна быть красной или синей, а верхняя фишка должна быть зеленой, фиолетовой или желтой? Как эта проблема связана с предыдущей?
Сколько существует различных стопок по три фишки, в которых ни один цвет не повторяется? Как насчет стеков из четырех фишек?
Предположим, вы хотите взять три фишки разного цвета и положить их в карман. Сколько различных вариантов у вас есть? Что, если вы хотите четыре фишки разного цвета? Как эти проблемы связаны с предыдущими?

Перестановка — это (возможная) перестановка объектов. Например, есть 6 перестановок букв a, b, c :

\begin{уравнение*} abc, ~~ acb, ~~ bac, ~~ bca, ~~ каб, ~~ cba.

\end{уравнение*}

Мы знаем, что у нас есть все перечисленные выше — есть 3 варианта, какую букву поставить первой, затем 2 варианта, какая буква будет следующей, что оставляет только 1 вариант для последней буквы. Мультипликативный принцип говорит, что мы умножаем $3\cdot 2 \cdot 1\text{.}$

Пример 1.3.1

Сколько существует перестановок букв a, b, c, d, e, f ?

Решение

Мы НЕ хотим пытаться перечислить все это. Однако, если бы мы это сделали, нам нужно было бы выбрать букву для записи в первую очередь. Есть 6 вариантов этой буквы. Для каждого выбора первой буквы есть 5 вариантов второй буквы (мы не можем повторить первую букву, мы переставляем буквы и имеем только по одной каждой), и для каждой из них есть 4 варианта третьей, 3 варианты для четвертого, 2 варианта для пятого и, наконец, только 1 вариант для последней буквы. Итак, есть $6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720$ перестановки 6 букв.

Здесь полезно использовать некоторые обозначения: $n!\text{,}$ читать как «$n$ факториал», это произведение всех положительных целых чисел, меньших или равных $n$ (для из соображений удобства мы также определяем 0! как 1). Таким образом, количество перестановок 6 букв, как видно из предыдущего примера, равно $6! = 6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1\text{.}$ Это обобщает:

Перестановки $n$ элементов

Существуют $n! = n\cdot (n-1)\cdot (n-2)\cdot \cdots \cdot 2\cdot 1$ перестановки $n$ (различных) элементов.

Example1.3.2 Подсчет биективных функций

Сколько функций $f:\{1,2,\ldots,8\} \to \{1,2,\ldots, 8\}$ являются биективными ?

Решение

Вспомните, что означает биективность функции: каждый элемент в домене кодов должен быть образом ровно одного элемента домена. Используя двухстрочную запись, мы могли бы записать одну из этих биекций как

. \begin{уравнение*} f = \twoline{1 \amp 2 \amp 3 \amp 4 \amp 5 \amp 6 \amp 7 \amp 8} {3 \amp 1 \amp 5 \amp 8 \amp 7 \amp 6 \amp 2 \amp 4} \end{уравнение*}

На самом деле мы просто переставляем элементы кодового домена, поэтому мы создаем перестановку из 8 элементов. На самом деле «перестановка» — это еще один термин, используемый для описания биективных функций из конечного множества в себя.

Если вы в это верите, то вы видите, что ответ должен быть $8! = 8 \cdot 7 \cdot\cdots\cdot 1 = 40320\text{.}$ Это можно увидеть и непосредственно: для каждого элемента домена, мы должны выбрать отдельный элемент кодового домена для сопоставления. Есть 8 вариантов, куда отправить 1, затем 7 вариантов, куда отправить 2, и так далее. Умножаем по принципу мультипликативности.

Иногда мы не хотим переставлять все буквы/цифры/элементы, которые нам даны.

Пример 1.3.3

Сколько 4-буквенных «слов» можно составить из букв от a до f без повторяющихся букв?

Решение

Это похоже на задачу перестановки 4 букв, только теперь у нас больше вариантов для каждой буквы. Для первой буквы есть 6 вариантов. Для каждого из них есть 5 вариантов второй буквы. Затем есть 4 варианта для третьей буквы и 3 варианта для последней буквы. Общее количество слов равно $6\cdot 5\cdot 4 \cdot 3 = 360\text{.}$. Это не $6!$, потому что мы никогда не умножали на 2 и 1. Мы могли бы начать с \ (6!\), а затем сократите 2 и 1 и, таким образом, напишите $\frac{6!}{2!}\text{.}$

В общем, мы можем спросить, сколько существует перестановок $k$ объектов, выбирающих эти объекты из большего набора $n$ объектов. (В приведенном выше примере $k = 4\text{,}$ и $n = 6\text{.}$) Мы пишем это число $P(n,k)$ и иногда называем его $k$-перестановка $n$ элементов . Из приведенного выше примера мы видим, что для вычисления $P(n,k)$ мы должны применить принцип умножения к $k$ числам, начиная с $n$ и считая в обратном порядке. Например

\begin{уравнение*} P(10, 4) = 10\cdot 9\кдот 8 \кдот 7. \end{уравнение*}

Еще раз обратите внимание, что $P(10,4)$ начинается с вида $10!\text{,}$, но мы останавливаемся после 7. Мы можем формально объяснить эту «остановку», отделив часть факториал нам не нужен:

\begin{уравнение*} P(10,4) = \frac{10\cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = \frac{10!}{6!}. \end{уравнение*}

Осторожно: факториал в знаменателе равен не $4!$, а $(10-4)!\text{.}$

$k$-перестановки $n$ элементов

$P(n,k)$ — количество $k$-перестановок $n$ элементов , количество способов расположить $k$ объектов, выбранных из $ п$ различных объектов.

\begin{уравнение*} P(n,k) = \frac{n!}{(n-k)!}. \end{уравнение*}

Обратите внимание, что когда $n = k\text{,}$ мы имеем $P(n,n) = \frac{n!}{(n-n)!} = n!$ (поскольку мы определили $ 0!$ на 1). Это имеет смысл — мы уже знаем, что $n!$ дает количество перестановок всех $n$ объектов.

Example1.3.4 Подсчет инъективных функций

Сколько функций $f:\{1,2,3\} \to \{1,2,3,4,5,6,7,8\}$ являются инъективными ?

Решение

Обратите внимание, что здесь не имеет смысла запрашивать число биекций , поскольку их нет (поскольку кодовый домен больше домена, сюръекций нет). Но чтобы функция была инъективной, мы просто не можем использовать элемент кодового домена более одного раза.

Нам нужно выбрать элемент из кодового домена, который будет изображением 1. Есть 8 вариантов. Затем нам нужно выбрать один из оставшихся 7 элементов, чтобы он был образом 2. Наконец, один из оставшихся 6 элементов должен быть образом 3. Таким образом, общее количество функций равно $8\cdot 7 \cdot 6 = Р(8,3)\текст{.}$

В целом это демонстрирует, что число инъекций $f:A \to B\text{,}$, где $\card{A} = k$ и $\card{B} = n \text{,}$ равно $P(n,k)\text{.}$

Вот еще один способ найти количество $k$-перестановок $n$ элементов: сначала выберите, какие $k$ элементов будут в перестановке, затем посчитайте, сколько существует способов их расположить. После того, как вы выбрали $k$ объектов, мы знаем, что есть $k!$ способов упорядочить (переставить) их. Но как выбрать $k$ объектов из $n\text{?}$ У вас есть $n$ объектов, и вам нужно выберите $k$ из них. Вы можете сделать это ${n \выбрать k}$ способами. Тогда для каждого выбора из этих $k$ элементов мы можем переставить из них $k!$ способов. Используя мультипликативный принцип, мы получаем другую формулу для $P(n,k)\text{:}$

\begin{уравнение*} P(n,k) = {n \выберите k}\cdot k!. \end{уравнение*}

Теперь, поскольку у нас уже есть замкнутая формула для $P(n,k)$, мы можем подставить ее в:

\begin{уравнение*} \frac{n!}{(n-k)!} = {n \выберите k} \cdot k!. \end{уравнение*}

Если мы разделим обе части на $k!$, мы получим замкнутую формулу для ${n \choose k}\text{.}$

Замкнутая формула для ${n \выбрать k}$

\begin{уравнение*} {n \выберите k} = \frac{n!}{(n-k)!k!} \end{уравнение*}

Мы говорим, что $P(n,k)$ подсчитывает перестановок , а ${n \choose k}$ подсчитывает комбинаций . Формулы для каждого из них очень похожи, просто в знаменателе ${n \choose k}\text{.}$ есть лишний $k!$ что ${n \choose k}$ не различает различные порядки, в которых могут появляться $k$ объекты. Мы просто выбираем (или выбираем) $k$ объекты, а не упорядочиваем их. Возможно, «комбинация» — обманчивый ярлык. Мы не имеем в виду кодовый замок (где порядок определенно имеет значение). Возможно, лучшая метафора — это сочетание вкусов — вам просто нужно решить, какие вкусы сочетать, а не в каком порядке их комбинировать.

Чтобы еще больше проиллюстрировать связь между комбинациями и перестановками, мы закончим пример.

Пример 1.3.5

Вы решили устроить званый обед. Несмотря на то, что вы невероятно популярны и у вас 14 разных друзей, у вас достаточно стульев, чтобы пригласить только 6 из них.

Сколько у вас есть вариантов, кого из 6 друзей пригласить?
Что, если вам нужно решить не только, кого из друзей пригласить, но и где их рассадить за длинным столом? Сколько вариантов у вас есть тогда?

Решение

Вы должны просто выбрать 6 друзей из 14. Это можно сделать ${14 \выберите 6}$ способами. Мы можем найти это число либо с помощью треугольника Паскаля, либо по закрытой формуле: $\frac{14!}{8!\cdot 6!} = 3003\text{.}$
Здесь вы должны подсчитать все способы, которыми вы можете переставить 6 друзей, выбранных из группы из 14. Таким образом, ответ равен $P(14, 6)\text{,}$, который можно рассчитать как $\frac{14 !}{8!} = 2192190\текст{.}$
Заметьте, что мы можем думать об этой задаче на счет как о счетных функциях: сколько инъективных функций имеется в вашем наборе из 6 стульев и в вашем наборе из 14 друзей (эти функции инъективны, потому что ни один стул не может двигаться). двум твоим друзьям).

Как связаны эти числа? Обратите внимание, что $P(14,6)$ намного на больше, чем ${14 \choose 6}\text{.}$ Это имеет смысл. ${14 \выбрать 6}$ выбирает 6 друзей, но $P(14,6)$ упорядочивает 6 друзей, а также выбирает их. На самом деле, мы можем точно сказать, насколько больше $P(14,6)$. В обеих задачах на подсчет мы выбираем 6 из 14 друзей. Для первого мы останавливаемся там, на 3003 способах. Но во второй задаче на подсчет каждый из этих 3003 вариантов выбора из 6 друзей можно упорядочить ровно $6!$ способами. Итак, теперь у нас есть $3003\cdot 6!$ вариантов, и это ровно $2192190\text{.}$

Можно также посмотреть на первую задачу иначе. Мы хотим выбрать 6 из 14 друзей, но нас не волнует порядок, в котором они выбираются. Чтобы выбрать 6 из 14 друзей, мы можем попробовать это:

\begin{уравнение*} 14 \cdot 13 \cdot 12 \cdot 11 \cdot 10 \cdot 9. \end{уравнение*}

Это разумное предположение, так как у нас есть 14 вариантов для первого гостя, затем 13 для второго и так далее. Но догадка неверна (на самом деле это произведение равно $2192190 = Р(14,6)$). Он различает разные порядки, в которых мы могли бы пригласить гостей. Чтобы исправить это, мы могли бы разделить на количество различных расстановок 6 гостей (чтобы все они считались одним исходом). Существует ровно $6!$ способов разместить 6 гостей, поэтому правильный ответ на первый вопрос

\begin{уравнение*} \frac{14 \cdot 13 \cdot 12 \cdot 11\cdot 10 \cdot 9}{6!}. \end{уравнение*}

Обратите внимание, что это можно записать как 9.0003

\begin{уравнение*} \frac{14!}{8!\cdot 6!}. \end{уравнение*}

, что у нас было изначально.

ПодразделУпражнения

1

Пиццерия предлагает 10 начинок.

Сколько пицц с тремя начинками они могли включить в свое меню? Предположим, что двойная начинка не допускается.
Сколько всего пицц возможно с от нуля до десяти начинок (но не с двойной начинкой)?
9{10} = 1024\) пицц. Скажите «да» или «нет» каждой начинке.
$P(10,5) = 30240$ способов. Назначьте каждому из 5 мест в левой колонке уникальную начинку для пиццы.

2

Кодовый замок состоит из циферблата с 40 цифрами. Чтобы открыть замок, вы поворачиваете циферблат вправо, пока не дойдете до первой цифры, затем влево, пока не дойдете до второй цифры, затем снова вправо до третьей цифры. Числа должны быть разными. Сколько различных комбинаций возможно? 93\)).

3

Используя цифры от 2 до 8, найдите количество различных пятизначных чисел, таких что:

Цифры могут использоваться более одного раза.
Цифры не могут повторяться, но могут идти в любом порядке.
Цифры не могут повторяться и должны быть записаны в возрастающем порядке.
Какой из приведенных выше вопросов на подсчет является комбинацией, а какой перестановкой? Объясните, почему это имеет смысл.

4

Сколько существует треугольников с вершинами из точек, показанных ниже? Обратите внимание, что мы не допускаем вырожденных треугольников, у которых все три вершины лежат на одной линии, но допускаем непрямоугольные треугольники. Объясните, почему ваш ответ правильный.

Подсказка

Вам нужно ровно две точки на оси $x$ или $y$, но не пересчитывайте прямоугольные треугольники.

5

Сколько четырехугольников можно нарисовать, используя точки внизу в качестве вершин (углов)?

Решение

${7\выберите 2}{7\выберите 2} = 441$ четырехугольников. Мы должны выбрать две из семи точек в верхнем ряду и две из семи точек в нижнем ряду. Однако не имеет значения, какую из двух точек (в каждой строке) мы выбираем первой, потому что после выбора этих четырех точек остается ровно один четырехугольник, который они определяют.

6

Сколько четырехугольников возможно в предыдущей задаче:

Квадраты?
Прямоугольники?
Параллелограммы?
Трапеции? ² Здесь, как и в исчислении, трапеция определяется как четырехугольник с по крайней мере одной парой параллельных сторон. В частности, параллелограммы — это трапеции.
Трапеции, не являющиеся параллелограммами?

Раствор

5 кв. Вам нужно пропустить ровно по одной точке сверху и снизу, чтобы длины сторон стали равными. Как только вы выбираете точку сверху, определяются остальные три точки.
${7 \выберите 2}$ прямоугольников. Как только вы выберете две точки сверху, будут определены две нижние.
Это сложно, так как вам нужно беспокоиться о нехватке места. Один из способов подсчета: разбить дела по расположению левого верхнего угла. Вы получаете ${7 \выберите 2} + ({7 \выберите 2}-1) + ({7 \выберите 2} — 3) + ({7 \выберите 2} — 6) + ({7 \выберите 2 } — 10) + ({7 \выберите 2} — 15) = 91$ параллелограммов.
Все
${7\выбрать 2}{7\выбрать 2} — \left[ {7 \выбрать 2} + ({7 \выбрать 2}-1) + ({7 \выбрать 2} — 3) + ({ 7 \выберите 2} — 6) + ({7 \выберите 2} — 10) + ({7 \выберите 2} — 15) \right]\text{.}$ Все, кроме параллелограммов.

7

Анаграмма слова — это просто перестановка его букв. Сколько существует различных анаграмм слова «не защищено авторским правом»? (Это самое длинное общеупотребительное английское слово без повторяющихся букв. )

8

Сколько существует анаграмм слова «оценки», начинающихся на букву «а»?

Решение

После первой буквы (а) мы должны переставить оставшиеся 7 букв. Есть только две буквы (s и e), так что на самом деле это всего лишь вопрос о битовой строке (представьте, что s — это 1, а e — 0). Таким образом, есть ${7 \выберите 2} = 21$ анаграмм, начинающихся с «а».

9

Сколько существует анаграмм слова «анаграмма»?

10

На деловом выезде ваша компания из 20 бизнесменов и деловых женщин играет в гольф.

Вам нужно разбиться на четверки (группы по 4 человека): первая четверка, вторая четверка и так далее. Сколько способов вы можете сделать это?
После всей вашей тяжелой работы вы понимаете, что на самом деле вы хотите, чтобы каждая четверка включала одного из пяти членов Совета. Сколько способов вы можете сделать это?

Решение

${20 \выбрать 4}{16 \выбрать 4}{12 \выбрать 4}{8 \выбрать 4}{4 \выбрать 4}$ способов. Выберите 4 из 20 человек для первой четверки, затем 4 из оставшихся 16 для второй четверки и так далее (используйте принцип умножения для объединения).
$5!{15 \выбрать 3}{12 \выбрать 3}{9 \выбрать 3}{6 \выбрать 3}{3 \выбрать 3}$ способов. Сначала определите время игры 5 членов правления, затем выберите 3 из 15 не членов правления для игры в гольф с первым членом правления, затем 3 из оставшихся 12 для игры в гольф со вторым и так далее.

11

Сколько различных рассадок возможно для короля Артура и его 9 рыцарей вокруг их круглого стола?

Решение

$9!$ (за столом сидят 10 человек, но не важно, где сидит король Артур, только кто сидит слева от него, два места слева от него и так далее). 9{10}\) функций. Существует 17 вариантов изображения каждого элемента в домене.

$P(17, 10)$ инъективных функций. Существует 17 вариантов изображения первого элемента домена, затем только 16 вариантов для второго и так далее.

13

Рассмотрим функции $f: \{1,2,3,4\} \to \{1,2,3,4,5,6\}\text{.}$

Сколько всего функций?
Сколько функций инъективны?
Сколько инъективных функций увеличивают ? Возрастание означает, что если $a \lt b$, то $f(a) \lt f(b)\text{,}$ или, другими словами, выходы становятся больше по мере увеличения входов.

14

Мы видели, что формула для $P(n,k)$ равна $\dfrac{n!}{(n-k)!}\text{.}$ Ваша задача состоит в том, чтобы объяснить , почему это это правильная формула.

Предположим, у вас есть 12 фишек разного цвета. Сколько разных стопок по 5 фишек можно составить? Объясните свой ответ и почему он аналогичен формуле для $P(12,5)\text{.}$
Снова используя сценарий с 12 фишками, сколько будет считаться $12!$? Что значит $7!$? Объяснять.
Объясните, почему имеет смысл делить $12!$ на $7!$ при вычислении $P(12,5)$ (в терминах чипов).
Ваше объяснение подходит для чисел, отличных от 12 и 5? Объясните формулу $P(n,k) = \frac{n!}{(n-k)!}$, используя переменные $n$ и $k\text{.}$

Вернуть все комбинации

Домашний
Функции
Формулы
Функции
Основы Excel Таблица Excel Расширенный фильтр Проверка данных Выпадающие списки Именованные диапазоны Решатель
Карты
Условное форматирование
Сводная таблица
VBA
Функции VBA Методы Характеристики Заявления Макросы Пользовательские функции Файлы и папки Флажки
Архив
Все статьи отсортированы по дате Категории Товары Продвинутый курс Excel
Контакт
Обо мне Блоги я прочитал

Автор: Оскар Кронквист Последнее обновление статьи 01 июля 2022 г.

Сегодня у меня есть две функции, которые я хотел бы продемонстрировать, они вычисляют все возможные комбинации из диапазона ячеек. Что такое комбинация? Чтобы объяснить комбинации, я должен объяснить разницу между комбинациями и перестановками.

Думайте о перестановках, как будто порядок важен, а о комбинациях, как будто порядок не важен. Если это сбивает с толку, посмотрите на следующие примеры.

Пример 1. Перестановки

Подумайте о номере телефона, каждая цифра может иметь от 0 до 9 или 10 различных значений. Пятизначный номер телефона содержит 100 000 перестановок (10x10x10x10x10 равно 100 000).

Теперь представьте себе номер телефона друга или коллеги. Если мы поменяем номера телефонов, вы, возможно, позвоните незнакомому человеку. Заказ важный .

Прочтите эту статью, чтобы узнать больше о перестановках:

Рекомендуемые статьи

Перестановки с повторением и без повторения
Я обсуждал разницу между перестановками и комбинациями в своем последнем посте, сегодня я хочу поговорить о двух видах […]

Пример 2 — Комбинации

Представьте, что вы собираетесь купить пиццу и можете выберите один из пяти ингредиентов: сыр, томатный соус, лук, ветчину и грибы. Неважно, в каком порядке вы говорите ингредиенты. Заказ не важен .

Пятизначный номер телефона имеет 100 000 возможных комбинаций, но пять из пяти ингредиентов пиццы имеют только одну комбинацию. Я думаю, что только математики используют слова перестановки, все остальные используют словосочетания, даже если они говорят о перестановках.

В следующей статье демонстрируется решение проблемы с помощью комбинаций, порядок не важен:

Рекомендуемые статьи

Идентификация чисел в сумме с помощью решателя Excel
Вот полезная функция, которую я недавно нашел в поиске примеров решателя Excel. Я суммировал некоторые случайные значения из […]

Пользовательские функции

Следующая пользовательская функция позволяет, например, увидеть все комбинации ингредиентов пиццы, которые вы можете выбрать, выбрав 5 из 7 ингредиентов.

Обновление от 01.07.2022! Теперь существует формула Excel 365, в которой также перечислены комбинации: Комбинации списка — формула Excel 365

Формула пользовательского массива в диапазоне ячеек E3:I23:

= Комбинации (B3:B9,5)

Вам нужно скопировать код VBA, приведенный ниже, в вашу книгу, прежде чем вы попробуете указанную выше функцию, определяемую пользователем.

Посмотрите это видео, чтобы узнать больше о UDF

Как ввести формулу массива

Выберите диапазон ячеек E3:I23
Нажмите левой кнопкой мыши в строке формул
Введите пользовательскую функцию
Нажмите и удерживайте CTRL + SHIFT
Нажмите Enter

Если вы все сделали правильно, формула теперь начинается и заканчивается фигурными скобками, например {=формула массива}. Они появляются автоматически, не вводите фигурные скобки самостоятельно.

Рекомендуемые статьи

Руководство для начинающих по формулам массива Excel
Формулы массива позволяют выполнять расширенные вычисления, которые невозможно выполнить с помощью обычных формул.

Код VBA

 'Измерение общедоступной переменной и объявление типа данных
Публичный результат () как вариант

'Имя определяемой пользователем функции
Комбинации функций (rng как диапазон, n как один)

'Сохраняем значения из диапазона ячеек rng в переменную массива rng1
rng1 = rng.Value

'Изменение результата переменной массива
Результат ReDim (n - 1, 0)

'Запустить пользовательскую рекурсивную функцию с параметрами rng1, n, 1, 0
Рекурсивный вызов (rng1, n, 1, 0)

'Удалить столбец значений из результата переменной массива
ReDim Preserve result(UBound(результат, 1), UBound(результат, 2) - 1)¨

'Транспонировать значения в результате переменной, а затем вернуть результат в пользовательскую функцию на листе
Комбинации = Application.Transpose(результат)

Конечная функция

 'Имя определяемой пользователем функции и параметров
Рекурсивная функция (r как вариант, c как один, d как один, e как один)

'Измерение переменных и объявление типов данных
Dim f как одиночный

'Для. .. Следующее утверждение
Для f = d To UBound(r, 1)

'Сохранить значение в переменной массива r, строка f, столбец 1, в строку результата переменной массива e и последний столбец
результат(e, UBound(результат, 2)) = r(f, 1)

'If... Then... Else... Конец оператора If
'Проверяем, что переменная в e равна c -1
Если е = (с - 1) Тогда

'Добавить еще один столбец в результат переменной массива
Результат ReDim Preserve (UBound (результат, 1), UBound (результат, 2) + 1)

'Для... Следующее утверждение
Для g = 0 To UBound (результат, 1)

'Сохранить значение в переменной массива, строка результата g, второй последний столбец, в строку результата g, последний столбец
результат(g, UBound(результат, 2)) = результат(g, UBound(результат, 2) - 1)
Следующая г

'Продолжить здесь, если e не равно c - 1
Еще

'Запустить пользовательскую рекурсивную функцию с параметрами r, c, f + 1, e + 1
Вызов рекурсивного (r, c, f + 1, e + 1)
Конец, если

Следующая ф

Конечная функция

Эти функции имеют ограничение в 65532 строки, если вам нужно больше, прочитайте этот комментарий.

Куда скопировать код vba?

Перейти к редактору VB (Alt + F11)
Нажмите левой кнопкой мыши на «Вставка» в меню
Нажмите левой кнопкой мыши на «Модуль»
Вставить код в кодовый модуль
Вернуться в Excel

Совет! Знаете ли вы, что Excel может подсчитать количество комбинаций за вас? Используйте функцию ОБЪЕДИНЕНИЕ:

=COMBIN(7,5) равно 21 комбинации.

Получить файл Excel

Combinations.xlsm

Категория комбинаций

Перестановки категории

Найдите числа, наиболее близкие к сумме
Excelxor — отличный сайт для вдохновения, меня очень впечатлил этот пост Какие числа дают в сумме […]

Список перестановок без повторения [UDF]
В этом сообщении блога описывается, как создавать перестановки, повторение НЕ разрешено. Перестановки — это элементы, расположенные в заданном порядке, что означает […]

Чередование уникальных групп без повторения
В этой статье демонстрируется формула Что находится на этой странице Формула вопроса Формула массива Объяснение формулы массива Получить файл Excel […]

Создать перестановки [UDF]
Крис спрашивает: Максимально допустимое число — 4 цифры, а число — от 0 до 9. После того, как я введу […]

Перестановки с повторением и без повторения
О разнице между перестановками и комбинациями я говорил в прошлом посте, сегодня хочу поговорить о двух видах […]

Список всех перестановок с условием
Недавно я получил вопрос о перестановках, по сути, как найти каждую перестановку между 0 и 9 […]

Список перестановок с повторением и количество вариантов для выбора
В этой статье демонстрируется макрос, который позволяет создать список перестановок, повторения разрешены на основе числа […]

Функции в этой статье

Комбинации

Более 1300 формул Excel

Категории формул Excel

AverageChooseCombine MergeCompareConcatenateConditional FormattingCountCount valuesDatesDuplicatesExtractFilterFilter recordsFiltered valuesFilterxmlHyperlinkIf cellIndex MatchLogicLookupsMatchMaxMinNumbers in sumOR logicOverlappingPartial matchRecordsSequenceSmallSort bySort valuesSumSumifsSumproductString manipulationTimeUnique distinct recordsUnique distinct valuesUnique recordsUnique valuesVlookupVlookup return values

Excel categories

Home page

Последние обновленные статьи.

Функции Excel

Более 300 функций Excel с подробной информацией, включая синтаксис, аргументы, возвращаемые значения и примеры для большинства функций, используемых в формулах Excel.

Формулы Excel

Более 1300 формул, организованных в подкатегории.

Таблицы Excel

Таблицы Excel упрощают работу с данными, добавляя или удаляя данные, фильтруя, суммируя, сортируя, улучшая читаемость с помощью форматирования ячеек, ссылок на ячейки, формул и многого другого.

Расширенный фильтр

Позволяет фильтровать данные на основе выбранного значения, заданного текста или других критериев. Он также позволяет фильтровать существующие данные или перемещать отфильтрованные значения в новое место.

Проверка данных

Позволяет контролировать, что пользователь может вводить в ячейку. Это позволяет вам указать условия и показать собственное сообщение, если введенные данные недействительны.

Раскрывающийся список

Позволяет пользователю работать более эффективно, отображая список, из которого пользователь может выбрать значение. Это позволяет вам контролировать то, что отображается в списке, и это быстрее, чем ввод в ячейку.

Именованные диапазоны

Позволяет назвать одну или несколько ячеек, это упрощает поиск ячеек с помощью поля Имя, чтение и понимание формул, содержащих имена вместо ссылок на ячейки.

Excel Solver

Excel Solver — это бесплатная надстройка, которая использует целевые ячейки, ограничения, основанные на формулах на листе, для выполнения анализа «что, если» и других проблем принятия решений, таких как перестановки и комбинации.

Диаграммы

Функция Excel, позволяющая визуализировать данные в виде графика.

Условное форматирование

Форматирование ячеек или значений ячеек на основе условия или критерия. Существует несколько встроенных инструментов условного форматирования, которые можно использовать, или использовать пользовательскую формулу условного форматирования.

Сводные таблицы

Позволяет быстро суммировать большие объемы данных в очень удобной для пользователя форме. Эта мощная функция Excel позволяет эффективно анализировать, упорядочивать и классифицировать важные данные.

VBA

VBA означает Visual Basic для приложений и представляет собой язык программирования, разработанный Microsoft. Он позволяет автоматизировать трудоемкие задачи и создавать пользовательские функции.

Макросы

Программа или подпрограмма, встроенная в VBA, которую может создать любой. Используйте средство записи макросов, чтобы быстро создавать собственные макросы VBA.

UDF

UDF расшифровывается как User Defined Functions и представляет собой настраиваемые функции, которые может создать каждый.

Архив

Список всех опубликованных статей.

Назад к основам: Часть 1. Перестановки и комбинации | by Becca R

Кажется, что независимо от того, сколько уроков продвинутой статистики я посещаю или сколько раз я возвращаюсь к этой теме, перестановки и комбинации продолжают ускользать от меня. Этот пост является первым в серии постов в блоге «Назад к основам», целью которых является создание математических основ науки о данных. Цель этого первого поста — помочь разобраться раз и навсегда, как выбрать эти надоедливые шарики из банки!

Перестановки и комбинации относятся к области математики, называемой комбинаторикой. В частности, это построено на обобщенном базовом принципе подсчета , , который гласит, что если вы проведете r экспериментов с n₁ возможными результатами в первом раунде, n₂ во втором раунде, …, nᵣ в rᵗʰ раунде, то существует n₁·n₂·…·nᵣ возможных исходов.

Предположим, мы проводим эксперимент с тремя раундами, например, выбираем шарики из банки, в которой два шарика, красный и синий. Мы выбираем два шарика каждый раунд. Сколько возможных исходов будет для всего эксперимента?

В первом раунде возможны два исхода. Для каждого из этих двух исходов есть два возможных исхода второго раунда, поэтому 2·2 = 4 возможных исхода. В третьем заключительном раунде у каждого из четырех вариантов есть еще два возможных исхода, поэтому 4·2 = 2·2·2=2³ = 8 возможных исходов.

Мы можем использовать этот общий принцип, чтобы найти варианты расположения элементов из данного набора с четырьмя критериями. Это можно разбить на два способа осмысления расположения элементов из набора объектов: Перестановки и комбинации . При перестановках порядок имеет значение. В этом случае выбор красного шарика, а затем синего шарика отличается от выбора синего шарика, а затем красного шарика. В комбинациях порядок не имеет значения, т. е. группа, содержащая один синий и один красный шарики, является одной и той же группой, независимо от того, какой из них был выбран первым. С любым из них мы можем либо заменить шарики в банке, либо нет.

Перестановки (порядок имеет значение)

а. С заменой

Сколькими способами мы можем выбрать два шарика из банки с тремя шариками с заменой, когда порядок не имеет значения? В этом первом примере есть три способа выбрать первый шарик, и для каждого из этих трех способов есть еще три способа выбрать следующий шарик. Следуя стрелкам, есть 9 различных возможных исходов, или 3².

Если бы мы хотели заменить шарики и выбрать в третий раз, было бы 3·3·3 = 3³ возможностей; в четвертом раунде у нас было бы 3·3·3·3 = 3⁴ возможных исходов и так далее. Вообще говоря, есть nʳ способов выбрать r объектов из набора n всего объектов.

б. БЕЗ замены

Сколько имеется заказанных композиций из трех шариков, если мы не не положим их обратно в банку? Для первого выбора снова есть три варианта. Для любого из этих трех вариантов останется только два варианта для второго шарика. На финальный шарик всегда будет оставаться только один, и мы будем вынуждены прекратить выбор после трех раундов. Таким образом, существует 3·2·1 = 6 возможных исходов или 3!.

А если мы не собираемся выбирать все шарики? Предположим, что в банке 5 шариков, и мы выберем только 2 из них. В этом случае есть 5 способов выбрать первый шарик и, поскольку мы не кладем его обратно в банку, 4 варианта выбора второго шарика. Это 5·4 = 20 возможных комбинаций. В качестве альтернативы, это то же самое, что и проблема выше, но «удаление» последних раундов, в которых мы продолжали заканчивать выбор всех шариков в банке. Итак, мы можем разделить эти возможности и переписать 5·4 как:

В общем случае количество способов выбрать r объектов из n всего объектов без замены составляет:

2. Комбинации (порядок не имеет значения)

а. БЕЗ замены

Давайте расширим приведенный выше пример и рассмотрим количество способов, которыми мы можем выбрать 2 шарика из пяти без замены их в банке.

Мы знаем, что когда мы выбираем 2 предмета из набора из 5 предметов, получается 5!/(5–2)! возможные исходы. Что здесь нового, так это проблема избыточности. Каждая цветовая пара имеет одну избыточную копию (например, красный+синий = синий+красный), поэтому мы можем разделить количество возможностей на 2·1 = 2!

Таким образом, общее количество возможностей равно:

Обобщая, количество способов составить группы из r объектов из n объектов без замены (т.

13. Перестановки с повторениями

Информатика — Перемножение количеств вариантов

AirPods (3‑го поколения) – Спецификации – Apple (RU)

AirPods без подзарядки в футляре MagSafe

AirPods с подзарядкой в футляре MagSafe

Модели iPhone

Модели iPod

Модели Mac

Модели iPad

Модели Apple Watch

Модели Apple TV

AirPods и окружающая

Тщательно отобранные материалы

Химические инновации

Экологически чистое производство

Экологичная упаковка

Apple и окружающая среда

Выберите свои AirPods.

AirPods 2‑го поколения

AirPods 3‑го поколения

AirPods Pro

AirPods Max

комбинаций и перестановок

Расследуй!8

Пример 1.3.1

Перестановки \(n\) элементов

Example1.3.2 Подсчет биективных функций

Пример 1.3.3

\(k\)-перестановки \(n\) элементов

Example1.3.4 Подсчет инъективных функций

Замкнутая формула для \({n \выбрать k}\)

Пример 1.3.5

ПодразделУпражнения

1

2

3

4

5

6

7

8

9

10

11

13

14

Вернуть все комбинации

Пример 1. Перестановки

Пример 2 — Комбинации

Пользовательские функции

Посмотрите это видео, чтобы узнать больше о UDF

Код VBA

Куда скопировать код vba?

Рекомендуемая литература

Получить файл Excel

Категория комбинаций

Перестановки категории

Функции в этой статье

Категории формул Excel

Excel categories

Назад к основам: Часть 1. Перестановки и комбинации | by Becca R

Добавить комментарий Отменить ответ