 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град.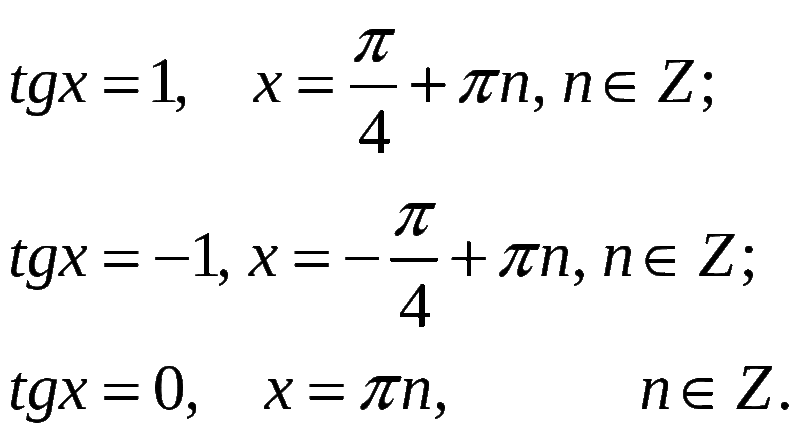 ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.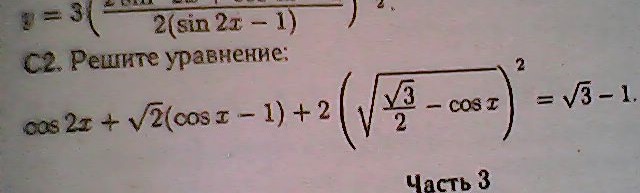 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.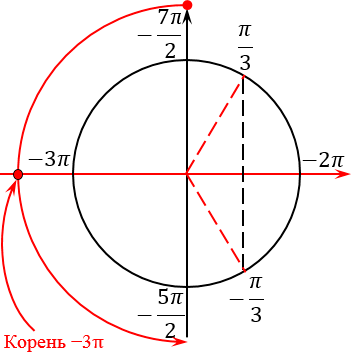 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.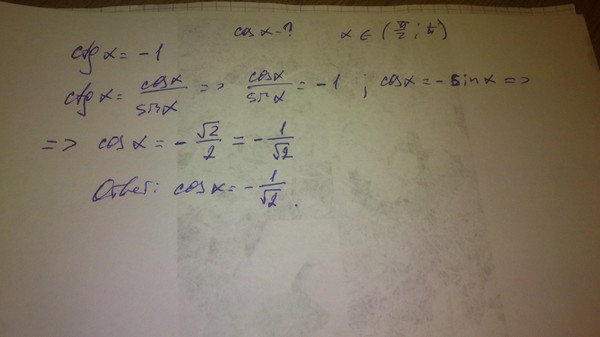 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
2 корень из 6 умножить на корень из 2 умножить на 8 корень из 3
Ответы
aslazer211124
16. 07.2020 12:24
07.2020 12:24
Два умножить на корень из трех умножить на корень из двух умножить на корень из двух умножить на корень из трех умножить на 8 умножить на корень из трех. получается: 96 умножить на корень из 3
вроде бы так
ПОКАЗАТЬ ОТВЕТЫ
artemtik2005 18.10.2020 01:06
ПОКАЗАТЬ ОТВЕТЫ
=-[2корень из 3-4]+2корень из 3=-2корень из 3+4+2корень из3=4
ответ:4
ПОКАЗАТЬ ОТВЕТЫ
Nikita12409
18. 10.2020 01:06
10.2020 01:06
Пошаговое объяснение:
1.
a) 7√3-√48+√27=7√3-√(16*3)+√(9*3)=7√3-4√3+3√2=6√3.
б) √2*(√8+4√2)=√2*(√(4*2)+4√2)=√2*(2√2+4√2)=√2*6√2=2*6=12.
в)(√3+5)²=(√3)²+2*√3*5+5²=3+10√3+25=28+10√3.
г) (√5+√3)(√5-√3)=(√5)²-(√3)²=5-3=2.
2.
2√6 ∨ 4√2
√(2²*6) ∨ √(4²*2)
√(4*6) ∨ √(16*2)
√24<√32.
4.
4/√11=4*√11/(√11*√11)=4√11/11.
√5/(√5-2)=√5*(√5+2)/((√5+2)*(√5-2))=(5+2√5)/(5-4)=5+2√5.
ПОКАЗАТЬ ОТВЕТЫ
Pmoshnek 18.10.2020 01:06
ответ:-6
Объяснение:
2 корня из трех * на минус корень из трех = -6
тангенс 300 градусов минус корень из трех.
ПОКАЗАТЬ ОТВЕТЫ
anyaradzivon
18. 10.2020 01:06
10.2020 01:06
ответ: -6.
Объяснение:
2√3 tg300° = 2√3 tg(360° — 60°) = 2√3 · (-tg60°) = 2√3 · (-√3) = -6
ПОКАЗАТЬ ОТВЕТЫ
ДанилкаМаксимка 18.10.2020 01:06
ПОКАЗАТЬ ОТВЕТЫ
pavlikpanov200oyp9mu 18.10.2020 01:06
ПОКАЗАТЬ ОТВЕТЫ
dasha45da 18.10.2020 01:06
2√13 * 5√2 * √ 26=2*5*(√ 26)²=26*10=260
ПОКАЗАТЬ ОТВЕТЫ
xlblacklxffff2
18. 2=4×5 =20
2=4×5 =20
ПОКАЗАТЬ ОТВЕТЫ
yecgaass121212 18.10.2020 01:06
7 в степени 2/3 это= корень из 7 в кубе* (корень из 7 в кубе)=7 в кубе или 343
2+343=345
ПОКАЗАТЬ ОТВЕТЫ
LoKotRon2017 18.10.2020 01:06
2√7 * 3√7 = (2*3) * (√7)² = 6 * 7 = 42
ПОКАЗАТЬ ОТВЕТЫ
dongrigoriew20 18.10.2020 01:06
2√3*√2*8√3= 96
ответ 96
ПОКАЗАТЬ ОТВЕТЫ
alexboyko95
18. 10.2020 01:06
10.2020 01:06
2 корень из 5 + 2 корень из 5 -3 корень из 5 =корень из 5
ответ корень из 5
ПОКАЗАТЬ ОТВЕТЫ
3743Dasha 18.10.2020 01:06
1/6*корень из 900= 1/6*30=5
ПОКАЗАТЬ ОТВЕТЫ
Милана1245 18.10.2020 01:06
1) 2√3·7√5 = 14√15
2) 14√15 : √15 = 14
ПОКАЗАТЬ ОТВЕТЫ
Saweretufio 18.10.2020 01:06
. 2=4×5=20
2=4×5=20
ПОКАЗАТЬ ОТВЕТЫ
ANiTEZ 18.10.2020 01:06
Вот фото с решением, надеюсь всё понятно
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Spamm 12.11.2020 07:50
Лёгкое задание — большие 256 нужно сделать 3;4…
Killyourself1 30.06.2019 08:30
Впарке сажали деревья два года: в 2005 г. 2−10x-25 принимает наибольшее значение?…
2−10x-25 принимает наибольшее значение?…
Инка1999 24.11.2020 22:30
Упростить выражение Номер 1 1)0,1x+3(1-x) 2)-3(2y+1)+4 3)-2-(7a-5) Номер 2 1)35+7(x-7) 2)2(c-3)-5(2-4c) 3)-(9-2x)+4 4)-4+4(5-x) 5)-2(x+5)+3(x-7) 6)-13-3(5-6x)…
vanya33251243 17.02.2021 15:57
Функции заданы формулами f(x)=14×2 и g(x)=16×2. Вычисли f(−10)g(9)…
massenia 25.11.2021 16:31
2sin(x-пи)=√2 на промежутке (0;2пи)…
proksi01
26.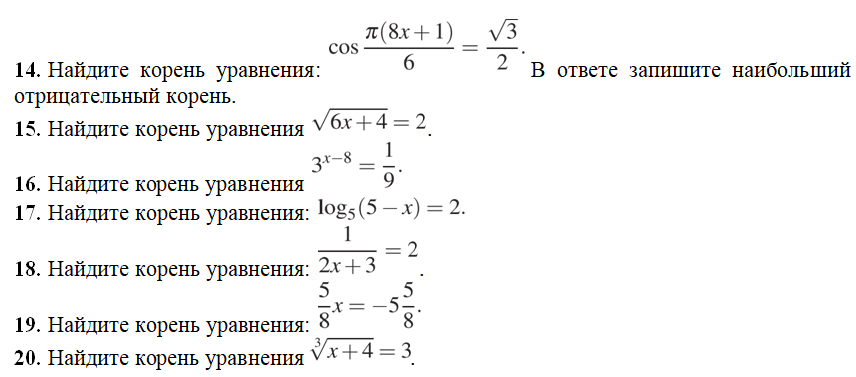 2…
2…
glushak527 30.08.2019 18:30
Выясните,имеет ли решения система и сколько: 4х-у=7 2у+14=8х…
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Если тангенс (А + В) = √3 и тангенс (А – В) = 1/√3, 0° В, то найти А и В
Тригонометрия — это, в основном, изучение отношений между углами и сторонами треугольника. Это одна из широко используемых тем математики, которая используется в повседневной жизни. Он включает в себя операции над прямоугольным треугольником, то есть треугольником, один из углов которого равен 90°. Есть некоторые термины, которые мы должны знать, прежде чем идти дальше. Эти термины,
Это одна из широко используемых тем математики, которая используется в повседневной жизни. Он включает в себя операции над прямоугольным треугольником, то есть треугольником, один из углов которого равен 90°. Есть некоторые термины, которые мы должны знать, прежде чем идти дальше. Эти термины,
- Гипотенуза — это сторона, противоположная прямому углу в прямоугольном треугольнике. Это самая длинная сторона прямоугольного треугольника. На стороне рисунка 1 AC — это гипотенуза.
- Перпендикуляр – Перпендикуляр треугольника, соответствующий особо острому углу θ, является стороной, противоположной углу θ. На стороне рисунка 1 перпендикуляр AB соответствует углу θ.
- Основание – это сторона, примыкающая к особенно острому углу θ. На рисунке 1 сторона ВС является основанием, соответствующим углу θ.
Рисунок 1
Тригонометрические функции
Как было сказано ранее, тригонометрия отображает соотношение между углами и сторонами прямоугольного треугольника. Это соотношение представлено стандартными отношениями и дается следующим образом:
Это соотношение представлено стандартными отношениями и дается следующим образом:
- Синус (sin) Синусом угла θ называется отношение длины перпендикуляра, соответствующего углу θ, к длине гипотенузы треугольника.
sin θ = перпендикуляр/гипотенуза =p/h
- Косинус (cos) Косинус угла θ представляет собой отношение длины основания, соответствующего углу θ, к длине гипотенузы треугольника.
cos θ = основание/гипотенуза=b/h
- Тангенс (tan) Тангенс угла θ – это отношение длины перпендикуляра, соответствующего углу θ, к длине основания для данного угла треугольника.
tan θ = перпендикуляр/основание=p/b
- Котангенс (котангенс) Это обратная величина тангенса.
cot θ = 1/tan θ = основание/перпендикуляр=b/p
- Секанс (сек) Это величина, обратная косинусу.
сек θ = 1/cos θ = гипотенуза/основание=h/b
- Косеканс (косек) Это величина, обратная синусу.

cosec θ =1/sin θ = гипотенуза/перпендикуляр=h/p
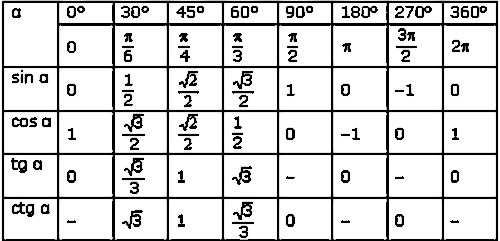
Некоторые тригонометрические соотношения вместе с некоторыми стандартными углами приведены в таблице ниже: °
119
 3
3Если тангенс (А + В) = √3 и тангенс (А – В) = 1/√3, 0°
< А + В ≤ 90°; A > B, затем найдите A и BРешение:
Дано,
tan(A + B) = √3
Так как A + B ≤ 90°,
Следовательно,
A ≤ 90° и B ≤ 90°
Согласно таблице угол, при котором tan принимает значение √3, равен 60°.
Следовательно,
tan(A + B) = √3 = tan 60°
tan(A + B) = tan 60°
A + B = 60° ⇢ (i)
tan(A – B ) = 1/√3
Согласно таблице угол, при котором тангенс приобретает значение 1/√3, равен 30°. Следовательно,
тангенс (A – B) = 1/√3 = тангенс 30°
тангенс (A – B) = тангенс 30°
A – B = 30° ⇢ (ii)
Сложение уравнений (i) и (ii),
2A = 90°
A = 45°
Подстановка значения A в уравнение (i),
45° + B = 60°
B = 60°- 45°
B = 15°
Следовательно, значения A и B, удовлетворяющие данному уравнению, равны 45° и 15° соответственно.

Аналогичные задачи
Вопрос 1: Если 2 sin 2 θ – 1= 0 и 0°< θ< 90°, то найдите значения следующих
а. cos θ + cos 2θ
б. sin θ × sin 2θ
Решение:
2 SIN 2 θ — 1 = 0
2SIN 2 θ = 1
2SIN 2 θ = 1
2SIN 2 θ = 1
2SIN 2 θ = 1
2 2 . 1/√2
Острый угол, для которого значение sin равно 1/√2 = 45°. Следовательно,
sin θ = 1/√2 = sin 45°
θ = 45°
Следовательно,
a. cos θ + cos 2θ
cos 45° + cos 2,45°
cos 45° + cos 90° (подставляем значения из таблицы)
1/√2 + 0 = 1/√2
б. sin θ × sin 2θ
sin 45° × sin 2,45°
sin 45° × sin 90°
1/√2 × 1
1/√2
6 90 sin(A – B) = 1/2 = cos(A + B) и A, B – острые углы.
Решение:
sin(A – B) = 1/2
Так как A, B — острые углы,
Следовательно, A – B также должен быть острым углом.
Острый угол, для которого значение sin равно 1/2 = 30°. Следовательно,
sin(A – B) = sin 30° = 1/2
A – B = 30° ⇢ (i)
Острый угол, для которого значение cos равно 1/2 = 60°, поэтому ,
cos(A + B) = cos 60° = 1/2
A + B = 60° ⇢ (ii)
Сложение уравнений (i) и (ii),
2A = 90°
A = 45°
Подставляя значение A в уравнение (i), получаем
45° – B = 30°
B = 45° – 30°
B = 15°
= cos θ, где 0°< θ< 90°.
Решение:
Острый угол, для которого значения cos и sin равны =45°, следовательно,
cos θ = sin θ = cos 45°
θ = 45°
, Следовательно
2 тангенс 2 θ + cos 2 θ -1
= 2 тангенс 45° × тангенс 45° + cos 45° × cos 45° -1
= 2 × 1 × 1 + 1/√2 × 1/√2 -1
= 2 + 1/2 — 1
= 3/2
Вопрос 4: Найдите θ для 0°<θ <90°, где (2sin θ – 1)(sin θ – 2)=0.
Решение:
(2sin θ — 1) (sin θ — 2) = 0
, глядя на уравнение, чтобы удовлетворить уравнение, либо
(2sin θ — 1) = 0
года = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0. или, (sin θ – 2) = 0sin θ = 1/2
sin θ = 2 (поскольку sin не может превышать 1, поэтому sin θ — 2 не может быть 0.)
sin θ = 1/2 = sin 30 °
θ = 30 °
Cos pi/3 — Найти значение Cos pi/3
LearnPracticeDownload
Значение cos pi/3 равно 0,5 . Cos pi/3 радиан в градусах записывается как cos ((π/3) × 180°/π), т. е. cos (60°). В этой статье мы обсудим методы определения значения cos pi/3 на примерах.
- Cos пи/3: 1/2
- Cos pi/3 в десятичной системе: 0,5
- Cos (-pi/3): 0,5 или 1/2
- Cos pi/3 в градусах: cos (60°)
Каково значение Cos pi/3?
Значение cos pi/3 в десятичной системе равно 0,5. Cos pi/3 также можно выразить с помощью эквивалента заданного угла (pi/3) в градусах (60°).
Cos pi/3 также можно выразить с помощью эквивалента заданного угла (pi/3) в градусах (60°).
Используя преобразование радиан в градусы, мы знаем, что θ в градусах = θ в радианах × (180°/pi)
⇒ пи/3 радиана = пи/3 × (180°/пи) = 60° или 60 градусов
∴ cos pi/3 = cos π/3 = cos(60°) = 1/2 или 0,5
Объяснение:
Для cos pi/3 угол pi/3 лежит между 0 и pi/2 (Первый квадрант). Поскольку функция косинуса положительна в первом квадранте, значение cos pi/3 = 1/2 или 0,5
Поскольку функция косинуса является периодической функцией, мы можем представить cos pi/3 как cos pi/3 = cos(pi/3 + n × 2pi), n ∈ Z.
⇒ cos pi/3 = cos 7pi/3 = cos 13pi/3 и так далее.
Примечание: Поскольку косинус — четная функция, значение cos(-pi/3) = cos(pi/3).
Методы определения значения Cos pi/3
Функция косинуса положительна в 1-м квадранте. Значение cos pi/3 принимается равным 0,5. Мы можем найти значение cos pi/3 по:
- Используя Unit Circle
- Использование тригонометрических функций
Cos pi/3 с помощью единичной окружности
Чтобы найти значение cos π/3 с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол пи/3 с положительной осью x.

- Косвенный коэффициент пи/3 равен координате х (0,5) точки пересечения (0,5, 0,866) единичной окружности и r.
Следовательно, значение cos pi/3 = x = 0,5
Cos pi/3 в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить cos pi/3 как:
- ± √(1-sin² (пи/3))
- ± 1/√(1 + tan²(pi/3))
- ± раскладушка(пи/3)/√(1 + раскладушка²(пи/3))
- ±√(косек²(пи/3) — 1)/косек(пи/3)
- 1/сек (пи/3)
Примечание: Поскольку pi/3 лежит в 1-м квадранте, окончательное значение cos pi/3 будет положительным.
Мы можем использовать тригонометрические тождества для представления cos pi/3 как
- -cos(pi — pi/3) = -cos 2pi/3
- -cos(pi + pi/3) = -cos 4pi/3
- sin(pi/2 + pi/3) = sin 5pi/6
- sin(pi/2 — pi/3) = sin pi/6
☛ Также проверьте:
- сек 3pi
- соз 13pi/6
- сек Пи
- грех 11pi/6
- соз 5pi/3
- sin пи/3
Примеры использования Cos pi/3
Пример 1.
 Используя значение cos pi/3, решите: (1-sin²(pi/3)).
Используя значение cos pi/3, решите: (1-sin²(pi/3)). Решение:
Мы знаем, (1-sin²(pi/3)) = (cos²(pi/3)) = 0,25
⇒ (1-sin²(pi/3)) = 0,25Пример 2. Найдите значение 2 cos(pi/3)/3 sin(pi/6).
Решение:
Используя тригонометрические тождества, мы знаем, что cos(pi/3) = sin(pi/2 — pi/3) = sin pi/6.
⇒ cos(pi/3) = sin(pi/6)
⇒ Значение 2 cos(pi/3)/3 sin(pi/6) = 2/3Пример 3. Найдите значение cos pi/3, если sec pi/3 равно 2.
Решение:
Так как cos pi/3 = 1/sec(pi/3)
⇒ cos пи/3 = 1/2 = 0,5
перейти к слайдуперейти к слайдуперейти к слайду
Готовы посмотреть на мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Cos pi/3
Что такое Cos pi/3?
Cos pi/3 — значение тригонометрической функции косинуса для угла, равного π/3 радиан. Значение cos pi/3 равно 1/2 или 0,5
Как найти cos pi/3 с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение cos pi/3 может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-sin²(pi/3))
- ± 1/√(1 + tan²(pi/3))
- ± раскладушка(пи/3)/√(1 + раскладушка²(пи/3))
- ±√(косек²(пи/3) — 1)/косек(пи/3)
- 1/сек (пи/3)
☛ Также проверьте: таблицу тригонометрии
Как найти значение Cos pi/3?
Значение cos pi/3 можно рассчитать, построив угол π/3 радиан с осью x, а затем найдя координаты соответствующей точки (0,5, 0,866) на единичной окружности. Значение cos pi/3 равно координате x (0,5).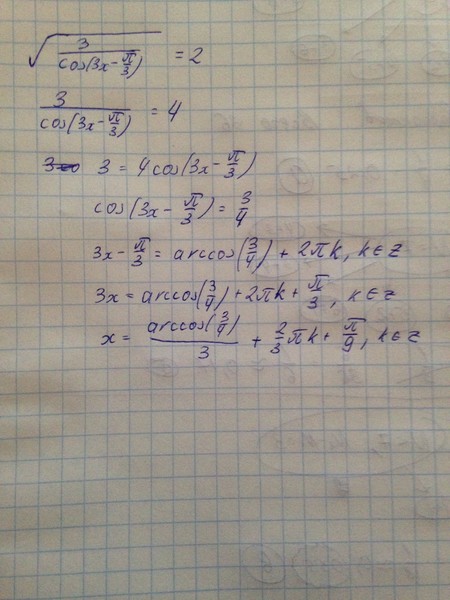



 Используя значение cos pi/3, решите: (1-sin²(pi/3)).
Используя значение cos pi/3, решите: (1-sin²(pi/3)).