7 5 корень: Mathway | Популярные задачи — Таловская средняя школа

Содержание

8; корень 50; 7,5; корень 65; корень

ответ: х = -1

объяснение: напомним основные свойства степени. пусть а > 0, b > 0, n, m — любые действительные числа. тогда

1) an am = an+m

−

3) (an)m = anm

4) (ab)n = an bn

(

)

6) an > 0

7) an > 1, если a > 1, n > 0

8) an < am, если a > 1, n < m

9) an > am, если 0< a < 1, n < m

в практике часто используются функции вида y = ax, где a — заданное положительное число, x — переменная. такие функции называют показательными. это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

определение. показательной функцией называется функция вида y = ax, где а — заданное число, a > 0,

≠

показательная функция обладает следующими свойствами

1) область определения показательной функции — множество всех действительных чисел.

это свойство следует из того, что степень ax где a > 0, определена для всех действительных чисел x.

2) множество значений показательной функции — множество всех положительных чисел.

чтобы убедиться в этом, нужно показать, что уравнение ax = b, где а > 0,

≠

, не имеет корней, если

≤

, и имеет корень при любом b > 0.

3) показательная функция у = ax является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 < a < 1.

это следует из свойств степени (8) и (9)

построим графики показательных функций у = ax при a > 0 и при 0 < a < 1.

использовав рассмотренные свойства отметим, что график функции у = ax при a > 0 проходит через точку (0; 1) и расположен выше оси oх.

если х < 0 и |х| увеличивается, то график быстро приближается к оси oх (но не пересекает её). таким образом, ось ох является горизонтальной асимптотой графика функции у = ax при a > 0.

если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

график функции у = ax при 0 < a < 1 также проходит через точку (0; 1) и расположен выше оси ох.

если х > 0 и увеличивается, то график быстро приближается к оси ох (не пересекая её). таким образом, ось ох является горизонтальной асимптотой графика.

если х < 0 и |х| увеличивается, то график быстро поднимается вверх.

показательные уравнения

рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. решение показательных уравнений часто сводится к решению уравнения ax = ab где а > 0,

≠

, х — неизвестное. это уравнение решается с свойства степени: степени с одинаковым основанием а > 0,

≠

равны тогда и только тогда, когда равны их показатели.

решить уравнение 23x • 3x = 576

так как 23x = (23)x = 8x, 576 = 242, то уравнение можно записать в виде 8x • 3x = 242, или в виде 24x = 242, откуда х = 2.

ответ х = 2

решить уравнение 3х + 1 — 2 • 3x — 2 = 25

вынося в левой части за скобки общий множитель 3х — 2, получаем 3х — 2(33 — 2) = 25, 3х — 2 • 25 = 25,

откуда 3х — 2 = 1, x — 2 = 0, x = 2

ответ х = 2

решить уравнение 3х = 7х

так как

≠

, то уравнение можно записать в виде

, откуда

(

)

, х = 0

ответ х = 0

решить уравнение 9х — 4 • 3х — 45 = 0

заменой 3х = t данное уравнение сводится к квадратному уравнению t2 — 4t — 45 = 0. решая это уравнение, находим его корни: t1 = 9, t2 = -5, откуда 3х = 9, 3х = -5.

уравнение 3х = 9 имеет корень х = 2, а уравнение 3х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.

ответ х = 2

решить уравнение 3 • 2х + 1 + 2 • 5x — 2 = 5х + 2х — 2

запишем уравнение в виде

3 • 2х + 1 — 2x — 2 = 5х — 2 • 5х — 2, откуда

2х — 2 (3 • 23 — 1) = 5х — 2( 5 2 — 2 )

2х — 2 • 23 = 5х — 2• 23

(

)

−

x — 2 = 0

ответ х = 2

решить уравнение 3|х — 1| = 3|х + 3|

так как 3 > 0,

≠

, то исходное уравнение равносильно уравнению |x-1| = |x+3|

возводя это уравнение в квадрат, получаем его следствие (х — 1)2 = (х + 3)2, откуда

х2 — 2х + 1 = х2 + 6х + 9, 8x = -8, х = -1

проверка показывает, что х = -1 — корень исходного уравнения.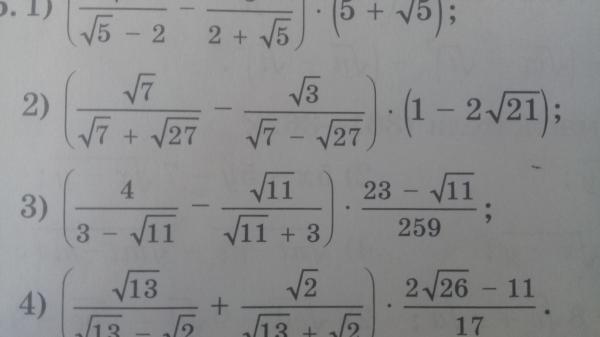

(36/5-корень из 7 + 88/7+корень из 5

Алгебра, 2020-11-17 18:48:05, ЕлизаветаСиянко

Ответ

Ответ разместил: aidar2002032

36 + 88 — 4 =
5 — √7 7+√ 5 √7 +√5

= 36(5 + √7) + 88(7-√ 5) — 4(√7- √5) =
(5 — √7) (5+ √7) (7+√ 5)(7-√ 5) (√7 +√5)(√7- √5)

= 36(5 + √7) + 88(7-√ 5) — 4(√7- √5) =
5² — √7² 7² -√ 5² √7² — √5²

= 36(5 + √7) + 88(7-√ 5) — 4(√7- √5) =
25 — 7 49 — 5 7 — 5

= 36(5 + √7) + 88(7-√ 5) — 4(√7- √5) =
18 44 2

=    2(5 + √7)     +    2(7-√ 5)     —    2 (√7- √5)        =
         1                     1           1
=    2(5 + √7)     +    2(7-√ 5)     —    2 (√7- √5)        =
=    10 + 2√7     +    14   — 2√ 5    —    2√7 + 2√5        = 10 + 14 = 24

Ответ

Ответ разместил: 2vovanavi

1 делить на 2 или 0,5

Ответ

Ответ разместил: luss55

1)9-8х=9
-8х=9-9
-8х=0
х=0
ответ: х=0
2)7-6х=7
-6х=7-7
-6х=0
х=0
ответ: х=0

Ответ

Ответ разместил: Nastya35116

1-й пример решаю с 2- мя условиями, тк не очень понятно записано условие

Ответ

Ответ разместил: mafa091

1. 2=1/7*7=1

Ответ

Ответ разместил: мили241

2√7 = √(4*7) = √28; 7√2 = √(49*2) = √98;

√25 < √28 < √36; √81 < √98 < √100;

5 < √28 < 6; 9 < √98 < 10;

В порядке возрастания:

5; √28; 6; 7; 8; 9; √98; 10.

2√7; 6; 7; 8; 9; 7√2;

Между числами 2√7 и 7√2 расположены целые числа: 6; 7; 8; 9.

Другие вопросы по: Алгебра

По норме рабочий должен изготовить 72 детали, а он изготовил 90 деталей. на сколько процентов рабочий выполнил норму и на сколько процентов он перевыполнил норму?…

Опубликовано: 28.02.2019 01:50

Ответов: 3

.(Вычислить площадь фигуры, заключенной между осью ох, прямой x=3,осью ох и линией y=x(в квадрате)-4х+5)….

Опубликовано: 28.02.2019 09:10

Ответов: 3

38.9. закон архимеда. однородное тело плавает на поверхности керосина так, что объем погруженной части составляет 0. 92 всего объема тела v. определить объем погруженной части vпогр…

Опубликовано: 28.02.2019 15:10

Ответов: 1

1. мерой каких свойств тела является его масса? 2. почему нагруженную тележку труднее разогнать или остановить, чем ненагруженную?…

Опубликовано: 02.03.2019 13:50

Ответов: 1

Составить по 6 слов муж. род, жен. род, сред. род…

Опубликовано: 02.03.2019 18:40

Ответов: 3

Сочинени на тему ‘смех’ в комедии «ревизор».напишите…

Опубликовано: 03.03.2019 07:10

Ответов: 1

Квадратный корень из 50 — Как найти квадратный корень из 50?

LearnPracticeDownload

Квадратный корень из 50 — это число, которое при умножении само на себя дает 50. Нахождение квадратного корня числа чрезвычайно важно для нахождения длины стороны квадрата по его площади. Теперь мы рассмотрим, как найти значение квадратного корня из 50, и решим некоторые задачи, которые помогут вам лучше понять это.

Квадратный корень из 50: √ 50 = 7,0710678…
Квадрат 50: 50 ² = 2500

1.	Что такое квадратный корень из 50?
2.	Является ли квадратный корень из 50 рациональным или иррациональным?
3.	Как найти квадратный корень из 50?
4.	Задающие вопросы
5.	Часто задаваемые вопросы о квадратном корне из 50

Что такое квадратный корень из 50?

Квадратный корень из числа — это число, которое при умножении само на себя дает исходное число.

Например, квадратный корень из 25 равен 5, так как 5 умножить на 5 дает 25. Однако у вас также могут быть квадратные корни некоторых чисел, которые не дают целых чисел, например 50. Мы можем выразить квадратный корень из 50 по-разному:

Десятичная форма: 7,071
Радикальная форма: √50 = 5√2
Форма экспонента: 50 ^1/2

Является ли квадратный корень из 50 рациональным или иррациональным?

Десятичная часть квадратного корня из 50 не является конечной. Это определение иррационального числа. Это также не может быть выражено как отношение p/q, которое говорит нам, что это иррационально.
Глядя на десятичную форму корня 50, мы видим, что он никогда не заканчивается: √50 = 7,0710678118…….
Таким образом, мы можем сделать вывод, что Квадратный корень из 50 иррационален.

Как найти квадратный корень из 50?

Есть 2 основных метода, которые мы используем для нахождения квадратного корня из 50:

Факторизация простых чисел
Длинное деление

Разложение на простые множители

Чтобы найти квадратный корень из 50, мы сначала выразим его через простые множители.

50 = 2 × 5 × 5

Далее это число можно уменьшить до 50 = 2 × 5 ²
Наконец, найти корень отсюда очень легко,

√50 = √(25 × 2) = 5√2 = 5 × 1,414 = 7,07

Следовательно, Квадратный корень из 50 ≅ 7,07

Шаг деления

цифры 50. Мы также соединяем 0 в десятичных дробях парами по 2 слева направо.
Шаг 2: Найдите такое число, чтобы при умножении его на себя произведение было меньше или равно 50. Мы знаем, что 7 × 7 = 49что меньше 50. Разделив 50 на 7, мы получим 7 в частном и 1 в остатке.
Шаг 3: Поместите десятичную дробь после частного, так как мы сейчас делим, используя 0 из десятичной части 50. Не забудьте перетащить пару нулей вниз, получив делимое 100. Кроме того, добавление 7 само по себе дает нам 14 который становится начальными цифрами нашего следующего делителя.

Шаг 4: Теперь у нас есть новый делитель 14X. Нам нужно найти такое значение X, чтобы 14X × X дало нам значение меньше 100. Только 0 заполняет позицию X, поэтому делимое равно 140, а частное теперь равно 7,0.
Шаг 5: Следующий делитель будет 140 + 0, а делимое будет 10000. Продолжаем делать те же шаги, пока не получим нужное количество десятичных знаков.

Таким образом, наше длинное деление теперь выглядит так:

Таким образом, Квадратный корень из 50 равен 7,071

Исследуйте Квадратные корни с помощью иллюстраций и интерактивных примеров

Квадратный корень из 10

Квадратный корень из 25
Квадратный корень из 5
Квадратный корень из 15

Загадочные вопросы

Чему равен квадратный корень из 450?
Является ли -7,071 корнем из 50? Если да, то почему?
Найдите квадратный корень из:
- 0,5
- 500000

Пример 1: Кевин хочет купить квадратный участок площадью 50 квадратных футов. Он планирует ограждать территорию и хочет рассчитать стоимость этого. Если стоимость километра ограждения 40 долларов, найдите стоимость ограждения всего периметра участка?
Решение:
- Во-первых, для расчета стоимости ограждения нам понадобится периметр земли.
- Чтобы найти периметр, нам нужно сначала найти длину стороны.
- Длина стороны равна квадратному корню из площади квадрата.
Следовательно, длина стороны здесь будет √50 = 7,071, а периметр в 4 раза больше.
Следовательно, общая стоимость ограждения = 4 × 7,071 × 40 = 1131,36 доллара.
Пример 2: 909:13 Рэндал едет по шоссе со средней скоростью 5√50 миль/ч в течение получаса. Какое расстояние он преодолевает?
Решение:
Нам нужно использовать формулу Расстояние = Скорость × Время
Скорость = 5√50 = 35,355 миль/ч
Время = 0,5 часа
Используя формулу, Расстояние = 35,355 × 0,5 = 17,677
Таким образом, Майкл преодолевает расстояние в 17,677 миль.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы о квадратном корне из 50
Что такое квадратный корень из 50?
Квадратный корень из 50 равен √50 = 7,071.
Чему равен квадрат 50?
Квадрат 50 равен 50 ² = 2500.
Чему равен квадратный корень из 50 в упрощенном виде?
Квадратный корень из 50 в упрощенной форме равен 5√2.
Является ли квадратный корень из 50 рациональным числом?
Квадратный корень из 50 является иррациональным числом, поскольку он не имеет конца. Оно не может быть выражено в форме p/q, что делает число рациональным.
Какова экспоненциальная форма корня 50?
Показатель степени, если корень 50 равен 50 ^1/2 .
Рабочие листы по математике и
наглядный курс
Рационализация знаменателя — ChiliMath
Поиск
Рационализировать знаменатель – значит исключить любые радикальные выражения в знаменателе, такие как квадратные корни и кубические корни. Основная идея состоит в том, чтобы умножить исходную дробь на соответствующее значение, чтобы после упрощения знаменатель больше не содержал радикалов.
Примечание: В этом уроке для простоты мы сосредоточимся только на квадратных корнях.
Когда знаменатель одночленный, основная стратегия состоит в том, чтобы применить тот факт, что
С другой стороны, если знаменатель двучленный, пригодится понятие сопряженного числа. Сопряжение бинома равно самому биному, однако средний знак изменяется или переключается .
Вот несколько примеров двучленов с соответствующими сопряженными.
Но что еще более важно, обратите внимание, что произведение данного бинома и его сопряженного является выражением без подкоренного символа.
Давайте рассмотрим несколько примеров!
Примеры рационализации знаменателя
Пример 1 : Рационализация знаменателя \large{{5 \over {\sqrt 2 }}}. Упростите дальше, если это необходимо.
Знаменатель содержит подкоренное выражение — квадратный корень из 2. Удалите подкоренное выражение, умножив его на себя, что равно \sqrt 2, поскольку \sqrt 2 \cdot \sqrt 2 = \sqrt 4 = 2 .
Однако тем самым мы меняем «значение» или значение исходной дроби. Чтобы сбалансировать это, сделайте то же самое сверху, умножив на то же значение.
Здесь мы умножаем исходную дробь на \large{{{\sqrt 2 } \over {\sqrt 2 }}}, что эквивалентно 1.
Помните, что любое число, умноженное на 1, возвращает исходное число, таким образом, мы меняем форму, но не исходное значение самого числа!
Итак, простое решение этой проблемы показано ниже.
Окончательный ответ содержит знаменатель без подкоренного символа, и поэтому мы можем утверждать, что успешно рационализировали его.
Пример 2 : Рационализируйте знаменатель \large{{6 \over {\sqrt 3 }}}. Затем упростите, если необходимо.
Обратите внимание, что знаменатель имеет квадратный корень из 3. Нам необходимо рационализировать его, избавившись от подкоренного символа.
Это означает, что мы должны умножить исходную дробь на \large{{{\sqrt 3 } \over {\sqrt 3 }}}.
Да, радикальный символ внизу исчез, но мы все еще можем что-то сделать. Упростите дальше, убрав общие факторы.
Пример 3 : Рационализация \large{\sqrt {{{27} \over {12}}}}.
Здесь мы имеем квадратный корень из целой дроби. Первым шагом является применение правила отношения квадратных корней . Это позволяет нам генерировать дробь с отличным числителем и знаменателем с радикальными символами.
ЧАСТНОЕ ПРАВИЛО КВАДРАТНЫХ КОРНЕЙ
Применяя приведенное выше правило, мы получаем более знакомую нам задачу.
«Новая» форма данной задачи имеет знаменатель root 12 , поэтому мы умножим его на \large{{{\sqrt {12} } \over {\sqrt {12} }}}.
Как видите, я не умножал на радикалы числителя, потому что число будет увеличиваться, а значит, упростить его будет труднее. Таким образом, мы сможем довольно легко упростить числитель, поскольку подкоренные числа меньше, если оставить их как есть.
Пример 4 : Упростите, рационализируя знаменатель \large{{{7\sqrt {10} } \over {\sqrt 2 }}}.
Умножьте числитель и знаменатель на \sqrt 2 . При этом радикал в знаменателе должен исчезнуть.
Мы пока не можем остановиться на этом, потому что подкоренное выражение в числителе содержит совершенный квадратный множитель. Продолжим наше упрощение.
Отмените общие множители, чтобы получить окончательный ответ. Вы видите, что \large{{{14} \over 2} = 7}.
Пример 5 : Упростите, рационализируя знаменатель \large{{{6 — \sqrt 5 } \over {\sqrt 8 }}}. 92}} \right) является совершенным квадратным числом.
Пример 6 : Рационализация \large{{2 \over {3 + \sqrt 3 }}}.
Эта задача немного отличается, потому что знаменатель теперь представляет собой двучлен, содержащий два члена. Чтобы избавиться от корня в знаменателе, умножим верх и низ на , сопряженное данного знаменателя.
Как получить сопряжение знаменателя? Возьмите тот же знаменатель, но поменяйте средний знак на 9.0913 .
Средний знак исходного знаменателя меняется с положительного на отрицательный. Мы выбрали множитель, который может рационализировать знаменатель: \large{{{3 — \sqrt 3 } \over {3 — \sqrt 3 }}}.
Вот наше решение.
Пример 7 : Рационализация \large{{3 \over {2 — \sqrt 2 }}}.
Знаменатель имеет отрицательный знак в середине , поэтому у сопряженного числа положительный средний знак.
Множитель, используемый для рационализации знаменателя, равен 9. 0907
Вот наше решение.
Нет общих множителей между числителем и знаменателем, поэтому это наш окончательный ответ.
Пример 8 : Рационализация \large{{{\sqrt 7} \over { — 3 — \sqrt 7 }}}.
Данным знаменателем является

, что делает его сопряженным
Учитывая задачу:
Умножьте числитель и знаменатель исходной дроби на , сопряженный знаменателю .
Распределите числители и СКОЛЬЗИТЕ знаменатели.
Средние члены знаменателя выпадут, потому что они «одинаковы» по значениям, но противоположны по знаку.
Упростите корни чисел с полным квадратом, т. е. \sqrt {49} = 7.
Вычтите значения в знаменателе, 9 — 7 = 2.
Если возможно, сократите дробь самые низкие его условия. Похоже, между верхом и низом нет ничего, что можно было бы компенсировать. Поэтому оставьте это как наш окончательный ответ.
Пример 9 : Рационализация \large{{{\sqrt 6 — \sqrt 2} \over {\sqrt 6 + \sqrt 2 }}}.
Переверните средний знак знаменателя, чтобы получить его сопряженное число. Это означает, что сопряжение \sqrt 6 + \sqrt 2 равно \sqrt 6 — \sqrt 2 .
Умножьте верх и низ на сопряженное.
Примените метод FOIL для раскрытия биномов.
После расширения с помощью FOIL средние члены числителя будут добавлены, а средние члены знаменателя будут удалены.
При каждой возможности упрощайте корни совершенных квадратных чисел
Сложите или вычтите целые числа, полученные после извлечения квадратного корня из совершенных квадратных чисел.
Теперь упростите
Не забудьте разбить его на произведение, один из множителей которого является числом в совершенном квадрате.
Очевидно, что 12 = 4 х 3. Это идеальный выбор множителей, поскольку число 4 — полный квадрат.
Перепишите радикал 12 как произведение радикалов его множителей .
Мы знаем, что квадратный корень из 4 равен 2!
Упростить путем умножения
Общий множитель числителя равен 4. Это означает, что мы можем вынести множитель 4 за скобки.
Отменить общие множители между числителем и знаменателем
Запишите окончательный ответ.
Пример 10 : Рационализация \large{{{\sqrt 2 + \sqrt 8} \over { — \sqrt 2 — \sqrt 8 }}}.
Умножьте данную дробь, как верхнюю, так и нижнюю, на сопряженную часть знаменателя.
А пока умножьте двучлены, расположив их рядом.
Расширьте биномы, используя метод FOIL.
Сократите термины, которые являются «одинаковыми», но противоположными по знаку.
Получить точные значения квадратных корней из совершенных квадратных чисел.
No related posts.