Алгебра – 9 класс. Системы неравенств
Дата публикации: .
Система неравенств
Ребята, вы изучили линейные и квадратные неравенства, научились решать задачи на эти темы. Теперь давайте перейдем к новому понятию в математике – система неравенств. Система неравенств похожа на систему уравнений. Вы помните системы уравнений? Системы уравнений вы изучали в седьмом классе, постарайтесь вспомнить, как вы их решали.
Введем определение системы неравенств.
Несколько неравенств с некоторой переменой х образуют систему неравенств, если нужно найти все значения х, при которых каждое из неравенств образует верное числовое выражение.
Любое значение x, при которых каждое неравенство принимает верное числовое выражение, является решением неравенства. Также может называться и частным решением.
А что есть частное решение? Например, в ответе мы получили выражение х>7. Тогда х=8, или х=123, или какое-либо другое число большее семи – частное решение, а выражение х>7 – общее решение.
Как мы объединяли систему уравнений? Правильно, фигурной скобкой, так вот с неравенствами поступают также. Давайте рассмотрим пример системы неравенств: $\begin{cases}x+7>5\\x-3
Если система неравенств состоит из одинаковых выражений, например, $\begin{cases}x+7>5\\x+7
Так, что же значит: найти решение системы неравенств?
Решение неравенства – это множество частных решений неравенства, которые удовлетворяют сразу обоим неравенствам системы.
Общий вид системы неравенств запишем в виде $\begin{cases}f(x)>0\\g(x)>0\end{cases}$
Обозначим $Х_1$ – общее решение неравенства f(x)>0.
$Х_2$ – общее решение неравенства g(x)>0.
$Х_1$ и $Х_2$ – это множество частных решений.
Решением системы неравенств будут числа, принадлежащие, как $Х_1$, так и $Х_2$.
 Итак, решением нашего неравенство будет множество $А= Х_1∩ Х_2$.
Итак, решением нашего неравенство будет множество $А= Х_1∩ Х_2$.Примеры решений систем неравенств
Давайте посмотрим примеры решения систем неравенств.
Решите систему неравенств.
а) $\begin{cases}3x-1>2\\5x-10 b) $\begin{cases}2x-4≤6\\-x-4
Решение.
а) Решим каждое неравенство отдельно.
$3х-1>2; \; 3x>3; \; x>1$.
$5x-10
Отметим наши промежутки на одной координатной прямой.
Решением системы будет отрезок пересечения наших промежутков. Неравенство строгое, тогда отрезок будет открытым.
Ответ: (1;3).
б) Также решим каждое неравенство отдельно.
$2x-4≤6; 2x≤ 10; x ≤ 5$.
$-x-4-5$.
Решением системы будет отрезок пересечения наших промежутков. Второе неравенство строгое, тогда отрезок будет открытым слева.
Давайте обобщим полученные знания.
Допустим, необходимо решить систему неравенств:
$\begin{cases}f_1 (x)>f_2 (x)\\g_1 (x)>g_2 (x)\end{cases}$.
Тогда, интервал ($x_1; x_2$) – решение первого неравенства. 2+36
2+36
Урок 28. системы неравенств с двумя переменными — Алгебра — 9 класс
Рассмотрим систему неравенств с двумя переменными.
y – x>5,
x2 – 1>y
Пара чисел 6 и 12 являются решением данной системы, так как при подстановке этих значений вместо переменных получаются верные числовые неравенства.
Сделаем вывод: пара чисел, которая является общим решением всех неравенств системы, называется решением системы неравенств с двумя переменными, а множеством решений системы неравенств с двумя переменными является пересечение множеств решений входящих в нее неравенств.
x2 + y2 ≤16
x – y ≤ 4
Для этого изобразим соответствующие графики функций на одной координатной плоскости. Графиком первой функции будет являться окружность с центром в точке начала отсчета и радиусом 4, а второй – прямая.

Множеством решений первого неравенства изначальной системы будет область внутри круга, включая точки окружности, а решением второго неравенства, полуплоскость, которая находится ниже прямой, включая все точки прямой.
Итак, множество точек, которые являются решением данной системы неравенств является часть плоскости, отмеченная на рисунке двойной штриховкой.
Рассмотрим еще один пример.
y>x2
x2 + y2<25
Множеством точек, задаваемым первым неравенством, является часть плоскость, расположенная выше параболы игрик равен икс в квадрате плюс три.
А второе неравенство задает множество точек, расположенных внутри круга с центром в точек нуль нуль и радусом 5.
Пересечение этих множеств является решением данной системы неравенств.
Решение систем неравенств с двумя переменными, алгебра ,9 класс
Предмет: | алгебра | |||||
Дата: 4. | ФИО учителя: Харченко Татьяна Викторовна | |||||
Класс: 9-Б | Кол-во присутствующих:17 | Кол-во отсутствующих:2 | ||||
Тема урока | Решение систем неравенств с двумя переменными | |||||
Цели обучения данного урока | -уметь решать системы неравенств с двумя переменными | |||||
Предполагаемый результат | Все учащиеся смогут:
| |||||
Большинство учащихся смогут: решать системы нелинейных неравенств с двумя переменными, содержащими квадратичную функцию и окружность, гиперболу и окружность, окружности с разными центрами, гиперболу, параболу и прямые. | ||||||
Некоторые учащиеся смогут: решать системынелинейных неравенств с двумя переменными с модулем, находитьобщее решение системы нелинейных уравнений с двумя переменными с модулем | ||||||
Языковая цель | Развитие навыков: построения графиков линейной, квадратичной, дробно-рациональной функций и окружности, нахождения решений систем неравенств с двумя переменными Основные термины и словосочетания:
Полиязычие:перевод терминовна казахский и английский языки; Используемый язык для диалога/письма на уроке: побуждающий диалог Вопросы для обсуждения:
| |||||
Ценности | — умение работать в команде; -умение ставить правильно проблемный вопрос; -умение анализировать и обобщать. | |||||
Предшествующие знания | Линейная функция и ее график, квадратичная функция и ее график, дробно-рациональная функция и ее график, уравнение окружности, точки пересечения графиков функций, решение неравенств с двумя переменными. | |||||
План | ||||||
Планируемое время | Запланированная деятельность | Ресурсы | ||||
Начало урока (10/) | I. Стадия вызова 1. Организационный момент. Создание положительного эмоционального настроя. Видеоролик « Что происходит в мире за 1 минуту». Исходя из просмотренного видеоролика, учитель предлагает попробовать следовать девиз «Сделай за минуту» и выполнить часть заданий урока в течение 1 минуты. 2.Анаграмма.(улучшение внимания). Из данного слова нужно составить как можно больше слов. Каждую букву разрешается использовать столько раз, сколько она встречается в слове. Тот, кто назовет больше всех слов – победит. На выполнение задания дается 1минуты. (слово – 1 балл, если из 3-5 букв, 2 балла- если из 5-8 букв, 3 балла- из 9 букв) Из слова «Математика» нужно составить как можно больше слов. Каждую букву разрешается использовать столько раз, сколько она встречается в слове, т.е. буквы «а» -три раза, «м», «т»-два раза, а остальные по одному. Возможные варианты ответов: актикт кит мак мат так там тик | тема мама такт тата аким | метка атака катет макет матка тетка мамка | аммиак татами | ||
Из 8-ми букв | ||||||
тематика | ||||||
Из 9-ти букв | ||||||
математик | ||||||
Высокий уровень мышления- из 6-9 букв
Средний уровень мышления- из 4-5 букв
Низкий уровень мышления – только из 3 букв
3. Выход на тему. Прием Мозговой штурм.(1 мин)
Выход на тему. Прием Мозговой штурм.(1 мин)
А) Какие темы мы изучили в 1 четверти и в каком порядке?
Б) Как вы думаете, какой может быть тема нашего урока, если она новая для вас и изучается после темы «Решение неравенств с двумя переменными»?
Б) Буквенно-картинный трехъязычный ребус позволит правильно произнести и записать тему урока (1 мин)
neravenstv
өзгермелі
Дескрипторы:
отгадывают изображения предметов
применяют правила по разгадыванию ребуса
переводят слова на русский язык
записывают предполагаемый ответ
ПК, интерактивная доска, видеоролик
(https://www.youtube.com/watch?v=q8QMa6PWk7w)
4.Актуализация жизненного опыта. Целеполагание.(1 мин)
Зная тему урока, сформулируйте цель нашего урока.
Предполагаемый ответ: научиться решать системы нелинейных неравенств с двумя переменными
4.Кроссенс. Девять картинок связаны одной центральной, расположите их в определенном порядке так, чтобы получился тематический последовательный круг. Объясните ваш выбор.
5. Собери пазл.Каждой группе предлагается пазл «Структурно-логическая таблица по теме: «Неравенства с двумя переменными». Участники команды за 1 минуту должны собрать пазл, который будет верным помощником при изучении новой темы. По истечении 1 минуты команда, закончившая первой, получает право зачитать на свое усмотрение любой из 3 пропущенных вопросов — пазлов и дать ответ на него. Если отвечающий не смог дать ответ, то члены команды вправе ему помочь. Далее отвечает команда, закончившая сбор пазла второй и третьей и т.д. Группа экспертов фиксирует результаты.Дескрипторы:
– собирают целое из частей
– вписывают недостающие термины
–записывают предполагаемый ответ
1. Вставьте пропущенное слово: «Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство
Вставьте пропущенное слово: «Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство
в … числовое неравенство».
2.Задайте неравенством с двумя переменными множество точек, расположенных вне круга с центром в точке(3;-2) и радиусом, равным 5.
3.Решение какого неравенство изображено на графике?
Ответы:
1. Верное
2.
3.
1.Какое неравенство задаёт множество точек круга, включая линию окружности, с центром в точке (-2;6) и радиусом, равным 3?
2. Графиком линейного уравнения с двумя переменными является ….
3.Решение какого неравенство изображено на графике?
Ответы:
1.
2.прямая
3.у
(Ф) После каждого этапа учащиеся отмечают результат своей работы
Я хорошо справился с заданиямиЯ не все понял при выполнении упражнении
Я ничего не понял, надо включаться в работу
Тест 19 эл учебник
Основная часть (20-25 минут)
II. Осмысление
Осмысление
1. Объяснение нового материала (10 мин)
Видеоурок «Системы неравенств с двумя переменными».
2.(Г) Первичное осмысление изученного.
ЗнаниеАналогия. Вспомните алгоритм решения систем неравенств с одной переменной и составьте алгоритм решения систем неравенств с двумя переменными
Заполните таблицу
1.Решить каждое неравенство отдельно2.Найти пересечение решений неравенств 3.Записать общий ответ
Первичная проверка понимания
ДА-НЕТ-ка
Верно ли, что
1.Если обе части неравенства умножить или разделить на одно и то же отрицательное число, то получится равносильное неравенство?
2.Если из одной части неравенства в другую перенести слагаемое с противоположным знаком, то получится верное неравенство?
3.Если к обеим частям неравенства прибавить
( отнять) одно и то же число( выражение) , то получится верное неравенство?
4. Решить систему неравенств с двумя переменными-значит найти множество пар чисел, обращающих каждое неравенство в неверное.
5. Решением системы неравенств является пересечение решений неравенств, входящих в систему.
Нет
Да
Да
Нет
Да
Применение новых знаний
Решите системы неравенств
«5 баллов»-
«4 балла»-
«3 балла»-
Анализ
«ТАНК» – развитие навыков аргументации
Т – тезис (Я считаю, что….)
А – аргументация (Так, как…)
Н – наглядность (Например,….)
К – кольцевание (Таким образом,….)
Математическая модель
Дескрипторы:
условие краткое к задаче-1 балл
математическая модель- 3 балла.
Составление системы неравенств и ее решение 3 балла
Ответ 1 балл.
Сотовая связь действует в радиусе 10 км- 30 км от станции. Нанесите на карту города область, в которой всегда будет работать связь, если станция имеет координаты (5,10)
Синтез
Найди ошибку
1.
Для решения каких проблем можно применять системы неравенств с двумя переменными
Оценка.
Метод «Дуэт». Найдите соответствие между системой неравенств и ее решением (5 мин)
2.3.
4.
5.
А)
В)
С)
D)
E)
Сверка с образцом.
Правильные ответы:
1-Е (2 балла), 2- D (1 балл), 3-А (2 балла), 4-С (3 балла),5-В ( 2 балла)
Итого- 10 баллов. Правильный ответ-1 балл
4. (Формативное оценивание).
Оцените свою работу на уроке с помощью фразеологизмов, приклеив стикеры
светлая голова
каша в голове
ни в зуб ногой
Проанализируйте уровень приобретенных знаний на данном этапе.
«светлая голова» – мне все ясно, я удовлетворен своей работой, могу применять в работе;
«каша в голове» – необходимо еще поработать над собой, чтобы до конца разобрать в материале, но сделаю это самостоятельно;
«ни в зуб ногой» – мне многие моменты не ясны, необходима консультация
III. Подведение итогов.
Подведение итогов.
Рефлексия.
ин)
Стадия рефлексии и оценки.
1. Итог урока.
0-6 баллов- «2»
7-10 баллов- «3»
11-15 баллов-«4»
16-20 баллов- «5»
Рефлексия содержания учебного материала
«Чемодан, мясорубка, корзина»
Чемодан– всё, что пригодится в дальнейшем
Мясорубка– информацию переработаю
Корзина – всё выброшу
Дома: параграф 7, № 117(б,г,д), № 119(б,г)
Творческое задание. Сферы применения неравенств с двумя переменными.
Дополнительная информацияДифференциация – Как вы планируете помогать учащимся? Какие задания вы планируете давать более способным ученикам?
Наблюдения
Были ли цели обучения/урока достижимыми?
Чему сегодня научились учащиеся?
Какой была атмосфера обучения?
Успешными ли были действия по дифференциации между учащимися?
Придерживался ли я временного графика? Какие отступления от плана я сделал и почему?
Итоговое оценивание
Назовите два наиболее успешных момента (как преподавания, так и обучения)
Назовите два момента, которые бы способствовали улучшению урока (как преподавания, так и обучения)
Что нового я узнал о классе и его отдельных учащихся, и как это отразится на проведении моего следующего урока?
Решение систем неравенств (9 класс)
1.
 Решение систем неравенств(9 класс)
Решение систем неравенств(9 класс)А. Нивен
3. Запомним
Решить систему неравенств –это значит найти значение
переменной, при котором верно
каждое из неравенств системы.
4. Запомним
Если надо решить систему неравенств,то:
1) решаем каждое неравенство
системы отдельно
2) изображаем полученные решения на
числовой прямой и смотрим
пересечения этих решений.
Эта общая часть и является
решением данной системы неравенств.
5. Содержание
• Решение систем линейныхнеравенств
• Решение двойных неравенств
• Решение систем, содержащих
квадратные неравенства
6. Решим систему неравенств (состоящую из линейных неравенств)
5х + 1 > 62х – 4
Решение: решим каждое неравенство отдельно
5х + 1 > 6
2х – 4
5х > 6 -1
2х
5х > 5
2х
х >1
х
1
3,5
х
Ответ: (1; 3,5)
7. Решим систему неравенств
5х + 12 ≤ 3х+ 20х
2х + 7 ≥ 0
Решение: решим каждое неравенство отдельно
5х + 12 ≤ 3х+ 20
5х – 3х ≤ — 12 + 20
2х ≤ 8
х≤4
х
х – 2х
2х ≥ -7
-х
х ≥ -7/2
х>-3
х ≥ -3,5
Изобразим на числовой прямой:
-3,5
Ответ: ( -3; 4]
-3
4
8.
 Работа в парах: Решить систему
Работа в парах: Решить системунеравенств:
1) 3х – 2 ≥ х + 1
4 – 2х ≤ х – 2
2) 3х > 12 + 11х
5х – 1 ≥ 0
Проверим ответы:
1) [2; +∞)
2) Нет решения
9. Примеры двойных неравенств
Прочитайте неравенства:-6
-1,2 ≤ х
0
10. Решение двойных неравенств
Решить неравенство: 0Решение: составим систему:
4х + 2 > 0
4х + 2 ≤ 6
Решим каждое неравенство системы отдельно:
1) 4х + 2 > 0
2) 4х + 2 ≤ 6
х > — 0,5
х≤1
Полученные результаты изобразим на числовой прямой:
-0,5
1
х
Ответ: -0,5
(-0,5; 1]
11. Решите неравенства, работая в парах
Решить неравенства:1)
2)
3)
4)
5)
-6 ≤ — 3х ≤ 3
4
-2 ≤ 6х + 7
0,3
0
Проверим
ответы:
1)
2)
3)
4)
5)
[-1; 2]
(2,5; 7]
[- 1,5; — 1)
(-2; 1)
(-4; 0)
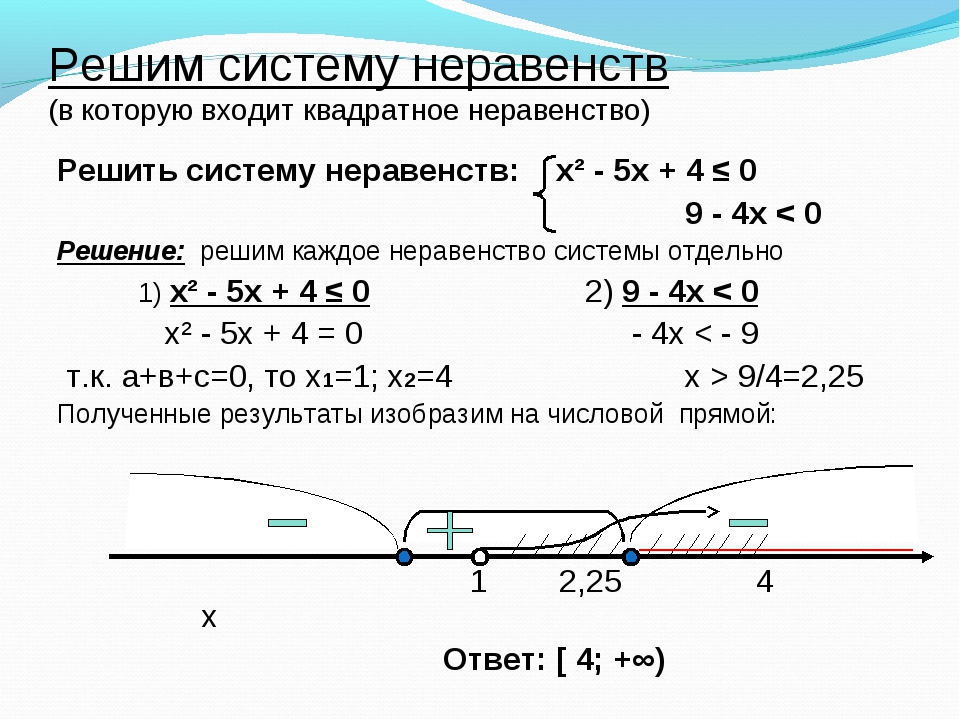
12. Решим систему неравенств (в которую входит квадратное неравенство)
Решить систему неравенств: х² — 5х + 4 ≤ 09 — 4х
Решение: решим каждое неравенство системы отдельно
1) х² — 5х + 4 ≤ 0
х² — 5х + 4 = 0
т.
 к. а+в+с=0, то х1=1; х2=4
к. а+в+с=0, то х1=1; х2=42) 9 — 4х
— 4х
х > 9/4=2,25
Полученные результаты изобразим на числовой прямой:
1
2,25
Ответ: [ 4; +∞)
4
х
13. Решим систему неравенств (в которую входит квадратное неравенство)
Решить систему неравенств:х² — 3х + 2
2х² — 3х – 5 > 0
Решение: решим каждое неравенство отдельно
х² — 3х + 2
2х² — 3х – 5 > 0
Найдем корни соответствующих квадратных уравнений
х² — 3х + 2 = 0
2х² — 3х – 5 = 0
По свойствам коэффициентов имеем:
х1 = 1 х 2 = 2
х1 = -1
Изобразим метод интервала на числовой оси:
-1
Ответ: (- ∞; -1) υ (2,5; +∞)
1
х2 = 5/2= 2,5
2
2,5
х
14. Решим системы неравенств,
1) 6х² — 5х + 1 > 04х – 1 ≥ 0
2) 4х² — 1 ≤ 0
х² > 1
3х² — 2х – 1
х² — х – 6 > 0
15. Решите системы неравенств
1) х² — 10х + 9 ≥ 012 – 3х
Проверим ответы:
2) 2х²- 5х + 2 > 0
4х – 1 ≥ 3
2) [1; 2)
3)
2х² — 7х + 5
2–х≥0
1) (4; 9]
3) (- ∞; 1)
Решение систем неравенств.
 (9 класс)
(9 класс)1. Решение систем неравенств
(9 класс)Разработано учителем математики
МОУ «СОШ» п. Аджером
Корткеросского района Республики Коми
Мишариной Альбиной Геннадьевной
А. Нивен
3. Запомним
Решить систему неравенств –это значит найти значение
переменной, при котором верно
каждое из неравенств системы.
4. Запомним
Если надо решить систему неравенств,то:
1) решаем каждое неравенство
системы отдельно
2) изображаем полученные решения на
числовой прямой и смотрим
пересечения этих решений.
Эта общая часть и является
решением данной системы неравенств.
5. Содержание
• Решение систем линейныхнеравенств
• Решение двойных неравенств
• Решение систем, содержащих
квадратные неравенства
6. Решим систему неравенств (состоящую из линейных неравенств)
5х + 1 > 62х – 4
Решение: решим каждое неравенство отдельно
5х + 1 > 6
2х – 4
5х > 6 -1
2х
5х > 5
2х
х >1
х
1
3,5
х
Ответ: (1; 3,5)
7.
 Решим систему неравенств 5х + 12 ≤ 3х+ 20
Решим систему неравенств 5х + 12 ≤ 3х+ 20х
2х + 7 ≥ 0
Решение: решим каждое неравенство отдельно
5х + 12 ≤ 3х+ 20
5х – 3х ≤ — 12 + 20
2х ≤ 8
х≤4
х
х – 2х
2х ≥ -7
-х
х ≥ -7/2
х>-3
х ≥ -3,5
Изобразим на числовой прямой:
-3,5
Ответ: ( -3; 4]
-3
4
8. Решите самостоятельно:
Решить системунеравенств:
1) 3х – 2 ≥ х + 1
4 – 2х ≤ х – 2
2) 3х > 12 + 11х
5х – 1 ≥ 0
Проверим ответы:
1) [2; +∞)
2) Нет решения
9. Примеры двойных неравенств
Прочитайте неравенства:-6
-1,2 ≤ х
0
10. Решение двойных неравенств
Решить неравенство: 0Решение: составим систему:
4х + 2 > 0
4х + 2 ≤ 6
Решим каждое неравенство системы отдельно:
1) 4х + 2 > 0
2) 4х + 2 ≤ 6
х > — 0,5
х≤1
Полученные результаты изобразим на числовой прямой:
-0,5
1
х
Ответ: -0,5
(-0,5; 1]
11.
 Решите неравенства, самостоятельно Решить неравенства:
Решите неравенства, самостоятельно Решить неравенства:1)
2)
3)
4)
5)
-6 ≤ — 3х ≤ 3
4
-2 ≤ 6х + 7
0,3
0
Проверим
ответы:
1)
2)
3)
4)
5)
[-1; 2]
(2,5; 7]
[- 1,5; — 1)
(-2; 1)
(-4; 0)
12. Решим систему неравенств (в которую входит квадратное неравенство)
Решить систему неравенств: х² — 5х + 4 ≤ 09 — 4х
Решение: решим каждое неравенство системы отдельно
1) х² — 5х + 4 ≤ 0
х² — 5х + 4 = 0
т.к. а+в+с=0, то х1=1; х2=4
2) 9 — 4х
— 4х
х > 9/4=2,25
Полученные результаты изобразим на числовой прямой:
1
2,25
Ответ: [ 4; +∞)
4
х
13. Решим систему неравенств (в которую входит квадратное неравенство)
Решить систему неравенств:х² — 3х + 2
2х² — 3х – 5 > 0
Решение: решим каждое неравенство отдельно
х² — 3х + 2
2х² — 3х – 5 > 0
Найдем корни соответствующих квадратных уравнений
х² — 3х + 2 = 0
2х² — 3х – 5 = 0
По свойствам коэффициентов имеем:
х1 = 1 х 2 = 2
х1 = -1
Изобразим метод интервала на числовой оси:
-1
Ответ: (- ∞; -1) υ (2,5; +∞)
1
х2 = 5/2= 2,5
2
2,5
х
14.
 Решите системы неравенств, работая самостоятельно 1) х² — 10х + 9 ≥ 0
Решите системы неравенств, работая самостоятельно 1) х² — 10х + 9 ≥ 012 – 3х
Проверим ответы:
2) 2х²- 5х + 2 > 0
4х – 1 ≥ 3
2) [1; 2)
3)
2х² — 7х + 5
2–х≥0
1) (4; 9]
3) (- ∞; 1)
http://krasdo.ucoz.ru/ee383358c499.png
Решение систем неравенств 9 класс
Просмотр содержимого документа
«Решение систем неравенств 9 класс»
(9 класс)
А. Нивен
Решить систему неравенств – это значит найти значение переменной , при котором верно каждое из неравенств системы.
Если надо решить систему неравенств, то :
- решаем каждое неравенство системы отдельно
- изображаем полученные решения на числовой прямой и смотрим пересечения этих решений.

Эта общая часть и является решением данной системы неравенств.
- Решение систем линейных неравенств
- Решение двойных неравенств
- Решение систем, содержащих квадратные неравенства
5х + 1 6
2х – 4 3
Решение: решим каждое неравенство отдельно
5х + 1 6 2х – 4 3
5х 6 -1 2х
5х 5 2х
х 1 х 3,5
1 3,5 х
Ответ: (1; 3,5)
— 3 х ≥ -3,5 Изобразим на числовой прямой: -3,5 -3 4 Ответ: ( -3; 4 ] «5х + 12 ≤ 3х+ 20
х 2х+3
2х + 7 ≥ 0
Решение: решим каждое неравенство отдельно
5х + 12 ≤ 3х+ 20 х 2х+3 2х + 7 ≥ 0
5х – 3х ≤ — 12 + 20 х – 2х
2х ≤ 8 -х
х ≤ 4 х — 3 х ≥ -3,5
Изобразим на числовой прямой:
-3,5 -3 4
Ответ: ( -3; 4 ]
12 + 11х 5х – 1 ≥ 0 Проверим ответы: 1) [ 2; +∞ ) 2) Нет решения «Решить систему
неравенств:
1) 3х – 2 ≥ х + 1
4 – 2х ≤ х – 2
2) 3х 12 + 11х
5х – 1 ≥ 0
Проверим ответы:
1) [ 2; +∞ )
2) Нет решения
Прочитайте неравенства :
-6 х 0
-1,2 ≤ х 3,5
0 х ≤ 5,9
0 4х + 2 ≤ 6 Решим каждое неравенство системы отдельно: 1) 4х + 2 0 2) 4х + 2 ≤ 6 х — 0,5 х ≤ 1 Полученные результаты изобразим на числовой прямой: -0,5 1 х Ответ: -0,5 х ≤ 1 или (-0,5; 1 ] «Решить неравенство: 0 4х +2 ≤ 6
Решение: составим систему: 4х + 2 0
4х + 2 ≤ 6
Решим каждое неравенство системы отдельно:
1) 4х + 2 0 2) 4х + 2 ≤ 6
х — 0,5 х ≤ 1
Полученные результаты изобразим на числовой прямой:
-0,5 1 х
Ответ: -0,5 х ≤ 1 или (-0,5; 1 ]
Решить неравенства:
Проверим
ответы:
1) [ -1; 2 ]
2) (2,5; 7 ]
3) [ — 1,5; — 1)
4) (-2; 1)
5) (-4; 0)
- -6 ≤ — 3х ≤ 3
- 4 2х – 1 ≤ 13
- -2 ≤ 6х + 7 1
- 0,3 0,5 + 0,1х 0,6
Решить систему неравенств: х ² — 5х + 4 ≤ 0
9 — 4х 0
Решение: решим каждое неравенство системы отдельно
1) х ² — 5х + 4 ≤ 0 2) 9 — 4х 0
х ² — 5х + 4 = 0 — 4х
т. к. а+в+с=0, то х 1 =1; х 2 =4 х 9/4=2,25
к. а+в+с=0, то х 1 =1; х 2 =4 х 9/4=2,25
Полученные результаты изобразим на числовой прямой:
1 2,25 4 х
Ответ: [ 4; + ∞ )
0 Решение: решим каждое неравенство отдельно х ² — 3х + 2 0 2х ² — 3х – 5 0 Найдем корни соответствующих квадратных уравнений х ² — 3х + 2 = 0 2х ² — 3х – 5 = 0 По свойствам коэффициентов имеем: х 1 = 1 х 2 = 2 х 1 = -1 х 2 = 5/2= 2,5 Изобразим метод интервала на числовой оси: -1 1 2 2,5 х Ответ: (- ∞; -1) υ (2,5; +∞) «Решить систему неравенств:
х ² — 3х + 2 0
2х ² — 3х – 5 0
Решение: решим каждое неравенство отдельно
х ² — 3х + 2 0 2х ² — 3х – 5 0
Найдем корни соответствующих квадратных уравнений
х ² — 3х + 2 = 0 2х ² — 3х – 5 = 0
По свойствам коэффициентов имеем:
х 1 = 1 х 2 = 2 х 1 = -1 х 2 = 5/2= 2,5
Изобразим метод интервала на числовой оси:
-1 1 2 2,5 х
Ответ: (- ∞; -1) υ (2,5; +∞)
0 4х – 1 ≥ 0 2) 4х ² — 1 ≤ 0 х ² 1 3х ² — 2х – 1 0 х ² — х – 6 0 «1) 6х ² — 5х + 1 0
4х – 1 ≥ 0
2) 4х ² — 1 ≤ 0
х ² 1
х ² — х – 6 0
0 4х – 1 ≥ 3 3) 2х ² — 7х + 5 0 2 – х ≥ 0 Проверим ответы: 1) (4; 9 ] 2) [ 1; 2) 3) (- ∞ ; 1 ) «1) х ² — 10х + 9 ≥ 0
12 – 3х 0
2) 2х ² — 5х + 2 0
4х – 1 ≥ 3
3) 2х ² — 7х + 5 0
2 – х ≥ 0
Проверим ответы:
1) (4; 9 ]
2) [ 1; 2)
3) (- ∞ ; 1 )
Как решать систему неравенств 8 класс
Основные понятия
Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Числовое неравенство — в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Типы неравенств
Строгие — используют только больше (>) или меньше (<)
- a < b — это значит, что a меньше, чем b.
- a > b — это значит, что a больше, чем b.
- a > b и b < a означают одно и тоже, то есть равносильны.
Нестрогие — используют сравнения ≥ (больше или равно) или ≤ (меньше или равно)
- a ≤ b — это значит, что a меньше либо равно b.
- a ≥ b — это значит, что a больше либо равно b.
- знаки ⩽ и ⩾ являются противоположными.
Другие типы
- a ≠ b — означает, что a не равно b.
- a ≫ b — означает, что a намного больше, чем b.

- a ≪ b — означает, что a намного меньше, чем b.
- знаки >> и << противоположны.
Система неравенств
Чтобы щелкать задачки, нам пригодятся свойства числовых неравенств. Вот они:
Если а > b , то b < а. Также наоборот: а < b, то b > а.
Если а > b и b > c, то а > c. И также если а < b и b < c, то а < c.
Если а > b, то а + c > b+ c (и а – c > b – c).
Если же а < b, то а + c < b + c (и а – c < b – c). К обеим частям можно прибавлять или вычитать одну и ту же величину.
Если а > b и c > d, то а + c > b + d.
Если а < b и c < d, то а + c < b + d.
Два неравенства одинакового смысла можно почленно складывать. Но важно перепроверять, т.к. возможны исключения. Например, если из 12 > 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если а > b и c < d, то а – c > b – d.
Если а < b и c > d, то а – c < b – d.
Из одного неравенства можно почленно вычесть другое противоположного смысла, оставляя знак того, из которого вычиталось.
Если а > b, m — положительное число, то mа > mb и
.Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
.
Если же а > b, n — отрицательное число, то nа < nb иОбе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.
Если а > b и c > d, где а, b, c, d > 0, то аc > bd.
Если а < b и c < d, где а, b, c, d > 0, то аc < bd.
Неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствием является: если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2. На множестве положительных чисел обе части можно возвести в квадрат.
На множестве положительных чисел обе части можно возвести в квадрат.
- Если а > b, где а, b > 0, то .
Если а < b , то .
Таблица числовых промежутков
Полезна тем, что с ее помощью удобно записывать множество решений.
Неравенство | Графическое решение | Форма записи ответа |
x < c | x ∈ (−∞; c) | |
x ≤ c | x ∈ (−∞; c] | |
x > c | x ∈ (c; +∞) | |
x ≥ c | x ∈ (c; +∞) |
Еще один важный шаг — запись ответа.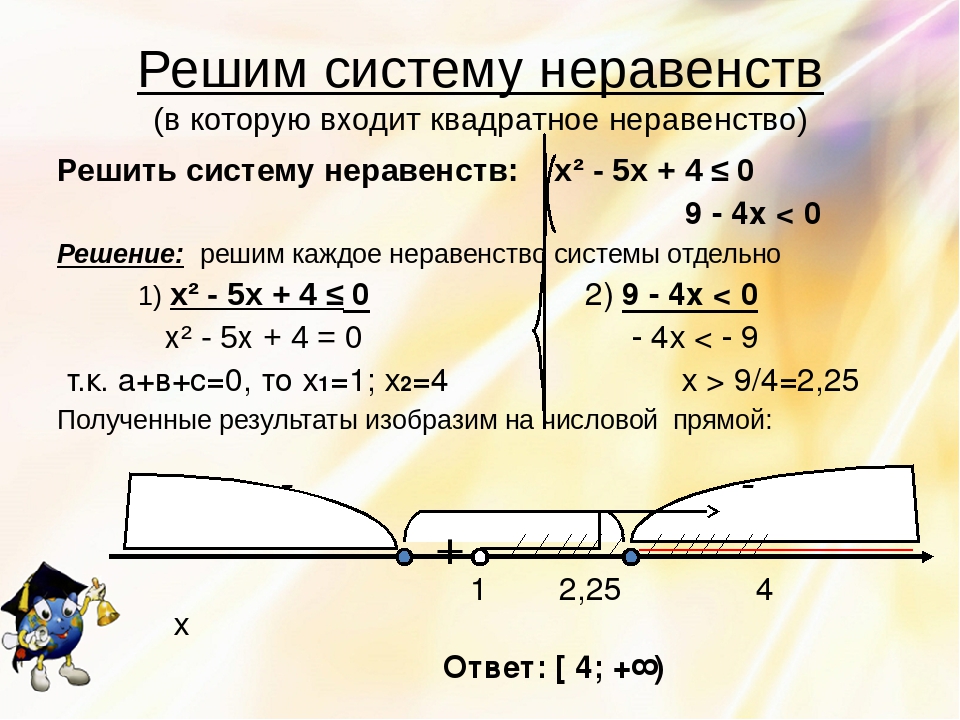 Вот, как правильно это делать:
Вот, как правильно это делать:
- Если знак строгий (>, <), точка на оси будет не закрашена, а скобка — круглой.
- Если знак нестрогий (≥, ≤), точка на оси будет закрашена, а скобка — квадратной.
- Скобка, рядом со знаком бесконечности всегда круглая.
Решение системы неравенств
Линейное неравенство — то, в котором неизвестное представлено в первой степени. Для его решения нужно, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице. Алгоритм решения:
1. Раскрыть скобки, перенести неизвестное в левую часть, числа в правую и привести подобные слагаемые. Получится одно из следующих видов:
- ax < b,
- ax ≤ b,
- ax > b,
- ax ≥ b.
2. Если получилось ax ≤ b.Для его решения необходимо поделить левую и правую часть на коэффициент перед неизвестным a.
3. Если a > 0, то x ≤ ba.
Если a < 0, то знак меняется на противоположный.
Получаем x ≥ ba.
4. Записываем ответ как он есть или в соответствии с таблицей числовых промежутков.
Решим пример
3 * (2 − x) > 18
Как решаем
Ответ: x < −4 или в числовом промежутке x ∈ (−∞; −4). |
И еще один
Как решаем
Ответ: х < – 2. |
Последний, чтобы разобраться наверняка
Как решаем
Ответ: числовой промежуток x ∈ (– 2; 0]. |
Запомнить все правила и научиться быстро их применять помогут на уроках математики в детской школе Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
Графические системы линейных неравенств — Элементарная алгебра
Системы линейных уравнений
Цели обучения
К концу этого раздела вы сможете:
- Определить, является ли упорядоченная пара решением системы линейных неравенств
- Решите систему линейных неравенств, построив график
- Решите приложения систем неравенств
Прежде чем начать, пройдите тест на готовность.
- График на числовой прямой.
Если вы пропустили эту проблему, просмотрите (рисунок). - Решите неравенство.
Если вы пропустили эту проблему, просмотрите (рисунок). - Определите, является ли заказанная пара решением для системы.
Если вы пропустили эту проблему, просмотрите (рисунок)
Определить, является ли упорядоченная пара решением системы линейных неравенств
Определение системы линейных неравенств очень похоже на определение системы линейных уравнений.
Система линейных неравенств
Два или более линейных неравенства, сгруппированных вместе, образуют систему линейных неравенств.
Система линейных неравенств выглядит как система линейных уравнений, но вместо уравнений в ней есть неравенства. Ниже представлена система двух линейных неравенств.
Для решения системы линейных неравенств мы найдем значения переменных, которые являются решениями обоих неравенств. Мы решаем систему, используя графики каждого неравенства, и показываем решение в виде графика.Мы найдем на плоскости область, содержащую все упорядоченные пары, удовлетворяющие обоим неравенствам.
Мы решаем систему, используя графики каждого неравенства, и показываем решение в виде графика.Мы найдем на плоскости область, содержащую все упорядоченные пары, удовлетворяющие обоим неравенствам.
Решения системы линейных неравенств
Решениями системы линейных неравенств являются значения переменных, которые делают все неравенства истинными.
Решение системы линейных неравенств показано заштрихованной областью в системе координат x-y , которая включает все точки, чьи упорядоченные пары делают неравенства истинными.
Чтобы определить, является ли упорядоченная пара решением системы двух неравенств, мы подставляем значения переменных в каждое неравенство. Если упорядоченная пара выполняет оба неравенства, это решение системы.
Определите, является ли заказанная пара решением для системы.
ⓐ (-2, 4) ⓑ (3,1)
Решение
- ⓐ Является ли упорядоченная пара (−2, 4) решением?
Упорядоченная пара (−2, 4) выполнила оба неравенства. Следовательно, (−2, 4) — решение этой системы.
Следовательно, (−2, 4) — решение этой системы.
- ⓑ Является ли упорядоченная пара (3,1) решением?
Упорядоченная пара (3,1) сделала одно неравенство истинным, а другое — ложным. Следовательно, (3,1) не является решением этой системы.
Определите, является ли заказанная пара решением для системы.
ⓐⓑ
Определите, является ли заказанная пара решением для системы.
ⓐⓑ
Решите систему линейных неравенств с помощью построения графиков
Решением единственного линейного неравенства является область на одной стороне граничной линии, которая содержит все точки, которые делают неравенство истинным.Решением системы двух линейных неравенств является область, содержащая решения обоих неравенств. Чтобы найти эту область, мы построим график каждого неравенства отдельно, а затем определим область, в которой оба неравенства верны. Решение всегда отображается в виде графика.
Как решить систему линейных неравенств
Решите систему, построив график.
Решите систему, построив график.
Решите систему, построив график.
Решите систему линейных неравенств с помощью построения графиков.
- Изобразите первое неравенство.
- Постройте граничную линию.
- Заштриховать сбоку от ограничивающей линии, где выполняется неравенство.
- На той же сетке нанесите график второго неравенства.
- Постройте граничную линию.
- Заштрихуйте сбоку от границы, на которой выполнено неравенство.
- Решением является область перекрытия штриховки.
- Проверьте, выбрав контрольную точку.
Решите систему, построив график.
Решите систему, построив график.
Решите систему, построив график.
Решите систему, построив график.
Решите систему, построив график.
Системы линейных неравенств с параллельными линиями границ могут не иметь решения. Мы увидим это на (Рисунок).
Решите систему, построив график.
Решение
Нет смысла в обеих заштрихованных областях, поэтому у системы нет решения.У этой системы нет решения.
Решите систему, построив график.
нет решения
Решите систему, построив график.
нет решения
Решите систему, построив график.
Решение
Ни одна точка на граничных линиях не включена в решение, так как обе линии пунктирны.
Решение — это дважды заштрихованная область, которая также является решением.
Решите систему, построив график.
Решите систему, построив график.
Решение приложений систем неравенств
Первое, что нам нужно сделать для решения приложений систем неравенств, — это преобразовать каждое условие в неравенство. Затем мы строим график системы, как делали выше, чтобы увидеть область, содержащую решения. Многие ситуации будут реалистичными только в том случае, если обе переменные положительны, поэтому на их графиках будет отображаться только Квадрант I.
Затем мы строим график системы, как делали выше, чтобы увидеть область, содержащую решения. Многие ситуации будут реалистичными только в том случае, если обе переменные положительны, поэтому на их графиках будет отображаться только Квадрант I.
Кристи продает свои фотографии в киоске на уличной ярмарке. В начале дня она хочет, чтобы на ее стенде было не менее 25 фотографий. Каждая небольшая фотография, которую она показывает, стоит ей 4 фунта стерлингов, а каждая большая фотография — 10 фунтов стерлингов. Она не хочет тратить больше 200 фунтов на фотографии для показа.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему в виде графика.
ⓒ Могла ли она показать 15 маленьких и 5 больших фотографий?
ⓓ Могла ли она показать 3 больших и 22 маленьких фотографии?
Решение
- ⓐ Пусть количество маленьких фото.
количество больших фото
Чтобы найти систему неравенств, переведите информацию.
У нас есть система неравенства. - ⓑ
Для графика, график x + y = 25 в виде сплошной линии.
Выберите (0, 0) в качестве тестовой точки. Поскольку это не делает неравенство
истинным, закрасьте сторону, на которой нет точки (0, 0), красным цветом.
Для построения графика, график 4 x + 10 y = 200 в виде сплошной линии.
Выберите (0, 0) в качестве тестовой точки. Поскольку это не делает неравенство
истинным, закрасьте сторону, которая включает точку (0, 0), синим.
Решение системы — это область графика, которая заштрихована дважды и поэтому заштрихована более темной. - ⓒ Чтобы определить, будут ли работать 10 маленьких и 20 больших фотографий, мы смотрим, находится ли точка (10, 20) в области решения. Нет. Кристи не показывала 10 маленьких и 20 больших фотографий.
- ⓓ Чтобы определить, будут ли работать 20 маленьких и 10 больших фотографий, мы смотрим, находится ли точка (20, 10) в области решения. Это. Кристи могла выбрать отображение 20 маленьких и 10 больших фотографий.
Обратите внимание, что мы также можем протестировать возможные решения, подставляя значения в каждое неравенство.
Прицеп может нести максимальный вес 160 фунтов и максимальный объем 15 кубических футов. Микроволновая печь весит 30 фунтов и имеет объем 2 кубических фута, в то время как принтер весит 20 фунтов и имеет 3 кубических фута пространства.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Можно ли перевозить на этом прицепе 4 микроволновые печи и 2 принтера?
ⓓ Можно ли перевозить на этом прицепе 7 микроволновых печей и 3 принтера?
- ⓐ
- ⓑ
- ⓒ да
- ⓓ нет
Мэри необходимо приобрести запасы листов для ответов и карандашей для стандартного теста, который будет проводиться среди младших классов в ее средней школе. Количество необходимых листов для ответов как минимум на 5 больше, чем количество карандашей.Карандаши стоят 2 фунта, а листы ответов — 1 фунт. Бюджет Мэри на эти принадлежности предусматривает максимальную стоимость в 400 фунтов стерлингов.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли Мэри приобрести 100 карандашей и 100 листов для ответов?
ⓓ Может ли Мэри приобрести 150 карандашей и 150 листов для ответов?
- ⓐ
- ⓑ
- ⓒ нет
- ⓓ нет
Омару нужно съесть не менее 800 калорий, прежде чем отправиться на командную тренировку.Все, что ему нужно, — это гамбургеры и печенье, и он не хочет тратить больше пяти фунтов стерлингов. В гамбургер-ресторане рядом с его колледжем каждый гамбургер содержит 240 калорий и стоит 1,40 фунта стерлингов. Каждое печенье содержит 160 калорий и стоит 0,50 фунтов стерлингов.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Сможет ли он съесть 3 гамбургера и 1 печенье?
ⓓ Сможет ли он съесть 2 гамбургера и 4 печенья?
Решение
ⓐ Давай количество гамбургеров.
количество файлов cookie
Чтобы найти систему неравенств, переведите информацию.
Калории из гамбургеров по 240 калорий каждый плюс калорий из печенья по 160 калорий в каждом должны быть больше 800.
Сумма, потраченная на гамбургеры по 1,40 фунтов стерлингов за каждый, плюс сумма, потраченная на печенье по цене 0,50 фунтов стерлингов, должна быть не более 5,00 фунтов стерлингов.
У нас есть система неравенства.
ⓑ
Решением системы является область графика, которая закрашена дважды и поэтому закрашена темнее.
ⓒ Чтобы определить, соответствуют ли 3 гамбургера и 2 печенья критериям Омара, мы смотрим, находится ли точка (3, 1) в области решения.Это. Он может съесть 3 гамбургера и 2 печенья.
ⓓ Чтобы определить, соответствуют ли 2 гамбургера и 4 печенья критериям Омара, мы смотрим, находится ли точка (2, 4) в области решения. Это. Он может съесть 2 гамбургера и 4 печенья.
Мы также можем проверить возможные решения, подставляя значения в каждое неравенство.
Tension необходимо съедать не менее 1000 дополнительных калорий в день, чтобы подготовиться к марафону. У него есть только 25 фунтов стерлингов, чтобы потратить на необходимое дополнительное питание, и он потратит их на 0 фунтов стерлингов.75 пончиков по 360 калорий в каждом и 2 энергетических напитка по 110 калорий.
У него есть только 25 фунтов стерлингов, чтобы потратить на необходимое дополнительное питание, и он потратит их на 0 фунтов стерлингов.75 пончиков по 360 калорий в каждом и 2 энергетических напитка по 110 калорий.
ⓐ Напишите систему неравенств, моделирующую эту ситуацию.
ⓑ Изобразите систему.
ⓒ Может ли он купить 8 пончиков и 4 энергетических напитка?
ⓓ Может ли он купить 1 пончик и 3 энергетических напитка?
- ⓐ
- ⓑ
- ⓒ да
- ⓓ нет
Врач Филиппа говорит ему, что он должен добавлять как минимум 1000 калорий в день к своему обычному рациону. Филип хочет купить протеиновые батончики по цене 1 фунт стерлингов.80 каждый и содержат 140 калорий и сок по цене 1,25 фунтов стерлингов за бутылку и содержат 125 калорий. Он не хочет тратить больше? 12.
ⓐ Напишите систему неравенств, моделирующую эту ситуацию.
ⓑ Изобразите систему.
ⓒ Может ли он купить 3 протеиновых батончика и 5 бутылок сока?
ⓓ Может ли он купить 5 протеиновых батончиков и 3 бутылки сока?
- ⓐ
- ⓑ
- ⓒ да
- ⓓ нет
Ключевые понятия
- Решение системы линейных неравенств с помощью построения графиков
- Изобразите первое неравенство.

- Постройте граничную линию.
- Заштриховать сбоку от ограничивающей линии, где выполняется неравенство.
- На той же сетке нанесите график второго неравенства.
- Постройте граничную линию.
- Заштрихуйте сбоку от границы, на которой выполнено неравенство.
- Решением является область перекрытия штриховки.
- Проверьте, выбрав контрольную точку.
- Изобразите первое неравенство.
Упражнения по разделам
Практика ведет к совершенству
Определить, является ли упорядоченная пара решением системы линейных неравенств
В следующих упражнениях определите, является ли каждая упорядоченная пара решением системы.
Решите систему линейных неравенств с помощью построения графиков
В следующих упражнениях решите каждую систему с помощью построения графиков.
Нет решения
Нет решения
Решение приложений систем неравенств
В следующих упражнениях переведите на систему неравенств и решите.
Кейтлин продает свои рисунки на окружной ярмарке. Она хочет продать не менее 60 рисунков, у нее есть портреты и пейзажи. Портреты она продает за 15 евро, пейзажи за 10 евро. Чтобы получить прибыль, ей нужно продать рисунков на сумму не менее 800 фунтов стерлингов.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Получит ли она прибыль, если продаст 20 портретов и 35 пейзажей?
ⓓ Получит ли она прибыль, если продаст 50 портретов и 20 пейзажей?
- ⓐ
- ⓑ
- ⓒ Нет
- ⓓ Есть
Джейк не хочет тратить больше 50 фунтов на мешки с удобрениями и торфяной мох для своего сада.Удобрение стоит 2 евро за мешок, а торфяной мох — 5 евро за мешок. Фургон Джейка вмещает не более 20 сумок.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли он купить 15 мешков удобрений и 4 мешка торфяного мха?
ⓓ Может ли он купить 10 мешков удобрений и 10 мешков торфяного мха?
Рэйко нужно отправить рождественские открытки и посылки по почте, и она хочет, чтобы ее почтовые расходы не превышали 500 фунтов стерлингов. Количество карточек минимум на 4 больше, чем в два раза больше пакетов.Стоимость пересылки открытки (с картинками) — 3 евро, посылки — 7 евро.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли она отправить 60 открыток и 26 пакетов?
ⓓ Может ли она отправить по почте 90 открыток и 40 пакетов?
- ⓐ
- ⓑ
- ⓒ Есть
- ⓓ Нет
Хуан готовится к выпускным экзаменам по химии и алгебре. Он знает, что у него всего 24 часа на обучение, и ему потребуется как минимум в три раза больше времени, чтобы изучать алгебру, чем химию.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли он потратить 4 часа на химию и 20 часов на алгебру?
ⓓ Может ли он потратить 6 часов на химию и 18 часов на алгебру?
Джоселин беременна и ей нужно съедать как минимум на 500 калорий в день больше, чем обычно. Когда однажды покупает продукты с бюджетом в 15 фунтов на дополнительную еду, она покупает бананы, каждый из которых содержит 90 калорий, и шоколадные батончики мюсли, каждый из которых содержит 150 калорий. Бананы стоят 0,35 фунта стерлингов каждый, а батончики мюсли — 2,50 фунта стерлингов каждый.
Бананы стоят 0,35 фунта стерлингов каждый, а батончики мюсли — 2,50 фунта стерлингов каждый.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли она купить 5 бананов и 6 батончиков мюсли?
ⓓ Может ли она купить 3 банана и 4 батончика мюсли?
- ⓐ
- ⓑ
- ⓒ Нет
- ⓓ Есть
Марк пытается нарастить мышечную массу, поэтому ему необходимо дополнительно съедать не менее 80 граммов белка в день. Бутылка протеиновой воды стоит 3 фунта.20, а протеиновый батончик стоит 1,75 фунтов стерлингов. Белковая вода содержит 27 граммов белка, а батончик — 16 граммов. Если он есть? 10 долларов на расходы
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Мог ли он купить 3 бутылки протеиновой воды и 1 протеиновый батончик?
ⓓ Мог ли он покупать не бутылки с протеиновой водой и 5 протеиновых батончиков?
Джоселин хочет увеличить потребление белка и калорий. Она хочет есть как минимум на 35 граммов больше белка каждый день и не более чем на 200 дополнительных калорий в день.Унция сыра чеддер содержит 7 граммов белка и 110 калорий. Унция сыра пармезан содержит 11 граммов белка и 22 калории.
Она хочет есть как минимум на 35 граммов больше белка каждый день и не более чем на 200 дополнительных калорий в день.Унция сыра чеддер содержит 7 граммов белка и 110 калорий. Унция сыра пармезан содержит 11 граммов белка и 22 калории.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Может ли она съесть 30 грамм сыра чеддер и 100 грамм сыра пармезан?
ⓓ Может ли она съесть 2 унции сыра чеддер и 30 грамм сыра пармезан?
- ⓐ
- ⓑ
- ⓒ Есть
- ⓓ Нет
Марк увеличивает свои физические нагрузки, бегая и ходя не менее 4 миль каждый день.Его цель — сжечь как минимум 1500 калорий с помощью этого упражнения. Ходьба сжигает 270 калорий на милю, а бег — 650 калорий.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Сможет ли он достичь своей цели, пройдя 3 мили и пробежав 1 милю?
ⓓ Сможет ли он достичь своей цели, пройдя 2 мили и пробежав 2 мили?
Повседневная математика
Билеты на матч Американской бейсбольной лиги для 3 взрослых и 3 детей стоят менее 75 фунтов стерлингов, а билеты для 2 взрослых и 4 детей — менее 62 фунтов стерлингов.
ⓐ Напишите систему неравенств для моделирования этой проблемы.
ⓑ Изобразите систему.
ⓒ Могли ли билеты стоить 20 евро для взрослых и 8 евро для детей?
ⓓ Могли ли билеты стоить? 15 для взрослых и 5? Для детей?
- ⓐ
- ⓑ
- ⓒ Нет
- ⓓ Есть
Дедушка и бабушка развлекают свою семью в кино. Билет на утренник стоит 4 евро для ребенка и 4 евро для взрослого. Вечерние билеты стоят 6 евро для ребенка и 8 евро для взрослого.Они планируют потратить не больше 80 фунтов на билеты на утренник и не более 100 на вечерние билеты.
ⓐ Напишите систему неравенств для моделирования этой ситуации.
ⓑ Изобразите систему.
ⓒ Могут ли они взять с собой 9 детей и 4 взрослых на оба спектакля?
ⓓ Могут ли они взять с собой 8 детей и 5 взрослых на оба спектакля?
Письменные упражнения
Изобразите неравенство. Как узнать, какую сторону линии нужно растушевать?
Изобразите систему. Что означает решение?
Что означает решение?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
Глава 5. Упражнения на повторение
Решение систем уравнений с помощью построения графиков
Определите, является ли упорядоченная пара решением системы уравнений .
В следующих упражнениях определите, являются ли следующие точки решениями данной системы уравнений.
Решение системы линейных уравнений с помощью построения графиков
В следующих упражнениях решите следующие системы уравнений с помощью построения графиков.
совпадающих линий
Определите количество решений линейной системы
В следующих упражнениях без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
бесконечно много решений, непротиворечивая система, зависимые уравнения
нет решений, несовместная система, независимые уравнения
Решение приложений систем уравнений с помощью построения графиков
ЛаВелле делает кувшин кофе мокко. На каждую унцию шоколадного сиропа она использует пять унций кофе. Сколько унций шоколадного сиропа и сколько унций кофе нужно ей, чтобы приготовить 48 унций кофе мокко?
ЛаВеллю нужно 8 унций шоколадного сиропа и 40 унций кофе.
Эли готовит коктейль для вечеринок, состоящий из крендельков и чекса. На каждую чашку крендельков он использует три чашки чекса. Сколько чашек кренделей и сколько чашек чекса ему нужно, чтобы приготовить 12 чашек коктейля для вечеринок?
Решите системы уравнений подстановкой
Решите систему уравнений подстановкой
В следующих упражнениях решите системы уравнений путем подстановки.
Решите приложения систем уравнений подстановкой
В следующих упражнениях переведите в систему уравнений и решите.
Сумма двух чисел равна 55. Одно число на 11 меньше другого. Найдите числа.
Цифры 22 и 33.
Периметр прямоугольника равен 128. Длина на 16 больше ширины. Найдите длину и ширину.
Размер одного из малых углов прямоугольного треугольника в 2 раза меньше, чем в 3 раза больше размера другого малого угла. Найдите размер обоих углов.
Размеры: 23 градуса и 67 градусов.
Габриэла работает в страховой компании, которая платит ей зарплату в размере 32 000 фунтов стерлингов плюс комиссию в размере 100 фунтов стерлингов за каждый проданный полис.Она рассматривает возможность перехода на другую работу в компанию, которая будет платить зарплату в размере 40 000 фунтов стерлингов плюс комиссию в размере 80 фунтов стерлингов за каждый проданный полис. Сколько полисов нужно продать Габриэле, чтобы общая сумма была такой же?
Сколько полисов нужно продать Габриэле, чтобы общая сумма была такой же?
Решите системы уравнений методом исключения
Решите систему уравнений методом исключения В следующих упражнениях решите системы уравнений методом исключения.
Решение приложений систем уравнений методом исключения
В следующих упражнениях переведите в систему уравнений и решите.
Сумма двух чисел равна. Их разница есть. Найдите числа.
Цифры и.
Омар каждый день останавливается в магазине пончиков по дороге на работу. На прошлой неделе он съел 8 пончиков и 5 капучино, что дало ему в общей сложности 3000 калорий. На этой неделе он съел 6 пончиков и 3 капучино, что в общей сложности составило 2160 калорий. Сколько калорий в одном пончике? Сколько калорий в одном капучино?
Выберите наиболее удобный метод решения системы линейных уравнений
В следующих упражнениях решите, что было бы удобнее решить систему уравнений путем подстановки или исключения.
Решение приложений с помощью систем уравнений
Перевести в систему уравнений
В следующих упражнениях переведите в систему уравнений. Не решайте систему.
Сумма двух чисел равна. Одно число на два меньше, чем в два раза больше другого. Найдите числа.
Четырехкратное число плюс трижды второе число. Дважды первое число плюс второе число — три.Найдите числа.
В прошлом месяце Джим и Дебби заработали 7200 фунтов стерлингов. Дебби заработала на 1600 фунтов больше, чем заработал Джим. Сколько они заработали?
Анри вложил 24 000 евро в акции и облигации. Сумма в акциях на 6 000 евро больше, чем в три раза больше, чем в облигациях. Сколько стоит каждое вложение?
Решение задач прямого перевода
В следующих упражнениях переведите в систему уравнений и решите.
Пэм на 3 года старше своей сестры Ян.Сумма их возрастов — 99. Найдите их возраст.
Молли хочет посадить 200 луковиц в своем саду. Она хочет все ирисы и тюльпаны. Она хочет посадить в три раза больше тюльпанов, чем ирисов. Сколько ирисов и сколько тюльпанов ей следует посадить?
Приложения Solve Geometry
В следующих упражнениях переведите в систему уравнений и решите.
Разница двух дополнительных углов составляет 58 градусов. Найдите размеры углов.
Размеры: 119 градусов и 61 градус.
Два угла дополняют друг друга. Мера большего угла в пять раз больше, чем в четыре раза меньшего угла. Найдите размеры обоих углов.
Бекка вешает 28-футовую цветочную гирлянду с двух сторон и наверху беседки, чтобы подготовиться к свадьбе. Высота на четыре фута меньше ширины. Найдите высоту и ширину беседки.
Пергола 8 футов в высоту и 12 футов в ширину.
Периметр городского прямоугольного парка составляет 1428 футов. Длина на 78 футов более чем в два раза больше ширины. Найдите длину и ширину парка.
Длина на 78 футов более чем в два раза больше ширины. Найдите длину и ширину парка.
Решение приложений с равномерным движением
В следующих упражнениях переведите в систему уравнений и решите.
Шейла и Ленор ехали в дом своей бабушки. Ленора ушла через час после Шейлы. Шейла ехала со скоростью 45 миль в час, а Ленора ехала со скоростью 60 миль в час. Сколько времени потребуется Леноре, чтобы догнать Шейлу?
Это займет у Леноры 3 часа.
Боб ушел из дома на своем велосипеде со скоростью 10 миль в час, чтобы добраться до озера. Шерил, его жена, уехала через 45 минут (час) спустя, двигаясь на своей машине со скоростью 25 миль в час. Сколько времени потребуется Шерил, чтобы догнать Боба?
Маркус может спуститься на своей лодке на 36 миль вниз по реке за три часа, но ему нужно четыре часа, чтобы вернуться вверх по течению. Найдите скорость лодки в стоячей воде и скорость течения.
Скорость лодки 10,5 миль в час. Скорость тока — 1.5 миль / ч.
Скорость тока — 1.5 миль / ч.
Пассажирский реактивный самолет может пролететь 804 мили за 2 часа с попутным ветром, но только 776 миль за 2 часа при встречном ветре. Найдите скорость струи в неподвижном воздухе и скорость ветра.
Решение смесей приложений с помощью системы уравнений
Приложения для растворения смесей
В следующих упражнениях переведите в систему уравнений и решите.
Линн заплатила в общей сложности 2780 фунтов стерлингов за 261 билет в театр. Студенческие билеты стоят 10 евро, взрослые — 15 евро.Сколько студенческих билетов и сколько взрослых билетов купила Линн?
Линн купила 227 студенческих билетов и 34 взрослых билета.
У Приама в машине есть десять центов и центов в подстаканнике. Общая стоимость монет — 4,21 фунта стерлингов. Количество десятицентовиков на три меньше, чем четырехкратное количество пенсов. Сколько центов и сколько центов в чашке?
Юми хочет приготовить 12 чашек смеси для вечеринок из конфет и орехов. Ее бюджет требует, чтобы вечеринка стоила ей 1 фунт.29 на чашку. Конфеты стоят 2,49 фунтов за чашку, а орехи — 0,69 фунтов за чашку. Сколько чашек конфет и сколько чашек орехов ей следует съесть?
Ее бюджет требует, чтобы вечеринка стоила ей 1 фунт.29 на чашку. Конфеты стоят 2,49 фунтов за чашку, а орехи — 0,69 фунтов за чашку. Сколько чашек конфет и сколько чашек орехов ей следует съесть?
Юми следует использовать 4 чашки конфет и 8 чашек орехов.
Ученому нужно 70 литров 40% раствора спирта. У него есть 30% и 60% раствор. Сколько литров 30% и сколько литров 60% растворов он должен смешать, чтобы получить 40% раствор?
Рассмотрение процентных заявок
В следующих упражнениях переведите в систему уравнений и решите.
У Джека есть 12 000 евро для инвестирования, и он хочет получать 7,5% годовых. Он поместит часть денег на сберегательный счет, приносящий 4% в год, а остальную часть — на счет CD, который приносит 9% в год. Сколько денег он должен положить на каждый счет?
Джек должен положить 3600 евро на сбережения и 8400 евро на компакт-диск.
Когда она закончит колледж, Линда будет должна 43 000 фунтов стерлингов в виде студенческих ссуд.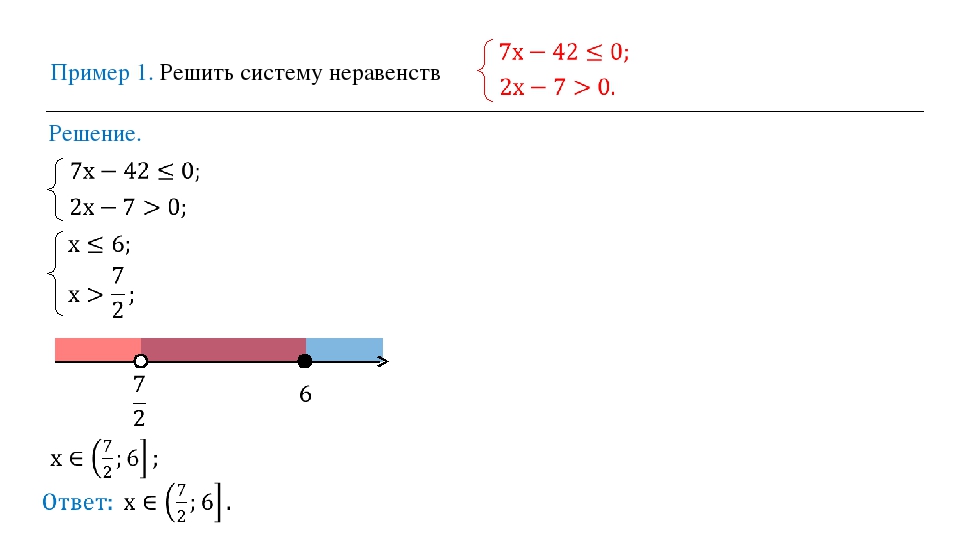 Процентная ставка по федеральным займам составляет 4,5%, а ставка по ссудам частных банков — 2%.Общая сумма процентов, которую она задолжала за один год, составила 1585 фунтов стерлингов. Какая сумма каждого кредита?
Процентная ставка по федеральным займам составляет 4,5%, а ставка по ссудам частных банков — 2%.Общая сумма процентов, которую она задолжала за один год, составила 1585 фунтов стерлингов. Какая сумма каждого кредита?
Графические системы линейных неравенств
Определить, является ли упорядоченная пара решением системы линейных неравенств
В следующих упражнениях определите, является ли каждая упорядоченная пара решением системы.
Решите систему линейных неравенств с помощью построения графиков
В следующих упражнениях решите каждую систему с помощью построения графиков.
Нет решения
Решение приложений систем неравенств
В следующих упражнениях переведите на систему неравенств и решите.
Роксана делает браслеты и ожерелья и продает их на фермерском рынке. Браслеты она продает по 12 фунтов за штуку, а ожерелья — по 18 фунтов. На рынке в следующие выходные у нее будет место, чтобы выставить не более 40 штук, и ей нужно продать не менее 500 фунтов стерлингов, чтобы получить прибыль.
- ⓐ Напишите систему неравенств, чтобы смоделировать эту ситуацию.
- ⓑ Изобразите систему.
- ⓒ Следует ли ей показать 26 браслетов и 14 ожерелий?
- ⓓ Следует ли ей показать 39 браслетов и 1 ожерелье?
ⓐ
ⓑ
ⓒ да
ⓓ нет
У Энни есть бюджет в 600 фунтов стерлингов на покупку книг в мягкой обложке и книг в твердом переплете для своего класса. Она хочет, чтобы количество книг в твердой обложке было как минимум в 5 раз больше, чем в три раза больше книг в мягкой обложке.Книги в мягкой обложке стоят 4 фунта каждая, а книги в твердой обложке — 15 фунтов.
- ⓐ Напишите систему неравенств, чтобы смоделировать эту ситуацию.

- ⓑ Изобразите систему.
- ⓒ Может ли она купить 8 книг в мягкой обложке и 40 книг в твердой обложке?
- ⓓ Может ли она купить 10 книг в мягкой обложке и 37 книг в твердой обложке?
Практический тест
В следующих упражнениях решите следующие системы с помощью построения графиков.
В следующих упражнениях решите каждую систему уравнений.Используйте либо замену, либо исключение.
бесконечно много решений
В следующих упражнениях переведите в систему уравнений и решите.
Сумма двух чисел равна −24. Одно число на 104 меньше другого. Найдите числа.
Цифры 40 и 64
Рамон хочет посадить в своем саду огурцы и помидоры.У него есть место для 16 растений, и он хочет посадить в три раза больше огурцов, чем помидоров. Сколько огурцов и сколько помидоров нужно посадить?
Два угла дополняют друг друга. Мера большего угла в шесть раз больше, чем мера меньшего угла, более чем в два раза. Найдите размеры обоих углов.
Мера большего угла в шесть раз больше, чем мера меньшего угла, более чем в два раза. Найдите размеры обоих углов.
Размеры углов: 28 градусов и 62 градуса.
В понедельник Лэнс бегал 30 минут и плавал 20 минут. Его фитнес-приложение сообщило ему, что он сжег 610 калорий.В среду фитнес-приложение сообщило ему, что он сжег 695 калорий, когда бегал 25 минут и плавал 40 минут. Сколько калорий он сжег за минуту бега? Сколько калорий он сжег за минуту плавания?
Кэти вышла из дома, чтобы дойти до торгового центра, быстро шагая со скоростью 4 мили в час. Ее сестра Эбби вышла из дома через 15 минут и ехала на велосипеде до торгового центра со скоростью 10 миль в час. Сколько времени понадобится Эбби, чтобы догнать Кэти?
Это займет у Кэти час (или 10 минут).
Самолету требуется несколько часов, чтобы преодолеть 2475 миль при встречном ветре из Сан-Хосе, Калифорния, в Лихуэ, Гавайи. Обратный рейс из Лихуэ в Сан-Хосе с попутным ветром занимает 5 часов. Найдите скорость струи в неподвижном воздухе и скорость ветра.
Найдите скорость струи в неподвижном воздухе и скорость ветра.
Лиз заплатила 160 фунтов за 28 билетов, чтобы отвести отряд Брауни в музей науки. Детские билеты стоят 5 евро, взрослые — 9 евро. Сколько билетов для детей и сколько билетов для взрослых купила Лиз?
Лиз купила 23 детских и 5 взрослых билетов.
Фармацевту необходимо 20 литров 2% физиологического раствора. У него есть 1% и 5% раствор. Сколько литров 1% и сколько литров 5% растворов она должна смешать, чтобы получить 2% раствор?
Переведите в систему неравенств и решите.
Энди хочет потратить не больше 50 фунтов стерлингов на Хэллоуинские угощения. Она хочет купить шоколадные батончики стоимостью 1 фунт каждый и леденцы стоимостью 0,50 фунтов стерлингов каждый, и она хочет, чтобы количество леденцов было как минимум в три раза больше, чем количество шоколадных батончиков.
- ⓐ Напишите систему неравенств, чтобы смоделировать эту ситуацию.
- ⓑ Изобразите систему.

- ⓒ Может ли она купить 20 шоколадных батончиков и 70 леденцов на палочке?
- ⓓ Может ли она купить 15 шоколадных батончиков и 65 леденцов на палочке?
ⓐ
ⓑ
ⓒ Нет
ⓓ Да
Глоссарий
- система линейных неравенств
- Два или более линейных неравенства, сгруппированных вместе, образуют систему линейных неравенств.
Устранение неравенств — объяснения и примеры
Что такое неравенство в математике?
Слово неравенство означает математическое выражение, в котором стороны не равны друг другу. По сути, неравенство сравнивает любые два значения и показывает, что одно значение меньше, больше или равно значению на другой стороне уравнения.
Как правило, для представления уравнений неравенства используются пять символов неравенства.
Символы неравенства
Эти символы неравенства: меньше ( <), больше (> ), меньше или равно ( ≤ ), больше или равно ( ≥ ) и символ неравенства ( ≠ ) .
Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, которые удовлетворяют условиям данной переменной.
Операции с неравенствами
Операции с линейными неравенствами включают сложение, вычитание, умножение и деление. Общие правила этих операций показаны ниже.
Хотя мы использовали символ <для иллюстрации, следует отметить, что те же правила применяются к>, ≤ и ≥.
- Символ неравенства не меняется, когда одно и то же число добавляется к обеим сторонам неравенства.Например, если a
- Вычитание обеих частей неравенства на одно и то же число не меняет знака неравенства. Например, если a
- Умножение обеих частей неравенства на положительное число не меняет знака неравенства. Например, если a
- Разделение обеих сторон неравенства на положительное число не меняет знака неравенства. Если a
- Умножение обеих сторон уравнения неравенства на отрицательное число изменяет направление символа неравенства.
 Например, если a b *
Например, если a b *- Аналогичным образом, разделение обеих сторон уравнения неравенства на отрицательное число изменяет символ неравенства. Если a b / c
- Вычитание обеих частей неравенства на одно и то же число не меняет знака неравенства. Например, если a
Как решать неравенства?
Подобно линейным уравнениям, неравенства можно решить, применяя аналогичные правила и шаги, за некоторыми исключениями. Единственная разница при решении линейных уравнений — это операция умножения или деления на отрицательное число.Умножение или деление неравенства на отрицательное число изменяет символ неравенства.
Линейные неравенства могут быть решены с помощью следующих операций:
- Сложение
- Вычитание
- Умножение
- Разделение
- Распределение собственности
Решение линейных неравенств с добавлением
Давайте посмотрим на несколько примеров ниже, чтобы понять это понятие.
Пример 1
Решите 3x — 5 ≤ 3 — x.
Решение
Начнем с добавления обеих сторон неравенства на 5
3x — 5 + 5 ≤ 3 + 5 — x
3x ≤ 8 — x
Затем сложим обе стороны на x.
3x + x ≤ 8 — x + x
4x ≤ 8
Наконец, разделите обе части неравенства на 4, чтобы получить;
x ≤ 2
Пример 2
Вычислите диапазон значений y, который удовлетворяет неравенству: y — 4 <2y + 5.
Решение
Сложите обе части неравенства на 4.
y — 4 + 4 <2y + 5 + 4
y <2y + 9
Вычтите обе части на 2y.
y — 2y <2y - 2y + 9
Y <9 Умножьте обе части неравенства на -1 и измените направление символа неравенства. y> — 9
Решение линейных неравенств с вычитанием
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 3
Решите x + 8> 5.
Решение
Изолируйте переменную x, вычтя 8 из обеих сторон неравенства.
x + 8-8> 5-8 => x> −3
Следовательно, x> −3.
Пример 4
Решите 5x + 10> 3x + 24.
Решение
Вычтите 10 из обеих сторон неравенства.
5x + 10-10> 3x + 24-10
5x> 3x + 14.
Теперь вычтем обе части неравенства на 3x.
5x — 3x> 3x — 3x + 14
2x> 14
x> 7
Решение линейных неравенств с умножением
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 5
Решить x / 4> 5
Решение:
Умножить обе стороны неравенства на знаменатель дроби
4 (x / 4)> 5 x 4
x> 20
Пример 6
Решите -x / 4 ≥ 10
Решение:
Умножьте обе стороны неравенства на 4.
4 (-x / 4) ≥ 10 x 4
-x ≥ 40
Умножьте обе стороны неравенства на -1 и измените направление символа неравенства на противоположное.
x ≤ — 40
Решение линейных неравенств с делением
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 7
Решите неравенство: 8x — 2> 0.
Решение
Прежде всего, сложите обе части неравенства на 2
8x + 2> 0 + 2
8x> 2
Теперь решите, разделив обе части неравенства на 8, чтобы получить;
x> 2/8
x> 1/4
Пример 8
Решите следующее неравенство:
−5x> 100
Решения сторон неравенства на -5 и измените направление символа неравенства
= −5x / -5 <100 / -5
= x <- 20
Решение линейных неравенств с использованием свойства распределения
Давайте посмотрим на несколько примеров ниже, чтобы понять эту концепцию.
Пример 9
Решить: 2 (x — 4) ≥ 3x — 5
Решение
2 (x — 4) ≥ 3x — 5
Примените свойство распределения, чтобы удалить скобки.
⟹ 2x — 8 ≥ 3x — 5
Сложить обе стороны на 8.
⟹ 2x — 8 + 8 ≥ 3x — 5 + 8
⟹ 2x ≥ 3x + 3
Вычесть обе стороны на 3.
⟹ 2x — 3x ≥ 3x + 3 — 3x
⟹ -x ≥ 3
⟹ x ≤ — 3
Пример 10
Студент набрал 60 баллов за первый тест и 45 баллов во втором тесте заключительного экзамена.Сколько минимальных баллов должен набрать ученик в третьем тесте, получив в среднем не менее 62 баллов?
Решение
Пусть в третьем тесте будет набрано x баллов.
(60 + 45 + x) / 3 ≥ 62
105 + x ≥ 196
x ≥ 93
Следовательно, учащийся должен набрать 93 балла, чтобы поддерживать среднее значение не менее 62 баллов.
Пример 11
Джастину требуется не менее 500 долларов для празднования своего дня рождения. Если он уже накопил 150 долларов, до этой даты осталось 7 месяцев. Какую минимальную сумму он должен откладывать ежемесячно?
Если он уже накопил 150 долларов, до этой даты осталось 7 месяцев. Какую минимальную сумму он должен откладывать ежемесячно?
Решение
Пусть минимальная ежемесячная экономия = x
150 + 7x ≥ 500
Решить для x
150-150 + 7x ≥ 500-150
x ≥ 50
Следовательно, Джастин должен экономить 50 долларов США или больше
Пример 12
Найдите два последовательных нечетных числа, которые больше 10 и имеют сумму меньше 40.
Решение
Пусть меньшее нечетное число = x
Следовательно, следующее число будет x + 2
x> 10 ………. больше 10
x + (x + 2) <40 …… сумма меньше 40
Решите уравнения.
2x + 2 <40
x + 1 <20
x <19
Объедините два выражения.
10 Следовательно, последовательные нечетные числа — 11 и 13, 13 и 15, 15 и 17, 17 и 19. Лучшим инструментом для представления и визуализации чисел является числовая линия. Линейные уравнения также можно решить графическим методом с использованием числовой прямой.Например, чтобы построить x> 1 на числовой прямой, вы обведите цифру 1 на числовой прямой и проведете линию, идущую от круга в направлении чисел, которые удовлетворяют утверждению о неравенстве. Пример 13 Если символ неравенства больше или равен или меньше или равен знаку (≥ или ≤), нарисуйте круг над числовым числом и заполните или заштрихуйте круг.Наконец, проведите линию, идущую от заштрихованного круга в направлении чисел, которая удовлетворяет уравнению неравенства. Пример 14 x ≥ 1 Та же процедура используется для решения уравнений, включающих интервалы. Пример 15 –2 < x <2 Пример 16 –10005 5 Неравенства и числовая линия
 Числовая линия определяется как прямая горизонтальная линия с числами, расположенными на равных отрезках или интервалах. У числовой прямой есть нейтральная точка в середине, известная как начало координат. Справа от начала координат на числовой прямой находятся положительные числа, а слева от начала координат — отрицательные числа.
Числовая линия определяется как прямая горизонтальная линия с числами, расположенными на равных отрезках или интервалах. У числовой прямой есть нейтральная точка в середине, известная как начало координат. Справа от начала координат на числовой прямой находятся положительные числа, а слева от начала координат — отрицательные числа.
05
Пример 17
–1 < x ≤ 2
Практические вопросыРешите следующие неравенства и представьте свой ответ на числовой прямой.
- 2x> 9
- x + 5> 13
- −3x <4
- 7x + 11> 2x + 5
- 2 (x + 3)
- -5 ≤ 2x — 7 ≤ 1
- 4x — 8 ≤ 12
Ответы
- x> 9/2
- x> 8
- x> −4/3
- x> −6/5
- x <−5.
- 1 ≤ x ≤ 4.
- x ≤ 5
REI.
 4.12 — Изобразите решения линейного неравенства с двумя переменными в виде полуплоскости (исключая границу в случае строгого неравенства) и изобразите набор решений системы линейных неравенств с двумя переменными как пересечение соответствующих полуплоскости. MAFS.912.A-REI.4.12 — Изобразите решения линейного неравенства с двумя переменными в виде полуплоскости (исключая границу в случае строгого неравенства) и изобразите набор решений для системы линейных неравенств в две переменные как пересечение соответствующих полуплоскостей.
4.12 — Изобразите решения линейного неравенства с двумя переменными в виде полуплоскости (исключая границу в случае строгого неравенства) и изобразите набор решений системы линейных неравенств с двумя переменными как пересечение соответствующих полуплоскости. MAFS.912.A-REI.4.12 — Изобразите решения линейного неравенства с двумя переменными в виде полуплоскости (исключая границу в случае строгого неравенства) и изобразите набор решений для системы линейных неравенств в две переменные как пересечение соответствующих полуплоскостей.Веб-сайт несовместим с используемой вами версией браузера. Не все функции могут быть доступны. Пожалуйста, обновите ваш браузер до последней версии.
Изобразите решения линейного неравенства с двумя переменными в виде полуплоскости
(исключая границу в случае строгого неравенства), и
графическое изображение множества решений системы линейных неравенств с двумя переменными
как пересечение соответствующих полуплоскостей.
Общая информация
Предметная область: Математика
Класс: 912
Домен-подобласть: Алгебра: рассуждения с помощью уравнений и неравенств
Кластер: Уровень 2: Базовое применение навыков и концепций
Дата принятия или изменения: 14. 02
02
Дата последней оценки: 14.02
Статус: Утверждено Государственным советом
Оценено: Да
Технические характеристики объекта испытаний
- Оценка:
MAFS. 912.A-CED.1.2
912.A-CED.1.2
Образцы тестовых заданий (1)
- Тестовый образец №: Образец образца 1
- Вопрос:
Показана система неравенства.
A. Используйте инструмент «Добавить стрелку» для построения граничных линий системы.
B. Перетащите звездочку в каждую область в наборе решений системы.
- Сложность: НЕТ
- Тип: GRID: графический элемент ответа
Связанные точки доступа
Альтернативная версия этого теста для учащихся со значительными когнитивными нарушениями.
Связанные ресурсы
Проверенные ресурсы преподаватели могут использовать для обучения концепциям и навыкам, связанным с этим тестом.
Формирующие оценки MFAS
Какой график ?: Студентам предлагается выбрать правильный график области решения данной системы двух линейных неравенств.
Оригинальные уроки по математике для учащихся — 9–12 классы
Графическое изображение линейных неравенств:Научитесь графически отображать линейные неравенства с двумя переменными, чтобы отображать их решения по мере выполнения этого интерактивного руководства.
Ресурсы для учащихся
Ресурсы, прошедшие проверку, учащиеся могут использовать для изучения концепций и навыков, используемых в этом тесте.
Оригинальное учебное пособие для студентов
Графическое изображение линейных неравенств:Научитесь графически отображать линейные неравенства с двумя переменными, чтобы отображать их решения по мере выполнения этого интерактивного руководства.
Тип: Оригинальное учебное пособие для учащихся
Обучающая игра
Решение неравенств: неравенства и графики неравенств: В этой сложной игре вы будете решать неравенства и работать с графиками неравенств.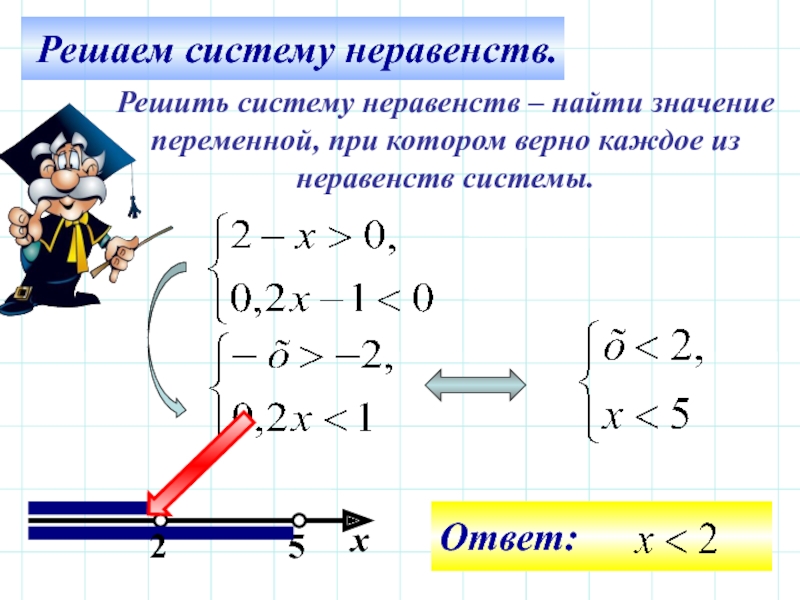 Используйте кнопку «Научи меня», чтобы просмотреть материалы перед испытанием. Во время задания вы получите одно бесплатное решение и две подсказки! После задания при необходимости просмотрите проблемы. Попробуйте еще раз, чтобы правильно ответить на все вопросы! Наборы вопросов различаются в зависимости от игры, поэтому не стесняйтесь играть в игру несколько раз по мере необходимости! Удачи!
Используйте кнопку «Научи меня», чтобы просмотреть материалы перед испытанием. Во время задания вы получите одно бесплатное решение и две подсказки! После задания при необходимости просмотрите проблемы. Попробуйте еще раз, чтобы правильно ответить на все вопросы! Наборы вопросов различаются в зависимости от игры, поэтому не стесняйтесь играть в игру несколько раз по мере необходимости! Удачи!
Тип: Обучающая игра
Задачи по решению проблем
Наборы решений: Типичная система уравнений или неравенств задачи дает систему и запрашивает график решения. Эта задача решает проблему. Он дает набор решений и запрашивает соответствующую ему систему. Цель этого задания — дать студентам возможность выйти за рамки типовой задачи и установить связи между точками на координатной плоскости и решениями неравенств и уравнений. Студенты должны сосредоточиться на том, что показывает график. Когда вы описываете регион, почему неравенство должно идти тем или иным путем? Когда вы выбираете точку, которая явно лежит в регионе, что должно быть правдой о ее координатах, чтобы она удовлетворяла соответствующей системе неравенств?
Эта задача решает проблему. Он дает набор решений и запрашивает соответствующую ему систему. Цель этого задания — дать студентам возможность выйти за рамки типовой задачи и установить связи между точками на координатной плоскости и решениями неравенств и уравнений. Студенты должны сосредоточиться на том, что показывает график. Когда вы описываете регион, почему неравенство должно идти тем или иным путем? Когда вы выбираете точку, которая явно лежит в регионе, что должно быть правдой о ее координатах, чтобы она удовлетворяла соответствующей системе неравенств?
Тип: Задача по решению проблем
Рыболовные приключения 3: Это задание является последним в серии из трех заданий, в которых неравенства используются в одном и том же контексте при увеличении сложности в 6-м, 7-м классе и по алгебре HS. Учащиеся пишут и решают неравенства, а также представляют решения графически.
Учащиеся пишут и решают неравенства, а также представляют решения графически.
Тип: Задача по решению проблем
Руководство
Ресурсы для родителей
Проверенные ресурсы, которые могут использовать опекуны, чтобы помочь учащимся изучить концепции и навыки, используемые в этом тесте.
Задачи по решению проблем
Наборы решений: Типичная система уравнений или неравенств задачи дает систему и запрашивает график решения. Эта задача решает проблему. Он дает набор решений и запрашивает соответствующую ему систему. Цель этого задания — дать студентам возможность выйти за рамки типовой задачи и установить связи между точками на координатной плоскости и решениями неравенств и уравнений. Студенты должны сосредоточиться на том, что показывает график. Когда вы описываете регион, почему неравенство должно идти тем или иным путем? Когда вы выбираете точку, которая явно лежит в регионе, что должно быть правдой о ее координатах, чтобы она удовлетворяла соответствующей системе неравенств?
Эта задача решает проблему. Он дает набор решений и запрашивает соответствующую ему систему. Цель этого задания — дать студентам возможность выйти за рамки типовой задачи и установить связи между точками на координатной плоскости и решениями неравенств и уравнений. Студенты должны сосредоточиться на том, что показывает график. Когда вы описываете регион, почему неравенство должно идти тем или иным путем? Когда вы выбираете точку, которая явно лежит в регионе, что должно быть правдой о ее координатах, чтобы она удовлетворяла соответствующей системе неравенств?
Тип: Задача по решению проблем
Рыболовные приключения 3: Это задание является последним в серии из трех заданий, в которых неравенства используются в одном и том же контексте при увеличении сложности в 6-м, 7-м классе и по алгебре HS. Учащиеся пишут и решают неравенства, а также представляют решения графически.
Учащиеся пишут и решают неравенства, а также представляют решения графически.
Тип: Задача по решению проблем
Загрузка….
Графические неравенства с программой «Пошаговое решение математических задач»
В предыдущих главах мы решали уравнения с одной неизвестной или переменной. Теперь мы изучим методы решения систем уравнений, состоящих из двух уравнений и двух переменных.
ТОЧКИ НА САМОЛЕТЕ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Представьте декартову систему координат и определите начало координат и оси.

- Для упорядоченной пары найдите эту точку в декартовой системе координат.
- Для данной точки в декартовой системе координат укажите связанную с ней упорядоченную пару.
Мы уже использовали числовую прямую, на которой мы представили числа в виде точек на прямой.
Обратите внимание, что это понятие содержит элементы из двух областей математики, строки из геометрии и чисел из алгебры. Рене Декарт (1596-1650) разработал метод соотношения точек на плоскости с алгебраическими числами.Эта схема называется декартовой системой координат (от Декарта) и иногда упоминается как прямоугольная система координат.
Эта система состоит из двух числовых линий, перпендикулярных в своих нулевых точках.
| Перпендикуляр означает, что две прямые расположены под прямым углом друг к другу. |
Внимательно изучите диаграмму, отмечая каждый из следующих фактов.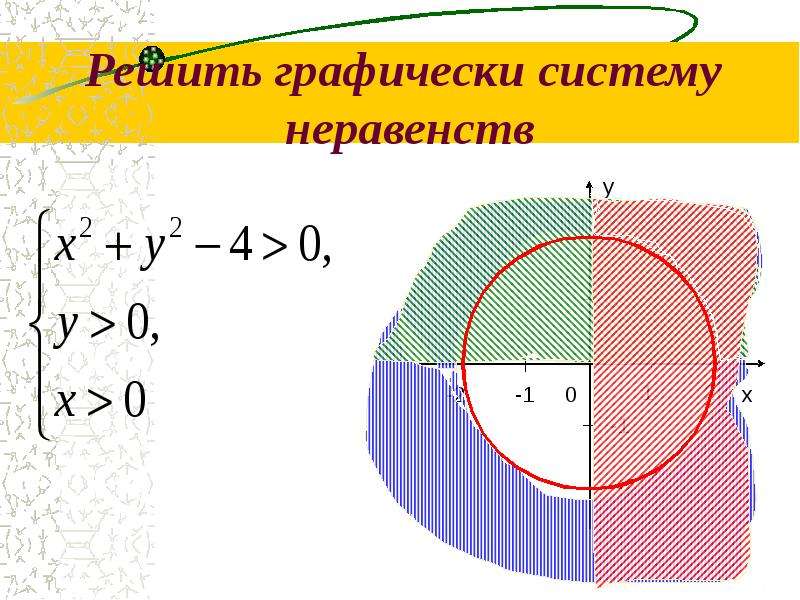
Числовые линии называются осями .Горизонтальная линия — это ось x , а вертикальная — ось y . Нулевая точка, в которой они перпендикулярны, называется началом .
| Оси множественного числа. Ось особенная. |
Положительный к справа и вверх ; отрицательный — слева и вниз .
| Стрелки указывают, что числовые линии продолжаются бесконечно. Таким образом, плоскость бесконечно простирается во всех направлениях. |
Самолет разделен на четыре части, которые называются квадрантами . Они пронумерованы в направлении против часовой стрелки, начиная с верхнего правого угла.
Точки на плоскости обозначаются упорядоченными парами чисел, записанных в скобках с запятой между ними, например (5,7). Это называется упорядоченной парой, потому что важен порядок, в котором написаны числа. Заказанная пара (5,7) — это , а не , как заказанная пара (7,5).Точки расположены на плоскости следующим образом.
Заказанная пара (5,7) — это , а не , как заказанная пара (7,5).Точки расположены на плоскости следующим образом.
Сначала начните с начала координат и посчитайте слева или справа количество пробелов, обозначенных первым числом в упорядоченной паре. Во-вторых, от точки на оси x, заданной первым числом, отсчитайте вверх или вниз количество пробелов, обозначенных вторым числом упорядоченной пары. Упорядоченные пары всегда сначала пишутся с x, а затем y, (x, y). Числа, представленные x и y, называются координатами точки (x, y).
| Это важно. Первое число упорядоченной пары всегда относится к горизонтальному направлению, а второе число всегда относится к вертикальному направлению. |
Пример 1 В следующей декартовой системе координат точки A (3,4), B (0,5), C (-2,7), D (-4,1), E (-3 , -4), F (4, -2), G (0, -5) и H (-6,0) обозначены. Проверьте каждый, чтобы определить, как они расположены.
| Каковы координаты начала координат? |
ИЗОБРАЖЕНИЕ ЛИНЕЙНЫХ УРАВНЕНИЙ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Найдите несколько упорядоченных пар, которые делают данное линейное уравнение истинным.
- Найдите эти точки в декартовой системе координат.
- Проведите прямую линию через те точки, которые представляют график этого уравнения.
График — это графическое изображение пронумерованных фактов. Есть много типов графиков, таких как гистограммы, круговые графики, линейные графики и так далее. Примеры таких графиков обычно можно найти в финансовом разделе газеты. Графики используются, потому что изображение обычно упрощает понимание числовых фактов.
В этом разделе мы обсудим метод построения графика уравнения с двумя переменными. Другими словами, мы нарисуем картину уравнения с двумя переменными.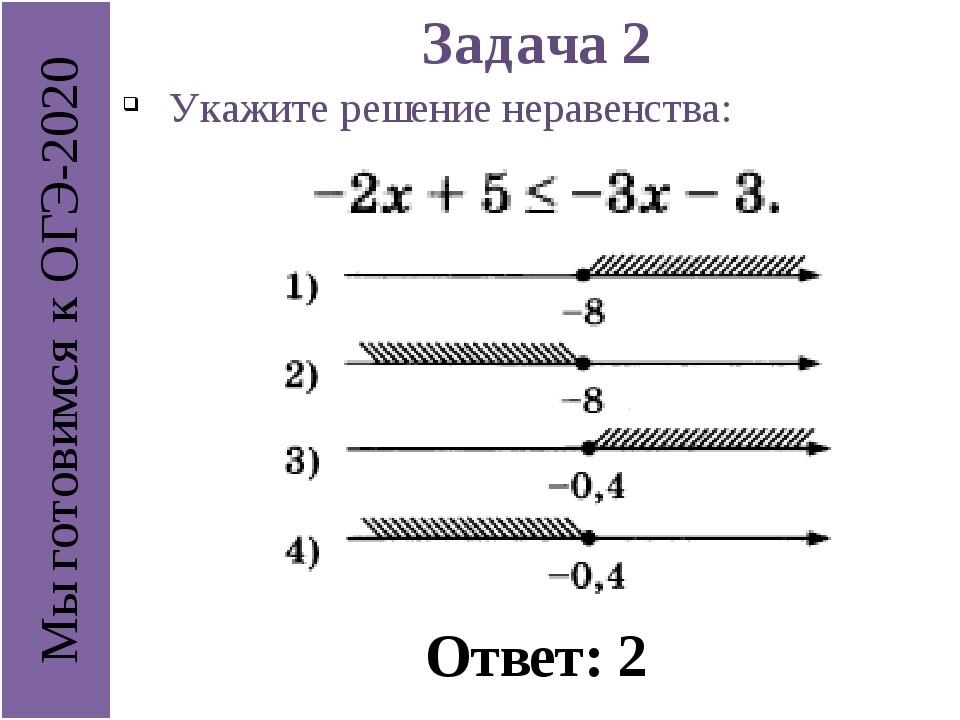
Рассмотрим уравнение x + y — 7 и заметим, что мы легко можем найти множество решений. Например, если x = 5, то y — 2, поскольку 5 + 2 = 7. Кроме того, если x = 3, то y = 4, поскольку 3 + 4 = 7. Если мы представим эти ответы в виде упорядоченных пар (x, y) , то у нас есть (5,2) и (3,4) как две точки на плоскости, которые представляют ответы на уравнение x + y = 7.
Все возможные ответы на это уравнение, расположенные в виде точек на плоскости, дадут нам график (или картинку) уравнения.
Конечно, мы никогда не сможем найти все числа x и y такие, что x + y = 7, поэтому мы должны довольствоваться наброском графика. Эскиз можно охарактеризовать как «кривую наилучшего соответствия». Другими словами, необходимо найти достаточно точек, чтобы получить достаточно точную картину уравнения.
| Помните, существует бесконечно много упорядоченных пар, которые удовлетворяли бы уравнению. |
Пример 1 Нарисуйте график 2x + y = 3.
Решение Мы хотим найти несколько пар чисел, которые сделают это уравнение истинным. Мы добьемся этого, выбрав число для x, а затем найдя соответствующее значение для y. Таблица значений используется для записи данных.
В верхней строке (x) мы разместим числа, которые мы выбрали для x. Затем в нижней строке (y) мы поместим соответствующее значение y, полученное из уравнения.
| Конечно, мы могли бы начать с выбора значений для y, а затем найти соответствующие значения для x. |
В этом примере мы позволим x принимать значения -3, -2, -1,0, 1,2,3.
| Эти значения произвольны. Мы могли выбирать любые ценности. |
Обратите внимание, что после того, как мы выбрали значение для x, значение для y определяется с помощью уравнения. |
| Эти значения x дают целые числа для значений y.Таким образом, это хороший выбор. Предположим, мы выбрали |
Эти факты дают нам следующую таблицу значений:
Теперь мы находим упорядоченные пары (-3,9), (-2,7), (-1,5), (0,3), (1,1), (2, -1), (3, -3) на координатной плоскости и соедините их линией.
Теперь у нас есть график 2x + y = 3.
| Линия показывает, что все точки на линии удовлетворяют уравнению, а также точки из таблицы.Стрелки указывают, что линия продолжается бесконечно. |
Графики всех уравнений первой степени с двумя переменными будут прямыми линиями. Этот факт будет использован здесь, хотя в математике будет гораздо позже, прежде чем вы сможете доказать это утверждение. Такие уравнения первой степени называются линейными уравнениями .
| Таким образом, любое уравнение вида ax + by — c, где a, b и c — действительные числа, является линейным уравнением. |
Уравнения с двумя неизвестными более высокой степени дают графики, которые представляют собой кривые разных типов.Вы изучите их на будущих курсах алгебры.
Поскольку график уравнения первой степени с двумя переменными представляет собой прямую линию, необходимо иметь только две точки. Однако ваша работа будет более точной, если вы найдете хотя бы три точки. Ошибки можно найти и исправить, если найденные точки не лежат на одной линии. Таким образом, мы называем третью точку «контрольной точкой».
| Это важно. Не пытайтесь сократить свою работу, найдя только два момента.Вы будете удивлены, как часто вы обнаружите ошибку, обнаружив все три точки. |
Пример 2 Нарисуйте график 3x — 2y — 7.
Решение Сначала составьте таблицу значений и выберите три числа, которые будут заменять x. Попробуем 0, 1,2.
| Опять же, вы также могли начать с произвольными значениями y. |
Ответ не так легко найти на графике, как целое число.Похоже, что x = 0 был не очень удачным выбором. Иногда можно заглянуть вперед и сделать лучший выбор для x.
| Поскольку и x, и y являются целыми числами, x = 1 было хорошим выбором. |
Точку (1, -2) будет легче найти. Если x = 2, у нас будет другая дробь.
Точку (3,1) легко найти.
| x = 3 был еще одним хорошим выбором. |
Скорректируем таблицу значений и будем использовать точки, дававшие целые числа. Это не всегда возможно, но попытка получить целые значения даст более точный набросок. Теперь у нас есть таблица для 3x — 2y = 7.
Это не всегда возможно, но попытка получить целые значения даст более точный набросок. Теперь у нас есть таблица для 3x — 2y = 7.
| Мы можем это сделать, поскольку выбор x был произвольным. |
Расположение точек (1, -2), (3,1), (- 1, -5) дает график 3x — 2y = 7.
| Сколько упорядоченных пар удовлетворяют этому уравнению? |
НАКЛОН ЛИНИИ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Свяжите наклон линии с ее крутизной.
- Запишите уравнение прямой в форме пересечения наклона.
- Постройте прямую линию, используя ее наклон и точку пересечения по оси Y.
Теперь мы хотим обсудить важную концепцию, называемую наклоном линии. Интуитивно мы можем думать об уклоне как о крутизне линии по отношению к горизонтали.
Ниже приведены графики из нескольких линий. Внимательно изучите их и мысленно ответьте на следующие вопросы.
Какая линия круче?
Как выглядит связь между коэффициентом при x и крутизной Какой график будет круче: линии, когда уравнение имеет вид y = mx?
| Какой график будет круче: y = 3x или y = 7x? |
Теперь изучите следующие графики.
Какая линия круче?
Как отрицательное значение m влияет на график?
| Какой график будет круче: y = 3x или y = 7x? |
Для графика y = mx следовало сделать следующие наблюдения.
- Если m> 0, то
- по мере увеличения значения m крутизна линии увеличивается и
- линия поднимается вправо и опускается влево.
- Если м
- по мере увеличения значения m крутизна линии уменьшается и
- линия поднимается влево и опускается вправо
Помните, m> 0 означает, что «m больше нуля. « « |
Другими словами, в уравнении вида y — mx, m управляет крутизной линии. В математике мы используем слово« наклон »для обозначения крутизны и формируем следующее определение:
В уравнении вида y = mx, m — это наклон графика уравнения.
Пример 1 Нарисуйте график y = 6x и укажите наклон линии.
Решение Сначала мы составим таблицу, показывающую три набора упорядоченных пар, которые удовлетворяют уравнению.
| Помните, нам нужны только две точки для определения линии, но мы используем третью точку в качестве проверки. |
Затем мы делаем набросок графика.
Значение m равно 6, следовательно, наклон равен 6. Мы можем просто написать m — 6.
Пример 2 Нарисуйте график и укажите наклон
.Решение Выбирая значения x, которые делятся на 3, получаем таблицу
| Зачем использовать значения, которые делятся на 3? |
Тогда график
Склон
Теперь мы хотим сравнить графики двух уравнений, чтобы установить другую концепцию.
Пример 3 Нарисуйте графики y 3x и y — 3x + 2 на одном и том же наборе координатных осей.
| Сравните коэффициенты при x в этих двух уравнениях. |
Решение
В примере 3 посмотрите на таблицы значений и обратите внимание, что для данного значения x, значение y в уравнении y = 3x + 2 на два больше, чем соответствующее значение y в уравнении y = 3x.
Теперь посмотрите на графики двух уравнений и обратите внимание, что график y = 3x + 2, кажется, имеет тот же наклон, что и y = 3x.Также обратите внимание, что если весь график y = 3x перемещается вверх на две единицы, он будет идентичен графику y = 3x + 2. График y = 3x пересекает ось y в точке (0,0). , а график y = 3x + 2 пересекает ось y в точке (0,2).
| Снова сравните коэффициенты при x в двух уравнениях. |
Сравните эти таблицы и графики, как в примере 3.
| Обратите внимание: когда две линии имеют одинаковый наклон, они параллельны. |
Наклон от одной точки на линии к другой определяется отношением изменения y к изменению x. То есть
| Если вы хотите произвести впечатление на своих друзей, вы можете написать , где греческая буква (дельта) означает «изменение». |
Обратите внимание, что изменение x равно 3, а изменение y равно 2.
Изменение x равно -4, а изменение y равно 1.
| Можно также сказать, что изменение x равно 4, а изменение y равно -1.Это приведет к той же строке. |
Пример 7 На графике y = 3x — 2 наклон равен 3.
Изменение x равно 1, а изменение y равно 3.
y = mx + b называется формой с пересечением наклона уравнения прямой линии. Если уравнение имеет такую форму, m — это наклон линии, а (0, b) — точка, в которой график пересекает (пересекает) ось y.
Если уравнение имеет такую форму, m — это наклон линии, а (0, b) — точка, в которой график пересекает (пересекает) ось y.
| Точка (0, b) называется точкой пересечения по оси y. |
Если уравнение прямой имеет форму пересечения наклона, можно нарисовать его график, не составляя таблицу значений. Используйте точку пересечения оси Y и наклон, чтобы нарисовать график, как показано в примере 8.
| Обратите внимание, что это уравнение имеет вид y = mx + b. |
Сначала найдите точку (0, -2). Это одна из точек на линии. Наклон показывает, что изменение x равно 4, поэтому из точки (0, -2) мы перемещаем четыре единицы в положительном направлении параллельно оси x.Поскольку изменение y равно 3, мы перемещаем три единицы в положительном направлении параллельно оси y. Получившаяся точка тоже находится на линии. Поскольку две точки определяют прямую линию, мы рисуем график.
Поскольку две точки определяют прямую линию, мы рисуем график.
| Всегда начинайте с точки пересечения оси Y. Распространенная ошибка, которую допускают многие студенты, — это путать точку пересечения оси y с точкой пересечения оси x (точка, в которой линия пересекает ось x). |
Пример 9 Задайте наклон и точку пересечения по оси Y и нарисуйте график y = 3x + 4.
Решение m = -3, точка пересечения по оси y = (0,4).
Чтобы выразить наклон в виде отношения, мы можем написать -3 как или. Если мы запишем наклон как, то из точки (0,4) мы перемещаем одну единицу в положительном направлении параллельно оси x, а затем перемещаем три единицы в отрицательном направлении параллельно оси y. Затем мы проводим линию через эту точку и (0,4).
Предположим, уравнение не имеет формы y = mx + b. Сможем ли мы найти наклон и точку пересечения по оси Y? Ответ на этот вопрос — да. Однако для этого мы должны изменить форму данного уравнения, применив методы, использованные в разделе 4-2.
Однако для этого мы должны изменить форму данного уравнения, применив методы, использованные в разделе 4-2.
| Раздел 4-2 посвящен решению буквальных уравнений. Вы можете просмотреть этот раздел. |
Пример 10 Найдите наклон и точку пересечения оси Y для 3x + 4y = 12.
Решение Сначала мы понимаем, что уравнение не в форме пересечения наклона, необходимой для ответа на заданные вопросы. Чтобы получить эту форму, решите данное уравнение относительно y.
| Нарисуйте здесь диаграмму. |
Пример 11 Найдите наклон и точку пересечения оси y для 2x — y = 7.
Решение Поместив уравнение в форму углового пересечения, мы получим
Нарисуйте график линии на сетке ниже. |
ГРАФИЧЕСКИЕ ЛИНЕЙНЫЕ НЕРАВЕНСТВА
ЗАДАЧИ
По завершении этого раздела вы сможете построить график линейных неравенств.
В главе 4 мы построили линейные графики неравенств, например
Это были неравенства с участием только одной переменной. Мы обнаружили, что во всех таких случаях график представлял собой часть числовой прямой. Поскольку уравнение с двумя переменными дает график на плоскости, кажется разумным предположить, что неравенство с двумя переменными будет отображаться как некоторая часть или область плоскости. На самом деле это так. Решение неравенства x + y
Пример 1 Каждая из следующих пар чисел в наборе решений x + y
Решение
| Набор решений состоит из всех упорядоченных пар, которые делают утверждение истинным. |
Подводя итог, следующие упорядоченные пары дают верное утверждение. (2,1), (3, -4), (0,0), (- 1,4) |
| Следующие упорядоченные пары дают ложное утверждение. (5,6), (3,2), (- 2,8) |
Ниже приведен график прямой x + y = 5. Точки из примера 1 указаны на графике с ответами на вопрос «Является ли x + y
| Обратите внимание, что все точки, удовлетворяющие уравнению, находятся слева и ниже линии, а все точки, которые не соответствуют, находятся сверху и справа. |
Обратите внимание, что все ответы «да» лежат на одной стороне линии x + y = 5, а все ответы «нет» лежат на другой стороне линии или на самой строке.
График прямой x + y = 5 делит плоскость на три части: саму линию и две стороны линий (называемые полуплоскостями).
х + у х + у
Если одна точка полуплоскости находится в наборе решений линейного неравенства, то все точки в этой полуплоскости входят в набор решений. Это дает нам удобный метод построения графиков линейных неравенств.
Это дает нам удобный метод построения графиков линейных неравенств.
Построение графика линейного неравенства
1. Замените символ неравенства знаком равенства и нанесите на график полученную линию.
2. Отметьте одну точку, которая, очевидно, находится в определенной полуплоскости этой прямой, чтобы увидеть, входит ли она в набор решений неравенства.
3. Если выбранная точка находится в наборе решений, то вся эта полуплоскость является набором решений. Если выбранная точка не входит в набор решений, тогда другая полуплоскость является набором решений.
| Почему нужно проверять только одну точку? |
Пример 2 Нарисуйте график 2x 4- 3y> 7.
Решение Шаг 1. Сначала нарисуйте график линии 2x + 3y = 7, используя таблицу значений или форму пересечения наклона.
Шаг 2: Затем выберите точку, которая не находится на прямой 2x + 3y = 7. [Если линия не проходит через начало координат, то точка (0,0) всегда является хорошим выбором.] Теперь обратимся к неравенство 2x + 3y>> 7, чтобы увидеть, находится ли выбранная точка в наборе решений.
Шаг 3: Точка (0,0) не входит в набор решений, поэтому полуплоскость, содержащая (0,0), не является набором решений. Следовательно, другая полуплоскость, определяемая линией 2x + 3y = 7, является множеством решений.
Поскольку сама линия не является частью решения, она показана пунктирной линией, а полуплоскость заштрихована, чтобы показать набор решений.
| Набор решений — это полуплоскость сверху и справа от прямой. |
Пример 3 Изобразите график решения линейного неравенства 2x — y ≥ 4.
Решение Шаг 1. Первый график 2x — y = 4. Поскольку линейный график для 2x — y = 4 не проходит через начало координат (0,0), проверьте эту точку в линейном неравенстве.
Шаг 2:
Шаг 3: Поскольку точка (0,0) не входит в набор решений, полуплоскость, содержащая (0,0), отсутствует в наборе. Следовательно, решение — другая полуплоскость. Обратите внимание, однако, что строка 2x — y = 4 включена в набор решений. Поэтому нарисуйте сплошную линию, чтобы показать, что это часть графика.
| Набор решений — это линия и полуплоскость ниже и правее линии. |
Пример 4 График x
Решение Первый график x = y. Затем проверьте точку не на линии. Обратите внимание, что график линии содержит точку (0,0), поэтому мы не можем использовать ее в качестве контрольной точки. Чтобы определить, какая полуплоскость является набором решений, используйте любую точку, которая явно не находится на прямой x = y. Точка (- 2,3) является такой точкой.
Используя эту информацию, построить график x
| Когда график линии проходит через начало координат, любая другая точка на оси x или y также будет хорошим выбором. |
ГРАФИЧЕСКОЕ РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Нарисуйте графики двух линейных уравнений в одной и той же системе координат.
- Найдите общее решение двух графиков.
Пример 1 Пара уравнений называется системой линейных уравнений.
Мы заметили, что каждое из этих уравнений имеет бесконечно много решений, и каждое из них будет образовывать прямую линию, когда мы построим его в декартовой системе координат.
Теперь мы хотим найти решения для системы. Другими словами, нам нужны все точки (x, y), которые будут на графике обоих уравнений.
Решение Мы рассуждаем следующим образом: если все решения 2x — y = 2 лежат на одной прямой, а все решения x + 2y = 11 лежат на другой прямой, то решение обоих уравнений будет их точками пересечение (если две прямые пересекаются).
| В этой таблице мы позволяем x принимать значения 0, 1 и 2. Затем мы находим значения для y с помощью уравнения. Сделайте это перед тем, как продолжить. В этой таблице мы позволяем y принимать значения 2, 3 и 6. Затем мы находим x, используя уравнение. Также проверьте эти значения. |
| Две прямые пересекаются в точке (3,4). |
Обратите внимание, что точка пересечения выглядит как (3,4). Теперь мы должны проверить точку (3,4) в обоих уравнениях, чтобы убедиться, что это решение системы.
| В качестве проверки мы подставляем упорядоченную пару (3,4) в каждое уравнение, чтобы увидеть, получим ли мы истинное утверждение. Существуют ли другие точки, которые удовлетворяли бы обоим уравнениям? Почему? |
Следовательно, (3,4) является решением системы.
Не все пары уравнений дают единственное решение, как в этом примере. На самом деле существует три возможности, и вы должны знать о них.
Поскольку мы имеем дело с уравнениями, которые представляют собой прямые линии, мы можем исследовать эти возможности, наблюдая за графиками.
1. Независимые уравнения Две прямые пересекаются в одной точке. В этом случае есть единственное решение.
| Приведенный выше пример представляет собой систему независимых уравнений. |
2. Несогласованные уравнения Две линии параллельны. В этом случае решения нет.
| Как бы далеко ни были протянуты эти линии, они никогда не пересекутся. |
3. Зависимые уравнения Два уравнения дают одну и ту же линию. В этом случае любое решение одного уравнения является решением другого.
| В этом случае общих решений будет бесконечно много. |
На более поздних курсах алгебры будут изучены методы распознавания несовместных и зависимых уравнений. Однако на этом уровне мы будем иметь дело только с независимыми уравнениями. Тогда вы можете рассчитывать, что для всех проблем, приведенных в этой главе, будут найдены уникальные решения.
| Это означает, что графики всех систем в этой главе будут пересекаться в одной точке. |
Решение системы двух линейных уравнений путем построения графика
1. Составьте таблицу значений и нарисуйте график каждого уравнения в той же системе координат.
2. Найдите значения (x, y), которые называют точку пересечения линий.
3. Отметьте эту точку (x, y) в обоих уравнениях.
| Опять же, в этой таблице мы произвольно выбрали значения x равными — 2, 0 и 5. Здесь мы выбрали для x значения 2, 4 и 6. Вы можете выбрать любые значения, которые хотите. Мы говорим «очевидный», потому что мы еще не проверили упорядоченную пару в обоих уравнениях. Как только он проверит, это определенно решение. |
Поскольку (3,2) проверяет оба уравнения, это решение системы.
ГРАФИЧЕСКОЕ РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Постройте два или более линейных неравенства на одном и том же наборе осей координат.
- Определите область плоскости, которая является решением системы.
Более поздние занятия по математике будут включать тему линейного программирования. Несмотря на то, что сама тема выходит за рамки этого текста, одна техника, используемая в линейном программировании, вполне доступна вам — построение графиков систем линейных неравенств — и мы обсудим это здесь.
В предыдущем разделе вы обнаружили, что решение системы линейных уравнений — это пересечение решений каждого из уравнений.Таким же образом решение системы линейных неравенств представляет собой пересечение полуплоскостей (и, возможно, прямых), которые являются решениями каждого отдельного линейного неравенства.
Другими словами, x + y> 5 имеет множество решений и 2x — y
имеет в качестве своего решения область плоскости, которая находится в наборе решений обоих неравенств.
Для построения графика решения этой системы мы наносим на график каждое линейное неравенство на одном и том же наборе координатных осей и указываем пересечение двух наборов решений.
| Обратите внимание, что решением системы линейных неравенств будет набор точек. |
| Опять же, используйте либо таблицу значений, либо форму уравнения с пересечением наклона для построения графика линий. |
Проверка точки (0,0) в неравенстве x + y> 5 показывает, что точка (0,0) не входит в набор ее решений. Мы указываем набор решений x + y> 5 экраном справа от пунктирной линии.
| Эта область находится справа и выше линии x + y = 5. |
Проверка точки (0,0) в неравенстве 2x — y
| Эта область находится слева и выше линии 2x — y = 4. |
Пересечение двух наборов решений — это та область плоскости, в которой пересекаются два экрана. Этот регион показан на графике.
| Обратите внимание еще раз, что решение не включает строки.Если, например, нас попросили построить график решения системы , который указывает, что решение включает точки на линии x + y = 5. |
Результаты показывают, что все точки в заштрихованной части графика будут в наборах решений x + y> 5 и 2x — y.
РЕШЕНИЕ СИСТЕМЫ ПУТЕМ ЗАМЕНЫ
ЗАДАЧИ
По завершении этого раздела вы должны уметь решать систему двух линейных уравнений методом подстановки.
В разделе 6-5 мы решили систему двух уравнений с двумя неизвестными с помощью построения графиков. Графический метод очень полезен, но он был бы непрактичным, если бы решения были дробными. Фактическую точку пересечения может быть очень сложно определить.
Существуют алгебраические методы решения систем. В этом разделе мы обсудим метод подстановки.
Пример 1 Решить методом подстановки:
Решение
Шаг 1 Мы должны найти одно неизвестное в одном уравнении.Мы можем выбрать x или y либо в первом, либо во втором уравнении. Наш выбор может быть основан на получении простейшего выражения. В этом случае мы решим относительно x во втором уравнении, получив x = 4 + 2y, потому что любой другой выбор привел бы к дроби.
| Посмотрите на оба уравнения и посмотрите, есть ли в одном из них переменная с коэффициентом, равным единице. |
Шаг 2 Подставьте значение x в другое уравнение.В этом случае уравнение
2х + 3у = 1.
Подставляя (4 + 2y) вместо x, мы получаем 2 (4 + 2y) + 3y = 1, уравнение только с одной неизвестной.
| Причина этого в том, что если x = 4 + 2y в одном из уравнений, то x должен быть равен 4 + 2y в другом уравнении. |
Шаг 3 Решите неизвестное.
| Помните, сначала удалите скобки. |
Шаг 4 Подставьте y = — 1 в любое уравнение, чтобы найти соответствующее значение для x.Поскольку мы уже решили второе уравнение относительно x через y, мы можем его использовать.
| Мы можем подставить y = — 1 в любое уравнение, поскольку y имеет одинаковое значение в обоих. |
Таким образом, у нас есть решение (2, -1).
| Помните, что x записывается первым в упорядоченной паре. |
Шаг 5 Проверьте решение в обоих уравнениях. Помните, что решение системы должно быть верным для каждого уравнения в системе.С
решение (2, -1) действительно проверяет.
| Это проверяет: 2x + 3y = 1 и x — 2y = 4. |
| Отметьте эту упорядоченную пару в обоих уравнениях. Ни в одном из этих уравнений не было переменной с коэффициентом, равным единице. В этом случае решение заменой — не лучший метод, но мы сделаем это так, чтобы показать, что это возможно. В следующем разделе будет предложен более простой метод. |
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ ДОПОЛНЕНИЕМ
ЗАДАЧИ
По завершении этого раздела вы должны уметь решать систему двух линейных уравнений методом сложения.
Метод сложения для решения системы линейных уравнений основан на двух фактах, которые мы использовали ранее.
Во-первых, мы знаем, что решения уравнения не меняются, если каждый член этого уравнения умножается на ненулевое число. Во-вторых, мы знаем, что если мы добавим одинаковые или равные количества к обеим сторонам уравнения, результаты все равно будут одинаковыми.
Пример 1 Решить сложением:
| Обратите внимание, что мы можем решить эту систему методом подстановки, решив первое уравнение относительно y.Решите эту систему методом подстановки и сравните свое решение с решением, полученным в этом разделе. |
Решение
Шаг 1 Наша цель — сложить два уравнения и исключить одно из неизвестных, чтобы мы могли решить полученное уравнение с одним неизвестным. Если мы сложим уравнения как есть, мы не удалим неизвестное. Это означает, что мы должны сначала умножить каждую сторону одного или обоих уравнений на число или числа, что приведет к исключению одного из неизвестных при сложении уравнений.
Внимательно изучив проблему, мы замечаем, что проще всего устранить неизвестное y. Это делается путем умножения каждой стороны первого уравнения на -2.
| Обратите внимание, что каждый член необходимо умножить на (- 2). |
Шаг 2 Добавьте уравнения.
Шаг 3 Решите полученное уравнение.
| В этом случае мы просто умножаем каждую сторону на (-1). |
Шаг 4 Найдите значение другого неизвестного, подставив это значение в одно из исходных уравнений.Используя первое уравнение,
| Подставьте x = 4 во второе уравнение и посмотрите, получите ли вы такое же значение для y. |
Шаг 5 Если мы проверим упорядоченную пару (4, -3) в обоих уравнениях, мы увидим, что это решение системы.
Пример 2 Решить сложением:
| Обратите внимание, что в этой системе ни одна переменная не имеет коэффициента, равного единице. Поэтому лучший метод решения — метод сложения. |
Решение
Шаг 1 Оба уравнения необходимо изменить, чтобы исключить одно из неизвестных. Ни одно из неизвестных не будет проще другого, поэтому удалите либо x, либо y.
Чтобы исключить x, умножьте каждую сторону первого уравнения на 3 и каждую сторону второго уравнения на -2.
| Если вы решили исключить y, умножьте первое уравнение на — 2, а второе уравнение на 3. Сделайте это и решите систему.Сравните ваше решение с полученным в примере. |
Шаг 2 Сложив уравнения, мы получаем
Шаг 3 Решение для урожайности
Шаг 4 Использование первого уравнения в исходной системе для нахождения значения другой неизвестной дает
Шаг 5 Убедитесь, что упорядоченная пара (- 1,3) является решением системы.
| Чек остается на ваше усмотрение. |
СТАНДАРТНАЯ ФОРМА
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Напишите линейное уравнение в стандартной форме.
- Решите систему двух линейных уравнений, если они заданы в нестандартной форме.
Уравнения в предыдущих разделах не содержали дробей, как неизвестные в левой части уравнения, так и неизвестные в том же порядке.
Такие уравнения называются стандартными. То есть они имеют вид ax + by = c, где a, b и c — целые числа. Перед решением методом сложения уравнения необходимо привести к стандартному виду.
Пример 1 Измените 3x = 5 + 4y на стандартную форму.
Решение 3x = 5 + 4y не в стандартной форме, потому что одно неизвестное находится справа. Если мы добавим -4y к обеим сторонам, мы получим 3x — 4y = 5, что в стандартной форме.
| Будьте осторожны. Многие студенты забывают умножить правую часть уравнения на 24. |
| Снова убедитесь, что каждый член умножен на 12. |
Теперь прибавьте — 24x к обеим сторонам, получив — 24x + 9y = -10, что в стандартной форме.Обычно уравнения пишутся так, что первый член положительный. Таким образом, мы умножаем каждый член этого уравнения на (- 1).
| Вместо того, чтобы говорить «первый член положительный», мы иногда говорим «ведущий коэффициент положительный». |
ПРОБЛЕМЫ СО СЛОВОМ С ДВУМЯ НЕИЗВЕСТНЫМИ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите, когда проблема со словом может быть решена с использованием двух неизвестных.
- Составьте уравнения и решите словесную задачу.
Многие проблемы со словами можно обрисовать и решить, используя два неизвестных.
Пример 1 Сумма двух чисел равна 5. Трижды первое число, добавленное к пяти умноженным на второе число, равно 9. Найдите числа.
Решение Пусть x = первое число
y = второе число
Первое утверждение дает нам уравнение
x + y = 5.
Второе утверждение дает нам уравнение
3x + 5 y = 9.
Теперь у нас есть система
, которую мы можем решить любым из известных нам методов, давая
x = 8 и y = — 3.
| Решите систему с помощью подстановки. |
Пример 2 Два работника получают в общей сложности 136 долларов за 8-часовую работу. Если одному работнику платят на 1 доллар в час больше, чем другому, найдите почасовую ставку для каждого.
Решение Пусть x = почасовая ставка одного работника
y = почасовая ставка другого работника.
| Обратите внимание, что очень важно сказать, что представляют x и y. |
Первое утверждение дает нам уравнение
8x + 8y = 136.
Второе утверждение дает уравнение
х = у + 1.
Теперь у нас есть система (в стандартной форме)
Решение дает x = 9 и y = 8. Ставка одного рабочего составляет 9 долларов в час, а другого — 8 долларов в час.
| Решите эту систему методом сложения. |
РЕЗЮМЕ
Ключевые слова
- Декартова система координат — это метод наименования точек на плоскости.
- Упорядоченные пары чисел используются для обозначения точек на плоскости.
- Линейное уравнение представляет собой прямую линию.
- Наклон от одной точки на линии до другой является отношением.
- Форма пересечения наклона уравнения прямой имеет вид y = mx + b.
- Линейное неравенство представляет собой часть плоскости.
- Система двух линейных уравнений состоит из линейных уравнений, для которых мы хотим найти совместное решение.
- Независимые уравнения имеют уникальные решения.
- Противоречивые уравнения не имеют решения.
- Зависимые уравнения имеют бесконечно много решений.
- Система двух линейных неравенств состоит из линейных неравенств, для которых мы хотим найти одновременное решение.
- Стандартная форма линейного уравнения — это ax + by = c, где a, b и c — действительные числа.
Процедуры
- Чтобы нарисовать график линейного уравнения, найдите упорядоченные пары чисел, которые являются решениями уравнения.Найдите эти точки в декартовой системе координат и соедините их линией.
- Чтобы нарисовать график линии, используя ее наклон:
Шаг 1 Запишите уравнение прямой в форме y — mx + b.
Шаг 2 Найдите точку пересечения j (0, b).
Шаг 3 Начиная с (0, b), используйте наклон m, чтобы найти вторую точку.
Шаг 4 Соедините две точки прямой линией. - Чтобы построить график линейного неравенства:
Шаг 1 Замените символ неравенства знаком равенства и нанесите на график полученную линию.
Шаг 2 Отметьте одну точку, которая явно находится в определенной полуплоскости этой прямой, чтобы увидеть, входит ли она в набор решений неравенства.
Шаг 3 Если выбранная точка находится в наборе решений, то вся эта полуплоскость является набором решений. Если выбранная точка не входит в набор решений, тогда другая полуплоскость является набором решений. - Чтобы решить систему двух линейных уравнений с помощью построения графиков, тщательно изобразите уравнения в одной и той же системе координат.Их точка пересечения и будет решением системы.
- Чтобы решить систему двух линейных неравенств с помощью построения графиков, определите область плоскости, которая удовлетворяет обоим утверждениям неравенства.
- Чтобы решить систему двух уравнений с двумя неизвестными путем подстановки, решите одну неизвестную одного уравнения через другое неизвестное и подставьте эту величину в другое уравнение. Затем подставьте полученное таким образом числовое значение в любое уравнение, чтобы найти значение другого неизвестного.Наконец, проверьте решение в обоих уравнениях.
- Чтобы решить систему двух уравнений с двумя неизвестными путем сложения, умножьте одно или оба уравнения на необходимые числа, чтобы при сложении уравнений одно из неизвестных было удалено. Решите оставшиеся неизвестные и подставьте это значение в одно из уравнений, чтобы найти другое неизвестное. Проверьте оба уравнения.
- Чтобы решить словесную задачу с двумя неизвестными, найдите два уравнения, которые показывают связь между неизвестными.Затем решите систему. Всегда проверяйте решение указанной проблемы.
Графические системы неравенств — A Plus Topper
Графические системы неравенствЕсли вы можете изобразить неравенство, вы можете изобразить и систему неравенств!
Просто изобразите каждое неравенство отдельно на одном и том же наборе осей. Область перекрытия штриховок — это решение системы неравенств.
Графики системы неравенств
- Изобразите каждое неравенство отдельно.Инструкции по графическому изображению неравенств можно найти в «Графическом изображении неравенств».
- Решением системы будет область, в которой штриховки от каждого неравенства накладываются друг на друга.
Изобразите следующую систему неравенств
Пример 1. Постройте график этой системы линейных неравенств и обозначьте область решения S:
y <2x - 6 и y> -3x + 4
- Замените символы неравенства знаками равенства и нанесите на график прямые линии.
y = 2x — 6 и y = -2x + 3
Эта задача связана со строгими неравенствами, поэтому прямые линии будут нарисованы пунктиром. - Определите, какая сторона каждой линии будет закрашена, чтобы обозначить ее неравенство. В этом примере используется контрольная точка (0,0).
y <2x - 6
0 <2 (0) - 6
0 <-6 False (закрасить другую сторону линии)
y> -3x + 4
0> -3 (0) + 4
0> 4 Неверно (закрасьте другую сторону линии)
Найдите перекрывающийся участок и пометьте его S.
Пример 2: Изобразите эту систему линейных неравенств и обозначьте область решения S:
2x + y ≥ 2 и 2x + y ≤ 6
- Замените символы неравенства знаками равенства и нанесите на график прямые линии.
Обратите внимание, что эти две линии имеют одинаковый наклон и параллельны.
y = -2x + 2 и y = -2x + 6
Эта задача касается двух неравенств «меньше или равно», поэтому обе линии нарисованы сплошными. - Определите, какая сторона каждой линии будет закрашена, чтобы обозначить ее неравенство.В этом примере используется контрольная точка (0,0).
y ≥ -2x — 2
0 ≥ -2 (0) — 2
0 ≥ -2 Верно (закрашиваем с той же стороны линии)
y ≤ -2x + 6
0 ≤ -2 (0) + 6
0 ≤ 6 Верно (заштрихуйте ту же сторону линии)
Найдите перекрывающийся участок и пометьте его S. Область между двумя параллельными линиями является решением.
Сайт «Мы продаем компакт-диски» планирует покупать объявления в местной газете, рекламирующие их сайт.Их операционный бюджет позволит им потратить не более 2200 долларов на это рекламное приключение. Они планируют разместить не более 20 рекламных объявлений. Реклама будет стоить 50 долларов за публикацию в дневной газете и 200 долларов за выходную. Подготовьте график, на котором будут представлены все возможные комбинации рекламы в этих условиях.
Решение:
Пусть x = количество объявлений выходного дня
Пусть y = количество объявлений будних дней
x + y ≤ 20 (будет не более 20 объявлений)
200x + 50y ≤ 2200 (стоимость рекламы самое большее 2200 долларов)
Для этой задачи x и y не могут быть отрицательными числами, поэтому ответ будет только в первом квадранте.
Решите каждое из неравенств выше для значения y.
С помощью графического калькулятора построите график
Y 1 = 20 — x (со значком «тень внизу»)
Y 2 = (2200 — 200x) / 50 (набор значков «затенение внизу»)
Установите окно для просмотра только первого квадранта.
Используйте опцию пересечения, чтобы найти вершины четырехугольника, площадь которого составляет пул ответов (перекрывающаяся заштрихованная область).
Как решить систему неравенств y3x5 и математику класса 9 CBSE
Подсказка: Теперь, чтобы решить неравенства, мы найдем соответствующее равенство и, следовательно, построим линию равенства.Теперь проверьте, удовлетворяет ли начало координат неравенству. Если он удовлетворяет неравенству, то исходная сторона — это множество решений, или в другом случае противоположная сторона — это множество решений. Следовательно, мы найдем множества решений на графе, и тогда решение неравенств будет пересечением обоих множеств решений. Полное пошаговое решение:
Теперь нам даны два линейных неравенства. Чтобы решить линейные уравнения, мы сначала построим график обоих неравенств, а затем найдем область пересечения этих двух неравенств.
Сначала рассмотрим $ y. Соответствующее линейное уравнение неравенству: $ y = 3x-5 $
Теперь построим линию $ y = 3x-5 $.
Теперь, подставляя значение x, мы найдем соответствующие значения y и, следовательно, найдем решение уравнения.
Теперь, подставив x = 0, мы получим y = — 5.
Аналогично, подставив x = 1, мы получим y = -2.
Следовательно, у нас есть точка (0, -5) и (1, -2) лежит в уравнении данной прямой.
Давайте начертим линию, нанеся точки и проведя линию, проходящую через точки.
Теперь рассмотрим неравенство $ y, следовательно, график неравенства:
Теперь аналогично рассмотрим уравнение $ y> -4x-7 $
Соответствующее уравнение будет $ y = -4x-7 $.
Теперь, подставив значение x = 0, мы получим y = — 7.
Теперь, подставив x = — 2, мы получим y = 1
Следовательно, точки (0, -7) и (-2, 1) лежат на уравнение.
Следовательно, мы построим точки и проведем линию, проходящую через точки.
Теперь рассмотрим неравенство $ y> -4x-7 $
Теперь мы видим, что точка (0, 0) удовлетворяет неравенству.Следовательно, требуемая область является областью исходной стороны линии.
Теперь решение двух одновременных неравенств является пересечением обеих областей.
Отсюда получаем:
Темно-розовая область — это необходимая область.
Примечание: Теперь обратите внимание, что при построении неравенства мы сначала построим соответствующее равенство. Теперь возьмите точку с любой стороны линии и проверьте, удовлетворяет ли она неравенству. Если точка удовлетворяет неравенству, то она находится в наборе решений неравенства, и, следовательно, эта сторона линии является всем набором решений.Если он не удовлетворяет неравенству, то противоположная сторона — это множество решений. Теперь мы можем взять любую точку, чтобы проверить это, но для простоты лучше взять начало.
Графики и решения систем линейных уравнений
Результаты обучения
- Графические системы уравнений
- Построить систему двух линейных уравнений
- Построить систему двух линейных неравенств
- Оценить заказанные пары как решения для систем
- Определить, является ли упорядоченная пара решением системы линейных уравнений
- Определить, является ли упорядоченная пара решением системы линейных неравенств
- Классифицируйте решения по системам
- Определите, какой тип решения будет иметь система, на основе ее графика
Путь течения реки зависит от многих переменных, включая размер реки, количество воды в ней, какие предметы плавают в реке, идет ли дождь или нет, и так далее.Если вы хотите лучше всего описать его поток, вы должны принять во внимание эти другие переменные. В этом может помочь система линейных уравнений.
Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Вы найдете системы уравнений во всех приложениях математики. Они являются полезным инструментом для обнаружения и описания взаимосвязи поведения или процессов.Например, редко можно найти схему транспортного потока, на которую влияет только погода. Несчастные случаи, время суток и крупные спортивные соревнования — это лишь некоторые из других переменных, которые могут повлиять на транспортный поток в городе. В этом разделе мы исследуем некоторые основные принципы построения графиков и описания пересечения двух линий, составляющих систему уравнений.
Построение системы линейных уравнений
В этом разделе мы рассмотрим системы линейных уравнений и неравенств с двумя переменными.Сначала мы попрактикуемся в построении графиков двух уравнений на одном и том же наборе осей, а затем изучим различные соображения, которые необходимо учитывать при построении графиков двух линейных неравенств на одном и том же наборе осей. Для построения графика системы линейных уравнений используются те же методы, что и для построения графиков отдельных линейных уравнений. Мы можем использовать таблицы значений, уклона и пересечения y или x и y -пересечения для построения графика обеих линий на одном и том же наборе осей.
Например, рассмотрим следующую систему линейных уравнений с двумя переменными.
[латекс] \ begin {array} {r} 2x + y = -8 \\ x-y = -1 \ end {array} [/ latex]
Давайте изобразим их, используя форму пересечения наклона на одном и том же наборе осей. Помните, что форма пересечения наклона выглядит как [latex] y = mx + b [/ latex], поэтому мы захотим решить оба уравнения для [latex] y [/ latex].
Сначала найдите y в [latex] 2x + y = -8 [/ latex]
[латекс] \ begin {array} {c} 2x + y = -8 \\ y = -2x — 8 \ end {array} [/ latex]
Во-вторых, решите относительно y в [latex] x-y = -1 [/ latex]
[латекс] \ begin {массив} {r} x-y = -1 \, \, \, \, \, \\ y = x + 1 \ end {array} [/ latex]
Теперь система записывается как
[латекс] \ begin {array} {c} y = -2x — 8 \\ y = x + 1 \ end {array} [/ latex]
Теперь вы можете построить оба уравнения, используя их наклоны и точки пересечения на одном и том же наборе осей, как показано на рисунке ниже.Обратите внимание на то, что графики имеют одну общую точку. Это их точка пересечения, точка, которая лежит на обеих линиях. В следующем разделе мы убедимся, что эта точка является решением системы.
В следующем примере вам будет предоставлена система построения графика, состоящая из двух параллельных линий.
Пример
Постройте график системы [латекс] \ begin {array} {c} y = 2x + 1 \\ y = 2x-3 \ end {array} [/ latex], используя наклоны и пересечения линий по оси Y.
Показать решениеСначала построим график [латекс] y = 2x + 1 [/ latex], используя наклон m = 2 и точку пересечения оси y (0,1)
Затем добавьте [латекс] y = 2x-3 [/ latex], используя наклон m = 2 и точку пересечения оси y (0, -3)
Обратите внимание на то, что это параллельные линии, и они не пересекаются.В следующем разделе мы обсудим, как не существует решений системы уравнений, представляющих собой параллельные прямые.
В следующем примере вам будет предоставлена система, уравнения которой выглядят по-разному, но после построения графика оказываются той же линией.
Пример
Изобразите систему [латекс] \ begin {array} {c} y = \ frac {1} {2} x + 2 \\ 2y-x = 4 \ end {array} [/ latex], используя x — и y -перехватывает.
Показать решениеСначала найдите точки пересечения по осям x и y [latex] y = \ frac {1} {2} x + 2 [/ latex]
Пересечение x будет иметь значение 0 для y, поэтому подставьте y = 0 в уравнение и выделите переменную x.
[латекс] \ begin {array} {c} 0 = \ frac {1} {2} x + 2 \\\ подчеркивание {\, \, \, \, \, \, \, \, — 2 \, \, \, \, \, \, — 2} \\ — 2 = \ frac {1} {2} x \\\ left (2 \ right) \ left (-2 \ right) = \ left (2 \ справа) \ frac {1} {2} x \\ — 4 = x \ end {array} [/ latex]
Х-точка пересечения [latex] y = \ frac {1} {2} x + 2 [/ latex] равна [latex] \ left (-4,0 \ right) [/ latex].
Угол пересечения по оси Y найти легче, поскольку это уравнение имеет форму пересечения с угловым коэффициентом. Y-точка пересечения равна (2,0).
Теперь мы можем построить [латекс] y = \ frac {1} {2} x + 2 [/ latex], используя точки пересечения
Теперь найдите перехватчики [latex] 2y-x = 4 [/ latex]
Подставьте y = 0 в уравнение, чтобы найти точку пересечения с x.
[латекс] \ begin {массив} {c} 2y-x = 4 \\ 2 \ left (0 \ right) -x = 4 \\ x = -4 \ end {array} [/ latex]
Х-точка пересечения [latex] 2y-x = 4 [/ latex] равна [latex] \ left (-4,0 \ right) [/ latex].
Теперь подставьте x = 0 в уравнение, чтобы найти точку пересечения оси y.
[латекс] \ begin {array} {c} 2y-x = 4 \\ 2y-0 = 4 \\ 2y = 4 \\ y = 2 \ end {array} [/ latex]
Y-пересечение [latex] 2y-x = 4 [/ latex] равно [latex] \ left (0,2 \ right) [/ latex].
ПОДОЖДИТЕ, это те же перехваты, что и [latex] y = \ frac {1} {2} x + 2 [/ latex]! Фактически, [latex] y = \ frac {1} {2} x + 2 [/ latex] и [latex] 2y-x = 4 [/ latex] на самом деле одно и то же уравнение, выраженное по-разному.Если бы вы записали их оба в форме пересечения наклона, вы бы увидели, что это одно и то же уравнение.
Если вы построите график, это одна и та же линия. В следующем разделе мы увидим, что системы с двумя одинаковыми уравнениями в них имеют бесконечное число решений.
Построение графика системы линейных уравнений состоит из выбора метода построения графиков, который вы хотите использовать, и построения графиков обоих уравнений на одном и том же наборе осей. Когда вы строите график системы линейных неравенств на одном и том же наборе осей, вам необходимо учесть еще несколько вещей.
Изобразите систему двух неравенств
Помните из модуля по построению графиков, что график одного линейного неравенства разбивает координатную плоскость на две области. По одну сторону лежат все решения неравенства. С другой стороны, решений нет. Рассмотрим график неравенства [латекс] y <2x + 5 [/ latex].
Пунктирная линия [латекс] y = 2x + 5 [/ latex]. Каждая упорядоченная пара в заштрихованной области под линией является решением [latex] y <2x + 5 [/ latex], поскольку все точки под линией делают неравенство истинным.Если вы сомневаетесь в этом, попробуйте подставить координаты x и y точек A и B в неравенство — вы увидите, что они работают. Итак, заштрихованной областью показаны все решения этого неравенства.
Граничная линия делит координатную плоскость пополам. В этом случае он показан пунктирной линией, поскольку точки на линии не удовлетворяют неравенству. Если бы неравенство было [латекс] y \ leq2x + 5 [/ латекс], то граница была бы сплошной.
Изобразим еще одно неравенство: [latex] y> −x [/ latex].Вы можете проверить пару точек, чтобы определить, какую сторону границы нужно заштриховать. Контрольные точки M и N дают верные утверждения. Итак, заштриховываем область над линией. Линия пунктирна, поскольку точки на линии не соответствуют действительности.
Чтобы создать систему неравенств, вам нужно построить график двух или более неравенств вместе. Давайте использовать [latex] y <2x + 5 [/ latex] и [latex] y> −x [/ latex], поскольку мы уже изобразили каждый из них.
Фиолетовая область показывает, где перекрываются решения двух неравенств.Эта область является решением системы неравенств . Любая точка в этой фиолетовой области будет верна как для [latex] y> −x [/ latex], так и для [latex] y <2x + 5 [/ latex].
В следующем примере вам дана система двух неравенств, граничные линии которых параллельны друг другу.
Примеры
Изобразите систему [latex] \ begin {array} {c} y \ ge2x + 1 \\ y \ lt2x-3 \ end {array} [/ latex]
Показать решениеГраницы для этой системы такие же, как и для системы уравнений из предыдущего примера:
[латекс] \ begin {array} {c} y = 2x + 1 \\ y = 2x-3 \ end {array} [/ latex]
Построение граничных линий будет аналогично, за исключением того, что неравенство [латекс] y \ lt2x-3 [/ latex] требует, чтобы мы нарисовали пунктирную линию, а неравенство [латекс] y \ ge2x + 1 [/ латекс] потребует сплошная линия.Графики будут выглядеть так:
Теперь нам нужно добавить регионы, представляющие неравенства. Для неравенства [латекс] y \ ge2x + 1 [/ latex] мы можем проверить точку по обе стороны от линии, чтобы увидеть, какую область закрасить. Давайте проверим [латекс] \ left (0,0 \ right) [/ latex], чтобы упростить задачу.
Заменить [латекс] \ left (0,0 \ right) [/ latex] на [latex] y \ ge2x + 1 [/ latex]
[латекс] \ begin {array} {c} y \ ge2x + 1 \\ 0 \ ge2 \ left (0 \ right) +1 \\ 0 \ ge {1} \ end {array} [/ latex]
Это неправда, поэтому мы знаем, что нам нужно заштриховать другую сторону граничной линии для неравенства [latex] y \ ge2x + 1 [/ latex].График теперь будет выглядеть так:
Теперь закрасим область, которая показывает решения неравенства [латекс] y \ lt2x-3 [/ latex]. Опять же, мы можем выбрать [latex] \ left (0,0 \ right) [/ latex] для тестирования, потому что это упрощает алгебру.
Заменить [латекс] \ left (0,0 \ right) [/ latex] на [latex] y \ lt2x-3 [/ latex]
[латекс] \ begin {array} {c} y \ lt2x-3 \\ 0 \ lt2 \ left (0, \ right) x-3 \\ 0 \ lt {-3} \ end {array} [/ latex ]
Это неправда, поэтому мы знаем, что нам нужно заштриховать другую сторону граничной линии для неравенства [латекс] y \ lt2x-3 [/ latex].График теперь будет выглядеть так:
У этой системы неравенства нет общих черт.
Как бы выглядел график, если бы система выглядела так?
[латекс] \ begin {массив} {c} y \ ge2x + 1 \\ y \ gt2x-3 \ end {array} [/ latex].
Проверка точки [latex] \ left (0,0 \ right) [/ latex] вернет положительный результат для неравенства [latex] y \ gt2x-3 [/ latex], и тогда график будет выглядеть следующим образом:
Фиолетовая область — это область перекрытия обоих неравенств.
В следующем разделе мы увидим, что точки могут быть решениями систем уравнений и неравенств. Проверим алгебраически, является ли точка решением линейного уравнения или неравенства.
Определить, является ли упорядоченная пара решением системы линейных уравнений
Линии на графике выше определены как
[латекс] \ begin {массив} {r} 2x + y = -8 \\ x-y = -1 \ end {array} [/ latex].
Они пересекаются в том, что выглядит как [латекс] \ left (-3, -2 \ right) [/ latex].
Используя алгебру, мы можем проверить, что эта общая точка на самом деле [latex] \ left (-3, -2 \ right) [/ latex], а не [latex] \ left (-2.999, -1.999 \ right) [/ latex ]. Подставляя значения x и y упорядоченной пары в уравнение каждой линии, вы можете проверить, находится ли точка на обеих линиях. Если подстановка приводит к истинному утверждению, значит, вы нашли решение системы уравнений!
Поскольку решение системы должно быть решением всех уравнений в системе, вам нужно будет проверить точку в каждом уравнении.В следующем примере мы заменим -3 на x и -2 на y в каждом уравнении, чтобы проверить, действительно ли это решение.
Пример
[латекс] \ left (-3, -2 \ right) [/ latex] решение системы
[латекс] \ begin {array} {r} 2x + y = -8 \\ x-y = -1 \ end {array} [/ latex]
Показать решение Сначала проверьте [латекс] 2x + y = -8 [/ latex]:[латекс] \ begin {массив} {r} 2 (-3) + (- 2) = -8 \\ — 8 = -8 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Теперь проверьте [латекс] x-y = -1 [/ latex].
[латекс] \ begin {array} {r} (- 3) — (- 2) = -1 \\ — 1 = -1 \\\ text {TRUE} \ end {array} [/ latex]
[латекс] \ left (-3, -2 \ right) [/ latex] является решением [латекса] x-y = -1 [/ latex]
Поскольку [latex] \ left (-3, -2 \ right) [/ latex] является решением каждого из уравнений в системе, [latex] \ left (-3, -2 \ right) [/ latex] это решение системы.
Ответ
[латекс] \ left (-3, -2 \ right) [/ latex] — это решение системы.
Пример
— это (3, 9) решение системы
[латекс] \ begin {array} {r} y = 3x \\ 2x – y = 6 \ end {array} [/ latex]
Показать решение Поскольку решение системы должно быть решением всех уравнений в системе, отметьте точку в каждом уравнении.Замените 3 на x и 9 на y в каждом уравнении.
[латекс] \ begin {array} {l} y = 3x \\ 9 = 3 \ left (3 \ right) \\\ text {TRUE} \ end {array} [/ latex]
(3, 9) представляет собой раствор [латекс] y = 3x [/ латекс].
[латекс] \ begin {array} {r} 2x – y = 6 \\ 2 \ left (3 \ right) –9 = 6 \\ 6–9 = 6 \\ — 3 = 6 \ text {FALSE } \ end {array} [/ latex]
(3, 9) — это , а не раствор [латекс] 2x – y = 6 [/ латекс].
Поскольку (3, 9) не является решением одного из уравнений системы, оно не может быть решением системы.
Ответ
(3, 9) не является решением системы.
Подумай об этом
[латекс] (- 2,4) [/ латекс] решение для системы
[латекс] \ begin {array} {r} y = 2x \\ 3x + 2y = 1 \ end {array} [/ latex]
Прежде чем производить какие-либо вычисления, посмотрите на заданную точку и первое уравнение в системе. Можете ли вы предсказать ответ на вопрос, не занимаясь алгеброй?
Показать решениеПодставьте -2 вместо x и 4 вместо y в первое уравнение:
[латекс] \ begin {array} {l} y = 2x \\ 4 = 2 \ left (-2 \ right) \\ 4 = -4 \\\ text {FALSE} \ end {array} [/ latex]
Вы можете остановить тестирование, потому что точка, которая является решением системы, будет решением обоих уравнений в системе.
[латекс] (- 2,4) [/ латекс] НЕ является решением для системы
[латекс] \ begin {array} {r} y = 2x \\ 3x + 2y = 1 \ end {array} [/ latex]
Помните, что для решения системы уравнений значения точки должны быть решением обоих уравнений. Как только вы найдете одно уравнение, для которого точка неверна, вы определили, что оно не является решением системы.
Мы можем использовать тот же метод, чтобы определить, является ли точка решением системы линейных неравенств.
Определить, является ли упорядоченная пара решением системы линейных неравенств
На приведенном выше графике вы можете видеть, что точки B и N являются решениями для системы, потому что их координаты делают оба неравенства истинными.
Напротив, точки M и A лежат вне области решения (фиолетовый). Хотя точка M является решением неравенства [latex] y> −x [/ latex], а точка A является решением неравенства [latex] y <2x + 5 [/ latex], ни одна из точек не является решением для система .В следующем примере показано, как проверить точку, чтобы увидеть, является ли она решением системы неравенств.
Пример
Является ли точка (2, 1) решением системы [латекс] x + y> 1 [/ latex] и [latex] 2x + y <8 [/ latex]?
Показать решение Проверьте суть каждого неравенства. Замените 2 вместо x и 1 на y . Является ли дело решением обоих неравенств?[латекс] \ begin {массив} {r} x + y> 1 \\ 2 + 1> 1 \\ 3> 1 \\\ text {TRUE} \ end {array} [/ latex]
(2, 1) — решение для [латекса] x + y> 1 [/ latex].
[латекс] \ begin {array} {r} 2x + y <8 \\ 2 \ left (2 \ right) +1 <8 \\ 4 + 1 <8 \\ 5 <8 \\\ text {TRUE} \ end {array} [/ latex]
(2, 1) — решение для [латекса] 2x + y <8. [/ Latex]
Поскольку (2, 1) является решением каждого неравенства, оно также является решением системы.
Ответ
Точка (2, 1) является решением системы [латекс] x + y> 1 [/ latex] и [latex] 2x + y <8 [/ latex].
Вот график системы в примере выше. Обратите внимание, что (2, 1) находится в фиолетовой области, которая является областью перекрытия для двух неравенств.
Пример
Является ли точка (2, 1) решением системы [латекс] x + y> 1 [/ latex] и [latex] 3x + y <4 [/ latex]?
Показать решениеОтметьте точку с каждым неравенством. Замените 2 вместо x и 1 на y . Является ли дело решением обоих неравенств?
[латекс] \ begin {массив} {r} x + y> 1 \\ 2 + 1> 1 \\ 3> 1 \\\ text {TRUE} \ end {array} [/ latex]
(2, 1) — решение для [латекса] x + y> 1 [/ latex].
[латекс] \ begin {array} {r} 3x + y <4 \\ 3 \ left (2 \ right) +1 <4 \\ 6 + 1 <4 \\ 7 <4 \\\ text {FALSE} \ end {array} [/ latex]
(2, 1) — это , а не решение для [латекса] 3x + y <4 [/ latex].
Поскольку (2, 1) — это , а не как решение одного из неравенств, это не решение системы.
Ответ
Точка (2, 1) не является решением системы [латекс] x + y> 1 [/ latex] и [latex] 3x + y <4 [/ latex].
Вот график этой системы. Обратите внимание, что (2, 1) не находится в фиолетовой области, которая является перекрывающейся областью; это решение одного неравенства (красная область), но не решение второго неравенства (синяя область).
Как показано выше, нахождение решений системы неравенств может быть выполнено путем графического отображения каждого неравенства и определения общей для них области. Ниже приведены дополнительные примеры, показывающие весь процесс определения области решений на графике для системы двух линейных неравенств. Общие шаги описаны ниже:
- Изобразите каждое неравенство в виде линии и определите, будет ли оно сплошным или пунктирным.
- Определите, с какой стороны каждой граничной линии представлены решения неравенства, проверив точку на каждой стороне
- Заштрихуйте область, которая представляет решения для обоих неравенств
Пример
Закрасьте область графика, которая представляет решения для обоих неравенств.[латекс] x + y \ geq1 [/ латекс] и [латекс] y – x \ geq5 [/ латекс].
Показать решение Изобразите одно неравенство. Сначала нарисуйте граничную линию, используя таблицу значений, пересечений или любой другой метод, который вы предпочитаете. Граница для [латекса] x + y \ geq1 [/ latex] — это [латекс] x + y = 1 [/ latex] или [латекс] y = −x + 1 [/ latex]. Поскольку знак равенства стоит вместе со знаком «больше», граница будет сплошной.Найдите упорядоченную пару по обе стороны от граничной линии. Вставьте значения x и y в неравенство [latex] x + y \ geq1 [/ latex] и посмотрите, какая упорядоченная пара дает истинное утверждение.
[латекс] \ begin {array} {r} \ text {Test} 1: \ left (−3,0 \ right) \\ x + y \ geq1 \\ — 3 + 0 \ geq1 \\ — 3 \ geq1 \\\ text {FALSE} \\\\\ text {Test} 2: \ left (4,1 \ right) \\ x + y \ geq1 \\ 4 + 1 \ geq1 \\ 5 \ geq1 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Поскольку (4, 1) приводит к истинному утверждению, область, которая включает (4, 1), должна быть заштрихована.
Проделайте то же самое со вторым неравенством. Постройте граничную линию, затем проверьте точки, чтобы определить, какая область является решением неравенства. В этом случае граница [латекс] y – x = 5 \ left (\ text {или} y = x + 5 \ right) [/ latex] сплошная.Контрольная точка (−3, 0) не является решением [latex] y – x \ geq5 [/ latex], а контрольная точка (0, 6) является решением.
Ответ
Фиолетовая область на этом графике показывает набор всех решений системы.
В этом разделе мы увидели, что решения систем линейных уравнений и неравенств могут быть упорядоченными парами. В следующем разделе мы будем работать с системами, у которых нет решений или есть бесконечно много решений.
Используйте график для классификации решений для систем
Напомним, что линейное уравнение отображается в виде линии, что означает, что все точки на линии являются решениями этого линейного уравнения.Есть бесконечное количество решений. Как мы видели в предыдущем разделе, если у вас есть система линейных уравнений, пересекающихся в одной точке, эта точка является решением системы. Что произойдет, если линии никогда не пересекаются, как в случае с параллельными линиями? Как бы вы описали решения для такой системы? В этом разделе мы исследуем три возможных результата решения системы линейных уравнений.
Три возможных исхода решений систем уравнений
Напомним, что решение системы уравнений — это значение или значения, которые верны для всех уравнений в системе.Есть три возможных исхода решений систем линейных уравнений. Графики уравнений внутри системы могут сказать вам, сколько решений существует для этой системы. Посмотрите на изображения ниже. На каждой показаны две линии, составляющие систему уравнений.
| Одно решение | Нет решений | Бесконечные решения |
|---|---|---|
| Если графики уравнений пересекаются, то существует одно решение, истинное для обоих уравнений. | Если графики уравнений не пересекаются (например, если они параллельны), то для обоих уравнений нет истинных решений. | Если графики уравнений одинаковы, то существует бесконечное количество решений, которые верны для обоих уравнений. |
- Одно решение: Когда система уравнений пересекается в упорядоченной паре, система имеет одно решение.
- Бесконечные решения: Иногда два уравнения отображаются в виде одной линии, и в этом случае у нас есть бесконечное количество решений.
- Нет Решение: Когда линии, составляющие систему, параллельны, решений нет, потому что эти две линии не имеют общих точек.
Пример
Используя график [latex] \ begin {array} {r} y = x \\ x + 2y = 6 \ end {array} [/ latex], показанный ниже, определите, сколько решений есть в системе.
Показать решение Линии пересекаются в одной точке. Таким образом, у этих двух линий есть только одна общая точка, есть только одно решение системы.Ответ
Есть одно решение этой системы.
Пример (расширенный)
Используя график [latex] \ begin {array} {r} y = 3,5x + 0,25 \\ 14x – 4y = -4,5 \ end {array} [/ latex], показанный ниже, определите, сколько решений имеет система. .
Показать решение Линии параллельны, то есть не пересекаются. Решения по системе нет.Ответ
Нет решений по системе.
Пример
Сколько решений имеет система [latex] \ begin {array} {r} y = 2x + 1 \\ — 4x + 2y = 2 \ end {array} [/ latex]?
Показать решение Сначала изобразите оба уравнения на одних и тех же осях.Два уравнения изображены на одной линии. Таким образом, каждая точка на этой линии является решением системы уравнений.
Ответ
Система [latex] \ begin {array} {r} y = 2x + 1 \\ — 4x + 2y = 2 \ end {array} [/ latex] имеет бесконечное количество решений.
В следующем разделе мы изучим некоторые алгебраические методы поиска решений систем уравнений.

 11.18
11.18




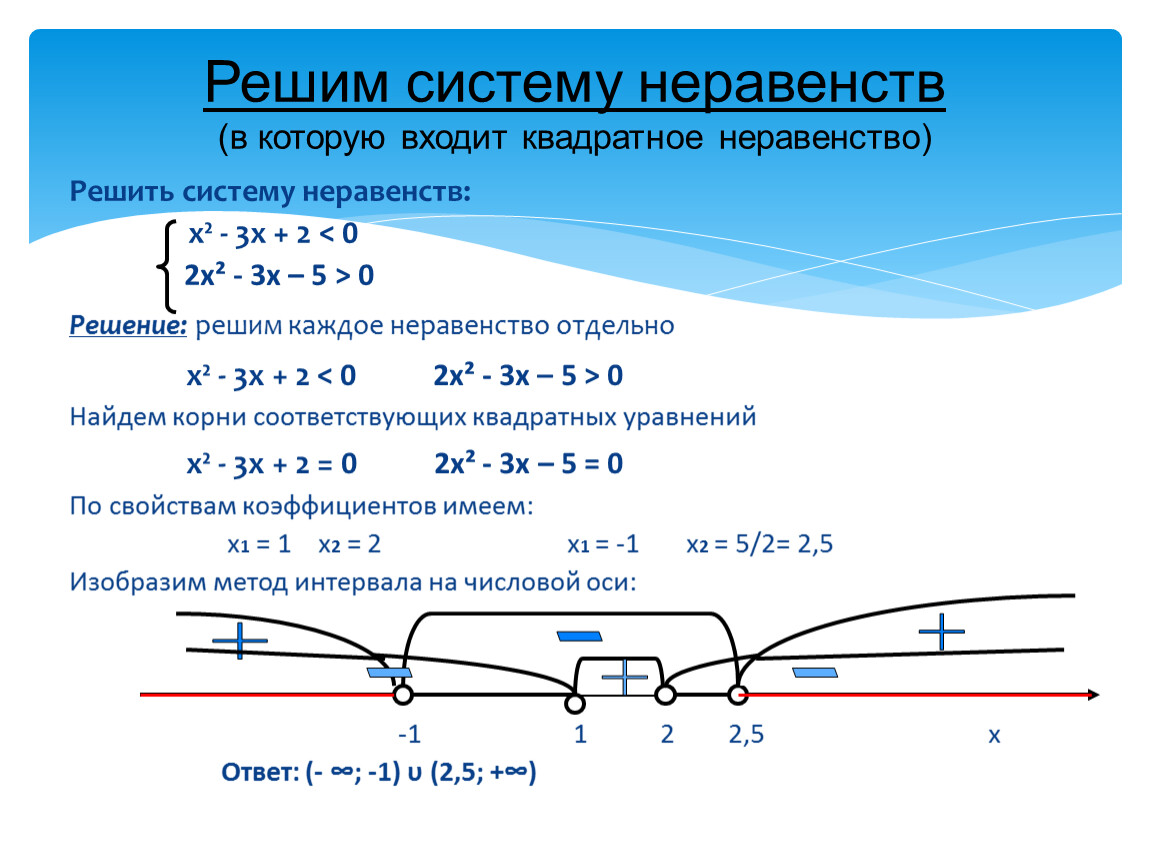 Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным. На множестве положительных чисел обе части можно возвести в квадрат.
На множестве положительных чисел обе части можно возвести в квадрат.
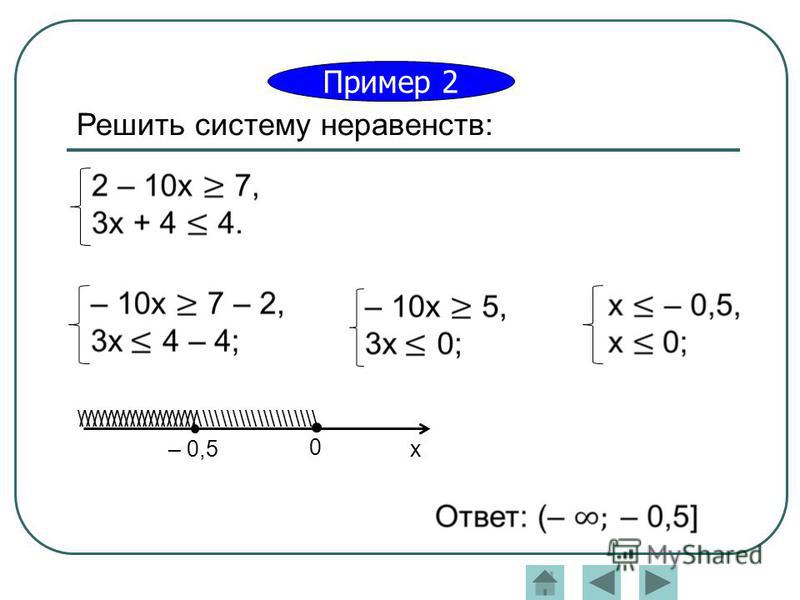




 Например, если a b *
Например, если a b *