Ранг матрицы калькулятор онлайн с решением: Онлайн калькулятор. Ранг матрицы.

Ранг матрицы, онлайн калькулятор с решением

Наш онлайн калькулятор позволяет найти ранг матриц всего в пару кликов. Для нахождения ранга матрицы выберите ее размер, заполните все элементы матрицы и нажмите кнопку «Вычислить», калькулятор выдаст ответ и пошаговое решение! Каждый шаг будет подробно расписан, это поможет вам проверить свое решение и понять, как был получен ответ.

Заполните элементы матрицы   Решили сегодня: раз, всего раз

Понравился сайт? Расскажи друзьям!

Как найти ранг матрицы онлайн

Ранг матрицы является для неё важнейшей числовой характеристикой. Его непременно следует определять, когда перед вами стоит задача проверить совместимость системы линейных уравнений. То есть, под понятием ранга подразумеваются все линейнонезависимые строки и столбцы в матрице. Существуют различные методы определения ранга матрицы. Чаще всего его вычисляют методом миноров или методом окантовки. Реже применяется метод Гаусса. Данный онлайн калькулятор прольёт свет на все те сложные преобразования, которые необходимы для вычисления ранга матрицы онлайн. Воспользовавшись им, вы сможете наглядно ознакомиться с различными вариантами определения данного показателя.

Для того чтобы найти ранг матрицы онлайн, вам необходимо совершить ряд простых операций. Для начала укажите размеры матрицы, кликнув на иконки «+» и «-» слева и внизу, соответствующие числу строк и столбцов. Далее введите в поля калькулятора элементы и нажмите кнопку «Вычислить». Готовый результат окажется на мониторе оперативно. Буквально через несколько секунд вы увидите значение ранга матрицы и детальную расшифровку его вычисления.

Пользование онлайн калькулятором имеет ряд плюсов: вы лучше усваиваете теорию на примере задания, проверяете свои расчёты, тщательно разбираетесь во всех способах вычисления ранга матрицы.

Онлайн калькулятор: Определение ранга матрицы

Ниже калькулятор, вычисляющий ранг матрицы. Под ним, как водится, немного теории.

Определение ранга матрицы

Ранг матрицы

 

save Сохранить extension Виджет

Update: Меня тут попросили сформулировать попроще, что такое ранг матрицы. Если попроще, то это максимальное число линейно-независимых строк/столбцов матрицы (число строк и число столбцов совпадает), то есть таких строк/столбцов, которые нельзя получить друг из друга элементарными преобразованиями.

Например, у этой матрицы
3 -1 1
6 -2 2
ранг равен 1, потому что вторая строка есть первая, умноженная на 2.

Итак, несколько определений.

Пусть дана матрица А размеров n x m и число k, не превосходящее наименьшего из чисел m и n. Выберем произвольно k строк матрицы и k столбцов (номера строк могут отличаться от номеров столбцов). Определитель матрицы, составленной из элементов, стоящих на пересечении выбранных k строк и k столбцов, называется минором порядка k матрицы A . (Что такое определитель матрицы можно посмотреть здесь Определитель (детерминант) матрицы).

Рангом матрицы А называется наибольший из порядков миноров матрицы А, отличных от нуля. Ранг нулевой матрицы считается равным нулю.

Ненулевой минор наибольшего порядка называется базисным минором. Или, что тоже самое, минор матрицы А является ее базисным минором, если он не равен нулю, и его порядок равен рангу матрицы А.

Теорема о базисном миноре
Столбцы матрицы А, входящие в базисный минор, образуют линейно независимую систему. Любой столбец матрицы А линейно выражается через столбцы из базисного минора.

Минор Mок матрицы А называют окаймляющим минором для минора М, если он получается из последнего добавлением одной новой строки и одного нового столбца матрицы А. Порядок окаймляющего минора Мок на единицу больше порядка минора М

Понятно, что ранг матрицы можно вычислить, перебирая все миноры, но в данном калькуляторе для вычисления ранга матрицы применяется

метод окаймляющих миноров, основанный на следующей теореме.

Теорема: Если для некоторого минора матрицы все окаймляющие его миноры равны нулю, то он является базисным. (А порядок, его, соответственно, равен рангу матрицы).

Метод окаймляющих миноров заключается в нахождении одного из базисных миноров матрицы и состоит в следующем:
Выбирается ненулевой минор первого порядка (ненулевой элемент матрицы). К очередному ненулевому минору последовательно добавляются такие строка и столбец, чтобы новый окаймляющий минор оказался ненулевым. Если этого сделать нельзя, то последний ненулевой минор является базисным.

Ранг матрицы методом окаймляющих миноров

Для того что бы вычислить ранг матрицы можно применить метод окаймляющих миноров или метод Гаусса. Рассмотрим метод Гаусса или метод элементарных преобразований.

Рангом матрицы называют максимальный порядок её миноров, среди которых есть хотя бы один, не равный нулю.

Рангом системы строк (столбцов) называется максимальное количество линейно независимых строк (столбцов) этой системы.

Алгоритм нахождения ранга матрицы методом окаймляющих миноров:

1. Минор M k-того порядка не равен нулю.
2. Если окаймляющие миноры для минора M (k+1)-го порядка, составить невозможно (т.е. матрица содержит k строк или k столбцов), то ранг матрицы равен k. Если окаймляющие миноры существуют и все равны нулю, то ранг равен k. Если среди окаймляющих миноров есть хотя бы один, не равный нулю, то пробуем составить новый минор k+2 и т.д.

Разберем алгоритм более подробно. Сначала рассмотрим миноры первого (элементы матрицы) порядка матрицы A. Если все они равны нулю, то rangA = 0. Если есть миноры первого порядка (элементы матрицы) не равные нулю

M₁ ≠ 0, то ранг rangA ≥ 1.

Проверим есть ли окаймляющие миноры для минора M₁. Если такие миноры есть, то они буду миноры второго порядка. Если все миноры окаймляющие минор M₁ равны нулю, то rangA = 1. Если есть хоть один минор второго порядка не равные нулю M₂ ≠ 0, то ранг rangA ≥ 2.

Проверим есть ли окаймляющие миноры для минора M₂. Если такие миноры есть, то они буду миноры третьего порядка. Если все миноры окаймляющие минор M₂ равны нулю, то rangA = 2. Если есть хоть один минор третьего порядка не равные нулю M₃ ≠ 0, то ранг rangA ≥ 3.

Проверим есть ли окаймляющие миноры для минора M₃. Если такие миноры есть, то они буду миноры четвертого порядка. Если все миноры окаймляющие минор M₃ равны нулю, то

rangA = 3. Если есть хоть один минор четвертого порядка не равные нулю M₄ ≠ 0, то ранг rangA ≥ 4.

Проверяем есть ли окаймляющий минор для минора M₄, и так далее. Алгоритм прекращается, если на каком-то этапе окаймляющие миноры равны нулю или окаймляющий минор нельзя получить (в матрице «закончились» строки или столбцы). Порядок не нулевого минора, который получилось составить будет рангом матрицы.

Пример

Рассмотрим данный метод на примере. Дана матрицы 4х5:

У данной матрице ранг не может быть больше 4. Так же у этой матрице есть не нулевые элементы (минор первого порядка), значит ранг матрицы ≥ 1.

Составим минор 2-ого порядка. Начнем с угла.

Найдем определитель данного минора.

Так определитель равен нулю, составим другой минор.

Найдем определитель данного минора.

Определить данного минора равен -2. Значит ранг матрицы ≥ 2.

Если данный минор был равен 0, то составили бы другие миноры. До конца бы составили все миноры по 1 и второй строке. Потом по 1 и 3 строке, по 2 и 3 строке, по 2 и 4 строке, пока не нашли бы минор не равный 0, например:

Если все миноры второго порядка равны 0, то ранг матрицы был бы равен 1. Решение можно было бы остановить.

Продолжим поиска ранга матрицы. Составим минор 3-го порядка.

Найдем определитель этого минора.

Минор получился не нулевой. значит ранг матрицы ≥ 3.

Если бы данный минор был нулевым, то нужно было бы составить другие миноры. Например:

Если все миноры третьего порядка равны 0, то ранг матрицы был бы равен 2. Решение можно было бы остановить.

Продолжим поиска ранга матрицы. Составим минор 4-го порядка.

Найдем определитель этого минора.

Определитель минора получился равный 0. Построим другой минор.

Найдем определитель этого минора.

Минор получился равным 0.

Построить минор 5-го порядка не получится, для этого нет строки в данной матрицы. Последний минор не равный нулю был 3-го порядка, значит ранг матрицы равен 3.

Найти ранг матрицы: способы и примеры

Определение. Рангом матрицы называется максимальное число линейно независимых строк, рассматриваемых как векторы.

Теорема 1 о ранге матрицы. Рангом матрицы называется максимальный порядок отличного от нуля минора матрицы.

Понятие минора мы уже разбирали на уроке по определителям, а сейчас обобщим его. Возьмём в матрице сколько-то строк и сколько-то столбцов, причём это «сколько-то» должно быть меньше числа строк и стобцов матрицы, а для строк и столбцов это «сколько-то» должно быть одним и тем же числом. Тогда на пересечении скольки-то строк и скольки-то столбцов окажется матрица меньшего порядка, чем наша исходная матрица. Определитель это матрицы и будет минором k-го порядка, если упомянутое «сколько-то» (число строк и столбцов) обозначим через k.

Определение. Минор (r+1)-го порядка, внутри которого лежит выбранный минор r-го порядка, называется называется окаймляющим для данного минора.

Наиболее часто используются два способа отыскания ранга матрицы. Это способ окаймляющих миноров и способ элементарных преобразований (методом Гаусса).

При способе окаймляющих миноров используется следующая теорема.

Теорема 2 о ранге матрицы. Если из элементов матрицы можно составить минор r-го порядка, не равный нулю, то ранг матрицы равен r.

При способе элементарных преобразований используется следующее свойство:

— если путём элементарных преобразований получена трапециевидная матрица, эквивалентная исходной, то рангом этой матрицы является число строк в ней кроме строк, полностью состоящих из нулей.

Окаймляющим минором называется минор большего порядка по отношению к данному, если этот минорм большего порядка содержит в себе данный минор.

Например, дана матрица

.

Возьмём минор

,

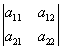окаймляющими будут такие миноры:

.

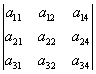
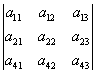
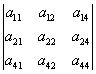Алгоритм нахождения ранга матрицы следующий.

1. Находим не равные нулю миноры второго порядка. Если все миноры второго порядка равны нулю, то ранг матрицы будет равен единице (r =1).

2. Если существует хотя бы один минор второго порядка, не равный нулю, то составляем окаймляющие миноры третьего порядка. Если все окаймляющие миноры третьего порядка равны нулю, то ранг матрицы равен двум (r =2).

3. Если хотя бы один из окаймляющих миноров третьего порядка не равен нулю, то составляем окаймляющие его миноры. Если все окаймляющие миноры четвёртого порядка равны нулю, то ранг матрицы равен трём (r =2).

4. Продолжаем так, пока позволяет размер матрицы.

Пример 1. Найти ранг матрицы

.

Решение. Минор второго порядка .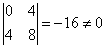

Окаймляем его. Окаймляющих миноров будет четыре:

,

,

,

.

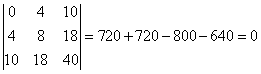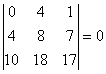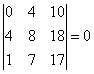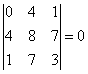Таким образом, все окаймляющие миноры третьего порядка равны нулю, следовательно, ранг данной матрицы равен двум (r =2).

Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы.

Пример 2. Найти ранг матрицы

.

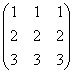Решение. Ранг данной матрицы равен 1, так как все миноры второго порядка этой матрицы равны нулю (в этом, как и в случаях окаймляющих миноров в двух следующих примерах, дорогим студентам предлагается убедиться самостоятельно, возможно, используя правила вычисления определителей), а среди миноров первого порядка, то есть среди элементов матрицы, есть не равные нулю.

Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы.

Пример 3. Найти ранг матрицы

.

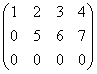Решение. Минор второго порядка этой матрицы 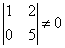, в все миноры третьего порядка этой матрицы равны нулю. Следовательно, ранг данной матрицы равен двум.

Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы.

Пример 4. Найти ранг матрицы

.

Решение. Ранг данной матрицы равен 3, так как единственный минор третьего порядка этой матрицы равен 3.

Проверить решение можно на калькуляторе онлайн Вычисление ранга матрицы.

Уже на примере 1 видно, что задача определения ранга матрицы способом окаймляющих миноров требует вычисления большого числа определителей. Существует, однако, способ, позволяющий свести объём вычислений к минимуму. Этот способ основан на использовании элементарных преобразований матриц и ещё называется также методом Гаусса.

Под элементарными преобразованиями матрицы понимаются следующие операции:

1) умножение какой-либо строки или какого либо столбца матрицы на число, отличное от нуля;

2) прибавление к элементам какой-либо строки или какого-либо столбца матрицы соответствующих элементов другой строки или столбца, умноженных на одно и то же число;

3) перемена местами двух строк или столбцов матрицы;

4) удаление «нулевых» строк, то есть таких, все элементы которых равны нулю;

5) удаление всех пропорциональных строк, кроме одной.

Теорема. При элементарном преобразовании ранг матрицы не меняется. Другими словами, если мы элементарными преобразованиями от матрицы A перешли к матрице B, то .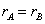

Используя эту теорему, отправляясь от любой матрицы A всегда можно прийти к такой матрице B, вычисление ранга которой не представляет затруднений. Для этого следует добиться, чтобы матрица B была трапециевидной.

Тогда ранг полученной матрицы будет равен числу строк в ней кроме строк, полностью состоящих из нулей.

Пример 5. Найти ранг матрицы

.

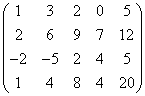Решение. Подвергнем эту матрицу следующим преобразованиям. Ко второй строке прибавим третью, умноженную на — 2, а затем к третьей строке прибывам первую, умноженную на 2, и, наконец, из четвёртой вычтем первую. После этих трёх последовательно выполненных преобразований получим матрицу

.

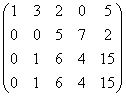Вычитая из четвёртой строки третью, а затем переставив местами вторую и третью строки, получаем матрицу

.

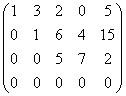Получили трапециевидную матрицу. Ранг полученной матрицы равен трём (r=3), так как после вычёркивания последней строки, полностью состоящей из нулей, в ней останется три строки.

Желающие могут проверить это решение способом окаймляющих миноров (минор третьего порядка, находящийся в левом верхнем углу, не равен нулю, а все миноры четвёртого порядка равны нулю).

Поделиться с друзьями

Начало темы «Матрицы»

Продолжение темы «Матрицы»

Другие темы линейной алгебры

Ранг матричного калькулятора

Поиск инструмента

Ранг матрицы

Инструмент для расчета ранга матрицы. В математике рангом матрицы M называется количество линейно независимых строк или столбцов.

Результаты

Ранг матрицы — dCode

Тег (-ы): Matrix

Поделиться

dCode и вы

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Инструмент для расчета ранга матрицы.В математике рангом матрицы M называется количество линейно независимых строк или столбцов.

Ответы на вопросы

Что такое ранг матрицы? (Определение)

Ранг матрицы (иногда обозначается как Rk) в основном определяется как максимальное количество векторов-строк (или векторов-столбцов), которые являются линейно независимыми.

Ранг матрицы также является размерностью векторного подпространства, созданного векторами (строками или столбцами) матрицы.

Ранг может быть вычислен как для строк, так и для столбцов, это будет одно и то же значение.

Как рассчитать ранг матрицы?

Чтобы вычислить ранг матрицы $ M $, сравните каждую из строк между ними и каждый из столбцов между ними, чтобы убедиться, что они линейно независимы два на два.

Пример: $$ M = \ begin {bmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 2 & 2 & 4 \ end {bmatrix} $$ Матрица $ M $ имеет ранг $ 2 $, поскольку строка 2 в два раза больше строки 1, они не являются линейно независимыми.
NB: столбец 3 представляет собой сумму столбцов 1 и 2, они не являются линейно независимыми.

Задайте новый вопрос

Исходный код

dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Рейтинг матрицы». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate), написанные на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.)) доступ к данным, скриптам или API не будет бесплатным, то же самое касается загрузки Rank of a Matrix для автономного использования на ПК, планшете, iPhone или Android!

Нужна помощь?

Пожалуйста, заходите в наше сообщество в Discord для получения помощи!

Вопросы / комментарии

Сводка

Инструменты аналогичные

Поддержка

Форум / Справка

Рекламные объявления

Ключевые слова

ранг матричный, линейно независимый

Ссылки

Источник: https: // www.dcode.fr/matrix-rank

© 2020 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокешинга / CTF. .

Matrix Рейтинг

Ранг — это количество строк, которые являются «уникальными»: не состоят из других строк. (То же для столбцов.)

Пример: Эта матрица

Второй ряд просто в 3 раза больше первого. Просто бесполезный подражатель. Не в счет.

Таким образом, несмотря на то, что есть 2 строки, ранг равен только 1.

А как насчет колонок? Второй столбец вдвое больше первого. И третий столбец в три раза больше первого (или 1.5 раз в секунду), так что тоже не в счет.

Значит, столбцы также показывают, что ранг равен только 1.

Пример: Эта матрица

Вторая строка не состоит из первой, поэтому ранг не менее 2.

А как насчет третьего ряда? Это первое и второе сложенные вместе, поэтому не в счет.

Таким образом, несмотря на то, что есть 3 строки, ранг только 2.

А как насчет колонок? Второй столбец хорош, но столбец 3 — это столбцы 1 и 2, сложенные вместе.

Значит, столбцы также показывают, что ранг всего 2.

Пример: Эта матрица

Вторая строка не состоит из первой, поэтому ранг не менее 2.

Третья строка выглядит нормально, но после долгого изучения мы обнаруживаем, что это первая строка минус два раза вторая. Подлый! Так что ранг всего 2.

И для столбцов: в этом случае столбец 3 — это столбцы 1 и 2, сложенные вместе. Таким образом, столбцы также показывают нам рейтинг 2.

Пример: Матрица идентичности

Все ряды — сильные независимые личности, не полагающиеся в своем существовании на других! Таким образом, рейтинг равен 3.

И точно так же для столбцов, они также говорят нам, что ранг равен 3.

Фактически, строки и столбцы всегда совпадают по рангу (удивительно, но факт!).

Когда мы говорим здесь о строках, мы можем сказать то же самое о столбцах.

Так что нам действительно не нужно работать над обоими.

Зачем искать ранг?

Ранг многое говорит нам о матрице.

Это полезно для того, чтобы сообщить нам, есть ли у нас шанс решить систему линейных уравнений: когда ранг равен количеству переменных, мы можем найти единственное решение.

Пример: яблоки и бананы

Если мы знаем, что

• 2 яблока и 3 банана стоят 7
долларов
• 3 яблока и 3 банана стоят 9
долларов

Тогда мы можем вычислить, что дополнительное яблоко должно стоить 2 доллара, а бананы стоят 1 доллар каждый.

(Есть 2 переменные, и ранг тоже 2.)

Но если бы мы только знали, что

• 2 яблока и 3 банана стоят 7
долларов
• 4 яблока и 6 бананов стоят 14
долларов

Мы не можем идти дальше, потому что вторая строка данных всего в два раза больше первой и не дает нам никакой новой информации.(Есть 2 переменные и рейтинг только 1.)

Он также используется для связи, стабильности систем и многого другого.

Линейная зависимость

Вместо «не сделаны из» мы говорим, что они линейно независимые , что является важной идеей.

Линейное означает, что мы можем умножать на константу, но не на степени или другие функции. Константа может быть любым действительным числом (0, 1, любым целым числом, дробью, отрицательными числами и т. Д.).

Зависимость означает, что они зависят друг от друга, другими словами, мы можем сложить некоторые (после умножения на константу), чтобы получить еще один.

Представьте, что они векторы (имеют направление и длину). Можем ли мы объединить другие векторы (при необходимости растянуть или сжать), чтобы получить тот же результат?

c = a + 2 b ,
поэтому c является линейно зависимым от a и b

Также обратите внимание, что:

• a и b вместе линейно независимы : мы не можем использовать a самостоятельно, чтобы добраться туда, где находится b , или наоборот.
• То же самое верно для b и c или a и c .
• Но a , b и c вместе линейно зависимы .

Думая примерно о a и b : мы действительно можем достичь в любом месте на плоскости, используя эти два вектора:

Векторы a и b охватывают всю плоскость.

Когда векторы линейно независимы и охватывают все пространство, мы говорим, что они являются «базисом » этого пространства.

Итак, a и b являются основой 2D плоскости.

Примечание. Пространство — это общий термин, охватывающий 1, 2, 3 или более высокие измерения, но мы часто называем двумерное пространство плоскостью.

Итак, a и b так же полезны, как оси x, y. То же самое можно сказать и о любых двух линейно независимых векторах в 2D-плоскости.

Самая основная пара линейно независимых векторов — это (1,0) и (0,1), которые образуют единичную матрицу 2×2:

По сути, они делают знакомыми осями x, y:

А в 3D:

А в 4D:

1

0

0

0

0

1

0

0

0

0

1

0

0

0

0

1

Хорошо, это немного сложно проиллюстрировать, но числа прекрасно подходят для любого количества измерений!

Как найти ранг

Обычно для определения ранга лучше всего использовать программное обеспечение. Существуют алгоритмы, которые играют со строками и столбцами для его вычисления.Но в некоторых случаях мы можем разобраться сами.

Для квадратной матрицы определитель может помочь: определитель ненулевой говорит нам, что все строки (или столбцы) являются линейно независимыми , так что это «полный ранг», и его ранг равен количеству строк.

Пример: Являются ли эти четырехмерные векторы линейно независимыми?

1

2

3

4

0

2

2

0

1

0

3

0

0

1

0

4

Определитель (используя Матричный калькулятор):

1 (2 (3 × 4-0 × 0) -2 (0 × 4-0 × 1) +0 (0 × 0-3 × 1)) — 2 (0 (3 × 4-0 × 0) — 2 (1 × 4-0 × 0) +0 (1 × 0-3 × 0)) + 3 (0 (0 × 4-0 × 1) -2 (1 × 4-0 × 0) +0 (1 × 1-0 × 0)) — 4 (0 (0 × 0-3 × 1) -2 (1 × 0-3 × 0) +2 (1 × 1-0 × 0)) = 8

Определитель ненулевой , поэтому все они должны быть линейно независимыми .

И так это полный ранг, а ранг 4 .

Итак, мы знаем, что на самом деле это основа для четырехмерного пространства: с помощью этих четырех векторов мы можем охватить все четырехмерное пространство.

Отличный пример, когда математика может сказать нам то, что мы не можем легко вообразить.

Другая недвижимость

Ранг не может быть больше наименьшего измерения матрицы.

Пример: для матрицы 2 × 4 ранг не может быть больше 2

Когда ранг равен наименьшему измерению, он называется «полным рангом», меньший ранг называется «недостаточным рангом».

Ранг не меньше 1, за исключением нулевой матрицы (матрицы, состоящей из всех нулей), ранг которой равен 0.

.

Matrix Рейтинг

Этот урок знакомит с концепцией матрицы ранга и объясняет, как ранг матрица раскрывается его эшелонированная форма.

Ранг матрицы

Вы можете представить себе матрицу r x c как набор строк r векторы, каждый имеет c элементов; или вы можете думать об этом как о наборе c векторы-столбцы, каждый из которых имеет r элементов.

Ранг матрицы определяется как (а) максимальное количество линейно независимых столбцов векторов в матрице или (б) максимальное количество линейно независимых строк векторов в матрице. Оба определения эквивалентны.

Для матрицы r x c ,

• Если r меньше c , то максимальный ранг матрицы составляет р .
• Если r больше c , то максимальный ранг матрицы c .

Ранг матрицы был бы равен нулю, только если бы матрица не имела элементов. Если бы матрица имела хотя бы один элемент, ее минимальный ранг был бы равен единице.

Как найти матрицу Рейтинг

В этом разделе мы описываем метод определения ранга любой матрицы.Этот метод предполагает знакомство с эшелонированные матрицы и эшелонные преобразования.

Максимальное количество линейно независимых векторов в матрице равно к количеству ненулевых строк в его матрица эшелонов строк. Следовательно, чтобы найти ранг матрицы, мы просто преобразовать матрицу к ее форме эшелона строк и подсчитать количество ненулевые строки.

Рассмотрим матрицу A и ее ряд строк. матрица, A _ref . Ранее мы показывали как найти форму эшелона строк для матрицы A .

Потому что рядный эшелон формирует A _ref имеет две ненулевые строки, мы знаем, что матрица A имеет два независимых вектора-строки; и мы знаем, что ранг матрицы A равен 2.

Вы можете убедиться, что это правильно. Ряд 1 и Ряд 2 матрицы A линейно независимый. Однако строка 3 — это линейная комбинация строк 1 и 2. В частности, строка 3 = 3 * (строка 1) + 2 * (строка 2). Следовательно, матрица A имеет только два независимых вектора-строки.

Матрицы полных рангов

Когда все векторов в матрице линейно независимый, матрица называется , полный ранг .Рассмотрим матрицы A и B ниже.

Обратите внимание, что строка 2 матрицы A является скалярным кратным ряд 1; то есть строка 2 равна удвоенной строке 1. Следовательно, строки 1 и 2 линейно зависимый. Матрица А имеет только одну линейно независимую строка, поэтому ее ранг равен 1. Следовательно, матрица A не имеет полного ранга.

Теперь посмотрим на матрицу B .Все его строки линейно Независимо, поэтому ранг матрицы B равен 3. Матрица B — полноразмерная.

Проверьте свое понимание

Проблема 1

Рассмотрим матрицу X , показанную ниже.

Какое у него звание?

(А) 0
(В) 1
(С) 2
(D) 3
(E) 4

Решение

Правильный ответ: (С).Поскольку в матрице больше нуля элементов, его ранг должен быть больше нуля. И поскольку в нем меньше строк, чем столбцов, его максимальный ранг равен максимальному количеству линейно независимые строки. И поскольку ни одна строка не зависит линейно от другой строки, матрица имеет 2 линейно независимых строки; так что его рейтинг 2.

Проблема 2

Рассмотрим матрицу Y , показанную ниже.

Какое у него звание?

(А) 0
(В) 1
(С) 2
(D) 3
(E) 4

Решение

Правильный ответ: (С). Поскольку в матрице больше нуля элементов, его ранг должен быть больше нуля.И поскольку в нем меньше столбцов, чем строк, его максимальный ранг равен максимальному количеству линейно независимых столбцы.

Столбцы 1 и 2 независимы, потому что ни один из них не может быть получен как скалярное кратное другому. Однако столбец 3 линейно зависит от столбцов 1 и 2, потому что столбец 3 равен столбцу 1 плюс столбец 2. Это оставляет матрицу максимум с двумя линейно независимые колонны; то есть., столбец 1 и столбец 2. Таким образом, ранг матрицы равен 2.

.Учебное пособие по ранжированию матриц

| Пример

Матрица — это массив чисел, упорядоченных по строкам и столбцам порядка m x n (m строк и n столбцов). Каждое отдельное число, присутствующее в матрице, называется элементом или записью. Ниже приведен пример матрицы порядка 3×3: [1 2 3] [4 5 6] [7 8 9]

Ранг матрицы:

Ранг матрицы определяется количеством имеющихся в ней независимых строк или столбцов.Строка или столбец считаются независимыми, если они удовлетворяют следующим условиям. 1. Строка / столбец должен иметь по крайней мере один ненулевой элемент для ранжирования. 2. Строка / столбец не должна совпадать с другой строкой / столбцом. 3. Строка / столбец не должна быть пропорциональной (кратной) другой строке / столбцу. 4. Строка / столбец не должна быть линейной комбинацией другой строки / столбца. Строка или столбец оцениваются только в том случае, если они соответствуют указанным выше условиям. Например, ранг матрицы ниже будет равен 1, поскольку вторая строка пропорциональна первой, а третья строка не имеет ненулевого элемента.[1 2 3] [2 4 6] [0 0 0]

Как рассчитать ранг матрицы:

В этом руководстве мы узнаем, как рассчитать ранг матрицы. Его можно рассчитать разными методами. Мы рассчитаем ранг на основе метода исключения Гаусса. Метод исключения Гаусса используется для вычисления ранга матрицы путем преобразования его в сокращенную форму эшелона строк. Ее можно назвать сокращенной формой эшелона строки, если она удовлетворяет следующим условиям.1. Первый элемент в первой строке должен быть ведущим элементом, т.е. 1. 2. Ведущий элемент в столбцах должен находиться справа от ведущего элемента предыдущей строки. 3. Если есть строки со всеми нулевыми элементами, они должны быть ниже строк ненулевых элементов. 4. Ведущий элемент должен быть единственным ненулевым элементом в каждом столбце. Если мы последуем вышеуказанным шагам, то матрица станет треугольной, то есть элементы ниже или выше главной диагонали станут нулевыми.Главная диагональ квадратной матрицы — это диагональ, идущая от верхнего левого угла к нижнему правому углу. Однако на этом занятии мы не будем рассматривать последний (четвертый) пункт, поскольку он не повлияет на ранг матрицы. Матрица может быть преобразована в сокращенную форму эшелона строк с помощью элементарных операций. В этом руководстве объясняются три основных элементарных операции. 1. Поменять местами две строки (или столбцы). 2. Умножение строки (или столбца) на ненулевое число.3. Умножение строки (или столбца) на ненулевое число и добавление результата к другой строке (или столбцу). Теперь, например, рассчитаем ранг матрицы. [1 2 3] [4 5 6] [7 8 9] а) Так как первый элемент первой строки является ведущим элементом, мы выполнили первое условие. Если первый элемент не равен 1, то нам нужно преобразовать элемент в 1, используя элементарные операции. б) Теперь сделаем нулевым первый элемент второй строки (чтобы сформировать треугольную матрицу).Умножьте первую строку на -4 и прибавьте ее ко второй строке. Результат представлен ниже. [1 2 3] [0–3–6] [7 8 9] c) Аналогичным образом проделаем тот же шаг для третьей строки, чтобы найти ранг матрицы. Умножьте первую строку на -7 и прибавьте ее к третьей строке. Вот результат. [1 2 3] [0–3–6] [0-6-12] г) Теперь давайте умножим вторую строку на -2 и добавим значения в третью строку, чтобы второй элемент третьей строки стал нулевым.Полученная матрица будет выглядеть, как показано ниже. [1 2 3] [0–3–6] [0 0 0] Теперь, когда он был преобразован в форму эшелона строк, мы можем найти ранг матрицы. Ранг матрицы равен 2, так как в третьей строке все элементы нулевые. Как мы видели в этом уроке, ранг можно найти простыми шагами, используя метод исключения Гаусса.

.