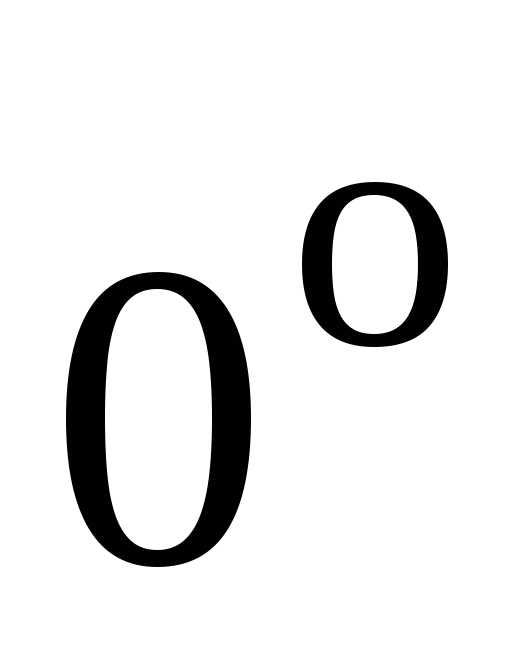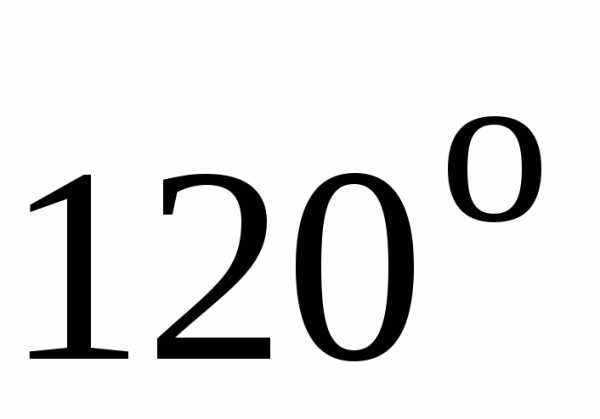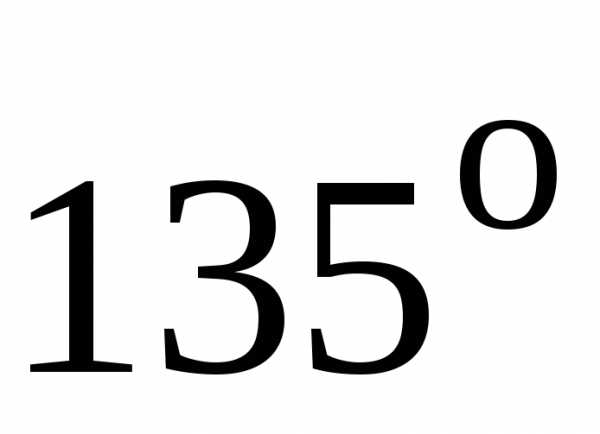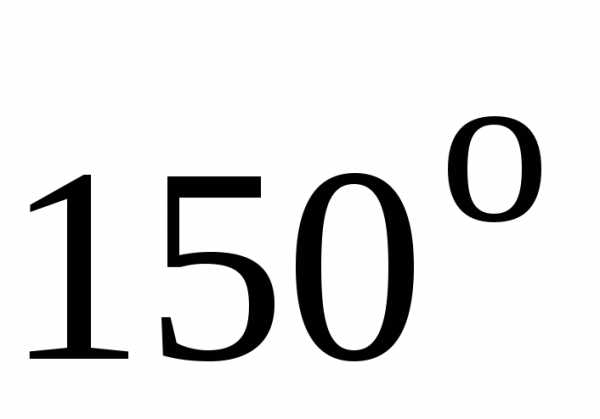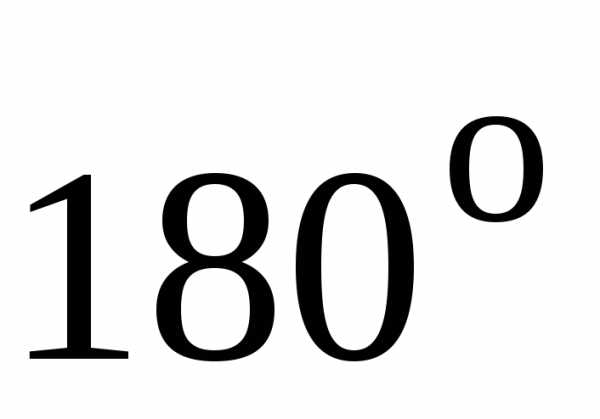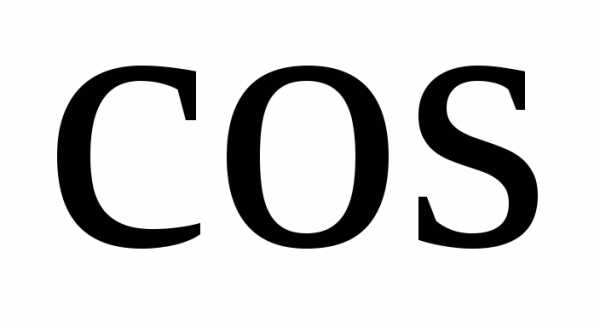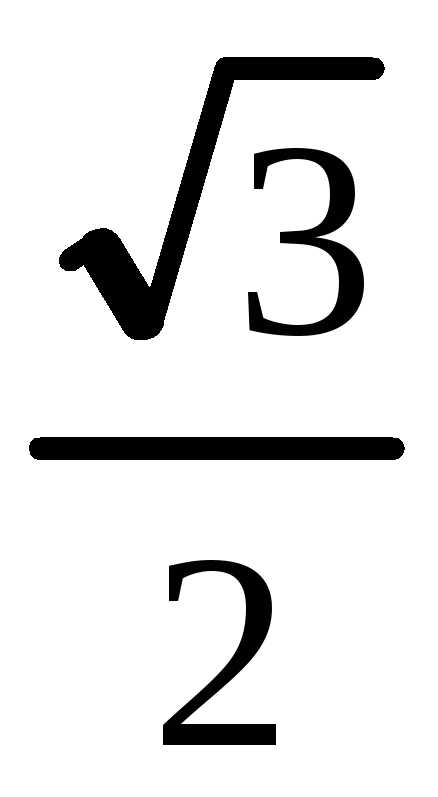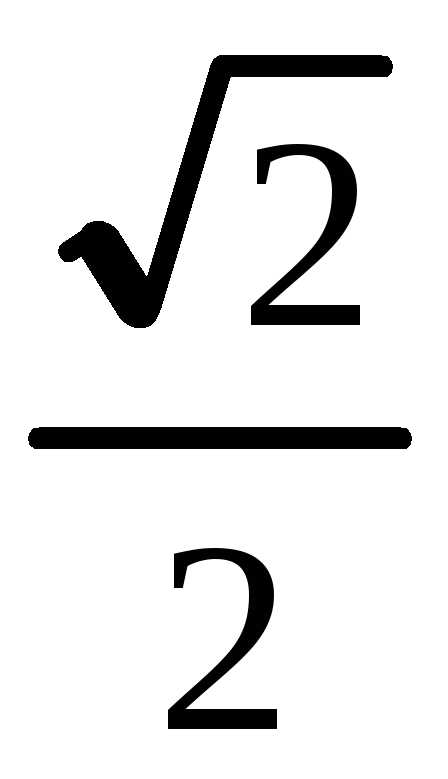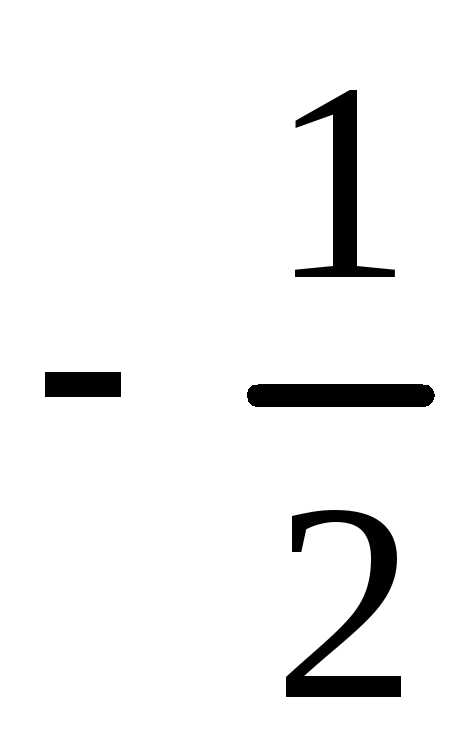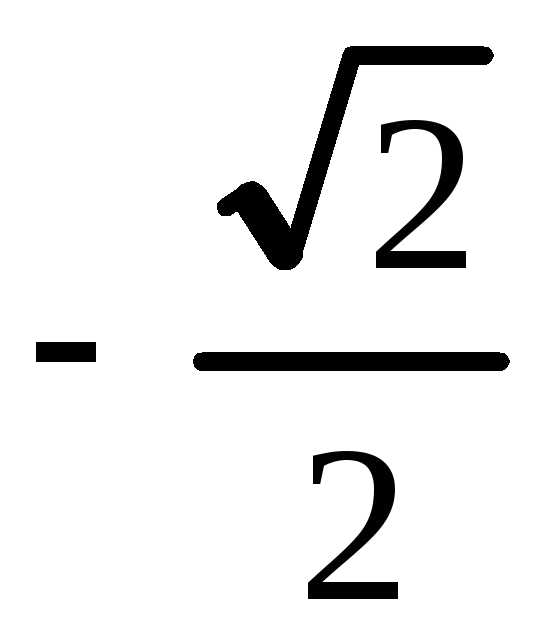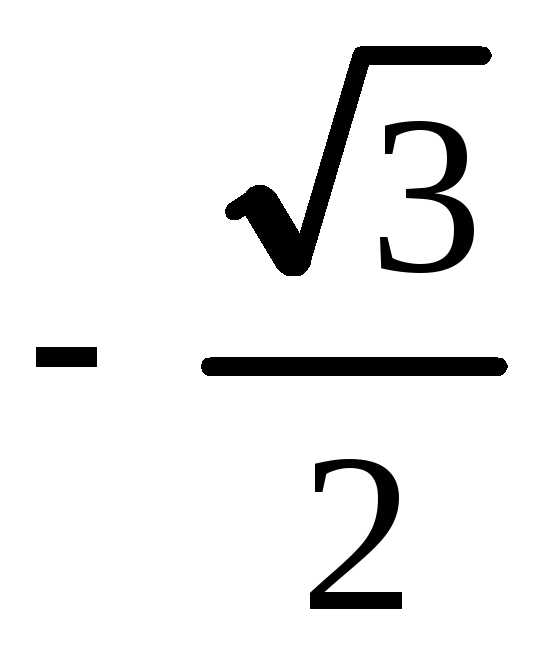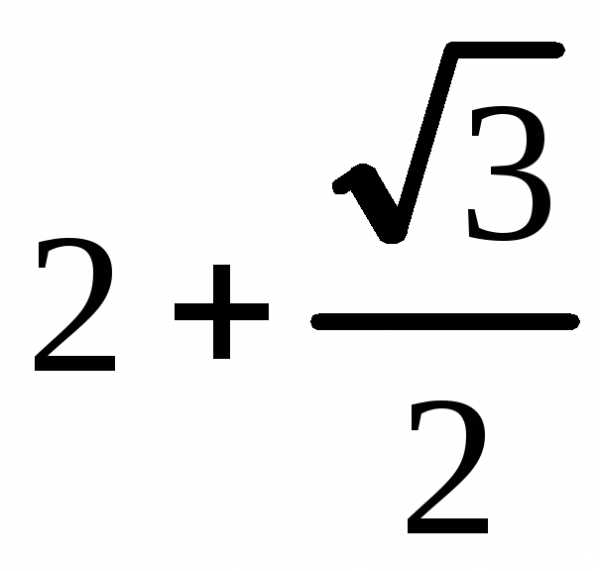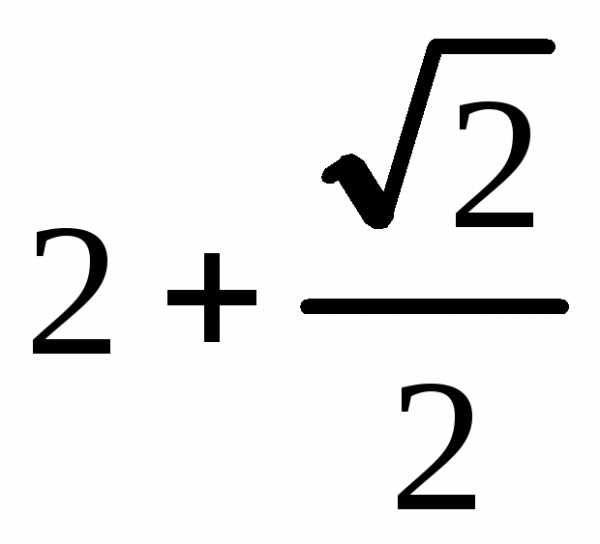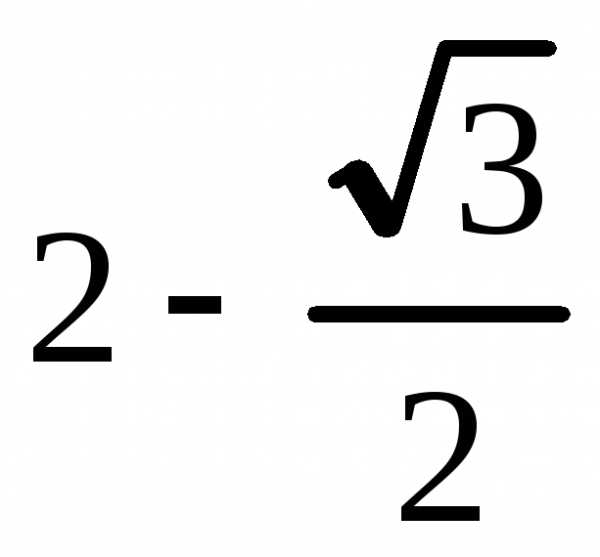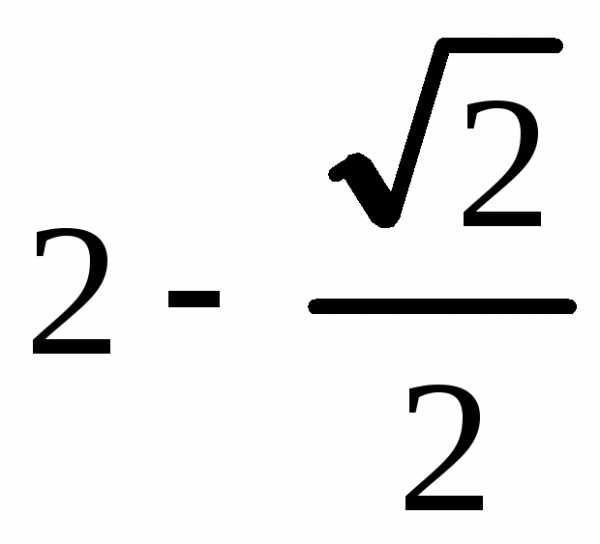Площадь фигуры ограниченной кривыми в прямоугольных координатах
Площадь фигуры между двумя кривыми в прямоугольных координатах определяется интегралом
от разницы кривых, где одна из них всегда принимает не меньшие значения чем другая , а также кривые непрерывны.
Пределы интегрирования — прямые x1=a, x2=b — ограничивают фигуру (a<b чаще всего это точки пересечения заданных кривых).
Данный цикл задач в первую очередь подойдет студентам мех-мата Львовского национального университета имени Ивана Франко для прохождения практикума из математического анализа.
Студенты других Вузов могут набираться практики на подобных интегралах, и изучать методику вычисления.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).
Пример 2.81 (2397). Найти площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах ax=y2, ay=x2,(a>0).
Вычисление: Построим графики функций, которые ограничивают искомую площадь фигуры:
На графике они будут иметь следующий вид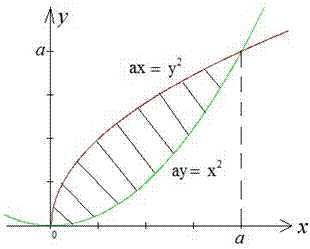
Площадь между кривыми и нужно найти. Как правило, Вам редко будет известно сам график, поэтому в заданиях где не заданы области на которой находить площадь в первую очередь необходимо найти точки пересечения кривых.
Найдем пределы интегрирования, то есть точки абсцисс пересечения заданных функций y1(x)=y2(x):
Как видите таким условием есть условие равенства функций.
Из последнего уравнения получим две точки x1=0, x2=a.
Дальше, когда Вы не видите графика функций необходимо установить какая из кривых принимает большие значения. Это нужно лишь для того, чтобы с первого раза получить положительное значение площади фигуры. Поскольку площадь всегда больше нуля, а интеграл может принимать произвольные значения, то без проверки следующего условия для нахождения площади интеграл нужно брать за модулем.
Выбираем произвольную точку из отрезка интегрирования [0;a] и убеждаемся в правильности неравенства , то есть проверяем которая из кривых принимает большее значения .
Как отмечалось выше, это нужно для того, чтобы после интегрирования получить положительную площадь фигуры между кривыми.
Вычисляем площадь фигуры, которая ограничена заданными кривыми интегрированиям:
Здесь мы имели достаточно простые функции, поэтому возведя их к табличным интегралам найти площадь достаточно легко. Следующие примеры будут содержать все более тяжелые функции, для интегрирования которых нужно применять знание практически всех формул интегрирования.
Следует заметить: значения площадей (во всех заданиях) измеряются в квадратных единицах (кв. од.), об этом Вы должны помнить, однако для экономии места и времени здесь будут приведены лишь значения определенных интегралов.
Пример 2.82 (2398) Вычислить площадь фигуры, ограниченной кривыми y=x2, x+y=2.
Вычисление: По методике записываем уравнение кривых, которые ограничивают площадь фигуры:
y1(x)=x2, y2(x)=2-x.
Здесь функции выразить достаточно просто.
Вычислим пределы интегрирования, приравняв между собой функции y1(x)=y2(x):
x2=2-x.
Переносим переменные по одну сторону от знака равенства и решаем квадратное уравнение
x2+x-2=0;
(x+2)(x-1)=0.
Следовательно, корни уравнения x1=-2, x2=1.
Сам график кривых и фигуры, площадь которой ищем, приведен на рисунку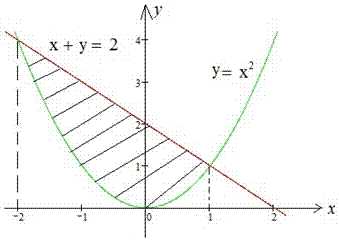
Подстановкой любой точки из промежутка [-2;1], например x=0 в функции убеждаемся, что выполняется неравенство
, поэтому .
Площадь фигуры вычисляем интегрированием разницы кривых в найденных пределах:
Площадь равна S=4,5 квадратных единиц.
По физическому содержанию площадь фигуры равна разнице площадей двух криволинейных трапеций. Первая отвечает за верхний график y2(x), нижняя криволинейная трапеция за функцию, которая принимает меньшие значения y2(x). Разница заключается в том, что здесь еще нужно определять пределы интегрирования.
Пример 2.83 (2399) Найти площадь фигуры, ограниченной кривыми y=2x-x2, x+y=0.
Вычисление: Запишем уравнение кривых, которые ограничивают искомую фигуру:
y1(x)=-x, y2(x)=2x-x2.
Из условия равенства функций y1(x)=y2(x) найдем пределы интегрирования:
2x-x2=-x;
x2-3x=0;
x (x-3) =0.
Следовательно, x1=0, x2=3.
Подстановкой единицы видим, что на промежутке [0;3] исполняется неравенство
, то есть .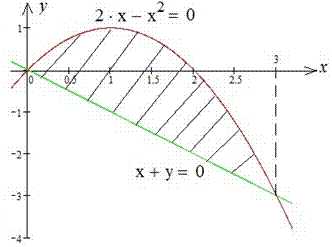
Находим площадь фигуры ограниченной заданными кривыми:
Под интегралом простая квадратичная функция, поэтому само интегрирование не сложно.
Следующие функции будут более сложными в плане интегрирования, однако используя табличные интегралы площадь найти удается.
Пример 2.84 (2400) Найти площадь фигуры, ограниченной кривыми y=2x, y=2, x=0.
Вычисление: Запишем подынтегральные функции:
y1(x)=2x, y2(x)=2, а также прямую x1=0 (ограничивает фигуру по оси абсцисс).
Найдем вторую границу интегрирования из условия равенства функций y1(x)=y2(x):
2x=2, 2x=21, отсюда имеем вторую точку x1=1.
На промежутке [0;1] исполняется неравенство , поэтому .
График степенной функции и прямой приведен ниже. 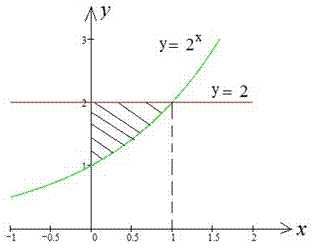
Площадь фигуры, которая ограничена кривыми равна интегралу:
При интегрировании получим логарифм.
На калькуляторах можете проверить, что площадь положительна.
Пример 2.85 (2401) Вычислить площадь фигуры, ограниченной кривыми y=x, y=x+sin2x, .
Вычисление: Запишем уравнение кривых, которые ограничивают площадь фигуры:
y1(x)=x, y2(x)=x+sin2x.
Дальше пределы интегрирования:
x1=0, x2=Pi (это известно нам по условию).
На промежутке справедливо неравенство
, поэтому . 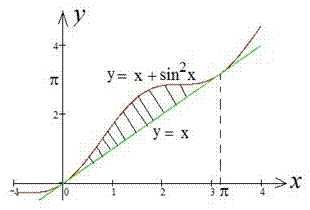
Если бы существовала дополнительная точка пересечения, то площадь была бы равна сумме двух интегралов.
Площадь фигуры вычисляем интегрированием: квадрат синуса под интегралом понижаем и выражаем с помощью косинуса двойного угла, а дальше за классической формулой интегрирования
Площадь равна Pi/2, что приблизительно равно 1,5708.
Пример 2.86 (2402) Найти площадь фигуры, ограниченной кривыми
Вычисление: Переписываем функции
Найдем пределы интегрирования, то есть точки абсцисс пересечения заданных функций из условия y1(x)=y2(x):
Поскольку функция парная
то найдем половину площади и результат умножим на двойку.
Из условия находим
что пределы равны плюс, минус бесконечности.
Чтобы легко представить, что мы интегрируем наведем график подынтегральных функций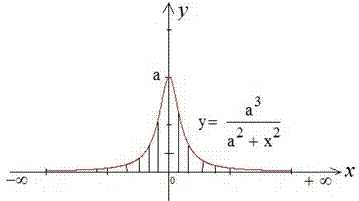
Учитывая четность функции интегрировать будем от 0 к бесконечности , а полученное значение умножим на двойку.
Получим несвойственный интеграл первого рода (детальнее о нем в части ІІІ).
Площадь фигуры вычисляем через предел интеграла:
В результате интегрирования получим арктангенс, который в предельном случае стремится к Pi/2.
Конечная формула достаточно компактна и удобна для расчетов, хотя с таким типом интегралов Вы знакомитесь впервые.
Пример 2.87 (2403) Вычислить площадь фигуры, ограниченной кривыми
Вычисление: Все Вы должны знать, что такой формулой задается уравнение эллипса.
Так как оси эллипса в канонической системе координат являются его осями симметрии, то эти оси делят эллипс на 4 равные части. Поэтому будем рассматривать часть эллипса, который находится в первом квадранте канонической (прямоугольной) системы координат.
Выражаем уравнение функции, которая ограничивает искомую площадь (четверть эллипса):
Запишем пределы интегрирования: из аналитической геометрии известно, что четверть эллипса ограничена прямыми x1=0, x2=a. 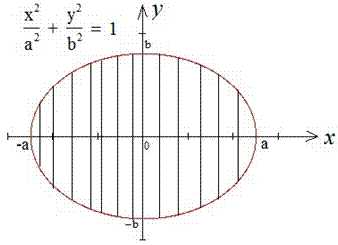
Для вычисления площади эллипса в самом интеграле необходимо выполнить замену переменных, что в свою очередь ведет к изменению пределов интегрирование. При этом придем к квадрату косинуса, который понижаем через косинус двойного угла.
В конце манипуляций приходим к табличным интегралам, которые легко интегрируем и подставляем пределы: 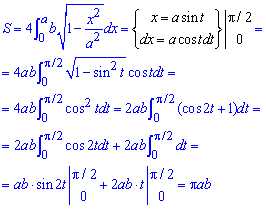
Получили классическую формулу площади эллипса S=Pi*a*b .
Видим, если эллипс вырождается в круг при (a=b=R), тогда формула площади круга S=Pi*R2.
Пример 2.88 (2404) Вычислить площадь фигуры, ограниченной кривыми y2=x2(a2-x2).
Вычисление: Так как все переменные в заданном уравнении входят в квадратах, то оси прямоугольной системы координат являются осями симметрии фигуры, которая ограничена этой линией, потому эти оси делят заданную фигуру на 4 равных части. Достаточно рассмотреть часть фигуры, которая заходиться в первом квадранте прямоугольной системы координат.
Построим график функции, которая ограничивает искомую площадь четвертины фигуры:
График неизвестной фигуры подобен на крылья бабочки. 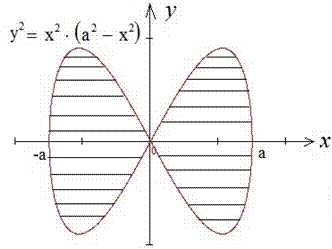
При y=0 имеем два корня уравнения x1=0 и x2=a.
Площадь фигуры равна 4 умножить на интеграл с найденными пределами.
Во время интегрирования выполняем замену переменных и пределов интегрирования
Это позволяет перейти к показательной функции, которая легко интегрируется.
Всегда помните, что замена переменных под интегралом ведет к изменению пределов интегрирования.
Пример 2.89 Найти площадь фигуры, ограниченную линиями
Вычисление: Запишем графику функций, которые ограничивают искомую площадь фигуры:
Определим пределы интегрирования из условия y1(x)=y2(x):
отсюда x1=0 и x2=1.
Между функциями справедлива зависимость на [0;1], поэтому .
График функций, что анализируем следующий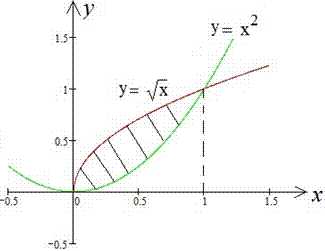
Площадь фигуры через определенный интеграл равна 1/3 (сравните 2.81 при a=1) :
Пример 2.90 Вычислить площадь фигуры, ограниченной кривыми
Вычисление: Вычислим пределы интегрирования из условия равенства функций y1(x)=y2(x):
Из биквадратного уравнения получим значение точек пересечения:
x1=-1 и x2=1.
Сами же функции в прямоугольных координатах будут иметь вид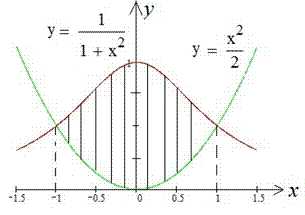
Интегрированием находим площадь фигуры (смотри рисунок и образец 2.89) :
Первый интеграл даст арктангенс, запомните хорошо эту формулу.
Пример 2.91 Вычислить площадь фигуры, ограниченной кривыми y=ex, y=e-x,x=1.
Вычисление: Из условия, которое Вы из-за повторяемости должны выучить y1(x)=y2(x) находим точки пересечения кривых:
ex=e-x,x=-x, 2x=0, следовательно, x1=0.
x2=1 (известно за условием).
График функций следующий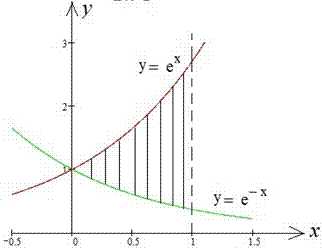
Экспоненту интегрировать не трудно, а площадь фигуры выражается формулой (смотри рисунок и образец 2.84) :
Пример 2.92 Найти площадь фигуры, ограниченной кривыми y=ln(x), y=ln2(x).
Вычисление: Пределы интегрирования из условия равенства функций y=ln(x), y=ln2(x) равны x1=1 и x2=e.
Интегрированием логарифмов находим площадь фигуры (смотри рисунок):
Здесь надо проинтегрировать по частям, положив ln(x) =u, (ln2(x)=u) и dx=dv. Попробуйте промежуточные действия провести самостоятельно.
Пример 2.93 Вычислить площадь фигуры, ограниченной кривыми
y=ln(x), y=ln(a), y=ln(b), x=0, где 0<a<b.
Вычисление: Построим графики функций, которые ограничивают искомую площадь фигуры:
x (y) =ey (то есть обратная функция к заданной функции y(x)=ln(x)) .
Такой прием применяют, когда пределы интегрирования параллельны оси Оx, то есть y=const.
Запишем пределы интегрирования:
y1=ln(a), y2=ln(b) (берем из начального условия).
График искомой фигуры следующий
Площадь фигуры, которая ограничена заданными кривыми:
Пример 2.94 Найти площадь фигуры, ограниченной кривыми
Вычисление: Пределы интегрирования в формуле площади находим из условия y1(x)=y2(x):
ln(x)/(4x)=x*ln(x).
Упростив на логарифм (если он больше нуля), получим
1=4x2; 4x2-1=0, x1=1/2.
Из условия на логарифм (=0) получим
ln(x) =0; x2=1.
ОДЗ: x>0.
График фигуры в прямоугольных координатах следующий
Площадь фигуры между кривыми (на [0,5;1]) находим интегрированием:
для вычисления интегралов используем метод замены переменных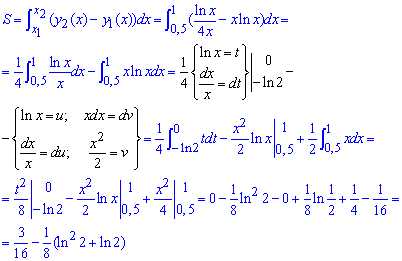
Вычисление не так просты, поэтому с превращениями попробуйте разобраться самостоятельно.
Пример 2.95 Вычислить площадь фигуры, ограниченной кривыми y=arcsin(x), y=arccos(x), y=0.
Вычисление: Находим точки пересечения кривых из равенства x1(y)=x2(y):
sin(x)=cos(y), отсюда y1=0 (известно за условием) и y1=Pi/4 (образец 2.93).
На графике это выглядит следующим образом
Учитывая справедливость неравенства вычисляем площадь фигуры:
Думаю, что с такими заданиями на экзамене или модулях Вы справитесь.
Пример 2.96 Найти площадь фигуры, ограниченной кривыми y=tg(x), y=2/3*cos(x), x=0.
Вычисление: Найдем пределы интегрирования, то есть абсциссы точек пересечения заданных функций y1(x)=y2(x):
tg(x)=2/3*cos(x), отсюда
(вторая точка известна за условием).
Кривые на плоскости имеют вид
Площадь фигуры, которая ограничена заданными кривыми () равна интегралу:
Пример 2.97 (2400) Вычислить площадь фигуры, ограниченной кривыми y=|ln(x)|, y=0, x=0,1; x=10.
Вычисление: Выписываем пределы интегрирования x1=0,1; x2=10 из начального условия.
Как строить модуль от логарифма Вы, по-видимому, еще не забыли
Площадь фигуры равна сумме двух интегралов, причем первый берем со знаком минус ():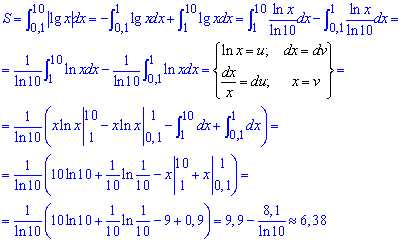
Во время интегрирования использовали интегрирование частями.
Пример 2.98 (2400) Найти площадь фигуры, ограниченной кривыми y=(x+1)2, x=sin(Pi*y), y=0 .
Вычисление: Построим график функций, которые ограничивают искомую площадь фигуры:
(здесь взяли обратную функцию к заданной y1(x)=(x+1)2), x2=sin(Pi*y).
Выпишем пределы интегрирования:
y1=0; y2=1 (известно за условием).
График функций приведен ниже
Неизвестную площадь фигуры вычисляем интегрированием ():
Пример 2.99 Вычислить площадь фигуры, ограниченной кривыми y=sin(x), y=cos(x), y=0
Вычисление: Из рисунку видно, что площадь S лучше разбить на две части: S=S1+S2.
Запишем уравнение функций, которые ограничивают искомую площадь фигуры:
Интегрируем синус и косинус функции и находим площадь.
Второй вариант заключается в интегрировании разницы обратных функций по y.
Пример 2407 Найти площадь фигуры, ограниченной кривыми (циссоида Диокла) x=2a (a>0).
Вычисление: Поскольку график функции симметричен относительно оси Ox, то будем рассматривать половину площади фигуры (над осью Ox) и результат умножим на 2.
В точке x=2a функция не определена, поэтому будем иметь интеграл второго рода (детальнее смотрите часть ІІІ), он совпадает и, следовательно, площадь будет выражена числом.
Запишем пределы интегрирования:
x1=0 (потому что ) x2=2a (за условием).
График функций следующий
Площадь фигуры, что ограниченна заданной кривой находится достаточно непростым интегрированием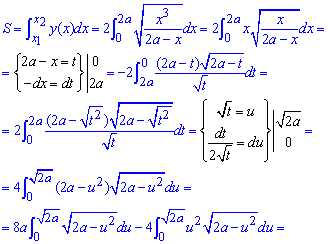
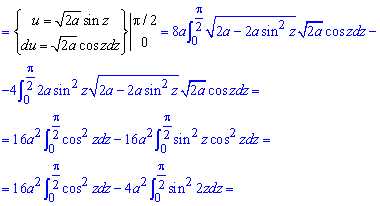
Здесь пришлось трижды выполнять замену переменных, чтобы прийти к правильному ответу.
Еще раз внимательно разберите интеграл.
Пример 2408 Вычислить площадь фигуры, ограниченной кривыми (трактриса), y=0.
Вычисление: Трактриса — кривая, по которой двигается объект, когда его тянуть по горизонтальной плоскости за бечевку фиксированной длины, если направление движения тягача является ортогональным к начальному положению бечевки и скорость тягача бесконечно малая величина.
Очевидно, что (смотри рисунок).
Принимая к сведению, что положительному приросту x отвечает отрицательный прирост y, и что фигура не квадрируема (в общем понимании), допускаем
где дифференциал за x находим через производную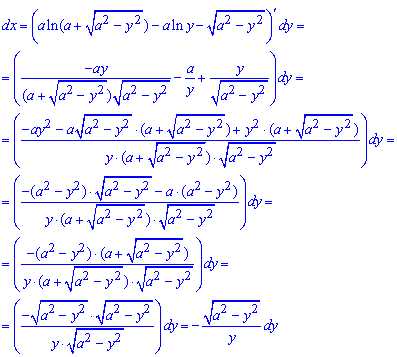
Площадь фигуры через определенный интеграл равна
Следующим идет материал из которого Вы научитесь находить площадь фигуры, ограниченной кривыми заданными параметрически.
yukhym.com
2.9.2. Площадь фигуры, ограниченной кривой, заданной параметрически
Если фигура
ограничена кривой, заданной параметрическими
уравнениями
,
прямымии осью 9рис. 5), то площадь ее вычисляется по
формулам:
9рис. 5), то площадь ее вычисляется по
формулам:
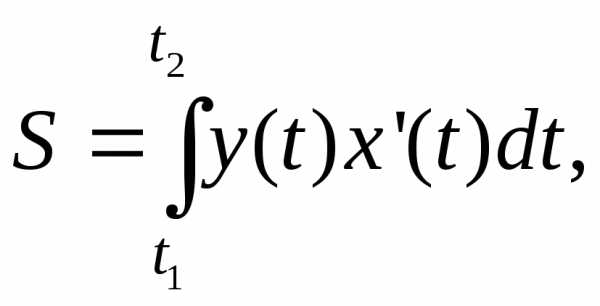 (42)
(42)
а пределы
интегрирования находятся из уравнений
на отрезка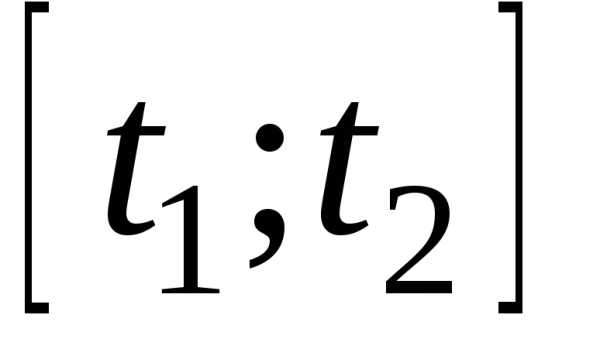 .
Порядок вычисления аналогичен п. 2.9.1.
.
Порядок вычисления аналогичен п. 2.9.1.
Пример. Найти площадь фигуры, ограниченной линиями, заданными уравнениями:.
Решение. Построим кривую, заданную параметрическими
уравнениями (рис. 5). Для этого вычислим
значения 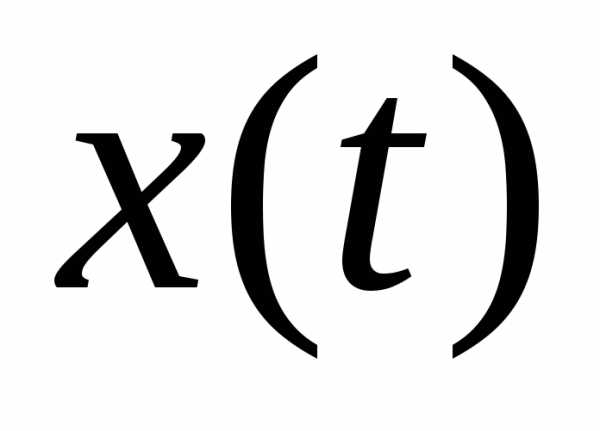 и
и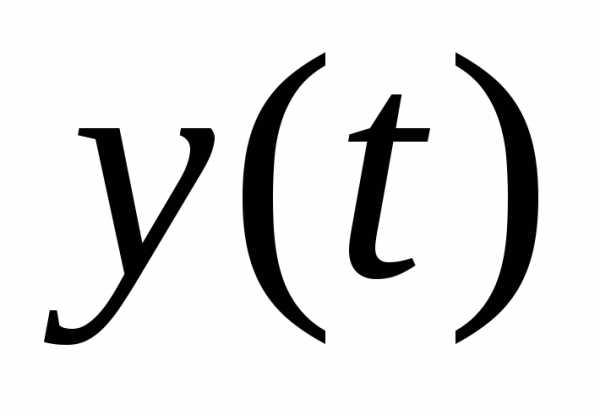
ОТРЕДАКТИРОВАТЬ
Таблица 5
Вспомогательная таблица для построения параметрически заданной кривой
Мы подставляли
значения  из верхней строки таблицы в параметрические
уравнения и последовательно получали
значения
из верхней строки таблицы в параметрические
уравнения и последовательно получали
значения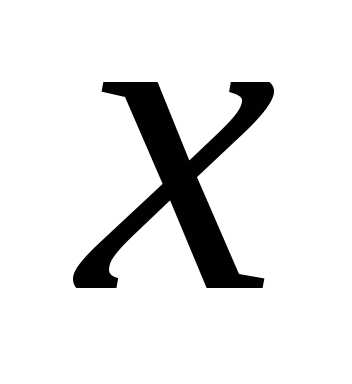 и
и .
Построим также и прямую
.
Построим также и прямую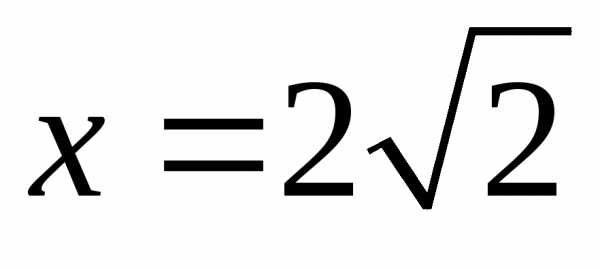 (см. рис. 6). Найдем пределы интегрирования.
Приравняем,
отсюда
(см. рис. 6). Найдем пределы интегрирования.
Приравняем,
отсюда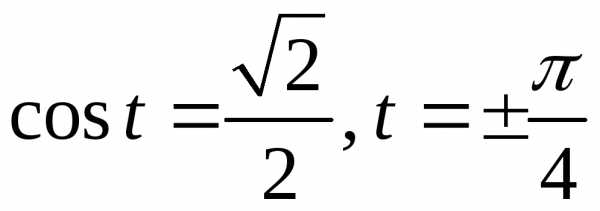 .
Поскольку
.
Поскольку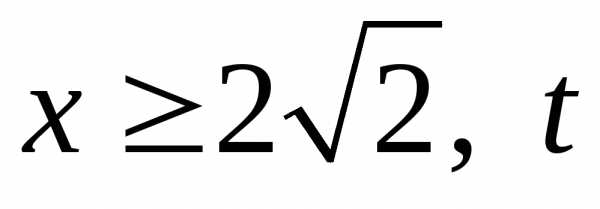 изменяется от
изменяется от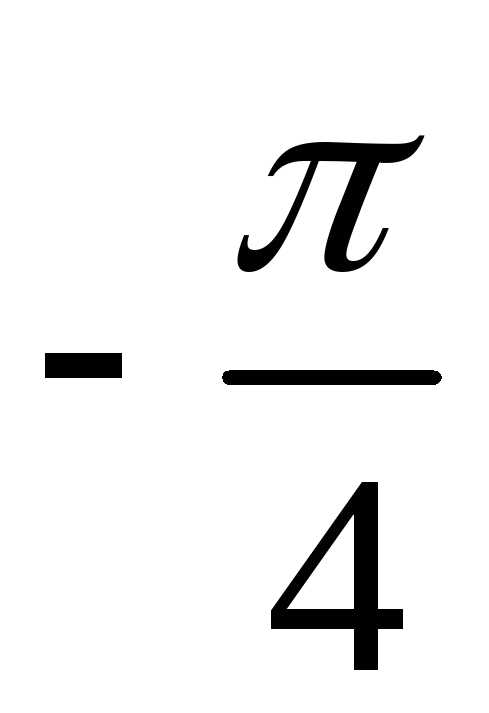 до
до
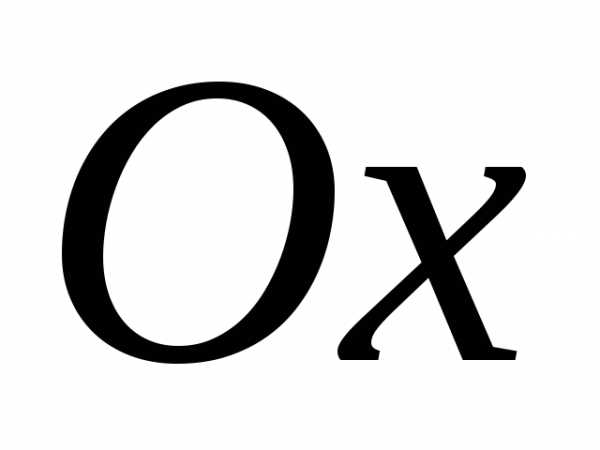 ,
то можно интегрировать от
,
то можно интегрировать от до
до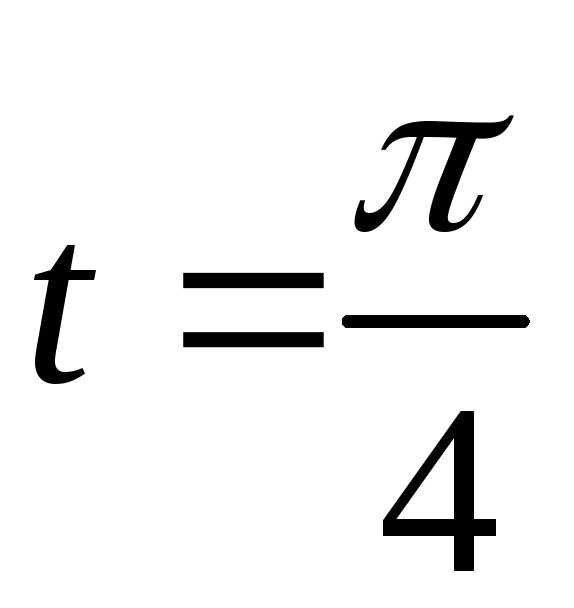 .
А результат затем удвоить. Подставляем
в формулу (42)::
.
А результат затем удвоить. Подставляем
в формулу (42)::.
Для вычисления интеграла воспользуемся формулами (22)-(27) из п. 1.7:
.
2.9.3. Площадь фигуры, ограниченной кривой, заданной в полярных координатах
Пусть кривая задана
в полярных координатах уравнением 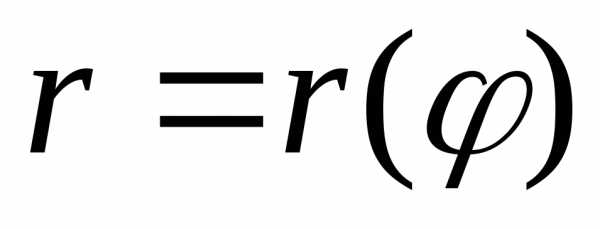 и двумя лучами
и двумя лучами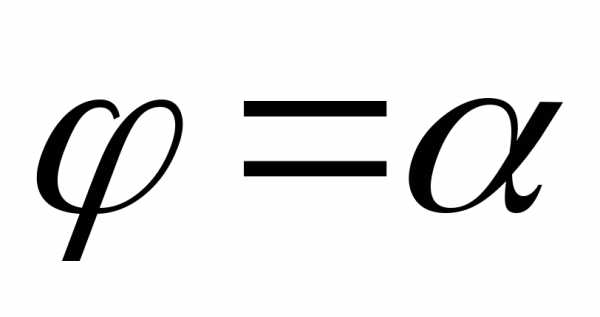 и,
тогда ее площадь (рис. 7) вычисляется по
формуле:
и,
тогда ее площадь (рис. 7) вычисляется по
формуле:
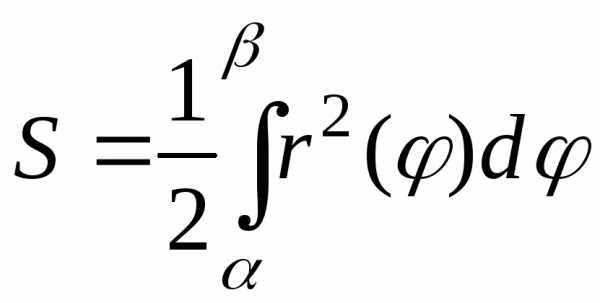
Порядок вычислений аналогичен п. 2.9.1.
Пример. Найти площадь фигуры, ограниченной линией , перейдя предварительно к полярным координатам.
Решение. Переход
от декартовых к полярным координатам
осуществляется по формулам: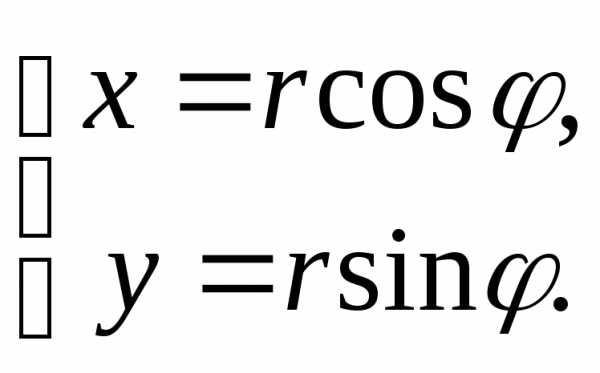 Подставив эти выражения в уравнение
кривой, получим:или.
Отсюда получаем уравнение кривой в
полярных координатах:
Подставив эти выражения в уравнение
кривой, получим:или.
Отсюда получаем уравнение кривой в
полярных координатах: .
.
Поскольку в правой
части уравнения стоит неотрицательная
величина, то полярный угол может принимать
любые значения
.
В силу периодичности функции вычислим подробно таблицу значений для
аргументов в промежутке
вычислим подробно таблицу значений для
аргументов в промежутке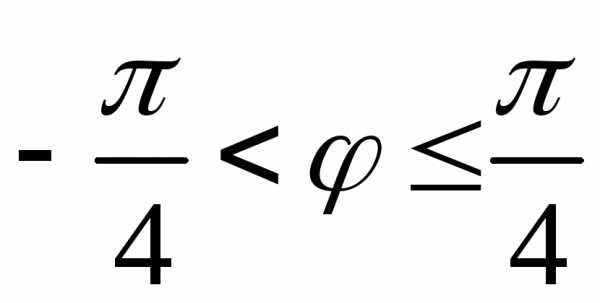
Таблица 6
Вспомогательная таблица для построения кривой, заданной в полярных координатах
Построим эту кривую
( четырехлепестковую розу). В силу
симметрии фигуры достаточно проинтегрировать
по  от
от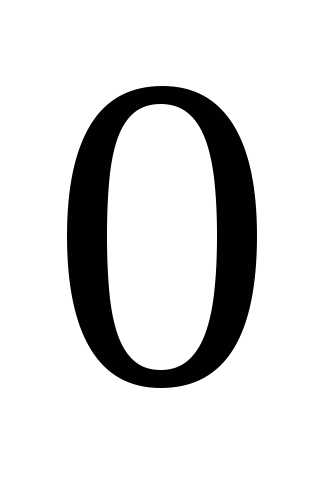 до
до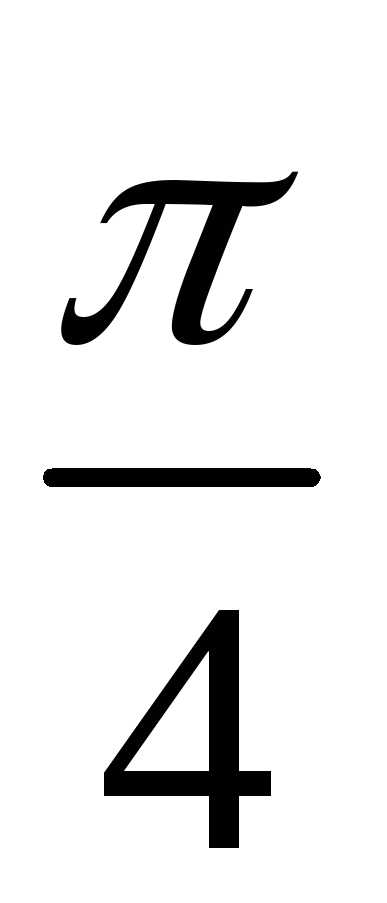 ,
а затем результат умножить на 8.
,
а затем результат умножить на 8.
Применим формулу (43): . Для вычисления интеграла воспользуемся формулой понижения степени (15) из п. 1.7:.
Вычислить интеграл
непосредственно зачастую весьма
непросто. Поэтому создаются специальные
таблицы интегралов. При затруднениях
в вычислении того или иного интеграла,
полученного при решении конкретной
технической задачи, можно ими
воспользоваться. Есть класс так называемых
«неберущихся» интегралов, т.е. класс
функций, первообразные для которых не
являются элементарными. Тем не менее,
интегралы от таких функций часто
встречаются в математике и приложениях.
Так, в теории вероятностей мы встретимся
с функцией 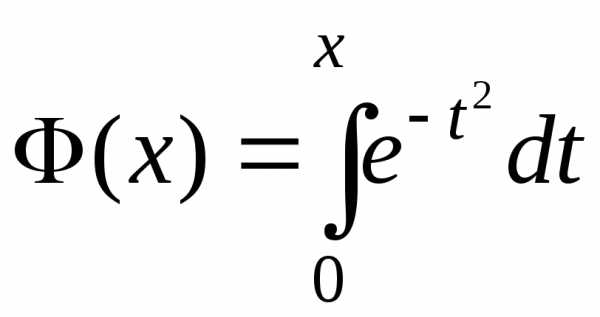
Для вычисления таких интегралов разработаны специальные методы. Например, формулы прямоугольников, трапеций, Симпсона или с помощью рядов.
Определенный интеграл применяется в математике для нахождения длин дуг кривых, объемов различных тел, площади поверхности тел вращения и др. Широко применяется определенный интеграл в механике и физике. Это вычисление статических моментов, моментов инерции плоских дуг кривых и фигур, координат центра тяжести, а также вычисление работы, давления и многого другого.
Приложение.
Вычисление длины кривой, заданной явным уравнением.
Если кривая задана явным уравнением в прямоугольных декартовых координатах
,
то . (1)
Пример.
Вычислить длину дуги куска графика логарифмической функции .
Решение. Подставляя
в формулу (1) 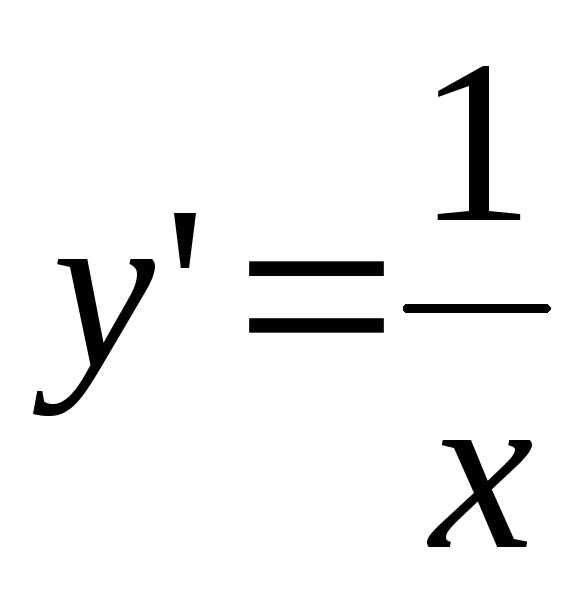 ,
получим:
,
получим:
.
Вычисление длины кривой, заданной параметрическим уравнением.
Если кривая задана параметрическим уравнением в прямоугольных декартовых координатах
,
то. (2)
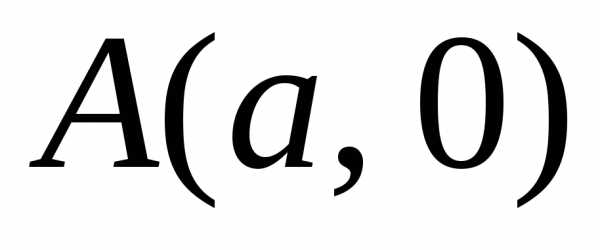 и.
и.
Решение. Найдем
вначале пределы интегрирования из
уравнений: 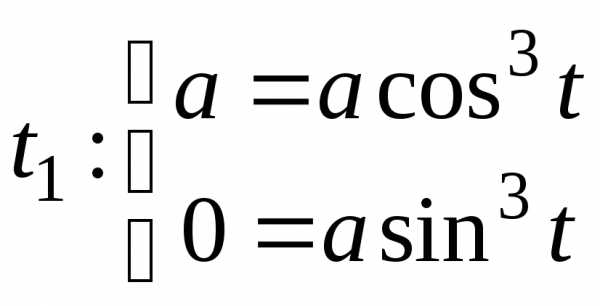 ,
,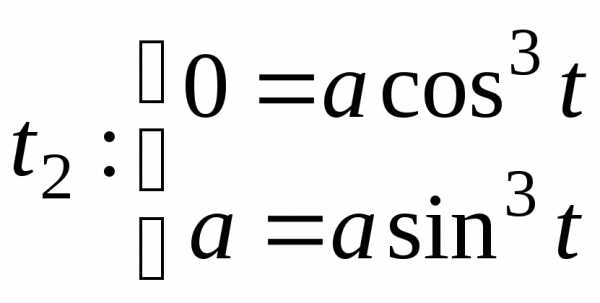 .
Отсюда
.
Отсюда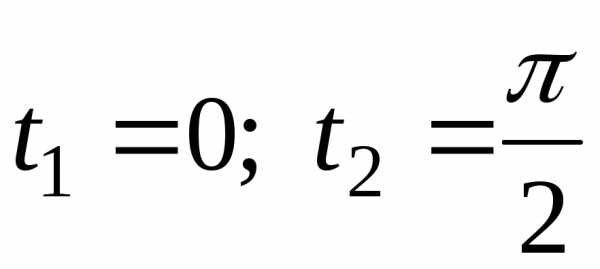 .
Вычислим также элементы подкоренного
выражения:.
Преобразуем подынтегральное выражение,
используя основное тригонометрическое
тождество:.
Подставив полученное выражение и пределы
интегрирования в формулу (2), окончательно
получаем выражение для длины дуги
четверти астроиды:
.
Вычислим также элементы подкоренного
выражения:.
Преобразуем подынтегральное выражение,
используя основное тригонометрическое
тождество:.
Подставив полученное выражение и пределы
интегрирования в формулу (2), окончательно
получаем выражение для длины дуги
четверти астроиды:
.
Вычисление длины кривой, заданной уравнением в полярных координатах.
Если кривая задана уравнением в полярных координатах
,
то. (3)
Пример. Вычислить
длину дуги одного витка логарифмической
спирали 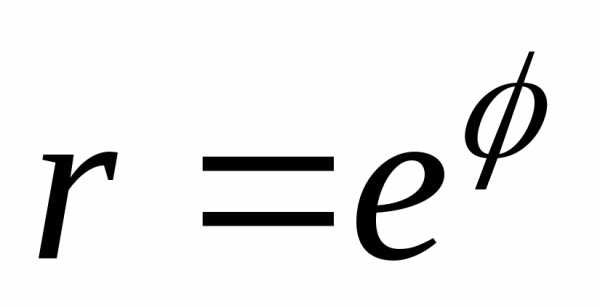 ,
где.
,
где.
Решение. Подставим 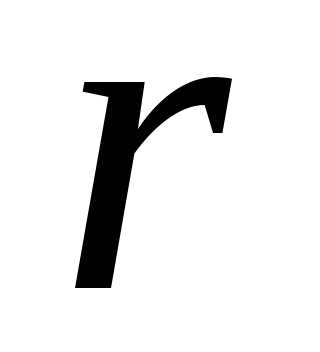 и
и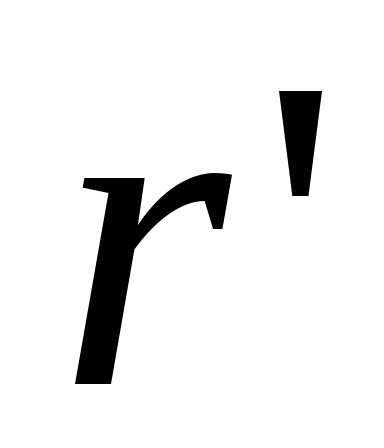 в формулу (3), получим:
в формулу (3), получим:
.
studfiles.net
Вычисление площадей плоских фигур с помощью определённого интеграла
Рассмотрим постановку задачи о площади криволинейной трапеции.
Вычислить площадь криволинейной трапеции, ограниченной линиями (рис. 1).
.
Рис. 1. Площадь криволинейной трапеции
Как мы пытались ее решить:
Первый способ.
Разбили отрезок на одинаковых отрезков, заменили искомую площадь площадью поступенчастой линии, легко ее сосчитали и получили приближенное решение нашей задачи. Далее устремили в пределе и
получили искомую площадь S. Ввели обозначение .
Это определенный интеграл. Вот таким образом мы пытались решить задачу. Мы знаем теперь, как приближенно ее решить, знаем обозначения для точного решения, но точного решения еще не знаем.
Затем мы получили точное решение задачи следующим образом: рис. 2:
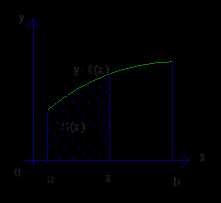
Рис. 2. Функция S (x)
Ввели функцию . Каждому площадь под соответствующей частью кривой . Так, введенная функция удовлетворяет единственному закону, а именно:
Каждому соответствует единственное значение .
Мы доказали, что производная этой же функции и доказали, что точная площадь вычисляется следующим образом. Надо найти любую первообразную от функциии взять приращение этих первообразных. То есть взять первообразную в точке и отнять первообразную в точке И в результате мы получили формулу, которой мы будем пользоваться для вычисления площадей.
.
Методику нахождения площади рассмотрим сначала на относительно простом примере.
Пример 1.
Найти площадь фигуры, ограниченной линиями
Решение.
Вот искомая площадь:
Рис. 3. Площадь
Вот формула:
Это общая формула. Конкретно к нашему случаю она применима так:
Пределы интегрирования .
=.
Вычислили площадь криволинейной фигуры.
Ответ:
В следующей задаче площадь искомой фигуры образовывается с помощью А именно:
Найти площадь фигуры, ограниченной линиями
Решение.
Посмотрим, как выглядит фигура (рис. 4).
Рис. 4. Фигура, ограниченная линиями
Формула та же самая:
В нашем случае . Итак, надо найти определенный интеграл
=-(-1)+1=1+1=2.
Искомая площадь найдена, и ответ получен.
Ответ: 2
Найти площадь фигуры, ограниченной линиями
Решение.
Рис. 5. Площадь фигуры, ограниченной линиями
Формула для площади та же самая:
В нашем случае .
Ответ:
В следующем примере ищется площадь под параболой.
Найти площадь фигуры, ограниченной линиями
Решение.
Схематически изобразим параболу Корни
Рис. 6. Парабола
Применим известную формулу
И применим ее для данной функции и пределов интегрирования
Искомая площадь найдена.
Ответ:
В предыдущих задачах площадь образовывалась с помощью разных кривых, но эта площадь находилась над осью . В следующей задаче наоборот.
Найти площадь фигуры, ограниченной линиями.
Решение.
Посмотрим, что это за фигура. График в пределах от Π до 2Π расположен под осью Ox (рис. 7).
Рис. 7. График в пределах от Π до 2Π
Ясно, что если возьмем определенный интеграл, то мы получим отрицательное число.
Вычисляем.
1. Сначала вычисляем определенный интеграл от π до 2π от подынтегральной функции
Надо найти первообразную.
По таблице первообразных: .
=-1-1=-2.
2. Для того чтобы найти площадь, надо взять модуль =2.
Ответ: 2.
Следующее усложнение – искомая площадь расположена между двумя кривыми.
А именно:
Найти площадь фигуры, ограниченной линиями (рис. 8)
Рис. 8. Площадь фигуры, ограниченной линиями
Решение.
Итак, площадь образуют 2 кривые, одна из них может находиться под осью .
Каким образом мы будем решать эту задачу?
Во-первых, мы можем сдвинуть фигуру на такое положительное , что площадь находится над осью . Рис. 9.
Рис. 9. Сдвиг фигуры
Затем мы возьмем соответствующий определенный интеграл и найдем площадь. Искомая площадь равна разности двух площадей.
Площадь под верхней кривой минус площадь под нижней кривой .
Каждую из площадей мы умеем находить.
Таким образом, в общем виде была поставлена задача, в общем виде получен ответ.
Ответ:
Обсудим и постановку задачи, и полученный важный результат.
Нам надо было найти площадь фигуры, ограниченной линиями
.
Мы использовали известный прием: эту площадь подняли на некоторое , и это Так вот, эту площадь теперь можно считать без введения . Правило следующее:
Площадь фигуры, ограниченной прямыми линиями непрерывных на отрезке и таких, что для всех из отрезка вычисляется по формуле, которую мы вывели:
Рассмотрим первый конкретный пример на нахождение площади между двумя линиями.
Найти площадь фигуры, ограниченную линиями
.
Решение. Для начала построим графики этих линий и поймем, где та площадь, которую нам надо искать.
График квадратичной функции – парабола. Корни – 0, 4, ветви вниз. График
– биссектриса первого координатного угла. Вот площадь, которую надо найти:
Рис. 10. Искомая площадь
Но для этого сначала надо найти точки пересечения и решить стандартную задачу.
1. Находим точки пересечения. Для этого решаем систему: .
Отсюда получаем квадратное уравнение относительно :
Мы нашли , то есть, пределы интегрирования. Это первое важное действие.
Теперь стандартное действие:
2. = =()
Искомая площадь равна 4,5
Ответ: 4,5
Во втором примере часть площади находится под осью , но на методику это не влияет.
Пример 6.
Итак, требуется найти площадь фигуры, ограниченной линиями
Решение.
Сначала построим графики, посмотрим, какую площадь нам нужно найти. Рис. 11.
Первая функция – парабола, ветви вниз. График второй функции – прямая линия.
Есть две точки пересечения, их придется найти, а именно взять пределы интегрирования, и тогда будем решать задачу по знакомому нам плану.
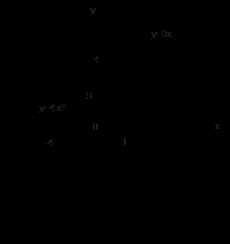
Рис. 11. Площадь фигуры, ограниченной линиями
Первое действие – найти пределы интегрирования и второе – найти площадь.
Пределы интегрирования найдем из системы.
То есть, пределы интегрирования найдены.
= ()
Ответ:
Итак, мы показали, каким образом можно вычислять площади плоских фигур с помощью определенного интеграла.
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Ru.scribd.com (Источник).
- Math5you.ru (Источник).
- Dok.opredelim.com (Источник).
Домашнее задание
- Найти площадь фигуры, ограниченной линиями , , ,
- Найти площадь фигуры, ограниченной линиями
- Алгебра и начала анализа, Мордкович А.Г.: № 1030, 1033, 1037, 1038.
interneturok.ru
Как найти площадь плоской фигуры, которая ограничена кривыми?
Разберем готовые ответы к примерам на нахождение площади плоской фигуры, которая ограничена кривыми через двойные интегралы.
Задание не сложные, а вся схема нахождения площади требует всего трех вещей:
знание элементарных функций и умение искать точки их пересечения;
понимание как через криволинейные интегралы искать площадь, умение правильно расставлять пределы;
хорошых знаний теории вычисления интегралов, поскольку к этому все сводится.
ЗАДАНИЕ 4.1 Найти площадь плоской фигуры, которая образована линиями:
x=4-y2, x+2y=4.
Решение: Фигура ограничена x=4-y2— параболой с вершиной в точке O(4;0) и ветками влево;
но x+2y=4 — прямой, которая отрезается на осях в точках (4;0) и (0;2).
Найдем точки пересечения графиков функций из системы уравнений:
При ее решении получим две точки
График параболы и прямой приведен на рисунку
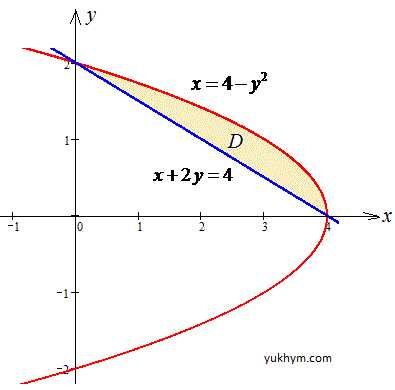
Запишем пределы интегрирования:
D: 0≤x≤4,
Здесь имеем y=√(4-x) — уравнение верхней части параболы x=4-y^2;
Вычислим площадь фигуры нахождением двойного интеграла: 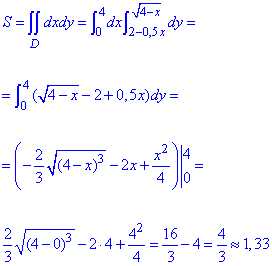
Площадь равна 1,33 единиц квадратных.
ЗАДАНИЕ 4.2 Найти площадь плоской фигуры, которая образована кривыми:
y=2-x, y2=4x+4.
Решение: y^2=4x+4 — парабола с вершиной в точке O (-1;0) и ветками вправо;
y=2-x, x+y=2 — прямая, которая отрезается на осях в точках (2;0) и (0;2).
Складываем систему уравнений для нахождения точек пересечения графиков заданных кривых:
При решении получим две точки
График области интегрирования имеет вид
Пределы в области D:
-6≤x≤2, 0,25y2-1≤y≤2-y.
Находим площадь фигуры через криволинейный интеграл: 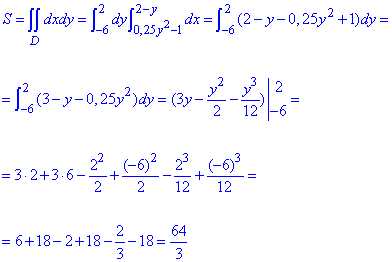
Кратный интеграл не трудно интегрировать.
ЗАДАНИЕ 4.3 Найти площадь плоской фигуры, которая образована линиями:
x2+y2=4, x2+y2=4x.
Решение: Область интегрирования ограничена x2+y2=4 — кругом с центром в точке O1(0;0) и радиусом R=2;
x2+y2=4x, x2-4x+4+y2=4, (x-2)2+y2=22 — круг с центром в точке O1(2;0) и радиусом R=2.
Найдем точки пересечения графиков заданных функций из системы уравнений:
отсюда
График фигуры, площадь которой ищем приведен на рисунку 
Расставим пределы в области D
(поскольку область симметрична относительно прямой y=0, то будем рассматривать ее половину, а результат умножим на 2):
D: 0≤y≤√3,
Здесь записали:
— уравнение левого полукруга (x-2)2+y2=4;
— уравнение правого полукруга x2+y2=4.
Вычислим площадь фигуры через двойной интеграл: 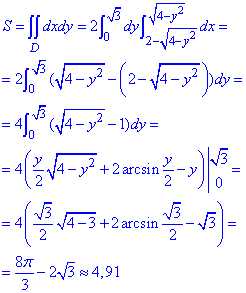
При интегрировании получили арксинусы, дальше подставили пределы интегрирования и округлили конечные значения.
ЗАДАНИЕ 4.4 Найти площадь плоской фигуры, которая образована кривыми:
x2+y2=2x, x2+y2=4x, y=x, y=0.
Решение: Начнем вычисление с анализа того, что собой представляет фигура, площадь которой нужно найти.
Сведем уравнения к простому виду
x2+y2=2x, x2-2x+1 +y2=1, (x-1)2+y2=12 — круг с центром в точке O1(1;0) и радиусом R=1.
x2+y2=4x, x2-4x+4+y2=4, (x-2)2+y2=22 — круг с центром в точке O1(2;0) и радиусом R=2.
y=x — прямая, которая является биссектрисой первой и третьей четверти.
Рисунок к задаче илюстрирует площадь которой фигуры нужно найти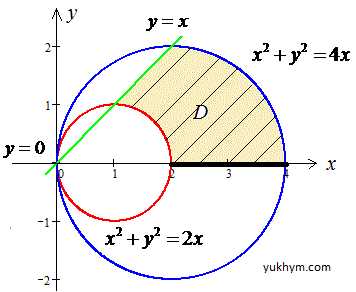
Поскольку поверхность ограничена кругами, то целесообразно перейти к полярным координатам.
Найдем якобиан перехода:
Запишем заданные функции в полярной системе координат:
отсюда
отсюда
y=0, тогда
y=x, тогда
Это нам нужно, чтобы знать пределы в новой системе координат.
Пределы интегрирования в полярной системе координат:
Вычислением кратного интеграла находим площадь фигуры, ограниченной заданными кривыми: 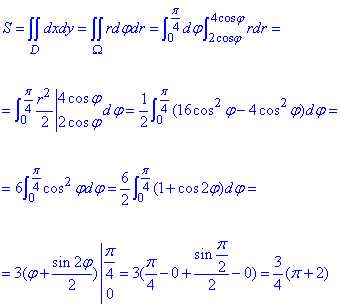
Конечное значение площади можно еще округлить.
Из этого примера Вы ознакомились как искать площадь в полярной системе координат.
В следующей статье разберем еще несколько примеров на нахождение площади фигур интегрированием.
yukhym.com
4.2. Вычисление площади фигуры, ограниченной линией, заданной параметрически
Пусть кривая задана
параметрическими уравнениями 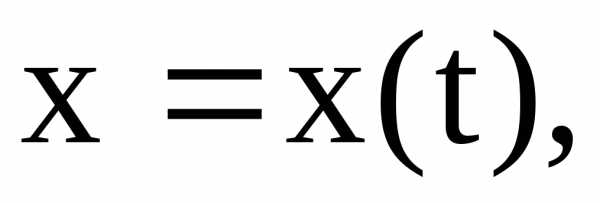
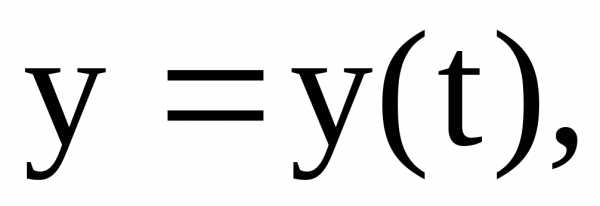 то площадь криволинейной трапеции,
ограниченной этой кривой, прямыми
то площадь криволинейной трапеции,
ограниченной этой кривой, прямыми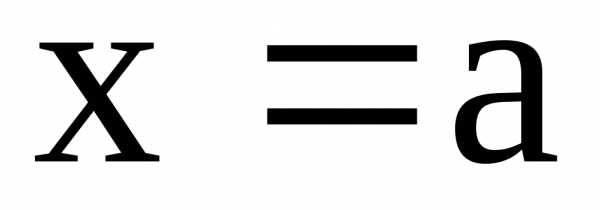 и
и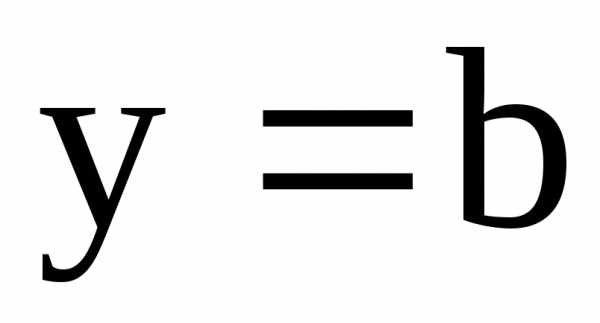 и отрезком [a,b]
оси ОХ, выражается формулой
и отрезком [a,b]
оси ОХ, выражается формулой
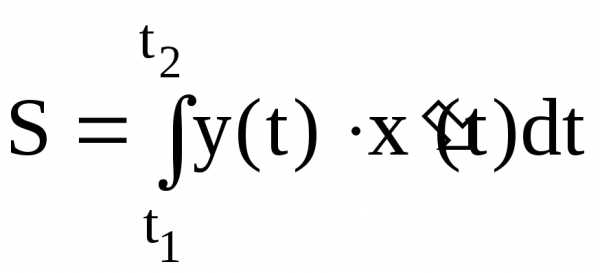 ,
(4.5)
,
(4.5)
где 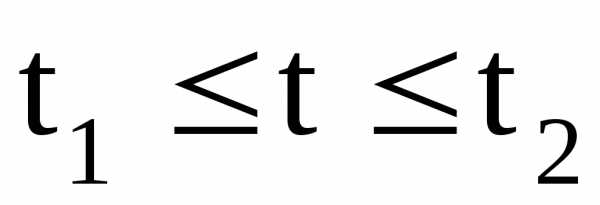 ,
,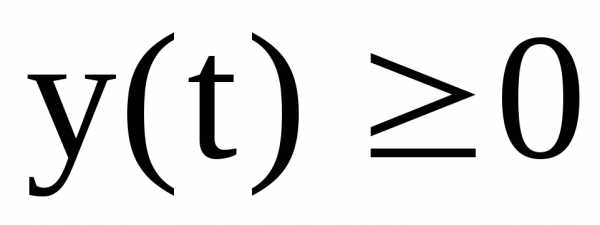 ,
, и
и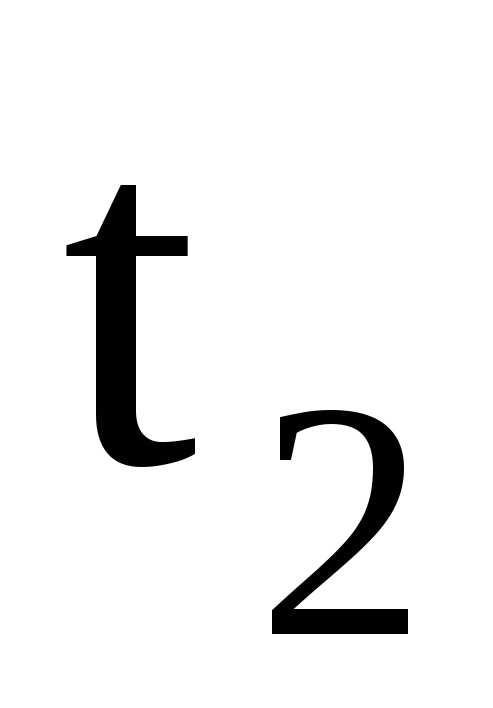 определяются из условий
определяются из условий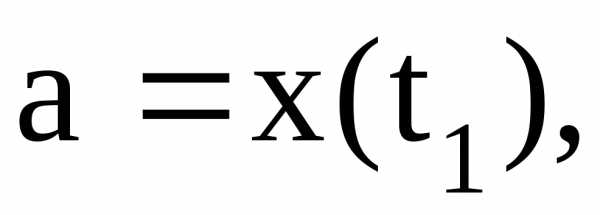
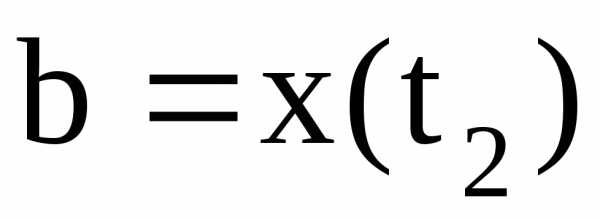 .
.
Пример 45. Найти площадь фигуры, ограниченной осью ОХ и одной аркой циклоиды
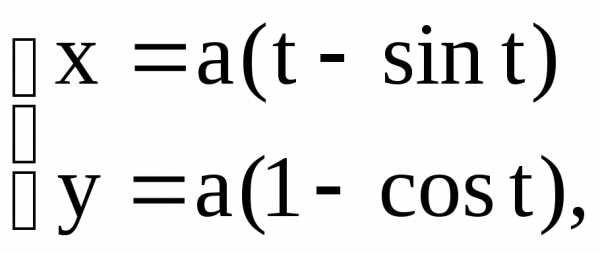 .
.
Решение. Воспользуемся формулой (4.5). Предварительно
найдем 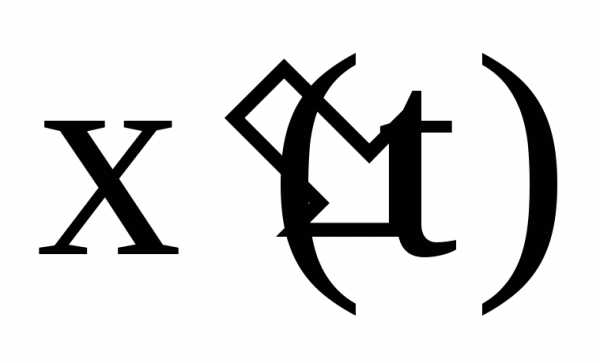 :
:
(кв.ед.)
4.3. Вычисление площади плоской фигуры в полярных координатах
В полярных
координатах положение точки на плоскости 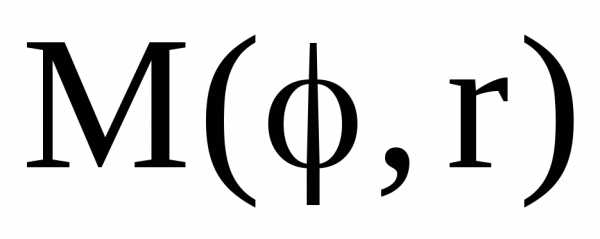 определяется двумя координатами:
полярным радиусом
определяется двумя координатами:
полярным радиусом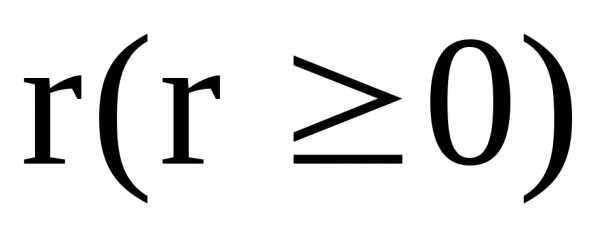 и полярным углом.
Связь между декартовыми координатами
(x,y)
и полярными (,
r)
осуществляется по формулам
и полярным углом.
Связь между декартовыми координатами
(x,y)
и полярными (,
r)
осуществляется по формулам
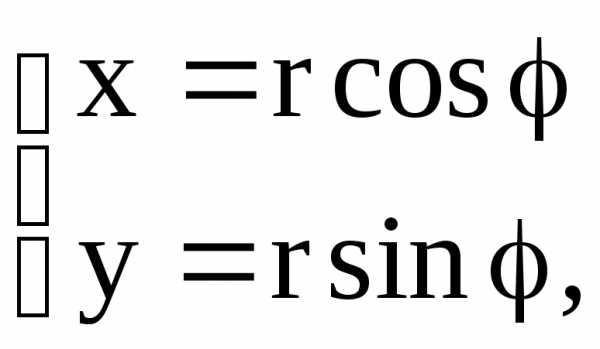 .
.
Площадь криволинейного сектора,
ограниченного
кривой  и двумя
и двумя
полярными радиусами 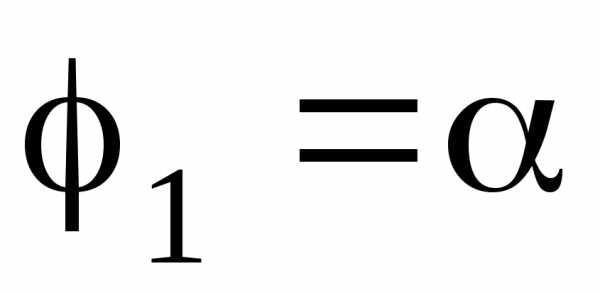 и
и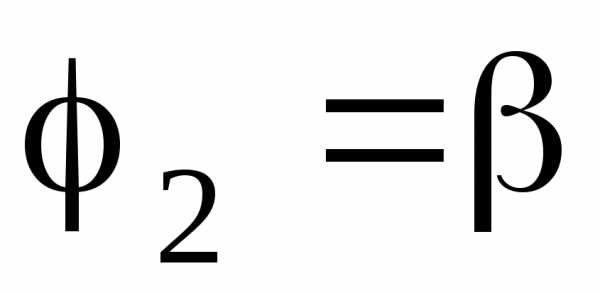
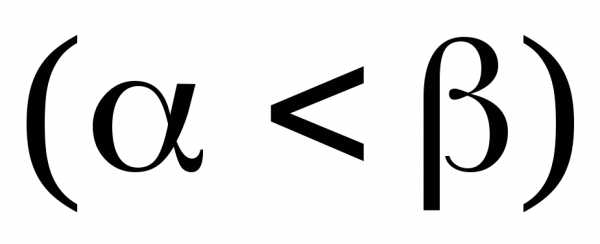 (рис.4.7), выражается
интегралом
(рис.4.7), выражается
интегралом
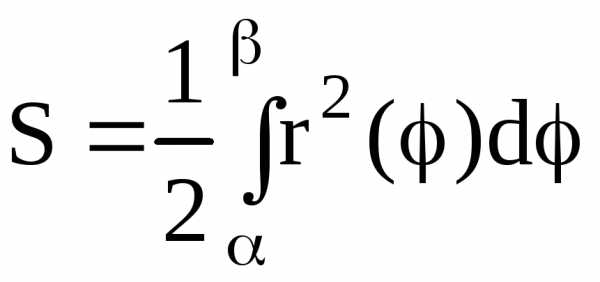 .
(4.6)
.
(4.6)
Пример 46. Найти площадь фигуры, ограниченной улиткой Паскаля .
Решение. Воспользуемся формулой (4.6). Чтобы найти пределы интегрирования и , необходимо построить чертеж кривой в полярных координатах. Результаты вычислений занесем в таблицу 1.
Таблица 1
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
| 0 |
|
|
| 1 |
3 |
|
| 2,5 | 2 | 1,5 |
|
| 1 |
Так как функция 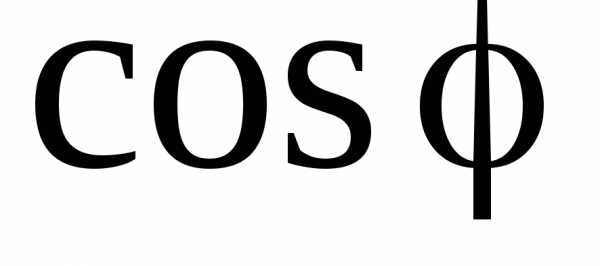
четная, то график функции
строим симметрично относительно
горизонтальной оси для значений углов
из промежутка.
Для построения графика функции припроводим полярную осьr;
на лучах, составляющих с осью r
углы, значение которых указано в таблице
1, откладываем соответствующее расстояние,
затем точки последовательно соединяем.
Получаем замкнутую кривую, называемую
улиткой Паскаля (рис.4.8).
четная, то график функции
строим симметрично относительно
горизонтальной оси для значений углов
из промежутка.
Для построения графика функции припроводим полярную осьr;
на лучах, составляющих с осью r
углы, значение которых указано в таблице
1, откладываем соответствующее расстояние,
затем точки последовательно соединяем.
Получаем замкнутую кривую, называемую
улиткой Паскаля (рис.4.8).
Площадь искомой фигуры равна
4.4. Вычисление длины дуги плоской кривой
Пусть функция f(x)
непрерывно дифференцируема на [a,b],
тогда длина дуги кривой 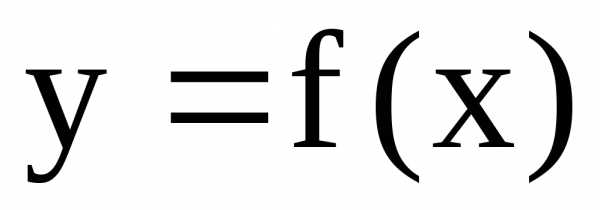 на указанном промежутке вычисляется
по формуле:
на указанном промежутке вычисляется
по формуле:
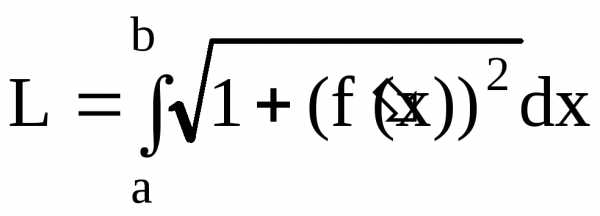 .
(4.7)
.
(4.7)
Если кривая гладкая
и задана параметрически, то длина дуги
этой кривой при 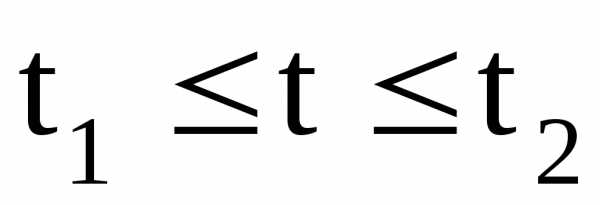 вычисляется по формуле:
вычисляется по формуле:
. (4.8)
Если гладкая кривая
задана в полярных координатах 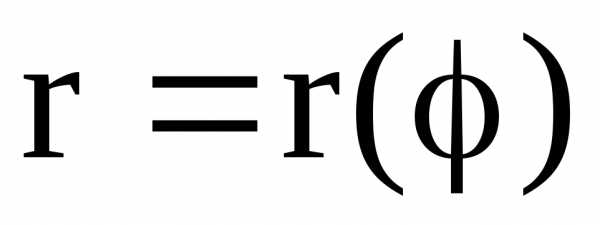 и,
то длина ее дуги равна
и,
то длина ее дуги равна
. (4.9)
Пример 47. Вычислить длину дуги развертки окружности
.
Решение. В нашем случае кривая задана параметрически.
Воспользуемся формулой (4.8), предварительно
находим производные 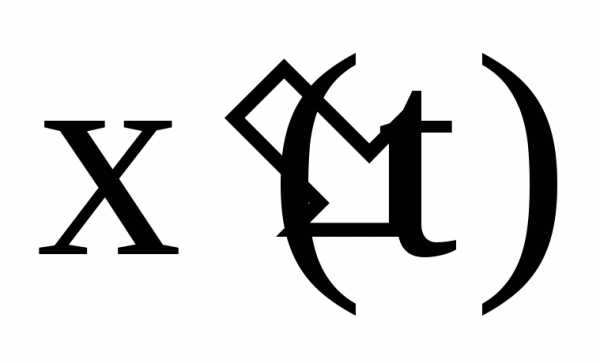 и
и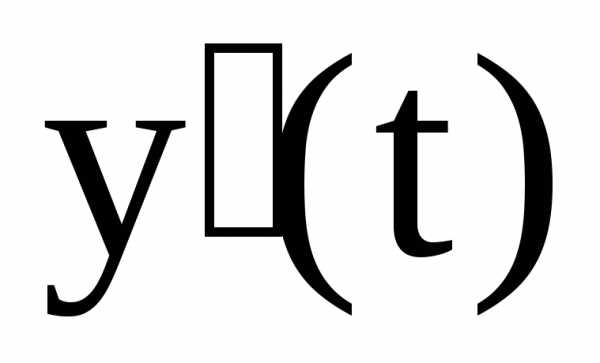 .
.

(ед.длины).
Пример 48. Найти длину дуги кривой 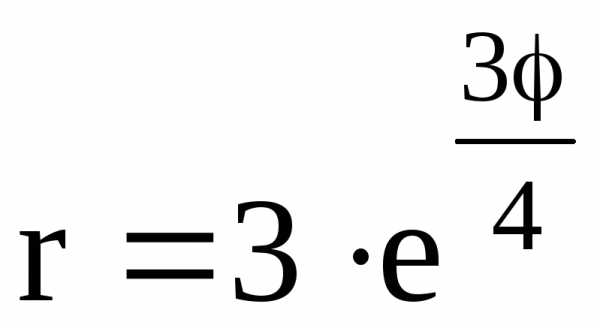 ,
,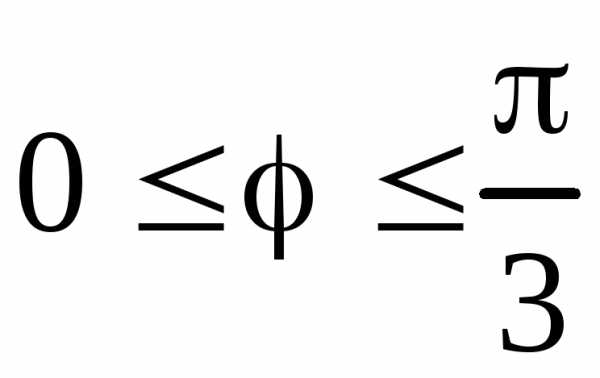 .
.
Решение. Кривая 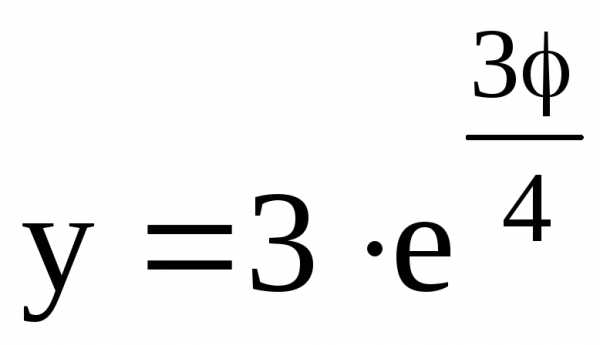 задана в полярных координатах.
Воспользуемся формулой (4.9). Находим
задана в полярных координатах.
Воспользуемся формулой (4.9). Находим
.
(ед.длины).
4.5. Вычисление объема тел вращения
Предположим, что
площадь сечения тела плоскостью,
перпендикулярной оси ОХ, может быть
выражена функцией от х: 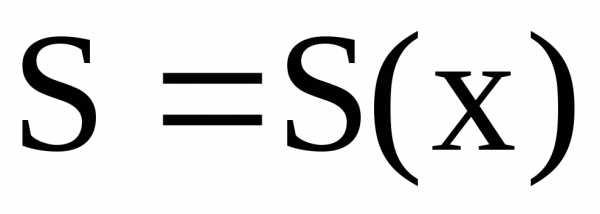 при,
тогда объем тела, заключенный между
перпендикулярными оси ОХ плоскостями
при,
тогда объем тела, заключенный между
перпендикулярными оси ОХ плоскостями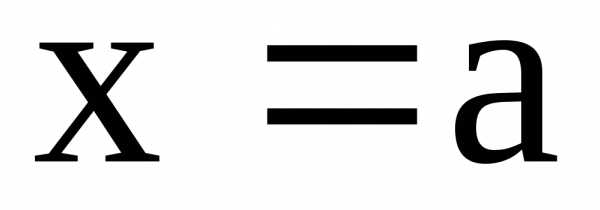 и
и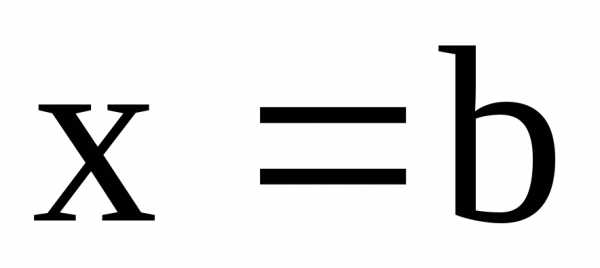 ,
находится по формуле
,
находится по формуле
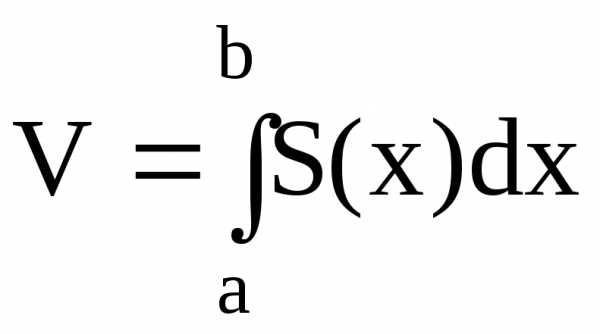 .
(4.10)
.
(4.10)
Если криволинейную трапецию (рис.4.10) вращать вокруг оси ОХ, то объем тела вращения будет равен
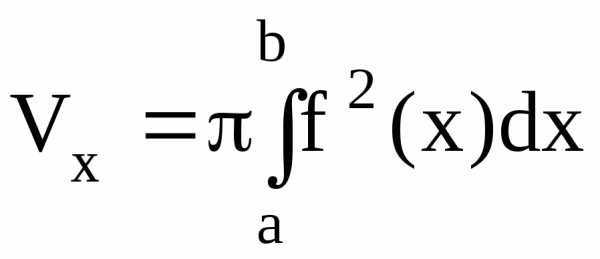 .
(4.11)
.
(4.11)
Если плоская
область, ограниченная кривыми 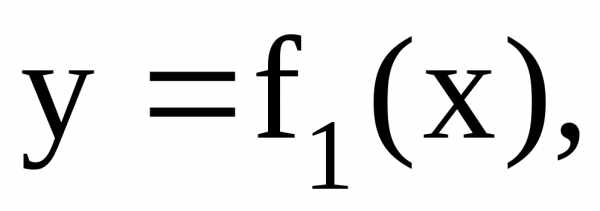
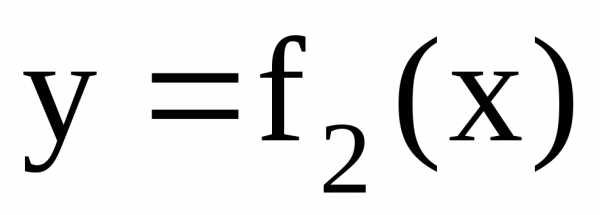 и прямыми
и прямыми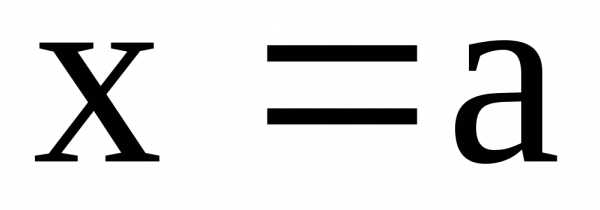 и
и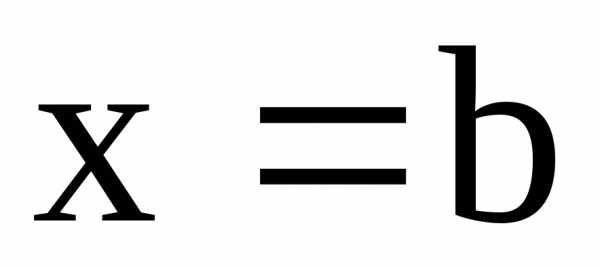 ,
вращается вокруг оси ОХ, то
,
вращается вокруг оси ОХ, то
(4.12)
Аналогично можно записать формулы для вычисления объемов тел вращения вокруг оси ОY:
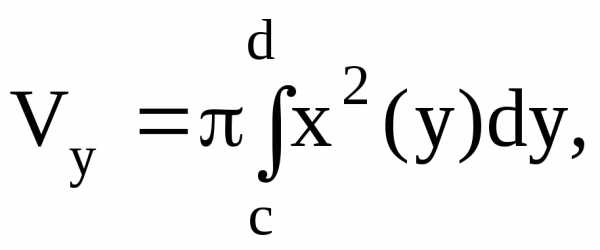 (4.13)
(4.13)
 (4.14)
(4.14)
Если кривые, ограничивающие плоскую область заданы в параметрическом виде, то к формулам (4.10 — 4.14) следует применить соответствующие замены переменной.
Если криволинейный сектор вращать вокруг полярной оси (см.рис.5.7), то
. (4.15)
Пример 49. Вычислить объем тела, полученного при
вращении дуги кривой 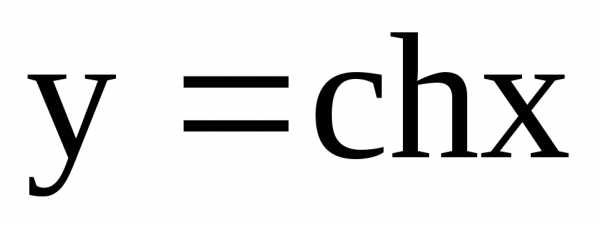 ,вокруг оси ОХ.
,вокруг оси ОХ.
Решение. Данная кривая  называется цепной линией. График ее
изображен на рис.4.9. Объем тела вращения
(рис.4.10) вычислим по формуле (4.11)
называется цепной линией. График ее
изображен на рис.4.9. Объем тела вращения
(рис.4.10) вычислим по формуле (4.11)
.
Пример 50. Найти объем параболоида вращения, радиус основания которого равен R, а высота Н.
Решение. Искомый параболоид вращения с указанными
параметрами получится, если будем
вращать вокруг оси ОY
параболу 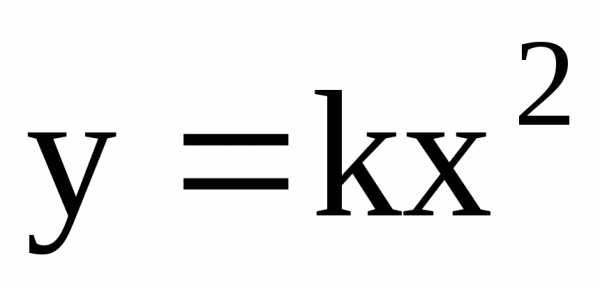 ,(рис.4.11; 4.12), где параметрk
легко вычислить исходя из данного
условия.
,(рис.4.11; 4.12), где параметрk
легко вычислить исходя из данного
условия.
Если 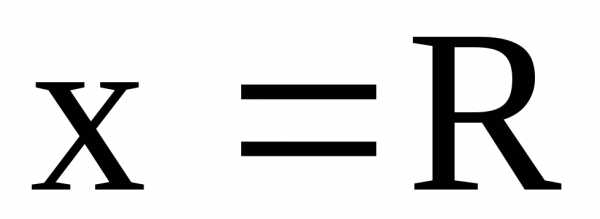 ,
то
,
то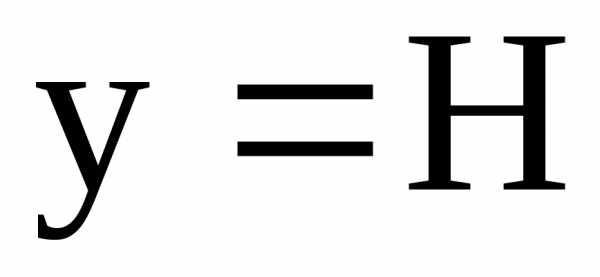 ,
поэтому
,
поэтому
.
Далее воспользуемся формулой (4.13)
 .
.
Если 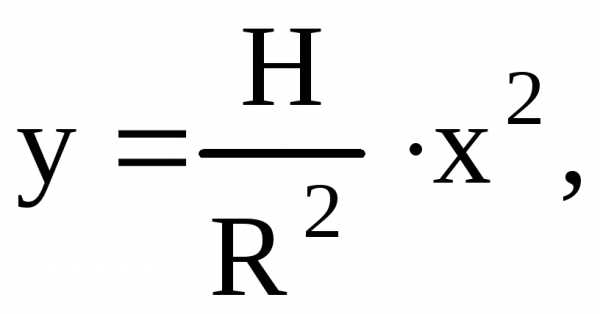 то
то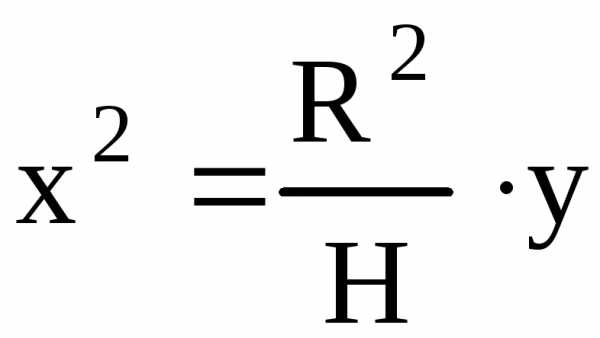
(ед3).
Пример 51. Найти объем тела вращения кривой ,вокруг оси ОХ.
Решение. Данная кривая задана в параметрическом виде
это эллипс (рис.4.13). Искомой фигурой вращения
является эллипсоид.
Найдем 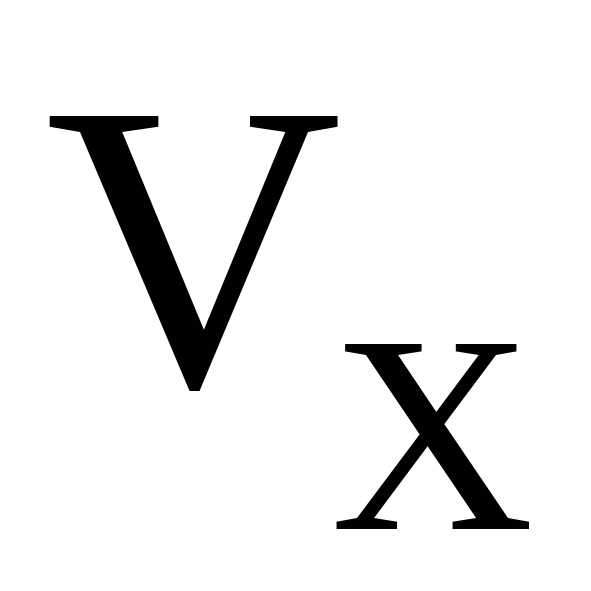 по формуле (4.11)
по формуле (4.11)
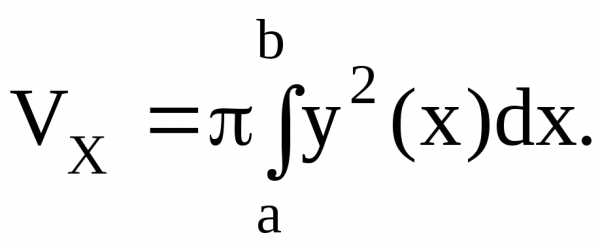
Если 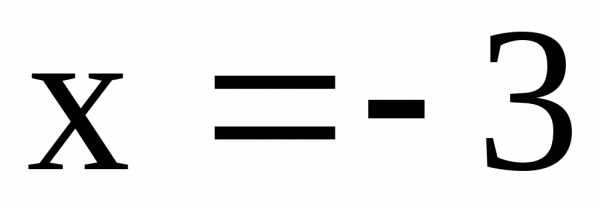 ,
то,
,
то,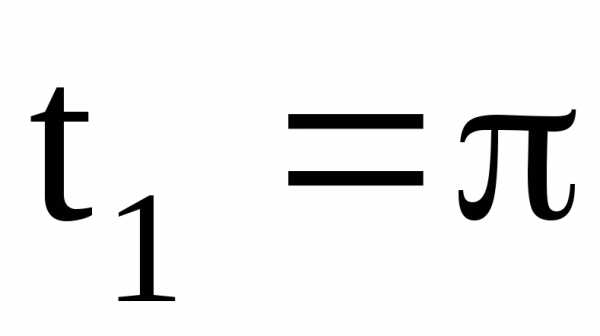 .
.
Если 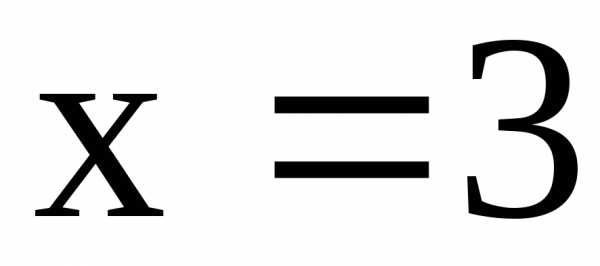 ,
то,
,
то,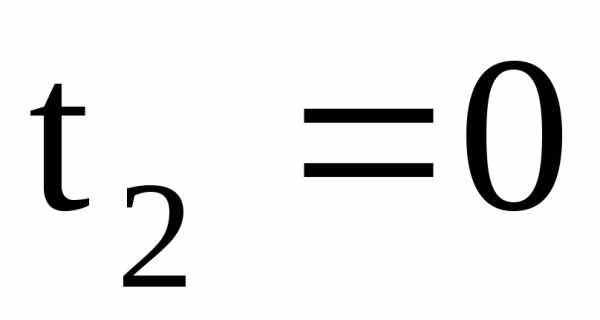 .
.
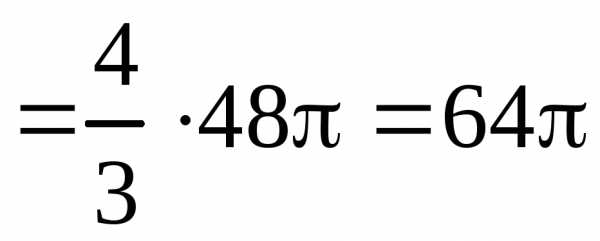 (куб.ед.).
(куб.ед.).
studfiles.net
как найти площадь фигуры ограниченной линиями заданными параметрически — 11 Августа 2013 — Примеры решений задач
Если кривая задана параметрическими уравнениями
то площадь криволинейной трапеции, ограниченной этой кривой, прямыми x=a, x=b и отрезком [a,b]оси Ox, выражается формулой
Пример. Найти площадь фигуры ограниченной одной аркой циклоиды
x=3(t-sint), y=3(1-cost), 0≤t≤2π и осью Ox.
Решение.
Шаг 1. Выполним построение графика функции заданной параметрически с помощью калькулятора
Вводим функцию и границы параметра, как указано в примере, нажимаем «Ok», получаем построение графика.
Шаг 2. Находим производную x'(t)
x'(t)=(3(t-sint))’=3(1-cost)
Выполнить дифференцирование можно с помощью калькулятора
Шаг 3. По формуле
, подставляем значения, имеем
Ответ: S=27π
Проверить вычисление площади фигуры ограниченной параметрически заданной кривой можно с помощью калькулятора
Замечание: в калькулятор вводим не саму функцию x(t) , а ее производную!
www.reshim.su
4.I. Вычисление площадей | Решение задач по математике и другим предмет
Внимательно изучите по учебнику Г. М. Фихтенгольца главу XII, п° 193—196. Разберите примеры, приведенные в п° 196. При решении задач с геометрическим содержанием всегда старайтесь сопроводить решение чертежом.
I. Уравнения кривых заданы в декартовой системе координат.
443. Вычислить площадь фигуры, ограниченной дугой параболы, прямыми X=I9 х — А и отрезком
оси абсцисс.
Решение. В теоретическом курсе показано, что площадь криволинейной трапеции численно равна определенному интегралу
В данном случае (рис. 5) криволинейная трапеция ABDC9 площадь которой мы вычисляем, ограничена параллельными прямыми AB и CD, отрезком прямой AC и отрезком кривой линии BD.
Искомая площадь равна:
444. Вычислить площадь трапеции, ограниченной дугой параболы и отрезком прямой х = 2.
Решение. Из рисунка 6 видно, что искомая площадь расположена симметрично относительно оси абсцисс и, следовательно,
445. Вычислить площадь фигуры, ограниченной кривыми;
Решение. На рисунке 7 изображена фигура, площадь которой мы должны вычислить. Как видно из рисунка, площадь фигуры OBMAO можно представить как разность двух площадей (пл. OBMPO и OAMPU1 где MP — перпендикуляр, опущенный из точки M на ось Ох).
Найдем координаты точки Al. Решая систему уравнений
получимСледов ат ельн о,
Легко видеть, что данную задачу можно решить и другим путем. Искомую площадь можно представить в виде разности двух площадей—пл. OAMNO и пл. OBMNO (MN — перпендикуляр, опущенный из точки M на ось Oy):
Тогда
Ясно, что значение площади OBMAO не зависит от способа ее вычисления.
446. Вычислить площадь фигуры, ограниченной петлей кривой:
Решение. Из уравнений кривой видно, что она расположена симметрично относительно оси Ох. Следовательно, можно легко вычислить половину искомой площади (см. рис. 8).
Рекомендуем провести самостоятельно подробное исследование кривой.
Записав уравнение кривой в виде легко найдем точки пересечения кривой с осью Ох, положив у = 0. Мы получим.Учитывая все сказанное, окончательно найдем:
447. Вычислить площадь фигуры, ограниченной синусоидой wИ осью Ох, если
Вся площадь петли равна:
Решение. Из рисунка 9 видно, что искомая площадь на сегментеРасположена над осью Ох, а на сегменте
Под осью Ох. Следовательно, достаточно вычислить площадь, ограниченную полуволной синусоиды на отрезке|, и удвоить полученный результат:
448. Найти всю площадь фигуры, ограниченной кривыми, прямыми X = 3, X = —2 и осью Ох.
Решение. Из рисунка 10 видно, что искомая площадь может быть представлена как сумма площадей:
где BA и MN—перпендикуляры, опущенные из точек В и Al на ось Ох.
Определим координаты точек В, С, М, Р. Для этого решим следующие системы уравнений:
Решая систему (I) уравнений, найдем координаты точек В и M : В (I, 2), M {— I, 2).
Решая систему (2) уравнений, найдем координаты точки С : С (3, К».
Решая систему (3) уравнений, найдем координаты точки P : Р(— 2, 5).
Найдем теперь значения промежуточных площадей:
Отсюда
449. Найти площадь фигуры, ограниченной линиями:
450. Найти площадь фигуры, ограниченной линиями:
451. Найти площадь фигуры, ограниченной параболами:
452. Найти площадь фигуры, ограниченной линиями:
453. Найти площадь фигуры, ограниченной линиями:
454. Найти площадь «Ьигуоы. огоаниченной линиями:
455. Найти площадь круга:
456. Найти площадь эллипса
457. Найти площадь, заключенную между кривыми
458. Найти площадь фигуры, ограниченной гипоци-лоидой
459. Найти площадь фигуры, ограниченной гиперболой
И прямой
460. Вычислить площадь фигуры, заключенной между параболой, осями координат и прямой х=3,5.
461. Найти площадь фигуры, заключенной между кривыми:
462. Найти площадь частей эллипса отсеченных гиперболой
463. Найти площадь фигуры, ограниченной кривой
464. Найти площадь фигуры, заключенной между кривыми
2. Кривые заданы параметрическими уравнениями. Если кривая, ограничивающая площадь плоской фигуры, задана параметрическими уравнениями:
где функцииНепрерывны вместе со своими про
изводными наТо для вычисления площади
плоской фигуры следует в определенном интеграле произвести замену переменной:
465. Вычислить площадь, ограниченную эллипсом!
Решение. Эллипс расположен симметрично относительно обеих осей (рис. Последовательно, можно вычислить сначала• часть площади данной фигуры. Вычислим площадь той части плоской фигуры, которая расположена в первом квадранте:
Найдем пределы интегрирования для переменной t из условий:
Имеем:
466. Найти площадь фигуры, ограниченной астроидой:
PsP ш е н и е. Искомая площадь изображена на рисунке 12. Вычислим сначала площадь тсй части плоской фигуры, которая расположена в первом квадранте, это будет
Рис. 12.
часть всей искомой площади. Найдем пределы интегрирования для переменной / из условий:
Следовательно,
467. Вычислить площадь, ограниченную одной аркой циклоиды:И осью Ох.
Решение. Из рисунка 13 видно, что при изменении параметра t от 0 до 2л точка (ху у) обегает всю арку циклоиды, причем х изменяется в промежутках от 0 до 2т. Следовательно,
Вся площадь, ограниченная астроидой, равна:
о
468. Вычислить площадь четверти круга: x = 2cos t, y = 2sint.
469. Найти площадь, ограниченную эволютой эллипса:
(.Эволютой кривой называется геометрическое место её центров кривизны. Эволютой эллипса является деформированная астроида.)
470. Найти площадь, ограниченную кардиоидой:
х = a(2cost — cos 21), у = a (2sin/— sin 2/).
3. Кривые заданы в полярной системе координат. Из
теоретического курса известно, что площадь S1 ограниченная неподвижным полярным радиусом г0, подвижным полярным радиусом г и кривой г — /(ф), может быть вычислена по следующей формуле:
<Р> Ч, г
S = — j J/-2 Лр = J — j /(<р)]2<*Ф.
90
471. Вычислить площадь, ограниченную первым витком спирали Архимеда г — а<р (рис. 14).
Решение. Найдем пределы интегрирования. Первый виток спирали образуется при изменении параметра t от О до 2зх. Следовательно,
,12*
D3 Д
472. Найти площадь, ограниченную одним лепестком кривой г = a sin 2<р.
Решение. Пределы интегрирования для <р найдем из условий:
О < 2<р<я.
Отсюда
и, следовательно,
473. Вычислить площадь, ограниченную кривой г = = a cos ф.
Решение. Данная кривая—окружность радиуса у,
проходящая через полюс, расположенная симметрично относительно полярной оси. Эго легко увидеть, если перейти к декартовым координатам. (Проделайте это самостоя-
а2 I
тельно.) Тогда S = я — — = —я;а2.
7 4 4
Можно было найти искомую площадь, используя полярное уравнение данной кривой. Пределы для q> найдут* ся из условия cos ф> 0, следовательно,
1C
T
S = J a® cos2 ф dq> =
TC TC
—< ф < —.
2 Y 2
Таким образом, имеем:
474. Вычислить площадь OAB (см. рис. 15), ограниченную полярными радиусамиг, = OA и r2 = OB и дугой логарифмической спирали
Решение. Будем считать, что полярному радиусу г, соответствует полярный угол фг, а полярному радиусу г2 соответствует полярный угол ф2. Тогда
475. Найти площадь петли листа Декарта:
Решение. Перейдем к полярным координатам с помощью известных соотношений:
Уравнение данной кривой в полярных координатах примет вид:
откуда
На получим
откуда
, в этом промежутке изменения полярного
углаф кривая опишет петлю. ПриИли
знаменатель стремится к нулю и, следовательно, р —» оо. Это значит, что существует асипмтота данной кривой. Найдем ее, пользуясь исходным уравнением кривой в лекап-товых координатах. Разделив обе части равенства
Из полученного уравнения кривой видно, чтоПри
HO
и, следовательно, таким образом,
Уравнение асимптоты:
Подставляя вместо k и b найденные значения, получим искомое уравнение асимптоты данной кривой:
Для построения данной кривой совместим полюс с началом декартовых координат и будем считать положительное направление оси Ox совпадающим с направлением полярной оси. Составим таблицу значений
Соединяя теперь плавной кривой полученные точки, получим петлю данной кривой (рис. 16).
Найдем площадь, ограниченную петлей листа Декарта. Из геометрических соображений видно, что полярный угол <р
изменяется от 0 до.Tаким образом, находим:
476. Вычислить площадь круга
477. Найти площадь, ограниченную петлей лемнискаты>
Построив предварительно данную кривую.
478. Найти площадь, ограниченную кривой:
P = a cos 4<р.
479. Найти площадь, ограниченную одним лепестком кривой:
P = a cos 2ф.
480. Найти площадь фигуры, ограниченной вторым витком спирали Архимеда р = аф и отрезком полярной оси, соединяющим концы первого и второго витков (см. рис. 14).
481. Найти площадь, ограниченную улиткой Паскаля:
P = 2а (2 cos ф).
482. Вычислить площадь, ограниченную кардиоидой:
P = а (I — cos ф).
| < Предыдущая | Следующая > |
|---|
matica.org.ua