Условная и абсолютная сходимость ряда
Числовой ряд
содержащий как положительные, так и отрицательные члены, называется знакопеременным. Такой ряд называется абсолютно сходящимся, если сходится ряд
составленный из модулей его членов, и условно (неабсолютно) сходящимся, если ряд (*) сходится, а ряд (**) расходится.
Из сходимости ряда (**) следует сходимость ряда (*), но из расходимости ряда (**) не следует расходимость ряда (*).
Ряд, у которого любые два соседних члена имеют разные знаки, называется знакочередующимся. Такой ряд записывают в виде:
или если первый член отрицателен
Признак Лейбница
Если члены ряда (***) таковы, что
и
то ряд сходится, причем его сумма
Остаток , удовлетворяющего условиям признака Лейбница, оценивается с помощью неравенства
Для сходимости знакочередующегося ряда не достаточно, чтобы его общий член стремился к нулю. Признак Лейбница утверждает лишь, что знакочередующийся ряд сходится, если абсолютная величина общего члена ряда стремится к нулю монотонно.
С другой стороны, для сходимости знакочередующегося ряда выполнение признака Лейбница не необходимо – знакочередующийся ряд может сходиться, если абсолютная величина его общего члена стремится к нулю не монотонно.
Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение или онлайн-помощь на зачете/экзамене 〉〉
Исследуем ряд на абсолютную сходимость.
Ряд, составленный из абсолютных величин членов знакочередующегося ряда:
Воспользуемся предельным признаком сходимости:
Гармоническим ряд
расходится
Предел конечный и отличный от нуля – ряды одновременно расходятся.
Исследуем ряд на условную сходимость:
Кроме того
По признаку Лейбница для знакочередующихся рядов ряд сходится
Ответ: сходится условно.
К оглавлению решебника по высшей математике 〉
100task.ru
Знакопеременные ряды, абсолютная и условная сходимость
Числовой ряд $\sum \limits _{n=1}^{\infty }u_{n} $, члены которого имеют произвольные знаки (+), (?), называется знакопеременным рядом.
Рассмотренные выше знакочередующиеся ряды являются частным случаем знакопеременного ряда; понятно, что не всякий знакопеременный ряд является знакочередующимся. Например, ряд $1-\frac{1}{2} -\frac{1}{3} +\frac{1}{4} +\frac{1}{5} -\frac{1}{6} -\frac{1}{7} +\ldots — $ знакопеременный, но не являющийся знакочередующимся рядом.
Отметим, что в знакопеременном ряде членов как со знаком (+), так и со знаком (-) бесконечно много. Если это не выполняется, например, ряд содержит конечное число отрицательных членов, то их можно отбросить и рассматривать ряд, составленный только из положительных членов, и наоборот.
Теорема 1 (достаточный признак сходимости знакопеременных рядов)
Знакопеременный ряд $\sum \limits _{n=1}^{\infty }u_{n} $ сходится, причём абсолютно, если сходится ряд, составленный из абсолютных величин его членов$\sum \limits _{n=1}^{\infty }\left|u_{n} \right| $.
Замечание
Теорема 1 даёт только достаточное условие сходимости знакопеременных рядов. Обратная теорема неверна, т.е. если знакопеременный ряд $\sum \limits _{n=1}^{\infty }u_{n} $ сходится, то не обязательно, что сходится ряд, составленный из модулей $\sum \limits _{n=1}^{\infty }\left|u_{n} \right| $ (он может быть как сходящимся, так и расходящимся). Например, ряд $1-\frac{1}{2} +\frac{1}{3} -\frac{1}{4} +…=\sum \limits _{n=1}^{\infty }\frac{(-1)^{n-1} }{n} $ сходится по признаку Лейбница, а ряд, составленный из абсолютных величин его членов, $\sum \limits _{n=1}^{\infty }\, \frac{1}{n} $ (гармонический ряд) расходится.
Свойство 4 (теорема Римана)
Если ряд условно сходится, то какое бы мы не взяли число А, можно переставить члены данного ряда так, чтобы его сумма оказалась в точности равной А; более того, можно так переставить члены условно сходящегося ряда, чтобы после этого он расходился.
Пример 1
Исследовать на условную и абсолютную сходимость ряд
\[\sum \limits _{n=1}^{\infty }\frac{(-1)^{n} \cdot 9^{n} }{n!} .\]Решение. Данный ряд является знакопеременным, общий член которого обозначим: $\frac{(-1)^{n} \cdot 9^{n} }{n!} =u_{n} $. Составим ряд из абсолютных величин $\sum \limits _{n=1}^{\infty }\left|u_{n} \right| =\sum \limits _{n=1}^{\infty }\frac{9^{n} }{n!} $ и применим к нему признак Даламбера. Составим предел $\mathop{\lim }\limits_{n\to \infty } \frac{a_{n+1} }{a_{n} } $, где $a_{n} =\frac{9^{n} }{n!} $, $a_{n+1} =\frac{9^{n+1} }{(n+1)!} $. Проведя преобразования, получаем $\mathop{\lim }\limits_{n\to \infty } \frac{a_{n+1} }{a_{n} } =\mathop{\lim }\limits_{n\to \infty } \frac{9^{n+1} \cdot n!}{(n+1)!\cdot 9^{n} } =\mathop{\lim }\limits_{n\to \infty } \frac{9^{n} \cdot 9\cdot n!}{n!\cdot (n+1)\cdot 9^{n} } =\mathop{\lim }\limits_{n\to \infty } \frac{9}{n+1} =0$. Таким образом, ряд $\sum \limits _{n=1}^{\infty }\left|u_{n} \right| =\sum \limits _{n=1}^{\infty }\frac{9^{n} }{n!} $ сходится, а значит, исходный знакопеременный ряд сходится абсолютно.Ответ: ряд $\sum \limits _{n=1}^{\infty }\frac{(-1)^{n} \cdot 9^{n} }{n!} $ абсолютно сходится.
spravochnick.ru
37. Знакопеременные ряды. Абсолютная и условная сходимость.
Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным.
Абсолютная и условная сходимость
Ряд называется абсолютно сходящимся, если ряд также сходится.
Если ряд сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.
Ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Пример 1
Исследовать на сходимость ряд .
Решение.
Применим достаточный признак Лейбница для знакочередующихся рядов. Получаем
поскольку . Следовательно, данный ряд сходится.
38. Знакочередующиеся ряды. Признак Лейбница.
Частным случаем знакопеременного ряда является знакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.
Признак Лейбница
Для знакочередующихся рядом действует достаточный признак сходимости Лейбница.
Пусть {an} является числовой последовательностью, такой, что
1. an+1 < an для всех n;
2.
Тогда знакочередующиеся ряды исходятся.
39. Функциональные ряды. Степенные ряды. Радиус сходимости. Интервал сходимости.
Понятие функционального ряда и степенного ряда
Обычный числовой ряд, вспоминаем, состоит из чисел:
Все члены ряда –это ЧИСЛА.
Функциональный же ряд состоит из ФУНКЦИЙ:
В общий член рядапомимо многочленов, факториалов и других подарков непременно входит буковка «икс». Выглядит это, например, так:
Как и числовой ряд, любой функциональный ряд можно расписать в развернутом виде:
Как видите, все члены функционального ряда это функции.
Наиболее популярной разновидностью функционального ряда является степенной ряд.
Определение:
Степенной ряд – это ряд, в общий член которого входят целые положительные степени независимой переменной.
Упрощенно степенной ряд во многих учебниках записывают так: , где– это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Простейший пример:
Посмотрим на это разложение и еще раз осмыслим определение: члены степенного ряда содержат «иксы» в целых положительных (натуральных) степенях.
Очень часто степенной ряд можно встретить в следующих «модификациях»: илигде а – константа. Например:
Строго говоря, упрощенные записи степенного ряда,илине совсем корректны. В показателе степени вместо одинокой буквы «эн» может располагаться более сложное выражение, например:
Или такой степенной ряд:
Лишь бы показатели степеней при «иксАх» были натуральными.
Сходимость степенного ряда
Интервал сходимости, радиус сходимости и область сходимости
Не нужно пугаться такого обилия терминов, они идут «рядом друг с другом» и не представляют особых сложностей для понимания. Лучше выберем какой-нибудь простой подопытный ряд и сразу начнём разбираться.
Прошу любить и жаловать степенной ряд Переменная может принимать любое действительное значение от «минус бесконечности» до «плюс бесконечности». Подставим в общий член ряда несколько произвольных значений «икс»:
Если х=1,то
Если х=-1,то
Если х=3,то
Если х=-0,2, то
Очевидно, что, подставляя в то или иное значение «икс», мы получаем различные числовые ряды. Некоторые числовые ряды будут сходиться, а некоторые расходиться. И наша задача найти множество значений «икс», при котором степенной рядбудет сходиться. Такое множество и называется областью сходимости ряда.
Для любого степенного ряда (временно отвлекаемся от конкретного примера) возможны три случая:
1) Степенной ряд сходится абсолютно на некотором интервале . Иными словами, если мы выбираем любое значение «икс» из интервалаи подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал и называется интервалом сходимости степенного ряда.Радиус сходимости, если совсем просто, это половина длины интервала сходимости:
Геометрически ситуация выглядит так:
В данном случае, интервал сходимости ряда: радиус сходимости ряда:
studfiles.net
Знакопеременные ряды. Абсолютная и условная сходимость
Знакочередующиеся ряды – частный случай знакопеременного ряда.
Теорема 1.
Если знакопеременный ряд (1)
таков, что ряд, составленный из абсолютных величин его членов
(2)
сходится, то и данный знакопеременный ряд также сходится.
Данная теорема позволяет судить о сходимости некоторых знакопеременных рядов. Исследование в данном случае сводится к исследованию ряда с положительными членами.
Данная теорема является достаточным признаком сходимости знакочередующегося ряда, но не необходимым: существуют такие знакопеременные ряды, которые сами сходятся, но ряды, составленные из абсолютных величин их членов, расходятся.
Определение:
Знакопеременный ряд (1)
называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов: (2)
Если же знакопеременный ряд (1) сходится, а ряд (2) расходится, то данный знакопеременный ряд (1) называется условно или неабсолютно сходящимся рядом.
Теорема 2:
Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.
Теорема 3:
Если ряд сходится условно, то какое бы мы ни задали число А, можно так переставить члены этого ряда, чтобы его сумма оказалась в точности равной А. Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный после перестановки, окажется расходящимся.
Пример:
Исследовать числовой ряд на абсолютную и условную сходимость.
Решение:
Исследуем данный числовой знакочередующийся ряд на абсолютную и условную сходимость, для чего составим ряд из абсолютных величин членов знакочередующегося ряда:
Исследуем полученный числовой ряд с положительными членами на сходимость, воспользовавшись предельным признаком сравнения. Сравним данный ряд с обобщенным гармоническим рядом . Так как , то ряд сходится.
Следовательно, оба ряда вместе сходятся.
Так как числовой ряд из абсолютных величин членов нашего знакочередующегося ряда сходится, то знакочередующийся числовой ряд сходится абсолютно.
Ответ: Ряд сходится абсолютно.
Пример.
Исследовать числовой ряд на абсолютную и условную сходимость.
Решение:
-знакочередующийся числовой ряд.
Воспользуемся признаком Лейбница:
, то есть члены ряда монотонно убывают по абсолютной величине.
Следовательно, знакочередующийся ряд сходится по признаку Лейбница.
Составим ряд из модулей членов нашего знакочередующегося ряда:
Исследуем полученный числовой ряд с положительными членами на сходимость, воспользовавшись предельным признаком сравнения. Сравним данный ряд с расходящимся гармоническим рядом .
Следовательно, оба ряда вместе расходятся.
Таким образом, сам знакочередующийся ряд сходится, а ряд из его модулей расходится. Следовательно, наш знакочередующийся числовой ряд сходится условно.
Ответ: Ряд сходится условно.
primer.by
§3. Знакопеременные числовые ряды. Абсолютная и условная сходимость. Признак Лейбница.
Перейдем к рассмотрению знакопеременных рядов.
Знакопеременнымназывается ряд, который содержит как положительные, так и отрицательные слагаемые. Опишем методы исследования таких рядов.
Важную информацию о поведении такого ряда можно получить, рассматривая ряд, членами которого являются абсолютные величины членов исходного ряда.
Определение.Рассмотрим ряд
,
где 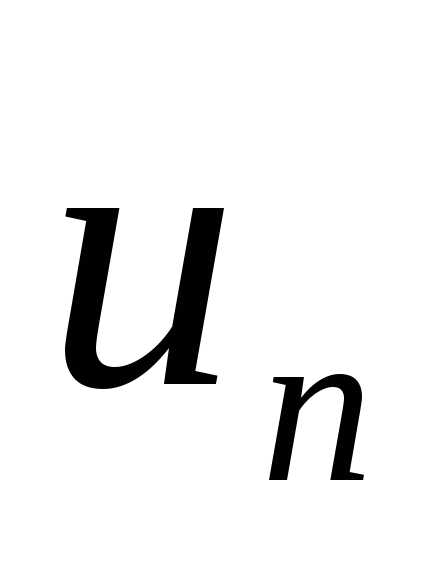 —
числа произвольного знака. Знакопеременный
ряд называетсяабсолютно сходящимся,
если сходится ряд, составленный из
модулей его членов.
—
числа произвольного знака. Знакопеременный
ряд называетсяабсолютно сходящимся,
если сходится ряд, составленный из
модулей его членов.
Теорема. Если ряд сходится абсолютно, то он сходится.
Другими словами, из сходимости ряда, составленного из модулей знакопеременного ряда, вытекает сходимость самого знакопеременного ряда.
Ряд, составленный из модулей членов знакопеременного ряда, является, очевидно, положительным и, следовательно, к нему применимы все рассмотренные выше признаки сходимости положительных рядов.
Задача №1. Исследовать на сходимость
ряд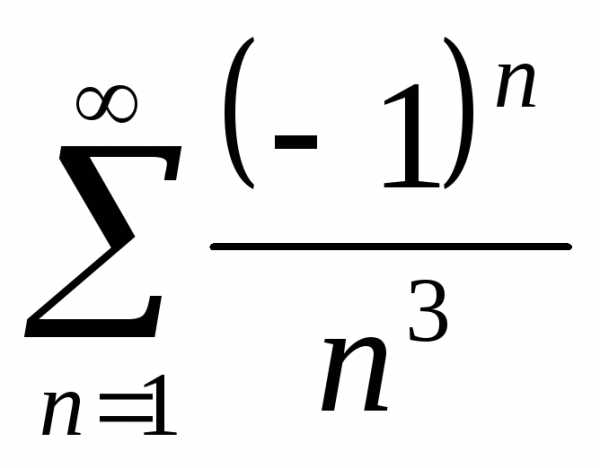 .
.
Решение.Исследуем ряд на абсолютную сходимость. Для этого запишем ряд
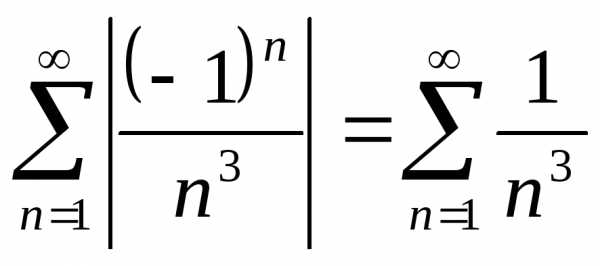 .
.
Получили положительный ряд, который
сходится, так как является обобщенным
гармоническим при 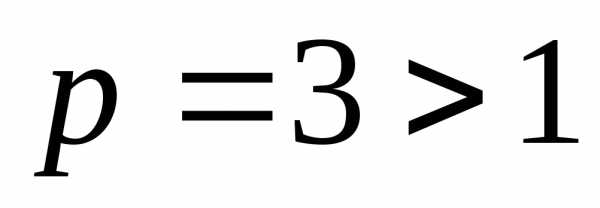 .
Делаем вывод, что исходный знакопеременный
ряд сходится абсолютно.
.
Делаем вывод, что исходный знакопеременный
ряд сходится абсолютно.
Ответ: ряд сходится абсолютно.
Задача №2.
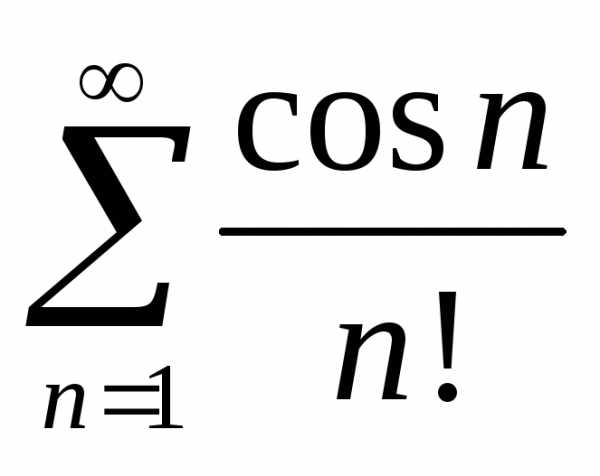 .
. Решение.Данный ряд является
знакопеременным, поскольку знак выражения меняется. Рассмотрим ряд, состоящий из
модулей исходного ряда:
меняется. Рассмотрим ряд, состоящий из
модулей исходного ряда:
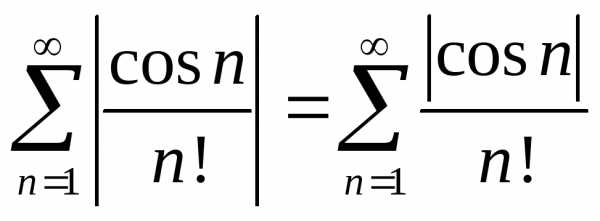 .
.
Получившийся положительный ряд можно
исследовать на сходимость с помощью
признака сравнения. Для любого
натурального 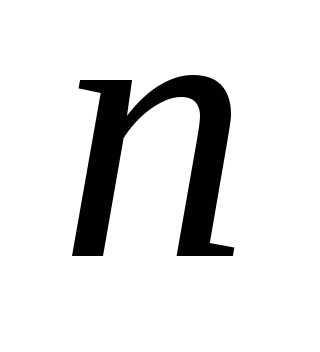 справедливо неравенство:
справедливо неравенство:
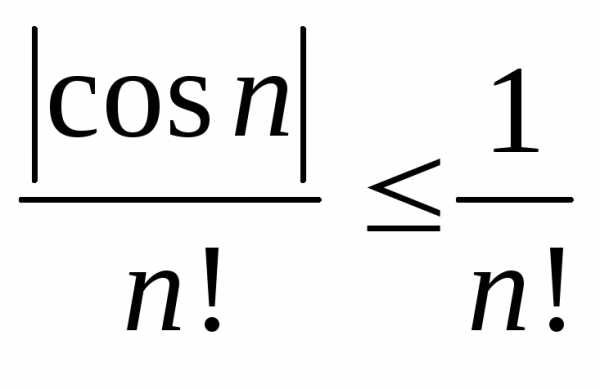 .
.
Ряд 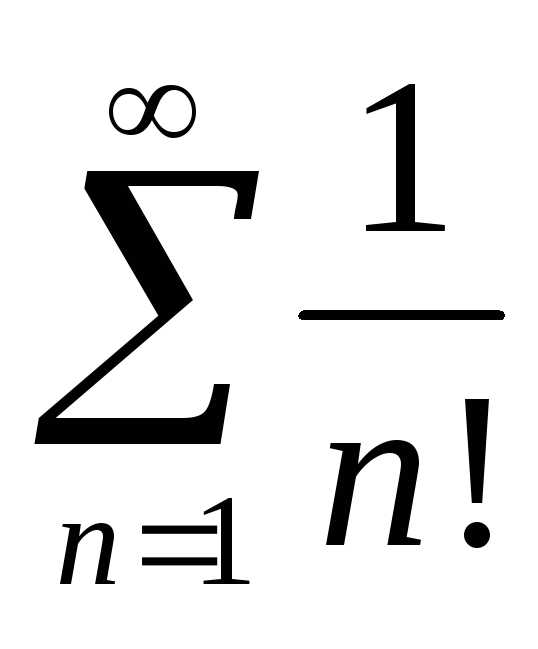 сходится, что можно показать по признаку
Даламбера,
сходится, что можно показать по признаку
Даламбера,
следовательно, по признаку сравнения
положительный ряд 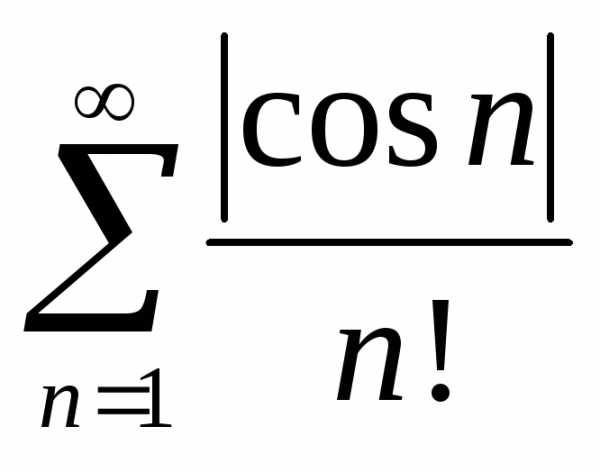 сходится, а исходный знакопеременный
ряд
сходится, а исходный знакопеременный
ряд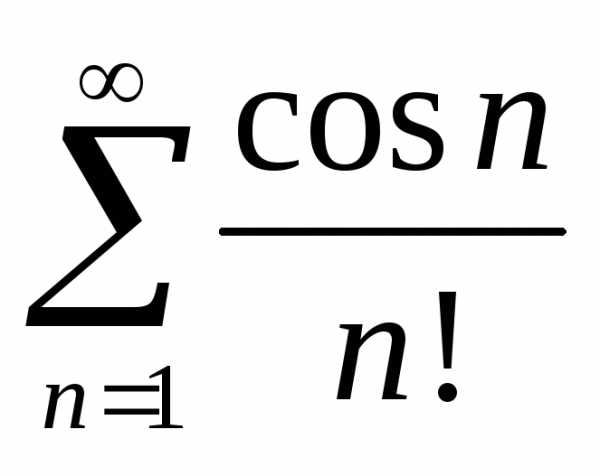 сходится абсолютно.
сходится абсолютно.
Ответ: ряд сходится абсолютно.
Заметим, что положительные ряды сходятся (имеют конечную сумму) за счет “быстрого” стремления к нулю общего члена ряда, для знакопеременных рядов существует еще одна возможность сходимости: сумма уменьшается за счет вычитания слагаемых. Поэтому для знакопеременных рядов может возникнуть ситуация, когда ряд, составленный из модулей, расходится, а сам знакопеременный ряд сходится. В этом случае говорят об условной сходимости.
Определение. Знакопеременный ряд называетсяусловно сходящимся, если он сходится, но не сходиться абсолютно.
Введем понятие знакочередующегося ряда:
Определение.Ряд
,
где 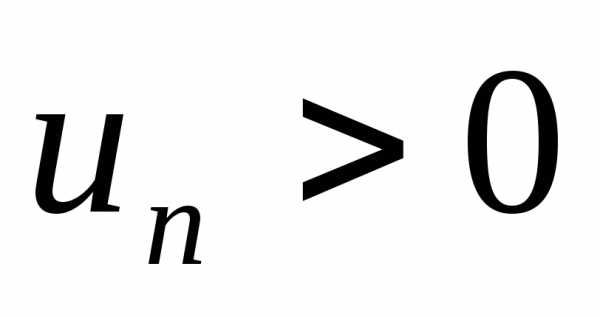 для всех
для всех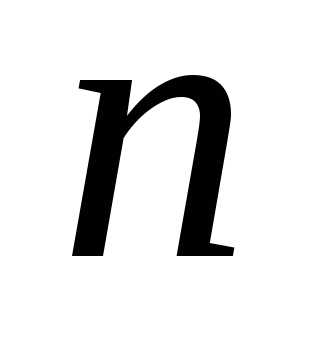
называется знакочередующимся.
Отметим, что в отличие от знакочередующихся рядов, в знакопеременных рядах знаки меняются произвольным образом. Следовательно, знакочередующиеся ряды являются частным случаем знакопеременных.
Для знакочередующихся рядов имеет место достаточный признак сходимости, принадлежащий Лейбницу.
Теорема (признак Лейбница сходимости знакочередующихся рядов).
Если для знакопеременного ряда
выполняются три условия:
1. Ряд является знакочередующимся.
2. Модули членов ряда монотонно убывают:
3. Модуль общего члена ряда стремиться к нулю, т.е.
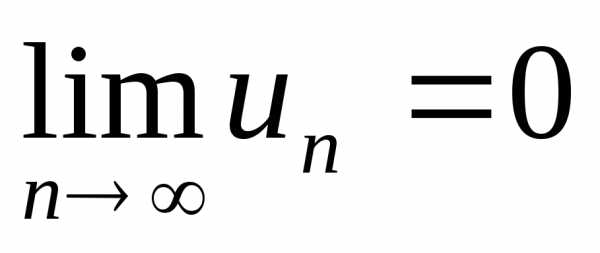 ,
,
то данный ряд сходится.
Подчеркнем, что все три условия признака Лейбница являются существенными и подлежат проверке.
Договоримся далее по тексту ряд, удовлетворяющий трем условиям признака Лейбница называть рядом Лейбница.
Сформулируем важное следствие теоремы Лейбница, используемое для приближенного вычисления суммы сходящегося ряда.
Можно показать, что для сходящегося ряда Лейбница верна оценка:
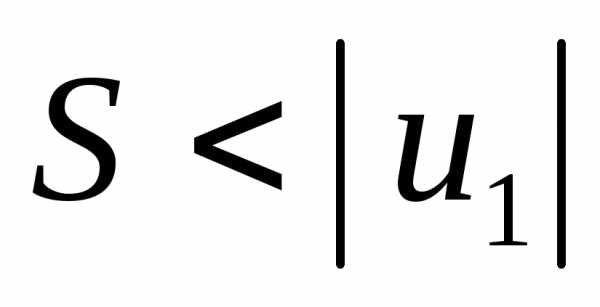 ,
тогда для остатка ряда имеем
,
тогда для остатка ряда имеем
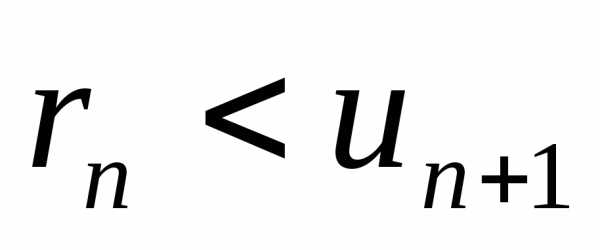 .
.
Задача №3.Исследовать на сходимость
ряд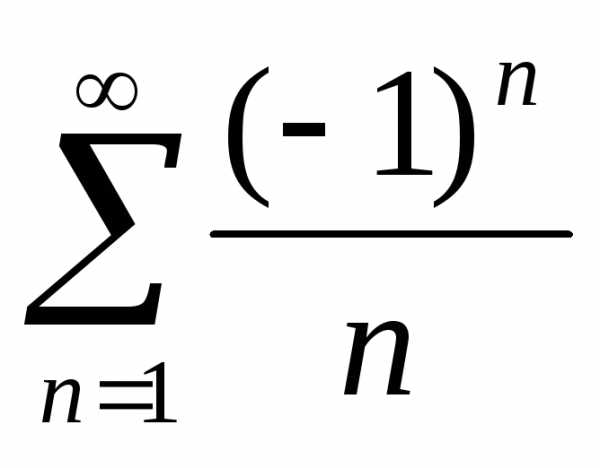 .
.
Решение.Покажем, что данный ряд является рядом Лейбница.
1. Действительно присутствует чередование знаков, т.к.
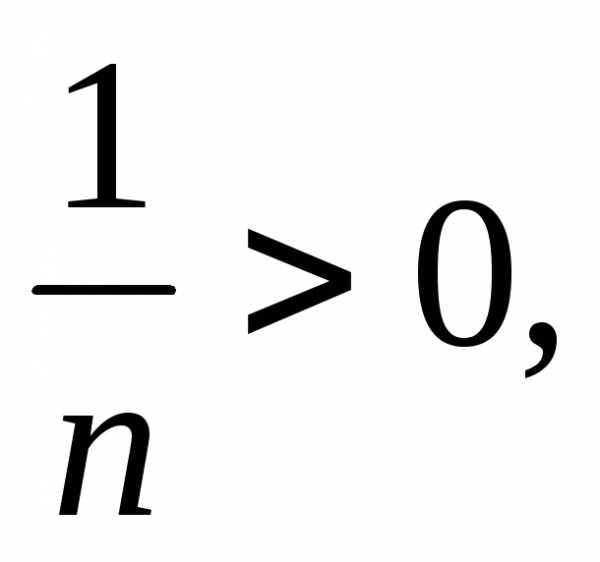 а
а
2. Имеем монотонное убывание модулей
членов ряда, поскольку для всех 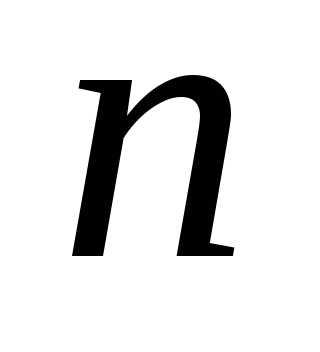 верно неравенство:
верно неравенство:
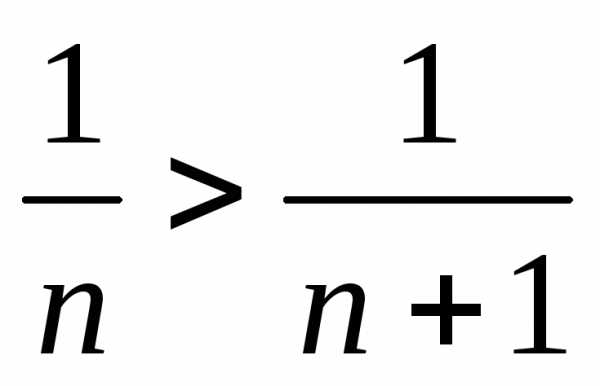 .
.
3. Третье условие также выполняется: 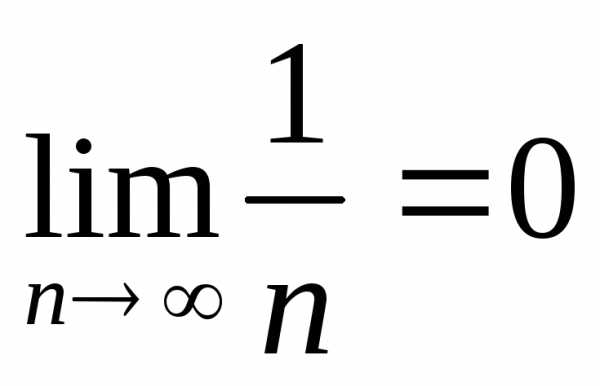 .
.
По признаку Лейбница делаем вывод о том, что ряд сходится.
Ответ: ряд сходится.
Задача №4. Исследовать на сходимость
ряд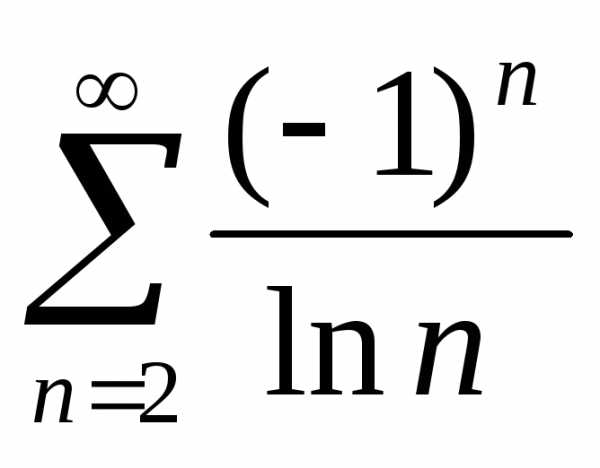 .
.
Решение.Проверим выполнение трех условий признака Лейбница.
1. За чередование знака отвечает множитель 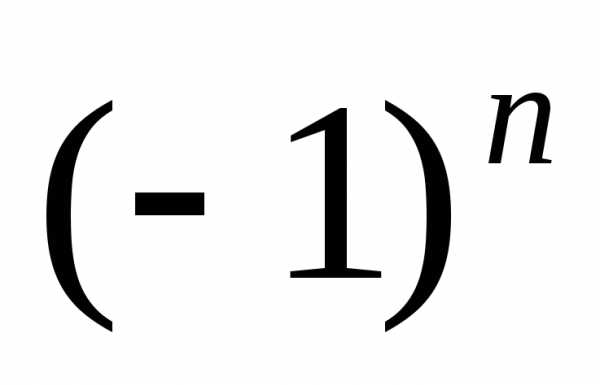 ,
знаменатель при этом остается больше
нуля:
,
знаменатель при этом остается больше
нуля:
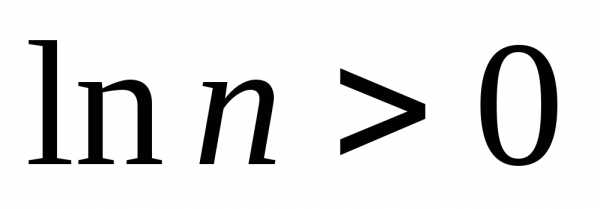 ,
для всех натуральных
,
для всех натуральных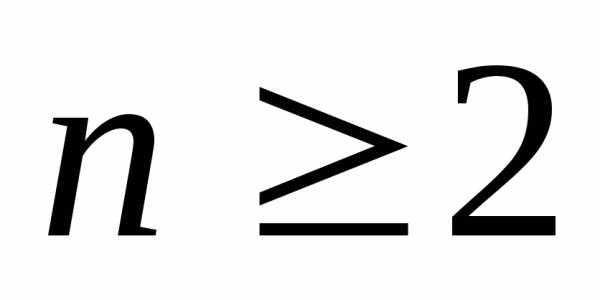 .
.
2. Из монотонного возрастания функции 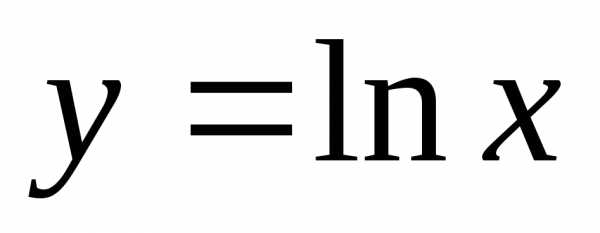 следует,
что для всех
следует,
что для всех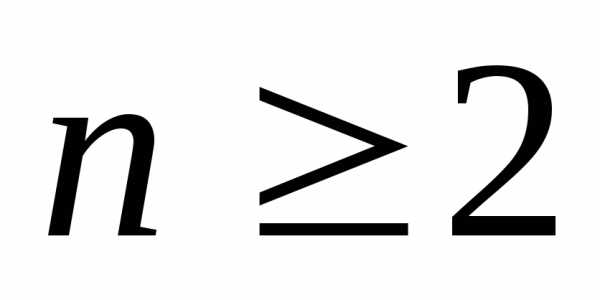 выполняется неравенство:
выполняется неравенство:
, отсюда
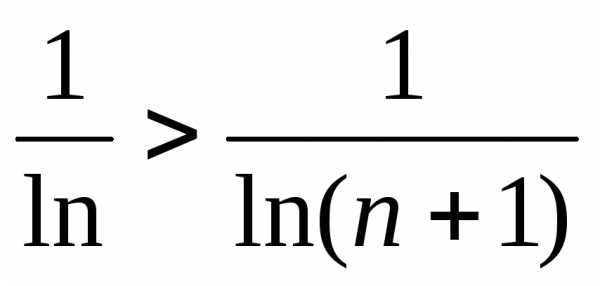 ,
т. е.
,
т. е.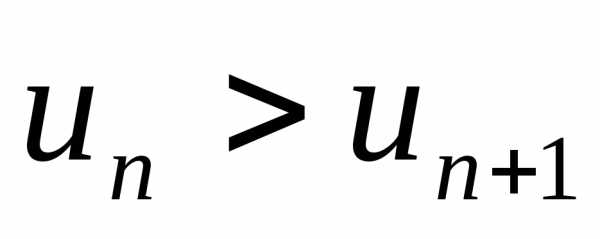 .
.
3. Справедливо и третье условие: 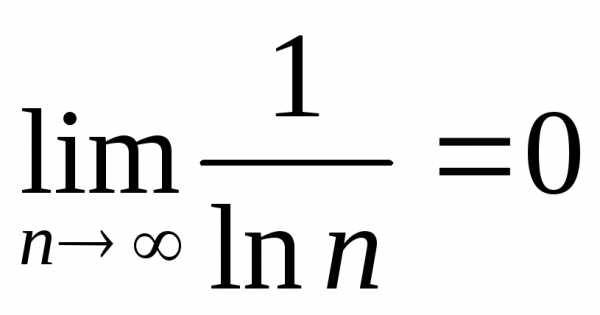 .
.
Ряд сходится условно по признаку Лейбница.
Ответ: ряд сходится.
Задача №5. Исследовать на сходимость
ряд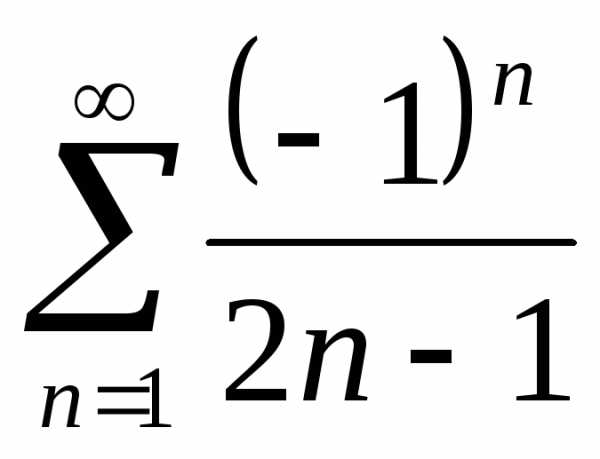 .
.
Решение.а). Исследуем ряд на абсолютную сходимость. Для этого рассмотрим ряд
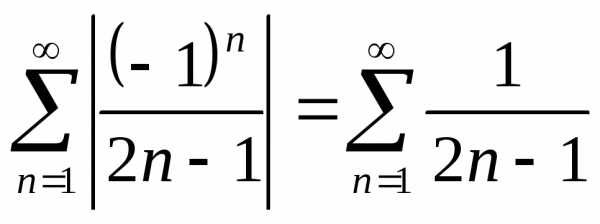 .
.
Полученный положительный ряд сравним
с гармоническим рядом 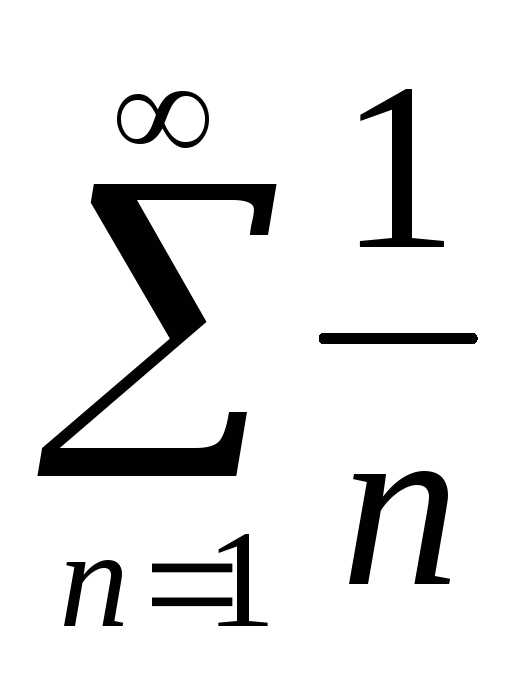 :
:
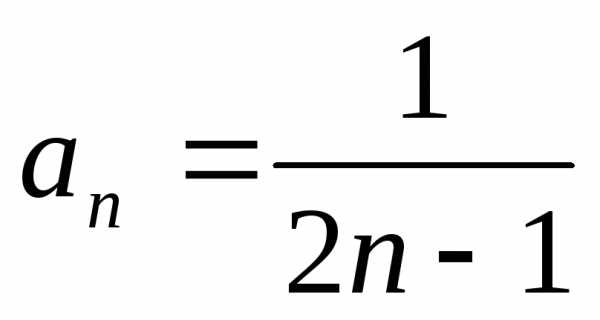 ,
,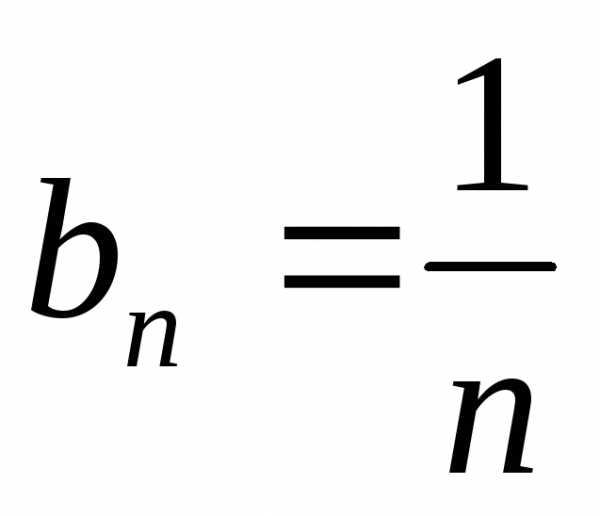 ,
,
тогда
Тогда по признаку сравнения ряд 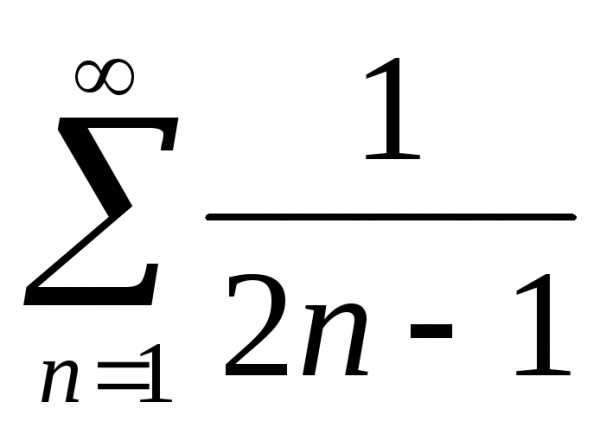 в смысле сходимости ведет себя также
как расходящийся гармонический ряд
в смысле сходимости ведет себя также
как расходящийся гармонический ряд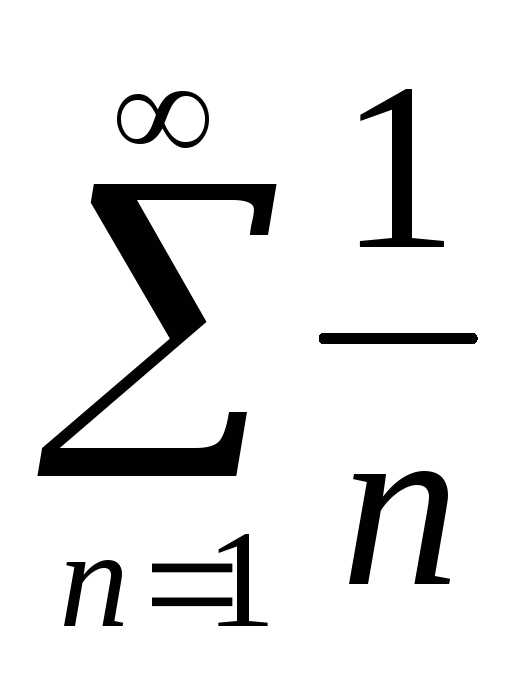 .
Ряд
.
Ряд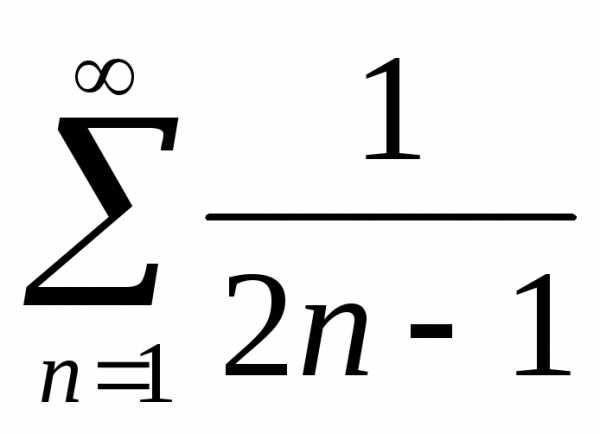 расходится, следовательно, исходный
ряд
расходится, следовательно, исходный
ряд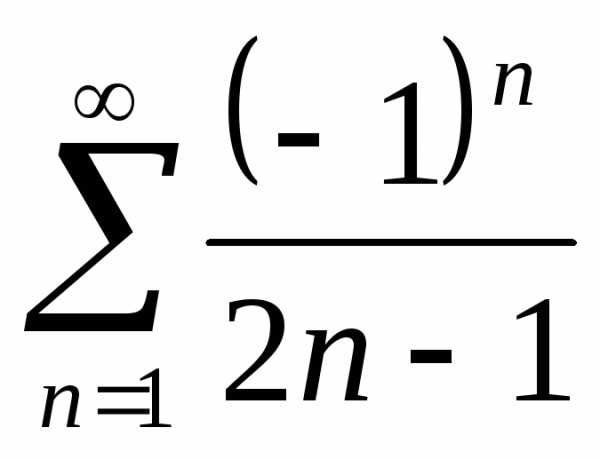 не
является абсолютно сходящимся.
не
является абсолютно сходящимся.
б). Исследуем ряд на условную сходимость. Воспользуемся признаком Лейбница.
1. Ряд 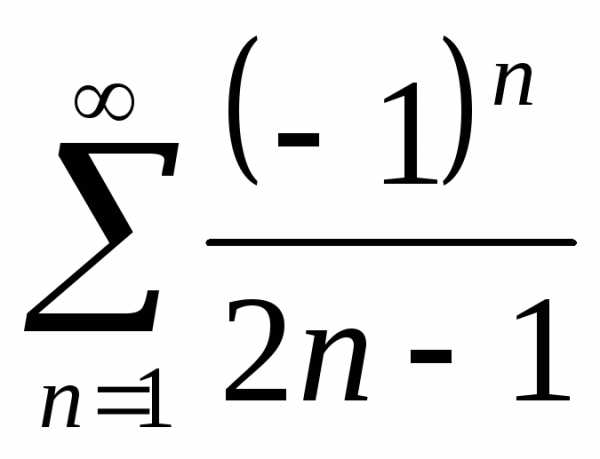 — знакочередующийся, т.к.для всех натуральных
— знакочередующийся, т.к.для всех натуральных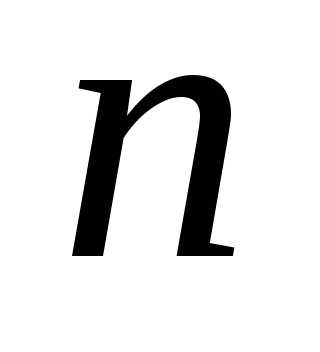 ,
а
,
а
.
2. , тогда
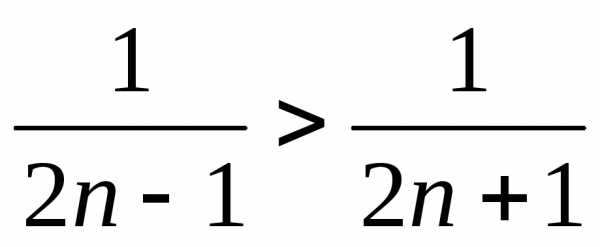 ,
,
что и означает монотонное убывание модулей членов ряда.
3. Верно, что 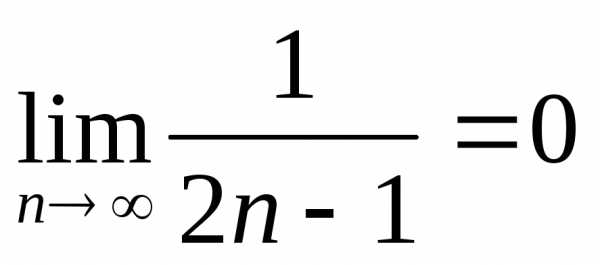 .
.
Ряд сходится по признаку Лейбница.
Ответ: ряд сходится.
studfiles.net
Исследование знакопеременных рядов на абсолютную сходимость.
Поиск ЛекцийПроще всего исследовать знакопеременный числовой ряд на абсолютную сходимость. В этом случае берем знакоположительный ряд , составленный из абсолютных величин членов исходного ряда, и применяем к нему подходящий достаточный признак сходимости из рассмотренных выше. Если ряд сходится, то исходный ряд является абсолютно сходящимся.
Пример.
Докажите, что знакопеременный числовой ряд абсолютно сходится.
Решение.
Соответствующих знакоположительный ряд будет иметь вид . Для него выполняется необходимое условие сходимости ряда, так как . Возьмем сходящийся знакоположительный ряд и воспользуемся вторым признаком сравнения: . Следовательно, ряд сходящийся, поэтому, исходный ряд сходится абсолютно.
К началу страницы
Расходимость знакопеременных рядов.
Если ряд расходится, то соответствующий знакопеременный ряд может, либо расходится, либо сходится условно.
Только признак Даламбера и радикальный признак Коши позволяют сделать вывод о расходимости знакопеременного ряда по расходимости ряда из модулей . Ряд также расходится, если не выполняется необходимое условие сходимости, то есть, если .
Пример.
Проверьте расходимость знакопеременного числового ряда .
Решение.
Модуль k-ого члена имеет вид . Исследуем ряд на сходимость по признаку Даламбера: . Следовательно, ряд расходится и можно утверждать, что исходный знакопеременный числовой ряд тоже расходится.
Пример.
Сходится ли знакочередующийся числовой ряд .
Решение.
Проверим выполнение необходимого условия сходимости числового ряда: .
Условие не выполняется, следовательно, ряд расходится. Предел был вычислен по правилу Лопиталя.
Осталось разобраться с условной сходимостью знакочередующихся рядов.
К началу страницы
Достаточные признаки условной сходимости числового ряда.
Признак Лейбница.
Если абсолютные величины членов знакочередующегося ряда монотонно убывают и предел модуля общего члена ряда равен нулю при , то ряд сходится.
Пример.
Определите характер сходимости знакочередующегося числового ряда .
Решение.
Ряд из абсолютных величин членов имеет вид . Для него выполняется необходимое условие сходимости . Возьмем гармонический ряд и воспользуемся вторым признаком сравнения:
Таким образом, ряд из модулей — расходящийся.
В свою очередь, знакочередующийся ряд сходится, так как выполняются условия признака Лейбница: последовательность монотонно убывает и .
Следовательно, исходный ряд условно сходящийся.
К началу страницы
Признак Абеля-Дирихле.
Числовой ряд сходится условно, если последовательность является невозрастающей и бесконечно малой, а последовательность частичных сумм числового ряда ограничена.
Пример.
Исследуйте числовой ряд на сходимость.
Решение.
Представим числовой ряд в виде
где — невозрастающая и бесконечно малая, а последовательность имеет ограниченную последовательность частичных сумм . Следовательно, условия признака Абеля-Дирихле выполнены и ряд условно сходится.
Признак Лейбница является частным случаем признака Абеля-Дирихле при или .
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Абсолютная и условная сходимость.
Признак Лейбница для знакочередующихся рядов.
Числовой ряд
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Числовой ряд называется знакочередующимся, если любые два стоящие рядом члена имеют противоположные знаки. Этот ряд является частным случаем знакопеременного ряда.
Признак сходимости Лейбница для знакочередующихся рядов. Если члены знакочередующегося ряда монотонно убывают по абсолютной величине и общий член un стремится к нулю при , то ряд сходится.
Этот признак служит достаточным признаком сходимости знакочередующихся рядов.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд
Составленный из абсолютных величин его членов, т.е. всякий абсолютно сходящийся ряд является сходящимся.
Если знакопеременный ряд сходится, а составленный из абсолютных величин его членов ряд расходится, то данный ряд называется условно (неабсолютно) сходящимся. Заметим, что из расходимости ряда в общем случае не следует расходимость ряда.
Для установления абсолютной сходимости знакопеременного (и знакочередующегося) ряда используются те же признаки, что и для сходимости ряда с положительными членами.
Для решения вопроса об абсолютной или условной сходимости знакочередующегося ряда необходимо рассмотреть ряд, составленный из абсолютных величин членов знакочередующегося ряда.
Если при исследовании этого ряда с помощью одного из признаков сходимости (признака Даламбера, признака сравнения рядов) ряд окажется сходящимся, то данный знакочередующийся ряд сходится абсолютно; если же ряд окажется расходящимся, то знакочередующийся ряд сходится условно.
Пример.Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:
Решение.
Члены данного ряда по абсолютной величине монотонно убывают: и . Следовательно, согласно признаку Лейбница, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.
Ряд составленный из абсолютных величин членов данного ряда, является гармоническим рядом, который, как известно, расходится. Поэтому данный ряд сходится условно.
Пример.Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:
Решение.
Используя признак Лейбница, получим
; , т.е. ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
Это геометрический ряд вида который сходится. Поэтому данный ряд сходится абсолютно.
Задание.Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:
Решение.
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ: данный ряд сходится условно.
Задание.Исследовать сходимость знакопеременного ряда:
Решение.
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ: данный знакопеременный ряд сходится абсолютно.
Вопросы для самоконтроля
- Что называется числовым рядом?
- Что называют частичными суммами ряда?
- Какой ряд называется геометрическим? гармоническим?
- В чем заключается необходимый признак сходимости ряда?
- Какие вы знаете достаточные признаки сходимости ряда с положительными членами?
- Какой ряд называется знакопеременным?
- В чем заключается признак сходимости Лейбница для знакочередующихся рядов?
Контрольное задание
1. Найдите первые четыре члена ряда по заданному общему члену:
u n =
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Найдите формулу общего члена ряда:
1 + + + …
_____________________________________________________________________________
3. Используя признак Даламбера, исследуйте сходимость ряда
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Исследуйте на абсолютную и условную сходимость ряд:
______________________________________________________________________________________________________________________________________________________________________________________________________
infopedia.su
