Алгебра формулы 9: Основные формулы по математике — Математика — Теория, тесты, формулы и задачи

‎App Store: Математика — геометрия алгебра

Описание

Подготовьтесь к урокам, ОГЭ и ГИА!

— Все темы школьного курса математики с 5 по 11 классы
— Все главные формулы с пояснением
— Поиск по темам
— Избранное
— Таблицы и постоянные

13 мар. 2022 г.

Версия 1.0.3

Привет! Немного улучшили интерфейс и обновили статьи!

Оценки и отзывы

Оценок: 108

Круто

Круто

Проверьте конспекты

Ошибка в разделе 9 класс §3 квадратный трёхчлен и его корни.

Квадратное уравнение имеет один корень, если дискриминант равен нулю. В вашем конспекте при дискриминанте меньше нуля.

Привет. Спасибо за отзыв. Действительно, там ошибка. Исправлю в ближайшем обновлении. Корректные шаги вычисления квадратного трёхчлена есть сейчас в разделе «Формулы». Воспользуйтесь алгоритмом оттуда, пожалуйста.

5*

Хорошее приложение, очень много формул, все подробно расписано, ясно и понятно. Есть конспекты по всем темам. Буду рекомендовать своим ученикам

Разработчик Danila Danilenko указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.

Данные, используе­мые для отслежи­вания информации

Следующие данные могут использоваться для отслеживания информации о пользователе в приложениях и на сайтах, принадлежащих другим компаниям:

• Геопозиция
• Идентифика­торы
• Данные об использова­нии
• Диагностика
• Другие данные

Связанные с пользова­телем данные

Может вестись сбор следующих данных, которые связаны с личностью пользователя:

• Геопозиция
• Идентифика­торы
• Данные об использова­нии
• Диагностика
• Другие данные

Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Подробнее

Информация

Провайдер

Danila Danilenko

Размер

42,7 МБ

Категория

Образование

Возраст

4+

Copyright

© night_coding

Цена

Бесплатно

• Поддержка приложения
• Политика конфиденциальности

Другие приложения этого разработчика

Вам может понравиться

Урок алгебры в 9-м классе по теме «Тригонометрические формулы и приемы их запоминания»

Цель урока: познакомить учащихся с мнемоническими правилами для запоминания формул приведения и значений тригонометрических функций некоторых углов; способствовать развитию логического мышления и устной математической речи при поиске решения поставленной проблемы;
воспитывать внимательность, наблюдательность и самостоятельность

Замечание: при проведении этого урока использовалась интерактивная доска и пульты дистанционного тестирования Activote, но провести его можно без этого оборудования, при помощи прилагаемой презентации.

Можно провести числовой анализ на каждом этапе тестирования – на начальном и итоговом, а можно сделать сравнительный анализ в конце урока, в качестве подведения итогов.

Ход урока

I. Организационный момент/

– Здравствуйте, ребята! Тригонометрия – один из интереснейших разделов математики, но почему-то большинство учащихся считают его самым трудным. Объяснить это, скорее всего можно тем, что в этом разделе формул больше, чем в любом другом – формулы приведения, формулы сложения, формулы двойного и половинного аргументов, формулы суммы и разности тригонометрических функций, формулы преобразования произведения тригонометрических функций в сумму. И самая первая группа формул, с которой вы познакомились в курсе геометрии 8 класса – основные тригонометрические тождества. Без знаний этих формул ни одно тригонометрическое выражение не преобразуешь. Сегодня на уроке, я хочу познакомить вас с некоторыми приемами запоминания тригонометрических формул.

Может, некоторые из них вам уже знакомы.

II. Входное (интерактивное) тестирование/

– Перед вами на парте лежат пульты дистанционного тестирования. Я предлагаю вам выполнить тест на знание тригонометрических формул и значений тригонометрических функций некоторых углов. Чтобы ответить на вопрос вам необходимо нажать на пульте кнопку с выбранным вами вариантом ответа.

III. Изучение нового материала (знакомство с приемами запоминания тригонометрических формул).

1. Табличные значения тригонометрических функций.

Вы уже знаете, что тригонометрическую функцию любого угла можно выразить через тригонометрическую функцию угла, не превышающего 90º. Поэтому необходимо знать табличные значения углов первой четверти.

Для запоминания значений синуса и косинуса для углов в 30º, 45º и 60º я предлагаю своим ученикам притчу.

– Пошли три дамы гулять.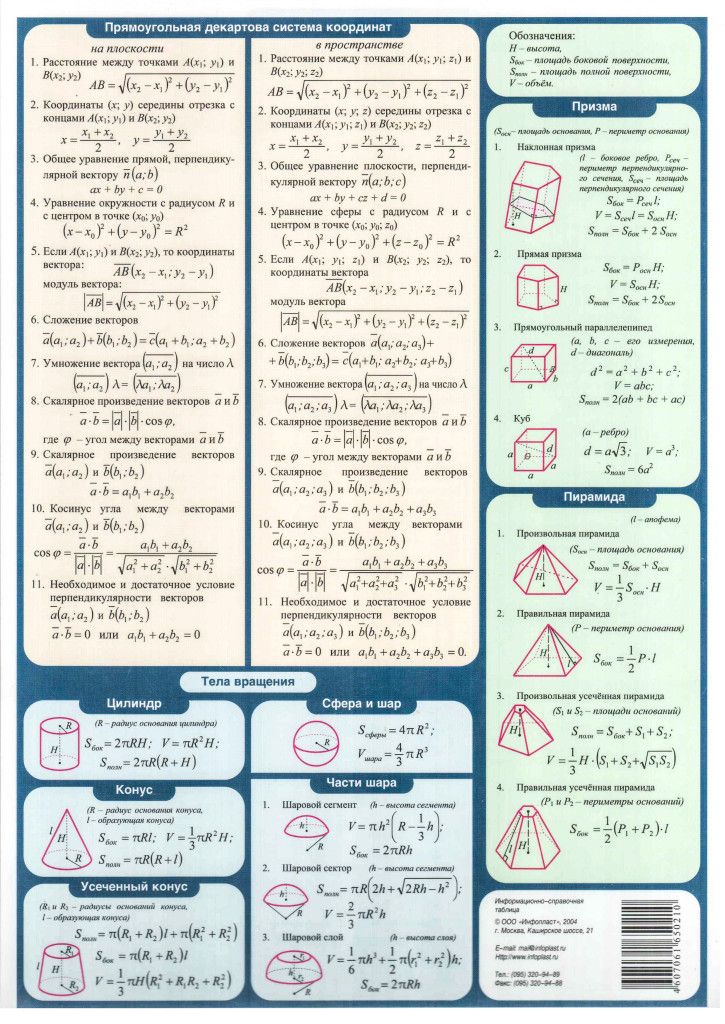 Первая дама, вторая дама и третья дама. И неожиданно пошел дождь. Все дамы открыли зонтики, и одели по паре калош. Прогулка была закончена, и дамы вернулись домой. Первая дама, вторая дама и третья дама пошли домой. (Сначала, в таблице, во второй строке по порядку указываются номера дам. За тем изображают корни – “зонтики”, и “надевают калоши” – в знаменателях пишут 2).

Чтобы указать значения тангенса и котангенса тех же углов достаточно вспомнить ОТТ, т.е ,

а котангенс взаимно обратная функция для тангенса.

2. Формулы приведения

Тригонометрические функции углов видамогут быть выражены через функции угла α с помощью формул, которые называют формулами приведения. Но запоминать эти формулы не обязательно. Для преобразования таких выражений достаточно знать знаки тригонометрических функций по четвертям и еще одну притчу.

– Жил забывчивый математик, и каждый раз преобразовывая тригонометрические функции углов вида , он спрашивал у своей лошади, жующей за окном сено, надо менять функцию на конфункцию или нет. А лошадь кивала головой по той оси, на которой располагался угол являющиеся границами первой и третьей четвертей соответственно, лежат на оси Оу, то лошадь кивком головы подтверждала смену функции на конфункцию. А для углов наоборот отрицала. Математику оставалось лишь записывать ответ, указывая знак данной функции.

3. Формулы сложения.

Формулы сложения – это та, группа формул которую нужно знать наизусть. Но для их запоминания можно тоже воспользоваться ассоциативным приемом. У косинуса функции одноименные, а у синуса разноименные. Не все в нашей жизни бывает “гладко” за белой полосой идет черная, и наоборот. Так и у наших функций, если функции идут одноименные, то знаки не совпадают, а если разноименные, то совпадают.

cos (α ­ β ) = cos α cos β + sin α sin β;
cos (α + β ) = cos α cos β – sin α sin β;
sin (α + β) = sin α cos β + cos α sin β;
sin (α – β) = sin α cos β – cos α sin β.

Для получения формулы тангенса суммы и тангенса разности достаточно применить ОТТ и разделить числитель и знаменатель полученной дроби на cos α cos β, где

cos α ≠ 0 и cos β ≠ 0.

Например, сos 97º cos 67º + sin 97º sin 67º = ños (97º– 67º) = ños 30º = ;

sin 25º

сos 20º + cos 25º sin 20º = sin (25º + 20º) = sin 45º = .

4. Формулы двойного угла

Чтобы получить тригонометрические формулы двойного аргумента достаточно в формулах сложения β заменить на α.

Например, cos 2α = cos (α + α ) = cos α cos α – sin α sin α = cos²α – sin²α;

sin 2α = sin (α + α ) = sin α cos α + sin α cos α = 2sin α cos α

tg2α = tg (α + α ) = .

Поэтому, 2 sin 65º cos 65º = sin (2∙ 65º) = sin130º = sin (180º – 50º) = sin 50º

Формулы суммы и разности тригонометрических функций

Если сложить косинус разности с косинусом суммы двух углов,то мы получим формулу суммы косинусов:

cos (α – β ) = cos α cos β + sin α sin β;
cos (α + β ) = cos α cos β – sin α sin β;
cos (α – β ) + cos (α + β ) = 2 cos α cos β (*)

Обозначим α – β ηа х, а α + β ηа у, тогда α = (х + у) и β =(х – у). Следовательно,

cos х + cos у = 2 cos(х+у) cos(х-у). Если обе части равенства (*) разделить на два, то мы получим формулу, позволяющую представлять произведение косинусов двух углов в виде суммы: cos α cos β =(cos (α – β ) + cos (α + β )). ΐналогичным способом мы получим:

cos х – cos у = -2 sin(х + у) sin(х – у) и sin α sin β = (cos (α – β ) – cos (α + β )).

Если сложить синус разности с синусом суммы двух углов, то мы получим формулу суммы синусов:

sin (α – β ) = sin α cos β – cos α sin β;
sin (α + β ) = sin α cos β + cos α sin β;
sin (α – β ) + sin (α + β ) = 2 sin α cos β (**)

Из чего мы получаем: sin α cos β =(sin (α – β ) + sin (α + β )) θ

sin х + sin у = 2 sin(х + у) cos (х – у).

Например, cos 80º– cos 40º = -2 sin(80º + 40º) sin(80º – 40º) = -2 sin60º sin 20º = -√3sin 20º.

sin 35º + sin 55º = 2 sin

(35º + 55º) cos (35º – 55º) = 2 sin45º cos 10º = √2 cos 10º.

IV. Инструктаж домашнего задания.

В качестве домашнего задания ребятам можно предложить, используя рассмотренные на уроке приемы, записать тригонометрические формулы. И сделать это нужно несколько раз.

V. Итог урока (интерактивное тестирование).

На интерактивной доске демонстрируются результаты тестирования на входе и выходе.

Все формулы по математике за 11 класс на листе А4

Шпаргалка

• формат doc
• размер 156.5 КБ
• добавлен 07 ноября 2011 г.

2011 г.
Содержание:
Алгебра формулы.
Формулы сложения.
Формулы двойного аргумента.
Формулы половинного аргумента.
Формулы преобразования суммы в произведение.
Формулы преобразования произведения в сумму.
Соотношения между функциями.
Формулы тройного аргумента.
Третья степень.
Arcsin….
Производная.
Прогрессии.
Квадратное уравнение ax2+bx+c=0 (a?0).
Первообразная.
Интеграл.
Логарифмы.
Степени.
Геометрия.
Соотношение между углами и сторонами треугольника.
Площади плоских фигур.
Объёмы и площади объёмных фигур.
Векторы.

Читать онлайн

Смотрите также

• формат pdf
• размер 3.47 МБ
• добавлен 02 апреля 2011 г.

Карманный справочник. Сборник формул по математике. 2003 Издательство: ООО издательство АСТРЕЛЬ Страниц: 160 Описание: В справочнике приведены все необходимые формулы как школьного курса математики, так и высшей математики, изучаемой на первых курсах высших учебных заведений. Структура данного справочника позволит учащимся за очень короткое время найти нужную формулу и воспользоваться ею. Книга адресована учащимся средних и высших учебных заведе…

• формат doc
• размер 21.76 КБ
• добавлен 17 августа 2009 г.

Шпаргалка содержит формулы по математике на следующие темы: Формулы сокращенного умножения. Свойства степеней. Геометрическая прогрессия. Модуль. Формулы cos и sin. Тригонометрические уравнения. Теоремы сложения. Правила дифференцирования. Уравнение касательной к графику функции. Площадь S фигуры, ограниченной прямыми x=a, x=b. Формула Ньютона-Лебница. Первообразная. Объемы и поверхности тел. Теорема синусов. Теорема косинусов. Неопределенные инт…

Шпаргалка

• формат doc
• размер 1.79 МБ
• добавлен 15 января 2012 г.

Автор неизвестен. 2011 год. Все формулы на 1 листе в виде таблицы. Степени. Корни. Сокращенное умножение. Квадратный трехчлен. Квадратное уравнение. Формулы Виета. Разложение трехчлена на множители. Логарифмы. основные тождества. Свойства логарифмов. Десятичный логарифм. Натуральный логарифм. Тригонометрия. Основные тождества. Простейшие тригонометрические уравнения. Некоторые значения тригонометрических функций. Формулы приведения. Сумма и разно…

• формат docx
• размер 38.13 МБ
• добавлен 16 июня 2011 г.

Сборник для государственной итоговой аттестации по математике за 9 класс.

Шпаргалка

• формат rtf
• размер 480.92 КБ
• добавлен 04 октября 2011 г.

Собраны и размещены все основные и необходимые формулы по школьному курсу математики на нескольких листах. Справочник пригодится ученикам 11-ых классов, сдающим ЕГЭ, и ученикам старших классов. Содержит: тригонометрические формулы(тождества), значения тригонометрических функций, графики степенных, логарифмических и др. функций, таблица производных, алгебраическая и геометрическая прогрессии, свойства степеней, корней, логарифмов, уравнение корней…

pottee

• формат jpg
• размер 130. 37 КБ
• добавлен 27 декабря 2009 г.

Шпаргалка пригодится ученикам 11-ых классов, сдающим ЕГЭ, и ученикам старших классов. Содержит: тригонометрические формулы(тождества), значения тригонометрических функций, графики степенных, логарифмических и др. функций, таблица производных, алгебраическая и геометрическая прогрессии, свойства степеней, корней, логарифмов, уравнение корней и теорема Виета, уравнение касательной, формулы сокращенного умножения, формулы понижения степени, формулы…

pottee

• формат pdf
• размер 51.17 КБ
• добавлен 05 мая 2009 г.

Собраны и размещены все основные и необходимые формулы по школьному курсу математики на одном листе. Шпаргалка содержит следующие материалы: Тригонометрические тождества Свойства логарифмов Свойства интегралов Таблица интегралов Таблица производных Свойства степеней и корней Формулы сложения тригонометрических функций Формулы приведения Формулы геометрической прогрессии Формулы алгебраической прогрессии Формулы по геометрии Формулы понижения ст…

Шпаргалка

• формат doc
• размер 477.5 КБ
• добавлен 15 декабря 2010 г.

Шпаргалка по математике. все основные формулы и таблицы. Содержание: Числа, дроби, модуль: Множества. Дроби. Арифметические операции с дробями. Пропорция. Модуль числа. Определение. Свойства модуля. формулы сокращенного умножения. степени и корни: Показательные неравенства. квадратные уравнения: Корни уравнения. Формулы Виета. Разложение квадратного трехчлена на множители. Приведенное уравнение. Квадратное неравенство. прогрессии: Арифметическая…

pottee

• формат doc
• размер 36.5 КБ
• добавлен 01 июня 2009 г.

Для подготовки и сдачи ЕГЭ (составлены в виде шпаргалки) На одном листе таблицы sin cos tg ctg формулы сложения, вычитания, разложения суммы и разности, разложение 2а, 3а и квадратов sin cos tg ctg, разложение tg, ctg, разложение произведений sin cos tg ctg, преобразование вида 2(sin или cos) а/2, и другие формулы sin cos tg ctg

Формулы алгебры для класса 9: Список важных формул

• Автор Принц
• Последнее изменение 10.11.2022

Алгебра Формулы для 9 класса: Алгебра — это раздел математики, в котором универсальные символы и буквы используются для представления величин и чисел в уравнениях и формулах. Алгебра делится на два раздела: элементарная алгебра и современная алгебра (абстрактная алгебра). Формулы алгебраических выражений для 9 классабыли включены в учебную программу CBSE, чтобы учащиеся могли понять значение алгебры в своей повседневной жизни.

В CBSE Class 9 вводится глава об алгебраических выражениях и тождествах. Алгебра — одна из самых простых и результативных тем. Однако, если вы не помните различные математические формулы для алгебры класса 9 и то, как их использовать в алгебраических выражениях и тождествах, это может стать проблемой. Чтобы облегчить учащимся, мы включили примеры алгебраических уравнений с ответами на эту страницу. Продолжайте читать, чтобы узнать больше.

Учащиеся, которые ищут полный список математических формул для 9 класса по алгебре, могут обратиться к таблице:

1. (a + b) 2 = a 2 + 2ab + b 2 2. (a − b) 2 = a 2 − 2ab + b 2 3. (a + b)(a – b) = a 2 – b 2 4. ( x + a)(x + b) = x 2 + (a + b)x + ab 5. (x + a)(x – b) = x 2 + (a – b)x – ab 6. (х – а)(х + Ь) = х 2 + (b – a)x – ab 7. (x–a)(x–b) = x 2 – (a+b)x + ab 8. (a + b) 3 = a 3 + b 3 + 3ab(a + b) 9. (a – b) 3 = a 3 – b 3 – 3ab(a – b) 10. (x + y + z) 2 = x 2 + y 2 + z 2 + 2xy + 2yz + 2xz 11. (x + y – z) 2 = x 1 2 2 + z 2 + 2xy – 2yz – 2xz 12. (x – y + z) 2 = x 2 + y 2 + z 2 — 2xy — 2yz + 2xz 13. (x — y — z) 2 = x 2 + y 2 + z 2 – 2xy + 2yz – 2xz 14. x 3 + y 3 + z 3 – 3xyz = (x + y + z)(x 2 + 2 y 2 x 0 90 2 + 0z – yz − xz) 15. x 2 + y 2 = 12[(x + y) 2 + (x – y) 2 ] 16. (x + a)(x + b )(x + c) = x 3 + (a + b + c)x 2 + (ab + bc + ca)x + abc 17. x 3 + y 3 = (x + y)(x 2 – xy + y 2 ) 8. 3 – y 3 = (x – y)(x 2 + xy + y 2 ) 19. x 2 + y 2 + z 900×2 1 x – z 900×2 2 900 1/2[(x − y) 2 + (y − z) 2 + (z − x) 2 ]

Алгебраические тождества для 9 класса по математике

Знаете ли вы разницу между алгебраическая формула (тождество) и алгебраическое выражение? Алгебраическая формула — это уравнение, представляющее собой правило, записанное с использованием математических и алгебраических символов. Он всегда включает алгебраические выражения с обеих сторон. Более того, равенство будет выполняться при любых значениях переменных.

С другой стороны, алгебраическое выражение не разделяется знаком равенства. Алгебраическое выражение содержит две вещи — переменные и константы. Значение переменной меняется в разных выражениях, а константа остается неизменной. Мы можем понять разницу между двумя по следующему примеру:

(a + b) ² = ² + 2AB + B ² — алгебрак. формула и здесь,

(a + b) ² — алгебраическое выражение.
a ² + 2ab + b ² — алгебраическое выражение.

Левая и правая стороны алгебраической формулы всегда равны для любых значений переменных в ней. Это свойство позволяет нам вывести результат по правой стороне, если мы знаем значения слева от выражения.

Ознакомьтесь с другими важными статьями по математике для 9 класса:

Алгебраические уравнения для 9-го класса: примеры с ответами

Теперь, когда мы представили все формулы алгебры для 9-го класса, давайте посмотрим на некоторые их примеры: идентификаторы:
(i) (2x – 1/x) ²
(ii) (2x + y) (2x – y)
Ответ: (i) (2x – 1/x) ²
Использование идентификатора: (a – b) ²  = a ²  + b ²  – 2ab, получаем:
(2x – 1/x) ²
= (2x) ²  + (1/x) ²  – 2 (2x)(1 x)
= 4x ² + 1/x ² – 4
(ii) (2x + y) (2x – y)
Используя тождество: (a – b)(a + b) = a ² — B ² , мы получаем:
(2x + y) (2x — y)
= (2x) ² — (Y) ²
= 4x ² — Y ²

Вопрос 2: Упростите следующее: (i) 175 x 175 +2 x 175 x 25 + 25 x 25 (ii) 322 x 322 – 2 x 322 x 22 + 22 x 22 Ответ: (i) Используя тождество: a 2 + b 2 +2ab = (a+b) 2 , получаем: 175 x 175 +2 x 175 x 25 + 25 x 25 = (175) 2  + 2 (175) (25) + (25) 2 = (175 + 25) 2 = (200) 2 = 40000 (ii) Использование тождества0021 + b 2 -2ab = (a-b) 2 , получаем: 322 х 322 – 2 х 322 х 22 + 22 х 22 = (322) 2 – 2 х 322 х 22 + (22 ) 2 = (322 — 22) 2 =

Вопрос 3: если М + 1/М = 110017

. 2 . Ответ: м + 1/м = 11 (Дано) Итак, (м+1/м) 2 = м 2 + 1/м 2 + 2 x M x 1/M ⟹ (M + 1/M) 2 = M 2 + 1/M 2 + 2 ⟹ (11) 2 + 2 ⟹ (11) 2 + 2 ⟹ (11) 2 = M 2 + 1/M 2 + 2 ⟹ 121 = M 2 + 1/M 2 + 2 ⟹ M 2 + 1/M 2. = 119

Вопрос 4: Запишите в развернутой форме следующее: (I) (A + 2B + C) 2 (II) (A 2 + B 2 + C 2 ) 2 (III) (A/BC BC. + b/ac + c/ab)  2 Ответ: Используя тождество: (x + y + z) 2  = x 2  + y 2 +  + z 9 0020 2 2 + 2xz, мы можем расширить алгебраические выражения. (i) (a + 2b + c) 2 = a 2  + (2b)  2  + c 2  + 2a(2b) + 2ac + 2(2b)c = A 2 + 4B 2 + C 2 + 4AB + 2AC + 4BC (II) (A 2 + B 2 + C 2 ) 2 = (A . 2 ) 2 + (B 2 ) 2 + (C 2 ) 2 + 2A 2 B 2 + 2B 2 C 2 + 2A 2 C 2 C 2 + 2A 2 C 2 C 2 + 2A 2 . 2 = а 4 + б 4 + в 4 + 2а 2 б 2 + 2б 2  c 2 + 2c 2 a 2 (iii) (a/bc + b/ac + c/ab) 2 = (a/bc) 2 + (b/ac) 2 + (c/ab) 2 + 2(a/bc)(b/ac) + 2(b/ac)(c/ab) + 2(c/ab)(a/bc) = A 2 /B 2 C 2 + B 2 /C 2 A 2 + C 2 /A 2 B 2 + 2 /A 2 + 2. /b 2 + 2/c 2

Также проверка k

Практические вопросы по формулам алгебраических выражений для 9-го класса

Здесь мы предоставили некоторые практические вопросы по формулам алгебраических выражений для 9-го класса:

Вопрос 1: Факторизация следующих алгебраических выражений:
(i) x ³  + x – 3x ²  – 3
(ii) a(a + b) ³  – 3a ² B (A + B)
(III) x (x ³ — Y ³ ) + 3xy (x — y)
(iv) A ² x ² + (AX ² +1) x+ A

Вопрос 2: Каковы возможные выражения для измерений кубоида, чей объем составляет 3X ²  – 12x.

Вопрос 3: Разложите на множители следующие алгебраические выражения:
(i) (x + 2) (x ² + 25) — 10x ² — 20x
(II) 2A ² + 26–ing 3B ²
(III) A ² + B ² + 2 (AB + BC + CA)
(IV) 4 (x — Y) ^{2020202020202020202020202020202020202 2}  – 12(x -y)(x + y) + 9(x + y) ²

Вопрос 4: Найдите H.C.F и L.C.M Следующих выражений:
(I) A ² + 2AB + B ²
(II) B ² 9009 – A ² + 2BC + C ²
(III) — B ² + A ² + 2CA + C 9 2 + 2CA + C 9 2 9009 + 2CA + C 2 9009 + 2CA + C 2 9009 + 2CA + C 2 9009 + 2CA + C 9 2 9009 + 2CA.

Часто задаваемые вопросы по формулам алгебры для класса 9

Q1: Как получить алгебраические выражения?

Ответ: Алгебраическое выражение представляет собой комбинацию констант, переменных и алгебраических операций (+, -, ×, ÷). Мы можем вывести алгебраическое выражение для данной ситуации или условия, используя эти комбинации.

Q2: В чем разница между алгебраическим выражением и полиномом?

Ответ: Разница между полиномиальными и алгебраическими выражениями заключается в том, что полиномы включают только переменные и коэффициенты с математическими операциями (+, -, ×), а алгебраические выражения также включают в себя иррациональные числа в степенях.
Более того, полиномы являются непрерывной функцией (например, x2 + 2x + 1), но алгебраическое выражение иногда может быть не непрерывным (например, 1/(x2 – 1) не является непрерывным в точке 1).

Q3: Какие существуют типы алгебраических выражений?

Ответ: Алгебраическое выражение может быть одного из следующих типов:
(i) мономиальное
(ii) биномиальное
(iii) трехчленное
(iv) линейное полиномиальное
(v) квадратичное полиномиальное
(vi) кубическое многочлен

Q4: Является ли 5x алгебраическим выражением?

Ответ: Да, любое выражение, содержащее переменные, числа и символы операций, называется алгебраическим выражением. Итак, 5x — это алгебраическое выражение. Это также моном, потому что он содержит только один термин.

Q5: Каковы основные законы алгебры?

Ответ: Основными законами алгебры являются ассоциативный, коммутативный и распределительный законы.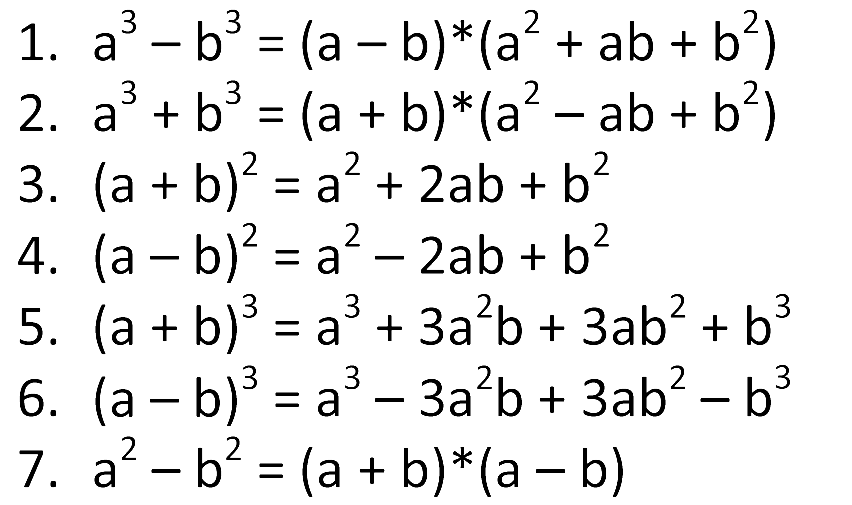 Ознакомьтесь со следующей таблицей, чтобы понять законы.

Алгебраические формулы для 9-го класса – Решенные примеры, PDF для скачивания

Алгебраические формулы для 9-го класса являются строительными блоками для алгебраических исследований более высокого уровня. Он включает в себя понимание алгебраических выражений и их решение. Изучение формул алгебры позволяет учащимся составлять уравнения и находить их решения. Помимо математики, эти формулы важны для развития жизненных навыков, применимых во многих различных профессиях и дисциплинах, таких как медицина, инженерия, химия, бюджетирование и так далее.

Список алгебраических формул 9-го класса

Ниже приведен список алгебраических формул 9-го класса, которые часто применяются при решении различных алгебраических уравнений.

• а ²  — б ² = (а — б)(а + б)
• (а + b) ² = а ² + 2ab + b ²
• a ² + b ² = (a + b) ²  — 2ab.
• (a — b) ² = a ²  — 2ab + b ²
• (а + b) ³ = а ³ + b ³ + 3ab(a + b)
• (a — b) ³ = a ³  — b ³  — 3ab(a — b)
• a ³  — b ³ = (a — b)(a ² + ab + b ² )
• a ³ + b ³ = (a + b)(a ²  — ab + b ² )
• х(а + б) = ха + хб
• х(а — б) = ха — хб
• (х — а)(х — б) = х ²  — (а + б)х + аб
• (х — а)(х + b) = х ² + (б — а)х — аб
• (x + a)(x — b)= x ² + (a — b)x — ab
• (х + а)(х + Ь)= х ² + (а + Ь)х + аб
• (x + y + z) ² = x ² + y ² + z ² + 2xy + 2yz + 2zx
• (x — y — z) ² = x ² + y ² + z ² — — 2xy + 2yz — 2zx

Применение алгебраических формул 9 класс

Понимание основ алгебраических формул 9 класс формирует фундаментальные знания для старших классов. Это помогает учащимся изучать различные темы, такие как тригонометрия, исчисление, геометрия и т. д. Формулы алгебры также составляют основу различных расчетов и анализов в реальной жизни. Давайте кратко рассмотрим применение формул алгебры класса 9 в реальном мире.

• Формулы алгебры класса 9 применяются в реальной жизни для составления бюджета наших расходов на сбережения. Эти формулы помогают нам принимать более разумные решения, тратя наши деньги.
• Оценивая варианты с помощью алгебраических формул, мы можем легко найти лучшие предложения по всем вопросам, от страховки до покупки вещей, чтобы сэкономить деньги.
• Алгебраические формулы применяются для рецептов и приготовления блюд. Анализ правильного количества ингредиентов требует алгебраических вычислений.
• Формулы алгебры применяются при планировании и оценке. Например, чтобы угадать количество краски, необходимое для окрашивания крыши, мы можем просто вычислить площадь прямоугольной крыши, чтобы узнать точное количество.

Советы по запоминанию алгебраических формул для 9-го класса

Переход от базовой арифметики к алгебраическим формулам в 9-м классе и символьному представлению поначалу может показаться пугающим для учащихся. Однако постепенно они могут усвоить эти формулы с практикой и некоторыми математическими приемами. Вот несколько советов учащимся, как упростить запоминание этих формул:

• В формулах 9-го класса по алгебре используются такие термины, как действительные корни, равные корни, мнимые корни, определители и т. д. Учащиеся должны убедиться, что они понимают смысл этих формул. необходимые термины перед запоминанием этих формул. Они могут получить помощь от учителей или своих друзей, чтобы прояснить то же самое.

• Получив кристально чистое знание терминов, используемых в формулах, учащиеся могут попробовать использовать некоторые забавные приемы, такие как фразы, чтобы лучше их запомнить. Кроме того, учащиеся могут поместить изображения формул в качестве обоев на свои гаджеты, что обеспечит их быстрый просмотр при использовании мобильного телефона или ноутбука.

• Ученики должны практиковаться в большом количестве задач и примеров, приведенных в учебнике, чтобы использовать эти формулы алгебры для 9 класса.

Algebra FormulasClass 9 Examples

Example 1: Factorise: 216x ³  — 27y ³

Solution: 216x ³ — 27y ³ = (6x) ³  — (3y) ³

, применив формулу A ³ -B ³ = (A-B) (A ² + AB + B ² ), мы получаем

216x ³ -27Y ³  = (6x — 3y) (36x ²  + 18xy + 9y ² )

Учащиеся могут скачать лист Math Formulas Class 9 для печати ниже.

 

Часто задаваемые вопросы по формулам алгебры 9 класса

Какие важные формулы алгебры 9 класса?

Некоторые из наиболее важных алгебраических формул класса 9 следующие:

(a — b) ³ = a ³  — b ³  — 3ab(a — b)

a ³  — b ³ = (a — b)(a ² + ab + b ² )

a ³ + b ³ = (a + b)(a ²  — ab + b ² )

х(а + б) = ха + хб

х(а — б) = ха — хб

Какие основные темы рассматриваются в классе 9 по алгебре?

Основные темы, охватываемые алгеброй в 9 классе, помогают учащимся определить тип полинома, решение полиномиального уравнения, корни и множители полиномиальных уравнений. Также эти основные формулы помогают реализовать четкое знание всех типов полиномиальных уравнений. Список всей базовой алгебры 9 классаформулы приведены в этой статье.

Почему важно решать все вопросы на основе формул алгебры 9 класса?

Важно решить все вопросы на основе формул алгебры 9 класса, чтобы понять, как оценивать различные типы полиномиальных уравнений и выражений. Это помогает студентам хорошо подготовиться к экзаменам и реализовать четкое понимание всех основных тем.

Сколько формул в алгебре 9 класса?

В 9 классе алгебры около 8 формулэто можно легко запомнить, если учащиеся будут следовать советам, упомянутым в этой статье, на постоянной основе. Ключевые формулы алгебры, включенные в математику класса 9, основаны на вычислении корней различных алгебраических выражений и уравнений.

Как запомнить формулы алгебры для 9 класса?

Один из лучших способов запомнить алгебраические формулы для 9-го класса — четко понимать все термины, используемые в формулах. Как только учащиеся формируют глубокое концептуальное понимание темы, они могут легко ее запомнить. Необходимо также обеспечить подготовку всех решенных примеров учебника с применением этих формул. Это обеспечит наиболее полный охват использования формулы в различных контекстах.

Скачать БЕСПЛАТНЫЕ учебные материалы

Математические формулы для 9 класса

Алгебраические формулы для 9 класса

Алгебра аналогична присвоению значений переменным, а также пониманию взаимосвязей между значениями в данном утверждении. Алгебра использует четыре математических операции, такие как сложение, вычитание, умножение и деление.

Чем математические удостоверения полезны для учащихся 9-го класса?

Математические тождества для 9-го класса обычно используются для упрощения сложных вычислений без использования автоматических электронных калькуляторов. Есть много математических тождеств, которые класс 9студенты могут использовать, чтобы уменьшить свои усилия в сложных математических задачах. Алгебра 9-го класса имеет огромный список алгебраических тождеств, которые могут использовать ученики 9-го класса. Большинство алгебраических тождеств используются при вычислении полиномиальных уравнений и выражений. Алгебраические тождества для математики 9-го класса также можно использовать для нахождения произведения больших чисел, а также их квадратов.

Алгебраические тождества для класса 9

Алгебраические тождества для класса 9 — это равенство, которое выполняется независимо от истинных значений, выбранных для вычисления. Это очень полезно во многих математических и научных вычислениях, включающих либо очень большое, либо очень маленькое число. Алгебраические формулы для 9 классаобычно представляются в виде переменных, которые могут принимать любое желаемое значение. Алгебра 9-го класса имеет обобщенные тождества, которые можно использовать во многих вычислениях.

Тождества по математике 9 класса с доказательствами:

Тождество 1:

Квадрат суммы любых двух чисел ‘a’ и ‘b’ определяется выражением (a + b)2 = a2 + b2 + 2ab

Доказательство :

(a + b)2 = (a + b) (a + b) = a2 + ab + ba + b2 = a2 + b2 + 2ab

Алгебраические тождества можно доказать с помощью метода деятельности.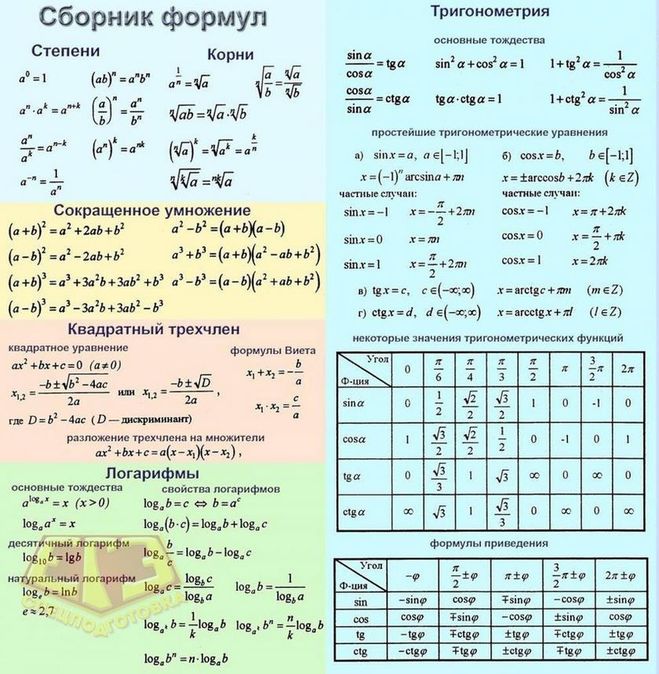

Тождество 2:

Квадрат разности любых двух чисел «a» и «b» определяется выражением (a — b)2 = a2 + b2 — 2ab.

Доказательство:

(a — b)2 = (a — b) (a — b) = a2 — ab — ba + b2 = a2 + b2 — 2ab

Тождество 3:

Произведение суммы и разности из 2 чисел ‘a’ и ‘b’ задается как (a + b) (a — b) = a2 — b2.

Доказательство:

(a + b) (a — b) = a2 — ab + ab — b2 = a2 — b2

Тождество 4:

(x + a) (x + b) = x2 + x ( а + б) + аб

Доказательство:

(x + a) (x + b) = x2 + xb + ax + ab = x2 + x (a + b) + ab 

Тождество 5: 

(x — a) (x + б) = x2 + x (b — a) — ab

Доказательство:

(x — a) (x + b) = x2 + xb — ax — ab = x2 + x (b — a) — ab

Тождество 6:

(x — a) (x — b) = x2 — x (a + b) + ab

Доказательство:

(x — a) (x — b) = x2 — xb — ax + ab = x2 — x (a + b) + ab 

Тождество 7:

Куб суммы любых двух чисел задается формулой (a + b)3 = a3 + b3 + 3ab (a + b)

Доказательство. b3 + 2ab2

= a3 + b3 + 3a2b + 3ab2

= a3 + b3 + 3ab (a + b)

Тождество 8:

Куб разности любых двух чисел равен (a — b)3 = a3 — b3 — 3ab (a — b)

Доказательство:

(a — b)3

= (a — b) (a — b)2

= (a — b) (a2 + b2 — 2ab)

= a3 + ab2 — 2a2b — ba2 — b3 + 2ab2

= a3 — b3 — 3a2b + 3ab2

= a3 — b3 — 3ab (a — b)

Тождество 9: 

Задан квадрат суммы трех чисел ‘a’, ‘b’ и ‘c’ по

(a + b + c)2 = a2 + b2 + c2 + 2ab +2bc + 2ca

Доказательство:

(a + b + c)2

= (a + b + c) (a + b + c)

= a2 + ab + ac + ba + b2 + bc + ca + cb + c2

= a2 + b2 + c2 + 2ab +2bc + 2ca

Тождества математических задач для 9 класса

1. Оцените квадрат 99 и 101, используя соответствующее алгебраическое тождество.