| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение |  ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Открытый урок по теме «Тригонометрические уравнения»
- Толмачёва Елена Евгеньевна
org/BreadcrumbList»> Разделы: МатематикаЦель урока: познакомить учащихся с однородными уравнениями, относительно cosx и sinx, с уравнениями, решаемыми с помощью разложения их левой части на множители.
Тип урока: комбинированный.
Оборудование: учебное пособие «Алгебра и начало анализа 10-11кл.» (А.Н. Колмогоров), тетрадь, карандаш, авторучка, линейка, справочник по алгебре, таблица формула корней простейших тригонометрических уравнений, составленная дома самостоятельно.
План урока:
| Этап урока: |
Цель этапа: | Время |
| 1. Организационный момент | Сообщение темы урока; постановка цели урока; сообщение этапов урока. |
2 минуты |
| 2. Проверка домашнего задания | Повторить решение тригонометрических уравнений, сводящихся к квадратным | 3 минуты |
| 3. Устный счет | Совершенствовать умение решать простейшие тригонометрические уравнения | 5 минут |
| 4. Самостоятельная работа | Выявить степень усвоения полученных на предыдущем уроке знаний | 10 минут |
| 5. Изучение нового материала | Познакомить с однородными уравнениями относительно cosx и sinx; с уравнениями, решаемыми с помощью разложения их левой части на множители | 10 минут |
| 6. Закрепление изученного материала | Первичное закрепление полученных знаний | 10 минут |
7. Итог урока |
Обобщение знаний полученных на уроке | 3 минуты |
| 8. Домашнее задание | Инструктаж по домашнему заданию. | 2 минуты |
I. Организационный момент
II. Проверка домашнего задания
III. Устное задание, заранее приготовленное на доске
Решить уравнения (можно пользоваться заранее приготовленной дома таблицей).
- cosx = 12
- sinx = -12
- sinx = -32
- cosx = 32
- tg x = 1
- ctgx = -1
- cos (x + π ) = 0
- sin (x — π3) = 0
- 5tgx = 0
IV. Самостоятельная работа
Работа проводится по учебному пособию
| Вариант 1 | Вариант 2 |
| 3sin2x – 5sinx – 2 = 0 6cos2x + cosx – 1 = 0 2cos2x + sinx +1 = 0 3tg2x + 2tgx – 1 = 0 |
4sin2x + 11sinx – 3 = 0 2sin2x + 3cosx = 0 8sin2x + cosx +1 = 0 2tg2x + 3tgx – 2 = 0 |
На обратной стороне доски заранее написаны ответы.
Можно предложить учащимся выполнить карандашом взаимопроверку, поменявшись вариантами, с последующим выставлением оценок.
V. Изучение нового материала
Опр. Однородные уравнения – это уравнения вида a•sinx + b•cosx = 0; a•sin2x + b•sinx•cosx + c•cos2x = 0
Пример 1.
2sinx + 5cosx = 0
Решение: Разделим обе части уравнения на cosx, получим:
2 tgx + 5 =0
tgx = -52
x = -arctg (52) + πn, nZ
Ответ: -arctg (52) + πn, nZ
Пример 2.
sin2x – 3sinxcosx – 4cos2x = 0
Решение: разделим обе части уравнения на cos2x, получим
tg2x – 3tgx – 4 = 0
tgx = 4, tgx = -2
x = arctg4 + πn, nZ, x = — π4+ πk, kZ
Ответ: — π4 + πk, kZ; arctg4 + πn, nZ
Пример 3.
cos2x + sinx = 0 (аналогично)
Ответ: π2 + 2 πn, (-1)n+1π6 + πk, n,kZ.
Пример 4.
cos6x + cos2x = 0
Ответ: π8 + πn4; π4 +πk2, n,kZ
VI. Закрепление изученного материала. Работа с методическим пособием
- 3sin2x + sinxcosx = 2cos2x
- 2cos2x – 3sinxcosx + sin2x = 0
- 4sin2x — sin2x = 3
- cos2x = 2cosx – 1
VII. Итог урока.
С какими способами решения тригонометрических уравнений вы знакомы теперь? (перечислить их).
VIII. Домашнее задание. Инструктаж по домашнему заданию.
Решить уравнения:
- 9sinxcosx – 7cos2x = 2sin2x
- 2sin2x – sinxcosx = cos2x
- sin2x – cosx = 0
- sin2x + 4cos2x = 1
Решить уравнение 12sin2x + 3sin2x – 2cos2x=2
(Данное уравнение не является однородным, но его можно преобразовать в однородное, заменив 3sin2x на 6sinxcosx и 2 на 2sin2x + 2cos2x.
После приведения подобных членов, получится однородное уравнение:
10sin2x + 6sinxcosx – 4cos2x = 0
Ответ: х = — π4 + πn, nZ, x = arctg 25 + πk, kZ.)
В начале следующего урока можно предложить самостоятельную работу:
(время выполнении 15-20 минут)
| Вариант I | Вариант II |
| 1) cos2x – 5sinx — 3 = 0 2) sin2x + cos2x = 0 3) cos2x – cos2x = sinx 4) sin4x – cos2x = 0 5) 5 – 5cos(π2 — x) = 2 cos2(π — x) |
1) cos2x + 3sinx = 2 2) sin2x – cos2x = 0 3) 6 – 10 cos22x + 4cos2x = sin2x 4) cosxcos2x = 1 5) 5 cos2(π2 + x) – 5 cos2(2π + x) = 32 |
Анализ усвоенности материала: Все учащиеся проявили интерес к данной теме.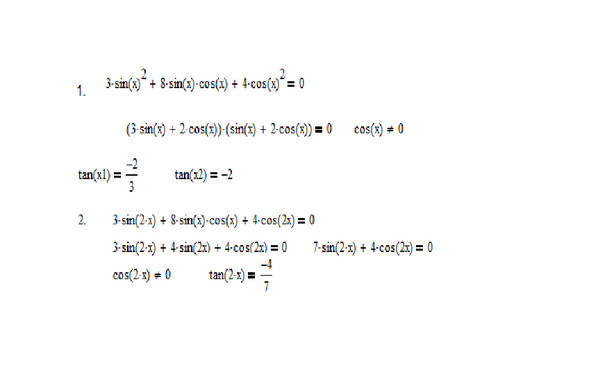
2x=0
Помогите пожалуйста — Учеба и наука
Лучший ответ по мнению автора
| |||||||||||||||||
08.17Другие ответы
| ||||||||||||
2x=0cosx*(sinx+cosx)=0
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
шайба массы m летит с горизонтальной скоростью в нулевое новости аш после удара плашмя поверхности льда шайба подскакивает на прежнюю высоту
Медиана равностороннего треугольника равна 13√3.
Найдите его сторону.
Решение плиз
Билеты по геометрии 7 класс Билет №1. 1. Точки. Прямые. Отрезки. 2. Сформулировать и доказать теорему, выражающую третий признак равенства
Обучение детей-сирот
Решите, пожалуйста
Пользуйтесь нашим приложением
тригонометрия — Общее решение $\sin 2x+\cos x=0$
Вопрос задан
Изменено 3 года, 11 месяцев назад
Просмотрено 442 раза
$\begingroup$
Решите тригонометрическое уравнение $\sin 2x+\cos x=0$
Моя попытка $$
2\sin x\cos x+\cos x=0\имплициты\cos x=0 \text{ или }\sin x=\frac{-1}{2}=\sin\frac{-\pi}{6} \\
x=(2n+1)\frac{\pi}{2} \text{ или}x=n\pi+(-1)^n\frac{-\pi}{6}\\
x=n\pi+\frac{\pi}{2} \text{или}x=2n\pi-\frac{\pi}{6}\text{или}x=2n\pi+\pi+\frac{\ пи {6}
$$ Ссылка $$
\cos x=-\sin 2x=\cos\Big(\frac{\pi}{2}+2x\Big)\имеется в виду x=2n\pi\pm\Big(\frac{\pi}{2}+ 2x\Большой)\\
-x=2n\pi+\frac{\pi}{2}\text{ или}3x=2n\pi-\frac{\pi}{2}\имеется в виду, что x=2m\pi-\frac{\pi}{ 2}\text{ или}x=\frac{2m\pi}{3}-\frac{\pi}{6}
$$
Но моя ссылка дает решение $x=2n\pi-\dfrac{\pi}{2}$ или $x=\dfrac{2n\pi}{3}-\dfrac{\pi}{6}$.
Я понимаю, как это достигается, и оба представляют собой одни и те же решения. Но как мне получить решение в моей ссылке из того, что я нашел в своей попытке? то есть
Как вывести $$ \bigg[x=n\pi+\frac{\pi}{2} \text{ или}x=2n\pi-\frac{\pi}{6}\text{ или}x=2n\pi+\pi+\ гидроразрыва {\ пи} {6} \ bigg] \\ \ подразумевает \bigg[x=2n\pi-\dfrac{\pi}{2}\text{ или}x=\dfrac{2n\pi}{3}-\dfrac{\pi}{6}\bigg] $$
- тригонометрия
$\endgroup$
2
$\begingroup$
Уравнение можно решить двумя способами.
Ваш метод: $2\sin x\cos x+\cos x=0$, поэтому $\cos x(2\sin x+1)=0$. Таким образом, мы имеем либо $\cos x=0$, либо $\sin x=-1/2$. Таким образом
\начать{выравнивать}
x&=\frac{\pi}{2}+2n\pi &\text{or}&& x&=-\frac{\pi}{2}+2n\pi && \text{(от $\cos x=0 $)} \\[4px]
x&=-\frac{\pi}{6}+2n\pi &\text{or}&& x&=\frac{7\pi}{6}+2n\pi && \text{(из $\sin x= -1/2$)}
\end{выравнивание}
(вы сгруппировали семейства решений $\cos x$ и $\sin x=-1/2$, но я предпочитаю разделять их).
Отличная работа.
Альтернативный метод: $\cos x=-\sin2x=\cos(\frac{\pi}{2}+2x)$. Поэтому либо $$ x=\frac{\pi}{2}+2x+2n\pi \to x=-\frac{\pi}{2}-2n\pi $$ или же $$ x = — \ frac {\ pi} {2} -2x + 2n \ pi \ to 3x = — \ frac {\ pi} {2} + 2n \ pi \ to x = \ frac {2n \ pi} {3} -\фракция {\ пи} {6} $$
Как восстановить предыдущие наборы решений?
Один комплект уже имеется. Для остальных трех рассмотрим случаи, когда $n=3k$, $n=3k+1$ или $n=3k+2$ с целым числом $k$. затем \начать{выравнивать} n&=3k & x&=\frac{6k\pi}{3}-\frac{\pi}{6}=2k\pi-\frac{\pi}{6} \\[4px] n&=3k+1 & x&=\frac{(6k+2)\pi}{3}-\frac{\pi}{6}=2k\pi+\frac{2\pi}{3}-\frac{ \pi}{6}=2k\pi+\frac{\pi}{2}\\[4px] n&=3k+2 & x&=\frac{(6k+4)\pi}{3}-\frac{\pi}{6}=2k\pi+\frac{4\pi}{3}-\frac{ \pi}{6}=2k\pi+\frac{7\pi}{6} \end{выравнивание} 9{-1}\left(\frac{-1}{2}\right) + 2\pi k = \frac{7 \pi}{6} + 2 \pi k$. В совокупности вы должны признать их своим решением, и одно из них вы цитируете из своей ссылки.
Вы уверены, что полностью скопировали ответ своей ссылки и правильно скопировали его $k$ коэффициенты?
$\endgroup$
3
$\begingroup$
У нас есть
, что эквивалентно
- $x=-\frac{\pi}2+2k\pi$
- $x=-\frac{\pi}6+\frac23k\pi$
, чтобы увидеть, что нарисуйте точки решения на тригонометрической окружности.
$\endgroup$
$\begingroup$
$$\sin(2x)+\cos(x)=0$$ $$2\sin(x)\cos(x)+\cos(x)=0$$ $$\cos(x)\left(2\sin(x)+1\right)=0$$ поэтому у вас есть два набора решений: $$\cos(x)=0,\,\sin(x)=-\frac{1}{2}$$ РЕДАКТИРОВАТЬ:
во-первых у них есть: $$x=2n\pi-\pi/2=\pi(2n-1/2)$$ и у вас есть: $$x=(2n+1)\pi/2$$ позволять: $$\pi/2(4n-1)=\pi/2(2m+1)$$ так: $$4n-1=2м+1$$ $$m=(4n-2)/2=2n-1$$ так что для всех целых значений $n$ $m$ также является целым числом, и поэтому они эквивалентны?
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
92(x)=5 $$
$$ 6(\frac{1}{2} — \frac{\cos(2x)}{2}) + \sin(x)\cos(x) -(\ frac{1}{2} + \frac{\cos(2x)}{2}) = 5 $$
$$ 3 — 3\cos(2x)+ \sin(x)\cos(x) — \ frac{1}{2} — \frac{\cos(2x)}{2} = 5$$
$$ \frac{7\cos(2x)}{2} — \sin(x)\cos( x) + \frac{5}{2} = 0 $$
$$ 7\cos(2x) — 2\sin(x)\cos(x) + 5 = 0 $$
$$ 7\cos (2x) — \sin(2x) + 5 = 0 $$
Итак, на данный момент я застрял, что делать, я попытался выполнить подпрограмму Вейерштрасса $\tan(\frac{x}{2}) = y $ и $\cos(x) = \frac{1-y^2}{1+y^2}$ и $\sin(x)=\frac{2y}{1+y^2} $, но я получил квартику, и я не смог ее решить.
9{-1}(-1/\sqrt{2})-\alpha)/2$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.