Раздел 2. Дифференциальное и интегральное исчисление
Раздел 2. Дифференциальное и интегральное исчисление
2.
Производная функции
2.1.
Дифференцирование функций
Сегодня вы изучите вопросы
-
Производная (или дифференцирование) функции. Задачи, приводящие к понятию производной
-
Односторонние производные
-
Примеры практического применения производной
-
Простейшие правила отыскания производных
-
Производная сложной функции
-
Производная обратной функции
-
Производные основных элементарных функций
-
Параметрическое задание функции и ее производная
-
Производная неявной функции
-
Таблица производных
Изучив тему занятия, вы сможете
-
определить область дифференцируемости функции;
-
найти производные функций, состоящих из основных элементарных функций;
-
найти производные от основных элементарных функций и любой комбинации образования функции от функции (суперпозиции функций), заданных как в явном, так и в неявном виде;
-
найти производные функций, заданных параметрически.

Основные понятия
-
производная функции
-
односторонние производные
-
основные элементарные функции
-
явное и неявное задание функции
-
параметрическое задание функции
2.1.1.
Производная (или дифференцирование) функции. Задачи, приводящие к понятию производной
Предварительно остановимся на понятии касательной к гладкой плоской линии в некоторой ее фиксированной точке. Здесь впервые введено новое понятие «гладкая плоская линия». Плоская линия называется гладкой, если она является непрерывной, не содержит особых точек, то есть в каждой своей точке имеет единственную касательную. К особым точкам относятся угловые точки (рис. 2.1), точки заострения (рис. 2.2) и узловые точки (рис. 2.3).
Рассмотрим на плоскости декартовых координат Оху гладкую линию L (рис. 2.4).
2.4).
Пусть М — произвольная точка этой линии. Возьмем по обе стороны от М произвольные точки и
Построим секущие и (рис. 2.4).
При стремлении точек и к точке М вдоль линии L секущие вращаются вокруг точки М, и в пределе при секущие примут предельное положение МТ. Это предельное положение секущих и называется касательной к плоской линии L в точке М.
Заметим, что в пределе секущая имеет с плоской гладкой линией единственную точку, называемую точкой касания, а в точках линий, содержащих угловые точки, узловые точки и точки заострения, предельные положения секущих не совпадают.
Задача Лейбница о касательной к плоской гладкой линии. На плоскости декартовых координат Оху дана плоская гладкая линия уравнением у = f(x) (рис. 2.5).
Пусть произвольная точка графика этой функции. Требуется найти уравнение касательной к графику этой функции в точке Пусть — произвольная точка графика функции. Построим касательную АТ и секущую АМ. Углы, образованные касательной и секущей с осью Ох, обозначим соответственно через φ и .
Предельным положением секущей АМ является касательная АТ. Введем обозначения: . При движении точки М по направлению к точке А вдоль линии у = f(x) приращение аргумента стремится к нулю; угол , следовательно, : . Так как , то окончательно находим, что:
. (32)
Известно, что уравнение касательной как прямой, проходящей через точку и образующей с осью Ох угол φ, имеет вид:
. (33)
С учетом равенства (32) окончательно находим уравнение искомой касательной:
. (34)
Таким образом, для отыскания уравнения касательной к плоской линии нам необходимо вычислить предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.
Задача Ньютона о мгновенной скорости. Вначале определим понятие мгновенной скорости. Пусть тело М движется вдоль оси Оs c произвольной скоростью (рис. 2.6). Пусть в момент времени t тело находилось в точке , а в момент времени тело находилось в точке Очевидно, пройденный телом М путь является функцией времени.
Пусть эта зависимость задается функцией .
Обозначим пройденные телом М пути соответственно следующим образом:
За величину скорости телаМ в момент времени t (или в точке А) принимается предел средней скорости на участке при (или при ).
Скорость в фиксированный момент времени t называется мгновенной скоростью в момент времени t и символически обозначается так: .
Таким образом, по определению:
. (35)
И вновь задача об отыскании мгновенной скорости свелась к вычислению предела отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.
Задача о производительности труда. Пусть функция выражает количество произведенной продукции u за время t и необходимо найти производительность труда в момент t0.
Очевидно, за период времени от t0 до количество произведенной продукции изменится от значения до значения ; тогда средняя производительность труда за этот период времени . Очевидно, что производительность труда в момент t 0 можно определить как предельное значение средней производительности за период времени от t0 до при , т.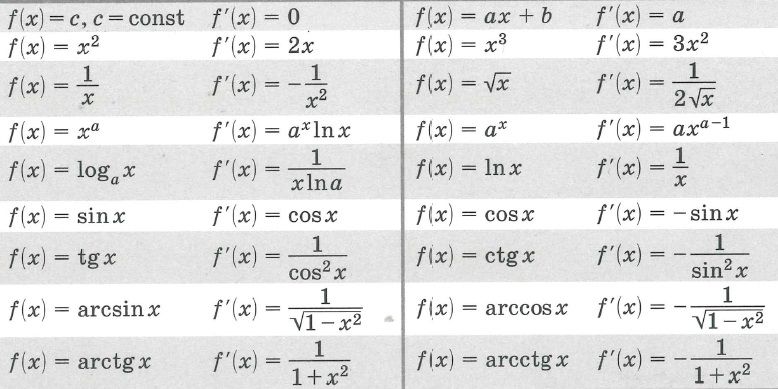 е.: .
е.: .
Рассматривая три различные по характеру задачи, мы пришли к пределу одного вида. Этот предел играет чрезвычайно важную роль в математическом анализе, являясь основным понятием дифференциального исчисления.
Пусть на отрезке [a, b] задана функция у = у(x). Пусть х = х0 — произвольная внутренняя точка этого отрезка, а y0 — соответствующее значение функции в точке х = х0: . Придадим приращение ∆x такое, чтобы не выйти за пределы заданного отрезка. Обозначим через y(x0 + ∆x) новое значение заданной функции, а через ∆y0 — приращение функции у = у(х) в т. х = х0:
Производной функции у = f(x) в точке x = x0
(36)
Символически производная от функции у = f(x) обозначается так:
или — по Лагранжу;
— по Лейбницу;
— по Ньютону.
Таким образом, по определению:
. (37)
(37)
Производная функции у = f(x) в произвольной внутренней точке области определения функции обозначается так:
. (38)
Если функция у = f(x) имеет производную в произвольной точке х некоторого множества значений х области определения функции у = f(x), то функция у = f(x) называется дифференцируемой на этом множестве.
Равенство (37) является частным значением производной в точке .
На основании введенного определения и рассмотренных нами задач, приводящих к понятию производной, заключаем, что уравнение касательной к графику функции в точке с абсциссой имеет вид:
, (39)
а мгновенная скорость равна:
, (40)
т.е. скорость материального тела в момент времени t равна производной от пути по времени, найденной для этого момента времени.
К примерам отыскания касательных к плоским линиям и мгновенной скорости мы обратимся после того, как научимся находить производные основных элементарных функций, сложных функций, обратных функций, изучим основные теоремы дифференцирования.
После определения понятия производной можно заключить, что:
, (41)
где — угол наклона касательной к графику функции у = f(x) в точке с абсциссой х. В этом и заключается геометрический смысл производной.
А мгновенная скорость равна:
, (42)
т.е. производной от пути по времени; в этом заключается физический смысл производной.
2.1.2.
Односторонние производные
Из определения производной следует, что производная есть предел функции. Из теории пределов следует, что предел (38) существует, если существуют односторонние пределы в точке , которые должны быть равны между собой. Что касается пределов для границ отрезка , то для этих точек нами были определены только односторонние пределы: для точки — предел справа, для точки — предел слева. По аналогии для производной функции у = f(x) на концах отрезка также вводятся понятия односторонних пределов
, (43)
называемых односторонними производными.
Таким образом, из определения производной функции у = f(x) следует, что для существования производной этой функции в точке необходимо и достаточно, чтобы существовали (конечные или бесконечные) в этой точке односторонние производные и , равные между собой:
= .
Геометрически равенство бесконечности производной в некоторой точке означает, что касательная к графику функции в точке, абсцисса которой равна , параллельна оси Оу (или перпендикулярна оси Ох).
На рис. 2.5 графиком функции у = f(x) является гладкая линия, односторонние производные (касательные слева и справа) в любой ее точке совпадают. На рисунках 2.1, 2.2, 2.3 функции, представленные своими графиками, имеют особые точки.
Как следует из рисунков, в особых точках эти касательные не совпадают, т.е. односторонние производные существуют, но не равны между собой.
При построении графиков функций существенную роль играет геометрическое представление равенства бесконечности односторонних пределов. На рис. 2.7 представлены возможные варианты равенства бесконечности односторонних производных.
Дадим некоторые пояснения к рисунку 2.7. На рис. а), б), в) имеется единственная касательная к графику функции в т. А. Если за х обозначить абсциссу точки А, то для случая а) , для варианта б) , для случая в) и г) односторонние пределы бесконечны, но отличны по знаку, для случая д) , для случая е) , для случая ж) .
Естественно, после введения понятия производной напрашивается вопрос: при каких условиях существует производная заданной функции?
Следующая теорема частично отвечает на поставленный вопрос.
Теорема 14 о непрерывности дифференцируемой функции — необходимое условие дифференцируемости функции.
Если функция у = f(x) дифференцируема в точке , то она непрерывна в этой точке.
Доказательство. По условию теоремы дано, что существует конечный предел:
. (44)
По теореме 2 о связи предела с б.м.в. имеем:
, (45)
где — б.м.в. при : .
Из равенства (45) следует, что:
. (46)
Отсюда находим, что:
Этим доказана непрерывность функции в точке .
Таким образом, из дифференцируемости функции в точке непременно следует ее непрерывность в этой точке. Это условие является необходимым. Однако обратное утверждение не всегда имеет место, т.е. из непрерывности функции еще не следует ее дифференцируемость. Наглядным примером тому являются функции, имеющие особые точки (рис. 2.1, 2.2, 2.3): на этих рисунках функции представлены неразрывными линиями (т.е. они представляют графики непрерывных функций), в особых же точках заданные функции не имеют производных (односторонние производные не равны между собой).
2.1, 2.2, 2.3): на этих рисунках функции представлены неразрывными линиями (т.е. они представляют графики непрерывных функций), в особых же точках заданные функции не имеют производных (односторонние производные не равны между собой).
Классическим примером такой функции является функция (рис. 2.8), которая непрерывна в точке х = 0, но производная этой функции в т. х = 0 не существует, так как , а .
Сформулируем четырехступенчатое правило отыскания производной.
Из определения производной следует, что для отыскания производной необходимо найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т.е. .
Отсюда следующее правило:
-
Придаем независимой переменной х приращение ; находим новое значение функции : для получения нового значения функции у = f(x) надо подставить в правую часть этого равенства вместо х выражение .
-
Находим приращение функции путем вычитания из нового значения старого значения :
.

-
Составляем отношение приращения функции к приращению аргумента: .
-
Находим предел .
В качестве примера найдем производную от постоянной величины, производную независимой переменной по самой переменной, производную от квадратичной функции, производную от логарифмической функции, производную от тригонометрической функции.
Пример 1. , где — const.
-
Новое значение функции равно .
-
Приращение функции равно:
= — =
-
Отношение приращения функции к приращению аргумента равно:
=
-
Находим предел
В силу существования предела по определению производной имеем: , или, подставляя вместо ее выражение , окончательно находим:
, (47)
т.е. производная постоянной величины равна нулю.
Пример 2.
-
Новое значение функции равно: .
-
Приращение функции равно:
= — = .
-
Отношение приращения функции к приращению аргумента равно:
-
Находим предел
В силу существования предела по определению производной имеем: , или, подставляя вместо ее выражение , окончательно находим:
, (48)
т.е. производная переменной по самой переменной равна 1.
Следовательно, и т.д.
Пример 3. .
-
Новое значение функции равно:
.
-
Приращение функции равно:
-
Отношение приращения функции к приращению аргумента равно:
.
-
Находим предел:
.

В силу существования предела по определению производной имеем: или, подставляя вместо функции ее выражение , окончательно находим:
. (49)
Пример 4. , где .
-
Новое значение функции равно:
.
-
Приращение функции равно:
-
Отношение приращения функции к приращению аргумента равно:
-
Находим предел:
В силу существования предела по определению производной имеем: , или, подставляя вместо функции у ее выражение , окончательно находим:
, (50)
или, с учетом равенства , окончательно получим:
. (51)
Отсюда, в частности, при будем иметь:
. (52)
Пример 5.
-
Новое значение функции равно .
-
Приращение функции равно:
-
Отношение приращения функции к приращению аргумента равно:
.

-
Находим предел:
В силу существования предела по определению производной имеем: , или, подставляя вместо у ее выражение , окончательно находим:
. (53)
2.1.3.
Примеры практического применения производной
Пример 6. Написать уравнение касательной и нормали к кривой:
f(x) = x2 + 4x + 5 в точке М0(-1; 2).
Уравнение касательной к плоской кривой определяется по формуле:
а нормали — по следующей формуле:
.
По условию задачи задана точка М0(-1; 2), лежащая на заданной кривой.
Следовательно, х0 = -1; у0 = 2.
Для нахождения искомых линий достаточно найти производную заданной функции при х = -1.
Находим:
Следовательно, искомыми касательная будут:
-
у — 2 = 2(х + 1), у — 2 = 2х + 2, у = 2х + 4.

-
— нормаль.
Пример 7. Тело движется вдоль оси Ох по закону .
Найти скорость движения в момент .
Решение. Находим .
Находим
2.1.4.
Простейшие правила отыскания производных
Пусть функции и — дифференцируемые функции на множестве .
Найдем, чему равны производные от функций, полученных из и путем арифметических действий:
(при ),
Теорема 15. Производная алгебраической суммы дифференцируемых функций равна алгебраической сумме производных этих функций, т.е.:
(54)
По условиям теоремы дано, что существуют конечные пределы:
(55)
Доказательство. Для простоты проведем доказательство для суммы. Введем обозначение: Y(x) = U(x) + V(x). Найдем производную функции по четырехступенчатому правилу.
-
Придадим х приращение Найдем новое (приращенное) значение функции:
.
-
Найдем приращение функции :
-
Найдем отношение:
.

-
Находим предел:
(56)
Из равенства (55) следует, что предел слева в равенстве (56) существует, следовательно, , или, с учетом введенного обозначения, окончательно получим:
ч.т.д.
Предоставляем читателю самостоятельно доказать справедливость равенства:
. (57)
Равенство (54) справедливо и при любом конечном числе слагаемых.
Теорема 16. Производная произведения двух дифференцируемых функций равна сумме произведений производной первой функции на вторую и производной второй функции на первую, т.е.:
(58)
По условиям теоремы дано, что существуют конечные пределы:
, .
Доказательство. Введем обозначение: Y(x) = U(x) ∙ V(x). Найдем производную функции по четырехступенчатому правилу.
-
Придадим приращение Найдем новое (приращенное) значение функции:
-
Найдем приращение функции :
-
Найдем отношение:
-
Находим предел:
.
 (59)
(59)
Из равенства (59) следует, что существует предел справа.
Следовательно, существует и предел слева:
,
или, с учетом введенного обозначения, окончательно получим:
, ч.т.д.
Следствие 1. В частности, если одна из функции есть постоянная величина, например , то из равенства (59) следует:
, (60)
т.е. постоянный множитель можно выносить за знак произведения.
Следствие 2. Производная произведения любого конечного числа дифференцируемых функций равна сумме произведений производной первой функции на все остальные плюс производная второй функции на все остальные и т.д. плюс производная последней функции на все остальные:
(61)
Доказательство предоставляем читателю.
Теорема 17. Производная частного двух дифференцируемых функций равна дроби, числитель которой равен разности произведений производной числителя на знаменатель и производной знаменателя на числитель, а знаменатель равен квадрату знаменателя данной дроби, если знаменатель отличен от нуля, т.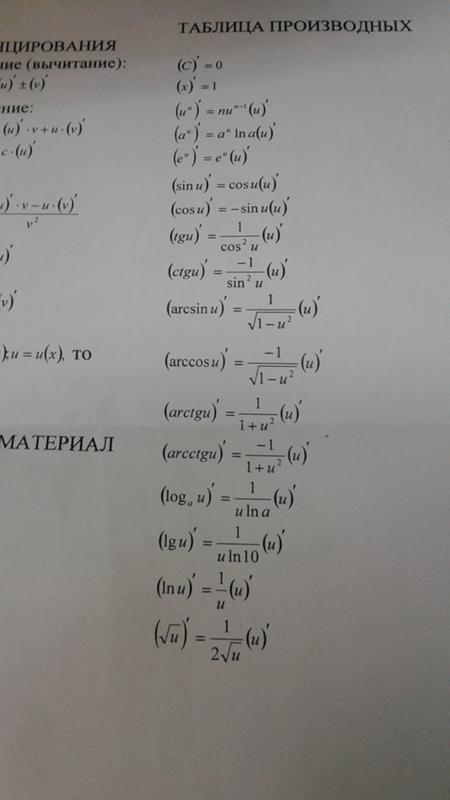 е.:
е.:
. (62)
По условиям теоремы дано, что существуют конечные пределы:
, и
Требуется доказать справедливость равенства (62).
Доказательство можно провести аналогично приведенному выше доказательству (доказательство предоставляется читателю).
Следствие 1. Если V(х) = с — константа, то формула (62) переписывается так:
. (63)
Следствие 2. Если V(х) = с — константа, то формула (62) переписывается так:
. (64)
2.1.5.
Производная сложной функции
Пусть у = f(u), где u ϵ U, а u = u(х), где х ϵ Х, u ϵ U. Тогда переменная у является сложной функцией независимой переменной х на множестве х ϵ Х, u — промежуточная переменная.
Найдем формулу для производной сложной функции по независимой переменной х при следующих предположениях: функция у = f(u) дифференцируема по u на множестве U, функция u = u(х) является дифференцируемой на множестве Х.
Докажем, что справедливо равенство:
, (65)
т.е. производная сложной функции по независимой переменной равна произведению производной этой функции по промежуточной переменной на производную промежуточной переменной по независимой переменной.
По условию существуют конечные пределы:
(66)
Из существования конечного предела следует, что:
, где ; или .
Отсюда находим:
(67)
В равенстве (67) перейдем к пределу при ∆х → 0.
(68)
По условию u = u(х) непрерывная функция, т.к. она дифференцируема. Следовательно, при ∆х → 0 и ∆u → 0.
Отсюда равенство (68) перепишется так:
.
В силу существования предела справа предел слева тоже существует и по определению называется т. о. имеем: , ч.т.д.
2.1.6.
Производная обратной функции
Если функция у = f(х) на множестве Х дифференцируема, то в точках, где ее производная отлична от нуля, обратная функция х = φ(у) дифференцируема и равна обратной величине производной прямой функции у = f(х), т.е.
(69)
Доказательство проведем для монотонной функции у = f(х). По условию прямая функция у = f(х) дифференцируема на множестве Х, следовательно, она непрерывна на этом множестве. Так как функция у = f(х) на множестве Х однозначна и монотонна, то для произвольной точки х ϵ Х справедливо следующее рассуждение: если изменить х на ∆х ≠ 0, то соответствующее значение функции у(х) изменится на ∆у ≠ 0.
Пусть Y — множество значений функции у = f(х).
По теореме о существовании обратной функции на множестве Y будет определена непрерывная и монотонная функция х = φ(у).
Для отыскания ее производной по переменной у найдем предел отношения:
. (70)
Т.к. функция у = f(х) непрерывна, то при ∆х → 0 и ∆у → 0, и наоборот. Следовательно, в (70) предел при ∆у → 0 можно заменить на ∆х → 0. Так как по условию пределы числителя и знаменателя существуют и предел знаменателя отличен от 0, то , или , ч.т.д.
2.1.7.
Производные основных элементарных функций
Производная логарифмической функции
На предыдущем занятии по четырехступенчатому правилу нами была найдена производная логарифмической функции:
, (71)
в частности, при а = е мы получили:
(72)
Рассмотрим сложную функцию удовлетворяющую всем условиям существования производной сложной функции.
Как будет выглядеть производная функции ? Последнюю функцию нужно рассматривать как сложную функцию , где .
По теореме о производной сложной функции имеем:
.
Таким образом, нами найдена производная сложной функции :
(73)
Отсюда, в частности, при а = е получим:
. (74)
Производная показательной функции
Рассмотрим показательную функцию
ϵ(-∞; +∞). (75)
Найдем производную функции (75), воспользовавшись производной логарифмической функции.
Прологарифмируем обе части равенства по основанию :
. (76)
Возьмем от обеих частей равенства (76) производную по х, рассматривая левую часть этого равенства как сложную функцию от х:
\
Подставляя вместо функции ее выражение , получим:
. (77)
Отсюда в частности при имеем:
. (78)
Рассмотрим сложную функцию которая удовлетворяет условиям существования сложной функции.
По теореме о производной сложной функции имеем:
.
Окончательно находим:
. (79)
В частности, при а = е получим:
. (80)
Производная степенной функции
Найдем производную степенной функции , где α — произвольное действительное число.
Прологарифмируем обе части равенства по основанию :
. (81)
Возьмем от обеих частей равенства (81) производную по х, воспользовавшись формулами (72) и (73):
.
Подставим в последнем равенстве вместо у(х) степенную функцию :
Окончательно получим:
(82)
В случае задания сложной степенной функции по аналогии с вышеизложенным получим:
, или
. (83)
Отсюда, в частности, при получим:
или окончательно:
. (84)
Отсюда при n = 2 получим:
. (85)
Производная показательно-степенной функции
Рассмотрим функцию заданную на множестве Х, где выполняются условия существования производной сложной функции: функции дифференцируемы, функция у дифференцируема по u и v.
Для отыскания искомой производной возьмем от обеих частей равенства натуральный логарифм:
. (86)
Возьмем от обеих частей равенства (86) производную по х, воспользовавшись формулой (73) и производной произведения:
(87)
Подставляя в равенстве (87) вместо показательно-степенную функцию получим:
,
или окончательно:
(88)
Из формулы (88) следует, что производная показательно-степенной функции равна сумме производных от функции , которая вначале рассматривается как показательная функция, а затем как степенная.
Производные тригонометрических функций
На предыдущем занятии (занятие 5) нами была найдена производная по четырехступенчатому правилу, и было установлено, что:
. (89)
Если дана сложная функция , то по формуле производной сложной функции находим:
(90)
Найдем у’, воспользовавшись формулами приведения и формулой (89).
Имеем:
,
где за u принята разность : .
Отсюда окончательно:
Таким образом,
. (91)
По аналогии, в случае задания сложной функции будем иметь:
.
Для отыскания производной воспользуемся формулой для производной дроби:
Таким образом,
(92)
В случае задания сложной функции по аналогии получим:
(93)
.
Для отыскания производной воспользуемся формулой приведения и формулой (93) для производной :
Таким образом, имеем:
(94)
В случае задания сложной функции будем иметь:
(95)
Производные обратных тригонометрических функций
-
.

Так как функция на заданном отрезке монотонна и непрерывна, то по теореме о существовании обратной функции функция имеет обратную функцию . Так как производная обратной функции отлична от нуля , то по теореме о производной обратной функции имеем:
. (96)
Здесь мы воспользовались основным тригонометрическим тождеством .
Отсюда находим, что . Перед радикалом в равенстве (96) взят знак «плюс», т.к. cos y на интервале является величиной положительной. Подставляя вместо у(x) обратную тригонометрическую функцию arcsinx, получим:
. (97)
В случае задания сложной функции получим:
. (98)
-
На интервале (-1; 1) функция монотонна и непрерывна. По теореме о существовании обратной функции функция имеет обратную функцию , которая на интервале по переменной у имеет производную, отличную от нуля. Следовательно, по теореме о производной обратной функции имеем:
или
(99)
По тем же соображениям перед радикалом взят знак «плюс», т.
 к. функция ] на интервале положительна.
к. функция ] на интервале положительна.В случае задания сложной функции по аналогии получим:
(100)
-
, .
Функция на заданном интервале монотонна и непрерывна, следовательно, на соответствующем интервале определена однозначная обратная функция . Заметим, что производная функции отлична от нуля. Тогда по теореме о производной обратной функции:
, или
(101)
В случае заданной сложной функции получим:
(102)
-
Функция на интервале монотонна и непрерывна. По теореме о существовании обратной функции заданная функция имеет обратную , которая на интервале также монотонна и непрерывна. Заметим, что при . Тогда, по теореме о производной обратной функции имеем:
, или
. (103)
В случае заданной сложной функции по аналогии будем иметь:
.
 (104)
(104)
2.1.8.
Параметрическое задание функции и ее производная
В качестве примера рассмотрим окружность в прямоугольной системе координат Оху (рис. 2.9).
Пусть М (х; у) — произвольная точка окружности; |ОМ|= R — радиус окружности.
По определению тригонометрических функций и имеем:
(105)
где .
Равенствами (105) зависимость функции у от х задается через угол α, который является параметром.
Легко заметить, что из равенства (105) следует:
что является известным каноническим уравнением окружности.
В общем случае функция у от переменной х называется заданной параметрически, если эта зависимость задается системой равенств (106):
(106)
где .
Найдем производную от функции, заданной параметрически равенствами (106). Пусть удовлетворяет всем условия дифференцируемости и существования обратной функции , где : функция монотонна и непрерывна на отрезке существует конечный предел , отличный от нуля.
Переменную у можно рассматривать как сложную функцию переменной х на отрезке :
.
По теореме о производной сложной функции имеем:
(107)
Так как производная обратной функции равна обратной величине производной прямой функции, т.е. , то равенство (107) можно переписать так:
. (108)
Пример. Функция переменной х задана параметрически:
Требуется найти . По формуле (108) имеем:
Найдем производную второго порядка от функции, заданной параметрически.
Функция является сложной функцией переменной х. По теореме о производной сложной функции имеем:
или окончательно . (109)
2.1.9.
Производная неявной функции
Пусть уравнение:
(110)
на множестве Х задает неявную функцию Общая формула для отыскания производной неявной функции задается в разделе функций многих переменных. Однако если в уравнении (110) рассматривать переменную y как функцию переменной х, то, взяв производную по х от обеих частей равенства (110) и разрешив относительно , можно найти искомую производную как функцию переменных х и у.
Действительно, уравнение
(111)
на множестве определяет неявную функцию .
Возьмем от обеих частей уравнения (111) производную по х:
(112)
Решив уравнение (112) относительно , находим:
.
На основе найденных производных основных элементарных функций составим таблицу производных. В нижеприведенную таблицу включены также основные правила дифференцирования.
2.1.10.
Таблица производных
1. |
14. |
2. |
15. |
3. |
16. |
4. |
17. |
5. |
18. |
6. |
19. |
7. |
|
8. |
|
9. |
22. |
10. |
23. |
11. |
24. |
12. |
25. |
13. |
Рассмотрим примеры на отыскание производных заданных функций по таблице производных и основным правилам взятия производных дифференцируемых функций.
Пример 1. Найти производную функции:
у = 2х4 + 4х2 + 3х2 + 5х — 2.
На основании правил дифференцирования и формулы производной степенной функции имеем:
y’ = (2х4 + 4х3 + 3х2 + 5х — 2)’ = (2x4)’ + (4x3)’ + (3x2)’ + (5x)’ — (2)’ = 2(x4)’ + 4(x3)’ + 3(x2)’ +
+ 5(x)’ — 0 = 2 ∙ 4x3 + 4 ∙ 3x2 + 3 ∙ 2x + 5 = 8x3 + 12x2 + 6x + 5.
Пример 2. Найти производную функции:
Имеем:
Пример 3. Дана функция f(x) = x3 — 4x — 1.
Вычислить , , , , .
-
Сначала находим производную заданной функции:
-
Подставляем в выражение первой производной вместо х последовательно числа -2; -1; 0; 1; 3:
Пример 4. Найти производную функции:
у = х2 sinx — x ∙ cosx.
Производную находим по правилу производной от алгебраической суммы и по формуле производной от произведения дифференцируемых функций.
Имеем:
Пример 5. Найти производную функции .
Искомую производную найдем по формуле производной от дроби:
Пример 6. Найти производную сложных функций:
1. Если предположить, что 4х = u, то функцию у = cos 4х можно рассматривать как сложную функцию:
y = cos u, u = 4x.
По правилу нахождения производной сложной функции имеем:
При нахождении производных сложных функций в дальнейшем мы будем пользоваться соответствующими формулами дифференцирования сложных функций.
.
.
Пример 7. Найти производную от функции, заданной неявно:
ху + sinу = 0.
Чтобы найти производную от неявной функции, нужно продифференцировать по х обе части заданного равенства, рассматривая переменную у как функцию от х, найти из полученного равенства.
Имеем:
Окончательно находим:
Контрольные вопросы
-
Дайте определение производной функции в точке.
-
Найдите по четырехступенчатому правилу производную функции у(х) = х2.
-
На основании основных правил взятия производных найдите производную функции у(х) = 5х2 — 3х + 4.
-
Непрерывность функции является необходимым или достаточным условием?
-
Для существования производной в точке каковы ее достаточные условия?
-
Перечислите наименования точек разрыва производной непрерывной функции.

-
Каков геометрический смысл производной?
-
Каков механический смысл первой производной?
-
Приведите пример применения понятия производной функции в экономике.
-
Дайте определение касательной к графику функции в точке и напишите уравнение касательной.
-
Какая функция называется неявно заданной?
-
Какая функция называется параметрически заданной?
-
Приведите формулы для нахождения производных арксинуса, арккосинуса, арктангенса и арккотангенса.
-
Приведите формулу для нахождения производной первого порядка параметрически заданной функции.
-
Сформулируйте правило нахождения производной неявно заданной функции.

Задания для самостоятельной работы
-
Воспользовавшись четырехступенчатым правилом дифференцирования, найдите производную функции .
-
Найдите производные следующих функций, пользуясь формулами и правилами дифференцирования:
1) ;
2) ;
3) ;
4) , вычислить ;
5) ;
6)
7) ;
8) ;
9) ;
10) ;
11) ;
12)
13) ;
14) ;
15) ;
16) ;
17) ;
18) ;
19) ;
20) .
-
Напишите уравнение касательной и нормали к параболе в точке, абсцисса которой равна .
-
Найдите мгновенную скорость движения тела в момент t = 2 ч.
 , если известно, что закон, выражающий зависимость пройденного пути от времени, имеет вид .
, если известно, что закон, выражающий зависимость пройденного пути от времени, имеет вид . -
Найдите производные следующих функций:
;
;
;
;
;
;
;
;
;
;
;
.
-
Найдите производные неявных функций:
;
;
.
-
Найдите производные функций, заданных параметрически:
-
Найдите уравнения касательной и нормали к плоской линии y = e3x в точке M0 (0; 1).

Понятие и свойства неопределённого интеграла, таблица интегралов
Неопределённый интеграл: 8 фактов, которые надо знать студенту
- Первообразная функция и неопределённый интеграл
- Геометрический смысл неопределённого интеграла
- Свойства неопределённого интеграла
- Таблица основных неопределённых интегралов
Факт 1. Интегрирование — действие, обратное дифференцированию, а именно, восстановление функции по известной производной этой функции. Восстановленная таким образом функция F(x) называется первообразной для функции f(x).
Определение 1. Функция F(x) называется первообразной для функции f(x)
на некотором промежутке X, если для всех значений x из этого промежутка выполняется
равенство F ‘(x)=f(x), то есть данная функция f(x) является производной
от первообразной функции F(x). .
.
Например, функция F(x) = sin x является первообразной для функции f(x) = cos x на всей числовой прямой, так как при любом значении икса (sin x)’ = (cos x).
Определение 2. Неопределённым интегралом функции f(x) называется совокупность всех её первообразных. При этом употребляется запись
∫
f(x)dx
,
где знак ∫ называется знаком интеграла, функция f(x) – подынтегральной функцией, а f(x)dx – подынтегральным выражением.
Таким образом, если F(x) – какая-нибудь первообразная для f(x) , то
∫
f(x)dx = F(x) +C
, (1)
где C — произвольная постоянная (константа).
Для понимания смысла множества первообразных функции как неопределённого интеграла уместна следующая аналогия. Пусть есть дверь (традиционная деревянная дверь). Её функция — «быть дверью». А из чего сделана дверь? Из дерева. Значит, множеством первообразных подынтегральной функции «быть дверью», то есть её неопределённым интегралом, является функция «быть деревом + С», где С — константа, которая в данном контексте может обозначать, например, породу дерева. Подобно тому, как дверь сделана из дерева при помощи некоторых инструментов, производная функции «сделана» из первообразной функции при помощи формулы, которую мы узнали, изучая производную.
Тогда таблица функций распространённых предметов и соответствующих им первообразных
(«быть дверью» — «быть деревом», «быть ложкой» — «быть металлом» и др.) аналогична таблице основных
неопределённых интегралов, которая будет приведена чуть ниже. В таблице неопределённых интегралов
перечисляются распространённые функции с указанием первообразных, из которых «сделаны» эти функции. В части
задач на нахождение неопределённого интеграла даны такие подынтегральные функции, которые без особых
услилий могут быть проинтегрированы непосредственно, то есть по таблице неопределённых интегралов. В
задачах посложнее подынтегральную функцию нужно предварительно преобразовать так, чтобы можно было
использовать табличные интегралы.
В части
задач на нахождение неопределённого интеграла даны такие подынтегральные функции, которые без особых
услилий могут быть проинтегрированы непосредственно, то есть по таблице неопределённых интегралов. В
задачах посложнее подынтегральную функцию нужно предварительно преобразовать так, чтобы можно было
использовать табличные интегралы.
Факт 2. Восстанавливая функцию как первообразную, мы должны учитывать произвольную постоянную (константу) C, а чтобы не писать список первообразной с различными константами от 1 до бесконечности, нужно записывать множество первообразных с произвольной константой C, например, так: 5x³+С. Итак, произвольная постоянная (константа) входит в выражение первообразной, поскольку первообразная может быть функцией, например, 5x³+4 или 5x³+3 и при дифференцировании 4 или 3, или любая другая константа обращаются в нуль.
Поставим задачу интегрирования: для данной функции f(x) найти такую функцию F(x), производная которой равна f(x).
Пример 1.Найти множество первообразных функции
Решение. Для данной функции первообразной является функция
так как
Функция F(x) называется первообразной для функции f(x), если производная F(x) равна f(x), или, что одно и то же, дифференциал F(x) равен f(x) dx, т.е.
или
(2)
Следовательно, функция — первообразная для функции . Однако она не является единственной первообразной для . Ими служат также функции
и вообще
где С – произвольная постоянная. В этом можно убедиться дифференцированием.
Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.
Таким образом, если для функции существует одна первообразная, то для неё существует бесконечное множество первообразных, отличающихся на постоянное слагаемое. Все первообразные для функции записываются в приведённом выше виде. Это вытекает из следующей теоремы.
Теорема (формальное изложение факта 2). Если F(x) – первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x) + C , где С – произвольная постоянная.
В следующем примере уже обращаемся к таблице интегралов, которая будет дана
в параграфе 3, после свойств неопределённого интеграла. Делаем это до ознакомления со всей таблицей, чтобы
была понятна суть вышеизложенного. А после таблицы и свойств будем пользоваться ими при интегрировании во всей полносте.
А после таблицы и свойств будем пользоваться ими при интегрировании во всей полносте.
Пример 2. Найти множества первообразных функций:
1)
2)
3)
Решение. Находим множества первообразных функций, из которых «сделаны» данные функции. При упоминании формул из таблицы интегралов пока просто примите, что там есть такие формулы, а полностью саму таблицу неопределённых интегралов мы изучим чуть дальше.
1) Применяя формулу (7) из таблицы интегралов при n = 3, получим
2) Используя формулу (10) из таблицы интегралов при n = 1/3, имеем
3) Так как
то по формуле (7) при n = -1/4 найдём
Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.
Под знаком интеграла пишут не саму функцию f, а её произведение на дифференциал dx. Это делается прежде всего для того, чтобы указать, по какой переменной ищется первообразная. Например,
, ;
здесь в обоих случаях подынтегральная функция равна , но её неопределённые интегралы в рассмотренных случаях оказываются различными. В первом случае эта функция рассматривается как функция от переменной x, а во втором — как функция от z.
Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции.
Для самопроверки при расчетах можно воспользоваться калькулятором неопределённых интегралов онлайн.
Пусть требуется найти кривую y=F(x) и мы уже знаем,что тангенс угла наклона касательной в каждой её точке есть заданная функция f(x) абсциссы этой точки.
Согласно геометрическому смыслу производной, тангенс угла наклона касательной в данной
точке кривой y=F(x) равен значению производной F'(x).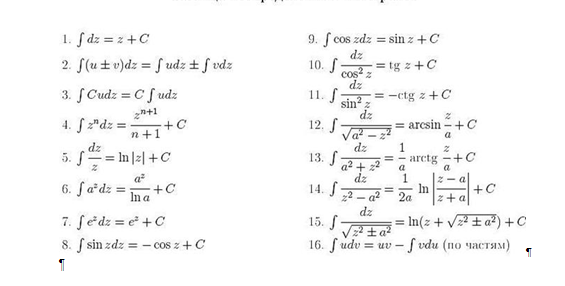 Значит, нужно найти такую функцию F(x), для которой F'(x)=f(x). Требуемая в задаче функция F(x) является первообразной от f(x). Условию задачи удовлетворяет не одна
кривая, а семейство кривых. y=F(x) — одна из таких кривых, а всякая другая кривая может быть получена
из неё параллельным переносом вдоль оси Oy.
Значит, нужно найти такую функцию F(x), для которой F'(x)=f(x). Требуемая в задаче функция F(x) является первообразной от f(x). Условию задачи удовлетворяет не одна
кривая, а семейство кривых. y=F(x) — одна из таких кривых, а всякая другая кривая может быть получена
из неё параллельным переносом вдоль оси Oy.
Назовём график первообразной функции от f(x) интегральной кривой. Если F'(x)=f(x), то график функции y=F(x) есть интегральная кривая.
Факт 3. Неопределённый интеграл геометрически представлен семеством всех интегральных кривых, как на рисунке ниже. Удалённость каждой кривой от начала координат определяется произвольной постоянной (константой) интегрирования C.
Факт 4. Теорема 1. Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.
Факт 5. Теорема 2. Неопределённый интеграл от дифференциала функции f(x) равен функции f(x) с точностью до постоянного слагаемого, т.е.
(3)
Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями.
Факт 6. Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.
(4)
Факт 7. Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.
(5)
Факт 8. Пользусь таблицей неопределённых интегралов,
свойствами неопределённого интеграла и методами интегрирования, можно отыскать неопределённый интеграл
любой функции.
Из определения неопределённого интеграла вытекают следующие формулы, которые в дальнейшем будем называть табличными интегралами:
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)
(25)
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Интеграл
Продолжение темы «Интеграл»
Найти неопределённый интеграл: начала начал, примеры
Метод замены переменной в неопределённом интеграле
Интегрирование подведением под знак дифференциала
Метод интегрирования по частям
Интегрирование дробей
Интегрирование рациональных функций и метод неопределённых коэффициентов
Интегрирование некоторых иррациональных функций
Интегрирование тригонометрических функций
Определённый интеграл
Несобственные интегралы
Площадь плоской фигуры с помощью интеграла
Объём тела вращения с помощью интеграла
Вычисление двойных интегралов
Длина дуги кривой с помощью интеграла
Площадь поверхности вращения с помощью интеграла
Определение работы силы с помощью интеграла
Поделиться с друзьями
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Основы обеспечения единства измерений: Обеспечение единства измерений — деятельность метрологических служб, направленная на достижение… Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает… Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Интересное: Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является. Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 5 из 6Следующая ⇒ Задание: 1) Вычислить интеграл по формуле трапеций. 2) Вычислить интеграл по формуле Симпсона при n=8; оценить погрешность результата, составив таблицу конечных разностей.
Теоретическая часть Метод трапеций Если функцию на каждом из частичных отрезков аппроксимировать прямой, проходящей через конечные значения, то получим метод трапеций. Площадь трапеции на каждом отрезке: Погрешность аппроксимации на каждом отрезке: Полная формула трапеций в случае деления всего промежутка интегрирования на отрезки одинаковой длины : Погрешность формулы трапеций: Метод парабол (метод Симпсона) Использовав три точки отрезка интегрирования, можно заменить подынтегральную функцию параболой. Обычно в качестве таких точек используют концы отрезка и его среднюю точку. В этом случае формула имеет очень простой вид Если разбить интервал интегрирования на 2N равных частей, то имеем , где Увеличение точности Приближение функции одним полиномом на всем отрезке интегрирования, как правило, приводит к большой ошибке в оценке значения интеграла. Для уменьшения погрешности отрезок интегрирования разбивают на части и применяют численный метод для оценки интеграла на каждой из них. При стремлении количества разбиений к бесконечности, оценка интеграла стремится к его истинному значению для аналитических функций для любого численного метода. Приведённые выше методы допускают простую процедуру уменьшения шага в два раза, при этом на каждом шаге требуется вычислять значения функции только во вновь добавленных узлах. Для оценки погрешности вычислений используется правило Рунге. Варианты заданий
№1. 1) ; 2) №2. 1) ; 2) №3. 1) ; 2) №4. 1) ; 2) №5. 1) ; 2) №6. 1) ; 2) №7. 1) ; 2) №8. 1) ; 2) №9. 1) ; 2) №10. 1) ; 2) №11. 1) ; 2) №12. 1) ; 2) №13. 1) 2) №14. 1) 2) №15. 1) 2) №16. 1) 2) №17. 1) 2) №18. 1) 2) №19. 1) 2) №20. 1) 2) №21. №22. 1) 2) №23. 1) 2) №24. 1) 2) №25. 1) 2) №26. 1) 2) №27. 1) 2) №28. 1) 2) №29. 1) 2) №30. 1) 2) Образец выполнения задания 1) 2) Задание №1. Решение методом трапеций Для решения интегралов по методу трапеций необходимо определить значение nтак, чтобы
Здесь где Находим Положим тогда неравенство (*) примет вид откуда т.е. возьмем . Вычисление интеграла производим по формуле Где Все расчеты приведены в табл. 7.
Таблица 7
Таким образом, Задание № 2.
Согласно условию поэтому Вычислительная формула имеет вид где Вычисление значений функции, а также сложение значений функции, имеющих одинаковые коэффициенты в формуле, производим в табл.8. Таблица8
Следовательно, Для оценки точности полученного результата составим таблицу конечных разностей функций до разностей четвертого порядка (табл. Таблица 9
Так как то остаточный член формулы Вычисления производились с четырьмя значащими цифрами, а потому величина остаточного члена на погрешность не влияет. Погрешность вычислений можно оценить из соотношения Значит, полученные четыре десятичных знака верны. Контрольные вопросы
1) Способ уменьшения погрешности нахождения интеграла в методе прямоугольников и трапеций. 2) Объяснить какой аппроксимирующей функцией в методе Симпсона заменяется подынтегральная функция. 3) Обязательно ли участок интегрирования разбивать при реализации метода на более мелкие участки. 4) Объяснить, какие изменения произойдут в алгоритме, если для построения аппроксимирующей функции средняя точка берется не в середине участка. 5) Назвать случаи использования автоматического подбора шага интегрирования. 6) Объяснить изменение погрешности нахождения интеграла при уменьшении числа разбиений n.
Лабораторная работа № 5. ⇐ Предыдущая123456Следующая ⇒ Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰). Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… |
Дифференцирование и интегрирование — формулы, примеры, различия
Дифференцирование и интегрирование являются важными ветвями исчисления, и формулы дифференцирования и интегрирования дополняют друг друга. Интегрируя производную функции, мы получаем в результате исходную функцию. Простыми словами, интегрирование — это процесс, обратный дифференцированию, поэтому интеграл еще называют первообразной. Дифференциация используется для разбиения функции на части, а интеграция используется для объединения этих частей в исходную функцию. Геометрически формула дифференцирования и интегрирования используется для нахождения наклона кривой и площади под кривой соответственно.
Геометрически формула дифференцирования и интегрирования используется для нахождения наклона кривой и площади под кривой соответственно.
Далее в этой статье мы рассмотрим правила дифференцирования и интегрирования, формулы и разницу между ними. Мы также решим несколько примеров на основе дифференциации и интеграции для лучшего понимания концепции.
| 1. | Что такое дифференциация и интеграция? |
| 2. | Формулы дифференцирования и интегрирования |
| 3. | Правила дифференциации и интеграции |
| 4. | Разница в дифференциации и интеграции |
| 5. | Часто задаваемые вопросы о дифференциации и интеграции |
Что такое дифференциация и интеграция?
Дифференцирование и интегрирование — это области исчисления, в которых мы определяем производную и интеграл функции.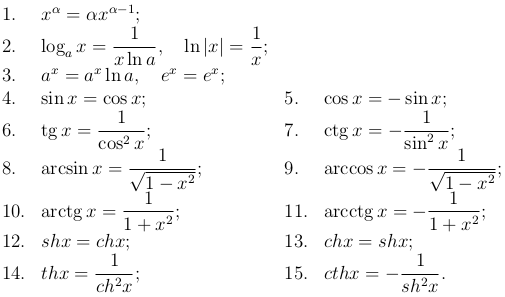 Дифференцирование — это процесс нахождения отношения небольшого изменения одной величины к малому изменению другой, зависящему от первой величины. С другой стороны, процесс нахождения площади под кривой функции называется интегрированием. Мы можем найти дифференцирование и интегрирование функции при определенных значениях и в определенном диапазоне конечных пределов. Интеграция функции, которая выполняется в определенных и конечных пределах, называется определенной интеграцией.
Дифференцирование — это процесс нахождения отношения небольшого изменения одной величины к малому изменению другой, зависящему от первой величины. С другой стороны, процесс нахождения площади под кривой функции называется интегрированием. Мы можем найти дифференцирование и интегрирование функции при определенных значениях и в определенном диапазоне конечных пределов. Интеграция функции, которая выполняется в определенных и конечных пределах, называется определенной интеграцией.
Основная формула для дифференцирования и интегрирования функции f(x) в точке x = a определяется выражением,
- Дифференцирование: f'(a) = lim h→0 [f (а+ч) — f(ч)]/ч
- Интегрирование: ∫f(x) dx = F(x) + C
Далее, в следующем разделе мы рассмотрим часто используемые формулы дифференцирования и интегрирования.
Формулы дифференцирования и интегрирования
Дифференцирование функции f(x) дает f'(x), которая является производной от f(x), а дальнейшее интегрирование f'(x) возвращает исходную функцию f(x). Также иногда обратный процесс интегрирования не может генерировать постоянные члены исходной функции, и поэтому к результатам интегрирования добавляется константа «C». В этом разделе мы рассмотрим различные наиболее часто используемые дифференцирования и формулы интегрирования для алгебраических функций, постоянной функции, показательной функции, логарифмической функции и тригонометрических функций.
Также иногда обратный процесс интегрирования не может генерировать постоянные члены исходной функции, и поэтому к результатам интегрирования добавляется константа «C». В этом разделе мы рассмотрим различные наиболее часто используемые дифференцирования и формулы интегрирования для алгебраических функций, постоянной функции, показательной функции, логарифмической функции и тригонометрических функций.
| Дифференциация | Интеграция |
|---|---|
| d(x n )/dx = nx n-1 | ∫x n dx = x n+1 /(n + 1) + C, n ≠ -1 |
| d(K)/dx = 0 | ∫К дх = Кх + С |
| d(e x )/dx = e x | ∫e x dx = e x + C |
| d(a x )/dx = a x log a | ∫a x dx = a x /log a + C |
| d(ln x)/dx = 1/x | ∫(1/x) dx = ln x + C |
| d(log a x)/dx = 1/(x ln a) | ∫log a x dx = x log a x — x/ln a |
Тригонометрические и обратные тригонометрические функции, формулы дифференцирования и интегрирования
Далее мы суммируем все тригонометрические формулы дифференцирования и интегрирования в таблице ниже. У нас есть шесть основных тригонометрических функций — sin x, cos x, tan x, cot x, sec x и cosec x. Также откроем формулы дифференцирования и интегрирования обратных тригонометрических функций — sin -1 x, cos -1 x, tg -1 x, ctg -1 x, sec -1 х, а cosec -1 х. Дифференцирование и интегрирование тригонометрических функций дополняют друг друга.
У нас есть шесть основных тригонометрических функций — sin x, cos x, tan x, cot x, sec x и cosec x. Также откроем формулы дифференцирования и интегрирования обратных тригонометрических функций — sin -1 x, cos -1 x, tg -1 x, ctg -1 x, sec -1 х, а cosec -1 х. Дифференцирование и интегрирование тригонометрических функций дополняют друг друга.
| Дифференциация | Интеграция |
|---|---|
| d(sin x)/dx = cos x | ∫sin x dx = -cos x + C |
| d(cos x)/dx = -sin x | ∫cos x dx = sin x + C |
| d(tan x)/dx = сек 2 x | ∫tan x dx = (1/a) ln |sec x| + С |
| d(cot x)/dx = -cosec 2 x | ∫cot x dx = (1/a) ln |sin x| + С |
| d(сек x)/dx = сек x тангенс x | ∫sec x dx = (1/a) ln |sec x + tan x| + С |
| d(cosec x)/dx = -cosec x cot x | ∫cosec x dx = (1/a) ln |cosec x — ctg x| + С |
| d(sin -1 x)/dx = 1/√(1 — x 2 ) | ∫sin -1 x dx = x sin -1 x + √(1 — x 2 ) + C |
| d(cos -1 x)/dx = -1/√(1 — x 2 ) | ∫cos -1 x dx = x sin -1 x — √(1 — x 2 ) + C |
| d(tan -1 x)/dx = 1/(1 + x 2 ) | ∫tan -1 x dx = x tan -1 x — (1/2) ln(1 + x 2 ) + C |
| d(кроватка -1 x)/dx = -1/(1 + x 2 ) | ∫кроватка -1 х дх = х кроватка -1 х + (1/2) ln(1 + х 2 ) + С |
| d(сек -1 x)/dx = 1/x√(x 2 — 1) | ∫сек -1 x dx = x сек -1 x — ln(|x| + √(x 2 — 1)) + C |
| d(cosec -1 x)/dx = -1/x√(x 2 — 1) | ∫cosec -1 x dx = x sec -1 x + ln(|x| + √(x 2 — 1)) + C |
Правила дифференциации и интеграции
Далее мы рассмотрим некоторые важные и часто используемые правила дифференцирования и интегрирования. Правилами, которые используются для дифференциации комбинаций функций, являются правило произведения, частное правило и цепное правило. Точно так же мы используем различные правила интегрирования функций, такие как основная теорема исчисления, и обычно используемые методы интегрирования, а именно метод подстановки, интегрирование по частям, интегрирование по неполным дробям и т. д. Ниже приведены правила дифференцирования и интегрирование и их формулы: 9б\) f(x)dx
Правилами, которые используются для дифференциации комбинаций функций, являются правило произведения, частное правило и цепное правило. Точно так же мы используем различные правила интегрирования функций, такие как основная теорема исчисления, и обычно используемые методы интегрирования, а именно метод подстановки, интегрирование по частям, интегрирование по неполным дробям и т. д. Ниже приведены правила дифференцирования и интегрирование и их формулы: 9б\) f(x)dx
Разница в дифференциации и интеграции
Теперь, когда мы поняли концепцию дифференциации и интеграции, давайте теперь поймем различия между дифференциацией и интеграцией. В приведенной ниже таблице показаны их различия и важные свойства дифференциации и интеграции.
Дифференциация VS Интеграция
| Дифференциация | Интеграция |
|---|---|
Дифференциация – это процесс определения скорости изменения количества по отношению к другому количеству. | Интеграция — это процесс объединения более мелких компонентов в единое целое, которое действует как один компонент. |
| Дифференцирование используется для нахождения наклона функции в точке. | Интегрирование используется для нахождения площади под кривой интегрируемой функции. |
| Производные считаются в точке. | Определенные интегралы функций рассматриваются на отрезке. |
| Дифференциация функции уникальна. | Интегрирование функции может быть неоднозначным, так как значение константы интегрирования C произвольно. |
Дифференциация и сходство интеграции
Далее мы рассмотрим некоторые общие свойства и сходства дифференциации и интеграции. Сходства и общие формулы, которым удовлетворяют как дифференцирование, так и интегрирование:
- Они удовлетворяют свойству линейности, то есть d(f(x) ± g(x))/dx = d(f(x)) /dx ± d(g(x))/dx и ∫[f(x) ± g(x)] dx = ∫f(x) dx ± ∫g(x) dx
- Дифференциация и интеграция — процессы, противоположные друг другу.

- Они удовлетворяют свойству скалярного умножения, то есть d(kf(x))/dx = kd(f(x))/dx и ∫kf(x) dx = k ∫f(x) dx
Важные замечания по дифференциации и интеграции:
- Дифференциация и интеграция являются обратными процессами друг друга. Следовательно, при интегрировании производной функции мы получаем в качестве результата исходную функцию вместе с константой интегрирования.
- Дифференциация дает небольшую скорость изменения количества. С другой стороны, интегрирование дает значение в непрерывных пределах и описывает кумулятивный эффект функции.
☛ Похожие темы:
- Дифференциальные уравнения
- Производные сложных функций
- Интеграция сек x тангенс x
Часто задаваемые вопросы о дифференциации и интеграции
Что такое дифференцирование и интегрирование в исчислении?
Дифференцирование и интегрирование являются важными разделами исчисления, а формулы дифференцирования и интегрирования дополняют друг друга. Дифференцирование — это процесс нахождения отношения небольшого изменения одной величины к малому изменению другой, зависящему от первой величины. С другой стороны, процесс нахождения площади под кривой функции называется интегрированием.
Дифференцирование — это процесс нахождения отношения небольшого изменения одной величины к малому изменению другой, зависящему от первой величины. С другой стороны, процесс нахождения площади под кривой функции называется интегрированием.
Какая связь между дифференциацией и интеграцией?
Дифференциация и интеграция являются процессами, обратными друг другу. При интегрировании производной функции в результате мы получаем исходную функцию, поэтому интеграл также называют первообразной. геометрически дифференцирование дает наклон функции, тогда как интегрирование дает площадь под кривой функции.
Как дифференциация и интеграция являются обратными процессами?
Когда мы интегрируем производную функции, мы получаем исходную функцию. Также интеграл функции называется ее первообразной. Основная теорема исчисления устанавливает связь между дифференцированием и интегрированием и показывает, как они являются процессами, обратными друг другу.
Почему дифференцирование и интегрирование являются линейными преобразованиями?
Дифференциация и интегрирование являются линейными преобразованиями, поскольку они удовлетворяют следующим свойствам:
- d(f(x) ± g(x))/dx = d(f(x))/dx ± d(g(x))/dx и ∫[f(x) ± g(x)] dx = ∫f(x) dx ± ∫g(x) dx
- d(kf(x))/dx = kd(f(x))/dx и ∫kf(x) dx = k ∫f(x) dx
Каковы различия и сходства между дифференциацией и интеграцией?
Некоторые из общих различий и сходств между дифференциацией и интеграцией:
- Дифференциация — это процесс определения скорости изменения количества по отношению к другой величине, а Интеграция — это процесс сведения меньших компонентов в единую единицу, которая действует как один компонент.

- Они оба удовлетворяют свойству линейности.
- Производные рассматриваются в точке, а определенные интегралы функций рассматриваются на интервале.
Формула дифференцирования и интегрирования
Дифференцирование и интегрирование являются весьма важными понятиями в исчислении, которые обычно используются для изучения изменений. Исчисление не ограничивается только математикой, но имеет огромное количество приложений в различных областях науки, а также в экономике. Кроме того, мы можем обнаружить исчисление в проведении анализа в финансах, а также на фондовом рынке. В этой главе мы изучим некоторые формулы дифференцирования и интегрирования с примерами помимо интересной концепции!
(Изображение будет загружено в ближайшее время)
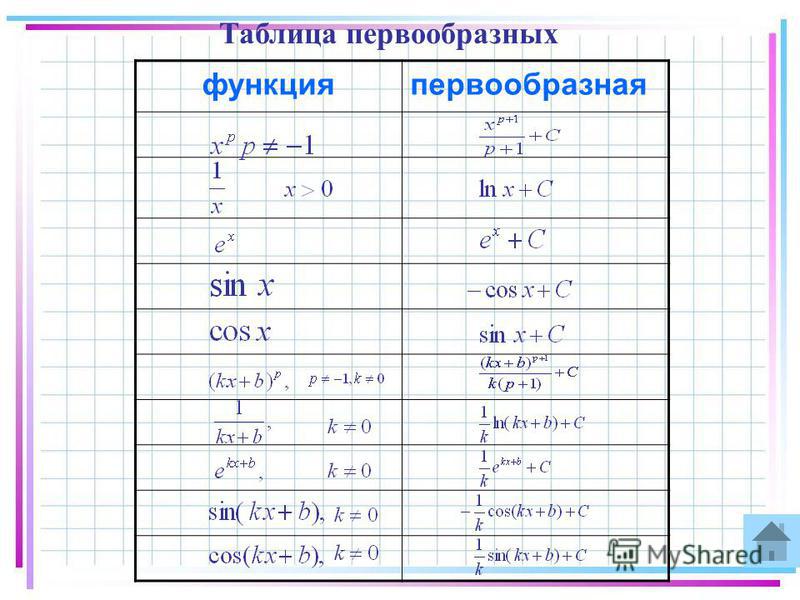
Ниже приведены некоторые основные формулы дифференцирования и интегрирования.
Формулы дифференцировки и интеграции
Формулы дифференциации | Форма интегрирования |
. |
Что такое дифференциация в математике?
Математическая концепция дифференциации помогает нам найти скорость изменения. Например, это позволяет нам определить скорость изменения скорости во времени (называемую ускорением). Кроме того, это также позволяет нам найти скорость изменения x по отношению к y, которая графически при y по отношению к x является градиентом кривой. Существует набор простых правил, которые можно использовать, чтобы легко различать ряд функций.
Если y = некоторая функция от x, то производная от y (по x) записывается как dy/dx.
Например: Узнать градиент кривой y = 2x 4 в точке (4, 56)?
Используя формулу, dy/dx = 8 x 2
Когда x = 4, dy/dx = 8 × 7 = 56.
Что такое интегрирование в математике?
Интегрирование — это математический метод нахождения функции g(x), производная которой Dg(x) эквивалентна заданной функции f(x). Это обозначается знаком интеграла «∫» или ∫f(x), обычно называемым неопределенным интегралом функции. Знак dx обозначает смещение бесконечно малого по x; поэтому ∫f(x) dx становится совокупной суммой произведения f(x) и dx. Определенный интеграл записывается в виде: — «∫a b
Это обозначается знаком интеграла «∫» или ∫f(x), обычно называемым неопределенным интегралом функции. Знак dx обозначает смещение бесконечно малого по x; поэтому ∫f(x) dx становится совокупной суммой произведения f(x) и dx. Определенный интеграл записывается в виде: — «∫a b
Когда «a» и «b» относятся к пределам интегрирования, эквивалентно (=) g(b) − g(a), где Dg(x) = f(x).
Полезность интегрирования
Интегрирование — это математический подход сложения срезов для нахождения целого. Применяя теорию интегрирования, мы можем легко найти площади, объемы, срединные точки многих полезных фигур. Тем не менее, проще всего начать с нахождения площади под кривой функции, как показано ниже:
(Изображение будет загружено в ближайшее время)
Дифференцирование под знаком интеграла
Дифференцирование под знаком интеграла — это алгебраическая операция в исчислении, которая выполняется для вычисления определенных интегралов. При достаточно свободной ситуации с интегрируемой функцией эта операция позволяет поменять местами порядок интегрирования и дифференцирования. В его упрощенной версии, называемой интегральным правилом Лейбница, дифференцирование под знаком интеграла моделирует полученное уравнение, законное по формуле: 9{1} (-2) = 6(4) -\frac{900}{16} = -\frac{129}{4} = -32,25\]
При достаточно свободной ситуации с интегрируемой функцией эта операция позволяет поменять местами порядок интегрирования и дифференцирования. В его упрощенной версии, называемой интегральным правилом Лейбница, дифференцирование под знаком интеграла моделирует полученное уравнение, законное по формуле: 9{1} (-2) = 6(4) -\frac{900}{16} = -\frac{129}{4} = -32,25\]
Таким образом, при x = −2 получается производная быть отрицательным и, следовательно, функция убывает при x = −2
Разница между дифференцированием и интегрированием [обновлено в 2022 г.]
Последнее обновление: 22 сентября 2022 г. / By Piyush Yadav / Проверка фактов / 4 минуты
Исчисление первоначально было известно как исчисление бесконечно малых или «исчисление бесконечно малых». Исчисление бесконечно малых появилось в 17 веке.
Это называется так, потому что это похоже на использование маленьких камешков для вычисления чего-либо. Дифференциация в исчислении разрезает что-то на маленькие кусочки, чтобы знать о его изменениях. Интеграция в исчислении объединяет маленькие кусочки вместе, чтобы узнать количество.
Дифференциация в исчислении разрезает что-то на маленькие кусочки, чтобы знать о его изменениях. Интеграция в исчислении объединяет маленькие кусочки вместе, чтобы узнать количество.
Исчисление — это изучение непрерывных изменений.
В математическом анализе используются две основные ветви: Дифференциация и Интеграция. Многие студенты и даже ученые не в состоянии понять его отличие.
Дифференциация против интеграцииОсновное различие между дифференцированием и интегрированием заключается в том, что дифференцирование используется для определения мгновенной скорости изменения и наклона кривых, тогда как если вам нужно вычислить площадь под кривыми, используйте интегрирование. Как видите, и дифференцирование, и интегрирование противоположны друг другу по математическому значению.
Таблица сравнения дифференцирования и интегрирования
| Параметры сравнения | Дифференцирование | Интегрирование |
|---|---|---|
| Назначение | Дифференцирование используется для расчета градиента кривой. Он используется для определения мгновенных скоростей перехода от одной точки к другой. Он используется для определения мгновенных скоростей перехода от одной точки к другой. | Интегрирование используется для расчета площади под кривыми или между ними. |
| Реальное применение | Дифференцирование используется для расчета мгновенной скорости. Он также используется, чтобы определить, является ли функция возрастающей или убывающей. | Интегрирование используется для расчета площади искривленных поверхностей. Он также используется для расчета объема объектов. |
| Сложение и деление | Дифференциация использует деление для вычисления мгновенной скорости или любых желаемых результатов. | Интеграция использует сложение для своих вычислений. |
| Прямо противоположно | Дифференциация – обратный процесс интеграции. | Интеграция — это обратный процесс дифференциации. |
| Роль | Дифференцирование используется для вычисления скорости функции, поскольку она вычисляет мгновенную скорость. | Интегрирование используется для расчета расстояния, пройденного любой функцией, так как вычисляет площадь под кривой. |
Что такое дифференциация?
В математике метод нахождения скорости изменения функции или нахождения производной известен как дифференцирование.
Три производных:
- Алгебраические функции- D ( x N ) = NX N — 1
- 4 — 1
- 15 . cos x
- Экспоненциальные функции- D ( e x ) = e x
Дифференциация используется для вычисления скорости кривой и изменения мгновенного градиента. одной точки в другую.
Существует «цепное правило», которое помогает различать составные функции. Расчет мгновенной скорости является одним из способов использования дифференцирования в реальном времени.
Что такое интеграция?
В исчислении интегрирование относится к формуле и методу, используемому для расчета площади под кривой. Он используется для расчета так, потому что это не идеальная форма, для которой можно просто вычислить площадь.
Интегрирование используется для определения расстояния, пройденного любой функцией. Расстояние, пройденное функцией, представляет собой площадь под кривой.
Main Differences Between Differentiation and Integration
9em\u0022\u003e \u003c/span\u003e>cspan style=\u0022font-size: inherit;text-indent: -0.9em\u0022\u003eИнтеграция и дифференциация в основном отличаются тем, как они применяются и их окончательные результаты.Основное отличие состоит в том, что они используются для получения разных ответов.Трудно получить градиенты нелинейных кривых, так как они имеют разные наклоны в любой заданной точке.Здесь вступает дифференцирование.Он используется для вычисления градиент кривой. Дифференциация — это алгебраическое выражение, которое используется для определения изменения, произошедшего от одной точки к другой. наследовать; текстовый отступ: -0,9em\u0022\u003eС другой стороны, алгебраическое выражение, используемое для вычисления площади под кривыми или между ними, представляет собой интеграцию. inherit;text-indent: -0.9em\u0022>И Дифференциация, и Интеграция являются важными понятиями исчисления, которые используются в сценариях реальной жизни. \u0022font-size: inherit;text-indent: -0.9em\u0022>Дифференциация в основном используется для расчета мгновенной скорости. Он используется, чтобы узнать, увеличивается функция или уменьшается.em>Интегрирование используется для вычисления площади криволинейных поверхностей. Он используется для расчета объема различных объектов. точка различия между дифференцированием и интегрированием заключается в методе, который они используют для вычислений. Результаты дифференцирования получаются путем деления, тогда как результаты интегрирования получаются путем сложения. -0,9em>И Дифференциация, и Интеграция прямо противоположны друг другу. Если кто-то использует дифференциацию, говорят, что он использует противоположность интеграции. Точно так же, если кто-то использует интеграцию, говорят, что он использует противоположность дифференцированию. -0.9em > > Дифференциация используется для вычисления скорости функции, поскольку она вычисляет мгновенную скорость, тогда как интегрирование используется для вычисления расстояния, пройденного любой функцией, поскольку она вычисляет площадь под кривой.\u003c/span> \u003c/li>», «selectedIcon»: «edit», «iconColor»: «#cf2e2e»} /–>
Он используется, чтобы узнать, увеличивается функция или уменьшается.em>Интегрирование используется для вычисления площади криволинейных поверхностей. Он используется для расчета объема различных объектов. точка различия между дифференцированием и интегрированием заключается в методе, который они используют для вычислений. Результаты дифференцирования получаются путем деления, тогда как результаты интегрирования получаются путем сложения. -0,9em>И Дифференциация, и Интеграция прямо противоположны друг другу. Если кто-то использует дифференциацию, говорят, что он использует противоположность интеграции. Точно так же, если кто-то использует интеграцию, говорят, что он использует противоположность дифференцированию. -0.9em > > Дифференциация используется для вычисления скорости функции, поскольку она вычисляет мгновенную скорость, тогда как интегрирование используется для вычисления расстояния, пройденного любой функцией, поскольку она вычисляет площадь под кривой.\u003c/span> \u003c/li>», «selectedIcon»: «edit», «iconColor»: «#cf2e2e»} /–>
Заключение
Одно из основных различий между дифференцированием и интегрированием состоит в том, что два алгебраических приложения прямо противоположны друг другу по своему применению.




 (59)
(59)
 к. функция ] на интервале положительна.
к. функция ] на интервале положительна. (104)
(104)


 , если известно, что закон, выражающий зависимость пройденного пути от времени, имеет вид .
, если известно, что закон, выражающий зависимость пройденного пути от времени, имеет вид .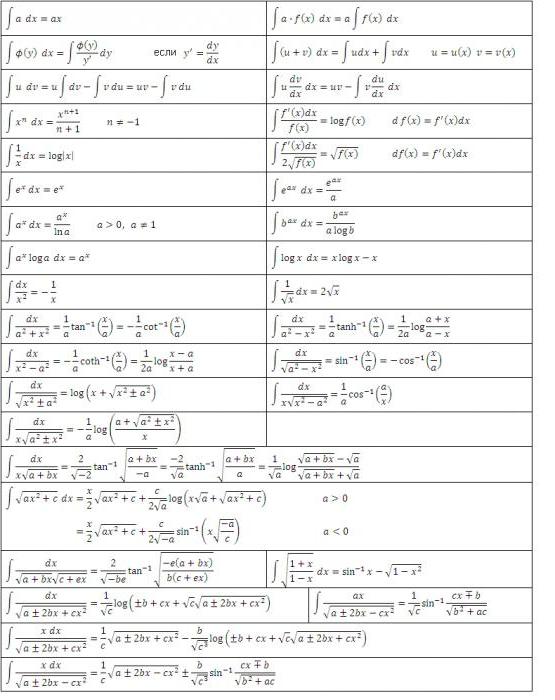
 — КиберПедия
— КиберПедия ..
..

 1) 2)
1) 2) Решение методом Симпсона
Решение методом Симпсона 9).
9).
 ..
..

 {x}\] 9{−1}x + C\]
{x}\] 9{−1}x + C\]