Алгебра логики — презентация онлайн
1. АЛГЕБРА ЛОГИКИ
Основнымипонятиями
алгебры логики являются понятие
логической переменной и логической функции.
Логической
переменной
(аргументом) называется величина
которая может принимать одно из двух значений («0» или «1»)
Логической функцией называется функция двоичных переменных
которая также может принимать одно из двух возможных состояний
(«0» или «1»)
Множество состояний (значений), которые могут принимать как
аргументы так и функции, равно двум.
Для этих состояний в алгебре логики определяются отношение
эквивалентности обозначаемое (=) и три операции:
логического сложения (дизъюнкции)
обозначаемое- + или V
логического умножения (конъюнкции)
обозначаемое- ● или Λ или &
логического отрицания (инверсии)
обозначаемое- ¯
При выполнении выше перечисленных операций отношения
эквивалентности имеют вид:
а) дизъюнкция
0+0=0
0+1=1
1+0=1
1+1=1
б) конъюнкция
0●0=0
0●1=0
1●0=0
1●1=1
в) инверсия
_
0=1
_
1=0
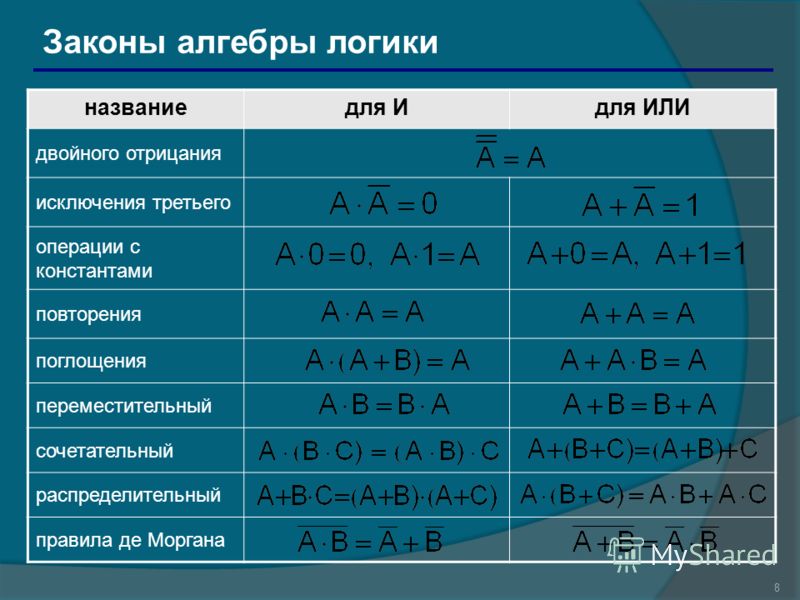
Законы алгебры логики:
1.
 Переместительный закон
Переместительный закондля логического сложения:
для логического умножения:
2. Сочетательный закон
для логического сложения:
для логического умножения:
x1 + x2= x2 +x1,
x1 x2= x2 x1.
(x1 + x 2)+x3= x1 +(x2 + x3),
(x1 x 2) x3 = x1(x2 x3).
3. Распределительные законы
первый распределительный закон: x1(x2+x3) = x1 x2+x1 x3, второй
распределительный закон: x1+x2 x3=(x1+x2)(x1+x3).
4. Законы отрицания (правило де Моргана)
для дизъюнкции:
x1 + x2 = x1 x2
для конъюнкции:
x1 x2 = x1 + x2
двойное отрицание:
x=x
5. Законы поглощения
дизъюнктивное поглощение: x1+x1 x2= x1 (1+x2)=x1
конъюнктивное поглощение: x1 (x1+x2)=x1 x1+x1 x2=x1+x1 x2=x2
6. Законы склеивания
дизъюнктивное склеивание: x1 x2+x1 x2=x1 (x2+x2)=x1
конъюнктивное склеивание: (x1+x2)(x1+x2)=x1+x1 x2+x1 x2=x1
Логическая связь НЕ (логическое отрицание)
Отрицанием высказывания х называют сложное высказывание F(х),
которое истинно, когда х ложно и ложно, когда х истинно.

Аналитическая функция, УГО и таблица истинности элемента НЕ
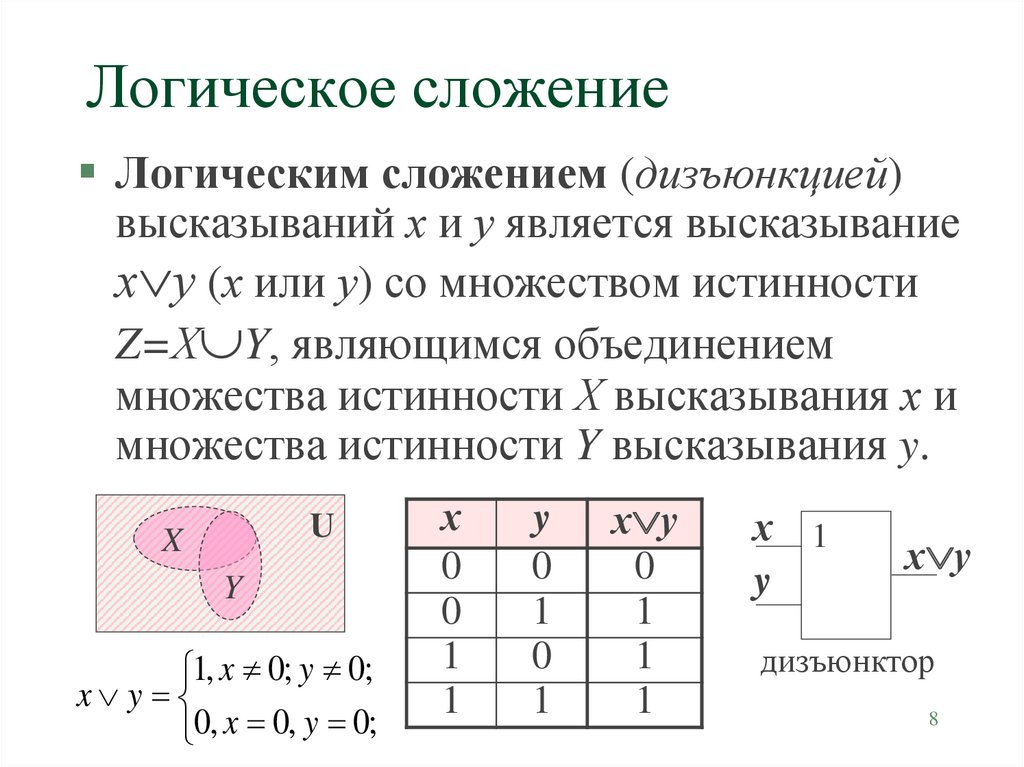
Логическая связь ИЛИ – сложение (дизъюнкция) высказываний
Дизъюнкцией двух высказываний х1 и х2 называется сложное
высказывание F(х1, х2), которое ложно только в одном случае,
когда х1 и х2 одновременно ложны (х1 = 0 и х2 = 0). Во всех
остальных случаях высказывание F(х1, х2) истинно.
Аналитическая функция, УГО и таблица истинности элемента ИЛИ
Логическая связь И (конъюнкция высказываний)
Конъюнкцией высказываний х1 и х2, называется сложное
высказывание F(х1, х2), которое истинно только в одном случае,
когда х1 и х2 одновременно истинны (х1 = 1 и х2 = 1). Во всех
остальных случаях высказывание F(х1, х2) ложно.
Аналитическая функция, УГО и таблица истинности элемента И
Логическая связь отрицание дизъюнкции (операция Пирса)
Логической связью отрицание дизъюнкции высказываний х1 и х2,
называется сложное высказывание F(х1, х2), которое истинно
только в том случае, когда х1 и х2 одновременно ложны (х1 = 0 и
х2 = 0).
 Во всех остальных случаях высказывание F(х1, х2)
Во всех остальных случаях высказывание F(х1, х2)ложно.
Аналитическая функция, УГО и таблица истинности элемента ИЛИНЕ
Логическая связь отрицание конъюнкции (операция Шеффера)
Логической связью отрицание конъюнкции высказываний х1 и х2,
называется сложное высказывание F(х1, х2), которое ложно
только в том случае, когда х1 и х2 одновременно истинны (х1 = 1
и х2 = 1). Во всех остальных случаях высказывание F(х1, х2)
истинно.
Аналитическая функция, УГО и таблица истинности элемента И-НЕ
Логическая связь отрицание равнозначности
(операция ИЛИ-ИЛИ)
Логической связью отрицание равнозначности высказываний х1 и х2,
называется сложное высказывание F(х1, х2), которое истинно
тогда, когда значения истинности высказываний х1 и х2 не
совпадают и ложно, когда значения истинности высказываний
х1 и х2 совпадают.
Аналитическая функция, УГО и таблица истинности элемента
исключающее ИЛИ
11. СИНТЕЗ ЛОГИЧЕСКИХ СХЕМ
Сущность задач синтеза заключается в том,чтобы спроектировать логическое устройство
Основные этапы синтеза логических схем
На первом этапе на основании заданного
алгоритма работы синтезируемого устройства
формируют словесное описание логической
функции.

Пример: Считать, что цель обнаружена (выходной
сигнал равен 1) только в тех случаях, когда не
менее чем два входных сигнала равны «1». Во всех
остальных случаях цель не обнаружена (выходной
сигнал равен 0).
На втором этапе на основе словесной формы логической функции
составляют табличную форму. Затем по таблице истинности
находят аналитическую форму представления логической
функции в виде СДНФ или СКНФ
Пример:
СДНФ примет вид :
СКНФ примет вид :
Третий этап. На этом этапе осуществляется минимизация СДНФ или
СКНФ с целью уменьшения числа логических элементов,
необходимых
для
разработки
функциональной
схемы
синтезируемого устройства. Для минимизации логических
функций используются как аналитические, так и графические
методы.
Сущность аналитических методов сводится к последовательному
применению законов алгебры логики и их следствий
F(X1,X2,X3)=X2X3(X1+X1)+X1X3(X2+X2)+X1X2(X3+X3) =>
F(X1,X2,X3)=X2X3+X1X3+X1X2
На четвертом этапе на основе минимизированной логической
функции
разрабатывается
функциональная
схема
синтезируемого устройства и проверяется правильность ее
работы.

15. Куб Карно
Куб Карно́ — графический способ минимизации переключательных(булевых) функций, обеспечивающий относительную простоту работы
с большими выражениями и устранение потенциальных гонок.
Представляет
собой
операции
попарного
неполного
склеивания
и
элементарного
поглощения.
Карты
Карно
рассматриваются
как
перестроенная
соответствующим
образом таблица истинности функции.
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и
усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и
были призваны помочь упростить цифровые электронные схемы.
В карту Карно булевы переменные передаются из таблицы истинности
и упорядочиваются с помощью кода Грея, в котором каждое следующее
число отличается от предыдущего только одним разрядом
16. Принципы минимизации
Основнымметодом
минимизации
логических
функций,
представленных в виде СДНФ или СКНФ, является операция
попарного неполного склеивания и элементарного поглощения.

Операция попарного склеивания осуществляется между двумя
термами (членами), содержащими одинаковые переменные,
вхождения которых (прямые и инверсные) совпадают для всех
переменных, кроме одной. В этом случае все переменные, кроме
одной, можно вынести за скобки, а оставшиеся в скобках прямое и
инверсное вхождение одной переменной подвергнуть склейке.
Например:
Аналогично для КНФ:
Возможность поглощения следует из очевидных равенств
На рисунке изображена простая таблица истинности для функции
из двух переменных, соответствующий этой таблице 2-мерный
куб (квадрат), а также 2-мерный куб с обозначением членов
СДНФ и эквивалентная таблица для группировки термов
В случае функции трёх переменных приходится иметь дело с
трёхмерным кубом. Это сложнее и менее наглядно, но технически
возможно. На рисунке в качестве примера показана таблица
истинности для булевой функции трёх переменных и соответствующий
ей куб.
Для упрощения работы с булевыми функциями большого числа
переменных был предложен следующий удобный приём.
 Куб,
Куб,представляющий собой структуру термов, разворачивается на
плоскость как показано на рисунке. Таким образом появляется
возможность представлять булевы функции с числом переменных
больше двух в виде плоской таблицы. При этом следует помнить,
что порядок кодов термов в таблице (00 01 11 10) не соответствует
порядку следования двоичных чисел, а клетки, находящиеся в
крайних столбцах таблицы, соседствуют между собой.
20. Синтез логической схемы
Синтезом логической схемы называется процедура получениялогической схемы реализующую заданную логические функцию.
При синтезе логических схем используются логические элементы.
Набор логических функций, с помощью которого можно
представить любую переключательную функцию называется
функционально полной системой или базисом. Обычно
функционально полными системами являются базисы 1) И, ИЛИ,
НЕ, 2) И, НЕ, 3) ИЛИ, НЕ, 4) И-ИЛИ-НЕ, 5) И-НЕ, 6) ИЛИ-НЕ.
Основным является базис И, ИЛИ, НЕ так как с помощью него
можно записать любую сложную функцию в виде СДНФ и
СКНФ.

При синтезе комбинационной схемы с несколькими выходами,
каждый выход рассматривается как функция входных значений.
Полученные функции минимизируются, и затем строится
логическая схема в одном из заданных базисов.
При синтезе цифровых автоматов , в таблицу функционирования
кроме выходных значений необходимо указывать и внутреннее
состояние устройства.
Пример синтеза комбинационной схемы.
Синтезировать комбинационную схему устройства управления
семисегментным индикатором в базисе И, ИЛИ, НЕ. Устройство
работает согласно таблицы
Составляем таблицу функционирования
устройства, используя символ индикации и
обозначение сегментов. При этом получаем
таблицу зависимости восьми функций а, b, c, d,
e, f, g от переменных (значений входных
сигналов). Затем используя карту Карно,
получаем минимальные дизъюнктивные
форму функций. Неопределенные значения
при этом заменяем на «0» или «1» в
зависимости от эффективности образования
групп и, следовательно, минимизации.

Используя
полученные
функции
синтезируем логическую схему устройства
в базисе И, ИЛИ, НЕ. Синтез выполняется в
направлении от значений входных сигналов
до
получения
выходных
значений.
Первоначально из входных переменных
получаем необходимые для функций
инверсные значения. Затем, поэтапно
применяя необходимые элементы для
реализации операций, получаем конечные
значения функций. Источник логической
единиц условно обозначаем точкой (1). При
положительной логике ей соответствует
напряжение питания всей схемы.
Репетиторы онлайн по алгебре логики. Дистанционные занятия по скайпу
1105
Популярные категории репетиторов математики: Подготовка к ЕГЭ Подготовка к ОГЭ (ГИА) Школьный курс Репетиторы на дом Занятия по скайпу Высшая математика
Найдено 1105 репетиторов
Сбросить фильтры
Сергей Александрович
Частный преподаватель Стаж 3 года
от 2 500 руб / час
свободенСергей Олегович
Преподаватель вуза Стаж 15 лет
от 2 500 руб / час
свободенДенис Дмитриевич
Частный преподаватель Стаж 3 года
У репетитора есть видеопрезентация смотреть видеопрезентация
от 1 600 руб / час
свободенКсения Сергеевна
Частный преподаватель Стаж 17 лет
от 3 000 руб / час
свободенМаксим Александрович
Частный преподаватель Стаж 21 год
У репетитора есть видеопрезентация смотреть видеопрезентация
от 3 000 руб / час
свободенДмитрий Сергеевич
Частный преподаватель Стаж 12 лет
от 5 000 руб / час
свободенМаксим Алексеевич
Частный преподаватель Стаж 13 лет
от 3 000 руб / час
свободенКирилл Вадимович
Студент Стаж 3 года
У репетитора есть видеопрезентация смотреть видеопрезентация
от 2 000 руб / час
свободенЧастный преподаватель Стаж 4 года
от 1 800 руб / час
свободенАрсений Владимирович
Частный преподаватель Стаж 4 года
У репетитора есть видеопрезентация смотреть видеопрезентация
от 2 500 руб / час
свободенБулева алгебра
Логические функции, в которых значения переменных истинны (1) или ложны (0).

Рекламные ссылки
В булевой алгебре значения переменных истинны (1) или ложны (0) .
BUF
y = a (1)
| a | y |
|---|---|
| 0 | 0 |
| 1 | 1 |
AND
y = a & b (2)
| a | b | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
или
Y = A | б (3)
| a | b | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
XOR
y = a ⊻ b (4)
| a | b | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Не
Y = A (5)
| A | Y |
|---|---|
| 0 |
NAND
y = a & b (6)
| a | b | y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Нор
9007 YNO
YNO
YNO
YNO
YNO
9004007 | b (7)| a | b | y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
XNOR
Y = A ⊻ B (8) Рекламные ссылки Добавляйте стандартные и настраиваемые параметрические компоненты, такие как балки с полками, пиломатериалы, трубопроводы, лестницы и т. Перевести О программе Engineering ToolBox! Мы не собираем информацию от наших пользователей. В нашем архиве сохраняются только электронные письма и ответы. Файлы cookie используются только в браузере для улучшения взаимодействия с пользователем. Некоторые из наших калькуляторов и приложений позволяют сохранять данные приложения на локальном компьютере. Эти приложения будут — из-за ограничений браузера — отправлять данные между вашим браузером и нашим сервером. Мы не сохраняем эти данные. Google использует файлы cookie для показа нашей рекламы и обработки статистики посетителей. Пожалуйста, прочитайте Конфиденциальность и условия Google для получения дополнительной информации о том, как вы можете контролировать показ рекламы и собираемую информацию. AddThis использует файлы cookie для обработки ссылок на социальные сети. Пожалуйста, прочитайте AddThis Privacy для получения дополнительной информации. Если вы хотите рекламировать свои товары или услуги в Engineering ToolBox, используйте Google Adwords. Вы можете настроить таргетинг на Engineering ToolBox с помощью управляемых мест размещения AdWords. Эту страницу можно цитировать как Изменить дату доступа. . . закрыть спросил Изменено
2 года, 10 месяцев назад Просмотрено
3к раз Недавно я изучал информатику и познакомился с булевой алгеброй. 2 Вы можете использовать булеву алгебру для многих вещей в программировании. это базовый метод вычисления, такой как сложение, вычитание или умножение чисел, многоцелевой инструмент , а не просто инструмент для сокращения количества строк кода в программе. Обратите внимание, что это не инструмент для просто , что также упрощает аппаратное обеспечение логических вентилей. Однако может иногда использоваться для таких случаев (как и для обратного, или совсем для других целей). Например, если ваша программа содержит слишком сложное логическое выражение или последовательность условных выражений, логическая алгебра может помочь вам упростить выражение и окружающий его код. Но это не обязательно приводит к уменьшению количества строк кода. На самом деле, иногда сложные однострочные логические фрагменты кода становятся более удобными в сопровождении, если вы разбиваете их на несколько строк кода, и булева алгебра может помочь вам в этом.0461 правильно . Итак, ИМХО, ваш вопрос похож на «Могу ли я использовать карманный калькулятор, чтобы найти кратчайший маршрут при путешествии из А в Б» 0019
a b y 0 0 1 0 1 0 1 0 0 1 1 1 Связанные темы
Связанные документы
Engineering ToolBox — Расширение SketchUp — 3D-моделирование в режиме онлайн!
 д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, интересными и бесплатными приложениями SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!
д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, интересными и бесплатными приложениями SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!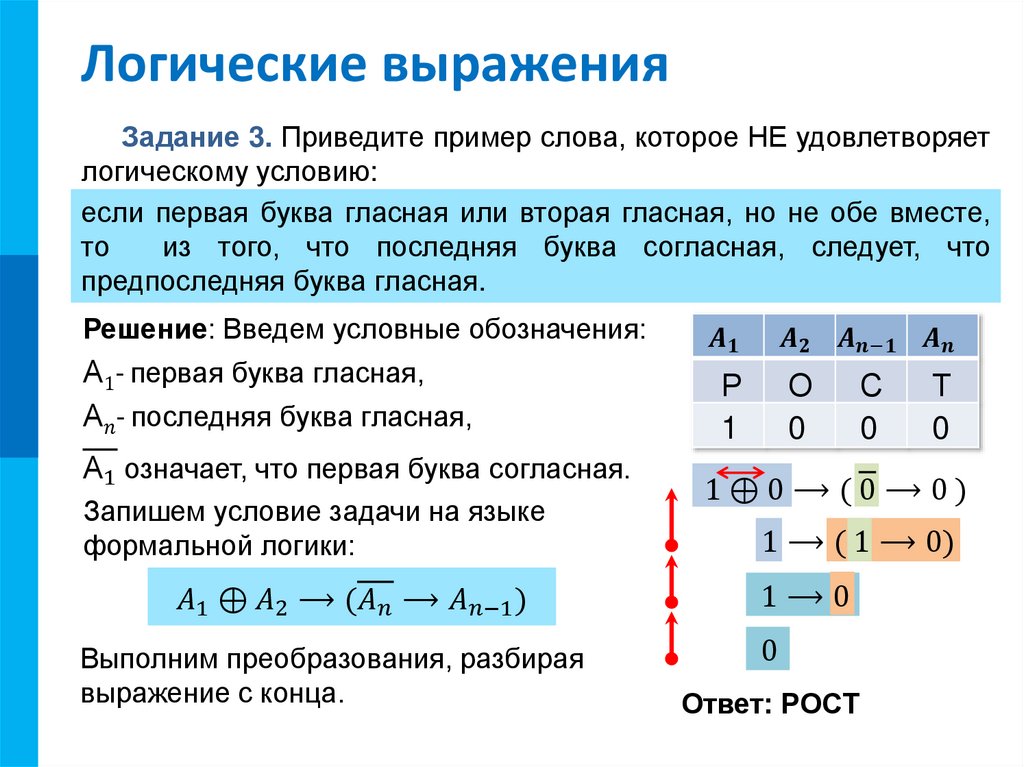
Реклама в ToolBox
Citation
Могу ли я использовать булеву алгебру, чтобы уменьшить количество строк в моем коде?
 Кажется, что булева алгебра используется для упрощения логических элементов в аппаратном обеспечении, чтобы сделать схему минимальной и, следовательно, более дешевой. Есть ли аналогичный способ, которым вы можете использовать его для уменьшения количества строк кода в вашем программном обеспечении на языках более высокого уровня, таких как C++, C# или любой другой язык?
Кажется, что булева алгебра используется для упрощения логических элементов в аппаратном обеспечении, чтобы сделать схему минимальной и, следовательно, более дешевой. Есть ли аналогичный способ, которым вы можете использовать его для уменьшения количества строк кода в вашем программном обеспечении на языках более высокого уровня, таких как C++, C# или любой другой язык?
Да, можно. Но должны ли вы?
Булева алгебра служит для приведения логических выражений к их минимальной форме, но хорошо это или плохо, остается на усмотрение программиста.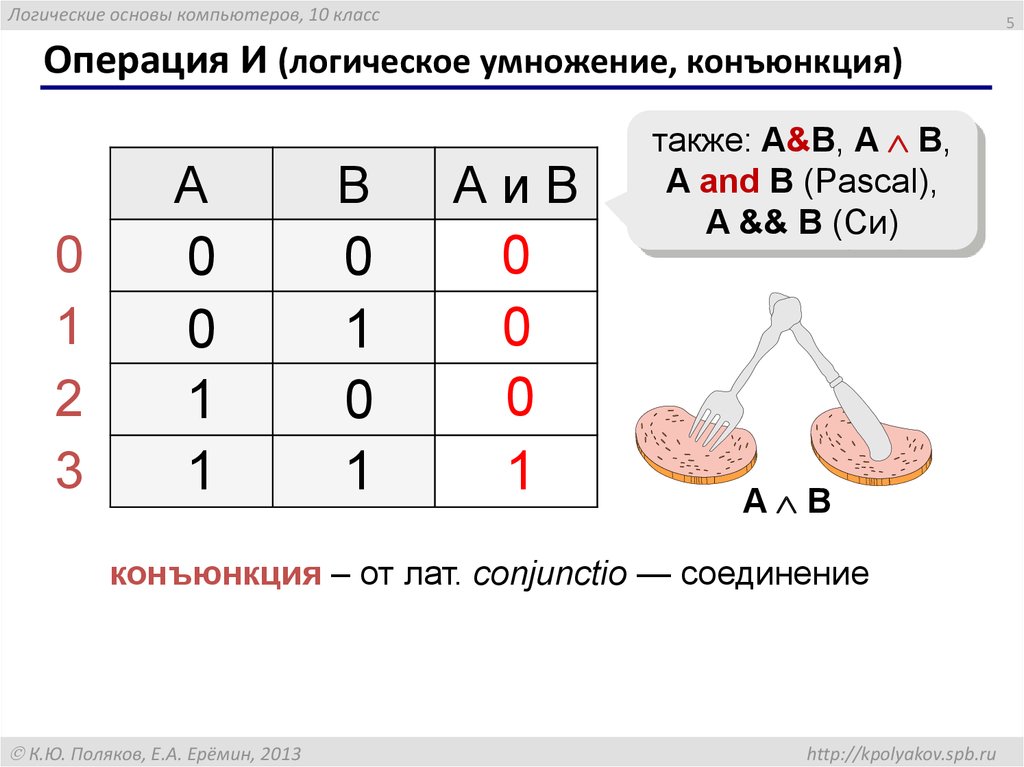 Возьмем этот код проверки:
Возьмем этот код проверки:
... если (person.Money == 0) вернуть; if (person.Money != 0 && person.Age < 15) return; если (person.Age > 90) вернуться; если (человек.Дети > 3) вернуться; если (person.HasWhiteShirt() && person.HasBlueSocks()) return; ...
Это список проверок объекта person , функция выйдет из функции, как только одна из них окажется истинной. Смысл этого довольно ясен, и любой, кто его читает, даже непрограммист, может понять, какие проверки мы делаем.
Однако это можно написать по-разному. Давайте перейдем к строкам кода и упростим его, как вы задали в своем вопросе, и посмотрим, что произойдет:
if (... || person.Money == 0 || person.Age < 15 || person.Age > 90 || person.Children > 3 || (person.HasWhiteShirt() && person.HasBlueSocks()) || ...) return;
Теперь у нас есть одна строка нечитаемых условных выражений, и в результате упрощения мы также потеряли информацию о том, что эта проверка на возраст до 15 лет как-то связана с деньгами. Редактировать этот код в будущем будет намного сложнее, поэтому его сокращение было ошибкой.
Редактировать этот код в будущем будет намного сложнее, поэтому его сокращение было ошибкой.
В заключение: всегда стремитесь к удобочитаемости, независимо от минимальной формы логического выражения.
7
Булева алгебра — это логика, сведенная к самой базовой форме. Она прекрасно соответствует двоичной системе счета, второй из основных возможных систем счета.
кажется, что булева алгебра используется для упрощения логических вентилей в аппаратных средствах
Не совсем. Это позволяет в первую очередь реализовать любую логику на аппаратном уровне. Как только вы это сделаете, вы можете использовать программное обеспечение, чтобы развить это и снова создать более сложную логику.
Так что нет, вы не уменьшите количество строк кода с помощью булевой алгебры. Вы используете его всякий раз, когда нужно сделать бинарный выбор. Если ваша проблема сложна, у вас будет много вариантов программного решения.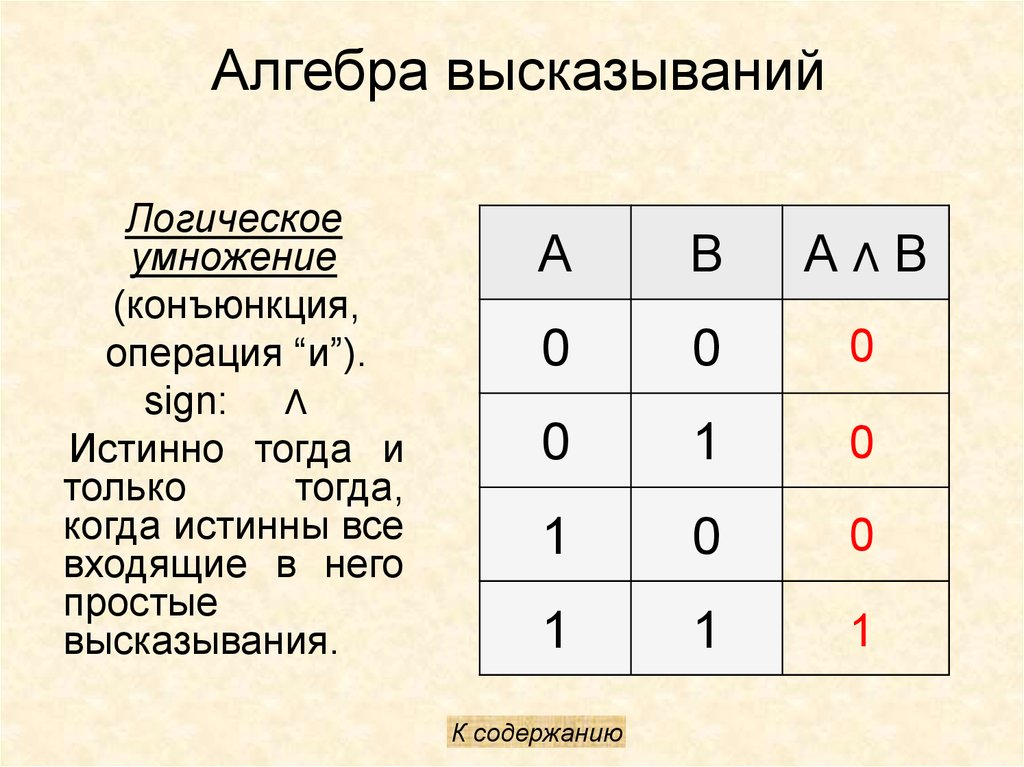
Так что дело обстоит наоборот: простая логика требует меньше булевой алгебры, сложная логика требует больше. И больше логики == больше кода.
Ну, хорошо. Причина, по которой инженеры-электронщики хотят уменьшить количество логических вентилей в схеме, вероятно, связана со стоимостью конструкции и эксплуатационными характеристиками их конечного продукта. Они строят именно то, что в конечном итоге сделает работу.
Когда вы программируете на любом языке, отличном от ассемблера, компьютер в конце концов будет выполнять не ваш код, а его преобразованную версию. Это преобразование языка, удобного для программиста, в язык, удобный для компьютера, можно назвать «компиляцией». Булева логика действительно используется компилятором для достижения операционной эффективности.
Вы можете программировать на ассемблере и выполнять работу компилятора самостоятельно, но с каждым днем это становится все менее и менее стоящим хлопот. Современные компиляторы знают все больше и больше трюков, и лучше вас.
Наоборот, если вы спросите, существует ли подобная практика в языках более высокого уровня, да, это называется «рефакторинг», что означает применение четко определенных преобразований к коду, изменяющему структуру, а не поведение. В 90-х годах Мартин Фаулер опубликовал книгу, представляющую собой каталог, вероятно, наиболее часто повторяющихся базовых рефакторингов в объектных языках.
Конечно, вы можете использовать Булеву алгебру для различных случаев в вашем проекте. Этот метод позволяет получить тот же результат с меньшим количеством шагов и компонентов при разработке схемы.
Однако в случае языков высокого уровня это может привести к большим проблемам. Языки HLL предназначены для удобочитаемости и простоты понимания. Вы можете упростить

В общем, я предлагаю не думать много о сокращении строк кода, а учитывать поведение программы во время выполнения, использование памяти и архитектурный дизайн. Обычно при подаче заявления Булева алгебра В ваших схемах вы выступаете в роли компилятора для большинства существующих языков.
Раньше я думал, что меняется:
if ($type == 'credit') {
общая сумма += сумма;
}
to:
$total += ($type == 'кредит') * $amount;
был умен, потому что удалял , если . Осторожно, хитрый код! Код должен быть читаем как программистом, так и машиной. Задача программиста — поддерживать код в сопровождении.
Обычно разбиение сложной строки на несколько более простых строк повышает читаемость без существенного снижения производительности. Только если бенчмаркинг показывает, что существует неприемлемая проблема с производительностью, вы должны провести рефакторинг для повышения производительности за счет удобочитаемости.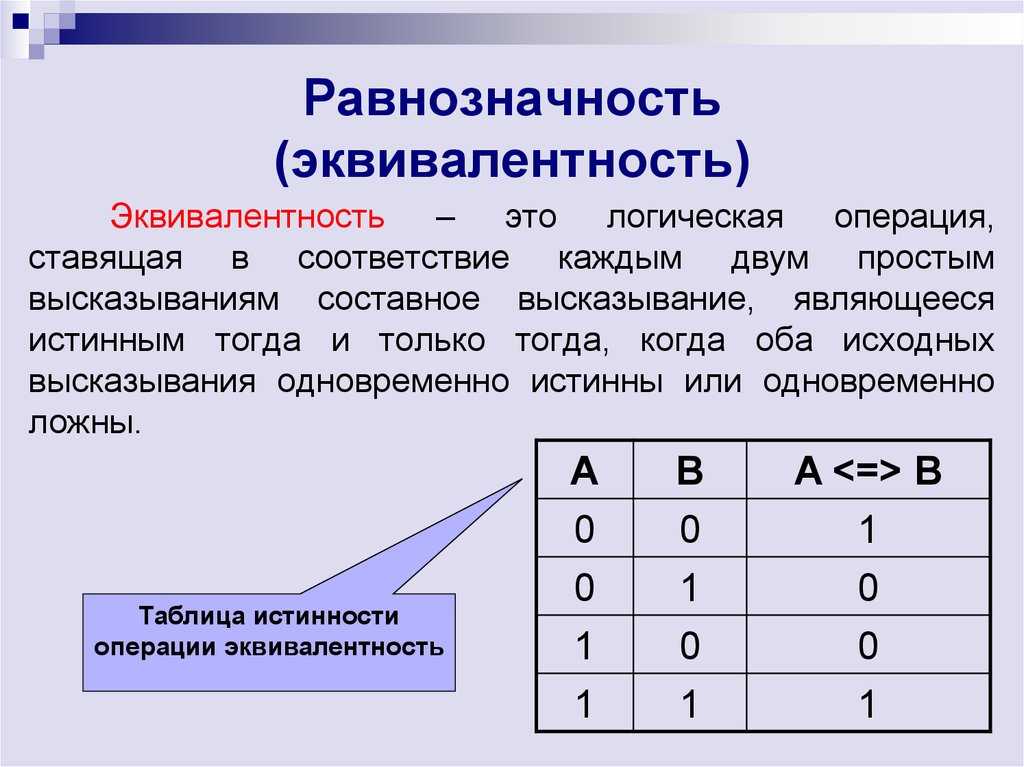
Булева логика, как и все остальное, должна использоваться ожидаемым образом, чтобы сделать код понятным.
В дополнение к существующему обсуждению, включая идею о том, что меньшее количество строк — это хорошо, если это также улучшает читабельность, я просто упомяну одну вещь, которую вы можете сделать с помощью булевой алгебры в языке, где все значения являются истинными или ложными, например Python . Вот решение FizzBuzz на Python, написанное в стиле, доступном практически для любого языка высокого уровня:
для i в диапазоне (1, 101):
с = ''
если i%3==0: s+= 'шипение'
если i%5==0: s+= 'Жужжание'
если s != '': печать(и)
иначе: напечатать (я)
Теперь давайте поговорим о том, что может Python, чего не могут некоторые языки. Для одного можно сократить
с != ''
до
с
, потому что строка правдива тогда и только тогда, когда она не пуста и не равна нулю (последнее здесь недостижимо). Таким образом, мы можем заменить двухстрочный оператор if/else на однострочный
print(s or i)
В Python «или» означает «вернуть первый аргумент, если он правдив, или второй, если нет».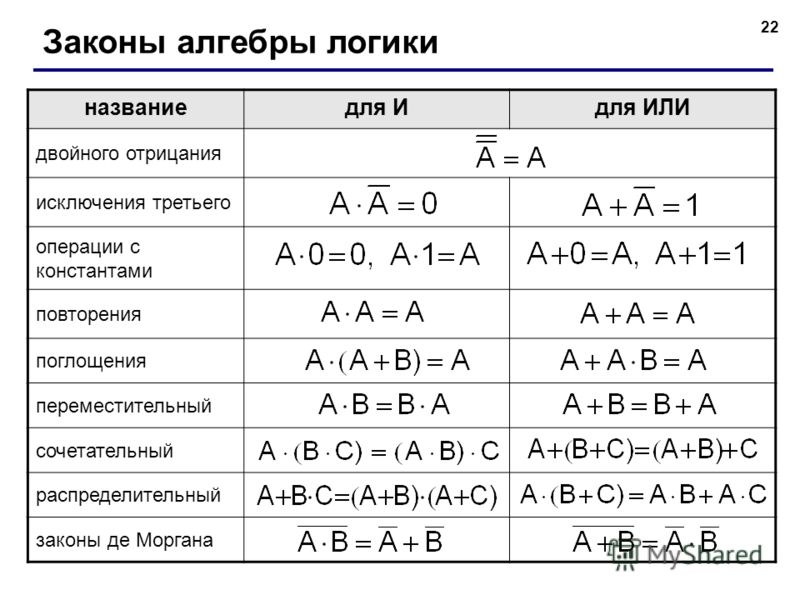 Как правило, эти значения не преобразуются в логические значения; он просто возвращает их как есть.
Как правило, эти значения не преобразуются в логические значения; он просто возвращает их как есть.
Я бы поддержал приведенный выше трюк с сокращением, потому что я думаю, что в этом случае он улучшает читаемость, хотя бы потому, что
- к тому времени, когда вы читаете Python, вы, надеюсь, уже знаете о истинных и ложных значениях (и если вы не знаете, что с ними делают булевы операторы, вам лучше научиться быстро, чтобы избежать веселых ошибок!), и
- это пример, когда меньшее количество строк также дает вам меньше понятий, о которых нужно думать при понимании всего блока.
В данном случае польза была в том, что одна и та же функция не должна упоминаться в двух строках, из которых вызывается только одна, и поэтому мы ищем выражение, которое равняется этому аргументу в каждом сценарии, и мы можем получить его, используя этот не-все — тот малоизвестный факт о том, как Python обрабатывает логические операторы. Я бы не хотел писать
s, если s еще я
или что-то еще менее лаконичное.
