§ 4. Примеры задач на использование законов алгебры логики и формализацию высказываний — ЗФТШ, МФТИ
Максимально упростить, это значит довести выражение до такого вида, когда невозможно применить ни один из законов алгебры логики, которые сокращают длину выражения.
Для того, чтобы не запутаться, можно использовать общую стратегию упрощения логических выражений.
1) Избавиться от операций импликации.
2) Продвинуть отрицание вглубь выражения. То есть применять законы де Моргана, и закон двойного отрицания пока знак отрицания не будет стоять только над переменными (но не над операциями).
После пункта 2 наступает относительная свобода действий. Можно использовать тождества поглощения или раскрывать скобки.
В нашей задаче операция импликации отсутствует, поэтому первый пункт мы пропускаем. Переходим к пункту 2. Применяем два раза второй закон де Моргана (для дизъюнкции) и закон двойного отрицания к правой скобке и получаем следующее логическое выражение:
`bar C vv ` (`A` & `C`) `vv` (`bar A` & `bar C` & `B`)
Если теперь внимательно посмотреть на выражение, то очевидно, что к первому и третьему слагаемому можно применить первый закон поглощения, так как отрицание переменной `C` является первым слагаемым и входит в третье в качестве множителя.
Поскольку дизъюнкцию ещё называют логическим сложением, её операнды называют слагаемыми, аналогично конъюнкция – это логическое умножение, и её операнды называют множителями.
После применения первого закона поглощения получается следующее логическое выражение:
`bar C` `vv` (`A` & `C`)
Применим второй (нестандартный для алгебры) закон дистрибутивности. Получаем:
(`bar C vv A`) & (`bar C vv C`)
Ко второй скобке применяем закон исключённого третьего, превращаем её в единицу, а затем применяем закон поглощения константы `1` и в итоге получаем выражение: `bar C vv A`, которое упростить уже нельзя.
Для лучшего понимания, рекомендуется выписать исходное логическое выражение, последовательно применить к нему все описанные действия и сравнить свой результат с приведённым в конце решения задачи.
Обратите внимание, что исходное логическое выражение зависело от трёх переменных (`A, B, C`) , в то время как упрощённое в итоге зависит от двух логических переменных (`A` и `C`). При этом выражения всё равно остаются равносильными! Это происходит потому, что в процессе упрощения применялись законы поглощения. Аналогичный результат мог бы получиться, если в процессе упрощения выражения используются законы поглощения переменных константами. Исчезновение переменной при упрощении означает, что в исходном выражении она является несущественной.
При этом выражения всё равно остаются равносильными! Это происходит потому, что в процессе упрощения применялись законы поглощения. Аналогичный результат мог бы получиться, если в процессе упрощения выражения используются законы поглощения переменных константами. Исчезновение переменной при упрощении означает, что в исходном выражении она является несущественной.
Чтобы решить эту задачу, необходимо провести процесс формализации условия, сформировать единое логическое выражение и провести его упрощение. Выделим из условия четыре простых высказывания: «`A` нарушил правила», «`B` нарушил правила», «`C` нарушил правила», и «`D` нарушил правила». Обозначим их соответственно буквами `A`, `B`, `C`, `D`. Тогда высказывания из условия формализуются следующим образом (конъюнкция не обозначается никак):
1) `A -> B`;
2) `B -> C` \/ `¬A`;
3) `¬D -> A¬ C`;
4) `D -> A`.
Нам известно, что выполняются все 4 высказывания, следовательно, нужно объединить их знаками конъюнкции и найти наборы, при которых получившееся общее высказывание будет истинным. Эти наборы и покажут нам, какие возможны ситуации (правила обмена нарушил тот, у кого переменная в итоговом наборе имеет значение «1»).
Эти наборы и покажут нам, какие возможны ситуации (правила обмена нарушил тот, у кого переменная в итоговом наборе имеет значение «1»).
Итак, строим логическое выражение:
`(A -> B)( B -> C` \/ `¬A)( ¬D -> A¬C)( D -> A)`.
Теперь будем его упрощать. По алгоритму первым делом избавляемся от операции импликации. Получаем следующее выражение:
`(¬A` \/ `B)( ¬B` \/ `C` \/ `¬A)( D` \/ `A¬C)( ¬D` \/ `A)`.
Раскрываем скобки. Первую перемножаем со второй, а третью с четвёртой.
`(¬A¬B` \/ `¬AC` \/ `¬A` \/ `BC` \/ `B¬A) ( DA` \/ `A¬C¬D` \/ `A¬C)`.
Напомним, что слагаемые, равные нулю по причине того, что в них входит сразу и переменная и её отрицание, мы не записываем. В первой скобке теперь можно применить тождество поглощения, и «съесть» все слагаемые, имеющие в своём составе `A` с отрицанием. Во второй скобке можно также применить тождество поглощения, и «съесть» второе слагаемое. В итоге получаем:
Во второй скобке можно также применить тождество поглощения, и «съесть» второе слагаемое. В итоге получаем:
`( ¬A` \/ `BC ) ( DA` \/ `A¬C)`.
При раскрытии оставшихся скобок три из четырёх слагаемых окажутся равными нулю, а последнее будет выглядеть следующим образом: `ABCD`. Из этого следует, что все четверо работников банка нарушили правило обмена валюты. (Только в этой ситуации предположения из условия задачи одновременно выполняются).
Правила обмена валюты нарушили все.
В заключение приведём общую схему решения текстовых логических задач, которую мы уже применяли на практике при разборе примеров.
Среди задач алгебры логики часто встречаются задачи на определение количества решений систем логических уравнений. Рассмотрим примеры некоторых их них.
Заметим, что часто перед решением больших систем логических уравнений сначала удобно упростить исходную систему с помощью законов алгебры логики, а также воспользоваться заменой переменных, если это возможно.
23 задание ЕГЭ по информатике
ЕГЭ по информатике выбирают будущие работники ИТ-сферы. Но для сдачи экзамена нужно не только уметь программировать. Многие задачи связаны с математикой, анализом данных, логикой. Чтобы без проблем решить их на экзамене, необходимо много практиковаться. Вы можете учиться самостоятельно, а можете записаться на курсы подготовки к ЕГЭ и ОГЭ, где преподаватели будут объяснять все сложные моменты. В статье мы разберем тему «Логические выражения». Она встречается в 23 номере ЕГЭ по информатике.
Алгебра логики
Прежде чем приступить к разбору заданий, нужно изучить теорию. Алгеброй логики называют один из разделов математической логики. Его особенность в том, что логические выражения анализируются с использованием алгебраических законов и правил. Создание науки связано с именем Дж. Буля (1815-1864). Ученый разработал собственный математический язык, записывал с его помощью уравнений. Истинность и ложность выражений доказывал с помощью алгебраических операций. Несмотря на то, что алгебра логики продолжает развиваться, принцип остается прежним.
Несмотря на то, что алгебра логики продолжает развиваться, принцип остается прежним.
Основой алгебры логики (и 23 задания ЕГЭ) являются логические высказывания — не вопросительные предложения, по поводу которых можно однозначно сказать, являются они истинными или ложными. Например, высказывание «снег белый» истинно, «солнце светит ночью» — ложно. Предложение «мороженое вкусное» не является логическим высказыванием, нельзя однозначно сказать о его правдивости. Если заменить его на «я люблю мороженое», то оно может принимать как истинное, так и ложное значение, это зависит от предпочтений человека.
В 23 задании по информатике встречаются двузначные высказывания, принимающие значения «правда» и «неправда». Но алгебра логики рассматривает также многозначные, имеющие значения «вероятно», «невозможно», «возможно». Элементарные высказывания обозначают латинскими буквами (например, A = «осенью деревья сбрасывают листву»). Сложные высказывания составляются из элементарных с использованием частиц «и», «или», «тогда и только тогда», «если. . то» (например, А и В = «осенью деревья сбрасывают листву и некоторые птицы улетают на юг»). В цифровом представлении истине соответствует число 1, а лжи число 0. Для вычисления примеров обычно используются таблицы истинности.
. то» (например, А и В = «осенью деревья сбрасывают листву и некоторые птицы улетают на юг»). В цифровом представлении истине соответствует число 1, а лжи число 0. Для вычисления примеров обычно используются таблицы истинности.
Основные операции алгебры логики
Для решения номера 23 по информатике нужно знать основные операции:
- инверсия (отрицание). Операция называется унарной, так как преобразует одну величину: «переворачивает» выражение, меняет истину на ложь и наоборот. Обозначается чертой над буквой, символом ᆨ, словом «not». В результате преобразования числа A получается высказывание ᆨA. Читается «не А», «отрицание А», «А ложно». Пример: A = 1 больше 0; Ā = 1 не больше 0. На рисунке А — множество точек, Ā — все точки, не принадлежащие множеству;
- конъюнкция (умножение). Обозначает величины (2 или больше), объединенные союзом И. Для математической записи используются знаки ∧, •, &, and. Иногда знак опускают, по аналогии с математикой.
 Высказывание истинно, когда все его части правдивы, например, A∧B = «химия изучает вещества и молекулы». На рисунке изображается множествами, их пересечение соответствует A∧B;
Высказывание истинно, когда все его части правдивы, например, A∧B = «химия изучает вещества и молекулы». На рисунке изображается множествами, их пересечение соответствует A∧B;
- дизъюнкция (сложение). Связывает 2 и более выражения союзом ИЛИ. Обозначается знаками ∨, +, |, or. Выражение истинно, если правдива одна часть или сразу обе. Пример: А∨В = «звезды состоят из газа или плазмы». На рисунке изображается объединением множеств;
- строго-разделительная (исключающая) дизъюнкция. Связывает высказывания союзом ИЛИ. Особенность в том, что союз является исключающим, то есть выражение истинно, когда правдива одна из его частей. Обозначают через ∨∨, ⊕, а читают «либо А, либо В». Пример: А⊕В = «валентность серы II или IV»;
- импликация. Соединяет выражения, указывающие на причину и следствие. Обозначается ⟶, ⊃, читается «из А следует В», «если А, то В», «А влечет В». Пример является ложью, когда причина правдива, а следствие — неправда.
 Пример: А⟶В = «если число делится только на себя и на 1, то оно сложное».
Пример: А⟶В = «если число делится только на себя и на 1, то оно сложное».
- эквивалентность. Операция объединяет высказывания связками ТОГДА И ТОЛЬКО ТОГДА, РАВНОСИЛЬНО, НЕОБХОДИМО И ДОСТАТОЧНО. Обозначается ~, ↔️, читается «А эквивалентно В». Выражение истинно, когда обе части одинаковы. Например: А~В = «число делится на 5 тогда, когда его последняя цифра 0 или 5». Эквивалентность противоположна строго-разделительной дизъюнкции.
На самом деле, для решения номеров достаточно трех операций: сложения, умножения, отрицания. Строго-разделительную дизъюнкцию можно представить как (ᆨА∧B)∧(А∧ᆨВ), импликацию — ᆨА∨B, эквивалентность (ᆨA∧ᆨB)∨(A∧B). Порядок выполнения действий при вычислении:
- инверсия;
- конъюнкция;
- дизъюнкция;
- остальные.
Примеры решения задач
Переходим к разбору 23 задания по информатике. Решим несколько задач.
Задача 1. Вычислите логическое значение: (ᆨ(15 < 3))∧(10 > 20).
Решение: Составим таблицу.
|
15 < 3 |
10 > 20 |
ᆨ(15 < 3) |
ᆨ(15 < 3)∧(10 > 20) |
|
0 |
1 |
1 |
0 |
Ответ: ложь.
Задача 2. Запишите высказывание с помощью логических операций, определите его значение: «если часы неправильно показывают время, то вы не успеете на занятия».
Решение: Пусть «часы неправильно показывают время» = А, «успеете на занятия» = В, а «не успеете на занятия» = ᆨВ. Логическое выражение: А⟶ᆨВ. Из причины сделал верный вывод, поэтому выражение является истинным.
Ответ: истина.
Задача 3. Определить значение ((х > 10) ∨ (х < 15)) → (х < 5) для 1) x = 9 и 2) х = 4.
Решение: Для х = 9: ((9 > 10) ∨ (9 < 15)) → (9 < 5) = ложь ∨ истина → ложь = истина → ложь = ложь.
Для х = 4: ((4 > 10) ∨ (4 < 15)) → (4 < 5) = ложь ∨ истина → истина = истина → истина = истина.
Ответ: 1) ложь; 2) истина.
Мы изучили основную теорию алгебры логики и разобрались, как решать 23 номер в ЕГЭ. Эта тема очень важна, поэтому не забывайте ее и постоянно практикуйтесь, чтобы подготовиться к экзамену лучше. Желаем вам легких вариантов и высоких баллов!
Алгебра логики примеры с решениями информатика – решение задач с помощью алгебры логики
Алгебра логика примеры
Одним из мощных методов решения логических задач является решение с помощью законов алгебры логики.
Алгоритм решения логических задач с помощью алгебры логики:

Задача1 » Кто преступник»
Определить участника преступления, исходя из двух
Посылок:
1) «Если Иванов не участвовал или Петров участвовал,
То Сидоров участвовал»;
2) «Если Иванов не участвовал, то Сидоров не
Участвовал».
Рассмотрим решение этой несложной задачи двумя Способами: с помощью таблиц истинности и с помощью Алгебраических преобразований.
1 способ
Составим выражения:
I — «Иванов участвовал в преступлении»;
P — «Петров участвовал в преступлении»;
S — «Сидоров участвовал в преступлении»
.
Запишем посылки в виде формул:
Из таблицы видно, что совершил преступление Иванов
Способ 2
Применим для решения этой же задачи преобразования с
Помощью законов алгебры логики:
= (I & P ˅S) &(I ˅S) = I&P˅ I & S˅ I &P &S ˅0=
Из последнего выражения видно, что выражение верно, если I=1, значит преступник — Иванов.
Задача 2 «Прогноз погоды»
НА вопрос, какая завтра будет погода, синоптик ответил: 1. Если не будет ветра, то будет пасмурная погода без дождя. 2. Если будет дождь, то будет пасмурно и без ветра. 3. Если будет пасмурная погода, то будет дождь и не будет ветра. Так какая же погода будет завтра?
Решим эту задачу средствами алгебры логики.
1. Выделим простые высказывания и запишем их через переменные :
A – «Ветра нет»
С – «Дождь» 2. Запишем логические функции (сложные высказывания) через введенные переменные:
Если не будет ветра, то будет пасмурная погода без дождя:
A → B & C
Если будет дождь, то будет пасмурно и без ветра:
С → B & A
Если будет пасмурная погода, то будет дождь и не будет ветра
B → C &
В) Запишем произведение указанных функций:
F=(A→ B & C) & (C→B & A) & (B→ C & A)
F=(A→ B & C) & (C→B & A) & (B→ C & A)
= (A v B & C) & (C v B&A) & (B v C&A) =
= (A v B & C) & (B v C&A) & (C v B&A) =
= (A & B v B&C&B v A&C&A v B&C&C&A) &
Ответ: погода будет ясная, без дождя, но ветреная.
Задача 3 «История с амфорой».
Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая удивительную находку, каждый высказал по два предположения.
Алеша: «Это сосуд греческий и изготовлен в V веке». Боря: «Это сосуд финикийский и изготовлен в III веке». Гриша: «Это сосуд не греческий и изготовлен в IV веке». Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
Введем следующие обозначения:
«Это сосуд греческий» — G;
«Это сосуд финикийский» — F;
«Сосуд изготовлен в III веке» — V3;
«Сосуд изготовлен в IV веке» — V4;
«Сосуд изготовлен в V веке» — V5. Формализуем задачу, записав в данных обозначениях условия задачи. Со слов учителя следует, что Алеша прав только в чем-то одном: или G = 1, или V5 = 1.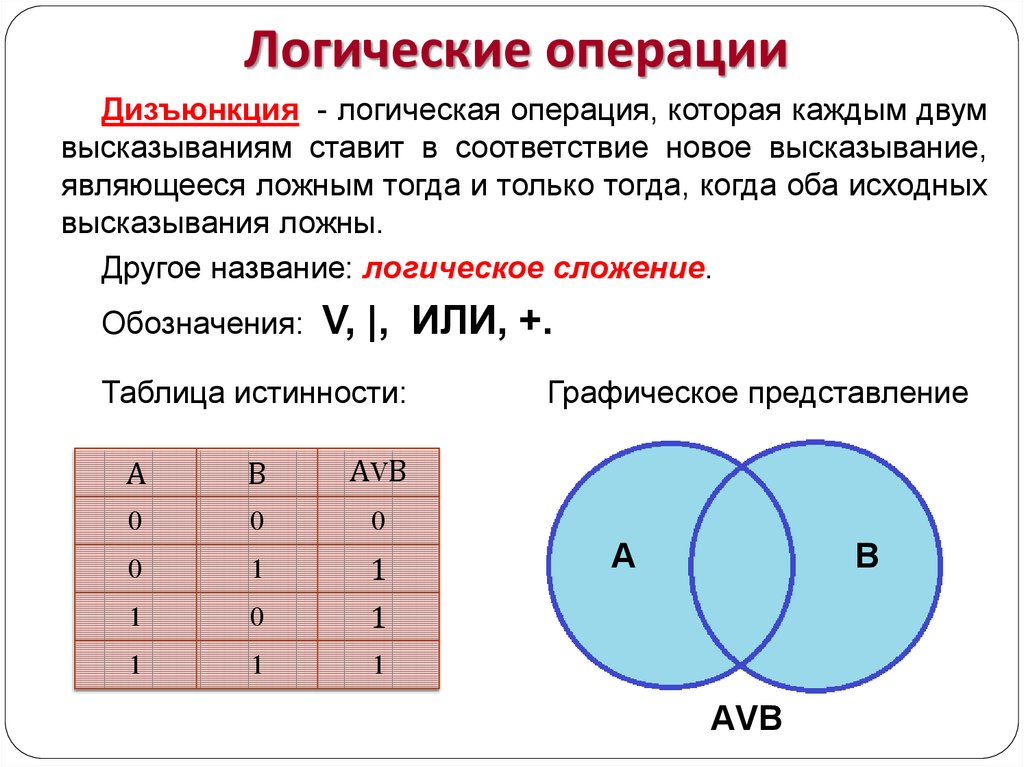 Таким образом, тождественно истинным будет высказывание: GV5 v GV5.=1 Аналогично, из слов Бори и учителя следует: FV3 v FV3 = 1, а из слов Гриши и учителя: GV4
Таким образом, тождественно истинным будет высказывание: GV5 v GV5.=1 Аналогично, из слов Бори и учителя следует: FV3 v FV3 = 1, а из слов Гриши и учителя: GV4
4 = 1. Кроме того, ясно, что сосуд может быть изготовлен только в одном из веков и только в одной из стран. Эти условия можно записать так: V3V4V5 ˅ V3V4V5 ˅ V3V4V5 = 1, Итак, мы получили пять тождественно истинных высказываний. Их нужно логически перемножить. Результат должен быть также тождественно истинным высказыванием: 1 = (GV5 v GV5) & (FV3 v FV3) & (GV4 v GV4) & (FG v FG) & (V3V4V5 ˅ V3V
4V5 ˅ V3V4V5) = (упростим: сначала перемножим первую и третью скобки и вторую и четвертую скобки)
4V5 ˅ V3V4V5) = учитывая, что, GG = 0, GG = G, GG = G, упростим выражения в первой и второй скобках: =(GV5V4 ˅ V5GV4 ) &( FV3G ˅V3 FG)& (V3V4V5 ˅ V3V4V5 ˅ V3V4V5) = (перемножим первую и вторую скобки и упростим полученное выражение) (GV5V4 FV3G ˅V5GV4FV3G˅GV5V4 V3 FG ˅ V5GV4V3 FG) & (V3V4V5 ˅ V3V4V5 ˅ (V3V4V5)= (V5V4FV3G˅GV5V4 V3 F) & (V3V4V5
˅ V3V4V5 ˅ V3V4V5)= GV5V4 V3 F GV5V4 V3 F=1, если G=1, V5=1, V4 =1, V3=1, F=1 Итак, сосуд финикийский и изготовлен в V веке.
Задача 4 «Поход в кино».
Андрей, Аня и Маша решили пойти в кино. Каждый из них высказал свои пожелания по поводу выбора фильма. Андрей сказал: «Я хочу посмотреть французский боевик». Маша сказала: «Я не хочу смотреть французскую комедию». Аня сказала: «Я хочу посмотреть американскую мелодраму». Каждый из них слукавил в одном из двух пожеланий. На какой фильм пошли ребята? 1. Выделим простые высказывания и запишем их через переменные: А — «Французский фильм» С — «Комедия» 2. Запишем логические функции (сложные высказывания). Учтем условие о том, что каждый из ребят оказался прав в одном предположении: а) «Французский боевик» A&B˅A&B б) «Американскую мелодраму» A&B˅ А &В
В) «Нефранцузская комедия» A&C˅A&C
3. Запишем произведение :
(A&B˅A&B) & (A&B˅ А&В)&( A&C˅A&C)=1. Упростим формулу: (A&B˅A&B) & (A&B˅ А&В)&( A&C˅A&C)= (A&B˅A&B) & (A&B˅ А&В)&( A&C˅A&C)= =(A&B& A&B˅ A&B& A&B˅A&B &А&В˅ A&B&A&B)&( A&C˅A&C)= =(A&B ˅A&B)&( A&C˅A&C)= A&B& A&C˅A&B& A&C˅ A&B&A&C˅A&B&A&C= = A&B&C˅ A&B&C =1 6. Составим таблицу истинности для выражения:
Упростим формулу: (A&B˅A&B) & (A&B˅ А&В)&( A&C˅A&C)= (A&B˅A&B) & (A&B˅ А&В)&( A&C˅A&C)= =(A&B& A&B˅ A&B& A&B˅A&B &А&В˅ A&B&A&B)&( A&C˅A&C)= =(A&B ˅A&B)&( A&C˅A&C)= A&B& A&C˅A&B& A&C˅ A&B&A&C˅A&B&A&C= = A&B&C˅ A&B&C =1 6. Составим таблицу истинности для выражения:
A&B&C˅ A&B&C: 7. Найдем по таблице значения переменных, для которых F=1. 8. Проанализируем результат: Результат Б) не является решением, т. к. в ответе Маши оба утверждения оказываются неверными, что противоречит условию задачи. Результат А) полностью удовлетворяет условию задачи и поэтому является верным решением.
к. в ответе Маши оба утверждения оказываются неверными, что противоречит условию задачи. Результат А) полностью удовлетворяет условию задачи и поэтому является верным решением.
Ответ: ребята выбрали американский боевик.
А
Решите самостоятельно задачи уровня 3
Применение инструмента алгебры логики при решении логических задач
История с амфорой
Антон, Борис и Григорий нашли в земле сосуд, о котором каждый высказал по два предположения:
Антон: «Сосуд греческий и изготовлен в V столетии»;
Борис: «Сосуд финикийский и изготовлен в III столетии»;
Григорий: «Сосуд не греческий и изготовлен в IV столетии».
Специалист сказал ученикам, что каждый из них не ошибся только в одном из двух предположений. Определить место и столетие изготовления сосуда.
Решение:
Введем следующие обозначения:
$G$ — «Сосуд греческий»;
$F$ — «Сосуд финикийский»;
$S_3$ — «Сосуд изготовлен в $III$ столетии»;
$S_4$ — «Сосуд изготовлен в $IV$ столетии»;
$S_5$ — «Сосуд изготовлен в $V$ столетии».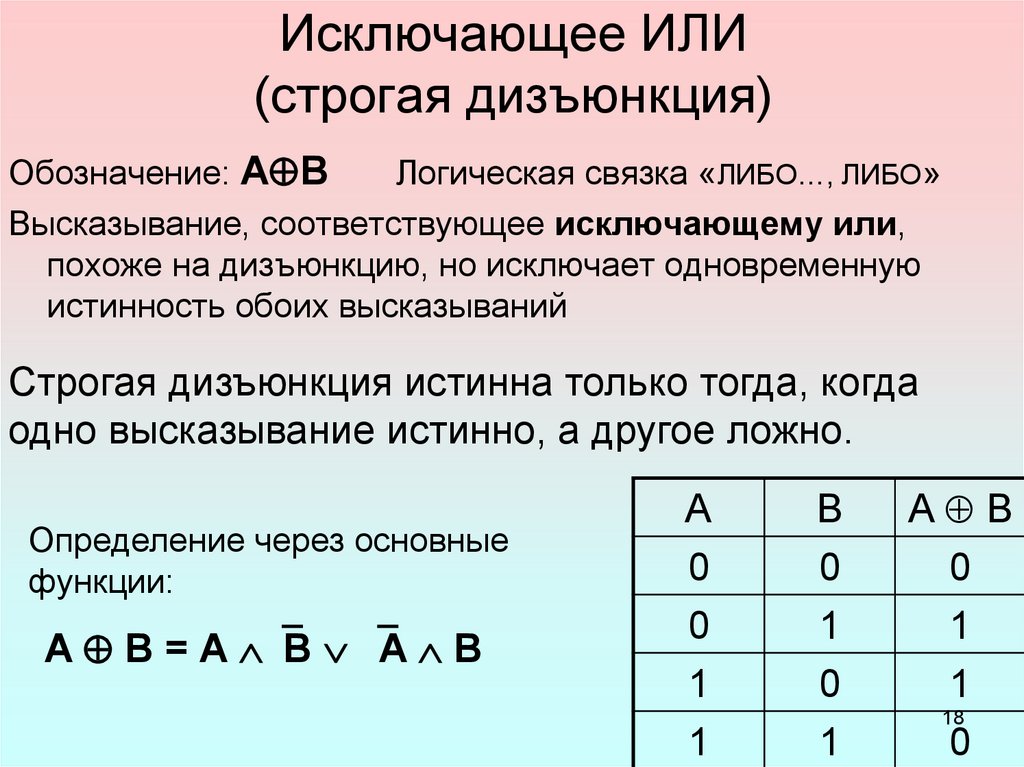
Запишем условие задачи с помощью обозначений:
Антон прав только в одном предположении: $G = 1$ или $S_5 = 1$. Тогда $G\overline\vee \overlineS_5=1$.
Аналогично для слов Бориса: $F\overline\vee \overlineS_3=1$.
Для слов Григория: $\overline\overline\vee GS_4=1$.
Т. к. сосуд может быть изготовлен только в одном из столетий и только в одной из стран, запишем условия:
\[S_3\overline\overline\vee \overlineS_4\overline\vee \overline\overlineS_5=1,\] \[F\overline\vee \overlineG=1.\]
Применим операцию логического умножения к полученным тождественно истинным высказываниям, результат которого также должен быть тождественно истинным:
\[\left(G\overline\vee \overlineS_5\right)\wedge \left(F\overline\vee \overlineS_3\right)\wedge \left(\overline\overline\vee GS_4\right)\wedge \left(F\overline\vee \overlineG\right)\wedge \] \[\wedge \left(S_3\overline\overline\vee \overlineS_4\overline\vee \overline\overlineS_5\right)=\]
Перемножим первую на третью скобку и вторую на четвертую:
\[=\left(G\overline\overline\overline\vee \overlineS_5\overline\overline\vee G\overlineGS_4\vee \overlineS_5GS_4\right)\wedge \] \[\wedge \left(F\overlineF\overline\vee \overlineS_3F\overline\vee F\overline\overlineG\vee \overlineS_3\overlineG\right)\wedge \left(S_3\overline\overline\vee \overlineS_4\overline\vee \overline\overlineS_5\right)=\]
Т. к. $G\overline=0$, $GG=G$, $\overline\overline=\overline$, упростим выражения:
к. $G\overline=0$, $GG=G$, $\overline\overline=\overline$, упростим выражения:
\[=\left(\overlineS_5\overline\vee G\overlineS_4\right)\wedge \left(F\overline\overline\vee \overlineS_3G\right)\wedge \left(S_3\overline\overline\vee \overlineS_4\overline\vee \overline\overlineS_5\right)=\]
Перемножим первые две скобки и упростим выражение:
\[=\left(\overlineS_5\overline\overlineS_3G\vee G\overlineS_4\overlineS_3G\vee \overlineS_5\overlineF\overline\overline\vee G\overlineS_4F\overline\overline\right)\wedge \] \[\wedge \left(S_3\overline\overline\vee \overlineS_4\overline\vee \overline\overlineS_5\right)=\] \[=\left(G\overlineS_4\overlineS_3\vee \overlineS_5\overlineF\overline\right)\wedge \left(S_3\overline\overline\vee \overlineS_4\overline\vee \overline\overlineS_5\right)=\] \[=\left(G\overlineS_4\overlineS_3\vee \overlineS_5\overlineF\overline\right)\wedge \left(S_3\overline\overline\vee \overlineS_4\overline\vee \overline\overlineS_5\right)=\overlineS_5\overlineF\overline;\]
$\overlineS_5\overlineF\overline=1$, что возможно только в случае:
\[\overline=1, S_5=1, \overline=1, F=1, \overline=1. \]
\]
Ответ: сосуд финикийский и изготовлен в $V$ столетии.
Решение логических задач средствами алгебры логики
- изучается условие задачи; вводится система обозначений для логических высказываний; конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи; определяются значения истинности этой логической формулы; из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.
A = «машина красного цвета»;
B = «машина была «Рено»;
C = «машина синего цвета»;
D = «машина была «Тойота»;
E = «машина была «Форд».
Из показаний Боба следует, что A \/ B истинно;
Из показаний Джона следует, что C \/ D истинно;
Из показаний Сэма следует, что A \/ E истинно.
Следовательно, истинна конъюнкция (A \/ B) /\ (C \/ D) /\ (A \/ E) = 1
Раскрывая скобки, получаем:
(A \/ B) /\ (C \/ D) /\ (A \/ E) = (A /\ C \/ A /\ D \/ B /\ C \/ B /\ D) /\ ( A \/ E) =
A /\ C /\ A \/ A /\ D /\ A \/ B /\ C /\ A \/ B /\ D /\ A \/ A /\ C /\ E \/ A /\ D /\ E \/ B /\ C /\ E \/ B /\ D /\ E = 1.
Из полученных восьми слагаемых семь (согласно условию) являются ложными. Остается единственное истинное слагаемое:
B /\ C /\ A = 1. Значит, нарушитель скрылся на автомобиле «Рено» синего цвета.
Ответ: РЕНО, СИНИЙ.
Пример.
Трое друзей, болельщиков автогонок «Формула-1», спорили о результатах предстоящего этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
Решение.
Введем обозначения для логических высказываний:
Ш — победит Шумахер;
Х — победит Хилл;
А — победит Алези.
Реплика Ника «Алези пилотирует самую мощную машину» не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Зафиксируем высказывания каждого из друзей:
Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание
Высказывание истинно только при Ш=1, А=0, Х=0.
Ответ.
Победителем этапа гонок стал Шумахер.
Задача для самопроверки:
На перемене в кабинете биологии 8 ребят баловались и разбили дорогой микроскоп. Их всех вызвали к директору и выслушали:
Ира: Это Антон разбил.
Наташа: Нет, Антон не бил!
Сергей: А я тоже знаю, что это Наташа разбила!
Антон: Нет, ни Наташа, ни Сергей этого не делали!
Оля: А я видела, что разбил Сергей!
Максим: Это кто-то чужой!
Костя: Это либо Наташа, либо Сергей – больше некому!
Кто разбил микроскоп, если известно, что из этих восьми высказываний истинны только два?
Ответ записать в виде первой буквы имени.
Презентация и конспект урока на тему «Решение задач по информатике с использованием элементов алгебры логики»
План — конспект урока
На тему: решение задач по информатике с использованием элементов алгебры логики
Формирование умения применять полученные знания на практике;
Развитие умения построения таблиц истинности по заданным формулам;
Развитие умения решать текстовые задачи с использованием законов логики.
Воспитательная – развитие познавательного интереса, логического мышления.
Образовательная – повторение основ математической логики, выполнение практических заданий.
Развивающая – развитие логического мышления, внимательности.
Организационный момент (2 мин)
Актуализация знаний. Повторение логических операций и законов. (5 мин)
Решение задач. Применение логических операций и законов на практике + задача модуль ЭОР(15 мин)
Практическая работа (модуль 31 ЭОР «Решение логических задач») (12 мин)
Физкультминутка (2 мин)
Работа с тренажером Логика (5 мин)
Итоги урока (2 мин)
Домашнее задание (1 мин)
Выставление оценок (1 мин)
Организационный момент
Сегодня мы с вами завершаем тему “Основы логики” и применим основные логические операции, законы преобразования для решения задач по информатике.
Урок идет параллельно с презентацией.
Актуализация знаний. Повторение логических операций и законов.
Алгебра логики – раздел математической логики, изучающий строение сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
1. Основоположник формальной логики? (Аристотель.)
2. Основоположник алгебры логики? (Джордж Буль. (сообщение))
3. Перечислите логические операции:
отрицание (инверсия)
&, /\ конъюнкция (“И”)
V дизъюнкция (“ИЛИ”)
Логическое следование (импликация)
4. В чем смысл закона двойного отрицания?
Двойное отрицание исключает отрицание.
5. Законы де Моргана (законы общей инверсии).
Отрицание дизъюнкции является конъюнкцией отрицаний:
(A V B) = A /\ B
Отрицание конъюнкции является дизъюнкцией отрицаний:
6. Как выразить импликацию через дизъюнкцию?
Решение задач. Применение логических операций и законов на практике
Применение логических операций и законов на практике
Для какого имени истинно высказывание:
(Первая буква имени гласная -> Четвертая буква имени согласная)?
Решение. Сложное высказывание состоит из двух простых высказываний:
А – первая буква имени гласная,
В – четвертая буква имени согласная.
(А В) = (A V В) = ( (А) /\ B) = A /\ B
Применяемые формулы:
1. Импликация через дизъюнкцию А В = A V В
2. Закон де Моргана (A V B) = A /\ B
3. Закон двойного отрицания.
(Первая буква имени гласная /\ Четвертая буква имени гласная)
Какое логическое выражение равносильно выражению (А \/ B)?
Решение. (А \/ B)= А /\ (B)= А /\ B
Составить таблицу истинности для формулы
Порядок выполнения логических операций:
Составить таблицу истинности.
Сколько строк будет в вашей таблице? 3 переменных: А, В, С; 2 3 =8
Одним из мощных методов решения логических задач является решение с помощью законов алгебры логики.
Алгоритм решения логических задач с помощью алгебры логики: 1) внимательно изучить условие; 2) выделить простые высказывания и обозначить их латинскими буквами; 3) записать условие задачи на языке алгебры логики; 4) составить конечную формулу, для этого объединить логическим умножением формулы каждого утверждения, приравнять произведение единице; 5) упростить формулу, проанализировать полученный результат или составить таблицу истинности, найти по таблице значения переменных, для которых F = 1, проанализировать результаты.
Задача1 » Кто преступник»
Рассмотрим решение этой несложной задачи двумя способами с помощью таблиц истинности и с помощью алгебраических преобразований.
Xn—-8sbanwvcjzh9e. xn--p1ai
07.03.2017 18:00:38
2017-03-07 18:00:38
Источники:
Https://xn—-8sbanwvcjzh9e. xn--p1ai/raznoe/algebra-logiki-primery-s-resheniyami-informatika-reshenie-zadach-s-pomoshhyu-algebry-logiki. html
html
Решение задач по алгебре логики: примеры и на заказ » /> » /> .keyword { color: red; }
Алгебра логика примеры
В этом разделе вы найдете бесплатные примеры Решений задач по алгебре логики. Затронем самые основы предмета: проверка формул алгебры логики, составление высказываний, решение логических задач и т. п. Ссылки на более сложные задачи о высказываниях и предикатах вы найдете ниже.
Другие примеры решений по математической логике:
- Таблицы истинности Булевы формулы
Исчисление высказываний Исчисление предикатов
Математическая логика: решения задач онлайн
Задача 1. Семья, состоящая из отца А, матери В и трех дочерей C, D, E купила телевизор. Условились, что в первый вечер будут смотреть передачи в таком порядке:
1. Когда отец А смотрит передачу, то мать В делает то же.
2. Дочери D и E, обе или одна из них, смотрят передачу.
3. Из двух членов семьи — мать В И дочь С — смотрят передачу одна и только одна.
4. Дочери C и D или обе смотрят, или обе не смотрят.
5. Если дочь Е смотрит передачу, то отец А и дочь D делают то же.
Кто из членов семьи в этот вечер смотрит передачу?
Задача 2. Построить таблицу истинности и определить выполнимость формулы:
$$ P \wedge Q \to (Q \wedge \bar \to R \wedge Q) $$
Задача 3. Даны высказывания:
1) То, что N делится на 15, есть необходимое условие того, чтобы N делилось на 3.
2) То, что N не делится на 3, влечёт то, что N не делится на 15.
3) N делится на 3 при условии, что N делится на 15.
4) N не делится на 3 только тогда, когда N не делится на 15.
5) N делится на 3 тогда и только тогда, когда N делится на 15.
Какие из них следуют из высказывания
6) Если N делится на 15, то N делится на 3.
Задача 4. Известно следующее: если Петя не видел Колю на улице, то либо Коля ходил в кино, либо Петя сказал правду; если Коля не ходил в кино, то Петя не видел Колю на улице, и Коля сказал правду; если Коля сказал правду, то либо он ходил в кино, либо Петя солгал. Выяснить, ходил ли Коля в кино.
Выяснить, ходил ли Коля в кино.
Как решать логические задачи?
Примеры решений логических задач вы найдете выше, здесь опишем Общую схему:
Исчисление предикатов.
Www. matburo. ru
27.02.2018 16:18:17
2018-02-27 16:18:17
Источники:
Https://www. matburo. ru/ex_dm. php? p1=dmlogika
Урок 11. алгебра логики. таблицы истинности — Информатика — 10 класс — Российская электронная школа » /> » /> .keyword { color: red; }
Алгебра логика примеры
Перечень вопросов, рассматриваемых в теме: высказывание, логическая переменная, логические операции (отрицание, конъюнкция, дизъюнкция, строгая дизъюнкция, импликация, эквиваленция), логические выражения, предикаты и их множества истинности, таблицы истинности и их анализ.
Глоссарий по теме: импликация, эквиваленция, предикат, примеры законов алгебры логики.
Основная литература по теме урока:
Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса
Базовый уровень: учебник для 10 класса
— М.: БИНОМ. Лаборатория знаний, 2017 (с.174—197)
Открытые электронные ресурсы по теме:
Теоретический материал для самостоятельного изучения:
Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними.
Алгебра логики возникла в середине XIX века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейно-контактных и электронно-ламповых схем. Логическое высказывание — это повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Например, предложение «Джордж Буль — основоположник алгебры логики» истинно, а «Солнце — спутник Земли» ложно.
Употребляемые в обычной речи логические связки «не», «и», «или», «если…то», «тогда и только тогда» и др. позволяют из уже заданных высказываний строить новые высказывания. Высказывания, образованные из других высказываний, называются составными. Высказывание, никакая часть которого не является высказыванием, называется элементарным. Например, из двух простых высказываний (каких?) можно получить следующее составное высказывание: «Алгебра логики является основой строения логических схем компьютеров и служит математической основой решения сложных логических задач». Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).
позволяют из уже заданных высказываний строить новые высказывания. Высказывания, образованные из других высказываний, называются составными. Высказывание, никакая часть которого не является высказыванием, называется элементарным. Например, из двух простых высказываний (каких?) можно получить следующее составное высказывание: «Алгебра логики является основой строения логических схем компьютеров и служит математической основой решения сложных логических задач». Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).
Обоснование истинности или ложности элементарных высказываний не является задачей алгебры логики. Эти вопросы решаются теми науками, к сфере которых относятся элементарные высказывания. Такое сужение интересов позволяет обозначать высказывания символическими именами (например, А, В, С).
Логическая переменная — это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь». Для логических значений «истина» — «ложь» могут использоваться следующие обозначения: И — Л, true — false, да — нет, 1 — 0.
Для логических значений «истина» — «ложь» могут использоваться следующие обозначения: И — Л, true — false, да — нет, 1 — 0.
Логическая операция полностью может быть описана Таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.
В алгебре логики имеется шесть логических операций. Из курса информатики 8—9 классов вам знакомы три из них:
— отрицание (инверсия, логическое НЕ)
Высказыванию ставится в соответствие новое высказывание, значение которого противоположно исходному.
— конъюнкция (логическое умножение, логическое И)
Высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.
— дизъюнкция (логическое сложение, логическое ИЛИ)
Высказывание ложно тогда и только тогда, когда ложны оба исходных высказывания.
Рассмотрим новые логические операции.
— Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда первое высказывание (посылка) истинно, а второе (следствие) — ложно, называется импликацией (от лат. implicatio — сплетение, тесная связь) или логическим следованием.
implicatio — сплетение, тесная связь) или логическим следованием.
Операция импликации обозначается символом и задается следующей таблицей истинности:
В разговорной речи импликации соответствуют предложения, содержащие связку «если…, то». Как правило, эту связку мы используем, когда хотим показать зависимость одного события от другого.
Импликацию можно заменить на выражение, использующее ранее изученные операции НЕ и ИЛИ:
— Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда только одно из двух высказываний истинно, называется строгой (исключающей) дизъюнкцией.
Строгая дизъюнкция обозначается символоми задается следующей таблицей истинности:
В русском языке строгой дизъюнкции соответствует связка «либо». Например, в пословице «Либо пан, либо пропал», выполнение обоих условий одновременно невозможно. В отличие от обычной дизъюнкции в высказывании, содержащем строгую дизъюнкцию, мы утверждаем, что произойдет только одно событие.
Строгую дизъюнкцию можно представить через базовые операции следующим образом:
Чтобы доказать это равенство, достаточно для всех возможных комбинаций и вычислить значения выражения, стоящего в правой части равенства, и сравнить их со значениями выражения для тех же исходных данных.
— Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным, когда оба исходных высказывания истинны или оба исходных высказывания ложны, называется эквиваленцией или равнозначностью.
В логике эквиваленция обозначается символом и задается следующей таблицей истинности:
В разговорной речи эквивалентности соответствует связка «тогда и только тогда, когда», а в математике — «необходимо и достаточно».
Если посмотреть внимательно на таблицы истинности для двух последних логических операций, то можно заметить, что эквивалентность — это обратная операция для операции «исключающее ИЛИ», т. е.
Можно заменить эквивалентность выражением, которое включает только базовые логические операции:
Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок.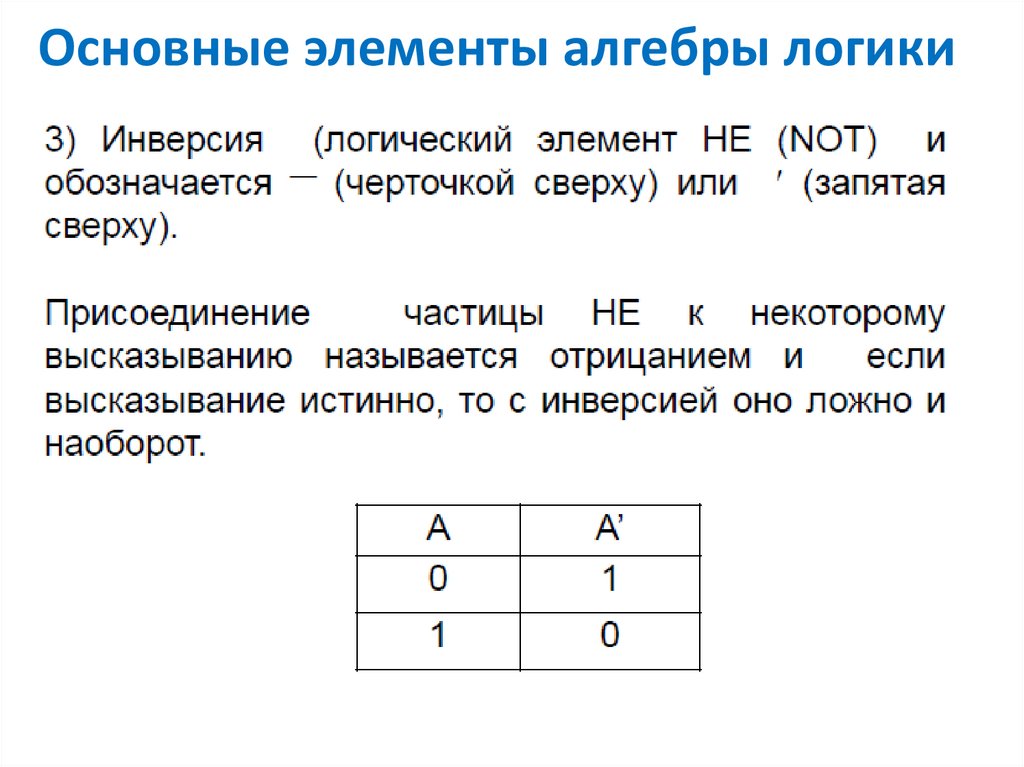
Для логического выражения справедливо:
При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом:
отрицание; конъюнкция; дизъюнкция, строгая дизъюнкция; импликация, эквиваленция.
Операции одного приоритета выполняются в порядке их следования, слева направо. Как в математике, скобки меняют порядок выполнения операций.
Операция импликации обозначается символом и задается следующей таблицей истинности:
Можно заменить эквивалентность выражением, которое включает только базовые логические операции:
Как правило, эту связку мы используем, когда хотим показать зависимость одного события от другого.
Resh. edu. ru
06.05.2020 12:46:57
2020-05-06 12:46:57
Источники:
Https://resh. edu. ru/subject/lesson/5426/conspect/
решение задач с помощью алгебры логики.
Одним
из мощных методов решения логических задач является решение с помощью законов
алгебры логики.
Алгоритм решения логических задач с помощью алгебры логики:
1) внимательно изучить условие;
2) выделить простые высказывания и обозначить их латинскими буквами;
3) записать условие задачи на языке алгебры логики;
4) составить конечную формулу, для этого объединить логическим умножением формулы каждого утверждения, приравнять произведение единице;
5) упростить формулу, проанализировать полученный результат или составить таблицу истинности, найти по таблице значения переменных, для которых F = 1, проанализировать результаты.
Задача1 » Кто преступник»
Определить участника преступления, исходя из двух
посылок:
1) «Если Иванов не участвовал или Петров участвовал,
то Сидоров участвовал»;
2) «Если Иванов не участвовал, то Сидоров не
участвовал».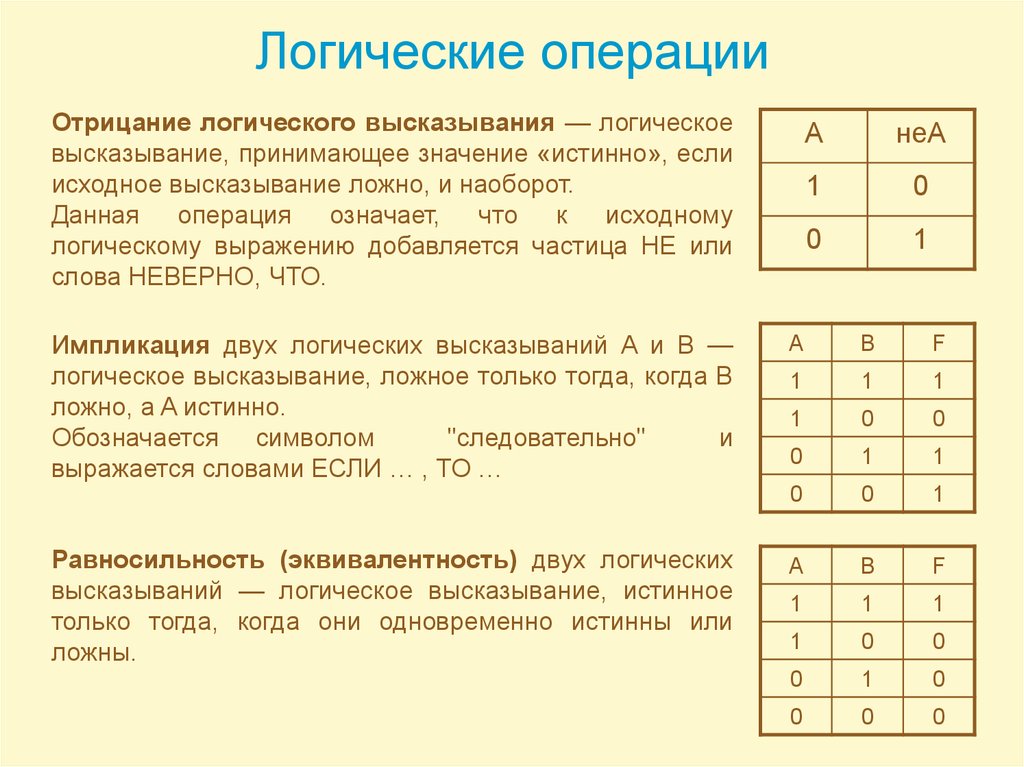
Рассмотрим решение этой несложной задачи двумя способами: с помощью таблиц истинности и с помощью алгебраических преобразований.
1 способ
Составим выражения:
I — «Иванов участвовал в преступлении»;
P — «Петров участвовал в преступлении»;
S — «Сидоров участвовал в преступлении»
.
Запишем посылки в виде формул:
¬I˅P→S и ¬I→¬S
Из таблицы видно, что совершил преступление Иванов
Способ 2
Применим для решения этой же задачи преобразования с
помощью законов алгебры логики:
( ¬I˅P→S) &( ¬I→¬S)=(¬(¬I˅P)˅S) & (I˅¬S) =
= (I & ¬P ˅S) &(I ˅¬S) = I&¬P˅ I & S˅ I &¬P &¬S ˅0=
= I&¬P ˅ I & S =I & (¬P˅S)
Из последнего выражения видно, что выражение верно, если I=1, значит преступник — Иванов.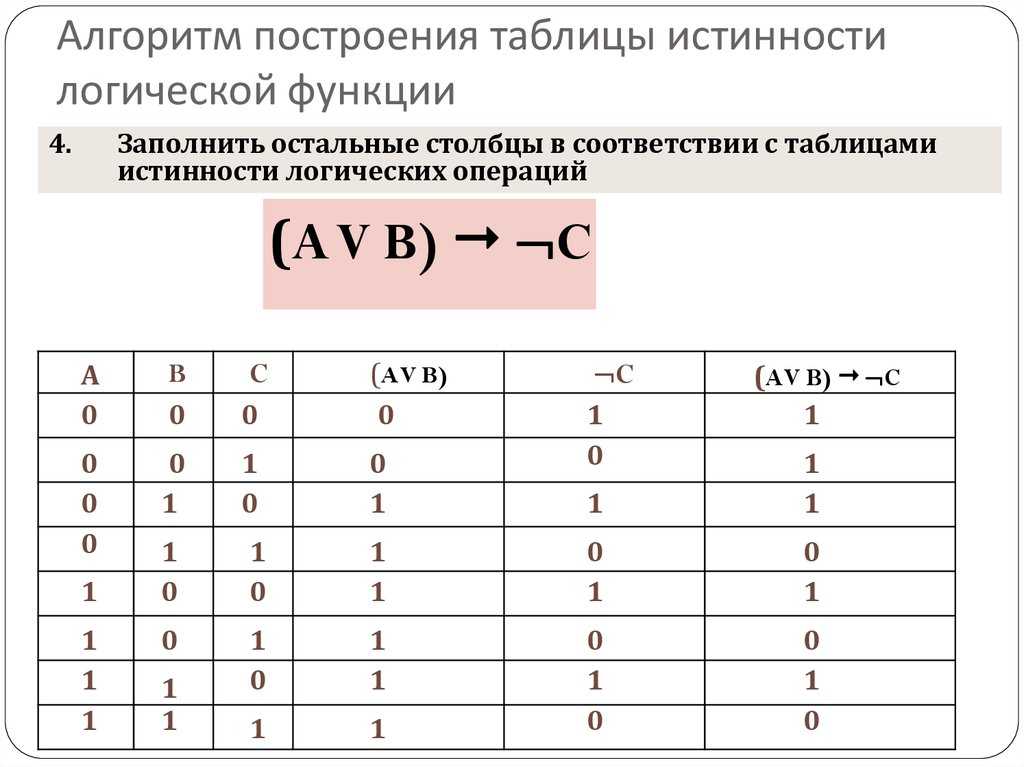
Задача 2 «Прогноз погоды»
На вопрос, какая завтра будет погода, синоптик ответил:
1. Если не будет ветра, то будет пасмурная погода без дождя.
2. Если будет дождь, то будет пасмурно и без ветра.
3. Если будет пасмурная погода, то будет дождь и не будет ветра.
Так какая же погода будет завтра?
Решим эту задачу средствами алгебры логики.
Решение:
1. Выделим простые высказывания и запишем их через переменные:
A – «Ветра нет»
B – «Пасмурно»
С – «Дождь»
2. Запишем логические функции (сложные высказывания) через введенные переменные:
Если не будет ветра, то будет пасмурная погода без дождя:
A → B & C
Если будет дождь, то будет пасмурно и без ветра:
С → B & A
Если будет пасмурная погода, то будет дождь и не будет ветра
B → C &
в) Запишем произведение указанных функций:
F=(A→ B & C) & (C→B & A) & (B→ C & A)
Упростим формулу (используются законы де Моргана, переместительный закон, закон противоречия):
F=(A→ B & ¬C) & (C→B & A) & (B→ C & A)
= (¬A v B & ¬C) & (¬C v B&A) & (¬B v C&A) =
= (¬A v B & ¬C) & (¬B v C&A) & (¬C v B&A) =
= (¬A &¬ B v B&¬C&¬B v ¬A&C&A v B&¬C&C&A) &
(C v B&A)=
= ¬A & ¬B &(C v B&¬A) =A&¬B&C v¬ A&¬B&B&¬A =
= ¬A&¬B&¬C
3. Приравняем результат единице, т.е. наше выражение должно быть истинным:F = ¬A &¬ B & ¬C = 1 и проанализируем результат:
Приравняем результат единице, т.е. наше выражение должно быть истинным:F = ¬A &¬ B & ¬C = 1 и проанализируем результат:
Логическое произведение равно 1, если каждый множитель равен 1.
¬A = 1; ¬B = 1; ¬C = 1.значит: A = 0; B = 0; C = 0;
Ответ: погода будет ясная, без дождя, но ветреная.
Задача 3 «История с амфорой».
Алеша, Боря и Гриша нашли в земле сосуд.
Рассматривая удивительную находку, каждый высказал по два предположения.
Алеша: «Это сосуд греческий и изготовлен в V веке». Боря: «Это сосуд финикийский и изготовлен в III веке». Гриша: «Это сосуд не греческий и изготовлен в IV веке».
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
Введем следующие обозначения:
«Это сосуд греческий» — G;
«Это сосуд финикийский» — F;
«Сосуд
изготовлен в III веке» — V3;
«Сосуд
изготовлен в IV веке» — V4;
«Сосуд
изготовлен в V веке» — V5.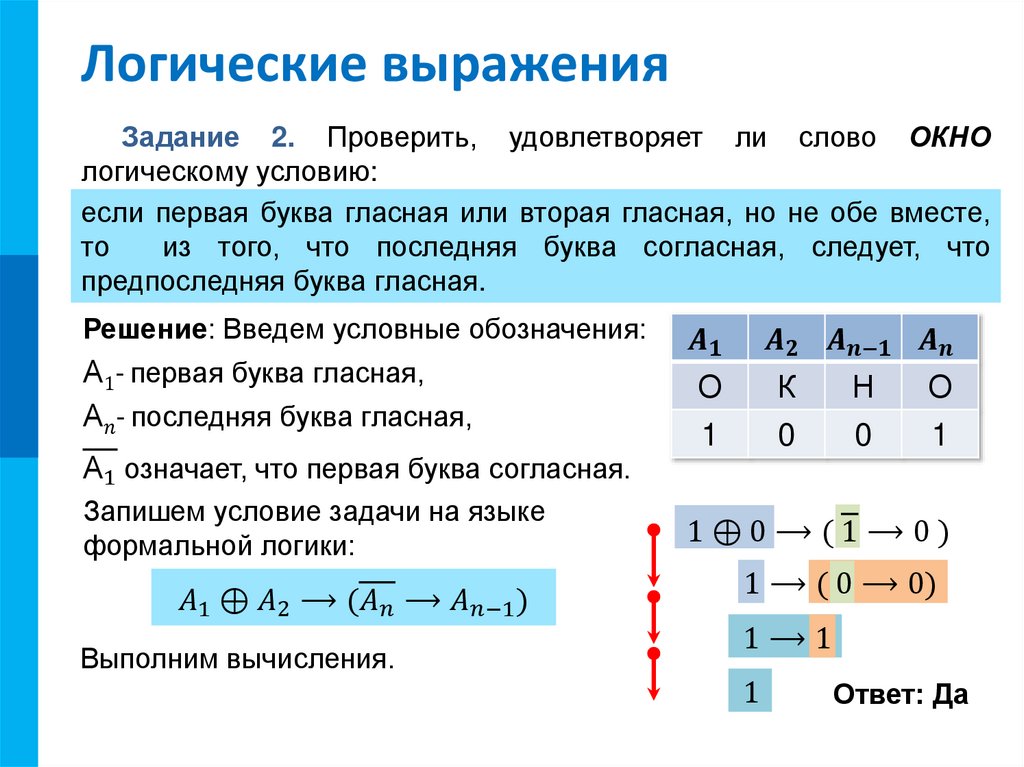
Формализуем задачу, записав в данных обозначениях условия задачи.
Со слов учителя следует, что Алеша прав только в чем-то одном: или G = 1, или V5 = 1.
Таким образом, тождественно истинным будет высказывание: G¬V5 v ¬GV5.=1
Аналогично, из слов Бори и учителя следует: F¬V3 v ¬FV3 = 1,
а из слов Гриши и учителя: ¬G¬V4 v GV4 = 1.
Кроме того, ясно, что сосуд может быть изготовлен только в одном из веков и только в одной из стран. Эти условия можно записать так:
V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ ¬V3¬V4V5 = 1,
F¬G v ¬FG = 1.
Итак, мы получили пять тождественно истинных высказываний. Их нужно логически перемножить. Результат должен быть также тождественно истинным высказыванием:
1 = (G¬V5 v ¬GV5) & (F¬V3 v ¬FV3) & (¬G¬V4 v GV4) & (F¬G v ¬FG) & (V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ ¬V3¬V4V5) =
(упростим: сначала перемножим первую и третью скобки и вторую и четвертую скобки)
=(G¬V5¬G¬V4˅¬GV5¬G¬V4 ˅ G¬V5GV4 ˅ ¬GV5 GV4)&( F¬V3 F¬G˅¬FV3 F¬G˅ F¬V3 ¬FG ˅ ¬FV3¬FG) & (V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ ¬V3¬V4V5) =
учитывая, что, G¬G = 0, GG = G,¬ G¬G =¬ G, упростим выражения в первой и второй скобках:
=(¬GV5¬V4 ˅ ¬V5GV4 ) &( ¬FV3G ˅¬V3 F¬G)& (V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ ¬V3¬V4V5) =
(перемножим первую и вторую скобки и упростим полученное выражение)
(¬GV5¬V4 ¬FV3G˅¬V5GV4¬FV3G˅¬GV5¬V4 ¬V3 F¬G ˅ ¬V5GV4¬V3 F¬G) & (V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ (¬V3¬V4V5)= (¬V5V4¬FV3G˅¬GV5¬V4 ¬V3 F) & (V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ ¬V3¬V4V5)= ¬GV5¬V4 ¬V3 F
¬GV5¬V4 ¬V3 F=1, если ¬G=1, V5=1, ¬V4=1, ¬V3=1, F=1
Итак, сосуд финикийский и изготовлен в V веке.
Задача 4 «Поход в кино».
Андрей, Аня и Маша решили пойти в кино. Каждый из них высказал свои пожелания по поводу выбора фильма.
Андрей сказал: «Я хочу посмотреть французский боевик».
Маша сказала: «Я не хочу смотреть французскую комедию».
Аня сказала: «Я хочу посмотреть американскую мелодраму».
Каждый из них слукавил в одном из двух пожеланий. На какой фильм пошли ребята?
Решение:
1. Выделим простые высказывания и запишем их через переменные:
А — «Французский фильм»
В — «Боевик»
С — «Комедия»
2. Запишем логические функции (сложные высказывания). Учтем условие о том, что каждый из ребят оказался прав в одном предположении:
Запишем логические функции (сложные высказывания). Учтем условие о том, что каждый из ребят оказался прав в одном предположении:
а) «Французский боевик» ¬A&B˅A&¬B
б) «Американскую мелодраму» ¬¬A&¬B˅¬ А &¬¬В
в) «Нефранцузская комедия» ¬¬A&C˅¬A&¬C
3. Запишем произведение :
(¬A&B˅A&¬B) & (¬¬A&¬B˅¬ А&¬¬В)&( ¬¬A&C˅¬A&¬C)=1.
Упростим формулу: (¬A&B˅A&¬B) & (¬¬A&¬B˅¬ А&¬¬В)&( ¬¬A&C˅¬A&¬C)=
(¬A&B˅A&¬B) & (A&¬B˅¬ А&В)&( A&C˅¬A&¬C)=
=(¬A&B& A&¬B˅ A&¬B& A&¬B˅¬A&B &¬А&В˅ A&¬B&¬A&B)&( A&C˅¬A&¬C)=
=(A&¬B ˅¬A&B)&( A&C˅¬A&¬C)= A&¬B& A&C˅¬A&B& A&C˅ A&¬B&¬A&¬C˅¬A&B&¬A&¬C=
= ¬A&B&¬C˅ A&¬B&C =1
6.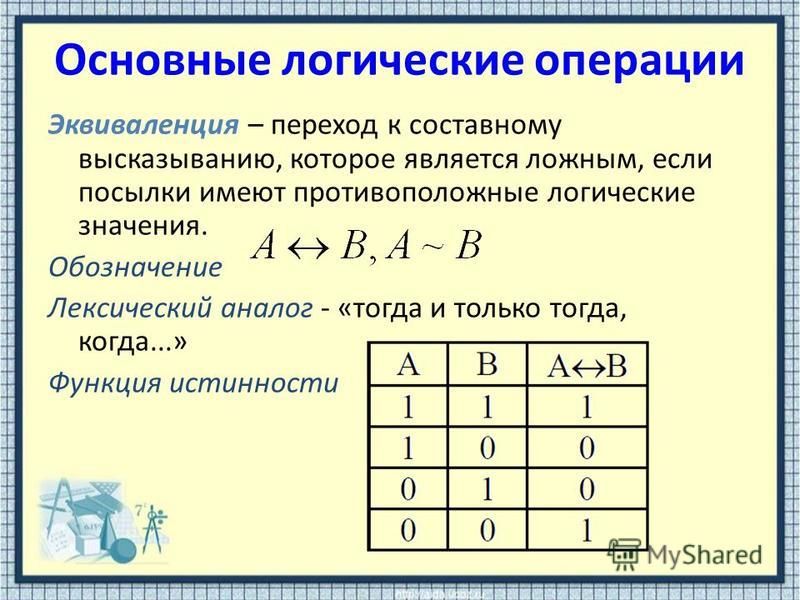 Составим таблицу истинности для выражения:
Составим таблицу истинности для выражения:
¬A&B&¬C˅ A&¬B&C:
¬A&B&¬C˅A&¬B&C | ||||
7. Найдем по таблице значения переменных, для которых F=1.
Найдем по таблице значения переменных, для которых F=1.
8. Проанализируем результат:
Результат Б) не является решением, т.к. в ответе Маши оба утверждения оказываются неверными, что противоречит условию задачи.
Результат А) полностью удовлетворяет условию задачи и поэтому является верным решением.
Ответ: ребята выбрали американский боевик.
А
Решите самостоятельно задачи уровня 3
Применение инструмента алгебры логики при решении логических задач
Содержание статьи
1. Алгоритм решения логических задач с помощью алгебры логики
2. Законы алгебры логики
Законы алгебры логики
3. Примеры решения логических задач с помощью алгебры логики
Решение логических задач с помощью алгебры логики является мощным средством.
Алгоритм решения логических задач с помощью алгебры логики
изучение условия;
выделение простых высказываний, которым даются имена;
запись условия задачи языком алгебры логики;
составление конечной формулы, для чего объединяются формулы каждого утверждения с помощью логического умножения и приравнивается полученная формула единице;
упрощение формулы, анализ полученного результата или составление таблицы истинности, нахождение по таблице значения переменных, для которых $F=1$, анализ результатов.
Законы алгебры логики
Рисунок 1.
Примеры решения логических задач с помощью алгебры логики
Пример 1
Задача «Кто преступник»
Определить участника преступления, зная, что:
«Если Иван не участвовал или Петр участвовал, то Семен участвовал»;
«Если Иван не участвовал, то Семен не участвовал».

Решим задачу с помощью таблиц истинности и с помощью алгебры логики.
Решение:
Решение с помощью таблицы истинности
Пусть:
$I$ — «Иван участвовал в преступлении»;
$P$ — «Петр участвовал в преступлении»;
$S$ — «Семен участвовал в преступлении».
Запишем условия задачи в виде формул:
$\overline{I}\vee P\to S$ и $\overline{I}\vee P\to \overline{S}$
Построим таблицу истинности для всех возможных наборов:
Рисунок 2.
Из таблицы видно, что преступление совершил Иван.
Решение с помощью алгебры логики
\[F\left(I,P,S\right)=\left(\overline{I}\vee P\to S\right)\wedge \left(\overline{I}\to \overline{S}\right)=\left(\left(\overline{\overline{I}\vee P}\right)\vee S\right)\wedge \left(I\vee \overline{S}\right)=\] \[=\left(I\wedge \overline{P}\vee S\right)\wedge \left(I\vee \overline{S}\right)=I\wedge \overline{P}\vee I\wedge S\vee I\wedge \overline{P}\wedge \overline{S}\vee 0=I\wedge \overline{P}\vee I\wedge S=\] \[=I\wedge \left(\overline{P}\vee S\right)\]
Из получившегося выражения получаем, что выражение верно, когда $I=1$.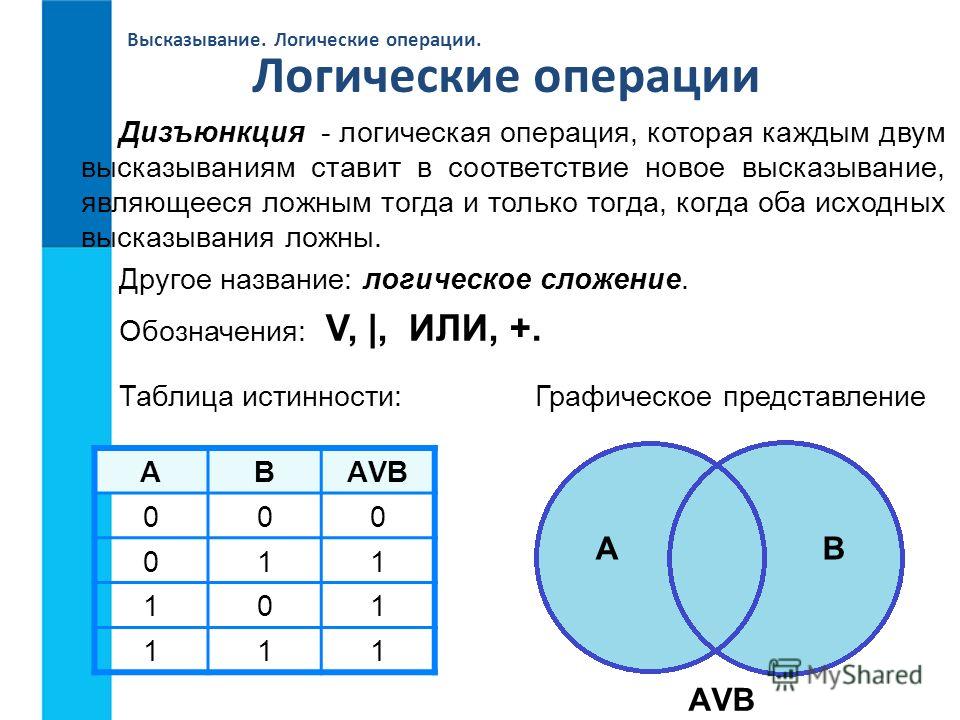 Таким образом, преступник — Иван.
Таким образом, преступник — Иван.
Пример 2
Задача о погоде
Определить погоду на завтра, если синоптик сказал, что:
Если не будет ветра, то будет пасмурная погода и не будет дождя.
Если будет дождь, то будет пасмурно и не будет ветра.
Если будет пасмурная погода, то будет дождь и не будет ветра.
Решим эту задачу средствами алгебры логики.
Решение:
Пусть:
$A$ — «Не будет ветра»;
$B$ — «Пасмурно»;
$C$ — «Дождь».
Запишем с помощью переменных $A$, $B$, $C$ высказывания синоптика:
Если не будет ветра, то будет пасмурная погода и не будет дождя:
\[A\to B\wedge \overline{C}\]Если будет дождь, то будет пасмурно и не будет ветра:
\[C\to B\wedge A\]Если будет пасмурная погода, то будет дождь и не будет ветра
\[B\to C\wedge A\]Составим конъюнкцию указанных функций:
\[F=\left(A\to B\wedge \overline{C}\right)\wedge \left(C\to B\wedge A\right)\wedge \left(B\to C\wedge A\right)\]Используя законы алгебры логики(закон де Моргана, переместительный закон, закон противоречия), упростим формулу:
\[F=\left(A\to B\wedge \overline{C}\right)\wedge \left(C\to B\wedge A\right)\wedge \left(B\to C\wedge A\right)=\] \[=\left(\overline{A}\vee B\wedge \overline{C}\right)\wedge \left(\overline{C}\vee B\wedge A\right)\wedge \left(\overline{B}\vee C\wedge A\right)=\] \[=\left(\overline{A}\vee B\wedge \overline{C}\right)\wedge \left(\overline{B}\vee C\wedge A\right)\wedge \left(\overline{C}\vee B\wedge A\right)=\] \[=\left(\overline{A}\wedge \overline{B}\vee B\wedge \overline{C}\wedge \overline{B}\vee \overline{A}\wedge C\wedge A\vee B\wedge \overline{C}\wedge C\wedge A\right)\wedge \left(\overline{C}\vee B\wedge A\right)=\] \[=\overline{A}\wedge \overline{B}\wedge \left(C\vee B\wedge \overline{A}\right)=\overline{A}\wedge \overline{B}\wedge C\vee \overline{A}\wedge \overline{B}\wedge B\wedge \overline{A}=\overline{A}\wedge \overline{B}\wedge \overline{C}\]Приравниваем результат к единице, т.
\[F=\overline{A}\wedge \overline{B}\wedge \overline{C}=1.\] е. проверяем, при каких условиях выражение будет истинным:
е. проверяем, при каких условиях выражение будет истинным:Проанализируем полученный результат:
Функция будет истинной, если каждый множитель будет истинным, т.е. $\overline{A}=1$, $\overline{B}=1$, $\overline{C}=1$. Отсюда следует, что $A=0$, $B=0$, $C=0$.
Ответ: погода будет без ветра, ясная и без дождя.
Пример 3
История с амфорой
Антон, Борис и Григорий нашли в земле сосуд, о котором каждый высказал по два предположения:
Антон: «Сосуд греческий и изготовлен в V столетии»;
Борис: «Сосуд финикийский и изготовлен в III столетии»;
Григорий: «Сосуд не греческий и изготовлен в IV столетии».
Специалист сказал ученикам, что каждый из них не ошибся только в одном из двух предположений. Определить место и столетие изготовления сосуда.
Решение:
Введем следующие обозначения:
$G$ — «Сосуд греческий»;
$F$ — «Сосуд финикийский»;
$S_3$ — «Сосуд изготовлен в $III$ столетии»;
$S_4$ — «Сосуд изготовлен в $IV$ столетии»;
$S_5$ — «Сосуд изготовлен в $V$ столетии».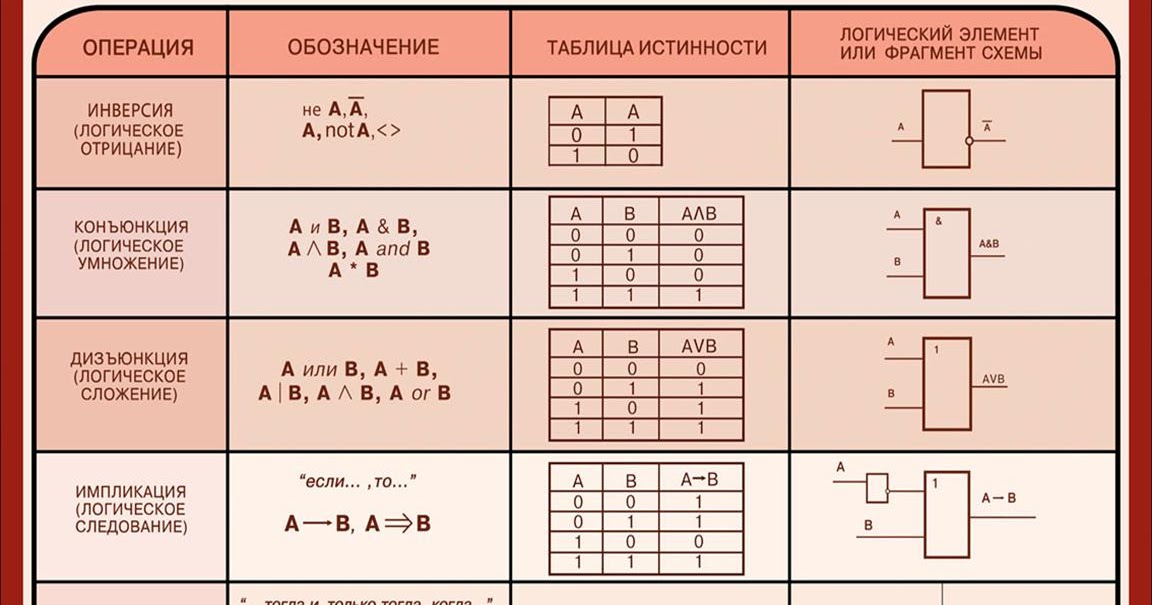
Запишем условие задачи с помощью обозначений:
Антон прав только в одном предположении: $G = 1$ или $S_5 = 1$. Тогда $G\overline{S_5}\vee \overline{G}S_5=1$.
Аналогично для слов Бориса: $F\overline{S_3}\vee \overline{F}S_3=1$.
Для слов Григория: $\overline{G}\overline{S_4}\vee GS_4=1$.
Т.к. сосуд может быть изготовлен только в одном из столетий и только в одной из стран, запишем условия:
\[S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5=1,\] \[F\overline{G}\vee \overline{F}G=1.\]
Применим операцию логического умножения к полученным тождественно истинным высказываниям, результат которого также должен быть тождественно истинным:
\[\left(G\overline{S_5}\vee \overline{G}S_5\right)\wedge \left(F\overline{S_3}\vee \overline{F}S_3\right)\wedge \left(\overline{G}\overline{S_4}\vee GS_4\right)\wedge \left(F\overline{G}\vee \overline{F}G\right)\wedge \] \[\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\]
Перемножим первую на третью скобку и вторую на четвертую:
\[=\left(G\overline{S_5}\overline{G}\overline{S_4}\vee \overline{G}S_5\overline{G}\overline{S_4}\vee G\overline{S_5}GS_4\vee \overline{G}S_5GS_4\right)\wedge \] \[\wedge \left(F\overline{S_3}F\overline{G}\vee \overline{F}S_3F\overline{G}\vee F\overline{S_3}\overline{F}G\vee \overline{F}S_3\overline{F}G\right)\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\]
Т. к. $G\overline{G}=0$, $GG=G$, $\overline{G}\overline{G}=\overline{G}$, упростим выражения:
к. $G\overline{G}=0$, $GG=G$, $\overline{G}\overline{G}=\overline{G}$, упростим выражения:
\[=\left(\overline{G}S_5\overline{S_4}\vee G\overline{S_5}S_4\right)\wedge \left(F\overline{S_3}\overline{G}\vee \overline{F}S_3G\right)\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\]
Перемножим первые две скобки и упростим выражение:
\[=\left(\overline{G}S_5\overline{S_4}\overline{F}S_3G\vee G\overline{S_5}S_4\overline{F}S_3G\vee \overline{G}S_5\overline{S_4}F\overline{S_3}\overline{G}\vee G\overline{S_5}S_4F\overline{S_3}\overline{G}\right)\wedge \] \[\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\] \[=\left(G\overline{S_5}S_4\overline{F}S_3\vee \overline{G}S_5\overline{S_4}F\overline{S_3}\right)\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\] \[=\left(G\overline{S_5}S_4\overline{F}S_3\vee \overline{G}S_5\overline{S_4}F\overline{S_3}\right)\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\overline{G}S_5\overline{S_4}F\overline{S_3};\]
$\overline{G}S_5\overline{S_4}F\overline{S_3}=1$, что возможно только в случае:
\[\overline{G}=1, S_5=1, \overline{S_4}=1, F=1, \overline{S_3}=1. \]
\]
Ответ: сосуд финикийский и изготовлен в $V$ столетии.
Сообщество экспертов Автор24
Автор этой статьи Дата написания статьи: 07.04.2016
Решение заданий ЕГЭ по информатике с использованим элементов алгебры логики
В настоящее время на вступительных экзаменах по информатике есть много заданий по теме “алгебра логики”. Цель данного урока – закрепление навыков решения заданий ЕГЭ по информатике с использованием элементов алгебры логики.
Цели урока:
- Формирование умения применять полученные знания на практике;
- Развитие умения построения таблиц истинности по заданным формулам;
- Развитие умения решать текстовые задачи с использованием законов логики.
Задачи урока:
- Воспитательная – развитие
познавательного интереса, логического мышления.

- Образовательная – повторение основ математической логики, выполнение практических заданий.
- Развивающая – развитие логического мышления, внимательности.
Ход урокаПовторение логических операций и законов.
Сегодня мы с вами завершаем тему “Основы логики” и применим основные логические операции, законы преобразования для решения заданий ЕГЭ по информатике.
Урок идет параллельно с презентацией. <Приложение1>
1. Повторение логических операций и законов.
Алгебра логики – раздел математической логики,
изучающий строение сложных логических
высказываний и способы установления их
истинности с помощью алгебраических методов.
Вопросы:
1. Основоположник формальной логики?
Аристотель.
2. Основоположник алгебры логики?
Джордж Буль.
3. Перечислите логические операции:
¬ отрицание (инверсия)
&, /\ конъюнкция (“И”)
V дизъюнкция (“ИЛИ”)
логическое следование (импликация)
равнозначность (эквивалентность)
4. В чем смысл закона двойного отрицания?
Двойное отрицание исключает отрицание.
5. Законы де Моргана (законы общей инверсии).
Отрицание дизъюнкции является конъюнкцией отрицаний:
¬(A V B) = ¬A /\ ¬B
Отрицание конъюнкции является дизъюнкцией отрицаний:
¬(A /\B) = ¬A V ¬B
6. Закон идемпотентности (одинаковости).
A V A = A
A /\ A = A
7. В чём смысл закона исключения третьего?
В чём смысл закона исключения третьего?
Из двух противоречащих высказываний об одном и том же одно всегда истинно, второе ложно, третьего не дано:
A V ¬А= 1
8. О чём закон противоречия?
Не могут быть одновременно истинны утверждение и его отрицание:
A /\ ¬А= 0
9. Закон исключения констант.
Для логического сложения:
A V 1 = 1 A V 0 = A
Для логического умножения:
A /\ 1 = A A /\ 0 = 0
10. Как выразить импликацию через дизъюнкцию?
А В = ¬A V В
2. Примение логических операций и законов на практике.
Пример 1. (Задание А11 демоверсии 2004 г.)
Для какого имени истинно высказывание:
¬ (Первая буква имени гласная -> Четвертая буква имени согласная)?
1) ЕЛЕНА
2) ВАДИМ
3) АНТОН
4) ФЕДОР
Решение.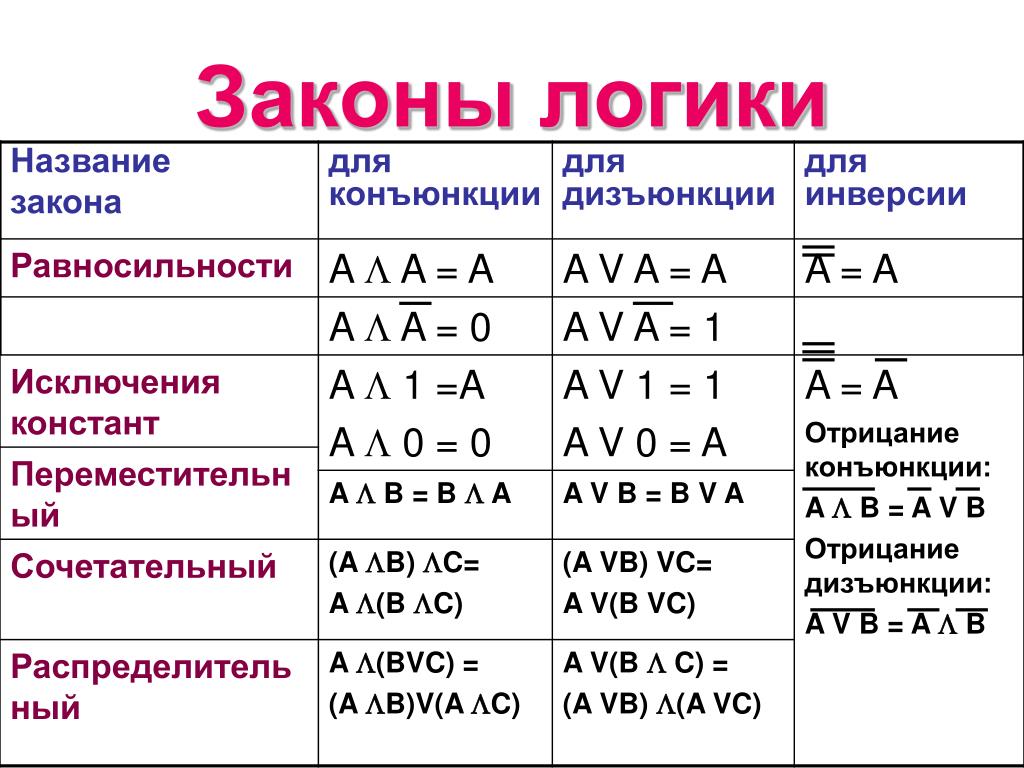 Сложное высказывание состоит из
двух простых высказываний:
Сложное высказывание состоит из
двух простых высказываний:
А – первая буква имени гласная,
В – четвертая буква имени согласная.
¬ (А В) = ¬ (¬A V В) = (¬ (¬А) /\ ¬B) = A /\ ¬B
Применяемые формулы:
1. Импликация через дизъюнкцию А ? В = ¬A V В
2. Закон де Моргана ¬(A V B) = ¬A /\ ¬B
3. Закон двойного отрицания.
(Первая буква имени гласная /\ Четвертая буква имени гласная)
Ответ: 3
Пример 2. (Задание А12 демоверсии 2004 г.)
Какое логическое выражение равносильно выражению ¬ (А \/ ¬B)?
1) A \/ B
2) A /\ B
3) ¬A \/ ¬B
4) ¬A /\ B
Решение. ¬ (А \/ ¬B)= ¬ А \/ ¬ (¬B)= ¬ А \/ B
Ответ: 4
Пример 3.
Составить таблицу истинности для формулы
¬ (B /\ C) V (A/\C B)
Порядок выполнения логических операций:
¬ (B /\ C) V (A/\C B)
2 1 5 3 4
Составить таблицу истинности.
Сколько строк будет в вашей таблице? 3 переменных: А, В, С; 23=8
Сколько столбцов? 5 операций + 3 переменных = 8
Решение:
| A | B | C | (B /\ C) | ¬ (B /\ C) | A/\C | (A/\C ? B) | ¬ (B /\ C) V (A/\C B) |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
Какие ответы получились в последнем столбце?
Ответ: 1
Логическое выражение называется тождественно-истинным,
если оно принимает значения 1 на всех наборах
входящих в него простых высказываний. Тождественно-истинные формулы называют тавтологиями.
Тождественно-истинные формулы называют тавтологиями.
Решим этот пример аналитическим методом:
упрощаем выражение
¬ (B /\ C) V (A/\C B)= (применим формулу для импликации)
¬ (B /\ C) V ¬ (A /\ C) V B = (применим 1 и 2 законы де Моргана)
(¬B V ¬C) V (¬A V ¬C) V B = (уберём скобки)
¬B V ¬C V ¬A V ¬C V B= (применим переместительный закон)
¬B V B V ¬C V ¬C V ¬A = (закон исключения третьего, закон идемпотентности)
1 V ¬С V ¬A = 1 V ¬A = 1 (закон исключения констант)
Ответ: 1, означает, что формула является тождественно-истинной или тавтологией.
Логическое выражение называется тождественно-ложным, если оно принимает значения 0 на всех наборах входящих в него простых высказываний.
(задание 3 домашнего задания)
Пример 4.
В таблице приведены запросы к поисковому
серверу. Расположите обозначения запросов в
порядке возрастания количества страниц, которые
найдёт поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” в запросе используется символ I, а для логической операции “И” – символ &.
А Законы & Физика Б Законы I (Физика & Биология) В Законы & Физика & Биология & Химия Г Законы I Физика I Биология
Решение:
Первый способ основан на рассуждении.
Рассуждая логически, мы видим, что больше всего
будет найдено страниц по запросу Г, так как при
его исполнении будут найдены и страницы со
словом “законы”, и страницы, со словом
“физика”, и страницы со словом “биология”.
Меньше всего будет найдено страниц по запросу В,
так как в нем присутствие всех четырех слов на
искомой странице. Осталось сравнить запросы А и
Б. По запросу Б будут найдены все страницы,
соответствующие запросу А, (так как в последних
обязательно присутствует слово “законы”), а
также страницы, содержащие одновременно слова
“физика” и “биология”. Следовательно по
запросу Б будет найдено больше страниц, чем по
запросу А. Итак, упорядочив запросы по
возрастанию страниц, получаем ВАБГ.
Осталось сравнить запросы А и
Б. По запросу Б будут найдены все страницы,
соответствующие запросу А, (так как в последних
обязательно присутствует слово “законы”), а
также страницы, содержащие одновременно слова
“физика” и “биология”. Следовательно по
запросу Б будет найдено больше страниц, чем по
запросу А. Итак, упорядочив запросы по
возрастанию страниц, получаем ВАБГ.
Ответ: ВАБГ.
Второй способ предполагает использование графического представления операций над множествами. (Смотри презентацию)
Пример 5. (Задание А16 демоверсии 2006 г.)
Ниже в табличной форме представлен фрагмент базы данных о результатах тестирования учащихся (используется стобалльная шкала)
| Фамилия | Пол | Математика | Русский язык | Химия | Информатика | Биология |
| Аганян | ж | 82 | 56 | 46 | 32 | 70 |
| Воронин | м | 43 | 62 | 45 | 74 | 23 |
| Григорчук | м | 54 | 74 | 68 | 75 | 83 |
| Роднина | ж | 71 | 63 | 56 | 82 | 79 |
| Сергеенко | ж | 33 | 25 | 74 | 38 | 46 |
| Черепанова | ж | 18 | 92 | 83 | 28 | 61 |
Сколько записей в данном фрагменте удовлетворяют условию
“Пол=’м’ ИЛИ Химия>Биология”?
1) 5
2) 2
3) 3
4) 4
Решение:
Выбираем записи: Мальчики (двое) и
Химия>Биология (трое, но один мальчик, уже
взялся 1 раз). В итоге 4 записи удовлетворяют
условию.
В итоге 4 записи удовлетворяют
условию.
Ответ: 4
Задание 6. (Задание В4 демоверсии 2007 г)
В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита. Самые горячие болельщики высказали свои предположения о распределении мест в дальнейших состязаниях.
Один считает, что первой будет Наташа, а Маша будет второй.
Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место.
Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов.
Какое место на чемпионате заняли Наташа, Маша, Люда, Рита?
(В ответе перечислите подряд без пробелов числа, соответствующие местам девочек в указанном порядке имен.)
Решение:
Обозначим высказывания:
Н1 = “первой будет Наташа”;
М2 = “второй будет Маша”;
Л2 = “второй будет Люда”;
Р4 = “четвертой будет Рита”;
Р3 = “третьей будет Рита”;
Н2 = “второй будет Наташа”.
Согласно условию:
из высказываний 1 болельщика следует, что Н1VМ2 истинно;
из высказываний2 болельщика следует, что Л2VР4 истинно;
из высказываний 3 болельщика следует, что Р3VН2 истинно.
Следовательно, истинна и конъюнкция
(Н1VМ2) /\ (Л2VР4) /\ (Р3VН2) = 1.
Раскрыв скобки получим:
(Н1VМ2) /\ (Л2VР4) /\ (Р3VН2) = (Н1/\Л2V Н1/\Р4 V М2/\Л2 V М2/\Р4) /\ (Р3VН2)=
Н1/\ Л2/\Р3 V Н1/\Р4/\Р3 V М2/\Л2/\Р3 V М2/\Р4/\Р3 V Н1/\Л2/\Н2 V Н1/\Р4/\Н2 V М2/\Л2/\Н2 V М2/\Р4/\Н2 = Н1/\ Л2/\Р3 V 0 V 0 V 0 V 0 V 0 V 0 V= Н1/\ Л2/\Р3
Наташа-1, Люда-2, Рита-3, а Маша-4.
Ответ: 1423
3. Объяснение домашнего задания.
Задание 1. (Задание В8 демоверсии 2007г)
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” в
запросе используется символ |, а для логической
операции “И” – &.
А волейбол | баскетбол | подача Б волейбол | баскетбол | подача | блок В волейбол | баскетбол Г волейбол & баскетбол & подача
Задание 2 (Задание В4 демоверсии 2008г)
Перед началом Турнира Четырех болельщики высказали следующие предположения по поводу своих кумиров:
A) Макс победит, Билл – второй;
B) Билл – третий. Ник – первый;
C) Макс – последний, а первый – Джон.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов.
Какое место на турнире заняли Джон, Ник, Билл, Макс?
(В ответе перечислите подряд без пробелов места
участников в указанном порядке имен. )
)
Оценки за урок.
Математика | Введение в логику высказываний | Набор 1
Что такое логика?Логика является основой всех математических рассуждений и всех автоматических рассуждений. Правила логики определяют значение математических утверждений. Эти правила помогают нам понять и обосновать такие утверждения, как —
, например, где
Что на простом английском языке означает «Существует целое число, которое не является суммой двух квадратов». Важность математической логики Правила логики придают точный смысл математическим утверждениям. Эти правила используются для различения действительных и недействительных математических аргументов. Помимо важности для понимания математических рассуждений, логика имеет множество применений в компьютерных науках, начиная от проектирования цифровых схем и заканчивая созданием компьютерных программ и проверкой правильности программ.
Логика высказываний Что такое предложение? Предложение является основным строительным блоком логики. Оно определяется как повествовательное предложение, которое либо истинно, либо ложно, но не то и другое одновременно. Значение истинности предложения является истинным (обозначается как T), если это истинное утверждение, и ложным (обозначается как F), если это ложное утверждение. Например,
Оно определяется как повествовательное предложение, которое либо истинно, либо ложно, но не то и другое одновременно. Значение истинности предложения является истинным (обозначается как T), если это истинное утверждение, и ложным (обозначается как F), если это ложное утверждение. Например,
1. Солнце встает на востоке и заходит на западе. 2. 1 + 1 = 2 3. «б» — гласная.
Все приведенные выше предложения являются предложениями, где первые два являются действительными (верными), а третье — недействительными (ложными). Некоторые предложения, которые не имеют истинностного значения или могут иметь более одного истинностного значения, не являются предложениями. Например,
1. Который час? 2. Выйдите и поиграйте. 3. x + 1 = 2.
Приведенные выше предложения не являются высказываниями, так как первые два не имеют истинностного значения, а третье может быть истинным или ложным. Для представления предложений используется пропозициональных переменных . По соглашению эти переменные представлены маленькими буквами, такими как . Область логики, которая имеет дело с предложениями, называется исчислением высказываний или логикой высказываний . Это также включает в себя создание новых предложений с использованием существующих. Предложения, составленные из одного или нескольких предложений, называются составные предложения . Предложения объединяются вместе с помощью логических связок или логических операторов .
По соглашению эти переменные представлены маленькими буквами, такими как . Область логики, которая имеет дело с предложениями, называется исчислением высказываний или логикой высказываний . Это также включает в себя создание новых предложений с использованием существующих. Предложения, составленные из одного или нескольких предложений, называются составные предложения . Предложения объединяются вместе с помощью логических связок или логических операторов .
Поскольку нам необходимо знать истинностное значение предложения во всех возможных сценариях, мы рассматриваем все возможные комбинации предложений, которые соединяются вместе логическими связками, чтобы сформировать данное сложное предложение. Эта компиляция всех возможных сценариев в табличном формате называется таблица истинности . Наиболее распространенные логические связки-
1. Отрицание – Если является предложением, то отрицание обозначается , что в переводе на простой английский означает- «Это не тот случай, что » или просто «не». Истинное значение является противоположным истинностному значению . Таблица истинности –
Отрицание – Если является предложением, то отрицание обозначается , что в переводе на простой английский означает- «Это не тот случай, что » или просто «не». Истинное значение является противоположным истинностному значению . Таблица истинности –
Пример. Отрицание «Сегодня идет дождь» — это «Это не тот случай, когда сегодня идет дождь» или просто «Сегодня не идет дождь».
2. Союз – Для любых двух предложений и их союз обозначается , что означает «и». Союз является истинным, когда оба и являются истинными, в противном случае – ложным. Таблица истинности –
. Пример. Соединение предложений – “Сегодня пятница” и – “Сегодня идет дождь” равно “Сегодня пятница и сегодня идет дождь”. Это утверждение верно только в дождливую пятницу и ложно в любой другой дождливый день или в пятницу, когда дождя нет.
3. Дизъюнкция — Для любых двух предложений и их дизъюнкция обозначается , что означает «или». Дизъюнкция является Истинной, когда либо или Истинна, либо Ложь в противном случае. Таблица истинности –
Дизъюнкция является Истинной, когда либо или Истинна, либо Ложь в противном случае. Таблица истинности –
. Пример. Дизъюнкция предложений – «Сегодня пятница» и – «Сегодня идет дождь» – «Сегодня пятница или сегодня идет дождь». Это утверждение верно в любой день, который является пятницей или дождливым днем (включая дождливую пятницу), и ложно в любой день, кроме пятницы, когда также не идет дождь.
4. Исключающее ИЛИ – Для любых двух предложений и их исключающее или обозначается , что означает «либо или но не оба». Исключающее или является истинным, когда одно или является истинным, и ложным, когда оба истинны или оба ложны. Таблица истинности –
Пример. Исключающее или предложений – «Сегодня пятница» и – «Сегодня идет дождь»: «Либо сегодня пятница, либо сегодня идет дождь, но не то и другое одновременно». Это утверждение верно в любой день, который является пятницей или дождливым днем (не считая дождливых пятниц), и ложно в любой день, кроме пятницы, когда не идет дождь или дождливые пятницы.
5. Импликация — Для любых двух предложений и утверждение «если, то» называется импликацией и обозначается . В импликации называется гипотезой или предшествующей или предпосылкой и называется заключением или следствием . Импликация также называется условным оператором . Импликация ложна, когда истинна, и ложна в противном случае. Таблица истинности –
Вы можете задаться вопросом, почему истинно, когда ложно. Это связано с тем, что импликация гарантирует, что если и истинны, то импликация верна. Но импликация ничего не гарантирует, если посылка ложна. Невозможно узнать, является ли вывод ложным, поскольку этого не произошло. Эта ситуация аналогична позиции «Невиновен, пока не доказана вина», что означает, что вывод считается верным, пока не будет доказано, что он неверен. Поскольку мы не можем назвать импликацию ложной, если она ложна, наша единственная альтернатива — назвать ее истинной. Это следует из Принцип взрыва , который гласит: «Ложное утверждение подразумевает что-либо». Условные утверждения играют очень важную роль в математических рассуждениях, поэтому для выражения используются различные термины, некоторые из которых перечислены ниже.
Это следует из Принцип взрыва , который гласит: «Ложное утверждение подразумевает что-либо». Условные утверждения играют очень важную роль в математических рассуждениях, поэтому для выражения используются различные термины, некоторые из которых перечислены ниже.
"если , то "" достаточно для "" когда ""необходимым условием для является "" только если "" если "" не следует из "
Пример «Если сегодня пятница, то сегодня идет дождь» является предложение, имеющее форму . Вышеприведенное утверждение верно, если сегодня не пятница (посылка ложна) или если сегодня пятница и идет дождь, и ложно, когда пятница, но дождя нет.
6. Биусловная или двойная импликация — Для любых двух суждений и утверждение «если и только если (ифф)» называется биусловным и обозначается . Оператор также называется биимпликацией . имеет то же истинностное значение, что и Импликация истинна, когда и имеет те же значения истинности, и ложна в противном случае. Таблица истинности is-
Таблица истинности is-
Некоторые другие распространенные способы выражения are-
"необходим и достаточен для""if then" и наоборот""iff"
Пример: «Сегодня идет дождь тогда и только тогда, когда сегодня пятница». это предложение, имеющее вид . Вышеприведенное утверждение верно, если сегодня не пятница и не идет дождь, или если сегодня пятница и идет дождь, и ложно, если не пятница или не идет дождь. Упражнение:
1) Рассмотрим следующие утверждения:
P: Хорошие мобильные телефоны недешевы. В: Дешевые мобильные телефоны не годятся. L: P подразумевает Q M: Q подразумевает P N: P эквивалентно Q
Что из следующего относительно L, M и N ВЕРНО? (Gate 2014)
(A) Только L ВЕРНО.
(B) Только M ИСТИНА.
(C) Только N ИСТИНА.
(D) L, M и N ИСТИННЫ.
Для решения см. GATE | ВОРОТА-CS-2014-(Комплект-3) | Вопрос 11
2) Что из следующего не эквивалентно p⇔q (Gate 2015)
Решение см. в GATE | ВОРОТА-CS-2015 (Комплект 1) | Вопрос 65
в GATE | ВОРОТА-CS-2015 (Комплект 1) | Вопрос 65
Ссылки- Логика высказываний – Википедия Принцип взрыва – Википедия
Дискретная математика и ее приложения, автор: Kenneth H Rosen
Читать следующую часть : Введение в логику высказываний. Чираг Манвани . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу [email protected]. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам. Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.
Как математика используется в информатике?
По своей сути компьютеры являются вычислительными машинами. Просто подумайте о слове «компьютер» — что-то, что вычисляет. Даже если вы используете свой ноутбук для отправки электронных писем чаще, чем для баланса своего банковского счета, внутри машины происходят математические операции.
Если вы стремитесь сделать карьеру в области компьютерных наук, вы можете задаться вопросом, сколько математики вам нужно знать, чтобы добиться успеха. Ответ зависит от того, что вы хотите делать в своей компьютерной карьере и насколько продвинуты вы хотите стать.
Нужна ли вам математика в компьютерных науках?
Поскольку математика является фундаментальной частью компьютерных систем, каждый программист и ученый-компьютерщик должен иметь базовые математические знания. Тип и уровень математики, которые вам нужны, зависят от того, в каких областях компьютерных наук вы хотите работать.
Некоторые карьерные пути в области компьютерных наук требуют лишь минимальных математических знаний. Например, если вы знаете основные языки программирования и умеете выполнять простые арифметические действия, вы можете разрабатывать базовые мобильные приложения.
Но если вы хотите продвинуться дальше в своей карьере в области информатики, возможно, изучая передовые области, такие как компьютерная безопасность или операционные системы, вам необходимо понимать некоторые математические концепции более высокого уровня. Никто не ожидает, что компьютерщики будут математиками, но изучение математики на уровне средней школы и колледжа может открыть двери.
Никто не ожидает, что компьютерщики будут математиками, но изучение математики на уровне средней школы и колледжа может открыть двери.
«[В обучении информатике] вы узнаете больше о структурах данных и алгоритмах. Это своего рода ядро, математическая сторона компьютерных наук.»
«[В курсе CS] вы узнаете больше о структурах данных и алгоритмах», — сказал Дэвид Джойнер, доктор философии и исполнительный директор по онлайн-обучению Колледжа вычислительной техники Технологического института Джорджии и инструктор курса edX Introduction to Python Programming Professional. Сертификационная программа.
«Это своего рода ядро, математическая сторона информатики. Это очень, очень важно, потому что дает вам более глубокое понимание того, что на самом деле представляет собой разработка с использованием компьютеров». Например, заключительный курс программы Python, которую читает Джойнер, Computing in Python IV: Objects & Algorithms, посвящен объектно-ориентированному программированию — популярной парадигме, которую Джойнер сравнивает с философией: «Объектно-ориентированное программирование говорит о моем общем Желание донести до людей, что информатика предназначена не только для тех, кто хорошо разбирался в математике в старшей школе. Это область программирования, которая на удивление тесно связана с философией, — сказал Джойнер. люди часто недооценивают карьеру в области компьютерных наук, потому что это очень творческие области».
Это область программирования, которая на удивление тесно связана с философией, — сказал Джойнер. люди часто недооценивают карьеру в области компьютерных наук, потому что это очень творческие области».
Какая математика используется в информатике?
Ученые-компьютерщики используют все виды математики. Тем, кто работает с передовыми алгоритмами и матрицами, такими как распознавание изображений для медицинской диагностики, необходимо понимать концепции более высокого уровня, такие как дифференциальные уравнения.
Но начинающим профессионалам и первокурсникам важнее овладеть теорией чисел и основными уравнениями. Вот несколько тем для изучения.
Двоичный и шестнадцатеричный счет
Двоичная система счисления использует только две цифры, 0 и 1, для выражения всех математических понятий. Компьютеры используют двоичную систему вместо более распространенной десятичной, поэтому специалистам по информатике необходимо знать, как она работает.
Компьютеры могут читать двоичные файлы, но людям это может быть неудобно. В качестве альтернативы компьютерное программирование превратилось в систему, называемую шестнадцатеричной, в которой используются все девять десятичных цифр и буквы от A до F. Это более понятно для людей и преобразуется электронным способом в двоичную систему.
В качестве альтернативы компьютерное программирование превратилось в систему, называемую шестнадцатеричной, в которой используются все девять десятичных цифр и буквы от A до F. Это более понятно для людей и преобразуется электронным способом в двоичную систему.
Пусть вас не пугает незнакомство с этими языками. Программы по информатике, как правило, охватывают их на раннем этапе, поэтому вы можете сразу же начать практиковаться.
Дискретная математика
Дискретная математика — это материальная математика. Он анализирует отношения между вещами, которые являются отдельными и отдельными. Понятия дискретной математики включают:
- Вероятность
- Комбинаторика
- Логика
- Теория чисел
- Теория графов
Процессы решения задач дискретной математики являются основой современной вычислительной техники. Они поддерживают как простые, так и сложные дисциплины, такие как:
- Компьютерная архитектура
- Функциональное программирование
- Распределенные системы
- Машинное обучение и искусственный интеллект
Как специалист в области информатики, вы можете использовать дискретную математику для проверки нескольких алгоритмов и определения наиболее эффективного из них. Между тем, логическое мышление, которое вы разовьете, когда будете изучать дискретную математику, поможет вам более методично подходить к задачам программирования и разработки.
Между тем, логическое мышление, которое вы разовьете, когда будете изучать дискретную математику, поможет вам более методично подходить к задачам программирования и разработки.
Статистика
В последние несколько лет данные становятся все более важным аспектом научных вычислений, от машинного обучения до производительности персонализированных приложений. Эта повышенная зависимость от данных сделала статистику важной темой изучения для всех студентов, изучающих информатику.
Статистика позволяет компьютерным программам делать точные обобщения и прогнозы на основе доступной информации. Понимание статистики может облегчить понимание таких понятий, как:
- Интеллектуальный анализ данных
- Машинное обучение
- Моделирование будущего
- Распознавание речи
- Реакция пользователя
- Анализ компьютерной графики
Чем больше вы узнаете о статистике, тем более искусными вы станете в управлении и использовании сложных структур данных. Это позволяет вам писать более продвинутые алгоритмы и расширять границы настройки программного обеспечения.
Это позволяет вам писать более продвинутые алгоритмы и расширять границы настройки программного обеспечения.
Линейная алгебра
Информатика и разработка программного обеспечения опираются на алгоритмы. Алгоритм — это формула, которая ведет вас от определенного ввода к правильному выводу. Если это звучит знакомо, возможно, это напоминает вам об алгебре в средней или старшей школе.
Алгебра включает такие понятия, как:
- Экспоненты
- Многочлены
- Линейные уравнения
- Квадратные уравнения
Каждая из этих концепций применима в реальных компьютерных науках. Понимание экспоненциальных отношений может помочь вам адаптировать визуальные эффекты так, чтобы они привлекали внимание. Решение линейных уравнений помогает при анализе алгоритмов, поскольку помогает выявлять неточности.
В разработке программного обеспечения можно обойтись без знания алгебры, но ее изучение может помочь вам достичь больших высот.
Исчисление
Если вы планируете получить степень в области компьютерных наук, вы, вероятно, когда-нибудь пройдёте курс исчисления.
Существует два различных типа исчисления: интегральное исчисление и дифференциальное исчисление. Вместе эти дисциплины помогут вам определить скорость изменения, которая является важным компонентом многих алгоритмов и программ.
Дифференциальные уравнения особенно важны. Дифференциальное уравнение вычисляет, как что-то меняется и как быстро это происходит, поэтому компьютер может предсказать будущие результаты. Это помогает:
- Моделирование проектирования
- Улучшение программ решения проблем
- Создание эффективных алгоритмов
- Разработка точных графиков
Слово «исчисление» пугает некоторых студентов, изучающих информатику, но оно гораздо менее пугающее, чем думает большинство людей. Ключ в том, чтобы найти курс, который проведет вас через то, что вам нужно знать, чтобы работать в своей области.
Математика и информатика: что нужно для начала?
Чем больше вы будете изучать математику, тем глубже станете понимать компьютеры. Но значит ли это, что вы должны стать математиком, прежде чем начать изучать информатику?
Абсолютно нет!
Современные преподаватели компьютерных наук знают, что у всех разный опыт. Они встраивают изучение математики в свою учебную программу, чтобы учащиеся имели наилучшие шансы на успех.
Знаете ли вы?
Если вы пройдете курс информатики edX, вы обнаружите, что математические концепции и практика встроены в ваше обучение. Например, курс Computing in Python I от Технологического института Джорджии включает в себя разделы программы, посвященные переменным и математическим операторам, в которых особое внимание уделяется тому, как эти навыки работают в вычислительной технике.
Вы можете начать заниматься информатикой, имея только имеющиеся у вас математические навыки, или пройти курс, чтобы освежить свои знания и обрести уверенность.
Начало работы: изучение математики с помощью edX
Всем специалистам в области информатики необходимы хотя бы некоторые знания по математике. Курсы по информатике, которые вы найдете на edX, включают в себя некоторое изучение математики, но некоторые студенты могут все еще чувствовать, что им нужна специальная курсовая работа по математике, прежде чем приступить к работе.
На платформе edX вы найдете множество математических курсов, актуальных для студентов, изучающих информатику. Варианты включают «Введение в линейную алгебру», «Основы статистики» и «Исчисление перед университетом». Узнайте больше о математических курсах edX сегодня и начните быстрый путь к карьере в области компьютерных наук.
Пять типов математики, используемых в информатике
Все мы знаем, что математика и компьютеры тесно связаны. Вещи, которые приносят развлечения, общение и информацию в наши дома и на кончики пальцев, в своей самой простой форме — это числа. Итак, чтобы по-настоящему понять компьютеры и науку, которая заставляет их работать, мы должны сначала понять математику, которая составляет их анатомию.
Итак, чтобы по-настоящему понять компьютеры и науку, которая заставляет их работать, мы должны сначала понять математику, которая составляет их анатомию.
Одной из математических программ, которые мы используем каждый день, являются системы GPS, такие как Google Maps!. Они работают сразу над несколькими сложными приложениями, сравнивая один маршрут с другим, чтобы найти для вас самый быстрый. Факторы, такие как данные о местоположении, исторические модели трафика и другие показатели, являются числами, которые составляют эти уравнения. Программное обеспечение, используемое в Google Maps, постоянно обновляется в режиме реального времени с помощью машинного обучения. Таким образом, предложения приложения всегда будут самыми актуальными, что поможет вам добраться до места назначения как можно быстрее.
Было бы невозможно свести математику информатики в одну статью, но вот несколько основных математических механик информатики. Давайте рассмотрим каждый:
Давайте рассмотрим каждый:
Двоичная математика:
Двоичная математика — это сердце компьютера и важная математическая область для компьютерного программирования. Для всех математических понятий двоичная система счисления использует только две цифры, 0 и 1. Она упрощает процесс кодирования и необходима для низкоуровневых инструкций, используемых при программировании оборудования. Компьютеры хранят данные, используя двоичную систему. Информация, которую мы храним на компьютерах, от картинок до игр и даже видео, хранится с использованием двоичной системы счисления.
Линейная алгебра:
Линейная алгебра — это язык машинного обучения. Сердцебиение компьютера находится в линейной алгебре. Этот раздел математики предоставляет концепции, имеющие решающее значение для многих областей компьютерных наук, включая графику, обработку изображений, криптографию, машинное обучение, компьютерное зрение, оптимизацию, графовые алгоритмы, квантовые вычисления, вычислительную биологию, поиск информации и веб-поиск. Линейная алгебра — это то, что делает ваши видеоигры такими захватывающими и дает ответы на любые вопросы, которые вы можете задать!
Линейная алгебра — это то, что делает ваши видеоигры такими захватывающими и дает ответы на любые вопросы, которые вы можете задать!
Исчисление:
Исчисление — это раздел математики. Он изучает скорость, с которой происходят изменения. Он часто используется в компьютерной графике, научных вычислениях, приложениях для решения проблем, программировании игр и компьютерной безопасности.
Исчисление — это исследование непрерывного изменения и скорости изменения. Он используется во множестве областей компьютерных наук, включая создание графиков или изображений, моделирование, приложения для решения проблем, кодирование в приложениях, создание статистических решателей, а также разработку и анализ алгоритмов. Существует два различных типа исчисления: интегральное исчисление и дифференциальное исчисление. Вместе эти дисциплины помогут вам определить скорость изменения, которая является важным компонентом многих алгоритмов и программ.
Дифференциальные уравнения особенно важны. Дифференциальное уравнение вычисляет, как что-то изменяется и как быстро это происходит, поэтому компьютер может предсказать будущие результаты
Дискретная математика:
Эта математическая дисциплина является основой информатики. Дискретная математика изучает математические структуры. Его природа различна и разделима, охватывая логику, вероятность, комбинаторику, деревья, теорию множеств, алгоритмы и графы. Иногда ее также называют математикой принятия решений или конечной математикой, она работает с объектами, которые могут иметь разные отдельные значения. Это считается очень эффективным подходом к развитию силы и решению проблем.
Статистика:
Этот раздел математики используется для нескольких целей, включая интеллектуальный анализ данных, сжатие данных, анализ изображений и искусственный интеллект. Статистика была особенно полезна в программном обеспечении для распознавания речи, таком как Siri от Apple. Получив ваш запрос, Siri записывает частоты и звуковые волны вашего голоса и переводит их в код. Затем Siri разбирает код, чтобы определить конкретные шаблоны, фразы и ключевые слова. Статистика также поддерживает такие программы, как Google Translate, который использует данные для выполнения онлайн-переводов. Статистика помогает компьютерам обрабатывать огромные объемы информации в мгновение ока. Вы можете поблагодарить статистику за революцию в том, как мы используем компьютеры!
Получив ваш запрос, Siri записывает частоты и звуковые волны вашего голоса и переводит их в код. Затем Siri разбирает код, чтобы определить конкретные шаблоны, фразы и ключевые слова. Статистика также поддерживает такие программы, как Google Translate, который использует данные для выполнения онлайн-переводов. Статистика помогает компьютерам обрабатывать огромные объемы информации в мгновение ока. Вы можете поблагодарить статистику за революцию в том, как мы используем компьютеры!
Существует тесная связь между информатикой и математикой. Он учит программистов использовать абстрактный язык, работать с алгоритмами, самостоятельно анализировать свое вычислительное мышление и точно моделировать реальные решения. Возможно, ваш ученик станет следующим инновационным программистом!
В Mathnasium мы приветствуем обучение во всех его формах и хотели бы помочь детям расширить свое математическое мышление. Посетите наш веб-сайт, чтобы просмотреть наш каталог и получить помощь по математике, необходимую им для отличного учебного года.
Почему логика важна для информатики и математики
Чешский перевод этой страницы доступен по адресу Scientific и технический перевод .
Шведский перевод этой страницы доступен по адресу Научный блог: https://www.expertoautorecambios.es/science/?p=998 .
Эстонский перевод этой страницы доступен по адресу:
https://www.espertoautoricambi.it/science/2017/11/03/miks-loogika-on-oluline-et-arvuti-teadust-ja-matemaatika/
89 Португальский перевод этой страницы доступен по адресу:
https://www.homeyou.com/~edu/ciencia-da-computacao-e-matematica
Логика связана с формами рассуждений. С
рассуждение участвует в большинстве интеллектуальных действий, логика имеет отношение к
широкий круг занятий. Изучение логики необходимо для школьников.
Информатика. Это также очень ценно для студентов, изучающих математику, и других
которые используют математические доказательства, например, студенты-лингвисты. в
процесс рассуждения делает выводы. В выводе используется
совокупность утверждений, предпосылок, чтобы оправдать другое утверждение,
вывод. Наиболее надежными типами умозаключений являются дедуктивные умозаключения,
в котором заключение должно быть истинным, если посылки верны. Вспомнить элементарно
геометрия: Предполагая, что постулаты верны, мы доказываем, что другие
утверждения, такие как теорема Пифагора, также должны быть истинными. Геометрический
доказательства и другие математические доказательства обычно используют множество дедуктивных выводов.
Изучение логики необходимо для школьников.
Информатика. Это также очень ценно для студентов, изучающих математику, и других
которые используют математические доказательства, например, студенты-лингвисты. в
процесс рассуждения делает выводы. В выводе используется
совокупность утверждений, предпосылок, чтобы оправдать другое утверждение,
вывод. Наиболее надежными типами умозаключений являются дедуктивные умозаключения,
в котором заключение должно быть истинным, если посылки верны. Вспомнить элементарно
геометрия: Предполагая, что постулаты верны, мы доказываем, что другие
утверждения, такие как теорема Пифагора, также должны быть истинными. Геометрический
доказательства и другие математические доказательства обычно используют множество дедуктивных выводов.
Большинство наших курсов логики включают точный анализ характеристик
дедуктивный вывод. Эти курсы вводят некоторые специальные символы в то, что
называется «формальными языками», но логика не является операцией с символами.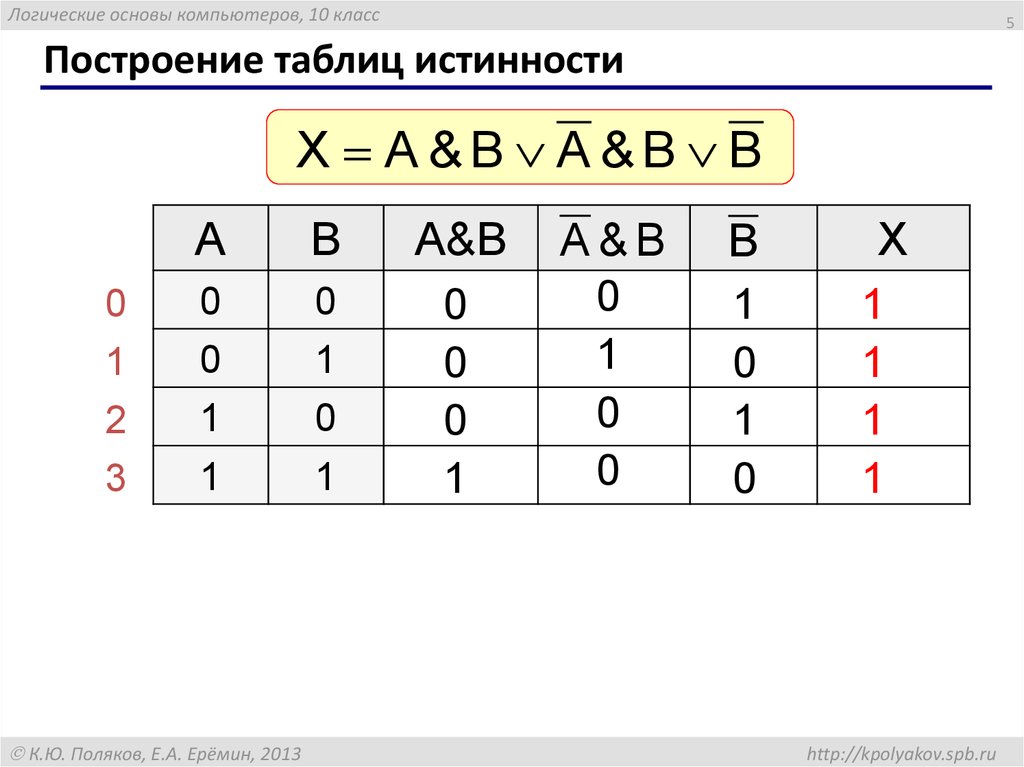 Курсы
обучать общим понятиям и методам, которые полезны независимо от формальных
языки. Студенты узнают, как строить доказательства на английском языке, а также на
формальный язык, так что понятия и методы, которые изучены, могут быть использованы в
разнообразие контекстов. Учатся даже доказывать теоремы о формальных
языки; это особенно важно для информатики, лингвистики и
некоторые разделы математики.
Курсы
обучать общим понятиям и методам, которые полезны независимо от формальных
языки. Студенты узнают, как строить доказательства на английском языке, а также на
формальный язык, так что понятия и методы, которые изучены, могут быть использованы в
разнообразие контекстов. Учатся даже доказывать теоремы о формальных
языки; это особенно важно для информатики, лингвистики и
некоторые разделы математики.
Идея компьютера общего назначения, машины Тьюринга, была изобретена в
курс исследований по логике. Программы для ЭВМ пишутся на специальных,
символьные языки, например, Fortran, C++, Lisp, Prolog.
Эти языки содержат черты логического символизма, а Лисп и Пролог
производные от формальных языков для логики. Благодаря таким связям изучение
логика может помочь в разработке программ. Другие математические методы
описанные в PHL 313K, например рекурсивные определения, широко используются в программах.
Теория множеств, описанная в PHL 313K, используется в современных проектах баз данных. Но
информатика — это не только программирование. включает в себя логические и
математический анализ программ. С помощью таких анализов можно доказать
корректность процедур и оценить количество шагов, необходимых для выполнения
заданную программу. В такой работе используется современная логика, и она заложена
в программы, которые помогают построить доказательства таких результатов. Логика тоже играет роль
в разработке новых языков программирования, и это необходимо для работы в
искусственный интеллект и когнитивная наука. Некоторые части логики используются
инженеры по схемотехнике.
Но
информатика — это не только программирование. включает в себя логические и
математический анализ программ. С помощью таких анализов можно доказать
корректность процедур и оценить количество шагов, необходимых для выполнения
заданную программу. В такой работе используется современная логика, и она заложена
в программы, которые помогают построить доказательства таких результатов. Логика тоже играет роль
в разработке новых языков программирования, и это необходимо для работы в
искусственный интеллект и когнитивная наука. Некоторые части логики используются
инженеры по схемотехнике.
Понимание предметов, преподаваемых в PHL 313K, требуется для
успешная специальность по информатике: 1. Так же, как исчисление
используется в инженерных курсах, основы логики и теории множеств используются во многих
курсы информатики. 2. Курсы CS для старших классов не являются программированием.
сверла; эти курсы охватывают общие принципы и требуют математических доказательств
об этих принципах. PHL 313K обучает основным принципам и методам
построение и оценка доказательств.
PHL 313K обучает основным принципам и методам
построение и оценка доказательств.
Математики рассуждают об абстрактных понятиях, например, непрерывных
функции, алгебраические системы, такие как «кольца», и топологические пространства. Самый
студенты-математики учатся писать доказательства таких вещей, следуя примерам в
их классы. Это часть изучения математики, но она медленная и часто приводит к
к путаницам. Специалисты по математике, изучающие логику, обнаруживают, что она помогает им в их учебе.
математическое мышление. Это помогает избежать путаницы и помогает в
построение ясных, убедительных доказательств. Изучение логики необходимо для работы
в основаниях математики, которая в значительной степени связана с природой
математической истины и с обосновывающими доказательствами математических объектов,
такие как целые числа, комплексные числа и бесконечные множества. Математические специальности в UT не
необходимо пройти курс логики, но те, кто это делает, почти всегда сообщают, что это
интересно и полезно.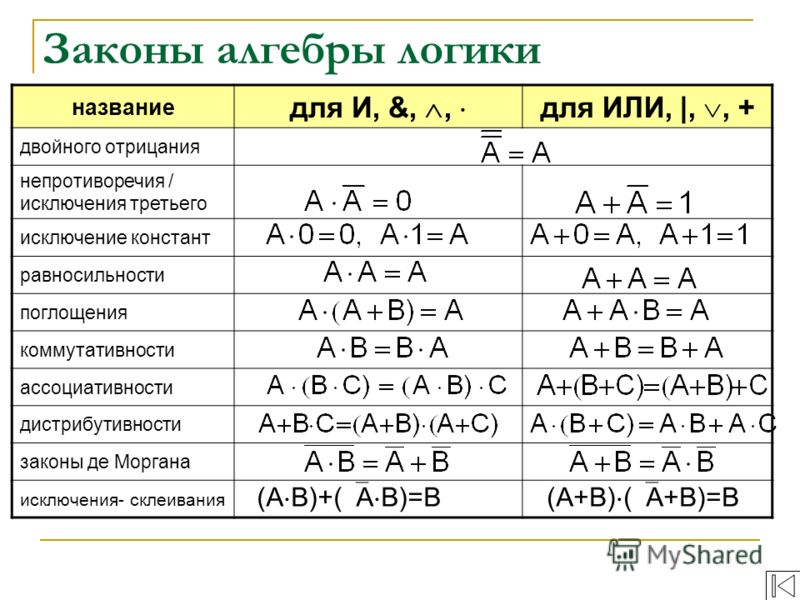
PHL 313K — введение в логику, элементарную теорию множеств, основы теории чисел и использования индукции и рекурсии. Это требует серьезного изучения, но он охватывает интересный и полезный материал. Хорошие курсы повышения квалификации, для студентов, заинтересованных в более продвинутой логике, есть PHL 344K (= M 344K) и PHL. 358.
Роберт Л. Кози
Обновление от RLC: 22.09.17
запрос ссылки — Является ли информатика разделом математики?
Если вы создаете граф Кэли группы, это математика? Что если смоделировать орбиту элемента из группы? Где математические модели перестают быть математикой? Натуральные числа по-прежнему ведут себя так, как в их точной модели, когда модель не используется кем-либо. Единственной целью компьютера является моделирование математических объектов.
Целью информатики является построение или описание модели математических объектов, даже если нет их реализации на каком-либо компьютере или способа получить результат, который программа должна вычислить.
Алгоритмы, по иронии судьбы, являются аспектом информатики, который оказывает наибольшее влияние на другие области математики.
Простой случай: если вы определили, что временная сложность алгоритма слишком велика для его реализации, это все равно будет вкладом в информатику. С другой стороны, если вы показываете, что две конструкции эквивалентны, скажем, задача решения клики и разложение больших чисел на множители, и существует алгоритм для выполнения одной из этих задач с меньшей временной сложностью, то должен существовать алгоритм такой же сложности для решения одной из этих задач. второе свойство. Вопрос в том, сколько информации можно избежать получения об одной проблеме от информации в решении или исчерпании другой? Временная сложность алгоритма — это его инвариантная мера, которая дает вам представление о том, насколько сложна проблема. Когда две проблемы не одинаково сложны, сложны или требуют много времени, более сложную задачу нельзя решить, используя только более простые решения (без обработки этих решений алгоритмом, который закрывает разницу в сложности в общем алгоритме).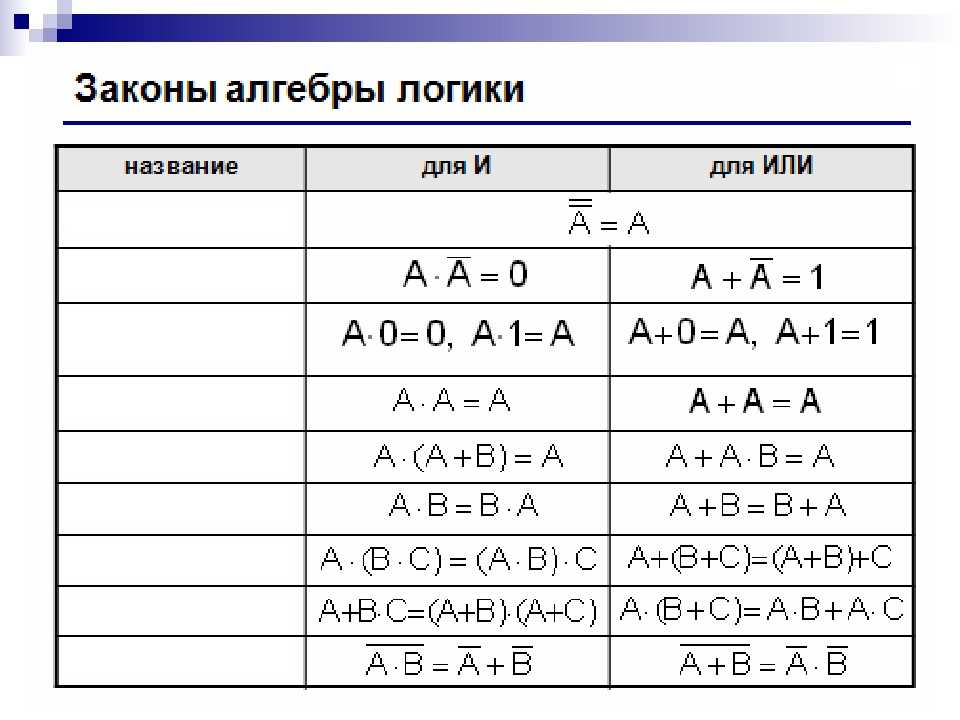 Изучая различные задачи и их временную сложность, вы видите, как общность проблемы соотносится с ее сложностью для решения в целом. Также полезно увидеть, например, логические вентили, реализованные как решение игры «Сапер», потому что они показывают, как выглядят и ощущаются свойства полной по Тьюрингу системы.
Изучая различные задачи и их временную сложность, вы видите, как общность проблемы соотносится с ее сложностью для решения в целом. Также полезно увидеть, например, логические вентили, реализованные как решение игры «Сапер», потому что они показывают, как выглядят и ощущаются свойства полной по Тьюрингу системы.
Однако эти вещи также могут быть обманчивы: сначала может показаться, что вы должны проверять каждую перестановку типа объекта, чтобы выяснить, какое подмножество этих перестановок удовлетворяет свойству, что указывает на серьезную проблему, если эти перестановки быстро растут, скажем, с размером множества перестановок. Однако у него может быть вторая стадия, когда происходит насыщение независимой информацией, и испробованные перестановки больше не способствуют решению проблемы сами по себе, или все они определяются объемом собранной информации. Например, набрать минимум 3 балла, чтобы определить круг.
Существуют также теоремы, характеризующие тип данных, являющихся жизнеспособными элементами пространства поиска.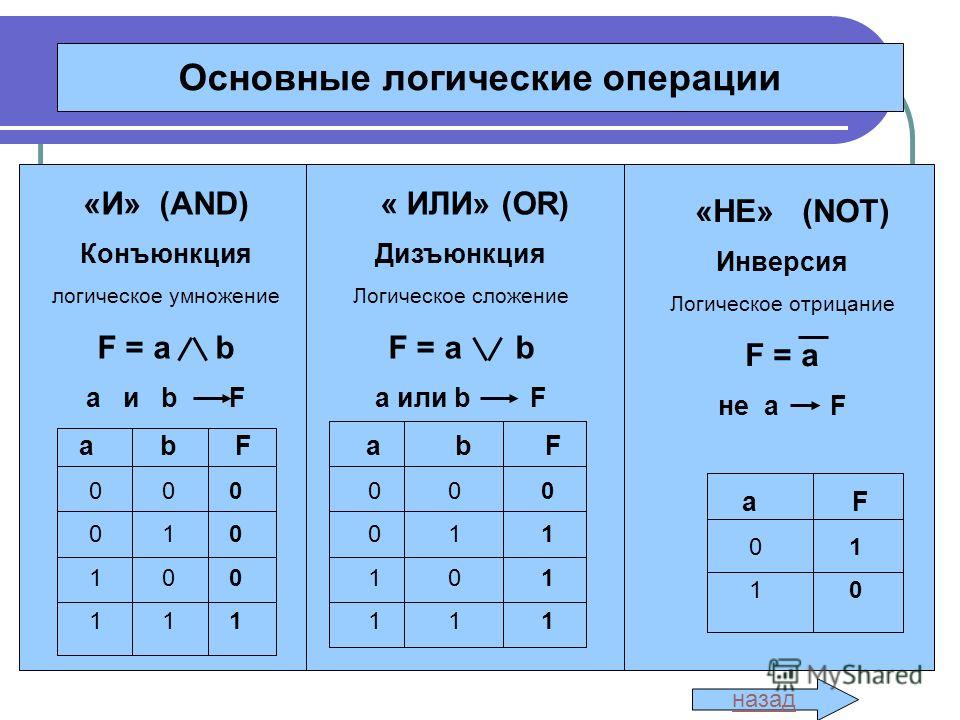 Это своего рода программа Мандельброта — используйте свои глаза, чтобы увидеть, как выглядят решения проблемы, найдите способ усилить эти характеристики и покажите, что они справедливы для всех возможных решений. Хорошим примером этого являются проективные плоскости, где диаграммы инцидентности для конечных плоскостей не обладают достаточной симметрией, чтобы решить, являются ли даже большие группы расположений, которые образуют частичные совпадения, жизнеспособными частями диаграммы инцидентности или нет, что приводит к тому, что большинство алгоритмов требуют на порядки выше возраста Вселенной, чтобы определить проективные плоскости данного порядка, и даже те, которым удалось найти вторую стадию, требуют огромных объемов поиска и объединения данных в течение многих лет фактического времени выполнения, чтобы прийти к вывод. Картина, которую я рисую здесь, — это не история успеха, это отражение реального непонимания того, на что похожи диаграммы инцидентности для проективных плоскостей, какие правила ими управляют.
Это своего рода программа Мандельброта — используйте свои глаза, чтобы увидеть, как выглядят решения проблемы, найдите способ усилить эти характеристики и покажите, что они справедливы для всех возможных решений. Хорошим примером этого являются проективные плоскости, где диаграммы инцидентности для конечных плоскостей не обладают достаточной симметрией, чтобы решить, являются ли даже большие группы расположений, которые образуют частичные совпадения, жизнеспособными частями диаграммы инцидентности или нет, что приводит к тому, что большинство алгоритмов требуют на порядки выше возраста Вселенной, чтобы определить проективные плоскости данного порядка, и даже те, которым удалось найти вторую стадию, требуют огромных объемов поиска и объединения данных в течение многих лет фактического времени выполнения, чтобы прийти к вывод. Картина, которую я рисую здесь, — это не история успеха, это отражение реального непонимания того, на что похожи диаграммы инцидентности для проективных плоскостей, какие правила ими управляют. Понимаемый объект должен иметь алгоритм, из изучения которого можно понять разницу между этим объектом и чистым шумом, стратегию, которая работает достаточно хорошо, чтобы делать предположения о природе решений. Так являются ли диаграммы падения проективных плоскостей чистым шумом? Глядя на диаграммы падения для небольших самолетов, они выглядят очень своеобразно, поэтому можно предположить, что типичный самолет не похож ни на один из известных самолетов. Но на самом деле этот общий шаблон может быть индуцирован в бинарной матрице, и показано, что он сохраняется в плоскостях в целом, что означает, что можно, начиная с этой характеристики, значительно сократить пространство поиска проблемы. Следовательно, характеристика пространства поиска сложной задачи очень похожа на характеристику самого объекта через инвариантные свойства.
Понимаемый объект должен иметь алгоритм, из изучения которого можно понять разницу между этим объектом и чистым шумом, стратегию, которая работает достаточно хорошо, чтобы делать предположения о природе решений. Так являются ли диаграммы падения проективных плоскостей чистым шумом? Глядя на диаграммы падения для небольших самолетов, они выглядят очень своеобразно, поэтому можно предположить, что типичный самолет не похож ни на один из известных самолетов. Но на самом деле этот общий шаблон может быть индуцирован в бинарной матрице, и показано, что он сохраняется в плоскостях в целом, что означает, что можно, начиная с этой характеристики, значительно сократить пространство поиска проблемы. Следовательно, характеристика пространства поиска сложной задачи очень похожа на характеристику самого объекта через инвариантные свойства.
Я бы сказал, что проблемы связаны со своей сложностью примерно так же, как расположение элементов бесконечного множества натуральных чисел связано с плотностью множества.
Но что такое алгоритм? Что такое программа?
Я отсылаю вас к Википедии для получения информации о теории типов Мартина-Лёфа и исчислении конструкций для некоторых конкретных реализаций вычислений. Полный охват см. в Практических основах языков программирования (Harper). Для рассмотрения теории предметной области я отсылаю вас к «Теории предметной области в логической форме» (Абрамски).
Один из ответов, данный Скоттом в теории предметных областей, заключается в том, что логическая структура программы как пространства свойств и выводов подобна решетке подалгебр или нормальных подалгебр абстрактной алгебры, которой не нужна голова. или абстрактная алгебра, содержащая их все, просто разветвленный или дефектный кристалл, сходящийся к пространству, где он должен был бы находиться, и что сформулировать рекурсивные определения программной логики означает найти неподвижные точки эндоморфизмов этой структуры порядка, которые эквивалентны непрерывным отображает на себя топологическое пространство, полученное из этой незавершенной решетки. Камень, двойственный этому, — это исполняемая программа, работающая по этой логике, которая является локалью, точками которой являются алгоритмы. В реальной теории предметных областей вы должны немного обобщить это, потому что области Скотта не образуют декартову закрытую категорию, а это означает, что они недостаточно похожи на топос для программ, представленных областями Скотта, чтобы быть произвольно выразительными.
Камень, двойственный этому, — это исполняемая программа, работающая по этой логике, которая является локалью, точками которой являются алгоритмы. В реальной теории предметных областей вы должны немного обобщить это, потому что области Скотта не образуют декартову закрытую категорию, а это означает, что они недостаточно похожи на топос для программ, представленных областями Скотта, чтобы быть произвольно выразительными.
Все это скрытая версия знаменитого утверждения Ловера о том, что между синтаксисом и семантикой существует связь Галуа. Точнее, между теорией и моделями теории или между логикой и пространством вычислений, которые она выполняет (денотационная семантика).
С другой стороны, существует связь между конструкциями объекта и доказательствами теоремы. Я не знаю, является ли это точным рассуждением, но если подумать, если предложения могут быть преобразованы в экзистенциальные, одновременно обладающие свойствами, то в совокупности они описывают вид объекта, определением которого является вещь, одновременно обладающая этими свойствами. так что доказать истинность этих утверждений — значит доказать, что тип занят какой-то реальной вещью. Соответствие Карри-Ховарда является доказательством того, что доказательства эквивалентны программам или конструкциям, и, в более общем смысле, что интуиционистские логики соответствуют типизированным лямбда-исчислениям, а, следовательно, и декартовым замкнутым категориям (что согласуется с тем, что для логиков топос — это просто категории). множеств для интуиционистской логики). Это довольно сильно влияет на дизайн языка, поскольку предоставляет средства вычисления с доказательствами вместо алгоритмов. Это основа философии теории гомотопических типов (Univalent Foundations Program), а также большей части интуиционистской логики и информатики.
так что доказать истинность этих утверждений — значит доказать, что тип занят какой-то реальной вещью. Соответствие Карри-Ховарда является доказательством того, что доказательства эквивалентны программам или конструкциям, и, в более общем смысле, что интуиционистские логики соответствуют типизированным лямбда-исчислениям, а, следовательно, и декартовым замкнутым категориям (что согласуется с тем, что для логиков топос — это просто категории). множеств для интуиционистской логики). Это довольно сильно влияет на дизайн языка, поскольку предоставляет средства вычисления с доказательствами вместо алгоритмов. Это основа философии теории гомотопических типов (Univalent Foundations Program), а также большей части интуиционистской логики и информатики.
Здесь присутствует некоторая степень взаимодействия между линейной логикой (т. е. некоммутативной геометрией) и информатикой. Физика, топология, логика и вычисления: Розеттский камень (Baez, Stay) показывает, что если вы замените декартовы замкнутые категории замкнутыми моноидальными категориями, вы можете обобщить изоморфизм Карри-Ховарда, чтобы получить все виды прекрасного квантового поведения и семантики. Двойственность Стоуна снова проявляется в изучении пространств Чу, которые представляют собой модель линейной логики, которая в конечном итоге очень похожа на теорию доменов.
Двойственность Стоуна снова проявляется в изучении пространств Чу, которые представляют собой модель линейной логики, которая в конечном итоге очень похожа на теорию доменов.
Итак, если все это относится к интуиционистской логике, то что такое классическая логика? Оказывается, некоторые реализации передачи продолжения, такие как call/cc из Scheme, а также введение передачи потока управления или процедурного программирования в чисто функциональный язык, такой как Haskell, сводится к тому, чтобы сделать его неконструктивной логикой. То, что делает Haskell таким надоедливым (многие говорят, что совершенно бесполезным), заключается в том, что вы не можете заставить программу общаться с внешним миром или зависеть от внешнего взаимодействия, даже от параметров, зависящих от времени выполнения, без полной остановки формата языка для говорить в процедурах с так называемой монадой IO или же уничтожать всю встроенную логику, которая проверяет поведение вашей программы. Итак, урок в том, что неконструктивная математика подобна интерактивной программе, а конструктивная математика подобна библиотеке.
Жизнь после исчисления | Кафедра математики
Введение
Если вы студент, сдающий стандартную последовательность математических вычислений бакалавриата, вам может быть интересно, что будет дальше. Видели ли вы лучшее, что может предложить математика? Или, как спрашивает наш заголовок, есть ли (математическая) жизнь после исчисления?
На самом деле, математика — это яркая, захватывающая область огромного разнообразия и глубины, для которой исчисление — только начало. Далее следует краткий обзор современного математического ландшафта, включая ключ к курсам факультета математики Корнелла, которые разбросаны по этому ландшафту. В то время как современная математика организована в многочисленные дисциплины и поддисциплины — официальное руководство по предметной классификации Американского математического общества занимает почти 100 страниц! — большинство предметов попадают в скромное число основных областей. Для курсов старшего уровня и курсов для выпускников мы используем среднюю цифру номеров наших курсов, чтобы определить область математики, к которой принадлежит курс:
1 и 2 для анализа;
3 для алгебры;
4 для комбинаторики;
5 и 6 для геометрии и топологии;
7 для вероятности и статистики;
8 для математической логики;
9 для курсов чтения.

Цифра 0 используется для различных целей, не связанных с классификацией предметов математики, таких как математическое образование, история математики и некоторые начальные курсы. Но что представляют собой эти области? Следующие описания помогут вам ориентироваться в разделе «Математика» каталога учебных курсов и выбирать курсы по математике, которые будут вам полезны.
Начальный уровень
При выборе курсов после линейной алгебры и векторного исчисления в первую очередь следует найти курс соответствующего уровня. Как правило, занятия по MATH на уровне 3000 предполагают минимальные навыки написания корректуры и являются хорошими начальными курсами для студентов, которым все еще неудобно писать корректуры. MATH 3040 (Prove It!) специально ориентирован на улучшение этих навыков. Большинство классов MATH с уровнем 4000 предполагают более глубокое знакомство с написанием корректуры. Особенно это касается курсов с отличием по алгебре и анализу. Тем не менее, учащиеся, завершившие курс MATH 2230–2240 на пятерку или выше, часто хорошо подготовлены к любому классу MATH уровня 4000.
Хотя студенты иногда посещают курсы МАТЕМАТИЧЕСКОГО уровня для выпускников, необходимо сделать несколько предостережений. Во-первых, курсы для выпускников подходят как продолжение, а не как замена полноценного бакалавриата по математике на уровне 4000. Основные курсы для выпускников (MATH 6110-6120, 6310-6320, 6510-6520) предполагают, что студенты имеют обширную подготовку по математике на уровне бакалавриата, включая, помимо прочего, курсы, эквивалентные нашим курсам с отличием по алгебре и анализу. Более продвинутые курсы для выпускников часто имеют дополнительные предварительные условия для выпускников. Ни один курс для выпускников не должен рассматриваться как замена его аналога для бакалавриата, и сама по себе МАТЕМАТИКА 2230-2240 совершенно неадекватна для подготовки к аспирантуре по математике. Студенты, которые заинтересованы в поступлении в магистратуру по математике, должны сначала проконсультироваться со своим руководителем и преподавателем курса.
Анализ
Анализ — это раздел математики, наиболее тесно связанный с исчислением и задачами, которые исчисление пытается решить. Он состоит из традиционных разделов исчисления дифференцирования, дифференциальных уравнений и интегрирования, а также их далеко идущих мощных расширений, которые играют важную роль в приложениях к физике и технике. Он также обеспечивает прочную теоретическую платформу, на которой могут быть построены прикладные методы. Анализ имеет две различные, но интерактивные ветви в зависимости от типов изучаемых функций: а именно, реальный анализ, который фокусируется на функциях, области определения которых состоят из действительных чисел, и комплексный анализ, который имеет дело с функциями комплексной переменной. Это кажется небольшим различием, но оказывается, что оно имеет огромное значение для теории и приводит к двум совершенно разным предметам. Оба имеют важные приложения.
Он состоит из традиционных разделов исчисления дифференцирования, дифференциальных уравнений и интегрирования, а также их далеко идущих мощных расширений, которые играют важную роль в приложениях к физике и технике. Он также обеспечивает прочную теоретическую платформу, на которой могут быть построены прикладные методы. Анализ имеет две различные, но интерактивные ветви в зависимости от типов изучаемых функций: а именно, реальный анализ, который фокусируется на функциях, области определения которых состоят из действительных чисел, и комплексный анализ, который имеет дело с функциями комплексной переменной. Это кажется небольшим различием, но оказывается, что оно имеет огромное значение для теории и приводит к двум совершенно разным предметам. Оба имеют важные приложения.
Изучение дифференциальных уравнений представляет центральный интерес для анализа. Они описывают явления реального мира, начиная от описания планетарных орбит и заканчивая электромагнитными силовыми полями, такими, например, как те, которые используются при компьютерной томографии. Такие уравнения традиционно классифицируются как обыкновенные дифференциальные уравнения (если они включают функции одной переменной) или дифференциальные уравнения в частных производных (если они включают функции более чем одной переменной). Каждая из этих двух областей соответствует активной подобласти анализа, которая, в свою очередь, делится на области, ориентированные на приложения, и области, сосредоточенные на теоретических вопросах.
Такие уравнения традиционно классифицируются как обыкновенные дифференциальные уравнения (если они включают функции одной переменной) или дифференциальные уравнения в частных производных (если они включают функции более чем одной переменной). Каждая из этих двух областей соответствует активной подобласти анализа, которая, в свою очередь, делится на области, ориентированные на приложения, и области, сосредоточенные на теоретических вопросах.
Алгебра
Алгебра берет свое начало в изучении чисел, которое во всех основных цивилизациях начиналось с практического, проблемного подхода. На Западе этот подход привел к развитию мощных общих методологий. Одна из таких методологий, восходящая к Евклиду и его школе, включает систематические доказательства свойств чисел. Другая методология связана с теорией уравнений, введенной арабскими математиками («алгебра» сама по себе имеет арабскую этимологию). Современная алгебра возникла в результате слияния этих методологий. Теория уравнений арабов была мощным инструментом для символических манипуляций, в то время как теория доказательств греков предоставила метод (аксиоматический метод) для выделения и систематизации ключевых аспектов алгебраических систем, которые затем изучаются сами по себе. Ярким примером такого слияния является теория групп, которую можно рассматривать как всесторонний анализ концепции симметрии. Теория групп является областью активных исследований и фундаментальным инструментом во многих разделах математики и физики.
Ярким примером такого слияния является теория групп, которую можно рассматривать как всесторонний анализ концепции симметрии. Теория групп является областью активных исследований и фундаментальным инструментом во многих разделах математики и физики.
Самый простой и широко известный пример современной алгебры — линейная алгебра, анализирующая системы уравнений первой степени. Линейная алгебра появляется практически во всех разделах прикладной математики, физики, математической экономики и т. д. Несмотря на то, что теория линейной алгебры к настоящему времени очень хорошо изучена, остается еще много интересных областей исследований, связанных с линейной алгеброй и вопросами вычислений.
Если перейти к системам уравнений второй степени и выше, то математика гораздо сложнее и сложнее. Эта область изучения известна как алгебраическая геометрия. Она важным образом взаимодействует с геометрией, а также с теорией чисел.
Наконец, теория чисел, с которой все началось, по-прежнему остается динамичной и сложной частью алгебры, возможно, сейчас, как никогда раньше, благодаря недавнему гениальному решению знаменитой 300-летней гипотезы Ферма. Хотя теорию чисел называют чистейшей частью чистой математики, в последние десятилетия она также играет важную практическую роль в приложениях к криптографии, компьютерной безопасности и кодам, исправляющим ошибки.
Хотя теорию чисел называют чистейшей частью чистой математики, в последние десятилетия она также играет важную практическую роль в приложениях к криптографии, компьютерной безопасности и кодам, исправляющим ошибки.
Комбинаторика
Комбинаторика, пожалуй, проще всего определяется как наука о счете. Более подробно комбинаторика имеет дело с числовыми отношениями и числовыми моделями, присущими сложным системам. В качестве простого примера рассмотрим любое многогранное тело и посчитаем количество ребер, вершин и граней. Это не случайные числа; комбинаторный анализ выявляет их взаимосвязь. Практические приложения комбинаторики изобилуют от планирования экспериментов до анализа компьютерных алгоритмов. Комбинаторика, возможно, является самым сложным предметом в математике, что некоторые объясняют тем фактом, что она имеет дело с дискретными явлениями, а не с непрерывными явлениями, причем последние обычно более регулярны и хорошо себя ведут. До последних десятилетий большая часть предмета состояла из классов сложных задач на счет вместе с оригинальными решениями. Однако с тех пор это радикально изменилось с введением и эффективным использованием важных методов и идей из соседних областей, таких как алгебра и топология, а также с использованием такими областями комбинаторных методов и результатов.
Однако с тех пор это радикально изменилось с введением и эффективным использованием важных методов и идей из соседних областей, таких как алгебра и топология, а также с использованием такими областями комбинаторных методов и результатов.
Геометрия и топология
Эти две области математики часто упоминаются вместе, потому что обе они связаны с изучением свойств пространства. Но в то время как геометрия фокусируется на свойствах пространства, включающих размер, форму и измерение, топология занимается менее осязаемыми свойствами относительного положения и связности.
Почти каждый старшеклассник хоть раз имел дело с евклидовой геометрией. Этот предмет оставался практически неизменным около 2000 лет, в течение которых он был жемчужиной в короне математики, архетипом логической точности и математической достоверности.
А потом, в семнадцатом веке, многое изменилось.
Основываясь на многовековых вычислительных методах, разработанных астрономами, астрологами, мореплавателями и механиками в их практических занятиях, Декарт систематически вводил теорию уравнений в изучение геометрии. Ньютон и другие изучали свойства кривых и поверхностей, описываемых уравнениями, используя новые методы исчисления, точно так же, как это делают сейчас студенты на текущих курсах исчисления. Эти методы и идеи в конечном итоге привели к тому, что мы называем сегодня дифференциальной геометрией, основным инструментом теоретической физики. Например, дифференциальная геометрия была ключевым математическим компонентом, использованным Эйнштейном при разработке теории относительности.
Ньютон и другие изучали свойства кривых и поверхностей, описываемых уравнениями, используя новые методы исчисления, точно так же, как это делают сейчас студенты на текущих курсах исчисления. Эти методы и идеи в конечном итоге привели к тому, что мы называем сегодня дифференциальной геометрией, основным инструментом теоретической физики. Например, дифференциальная геометрия была ключевым математическим компонентом, использованным Эйнштейном при разработке теории относительности.
Еще одно развитие достигло кульминации в девятнадцатом веке, свергнув евклидову геометрию как бесспорную основу для изучения пространства. Другие геометрии также считались возможными. Это аксиоматическое исследование неевклидовых геометрий идеально согласуется с дифференциальной геометрией, поскольку последняя допускает неевклидовы модели пространства. В настоящее время нет единого мнения относительно того, какая геометрия лучше всего описывает вселенную, в которой мы живем.
Наконец, в восемнадцатом и девятнадцатом веках зародилась топология (или, как ее тогда называли, анализ положения), так называемая геометрия положения. Топология изучает геометрические свойства, которые остаются неизменными при непрерывной деформации. Например, как бы ни изменялась окружность при непрерывном деформировании плоскости, точки, находящиеся внутри ее периметра, остаются внутри новой кривой, а точки снаружи остаются снаружи. Другой пример: никакая непрерывная деформация не может превратить сферу в плоскость. Поэтому они топологически различны.
Топология изучает геометрические свойства, которые остаются неизменными при непрерывной деформации. Например, как бы ни изменялась окружность при непрерывном деформировании плоскости, точки, находящиеся внутри ее периметра, остаются внутри новой кривой, а точки снаружи остаются снаружи. Другой пример: никакая непрерывная деформация не может превратить сферу в плоскость. Поэтому они топологически различны.
Топологию можно рассматривать как естественное дополнение к уже описанным революционным изменениям в геометрии. Ибо, как только кто-то признает, что существует более одного возможного способа геометризирования мира, то есть больше, чем просто евклидов способ измерения размеров и форм, становится важным выяснить, какие свойства пространства не зависят от такого измерения. Топология, которая, наконец, стала самостоятельной в двадцатом веке, является фундаментальным предметом, который дает ответы на подобные вопросы. Это основной инструмент для физиков и астрономов, которые пытаются понять структуру и эволюцию Вселенной. В самом деле, недавние астрономические наблюдения вместе с основными результатами топологии открывают захватывающую перспективу того, что вскоре мы получим глобальную топологическую структуру космоса.
В самом деле, недавние астрономические наблюдения вместе с основными результатами топологии открывают захватывающую перспективу того, что вскоре мы получим глобальную топологическую структуру космоса.
Вероятность и статистика
Каждый хоть раз имел дело с понятием вероятности, и каждый видел бесчисленное количество ссылок на статистику.
Наука о вероятности была разработана европейскими математиками восемнадцатого и девятнадцатого веков в связи с азартными играми. Для игры, характеристики которой были известны, они придумали способ присваивать каждому исходу число от 0 до 1, так что, если в игру играть большое количество раз, число, известное как вероятность исхода, давало бы хорошее приближение к относительной частоте возникновения этого исхода. С этого простого начала теория вероятностей превратилась в один из фундаментальных инструментов для работы с неопределенностью и случайными колебаниями в науке, экономике, финансах, актуарной науке, технике и т. д.
Один из взглядов на статистику состоит в том, что она ставит теорию вероятностей с ног на голову. То есть человек сталкивается с исходами, скажем, азартной игры, из которых надо угадать основные правила игры. Таким образом, статистика стремится восстановить законы или правила из числовых данных, тогда как вероятность предсказывает (с некоторой погрешностью), какими будут данные при заданных правилах.
То есть человек сталкивается с исходами, скажем, азартной игры, из которых надо угадать основные правила игры. Таким образом, статистика стремится восстановить законы или правила из числовых данных, тогда как вероятность предсказывает (с некоторой погрешностью), какими будут данные при заданных правилах.
Элементарные теории вероятности и статистики обычно включают дискретные модели и в значительной степени используют комбинаторику. Более продвинутые части каждого предмета в значительной степени зависят от реального анализа, особенно теории интеграции и ее ответвления, теории меры.
Математическая логика
Математическая логика имеет древние корни в работах Аристотеля и Лейбница и более современные истоки в работах начала двадцатого века Дэвида Гильберта, Бертрана Рассела, Альфреда Норта Уайтхеда и Курта Гёделя по логическим основаниям математики. Но он также играет центральную роль в современной компьютерной науке, например, при проектировании компьютеров, изучении компьютерных языков, анализе искусственного интеллекта.
Математическая логика изучает логическую структуру математики, начиная от таких локальных вопросов, как природа математического доказательства и обоснованной аргументации, до таких глобальных вопросов, как структура основанных на аксиомах математических теорий и моделей для таких теорий. Одним из ключевых инструментов является понятие рекурсивной функции, введенное впервые Гёделем и тесно связанное с понятиями вычислимости и теории сложности в компьютерных науках.
В дополнение к своему вкладу в математические основы и информатику, математическая логика и ее методы также привели к решению ряда важных проблем в других областях математики, таких как теория чисел и анализ.
И далее…
Из соображений экономии места и поскольку мы хотели описать области, хорошо представленные Корнеллским математическим факультетом, вышеизложенное пришлось опустить основные аспекты математики, например, многие важные области прикладной математики. Тем не менее, наши наброски описывают большинство важных областей фундаментальной математики.

 Высказывание истинно, когда все его части правдивы, например, A∧B = «химия изучает вещества и молекулы». На рисунке изображается множествами, их пересечение соответствует A∧B;
Высказывание истинно, когда все его части правдивы, например, A∧B = «химия изучает вещества и молекулы». На рисунке изображается множествами, их пересечение соответствует A∧B;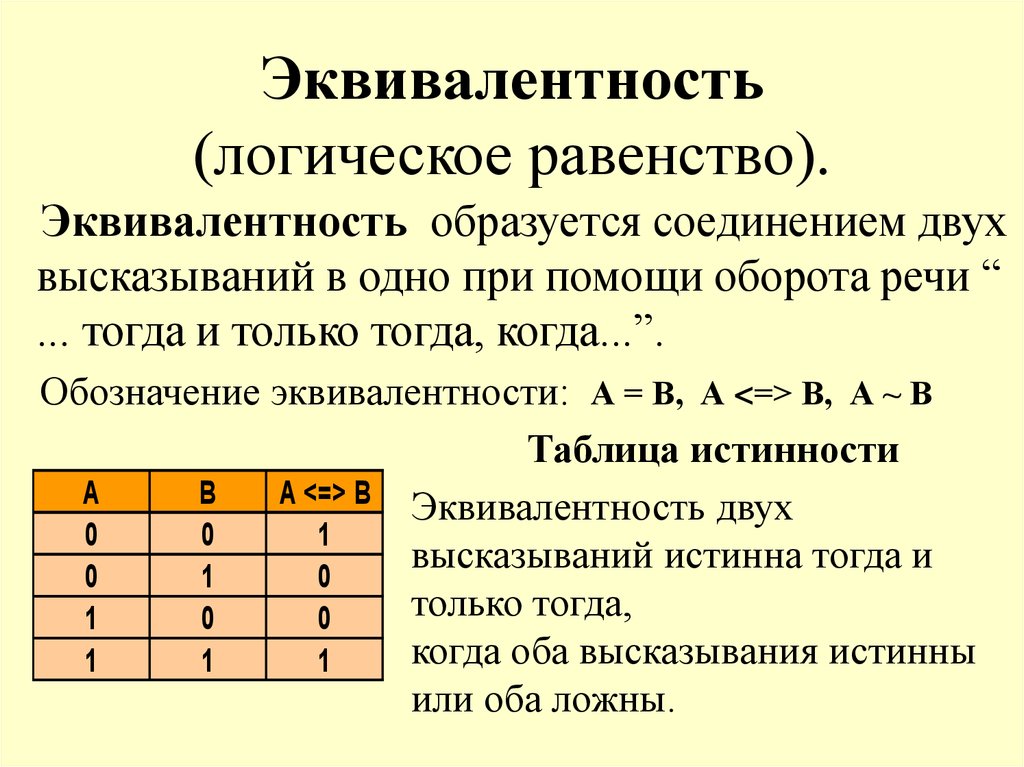 Пример: А⟶В = «если число делится только на себя и на 1, то оно сложное».
Пример: А⟶В = «если число делится только на себя и на 1, то оно сложное». 
 е. проверяем, при каких условиях выражение будет истинным:
е. проверяем, при каких условиях выражение будет истинным: