8 класс. Алгебра. Алгебраические дроби. — Преобразование рациональных выражений.
Комментарии преподавателяУрок: Преобразование рациональных выражений
Вспомним сначала определение рационального выражения.
Определение. Рациональное выражение – алгебраическое выражение, не содержащее корней и включающее только действия сложения, вычитания, умножения и деления (возведения в степень).
Под понятием «преобразовать рациональное выражение» мы имеем в виду, прежде всего, его упрощение. А это осуществляется в известном нам порядке действий: сначала действия в скобках, затем произведение чисел (возведение в степень), деление чисел, а затем действия сложения/вычитания.
Основной целью сегодняшнего урока будет приобретение опыта при решении более сложных задач на упрощение рациональных выражений.
Пример 1. Упростить рациональное выражение .
Решение. Сначала может показаться, что указанные дроби можно сократить, т. к. выражения в числителях дробей очень похожи на формулы полных квадратов соответствующих им знаменателей. В данном случае важно не спешить, а отдельно проверить, так ли это.
Проверим числитель первой дроби: . Теперь числитель второй: .
Как видно, наши ожидания не оправдались, и выражения в числителях не являются полными квадратами, т. к. у них отсутствует удвоение произведения. Такие выражения, если вспомнить курс 7 класса, называют неполными квадратами. Следует быть очень внимательными в таких случаях, т. к. перепутывание формулы полного квадрата с неполным – очень частая ошибка, а подобные примеры проверяют внимательность учащегося.
Поскольку сокращение невозможно, то выполним сложение дробей.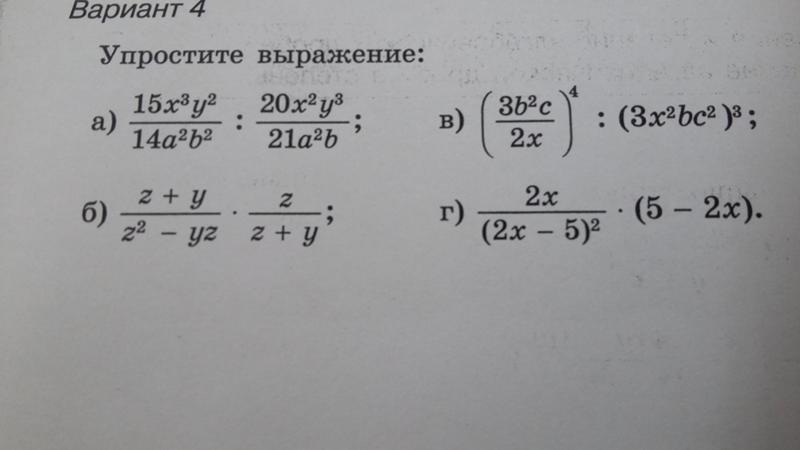 У знаменателей нет общих множителей, поэтому они просто перемножаются для получения наименьшего общего знаменателя, а дополнительным множителем для каждой из дробей является знаменатель другой дроби.
У знаменателей нет общих множителей, поэтому они просто перемножаются для получения наименьшего общего знаменателя, а дополнительным множителем для каждой из дробей является знаменатель другой дроби.
Конечно же, далее можно раскрыть скобки и привести затем подобные слагаемые, однако, в данном случае можно обойтись меньшими затратами сил и заметить, что в числителе первое слагаемое является формулой суммы кубов, а второе – разности кубов. Для удобства вспомним эти формулы в общем виде:
и .
В нашем же случае выражения в числителе сворачиваются следующим образом:
, второе выражение аналогично. Имеем:
.
Ответ. .
Пример 2. Упростить рациональное выражение .
Решение. Данный пример похож на предыдущий, но здесь сразу видно, что в числителях дробей находятся неполные квадраты, поэтому сокращение на начальном этапе решения невозможно. Аналогично предыдущему примеру складываем дроби:
Аналогично предыдущему примеру складываем дроби:
, здесь мы аналогично способу, указанному выше, заметили и свернули выражения по формулам суммы и разности кубов.
Ответ. .
Пример 3. Упростить рациональное выражение .
Решение. Можно заметить, что знаменатель второй дроби раскладывается на множители по формуле суммы кубов. Как мы уже знаем, разложение знаменателей на множители является полезным для дальнейшего поиска наименьшего общего знаменателя дробей.
.
Укажем наименьший общий знаменатель дробей, он равен: , т. к. делится на знаменатель третьей дроби, а первое выражение вообще является целым, и для него подойдет любой знаменатель. Указав очевидные дополнительные множители, запишем:
.
Ответ.
Рассмотрим более сложный пример с «многоэтажными» дробями.
Пример 4. 2+ab+ac+bc)}{(b+c)(a+c)(a+b)} = \frac{a(a+b)+c(a+b)}{(a+c)(a+b)} = \frac{(a+c)(a+b)}{(a+c)(a+b)} = 1$$
2+ab+ac+bc)}{(b+c)(a+c)(a+b)} = \frac{a(a+b)+c(a+b)}{(a+c)(a+b)} = \frac{(a+c)(a+b)}{(a+c)(a+b)} = 1$$
Что и требовалось доказать.
Упрощение выражений и объединение сходных терминов
Алгебра — это раздел математики, изучающий математические выражения. Он содержит переменные, коэффициенты, операторы и константы. Пример: пусть 3x + 4 будет алгебраическим выражением. Тогда 3 — коэффициент, x — переменная, + — оператор, 4 — константа. Алгебра помогает вывести неизвестные величины. Давайте пройдемся по компонентам алгебры один за другим.
- Переменная: — неизвестное количество. Это не фиксировано. Мы оцениваем значение переменных на основе некоторых других условий.
- Коэффициент: — это количество, умноженное на переменную.
- Оператор: операторов +, -, / ×.
- Константа: является фиксированной величиной и не имеет связанных с ней переменных.
Термины
Терм – это число, переменное произведение двух чисел, произведение двух переменных или произведение переменной и коэффициента.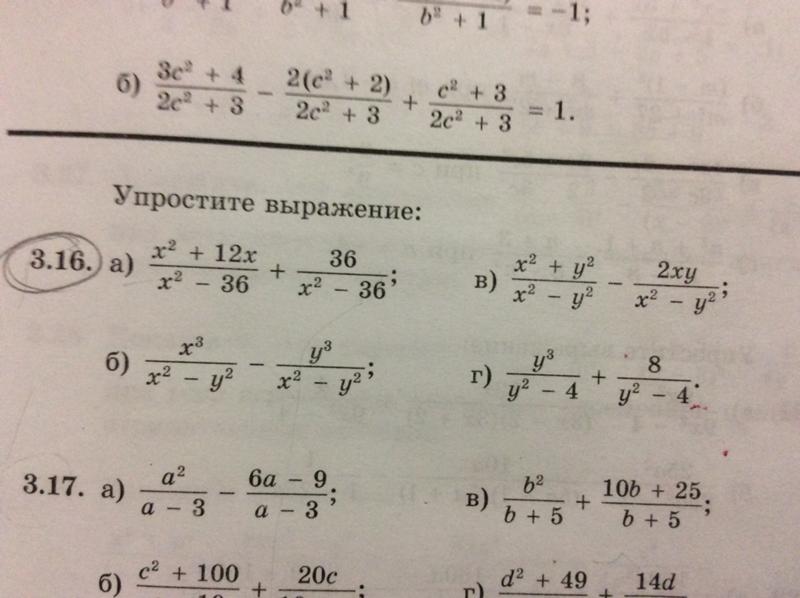 Например: В выражении x – 4y, x и -4y являются терминами. Термины можно разделить на две части,
Например: В выражении x – 4y, x и -4y являются терминами. Термины можно разделить на две части,
- Подобные термины: Термины с одинаковой мощностью и одинаковыми переменными. Коэффициенты могут варьироваться, но условие является переменным, и их показатели должны быть одинаковыми. Мы в основном объединяем подобные термины и помогаем в упрощении алгебраических выражений. Например: 4х + 6х = 10х. Здесь переменные одни, коэффициенты разные и степени тоже одинаковые.
- В отличие от терминов: Термины, которые имеют разные степени, разные переменные и коэффициенты, также могут различаться. Их нельзя упростить. Например: 4x + 6y + 2x 2 переменные, мощность разные.
Как объединить похожие термины и упростить?
Ответ:
Термы с одинаковыми переменными и одинаковыми степенями можно упростить. Сначала мы перестраиваем все выражение, комбинируя похожие и неодинаковые термины.
Одинаковые термины выделяются с одной стороны, а разные термины сохраняются с другой. Затем выполняется операция подобных термов. Например: Вычислить x 2 + 3x + y 2 +4x. В этом выражении степень x одинакова, поэтому мы выполняем операцию сложения 4x и 3x, что равно 7x. Результирующее выражение будет x 2 + 7x + y 2 .
Примеры вопросов
Вопрос 1: Оцените 3x + 4x + 5x 2 + 7x 2 + 4x.
Решение:
Объедините одинаковые члены x и x 2 .
3x + 4x + 4x = 11x
5x 2 + 7x 2 = 12x 2
Результат: 11x + 12x 2
Вопрос 2: Решите 4a + 3b +5c +6a + 9d.
Решение:
Объедините подобные члены,
4a + 6a = 10a
Результат: 10a + 3b + 5c + 9d.
Вопрос 3: выполнить вычитание x 3 – y из x 2 – 2y -9y.
Решение:
x 2 -2y -9y -(x 3 -Y)
= x 2 -11y -x 3 +y
= x 2 -10y -x 3
9006. : Найдите сумму подобных слагаемых 5ab + 6ab + 7ab + 8ba + 90ba. Отсюда найдите значение, когда a = 1, b = 2.
Решение:
Как мы все знаем, умножение коммутативно, поэтому ba = ab
Следовательно, в данном вопросе все термины подобны терминам. Сложение этих членов равно 116ba
Следовательно, положим a = 1, b = 2
Ответ: 116 × 1 × 2 = 232.
Вопрос 5: Найдите x, если углы треугольника равны 8x, 3x и 4x.
Решение:
Все углы похожи на термины
Сумма углов треугольника составляет 180 °
8x + 3x + 4x = 180
=> 15x = 180
=> x = 12
.Углы равны 96, 36, 48.
Вопрос 6: Если f(x) = x 2 + 5x + 9 и g(x) = 3x 2 + 9y + 9x найти f(x) + g(x).
Решение:
Подобные члены в f(x) и g(x) равны x 2 и x, поэтому мы выполняем сложение,
x 2 + 3x 2 9x + 9y + 9
= 4x 2 + 14x + 9y + 9
= (а + б) 2
Решение:
f(x) = g(x)
=> (a – b) 2 = (a + b) 2
=> a 3 4 + 9003 -2ab = a 2 + b 2 + 2ab
Выполняя операции подобных членов, получаем,
=> 4ab = 0
Это условие проверки равенства двух функций.
Выражения и уравнения — Common Core: Математика для 8-го класса
All Common Core: Математические ресурсы для 8-го класса
7 Диагностические тесты 75 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 … 22 23 Следующая →
Common Core: Справка по математике для 8-го класса » Выражения и уравнения
Упростите выражение:
Возможные ответы:
Нельзя упростить
3
30260 Правильный ответ: Объяснение:
Начните с распределения показателя степени через круглые скобки. Правило степени диктует, что увеличение степени до другой степени означает, что два показателя степени умножаются:
Правило степени диктует, что увеличение степени до другой степени означает, что два показателя степени умножаются:
Любые отрицательные степени могут быть преобразованы в положительные степени в знаменателе дроби:
Подобные термины могут быть упрощены вычитание степени знаменателя из степени числителя:
Сообщить об ошибке
Упрощение:
Возможные ответы:
Правильный ответ:3
7
Объяснение:
Используйте правило мощности для распределения показателя:
Отчет о ошибке
Упрощение:
Возможные ответы:
Правильный ответ:
0
Объяснение:
Чтобы упростить это, нам нужно будет использовать правило мощности и порядок операций.
Оценить первый член. Это будет сделано двумя способами, чтобы показать, что правило степени будет работать для показателей степени за скобками для одного члена.
Для второго члена мы не можем распределить и с показателем степени вне круглых скобок, потому что это не один член. Вместо этого мы должны сначала оценить термины в скобках.
Оцените второй член.
Возведите в квадрат значение в скобках.
Вычесть значение второго члена из первого члена.
Сообщить об ошибке
Что из следующего эквивалентно выражению ?
Возможные ответы:
Правильный ответ:
Объяснение:
Что из следующего эквивалентно выражению ?
Мы можем переписать данное выражение, распределив экспоненту снаружи.
Теперь это может выглядеть немного запутаннее, но нам нужно вспомнить, что когда мы распределяем показатель степени через круглые скобки, как мы пытались сделать выше, нам нужно умножить показатель степени внутри на число снаружи.
В общем виде это выглядит так:
Для нашей конкретной проблемы это выглядит так:
Сообщить об ошибке
Упростить.
Возможные ответы:
Правильный ответ:
Объяснение:
Когда показатель степени повышается на другой показатель степени, мы просто умножаем степени показателей степени и сохраняем основание прежним.
Сообщить об ошибке
Упрощение.
Возможные ответы: Правильный ответ:
Объяснение:
Когда показатель степени повышается на другой показатель степени, мы просто умножаем степени показателей степени и сохраняем основание прежним.
Сообщить об ошибке
Упрощение.
Возможные ответы:
Правильный ответ:
Объяснение:
Когда показатель степени повышается на другой показатель степени, мы просто умножаем степени показателей степени и сохраняем основание прежним.
Сообщить об ошибке
Упростите выражение
Возможные ответы: Правильный ответ:
Объяснение:
Сообщить об ошибке
Оценить
Возможные ответы:
Правильный ответ:
2
Объяснение: Если вы разделите два экспоненциальных выражения с одним и тем же основанием, вы можете просто вычесть показатели степени.
 Правило степени диктует, что увеличение степени до другой степени означает, что два показателя степени умножаются:
Правило степени диктует, что увеличение степени до другой степени означает, что два показателя степени умножаются:
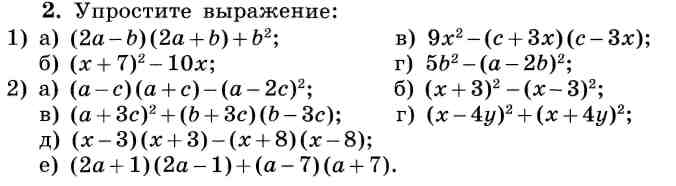


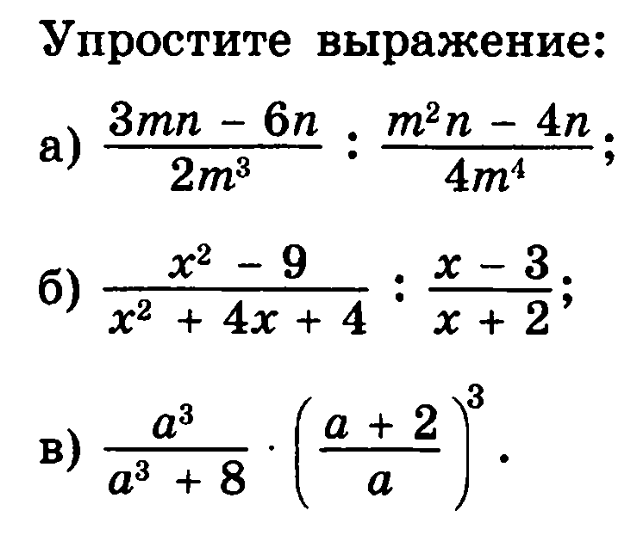 Одинаковые термины выделяются с одной стороны, а разные термины сохраняются с другой. Затем выполняется операция подобных термов. Например: Вычислить x 2 + 3x + y 2 +4x. В этом выражении степень x одинакова, поэтому мы выполняем операцию сложения 4x и 3x, что равно 7x. Результирующее выражение будет x 2 + 7x + y 2 .
Одинаковые термины выделяются с одной стороны, а разные термины сохраняются с другой. Затем выполняется операция подобных термов. Например: Вычислить x 2 + 3x + y 2 +4x. В этом выражении степень x одинакова, поэтому мы выполняем операцию сложения 4x и 3x, что равно 7x. Результирующее выражение будет x 2 + 7x + y 2 .
