| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.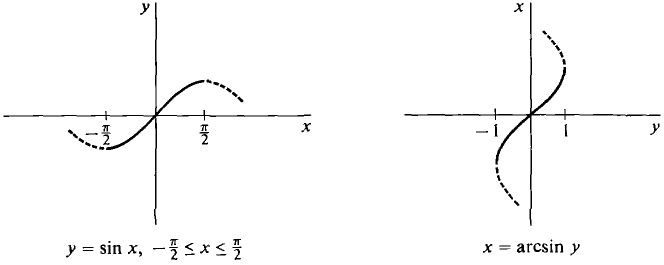 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.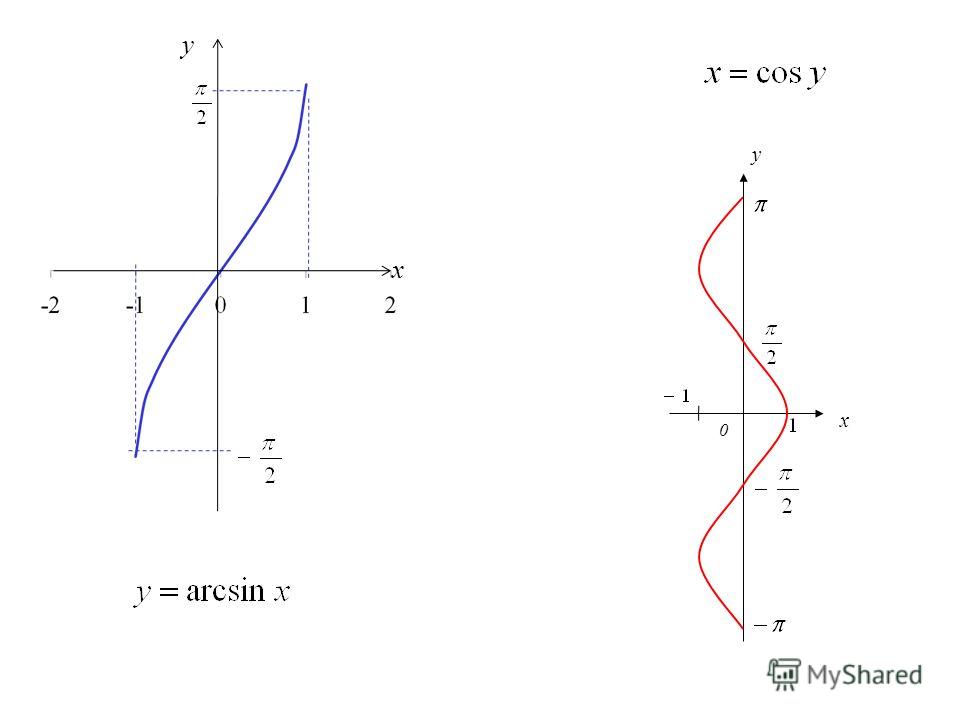 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | sin(120 град.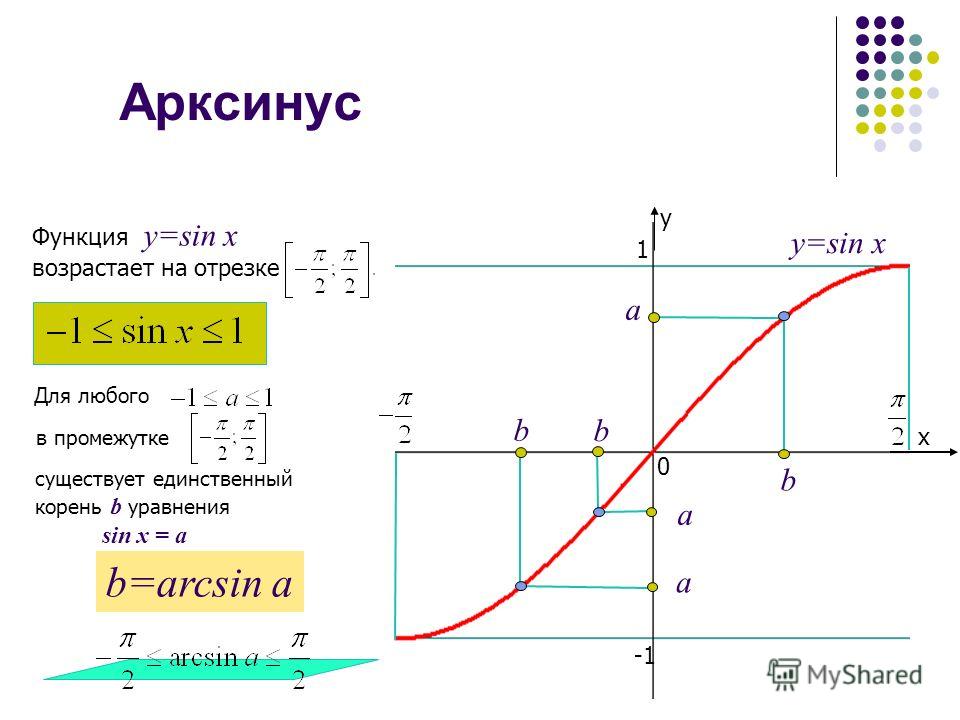 ) ) | ||
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Руководство пользователя > ГрафикиГрафик функции f(x) = x
График функции f(x) = x2
График функции f(x) = x3
График функции f(x) = sqrt(x)
График многочлена
При построении графика многочлена будет предложен диалог, в котором необходимо указать коэффициенты при степенях x. График функции f(x) = sin(x)
График функции f(x) = cos(x)
График функции f(x) = tg(x)
График функции f(x) = ctg(x)
График функции f(x) = arcsin(x)
График функции f(x) = arccos(x)
График функции f(x) = arctg(x)
График функции f(x) = arcctg(x)
График функции f(x) = ex
График функции f(x) = ln(x)
График плотности нормального распределения
При построении графика плотности нормального распределения будет предложен диалог, в котором необходимо указать математическое ожидание и стандартное отклонение. Чтобы построить График простейшей функции, достаточно вызвать соответствующую команду. Если на листе присутствуют два или более фрейма, то дополнительно потребуется указать фрейм, где будет создан график. В результате работы инструмента будут созданы сразу два объекта: выбранная простейшая функция и ее график. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Методика преподавания обратных тригонометрических функций в школах и классах с углубленным изучением математики
Методика преподавания обратных тригонометрических функций в школах и классах с углубленным изучением математики
Скачать все файлы (482 kb.)
Доступные файлы (16):
| n2.doc | 41kb. | 19.05.2004 01:25 | скачать |
| n3.doc | 1456kb. | 17.05.2004 08:59 | скачать |
| n4.doc | 1413kb. | 17.05.2004 08:28 | скачать |
n5. doc doc | 1124kb. | 17.05.2004 09:00 | скачать |
| n6.doc | 472kb. | 17.05.2004 08:49 | скачать |
| n7.doc | 64kb. | 17.05.2004 03:28 | скачать |
| n8.doc | 1582kb. | 17.05.2004 09:00 | скачать |
| n9.doc | 1123kb. | 17.05.2004 09:02 | скачать |
| n10.doc | 22kb. | 17.05.2004 04:04 | скачать |
| n11.doc | 623kb. | 17.05.2004 09:03 | скачать |
| n12.doc | 30kb. | 10.05.2004 16:40 | скачать |
| n13.doc | 21kb. | 18.05.2004 21:02 | скачать |
| n14.doc | 27kb. | 19.05.2004 00:08 | скачать |
| n15.doc | 26kb. | 19.05.2004 01:25 | скачать |
| n16.doc | 22kb. | 17.05.2004 04:29 | скачать |
| n17.doc | 29kb. | 15.06.2011 20:13 | скачать |
Введение
Одной из важнейших задач курса математики старших классов является логическое завершение всех основных линий, входящих в программу школьного математического образования, в том числе и линии функции.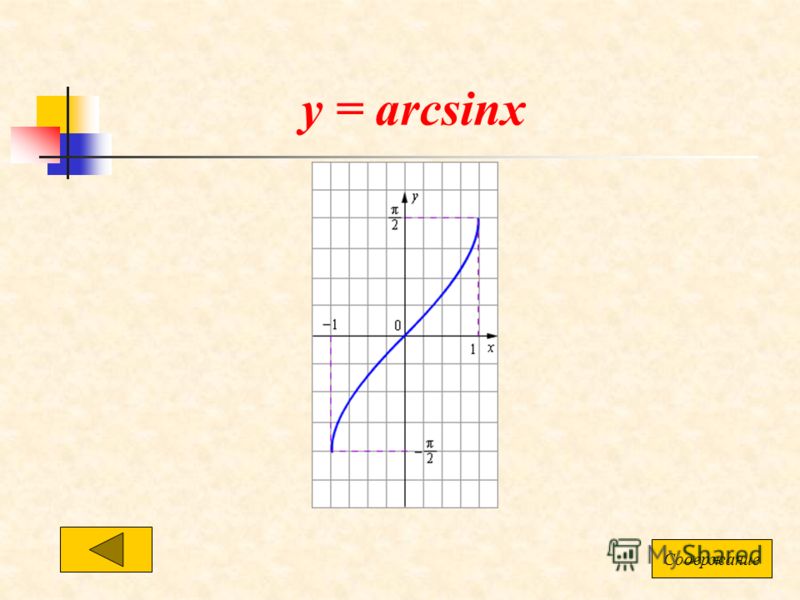 Изучение темы «Обратные тригонометрические функции» входит в программу как основной компонент, и на итоговом тестировании в задания групп B и C входят примеры на эту тему. Однако в том, что изучение обратных тригонометрических функций представляет для учащихся большие трудности, сомневаться не приходится. Учащиеся не справляются с решением даже элементарных заданий, не говоря уже о примерах повышенной сложности, нередко производят над ними необдуманные действия, совершая глупые ошибки, выполняют решение формально, «по стандарту». Учитель должен быть хорошим стратегом и вовремя создавать для интеллекта детей посильные трудности. В этом и заключается трудность: уметь не ликвидировать все преграды на пути ребят к вершине знания, а планомерно создавать их, что позволит детям не только осознано владеть школьной программой, но и продвинуться на пути формирования своей личности.
Изучение темы «Обратные тригонометрические функции» входит в программу как основной компонент, и на итоговом тестировании в задания групп B и C входят примеры на эту тему. Однако в том, что изучение обратных тригонометрических функций представляет для учащихся большие трудности, сомневаться не приходится. Учащиеся не справляются с решением даже элементарных заданий, не говоря уже о примерах повышенной сложности, нередко производят над ними необдуманные действия, совершая глупые ошибки, выполняют решение формально, «по стандарту». Учитель должен быть хорошим стратегом и вовремя создавать для интеллекта детей посильные трудности. В этом и заключается трудность: уметь не ликвидировать все преграды на пути ребят к вершине знания, а планомерно создавать их, что позволит детям не только осознано владеть школьной программой, но и продвинуться на пути формирования своей личности.
Кроме того, перед учителями школ стоит теперь новая задача – подготовить учеников к успешному прохождению централизованного тестирования. А это задача отнюдь не простая, учитывая соответствие уровня сложности заданий (особенно групп B и C) и количества часов, отводимых по программе на изучение темы. На изучение обратных тригонометрических функций в общеобразовательных школах отводится всего 2 часа (а по учебнику Алимова вообще рассматривается как сложный, дополнительный материал), хотя значение этой темы достаточно велико – она составляет необходимую основу для решения тригонометрических уравнений и неравенств, изучаемых позднее. Кроме того, обратные тригонометрические функции помогают в упрочении навыков работы с обратными функциями, закреплении понятия взаимно однозначных отображений.
А это задача отнюдь не простая, учитывая соответствие уровня сложности заданий (особенно групп B и C) и количества часов, отводимых по программе на изучение темы. На изучение обратных тригонометрических функций в общеобразовательных школах отводится всего 2 часа (а по учебнику Алимова вообще рассматривается как сложный, дополнительный материал), хотя значение этой темы достаточно велико – она составляет необходимую основу для решения тригонометрических уравнений и неравенств, изучаемых позднее. Кроме того, обратные тригонометрические функции помогают в упрочении навыков работы с обратными функциями, закреплении понятия взаимно однозначных отображений.
Надо отметить, что исследования в области обратных тригонометрических функций продолжались и продолжаются, они стали более актуальными в связи с применением в исследованиях электронных вычислительных средств. Отсюда вытекают и требования различных вузов, которые они предъявляют выпускникам школ по теме «Обратные тригонометрические функции».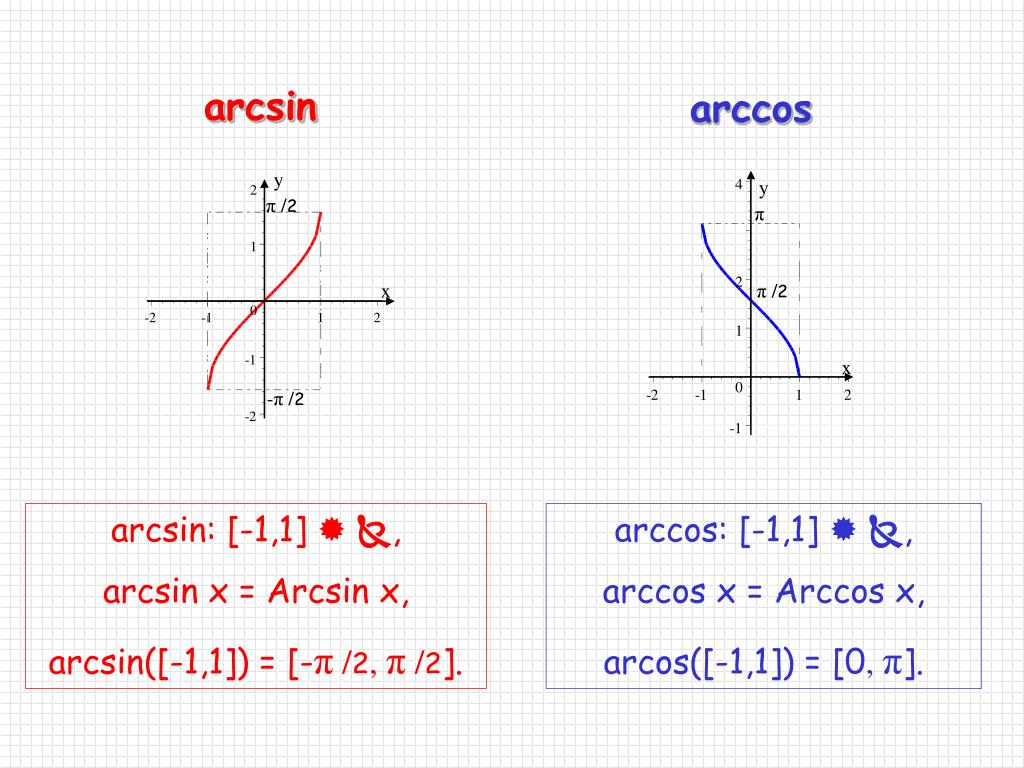 Ведь при выполнении экзаменационной работы ученик демонстрирует не только знание математики, но и способности к научно-исследовательской деятельности.
Ведь при выполнении экзаменационной работы ученик демонстрирует не только знание математики, но и способности к научно-исследовательской деятельности.
Возникает проблема: «Где ученикам школ взять знания и навыки овладения этим вопросом?» Следовательно, разработка и исследование методики изучения обратных тригонометрических функций в классах с углубленным изучением математики более чем актуальна.
В связи с этим объектом исследования является процесс обучения в общеобразовательных школах и классах с углубленным изучением математики.
Предметом исследования служит обучение теме «Обратные тригонометрические функции».
Научная проблема состоит в обосновании и разработке методических положений по изучению темы «Обратные тригонометрические функции».
Целью работы является формирование понятий обратных тригонометрических функций, а также разработка методики обучения данной темы в школах и классах с углубленным изучением математики.
Исходя из поставленной цели, сформулируем гипотезу исследования. Итак, гипотеза исследования заключается в том, что разработанная методика обучения будет способствовать наиболее качественному усвоению материала по рассматриваемой теме.
Итак, гипотеза исследования заключается в том, что разработанная методика обучения будет способствовать наиболее качественному усвоению материала по рассматриваемой теме.
Для успешной реализации поставленной цели и подтверждения гипотезы необходимо решить следующие задачи:
— обобщить и систематизировать материал по теме «Обратные тригонометрические функции»;
— разработать уроки по данной теме;
— разработать методические рекомендации, которые будут способствовать наиболее качественному проведению уроков по теме «Обратные тригонометрические функции»;
— создать обучающе-контролирующую программу;
— провести апробацию результатов выполненной работы.
Решение поставленных задач потребовало привлечения следующих методов исследования:
— анализ методической, математической и психолого-психологической литературы, а также периодических изданий;
— рассмотрение работ по истории математики;
— изучение опыта работы учителей физико-математической школы при СГПИ.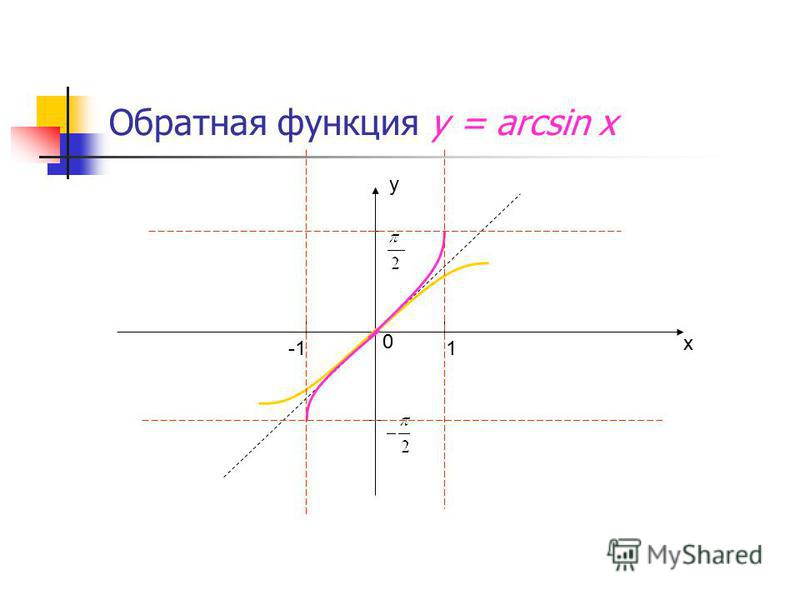
Практическая значимость данной работы определяется тем, что в ней разработаны учебные материалы для преподавания темы «Обратные тригонометрические функции». Подобраны системы задач по указанной теме, в том числе: устных, опорных, стандартных, нестандартных и исследовательских. Разработаны методические рекомендации для учителей по организации обучения по представленному материалу. Кроме того, ученики могут воспользоваться данной работой при самостоятельном изучении обратных тригонометрических функций, в этом им поможет разработанная обучающе-контролирующая программа. Курсовая работа может использоваться студентами педагогических вузов при изучении таких дисциплин как «Элементарная математика и ПРМЗ», «ТиМОМ», а также при подготовке к педагогической практике.
Arcsin — Формула, График, Домен и Диапазон, Примеры
Arcsin — одна из шести основных обратных тригонометрических функций. Это обратная тригонометрическая функция синуса. Арксинус также называется обратным синусом и математически записывается как arcsin x или sin -1 x (читается как синус, обратный x). Важно отметить, что sin -1 x не то же самое, что (sin x) -1 , то есть sin -1 x не является обратной функцией sin x. В обратной тригонометрии у нас есть шесть обратных тригонометрических функций: arccos, arcsin, arctan, arcsec, arccsc и arccot.
Важно отметить, что sin -1 x не то же самое, что (sin x) -1 , то есть sin -1 x не является обратной функцией sin x. В обратной тригонометрии у нас есть шесть обратных тригонометрических функций: arccos, arcsin, arctan, arcsec, arccsc и arccot.
Arcsin x определяет угол, соответствующий отношению перпендикуляра к гипотенузе прямоугольного треугольника. В этой статье мы рассмотрим понятие арксинуса и выведем его формулу. Мы также обсудим область значений и диапазон значений arcsin x и, следовательно, построим их график. Мы также решим различные примеры, используя тождества arcsin x, чтобы лучше понять его приложения и концепцию.
| 1. | Что такое арксинус? |
| 2. | Arcsin x Формула |
| 3. | Диаграмма арксинуса |
| 4. | Домен и диапазон Arcsin |
| 5. | Идентификационные данные Arcsin |
6. | Часто задаваемые вопросы по Arcsin |
Что такое арксинус?
Арксинус является обратной тригонометрической функцией синуса. Он дает меру угла для соответствующего значения функции синуса. Мы обозначаем функцию арксинуса для действительного числа x как arcsin x (читается как арксинус x) или sin -1 x (читается как инверсия синуса x), которая является обратной величиной sin y. Если sin y = x, то мы можем записать это как y = arcsin x. Arcsin — одна из шести важных обратных тригонометрических функций. Шесть обратных тригонометрических функций:
- Arcsin: функция, обратная синусу, обозначается arcsin x или sin -1 x
- Arccos: функция, обратная косинусу, обозначается arccos x или cos -1 x
- Arctan: функция, обратная тангенсу, обозначается arctan x или tan -1 х
- Arccot: Функция, обратная котангенсу, обозначается arccot x или cot -1 x
- Arcsec: функция, обратная секансу, обозначается arcsec x или sec -1 x
- Arccsc: Функция, обратная косекансу, обозначается arccsc x или csc -1 x
Функция arcsin помогает нам найти меру угла, соответствующую значению функции синуса.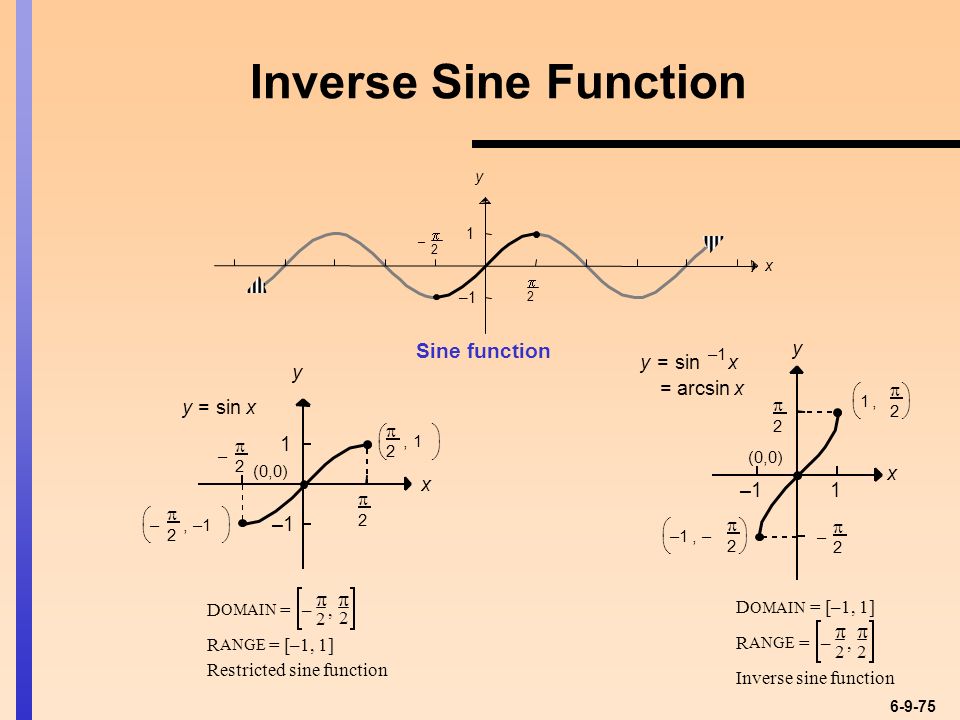 Давайте посмотрим на несколько примеров, чтобы понять его функционирование. Мы знаем значения функции синуса для некоторых конкретных углов, используя тригонометрическую таблицу.
Давайте посмотрим на несколько примеров, чтобы понять его функционирование. Мы знаем значения функции синуса для некоторых конкретных углов, используя тригонометрическую таблицу.
- Если sin 0 = 0, то arcsin 0 = 0
- sin π/6 = 1/2 подразумевает arcsin (1/2) = π/6
- sin π/3 = √3/2 подразумевает arcsin (√3/2) = π/3
- Если sin π/2 = 1, то arcsin (1) = π/2
Arcsin x Формула
Мы можем использовать формулу арксинуса, когда задано значение синуса угла, и мы хотим вычислить точную величину угла. Рассмотрим прямоугольный треугольник. Мы знаем, что sin θ = Противоположная сторона / Гипотенуза. Поскольку arcsin является обратной функцией синуса, поэтому мы имеем θ = arcsin (противоположная сторона / гипотенуза). Следовательно, формула для arcsin x такова:
θ = арксинус (противоположная сторона / гипотенуза)
Мы также можем использовать закон синусов для получения формулы арксинуса. Для треугольника ABC со сторонами AB = c, BC = a и AC = b имеем sin A/a = sin B/b = sin C/c.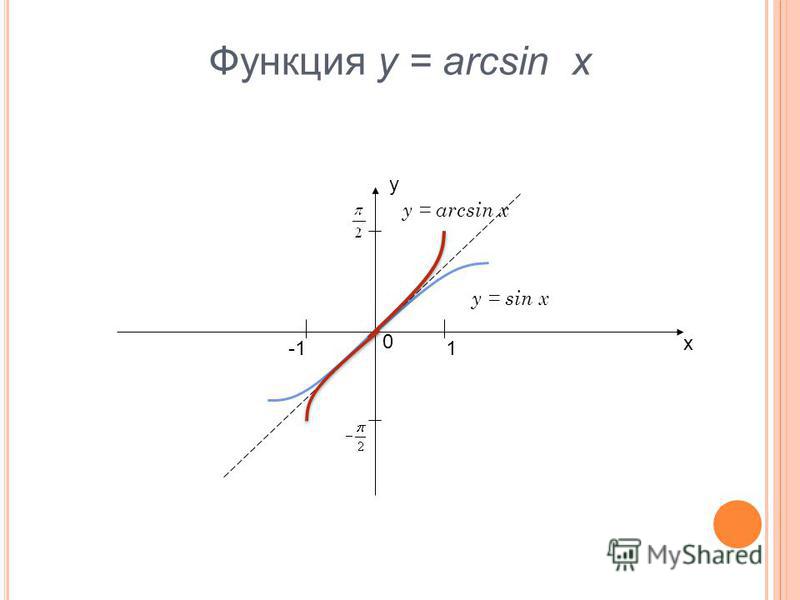 Тогда, взяв два за раз, мы имеем
Тогда, взяв два за раз, мы имеем
sin A / a = sin B / b
⇒ sin A = (a/b) sin B
⇒ A = arcsin [(a/b) sin B]
Точно так же мы можем найти величину углов B и C, используя тот же метод.
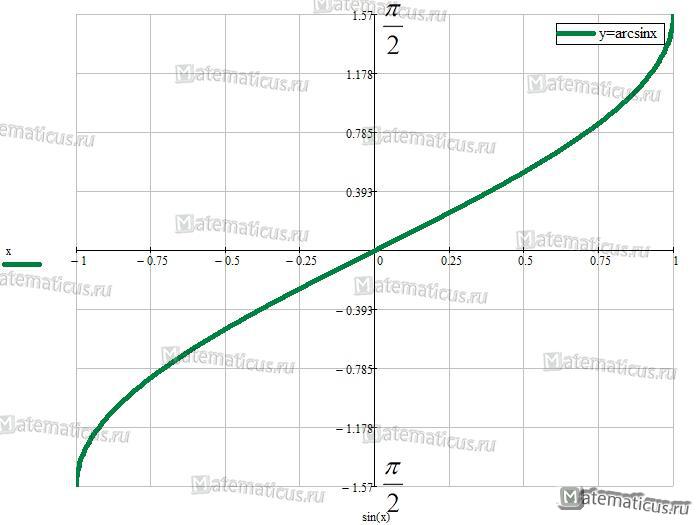
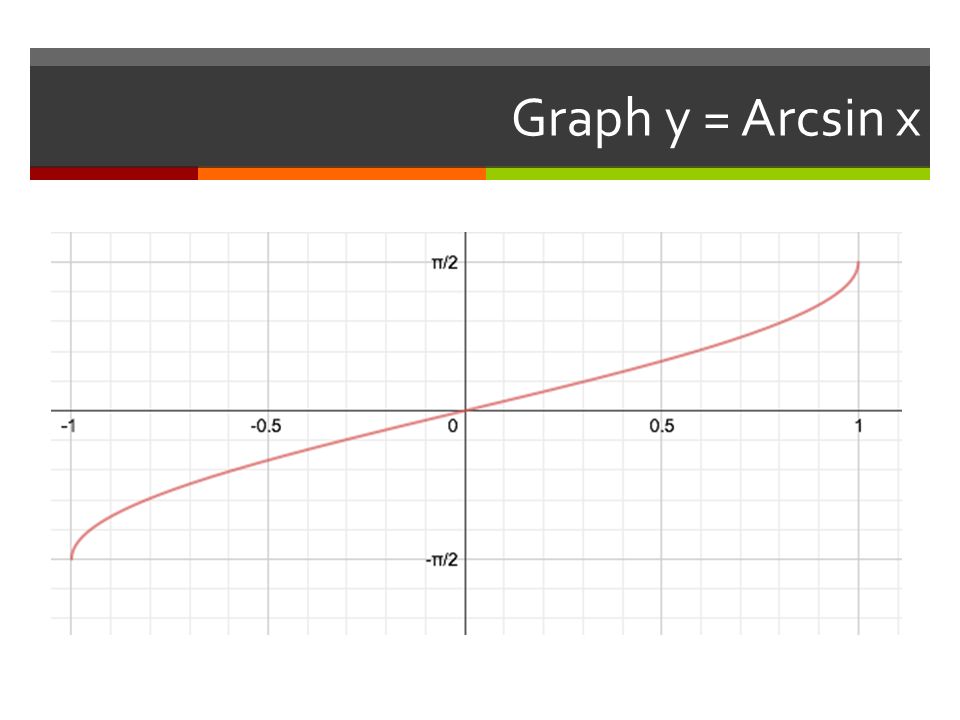
График дугового синуса
Теперь, когда мы знаем формулу арксинуса, построим график арксинуса x, используя некоторые его точки. Как обсуждалось функционирование arcsin, мы знаем значения функции синуса для некоторых конкретных углов и, используя тригонометрические формулы, имеем
- sin 0 = 0 подразумевает arcsin 0 = 0 → (0, 0)
- sin π/6 = 1/2 подразумевает arcsin (1/2) = π/6 → (1/2, π/6)
- sin π/3 = √3/2 подразумевает arcsin (√3/2) = π/3 → (√3/2, π/3)
- sin π/2 = 1 подразумевает arcsin (1) = π/2 → (1, π/2)
- sin (-π/4) = -1/√2 подразумевает arcsin (-1/√2) = -π/4 → (-1/√2, -π/4)
- sin (-π/6) = -1/2 подразумевает arcsin (-1/2) = -π/6 → (-1/2, -π/6)
Теперь, нанеся указанные выше точки на график, мы получим приведенный ниже график арксинуса:
Домен и диапазон Arcsin
Поскольку мы знаем, что две функции являются обратными друг другу, если они взаимно однозначны, а область определения и область определения функции становятся соответственно областью определения и областью определения обратной функции.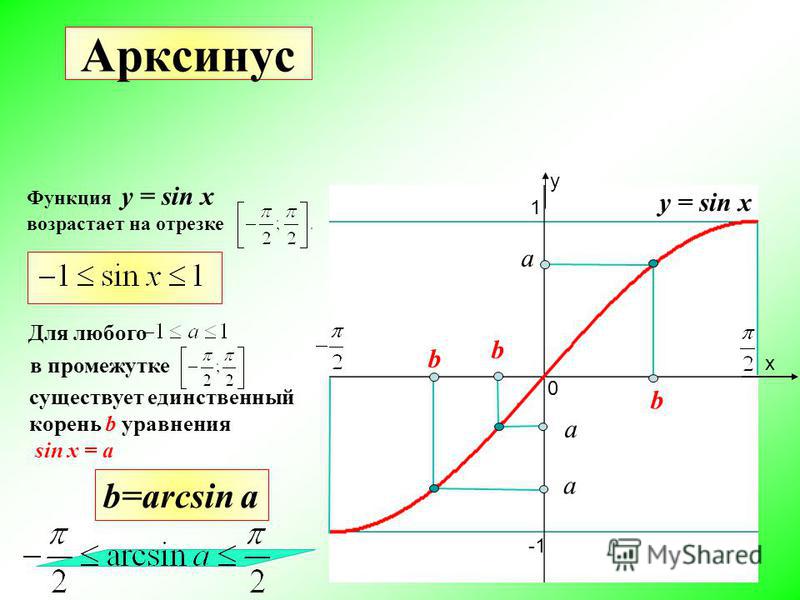 Мы знаем, что областью определения sin x являются все действительные числа, а его диапазон равен [-1, 1]. Но с этой областью sin x не является биективным. Итак, мы ограничиваем область определения синусоидальной функции до [–π/2, π/2], тогда sin x становится биективным с областью определения [–π/2, π/2] и диапазоном [-1, 1]. Когда область определения sin x ограничена [–3π/2, –π/2], [–π/2, π/2] или [π/2, 3π/2] и т. д., и диапазон [ -1, 1], то sin x биективен и, следовательно, соответственно мы можем определить arcsin с областью определения [-1, 1] и диапазоном [–3π/2, –π/2], [–π/2, π/2 ] или [π/2, 3π/2] и так далее.
Мы знаем, что областью определения sin x являются все действительные числа, а его диапазон равен [-1, 1]. Но с этой областью sin x не является биективным. Итак, мы ограничиваем область определения синусоидальной функции до [–π/2, π/2], тогда sin x становится биективным с областью определения [–π/2, π/2] и диапазоном [-1, 1]. Когда область определения sin x ограничена [–3π/2, –π/2], [–π/2, π/2] или [π/2, 3π/2] и т. д., и диапазон [ -1, 1], то sin x биективен и, следовательно, соответственно мы можем определить arcsin с областью определения [-1, 1] и диапазоном [–3π/2, –π/2], [–π/2, π/2 ] или [π/2, 3π/2] и так далее.
Мы получаем разные ветви функции arcsin для каждого интервала. Ветвь arcsin, соответствующая домену [-1, 1] и диапазону [–π/2, π/2], называется ветвью главного значения. Итак, arcsin определяется как arcsin: [-1, 1] → [–π/2, π/2]. Следовательно, домен и диапазон arcsin:
- Домен Arcsin: [-1, 1]
- Диапазон арксинуса: [–π/2, π/2]
Идентификация Arcsin
Теперь мы обсудим некоторые важные свойства и тождества функции арксинуса, которые помогают нам упростить и решить различные задачи тригонометрии.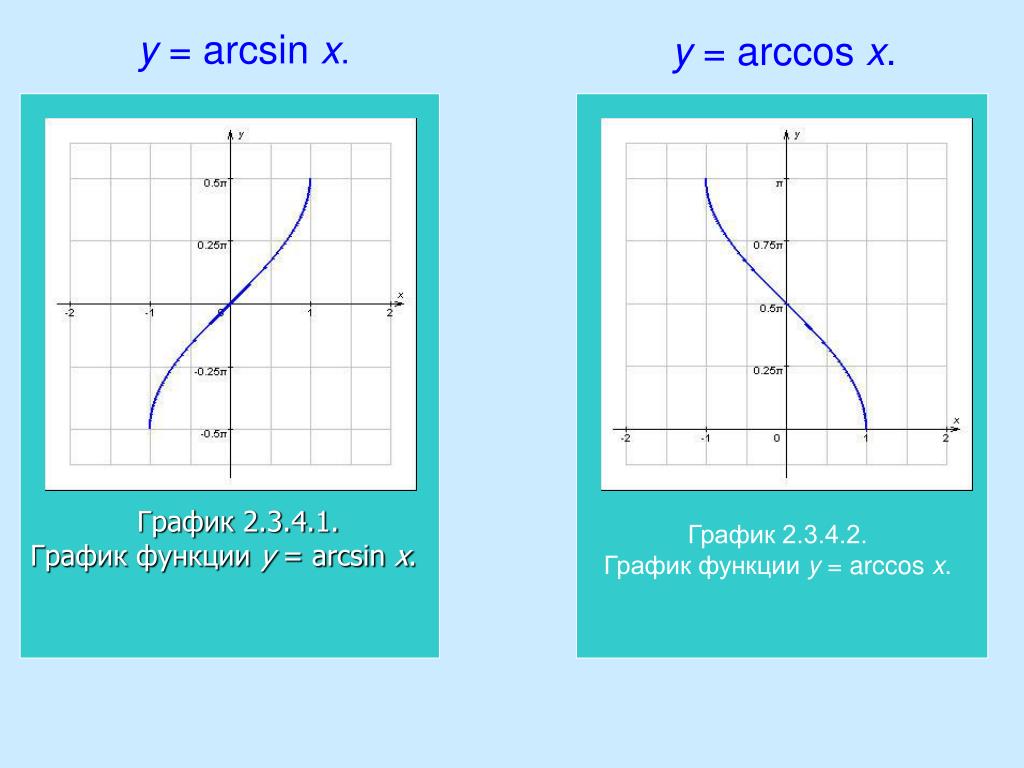
- sin (arcsin x) = x, если x находится в [-1, 1]
- arcsin (sin x) = x, если x находится в [–π/2, π/2]
- arcsin (1/x) = arccsc x, если x ≤ -1 или x ≥ 1
- arcsin (–x) = — arcsin x, если x ∈ [-1, 1]
- arcsin x + arccos x = π/2, если x ∈ [-1, 1]
- 2 arcsin x = arcsin (2x √(1 — x 2 )), если -1/√2 ≤ x ≤ 1/√2
- 2 arccos x = arcsin (2x √(1 — x 2 )), если 1/√2 ≤ x ≤ 1
- arcsin x + arcsin y = arcsin [x√(1 — y 2 ) + у√(1 — х 2 )]
Важные примечания по арксинусу
- Арксинус является функцией, обратной функции синуса.
- Домен и диапазон arcsin равны [-1, 1] и [–π/2, π/2] соответственно.
- Производная арксинуса равна 1/√(1 — x²).
- Интеграл от arcsin равен ∫arcsin x dx = x sin -1 x + √(1 — x 2 ) + C
☛ Похожие темы:
- Sin 1 в градусах
- Обратные тригонометрические соотношения
- Обратные триггерные производные
Арксинус Примеры
Пример 1: Докажите формулу арксинуса 2 arcsin x = arcsin (2x √(1 — x 2 )), если -1/√2 ≤ x ≤ 1/√2.

Решение: Предположим, что arcsin x = y, тогда мы имеем sin y = x. Рассмотрим RHS
RHS = arcsin (2x √(1 — x 2 ))
= arcsin [2 sin y √(1 — sin 2 y)]
= arcsin [2 sin y √(cos 2 y)] — [Используя тригонометрическую формулу sin 2 A + cos 2 A = 1, откуда следует cos 2 A = 1 — sin 2 A]
= arcsin [2 sin y cos y]
= arcsin [sin2y] — [Используя тригонометрическую формулу sin2A = 2 sinA cosA]
= 2y
= 2 arcsin x — [Потому что arcsin x = y]
Ответ: Следовательно, мы доказали, что 2 arcsin x = arcsin (2x √(1 — x 2 )), если -1/√2 ≤ x ≤ 1/√2
Пример 2: Найдите значение arcsin (sin 3π/5).
Решение: Мы знаем, что arcsin (sin x) = x, поэтому мы имеем arcsin (sin 3π/5) = 3π/5, но 3π/5 ∉ [–π/2, π/2]. Итак, нам нужно найти значение, эквивалентное sin 3π/5, такое, что угол лежит в интервале [–π/2, π/2].
 Используя тригонометрическую формулу sin x = sin (π — x), мы имеем
Используя тригонометрическую формулу sin x = sin (π — x), мы имеемsin (3π/5) = sin (π — 3π/5)
= sin (5π/5 — 3π/5)
= sin (2π/5)
Также обратите внимание, что 2π/5 ∈ [–π/2, π/2].
Итак, у нас есть arcsin (sin 3π/5) = 2π/5
Ответ: arcsin (sin 3π/5) = 2π/5
Пример 3: Докажите, что arcsin (3/5) – arcsin (8/17) = arccos (84/85)
Решение: Предположим, что A = arcsin (3/5) и B = arcsin (8/ 17), тогда мы имеем sin A = 3/5 и sin B = 8/17. Затем, используя тригонометрическую формулу, sin 2 x + cos 2 x = 1, имеем
cos A = √ (1 — sin 2 A)
= √ (1 — (3/5) 2 )
= √(1 — 9/25) )
= √(16/25)
= 4/5
cos B = √ (1 — sin 2 B)
= √ (1 — (8/17) 2 ) ) √(1 — 64/289)
= √(225/289)
= 15/17
Теперь, используя формулу cos (A — B) = cos A cos B + sin A sin B
= 4 /5 × 15/17 + 3/5 × 8/17
= 60/85 + 24/85
= 84/85
⇒ A — B = arccos (84/85)
⇒ arcsin (3/5) – arcsin (8/17) = arccos (84/85) — [A = arcsin ( 3/5) и B = arcsin (8/17)]
Ответ: Таким образом, мы доказали, что arcsin (3/5) – arcsin (8/17) = arccos (84/85)
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по Arcsin Questions
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по Arcsin
Что такое арксинус в тригонометрии?
Арксинус является обратной тригонометрической функцией синуса. Мы обозначаем функцию арксинуса для действительного числа x как arcsin x (читается как арксинус x) или sin -1 x (читается как обратный синус x). Это одна из шести основных обратных тригонометрических функций: arccos, arcsin, arctan, arcsec, arccsc и arccot. Важно помнить, что грех -1 х не является обратной величиной синуса.
Что такое формула арксинуса?
Формула для арксинуса определяется следующим образом: θ = арксинус (противоположная сторона/гипотенуза), где θ — угол в прямоугольном треугольнике. Функция arcsin помогает нам найти меру угла, соответствующую значению функции синуса. Мы также можем найти меру угла в треугольнике, используя формулу арксинуса, полученную с использованием закона синусов.
Мы также можем найти меру угла в треугольнике, используя формулу арксинуса, полученную с использованием закона синусов.
Что такое производная от Arcsin x?
Производная arcsin определяется как d/dx(arcsin x) = 1/√(1 — x²). Мы можем вывести эту формулу, используя первый принцип производных и метод дифференцирования по цепному правилу.
Как интегрировать Arcsin?
Интеграл от arcsin определяется выражением ∫arcsin x dx = x sin -1 x + √(1 — x 2 ) + C, где C — постоянная интегрирования. Его можно получить с помощью различных методов, таких как интегрирование по частям и метод замещения с последующим интегрированием по частям.
Что такое домен и диапазон Arcsin?
Домен и диапазон arcsin:
- Домен Arcsin: [-1, 1]
- Диапазон арксинуса: [–π/2, π/2]
Мы ограничиваем область определения функции синуса до [–π/2, π/2], чтобы сделать ее биективной, и, следовательно, определяем функцию арксинуса как две функции, обратные друг другу, если они взаимно однозначны. Ветвь arcsin, соответствующая домену [-1, 1] и диапазону [–π/2, π/2], называется ветвью главного значения.
Ветвь arcsin, соответствующая домену [-1, 1] и диапазону [–π/2, π/2], называется ветвью главного значения.
Как построить график арксинуса?
Используя определение и функционирование арксинуса, мы можем нанести некоторые точки на график с помощью тригонометрической таблицы. Некоторые из пунктов:
- sin 0 = 0 подразумевает arcsin 0 = 0 → (0, 0)
- sin π/6 = 1/2 подразумевает arcsin (1/2) = π/6 → (1/2, π/6)
- sin π/3 = √3/2 подразумевает arcsin (√3/2) = π/3 → (√3/2, π/3)
- sin π/2 = 1 подразумевает arcsin (1) = π/2 → (1, π/2)
- sin (-π/4) = -1/√2 подразумевает arcsin (-1/√2) = -π/4 → (-1/√2, -π/4)
- sin (-π/6) = -1/2 подразумевает arcsin (-1/2) = -π/6 → (-1/2, -π/6)
Затем, нанеся эти точки на график и соединив их кривой, мы получим график арксинуса.
Является ли Arcsin обратной стороной Sin?
Arcsin является обратной тригонометрической функцией sin. Когда функция arcsin определяется как arcsin: [-1, 1] → [–π/2, π/2], мы говорим, что она обратна sin: [–π/2, π/2] → [ -1, 1].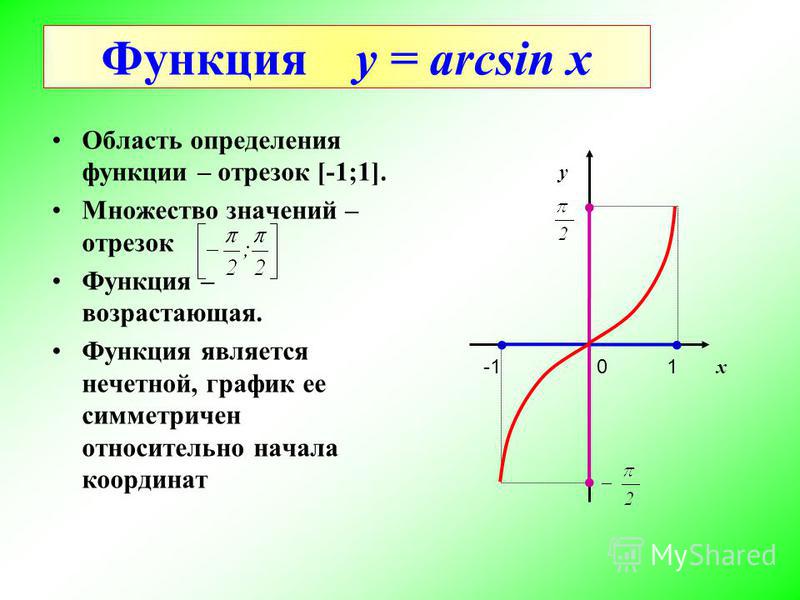
В чем разница между Sin и Arcsin?
Синус — это тригонометрическая функция, которая отображает вещественное число в угол, тогда как арксинус является обратной функцией синуса. Обе функции определяются как arcsin: [-1, 1] → [–π/2, π/2], тогда мы говорим, что это обратная функция sin: [–π/2, π/2] → [-1 , 1] и являются обратными друг другу.
Почему Arcsin (-2) не определен?
Arcsin (-2) не определен, поскольку область определения arcsin ограничена [-1, 1], а -2 не лежит в интервале [-1, 1].
Каковы личности Arcsin?
Вот некоторые важные формулы и тождества arcsin:
- sin (arcsin x) = x, если x находится в [-1, 1]
- arcsin (sin x) = x, если x находится в [–π/2, π/2]
- arcsin (1/x) = arccsc x, если x ≤ -1 или x ≥ 1
- arcsin (–x) = — arcsin x, если x ∈ [-1, 1]
- arcsin x + arccos x = π/2, если x ∈ [-1, 1]
- 2 arcsin x = arcsin (2x √(1 — x 2 )), если -1/√2 ≤ x ≤ 1/√2
Что такое арксинус греха?
Формула для arcsin от sin дается следующим образом: arcsin (sin x) = x, если x находится в [–π/2, π/2].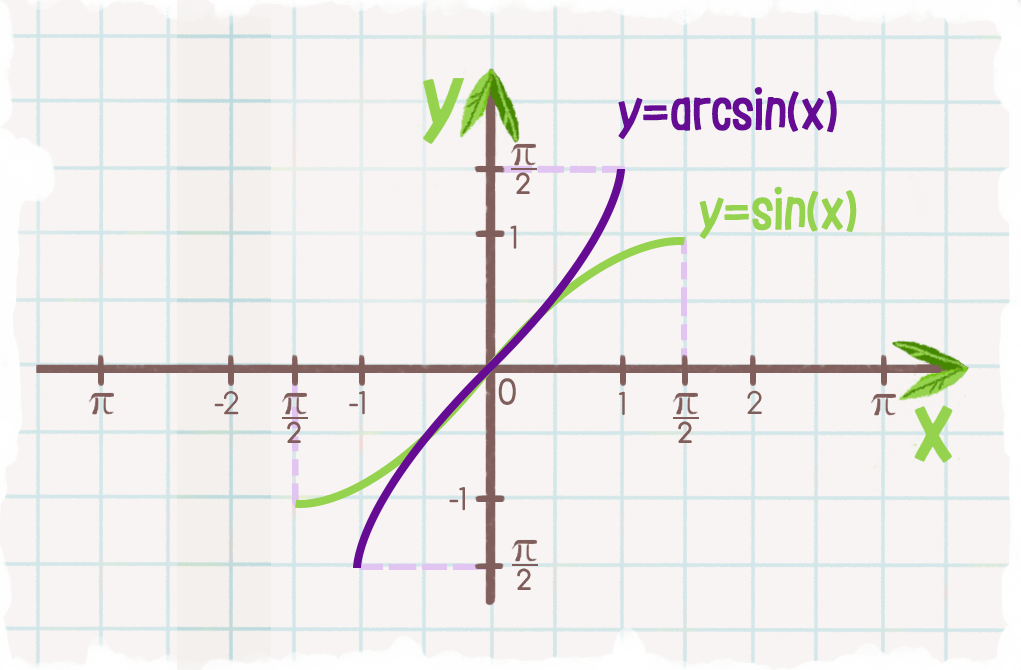
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктический(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы | 45 | |
| 33 | Найти точное значение 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | желтовато-коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | соз(210) | |
| 52 | Найти точное значение | сек (60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-(квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт.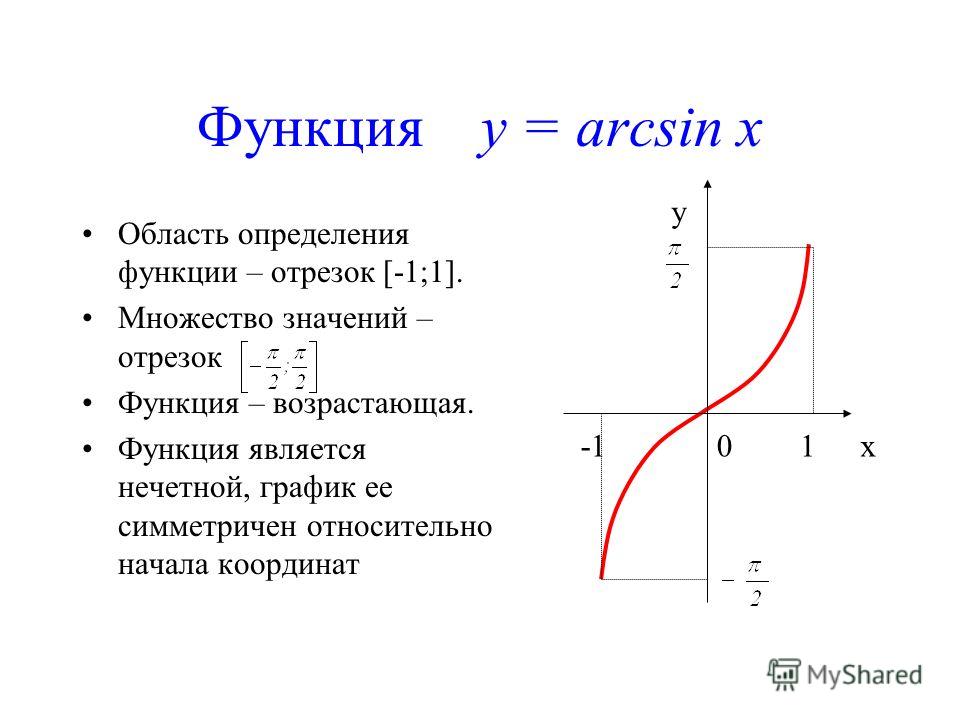 )/4 )/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
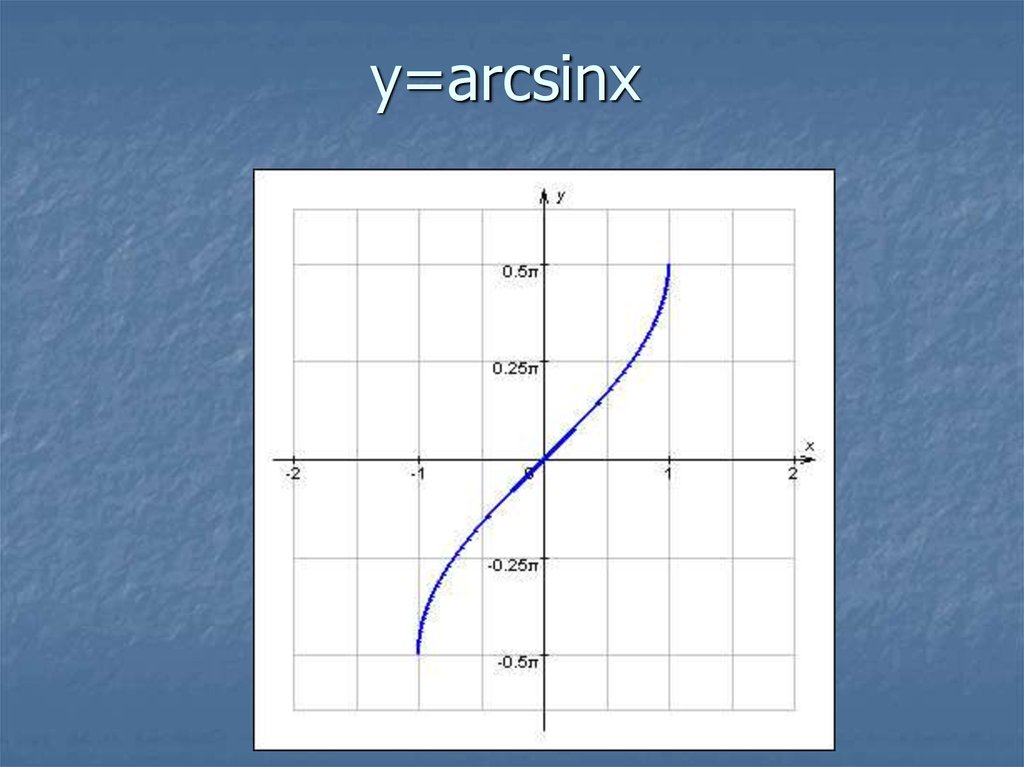
графическое представление функции arcsin(x)
Программное обеспечение для построения графиков онлайн , также известное как графопостроитель ,
это онлайн-график , который позволяет отображать функции в режиме онлайн.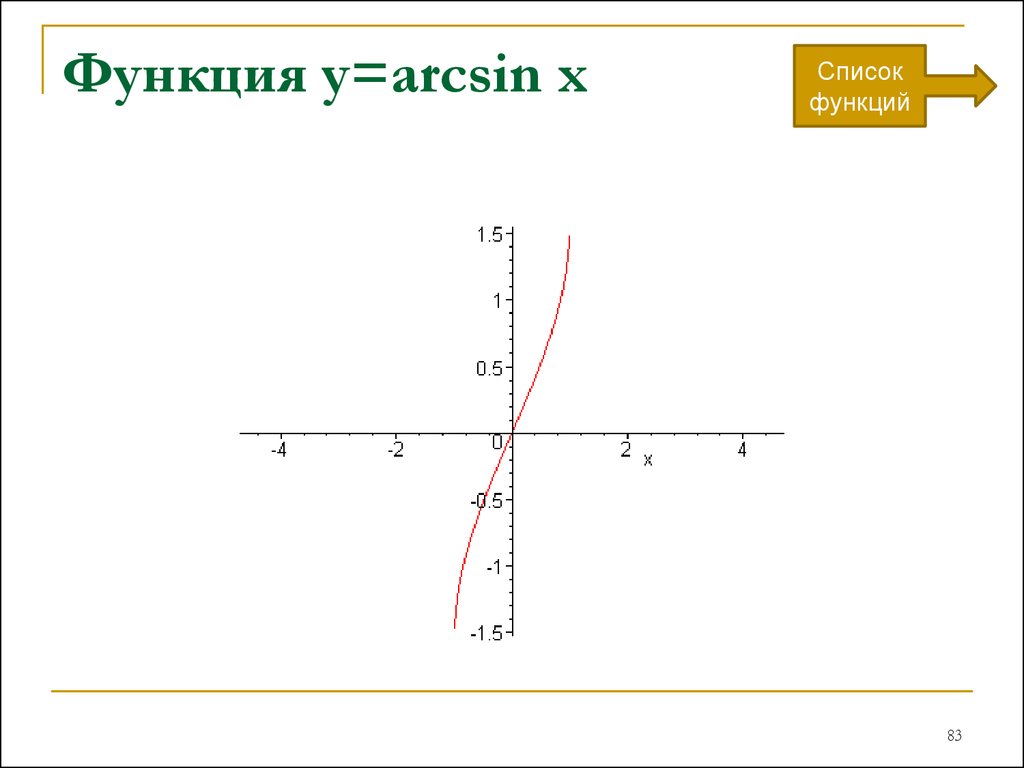 Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функционального исследования ,
позволяет получить графическое представление функции из уравнения кривой,
его можно использовать для определения вариации, минимума, максимума функции.
Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функционального исследования ,
позволяет получить графическое представление функции из уравнения кривой,
его можно использовать для определения вариации, минимума, максимума функции.
Онлайн-плоттер также может рисовать параметрические кривые. и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
В графическом калькуляторе для записи математических функций должны использоваться следующие операторы: 9Для мощности
Это программное обеспечение для построения кривых позволяет использовать следующие обычных математических функций :
- абс (абсолютное значение), график абсолютного значения
- арккос (арккосинус), арккосинус графика
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- опыта (экспоненциальный), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- абс.
 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения - арккос (арккосинус), арккосинус графика
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- опыта (экспоненциальный), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- Графические функции онлайн
Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно ,
просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн .
Переменная, которая будет использоваться для представления функций, — «x».
Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.
Кривые можно удалить из плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.
Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования.
онлайн-плоттер имеет несколько опций, позволяющих настроить график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов,
чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.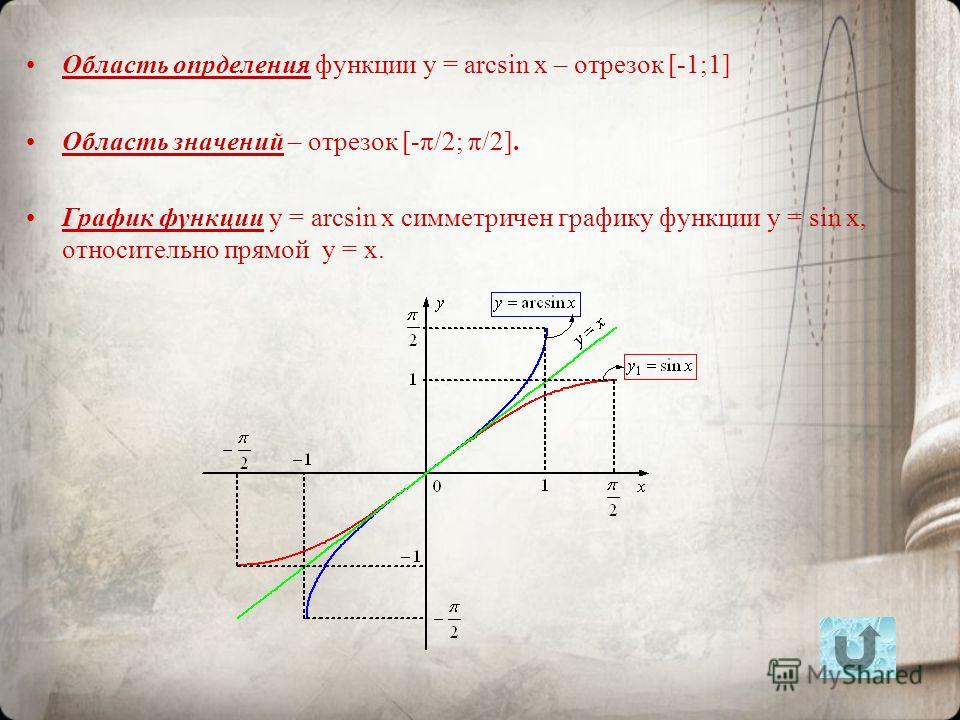
- Проведение касательной функции к точке
- График производной функции
Онлайн-плоттер позволяет провести тангенс функции в точке для этого, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
Онлайн-плоттер позволяет вам построить производную функции для этого,
вы просто рисуете нужную функцию, затем после того, как функция нарисована,
нажмите на меню, на параметры, затем на появившуюся производную кнопку,
затем строится производная функции.
9Построитель кривых 0003 также можно использовать для вычисления производной функции и к участок он для этого, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).
Плоттер позволяет рисовать параметрическую кривую , для этого
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «Построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения нужных точек.
Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.
Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея.
Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это,
используйте область в правом нижнем углу графиков.
Сделать это,
используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых,
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как
изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков.
Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно скопировать изображение.
Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.



 Используя тригонометрическую формулу sin x = sin (π — x), мы имеем
Используя тригонометрическую формулу sin x = sin (π — x), мы имеем (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения