Первая часть
Вторая часть
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
Ряд Тейлора онлайн
Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора:,
где rn – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:
, где число x заключено между х и а.
- Решение онлайн
- Видеоинструкция
f(x)=
в точке x0= Количество элементов ряда34567
Использовать разложение элементарных функций
ex, cos(x), sin(x), ln(1+x), (1+x)m
Правила ввода функций
Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если:
- она имеет производные всех порядков;
- построенный ряд сходится в этой точке.

При а=0 получаем ряд, называемый рядом Маклорена:
Разложение простейших (элементарных) функций в ряд Маклорена:Показательные функции
, R=∞
Тригонометрические функции
, R=∞
, R=∞
, (-π/2 < x < π/2), R=π/2
Функция actgx не разлагается по степеням x, т.к. ctg0=∞
Гиперболические функции
, -1<x<1, R = 1
Биномиальные ряды
.
Пример №1. Разложить в степенной ряд функцию f(x)=2x.
Решение. Найдем значения функции и ее производных при х=0
f(x) = 2x, f(0) = 20=1;
f'(x) = 2xln2, f'(0) = 20 ln2= ln2;
f»(x) = 2x ln22, f»(0) = 20 ln22= ln22;
…
f(n)(x) = 2x lnn2, f(n)(0) = 20 lnn2= lnn2.
Подставляя полученные значения производных в формулу ряда Тейлора, получим:
Пример №2. Написать ряд Тейлора по степеням (х+4) для функции f(x)=ex.
Решение. Находим производные функции ex и их значения в точке х=-4.
f(x) = еx, f(-4) = е-4;
f'(x) = еx, f'(-4) = е-4;
f»(x) = еx, f»(-4) = е-4;
…
f(n)(x) = еx, f(n)( -4) = е-4.
Следовательно, искомый ряд Тейлора функции имеет вид:
Данное разложение также справедливо для -∞<x<+∞.

Пример №3. Разложить функцию f(x)=lnx в ряд по степеням (х-1),
( т.е. в ряд Тейлора в окрестности точки х=1).
Решение. Находим производные данной функции.
f(x)=lnx, , , ,
f(1)=ln1=0, f'(1)=1, f»(1)=-1, f»'(1)=1*2,…, f(n)=(-1)n-1(n-1)!
Подставляя эти значения в формулу, получим искомый ряд Тейлора:
Пример №4. Разложить в степенной ряд функцию .
Решение
, -∞<x<∞
Пример №5. Разложить в ряд Маклорена функцию .
Разложить в ряд Маклорена функцию .
Решение. Имеем
Пользуясь формулой (4), можем записать:
подставляя вместо х в формулу –х, получим:
Отсюда находим: ln(1+x)-ln(1-x) = —
Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим
. Этот ряд сходится в интервале (-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.
Замечание.
Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а)m, где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t=х-а и раскладывать полученную функцию относительно t в ряд Маклорена.
Этот метод основан на теореме о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.
Пример №5а. Разложить в ряд Маклорена функцию , указать область сходимости.
Решение. Сначала найдем 1-x-6x2=(1-3x)(1+2x), далее разложим дробь с помощью сервиса.
на элементарные:
Дробь 3/(1-3x) можно рассматривать как сумму бесконечно убывающей геометрической прогрессии знаменателем 3x, если |3x| < 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
с областью сходимости |x| < 1/3.Пример №6. Разложить функцию в ряд Тейлора в окрестности точки х=3.
Решение. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х=3. Однако проще будет воспользоваться имеющимся разложением (5):
=
Полученный ряд сходится при или –3<x-3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции. Пример №7. Написать ряд Тейлора по степеням (х-1) функцииln(x+2).
Решение.
Ряд сходится при , или -2 < x < 5.
Пример №8. Разложить функцию f(x)=sin(πx/4) в ряд Тейлора в окрестности точки x=2.
Решение. Сделаем замену t=х-2:
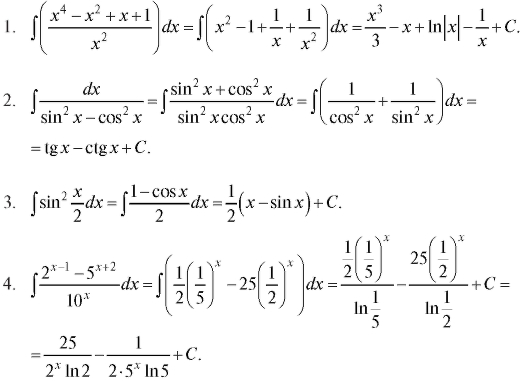 е. при (-∞<x<+∞).
е. при (-∞<x<+∞).
Таким образом,
, (-∞<x<+∞)
Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.- если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена.

- если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.
- в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа: a<c<x (или x<c<a).
Пример №1. Вычислить ln(3) с точностью до 0,01.
Решение. Воспользуемся разложением , где x=1/2 (см. пример 5 в предыдущей теме):
Пример №2. Вычислить с точностью до 0,0001.
Решение. Воспользуемся биномиальным рядом. Так как 53 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=53+5.

Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подынтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.
Пример №3. Вычислить интеграл ∫014sin(x)x с точностью до 10-5.
Решение. Соответствующий неопределенный интеграл не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
Разделив почленно ряд для sinx на x , получим:
Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:
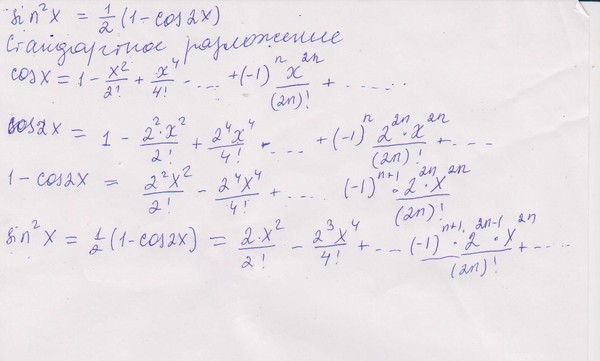
Таким образом, находим
Пример №4. Вычислить интеграл ∫014ex2 с точностью до 0,001.
Решение.
≈0.0001<0.001
Следовательно, .|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 4 из 4 1. Имеем ; , и по формуле (5.2) получаем . (5.3) Областью сходимости этого степенного ряда является интервал . 2. Имеем: , , , , , откуда , , , , и т.д. Очевидно, что производные четного порядка , а нечетного порядка , , и по формуле (5.2) имеем (5.4) Область сходимости ряда . 3. . Рассматривая аналогично функции , получим: (5.5) Область сходимости ряда . 4. , где – любое действительное число. Имеем , , , , …, , … При : , , , , …, и по формуле (5.2) получаем (5.6) Найдем интервал сходимости ряда: Ряд, составленный из модулей , исследуем с помощью признака Даламбера: . Следовательно, интервал сходимости ряда . На концах интервала при сходимость ряда зависит от конкретных значений . Ряд (5.6) называется биномиальным. Если – целое положительное число, то биномиальный ряд представляет формулу бинома Ньютона, так как при сомножитель равен нулю, следовательно, -йчлен ряда и все последующие равны нулю, т.е. ряд обрывается, и вместо бесконечного разложения получается конечная сумма. Выпишем некоторые разложения функции при различных . : , (5.7) Если в это разложение подставить вместо , получим: (5.8) : , (5.9) : , (5.10) 5. . Получить разложение для этой функции, непосредственно вычисляя коэффициенты с помощью производных, не очень просто, поэтому мы воспользуемся разложением (5.7) и свойством 2) степенных рядов. Интегрируя почленно равенство (5.7) в интервале , где , с учетом того, что , получим (5.11) Область сходимости ряда (после выяснения сходимости на концах интервала) есть . 6. Проделаем то же самое, что и в предыдущем случае, воспользовавшись разложением (5. (5.12) Область сходимости ряда . 7. Воспользуемся разложением (5.10), подставив в него вместо : Интегрируя в интервале , где , получаем: (5.13) Область сходимости ряда Можно доказать, что ряды, приведенные в формулах (5.3) – (5.13), сходятся к функциям, для которых они составлены. При разложении более сложных функций часто используют готовые разложения (5.3) – (5.13). Примеры 1) Разложить в ряд Маклорена функцию Решение. Воспользуемся известной тригонометрической формулой Разложим в ряд Маклорена функцию , заменяя в разложении (5.5) на : Тогда Это и есть разложение в ряд Маклорена функции . Очевидно, что оно справедливо при любом . 2) Разложить в ряд Тейлора по степеням функцию Решение. Преобразуем данную функцию так, чтобы можно было воспользоваться разложением (5.7): Полученное разложение справедливо, когда . Применение рядов в приближенных вычислениях Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, определенных интегралов, которые являются «не берущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения. Примеры I. Вычислить приближенно с точностью до 0,0001: а) Решение. Для вычисления запишем ряд (5.3) при , принадлежащем области сходимости : Взяв первые пять членов разложения, на основании следствия из теоремы Лейбница для сходящегося знакочередующегося ряда, мы допустим погрешность , не превышающую первого отброшенного члена (по абсолютной величине), т.е. . Итак, б) Решение. Воспользуемся разложением (5.11), подставив в него , входящее в область сходимости : Так как данный числовой ряд не является знакопеременным, то о погрешности нельзя судить по величине первого отбрасываемого члена. Если в качестве взять сумму первых трех членов, мы допустим погрешность (здесь мы учли, что сумма сходящегося геометрического ряда в скобках равна ) Итак, в) Решение. Для вычисления запишем ряд (5.4) при , принадлежащем области сходимости : (необходимо взять два члена, так как при этом погрешность ). Итак, . II. Вычислить приближенно с точностью до 0,001 следующие интегралы: a) Решение. Так как интеграл «не берущийся», «точное» интегрирование здесь невозможно. Воспользуемся разложением (5.4). Разделив обе части на , получим , причем ряд сходится при всех значениях . Интегрируя почленно, получим: Возьмем первые три члена разложения, т.к. . Итак, б) Решение. Заменив на в разложении (5.3), получим: . Умножая полученный ряд на : , и почленно интегрируя в интервале , принадлежащем интервалу сходимости ряда , имеем: При этом . Задачи Разложить в ряд Маклорена следующие функции, указав промежутки сходимости полученных рядов. 86. 87. 88. 89. 90. 91. 92. Разложить в ряд Тейлора следующие функции и найти область сходимости полученного ряда. 93. по степеням 94 по степеням 95. по степеням 96. по степеням 97. по степеням 98. по степеням Вычислить приближенно с точностью до 0,0001: 99. 100. 101. 102. 103. 104. Вычислить приближенно, взяв первые два члена разложения в ряд подынтегральной функции, и оценить допущенные при этом погрешности: 105. 106. Ответы В задачах1, 3, 6, 7, 8, 9, 10, 12, 13, 15, 17, 18, 19, 21, 22, 23, 31, 32, 33, 34, 35, 37, 38, 42, 43, 44 – ряды сходятся. В задачах 2, 4, 5, 11, 14, 16, 20, 24, 25, 26, 27, 28, 29, 30, 36, 39, 40, и 41 – ряды расходятся. В задачах 45, 46, 47, 49, 50, 51, 55 – ряды абсолютно сходятся. В задачах 48, 53, 54, 57 – ряды сходятся условно. В задачах 52, 56, 58, 59 – ряды расходятся. 60.(-1;1],61.[-1/2;1/2),62.{0},63.(-1/3;1/3],64.(-1;1),65.[0;2],66.[-10;10),67.(-∞;∞), 68.(-7;-1), 69. [-4;4), 70. (-2;2), 71. , 72. [1;3), 73. (-1/3;1/3), 74. (-∞;∞), 75. [-1;1], 76. [-1;1), 77. (1;5], 78. (-1/4;1/4), 79. (-1/3;1/3), 80. (-3;1], 81. (-1;1], 82. (-∞;∞), 83. , 84. , 85. [-1/e;1/e), 86. 87. 88. 89. 90. 91. 92. 93. 94. 95. 96. 97. 98. 99. 100. 101. 102. 103. 104. 105. 106. .
Оглавление §1. Основные понятия. 4 §2. §3. Признаки сходимости знакопеременных рядов. 22 §4. Степенные ряды.. 27 §5. Ряды Маклорена и Тейлора. 32 §6. Применение рядов в приближенных вычислениях. 39 Ответы.. 43 Подписано в печать 2012 г. Формат 60´84/16. Бумага писчая. Отпечатано на ризографе. Уч. изд. листов 2.
Московский государственный университет тонких химических технологий им. М.В.Ломоносова Издательско-полиграфический центр 117571, Москва, просп. Вернадского, 86.
* Напомним, что степенью степенного выражения называется наибольшая из степеней входящих в него слагаемых, само это слагаемое называется старшим, а его коэффициент называется старшим коэффициентом. Например, у степенного выражения старшее слагаемое имеет степень 1,5, а старший коэффициент равен 5. ⇐ Предыдущая1234 Читайте также: Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Решение задач с использованием генеалогического метода История происхождения и развития детской игры |
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 611; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.028 с.) |
6.3 Серия Тейлора и Маклорена. Исчисление, том 2
Цели обучения
- 6.3.1 Описать процедуру нахождения полинома Тейлора заданного порядка для функции.
- 6.3.2
Объясните смысл и значение теоремы Тейлора с остатком.

- 6.3.3 Оцените остаток для аппроксимации ряда Тейлора данной функции.
В предыдущих двух разделах мы обсуждали, как находить представления степенных рядов для определенных типов функций, в частности, функций, связанных с геометрическими рядами. Здесь мы обсуждаем представления степенных рядов для других типов функций. В частности, мы обращаемся к следующим вопросам: какие функции могут быть представлены степенными рядами и как мы находим такие представления? Если мы можем найти представление в виде степенного ряда для конкретной функции ff, и этот ряд сходится на каком-то интервале, как мы докажем, что этот ряд действительно сходится к f?f?
Обзор серии Taylor/Maclaurin
Рассмотрим функцию ff, которая имеет представление в виде степенного ряда при x=a.x=a. Тогда ряд имеет вид
∑n=0∞cn(x−a)n=c0+c1(x−a)+c2(x−a)2+⋯.∑n=0∞cn(x−a)n=c0+c1( х-а)+с2(х-а)2+⋯.
(6.4)
Какими должны быть коэффициенты? На данный момент мы игнорируем вопросы сходимости, а вместо этого сосредоточимся на том, каким должен быть ряд, если он существует. Мы вернемся к обсуждению сходимости позже в этом разделе. Если ряд Уравнение 6.4 является представлением для ff при x=a,x=a, мы, безусловно, хотим, чтобы ряд равнялся f(a)f(a) при x=a.x=a. Вычисляя ряд при x=a,x=a, мы видим, что
Мы вернемся к обсуждению сходимости позже в этом разделе. Если ряд Уравнение 6.4 является представлением для ff при x=a,x=a, мы, безусловно, хотим, чтобы ряд равнялся f(a)f(a) при x=a.x=a. Вычисляя ряд при x=a,x=a, мы видим, что
∑n=0∞cn(x−a)n=c0+c1(a−a)+c2(a−a)2+⋯=c0.∑n=0∞cn(x−a)n=c0+ c1(a−a)+c2(a−a)2+⋯=c0.
Таким образом, ряд равен f(a)f(a), если коэффициент c0=f(a).c0=f(a). Кроме того, мы хотели бы, чтобы первая производная степенного ряда равнялась f′(a)f′(a) при x=a.x=a. Дифференцируя уравнение 6.4 почленно, мы видим, что
ddx(∑n=0∞cn(x−a)n)=c1+2c2(x−a)+3c3(x−a)2+⋯.ddx(∑n=0∞cn(x−a)n )=c1+2c2(x−a)+3c3(x−a)2+⋯.
Следовательно, при x=a,x=a производная равна
ddx(∑n=0∞cn(x−a)n)=c1+2c2(a−a)+3c3(a−a)2+⋯=c1.ddx(∑n=0∞cn(x−a )n)=c1+2c2(a−a)+3c3(a−a)2+⋯=c1.
Следовательно, производная ряда равна f′(a)f′(a), если коэффициент c1=f′(a).c1=f′(a). Продолжая в том же духе, мы ищем коэффициенты c n такие, что все производные степенного ряда (6. 4) согласуются со всеми соответствующими производными от ff при x=a.x=a. Вторая и третья производные уравнения 6.4 равны
4) согласуются со всеми соответствующими производными от ff при x=a.x=a. Вторая и третья производные уравнения 6.4 равны
d2dx2(∑n=0∞cn(x−a)n)=2c2+3·2c3(x−a)+4·3c4(x−a)2+⋯d2dx2(∑n=0∞cn(x− а)n)=2c2+3·2c3(x−a)+4·3c4(x−a)2+⋯
и
d3dx3(∑n=0∞cn(x−a)n)=3·2c3+4·3·2c4(x−a)+5·4·3c5(x−a)2+⋯.d3dx3(∑n =0∞cn(x−a)n)=3·2c3+4·3·2c4(x−a)+5·4·3c5(x−a)2+⋯.
Следовательно, при x=a,x=a вторая и третья производные
d2dx2(∑n=0∞cn(x−a)n)=2c2+3·2c3(a−a)+4·3c4(a−a)2+⋯=2c2d2dx2(∑n=0∞cn(x −a)n)=2c2+3·2c3(a−a)+4·3c4(a−a)2+⋯=2c2
и
d3dx3(∑n=0∞cn(x−a)n)=3·2c3+4·3·2c4(a−a)+5·4·3c5(a−a)2+⋯=3·2c3d3dx3( ∑n=0∞cn(x−a)n)=3·2c3+4·3·2c4(a−a)+5·4·3c5(a−a)2+⋯=3·2c3
равно f″(a)f″(a) и f‴(a),f‴(a) соответственно, если c2=f″(a)2c2=f″(a)2 и c3=f‴(a )3·2.c3=f‴(a)3·2. В более общем виде мы видим, что если ff имеет представление степенного ряда при x=a,x=a, то коэффициенты должны быть заданы как cn=f(n)(a)n!.cn=f(n)(a) н!. То есть ряд должен быть
∑n=0∞f(n)(a)n!(x−a)n=f(a)+f′(a)(x−a)+f″(a)2!(x−a) 2+f‴(a)3!(x−a)3+⋯. ∑n=0∞f(n)(a)n!(x−a)n=f(a)+f′(a)( x−a)+f″(a)2!(x−a)2+f‴(a)3!(x−a)3+⋯.
∑n=0∞f(n)(a)n!(x−a)n=f(a)+f′(a)( x−a)+f″(a)2!(x−a)2+f‴(a)3!(x−a)3+⋯.
Этот степенной ряд для ff известен как ряд Тейлора для ff в п.в. Если a=0,a=0, то этот ряд известен как ряд Маклорена для ф.ф.
Определение
Если ff имеет производные всех порядков в точках x=a,x=a, то ряд Тейлора для функции ff в точках aa равен
∑n=0∞f(n)(a)n!(x−a) n=f(a)+f′(a)(x−a)+f″(a)2!(x−a)2+⋯+f(n)(a)n!(x−a)n+⋯ .∑n=0∞f(n)(a)n!(x−a)n=f(a)+f′(a)(x−a)+f″(a)2!(x−a) 2+⋯+f(n)(a)n!(x−a)n+⋯.
(6.5)
Ряд Тейлора для ff в точке 0 известен как ряд Маклорена для ff.
Позже в этом разделе мы покажем примеры нахождения ряда Тейлора и обсудим условия, при которых ряд Тейлора для функции будет сходиться к этой функции. Здесь мы сформулируем важный результат. Напомним из уникальности степенных рядов, что представления степенных рядов уникальны. Следовательно, если функция ff имеет степенной ряд в точках a, a, то она должна быть рядом Тейлора для ff в точках a. a.
a.
Теорема 6,6
Уникальность ряда Тейлора
Если функция ff имеет степенной ряд в точках и , который сходится к ff на некотором открытом интервале, содержащем и , то этот степенной ряд является рядом Тейлора для ff в точках и .
Доказательство следует непосредственно из уникальности степенного ряда.
Чтобы определить, сходится ли ряд Тейлора, нам нужно посмотреть на его последовательность частичных сумм. Эти частичные суммы представляют собой конечные полиномы, известные как полиномы Тейлора.
СМИ
Посетите архив MacTutor History of Mathematics, чтобы прочитать краткие биографии Брука Тейлора и Колина Маклорена и то, как они разработали концепции, названные в их честь.
Полиномы Тейлора
n -я частичная сумма ряда Тейлора для функции ff при aa известна как n -й полином Тейлора. Например, 0-я, 1-я, 2-я и 3-я частичные суммы ряда Тейлора равны
Например, 0-я, 1-я, 2-я и 3-я частичные суммы ряда Тейлора равны
p0(x)=f(a),p1(x)=f(a)+f′(a)(x−a),p2(x)=f(a)+f′(a)(x− а)+f″(a)2!(x−a)2,p3(x)=f(a)+f′(a)(x−a)+f″(a)2!(x−a) 2+f‴(a)3!(x−a)3,p0(x)=f(a),p1(x)=f(a)+f′(a)(x−a),p2(x )=f(a)+f′(a)(x−a)+f″(a)2!(x−a)2,p3(x)=f(a)+f′(a)(x− а)+f″(a)2!(x−a)2+f‴(a)3!(x−a)3,
соответственно. Эти частичные суммы известны как 0-й, 1-й, 2-й и 3-й многочлены Тейлора от ff в точках a, a соответственно. Если a=0,a=0, то эти полиномы известны как полиномы Маклорена для ф.ф. Дадим формальное определение полиномов Тейлора и Маклорена для функции f.f.
Определение
Если ff имеет n производных в точках x=a,x=a, то n -й полином Тейлора для ff в точке aa равен
pn(x)=f(a)+f′(a)(x −a)+f″(a)2!(x−a)2+f‴(a)3!(x−a)3+⋯+f(n)(a)n!(x−a)n. pn(x)=f(a)+f′(a)(x−a)+f″(a)2!(x−a)2+f‴(a)3!(x−a)3+⋯ +f(n)(a)n!(x−a)n.
n -й полином Тейлора для ff в точке 0 известен как n -й полином Маклорена для ff.
Теперь мы покажем, как использовать это определение, чтобы найти несколько полиномов Тейлора для f(x)=lnxf(x)=lnx при x=1.x=1.
Пример 6.11
Нахождение полиномов Тейлора
Нахождение полиномов Тейлора p0,p1,p2p0,p1,p2 и p3p3 для f(x)=lnxf(x)=lnx при x=1.x=1. Используйте графическую утилиту, чтобы сравнить график ff с графиками p0,p1,p2p0,p1,p2 и p3.p3.
Решение
Чтобы найти эти полиномы Тейлора, нам нужно вычислить ff и его первые три производные при x=1.x=1.
f(x)=lnxf(1)=0f′(x)=1xf′(1)=1f″(x)=−1x2f″(1)=−1f‴(x)=2x3f‴(1)= 2f(x)=lnxf(1)=0f′(x)=1xf′(1)=1f″(x)=−1x2f″(1)=−1f‴(x)=2x3f‴(1)=2
Следовательно,
p0(x)=f(1)=0,p1(x)=f(1)+f′(1)(x−1)=x−1,p2(x)=f(1 )+f′(1)(x−1)+f″(1)2(x−1)2=(x−1)−12(x−1)2,p3(x)=f(1)+ f′(1)(x−1)+f″(1)2(x−1)2+f‴(1)3!(x−1)3=(x−1)−12(x−1) 2+13(x−1)3.p0(x)=f(1)=0,p1(x)=f(1)+f′(1)(x−1)=x−1,p2(x )=f(1)+f′(1)(x−1)+f″(1)2(x−1)2=(x−1)−12(x−1)2,p3(x)= f(1)+f′(1)(x−1)+f″(1)2(x−1)2+f‴(1)3!(x−1)3=(x−1)−12 (х-1)2+13(х-1)3.
Графики y=f(x)y=f(x) и первых трех полиномов Тейлора показаны на рис. 6.5.
Рисунок 6,5 На этом графике нанесены функция y=lnxy=lnx и полиномы Тейлора p0,p1,p2p0,p1,p2 и p3p3 при x=1x=1.
Контрольно-пропускной пункт 6.10
Найдите полиномы Тейлора p0,p1,p2p0,p1,p2 и p3p3 для f(x)=1x2f(x)=1×2 при x=1.x=1.
Теперь мы покажем, как найти полиномы Маклорена для e x , sinx,sinx и cosx.cosx. Как указывалось выше, полиномы Маклорена — это полиномы Тейлора с центром в нуле.
Пример 6.12
Нахождение полиномов Маклорена
Для каждой из следующих функций найдите формулы для полиномов Маклорена p0,p1,p2p0,p1,p2 и p3.p3. Найдите формулу для многочлена Маклорена n th и запишите ее, используя сигма-нотацию. Используйте графическую утилиту, чтобы сравнить графики p0,p1,p2p0,p1,p2 и p3p3 с f.f.
- f(x)=exf(x)=ex
- f(x)=sinxf(x)=sinx
- f(x)=cosxf(x)=cosx
Решение
- Поскольку f(x)=ex,f(x)=ex, мы знаем, что f(x)=f′(x)=f″(x)=⋯=f(n)(x)=exf(x )=f′(x)=f″(x)=⋯=f(n)(x)=ex для всех натуральных чисел n .
 Следовательно,
Следовательно,f(0)=f′(0)=f″(0)=⋯=f(n)(0)=1f(0)=f′(0)=f″(0)=⋯=f (n)(0)=1
для всех положительных целых чисел n . Таким образом, имеемp0(x)=f(0)=1,p1(x)=f(0)+f′(0)x=1+x,p2(x)=f(0)+f′ (0)x+f″(0)2!x2=1+x+12×2,p3(x)=f(0)+f′(0)x+f″(0)2×2+f‴(0)3 !x3=1+x+12×2+13!x3,pn(x)=f(0)+f′(0)x+f″(0)2×2+f‴(0)3!x3+⋯+f(n )(0)n!xn=1+x+x22!+x33!+⋯+xnn!=∑k=0nxkk!.p0(x)=f(0)=1,p1(x)=f(0) +f′(0)x=1+x,p2(x)=f(0)+f′(0)x+f″(0)2!x2=1+x+12×2,p3(x)=f (0)+f′(0)x+f″(0)2×2+f‴(0)3!x3=1+x+12×2+13!x3,pn(x)=f(0)+f′( 0)x+f″(0)2×2+f‴(0)3!x3+⋯+f(n)(0)n!xn=1+x+x22!+x33!+⋯+xnn!=∑k= 0нкскк!.
Функция и первые три полинома Маклорена показаны на рис. 6.6.Рисунок 6,6 На графике показаны функция y=exy=ex и полиномы Маклорена p0,p1,p2p0,p1,p2 и p3.p3.
- Для f(x)=sinx,f(x)=sinx значения функции и ее первых четырех производных при x=0x=0 задаются следующим образом:
f(x)=sinxf(0)=0f′ (x)=cosxf′(0)=1f″(x)=−sinxf″(0)=0f‴(x)=−cosxf‴(0)=−1f(4)(x)=sinxf(4)( 0)=0.
 f(x)=sinxf(0)=0f′(x)=cosxf′(0)=1f″(x)=−sinxf″(0)=0f‴(x)=−cosxf‴( 0)=−1f(4)(x)=sinxf(4)(0)=0.
f(x)=sinxf(0)=0f′(x)=cosxf′(0)=1f″(x)=−sinxf″(0)=0f‴(x)=−cosxf‴( 0)=−1f(4)(x)=sinxf(4)(0)=0.
Поскольку четвертая производная sinx,sinx, шаблон повторяется. То есть f(2m)(0)=0f(2m)(0)=0 и f(2m+1)(0)=(−1)mf(2m+1)(0)=(−1)m для m≥0.m≥0. Таким образом, имеемp0(x)=0,p1(x)=0+x=x,p2(x)=0+x+0=x,p3(x)=0+x+0−13!x3 =x−x33!,p4(x)=0+x+0−13!x3+0=x−x33!,p5(x)=0+x+0−13!x3+0+15!x5=x −x33!+x55!,p0(x)=0,p1(x)=0+x=x,p2(x)=0+x+0=x,p3(x)=0+x+0−13 !x3=x−x33!,p4(x)=0+x+0−13!x3+0=x−x33!,p5(x)=0+x+0−13!x3+0+15!x5 =x−x33!+x55!,
и для m≥0,m≥0,p2m+1(x)=p2m+2(x)=x−x33!+x55!−⋯+(−1) mx2m+1(2m+1)!=∑k=0m(−1)kx2k+1(2k+1)!.p2m+1(x)=p2m+2(x)=x−x33!+x55!− ⋯+(−1)mx2m+1(2m+1)!=∑k=0m(−1)kx2k+1(2k+1)!.
Графики функции и ее полиномов Маклорена показаны на рис. 6.7.Рисунок 6.7 График показывает функцию y=sinxy=sinx и полиномы Маклорена p1,p3p1,p3 и p5.p5.
- Для f(x)=cosx,f(x)=cosx значения функции и ее первых четырех производных при x=0x=0 задаются следующим образом:
f(x)=cosxf(0)=1f′ (x)=−sinxf′(0)=0f″(x)=−cosxf″(0)=−1f‴(x)=sinxf‴(0)=0f(4)(x)=cosxf(4)( 0)=1.
 f(x)=cosxf(0)=1f′(x)=−sinxf′(0)=0f″(x)=−cosxf″(0)=−1f‴(x)=sinxf‴ (0)=0f(4)(x)=cosxf(4)(0)=1.
f(x)=cosxf(0)=1f′(x)=−sinxf′(0)=0f″(x)=−cosxf″(0)=−1f‴(x)=sinxf‴ (0)=0f(4)(x)=cosxf(4)(0)=1.
Поскольку четвертая производная равна cosx,cosx, шаблон повторяется. Другими словами, f(2m)(0)=(−1)mf(2m)(0)=(−1)m и f(2m+1)=0f(2m+1)=0 для m≥0. м≥0. Следовательно,p0(x)=1,p1(x)=1+0=1,p2(x)=1+0−12!x2=1−x22!,p3(x)=1+0−12! x2+0=1−x22!,p4(x)=1+0−12!x2+0+14!x4=1−x22!+x44!,p5(x)=1+0−12!x2+0 +14!x4+0=1−x22!+x44!,p0(x)=1,p1(x)=1+0=1,p2(x)=1+0−12!x2=1−x22! ,p3(x)=1+0−12!x2+0=1−x22!,p4(x)=1+0−12!x2+0+14!x4=1−x22!+x44!,p5( x)=1+0−12!x2+0+14!x4+0=1−x22!+x44!,
и для n≥0,n≥0,p2m(x)=p2m+1(x )=1−x22!+x44!−⋯+(−1)mx2m(2m)!=∑k=0m(−1)kx2k(2k)!.p2m(x)=p2m+1(x)=1− x22!+x44!−⋯+(−1)mx2m(2m)!=∑k=0m(−1)kx2k(2k)!.
Графики функции и полиномов Маклорена представлены на рис. 6.8.Рисунок 6,8 На этом графике изображены функция y=cosxy=cosx и полиномы Маклорена p0,p2p0,p2 и p4p4.
Контрольно-пропускной пункт 6.11
Найдите формулы для полиномов Маклорена p0,p1,p2p0,p1,p2 и p3p3 для f(x)=11+x. f(x)=11+x. Найдите формулу для многочлена Маклорена n th. Запишите ответ, используя сигма-нотацию.
f(x)=11+x. Найдите формулу для многочлена Маклорена n th. Запишите ответ, используя сигма-нотацию.
Теорема Тейлора с остатком
Напомним, что n -й полином Тейлора для функции ff при a является n -й частичной суммой ряда Тейлора для ff при a . Следовательно, чтобы определить, сходится ли ряд Тейлора, нам нужно определить, сходится ли последовательность полиномов Тейлора {pn}{pn}. Однако мы не только хотим знать, сходится ли последовательность полиномов Тейлора, мы хотим знать, сходится ли она к f.f. Чтобы ответить на этот вопрос, определим остаток Rn(x)Rn(x) как
Rn(x)=f(x)−pn(x).Rn(x)=f(x)−pn(x).
Чтобы последовательность полиномов Тейлора сходилась к f,f, нам нужно, чтобы остаток R n сходился к нулю. Чтобы определить, сходится ли R n к нулю, введем теорему Тейлора с остатком. Эта теорема полезна не только для доказательства того, что ряд Тейлора сходится к связанной с ним функции, но также позволяет нам количественно определить, насколько хорошо n -й многочлен Тейлора аппроксимирует функцию.
Эта теорема полезна не только для доказательства того, что ряд Тейлора сходится к связанной с ним функции, но также позволяет нам количественно определить, насколько хорошо n -й многочлен Тейлора аппроксимирует функцию.
Здесь мы ищем границу |Rn|.|Rn|. Рассмотрим простейший случай: n=0.n=0. Пусть p 0 будет 0-м многочленом Тейлора от a для функции f.f. Остаток R 0 удовлетворяет
R0(x)=f(x)−p0(x)=f(x)−f(a).R0(x)=f(x)−p0(x)=f(x)−f(a) .
Если ff дифференцируемо на интервале I , содержащем a и x , то по теореме о среднем значении существует действительное число c между a и x так, что f(x)−f(a)=f′(c)(x−a).f(x)−f(a)=f′(c)(x− а). Следовательно,
Следовательно,
R0(x)=f′(c)(x−a).R0(x)=f′(c)(x−a).
Используя теорему о среднем значении в аналогичном рассуждении, мы можем показать, что если ff дифференцируемо в n раз на интервале I , содержащем a и x , то n -й остаток R
n n удовлетворяетRn(x)=f(n+1)(c)(n+1)!(x−a)n+1Rn(x)=f(n+1)(c)(n+1)!(x −а)n+1
для некоторого действительного числа c между a и x . Важно отметить , что значение c в числителе выше — это не центр a , а скорее неизвестное значение c между a и x . Эта формула позволяет нам получить оценку остатка R n . Если нам случится узнать, что |f(n+1)(x)||f(n+1)(x)| ограничен некоторым действительным числом M на этом интервале I , затем
Если нам случится узнать, что |f(n+1)(x)||f(n+1)(x)| ограничен некоторым действительным числом M на этом интервале I , затем
|Rn(x)|≤M(n+1)!|x−a|n+1|Rn(x)|≤M(n+1)!|x−a|n+1
для всех x в интервале I .
Теперь сформулируем теорему Тейлора, которая устанавливает формальную связь между функцией ff и ее полиномом Тейлора n -й степени pn(x).pn(x). Эта теорема позволяет нам ограничить ошибку при использовании полинома Тейлора для аппроксимации значения функции и будет важна при доказательстве того, что ряд Тейлора для ff сходится к ff.
Теорема 6.7
Теорема Тейлора с остатком
Пусть ff — функция, которую можно дифференцировать n+1n+1 раз на интервале I , содержащем действительное число a . Пусть p n будет n -м многочленом Тейлора от ff при a , и пусть
Пусть p n будет n -м многочленом Тейлора от ff при a , и пусть
Rn(x)=f(x)−pn(x)Rn(x)=f(x)−pn (x)
будет n -м остатком. Тогда для каждых x в интервале I существует действительное число c между a и x так, что
Rn(x)=f(n+1)(c)(n+1)!(x−a)n+1.Rn(x)=f (n+1)(c)(n+1)!(x−a)n+1.
Если существует действительное число M такое, что |f(n+1)(x)|≤M|f(n+1)(x)|≤M для всех x∈I,x∈I, то
|Rn(x)|≤M(n+1)!|x−a|n+1|Rn(x)|≤M(n+1)!|x−a|n+1
для всех x в I .
Доказательство
Зафиксируем точку x∈Ix∈I и введем функцию g такую, что
g(t)=f(x)−f(t)−f′(t)(x−t)−f″(t)2!(x−t)2−⋯−f(n)(t) n!(x−t)n−Rn(x)(x−t)n+1(x−a)n+1. g(t)=f(x)−f(t)−f′(t) (x−t)−f″(t)2!(x−t)2−⋯−f(n)(t)n!(x−t)n−Rn(x)(x−t)n+1 (х-а)n+1.
g(t)=f(x)−f(t)−f′(t) (x−t)−f″(t)2!(x−t)2−⋯−f(n)(t)n!(x−t)n−Rn(x)(x−t)n+1 (х-а)n+1.
Мы утверждаем, что g удовлетворяет критериям теоремы Ролля. Поскольку g является полиномиальной функцией (в t ), это дифференцируемая функция. Кроме того, г равно нулю при t=at=a и t=xt=x, потому что
g(a)=f(x)−f(a)−f′(a)(x−a)−f″(a)2!(x−a)2+⋯+f(n)(a) n!(x−a)n−Rn(x)=f(x)−pn(x)−Rn(x)=0,g(x)=f(x)−f(x)−0−⋯− 0=0.g(a)=f(x)−f(a)−f′(a)(x−a)−f″(a)2!(x−a)2+⋯+f(n) (a)n!(x−a)n−Rn(x)=f(x)−pn(x)−Rn(x)=0,g(x)=f(x)−f(x)−0 −⋯−0=0.
Следовательно, g удовлетворяет теореме Ролля, и, следовательно, существует c между a и x такое, что g′(c)=0.g′(c)=0. Теперь вычислим g′.g′. Используя правило произведения, заметим, что
ddt[f(n)(t)n!(x−t)n]=−f(n)(t)(n−1)!(x−t)n−1+f(n+1)( t)n!(x−t)n. ddt[f(n)(t)n!(x−t)n]=−f(n)(t)(n−1)!(x−t)n −1+f(n+1)(t)n!(x−t)n.
ddt[f(n)(t)n!(x−t)n]=−f(n)(t)(n−1)!(x−t)n −1+f(n+1)(t)n!(x−t)n.
Следовательно,
g′(t)=−f′(t)+[f′(t)−f″(t)(x−t)]+[f″(t)(x−t)−f‴(t) 2!(x−t)2]+⋯+[f(n)(t)(n−1)!(x−t)n−1−f(n+1)(t)n!(x−t )n]+(n+1)Rn(x)(x−t)n(x−a)n+1.g′(t)=−f′(t)+[f′(t)−f″ (t)(x−t)]+[f″(t)(x−t)−f‴(t)2!(x−t)2]+⋯+[f(n)(t)(n− 1)!(x−t)n−1−f(n+1)(t)n!(x−t)n]+(n+1)Rn(x)(x−t)n(x−a )n+1.
Обратите внимание на эффект телескопирования. Следовательно,
g′(t)=−f(n+1)(t)n!(x−t)n+(n+1)Rn(x)(x−t)n(x−a)n+1.g ′(t)=−f(n+1)(t)n!(x−t)n+(n+1)Rn(x)(x−t)n(x−a)n+1.
По теореме Ролля мы заключаем, что существует число c между a и x такое, что g′(c)=0.g′(c)=0. С
g′(c)=−f(n+1)(c)n!(x−c)n+(n+1)Rn(x)(x−c)n(x−a)n+1g′( c)=−f(n+1)(c)n!(x−c)n+(n+1)Rn(x)(x−c)n(x−a)n+1
делаем вывод, что
−f(n+1)(c)n!(x−c)n+(n+1)Rn(x)(x−c)n(x−a)n+1=0.−f(n+ 1)(c)n!(x−c)n+(n+1)Rn(x)(x−c)n(x−a)n+1=0.
Добавление первого члена в левой части к обеим частям уравнения и деление обеих частей уравнения на (n+1)(x-c)n(x-a)n+1, (n+1)(x-c)n (x-a)n+1, заключаем, что
Rn(x)=f(n+1)(c)(n+1)!(x−a)n+1Rn(x)=f(n+1)(c)(n+1)!(x −а)n+1
по желанию. Из этого факта следует, что если существует M таких, что |f(n+1)(x)|≤M|f(n+1)(x)|≤M для всех x в I , затем
Из этого факта следует, что если существует M таких, что |f(n+1)(x)|≤M|f(n+1)(x)|≤M для всех x в I , затем
|Rn(x)|≤M(n+1)!|x−a|n+1.|Rn(x)|≤M(n+1)!|x−a|n+1.
□
Теорема Тейлора не только позволяет нам доказать, что ряд Тейлора сходится к функции, но также позволяет оценить точность полиномов Тейлора при аппроксимации значений функции. Мы начнем с рассмотрения линейных и квадратичных аппроксимаций f(x)=x3f(x)=x3 при x=8x=8 и определим, насколько точны эти аппроксимации при оценке 113,113.
Пример 6.13
Использование линейной и квадратичной аппроксимации для оценки значений функций
Рассмотрим функцию f(x)=x3.f(x)=x3.
- Найдите первый и второй полиномы Тейлора для ff при x=8.x=8. Используйте графическую утилиту, чтобы сравнить эти полиномы с ff вблизи x=8.x=8.
- Используйте эти два полинома для оценки 113,113.

- Используйте теорему Тейлора, чтобы ограничить ошибку.
Решение
- Для f(x)=x3,f(x)=x3 значения функции и ее первых двух производных при x=8x=8 следующие:
f(x)=x3f(8)=2f′(x)=13×2/3f′(8)=112f″(x)=−29×5/3f″(8)=−1144.f(x)=x3f( 8)=2f′(x)=13×2/3f′(8)=112f″(x)=−29×5/3f″(8)=−1144.
Таким образом, первый и второй полиномы Тейлора при x=8x=8 задаются какp1(x)=f(8)+f′(8)(x−8)=2+112(x−8)p2 (x)=f(8)+f′(8)(x−8)+f″(8)2!(x−8)2=2+112(x−8)−1288(x−8)2 .p1(x)=f(8)+f′(8)(x−8)=2+112(x−8)p2(x)=f(8)+f′(8)(x−8) +f″(8)2!(x−8)2=2+112(x−8)−1288(x−8)2.
Функция и полиномы Тейлора показаны на рис. 6.9.Рисунок 6,9 Графики f(x)=x3f(x)=x3 и линейная и квадратичная аппроксимации p1(x)p1(x) и p2(x).p2(x).
- Используя первый многочлен Тейлора при x=8,x=8, мы можем оценить 8)=2,25.
Используя второй полином Тейлора при x=8,x=8, получаем )=2+112(11−8)−1288(11−8)2=2,21875.
- По теореме Тейлора с остатком существует c в интервале (8,11)(8,11) такое, что остаток при аппроксимации 113113 первым полиномом Тейлора удовлетворяет
R1(11)=f″(c)2!(11−8)2.R1(11)=f″(c)2!(11−8)2.
Мы не знаем точного значения c , поэтому мы находим верхнюю границу R1(11)R1(11), определяя максимальное значение f″f″ на интервале (8,11).(8) ,11). Поскольку f″(x)=−29×5/3,f″(x)=−29×5/3, наибольшее значение для |f″(x)||f″(x)| на этом интервале происходит при x=8.x=8. Используя тот факт, что f″(8)=−1144,f″(8)=−1144, получаем|R1(11)|≤1144·2!(11−8)2=0,03125.|R1(11) |≤1144·2!(11−8)2=0,03125.
Аналогично, для оценки R2(11),R2(11) мы используем тот факт, чтоR2(11)=f‴(c)3!(11−8)3.R2(11)=f‴(c)3!(11−8)3.
Поскольку f‴(x)=1027×8/3,f‴(x)=1027×8/3, максимальное значение f‴f‴ на интервале (8,11)(8,11) равно f‴(8) ≈0,0014468.f‴(8)≈0,0014468. Следовательно, имеем|R2(11)|≤0,00114683!(11−8)3≈0,0065104.
 |R2(11)|≤0,00114683!(11−8)3≈0,0065104.
|R2(11)|≤0,00114683!(11−8)3≈0,0065104.
Контрольно-пропускной пункт 6.12
Найдите первый и второй полиномы Тейлора для f(x)=xf(x)=x при x=4.x=4. Используйте эти полиномы для оценки 6.6. Используйте теорему Тейлора, чтобы ограничить ошибку.
Пример 6.14
Аппроксимация sin
x Использование полиномов МаклоренаИз примера 6.12b полиномы Маклорена для sinxsinx задаются как
p2m+1(x)=p2m+2(x)=x−x33!+x55!− x77!+⋯+(−1)mx2m+1(2m+1)!p2m+1(x)=p2m+2(x)=x−x33!+x55!−x77!+⋯+(−1)mx2m +1(2м+1)!
для m=0,1,2,….m=0,1,2,….
- Используйте пятый полином Маклорена для sinxsinx, чтобы аппроксимировать sin(π18)sin(π18) и ограничить ошибку.
- Для каких значений x приближает ли пятый полином Маклорена sinxsinx с точностью до 0,0001?
Решение
- Пятый полином Маклорена равен
p5(x)=x−x33!+x55!.
 p5(x)=x−x33!+x55!.
p5(x)=x−x33!+x55!.
Используя этот полином, мы можем оценить следующим образом: =π18−13!(π18)3+15!(π18)5≈0,173648.
Чтобы оценить ошибку, используйте тот факт, что шестой полином Маклорена равен p6(x)=p5(x)p6(x)=p5(x), и вычислите границу R6(π18).R6(π18). По уникальности ряда Тейлора остаток равенR6(π18)=f(7)(c)7!(π18)7R6(π18)=f(7)(c)7!(π18)7
для некоторых c между 0 и π18.π18. Используя тот факт, что |f(7)(x)|≤1|f(7)(x)|≤1 для всех x , мы находим, что величина ошибки не превышает17!·(π18) 7≤9,8×10−10,17!·(π18)7≤9,8×10−10.
- Нам нужно найти такие значения x , что
17!|x|7≤0,0001,17!|x|7≤0,0001.
Решая это неравенство для x , получаем, что пятый полином Маклорена дает оценку с точностью до 0,0001, если |x|<0,907.|х|<0,907.
Контрольно-пропускной пункт 6.13
Используйте четвертый полином Маклорена для cosxcosx для аппроксимации cos(π12). cos(π12).
cos(π12).
Теперь, когда мы можем оценить остаток Rn(x),Rn(x), мы можем использовать эту оценку, чтобы доказать, что ряд Тейлора для ff в точках a сходится к f.f.
Представление функций с помощью ряда Тейлора и Маклорена
Обсудим теперь вопросы сходимости рядов Тейлора. Мы начнем с того, что покажем, как найти ряд Тейлора для функции и как найти ее интервал сходимости.
Пример 6.15
Нахождение ряда Тейлора
Нахождение ряда Тейлора для f(x)=1xf(x)=1x при x=1.x=1. Определить интервал сходимости.
Решение
Для f(x)=1x,f(x)=1x значения функции и ее первых четырех производных при x=1x=1 равны
f(x)=1xf(1)=1f′(x) =−1x2f′(1)=−1f″(x)=2x3f″(1)=2!f‴(x)=−3·2x4f‴(1)=−3!f(4)(x)=4 ·3·2x5f(4)(1)=4!.f(x)=1xf(1)=1f′(x)=−1x2f′(1)=−1f″(x)=2x3f″(1)= 2!f‴(x)=−3·2x4f‴(1)=−3!f(4)(x)=4·3·2x5f(4)(1)=4!.
То есть имеем f(n)(1)=(−1)nn!f(n)(1)=(−1)nn! для всех n≥0. n≥0. Таким образом, ряд Тейлора для ff при x=1x=1 равен
n≥0. Таким образом, ряд Тейлора для ff при x=1x=1 равен
∑n=0∞f(n)(1)n!(x−1)n=∑n=0∞(−1)n( x−1)n.∑n=0∞f(n)(1)n!(x−1)n=∑n=0∞(−1)n(x−1)n.
Чтобы найти интервал сходимости, мы используем критерий отношения. Получаем, что
|an+1||an|=|(−1)n+1(x−1)n+1||(−1)n(x−1)n|=|x−1| .|an+1||an|=|(−1)n+1(x−1)n+1||(−1)n(x−1)n|=|x−1|.
Таким образом, ряд сходится, если |x−1|<1.|x−1|<1. То есть ряд сходится при 0 ∑n=0∞(−1)n(2−1)n=∑n=0∞(−1)n∑n=0∞(−1)n(2−1)n=∑n=0 ∞(−1)n расходится по критерию расходимости. Аналогично, при x=0,x=0, ∑n=0∞(−1)n(0−1)n=∑n=0∞(−1)2n=∑n=0∞1∑n= 0∞(−1)n(0−1)n=∑n=0∞(−1)2n=∑n=0∞1 расходится. Следовательно, интервал сходимости равен (0,2).(0,2). Найдите ряд Тейлора для f(x)=12xf(x)=12x при x=2x=2 и определите его интервал сходимости. Мы знаем, что найденный в этом примере ряд Тейлора сходится на интервале (0,2),(0,2), но откуда мы знаем, что он на самом деле сходится к f?f? Мы рассмотрим этот вопрос в более общем виде через мгновение, но для этого примера мы можем ответить на этот вопрос, написав f(x)=1x=11−(1−x). То есть ff можно представить геометрическим рядом ∑n=0∞(1−x)n.∑n=0∞(1−x)n. Поскольку это геометрический ряд, он сходится к 1x1x, пока |1−x|<1.|1−x|<1. Следовательно, ряд Тейлора из примера 6.15 сходится к f(x)=1xf(x)=1x на (0,2).(0,2). Теперь рассмотрим более общий вопрос: если ряд Тейлора для функции ff сходится на некотором интервале, как мы можем определить, действительно ли он сходится к f?f? Чтобы ответить на этот вопрос, вспомним, что ряд сходится к определенному значению тогда и только тогда, когда его последовательность частичных сумм сходится к этому значению. Учитывая серию Тейлора для ff в a , частичная сумма n th определяется полиномом Тейлора n p n . Следовательно, чтобы определить, сходится ли ряд Тейлора к f,f, нам нужно определить, является ли limn→∞pn(x)=f(x).limn→∞pn(x)=f(x). Поскольку остаток Rn(x)=f(x)−pn(x),Rn(x)=f(x)−pn(x), ряд Тейлора сходится к ff тогда и только тогда, когда limn→∞Rn(x)=0. Сформулируем теперь эту теорему формально. Предположим, что ff имеет производные всех порядков на интервале I , содержащем a . Тогда ряд Тейлора ∑n=0∞f(n)(a)n!(x−a)n∑n=0∞f(n)(a)n!(x−a)n сходится к f(x)f(x) для всех x в I тогда и только тогда, когда limn→∞Rn(x)=0limn→∞Rn(x)=0 для всех x в I . С помощью этой теоремы мы можем доказать, что ряд Тейлора для ff в точке a сходится к ff, если мы можем доказать, что остаток Rn(x)→0.Rn(x)→0. Чтобы доказать, что Rn(x)→0,Rn(x)→0, мы обычно используем оценку |Rn(x)|≤M(n+1)!|x−a|n+1|Rn(x)|≤M(n+1)!|x−a|n+1 из теоремы Тейлора с остатком. В следующем примере мы находим ряды Маклорена для e x и sinxsinx и показываем, что эти ряды сходятся к соответствующим функциям для всех действительных чисел, доказывая, что остатки Rn(x)→0Rn(x)→0 для всех действительных чисел х . Для каждой из следующих функций найдите ряд Маклорена и его интервал сходимости. Используйте теорему Тейлора с остатком, чтобы доказать, что ряд Маклорена для ff сходится к ff на этом интервале. ∑n=0∞xnn!.∑n=0∞xnn!. |an+1||an|=|x|n+1(n+1)!·n!|x|n=|x|n+1,|an+1||an|=|x| n+1(n+1)!·n!|x|n=|x|n+1, limn→∞|an+1||an|=limn→∞|x|n+1 =0limn→∞|an+1||an|=limn→∞|x|n+1=0 |Rn(x)|≤eb(n+1)!|x|n+1.|Rn(x)|≤eb(n+1)!|x|n+1. ∑n=0∞|x|nn!∑n=0∞|x|nn! limn→∞|x|n+1(n+1)!=0limn→∞|x|n+1(n+1)!= 0 ∑n=0∞(−1)nx2n+1(2n+1)!.∑n=0∞(−1)nx2n+1(2n+1)!. |an+1||an|=|x|2n+3(2n+3)!·(2n+1)!|x|2n+1=|x| 2(2n+3)(2n+2).|an+1||an|=|x|2n+3(2n+3)!·(2n+1)!|x|2n+1=|x| 2(2n+3)(2n+2). limn→∞|x|2(2n+3)(2n+2)=0limn→∞|x|2(2n+3)(2n+2)=0 Rn(x)=f(n+1)(c)(n+1)!xn+1.Rn(x)=f(n+1)(c) (n+1)!xn+1. |Rn(x )|≤|x|n+1(n+1)!|Rn(x)|≤|x|n+1(n+1)! Найдите ряд Маклорена для f(x)=cosx.f(x)=cosx. Используйте тест отношения, чтобы показать, что интервал сходимости равен (−∞,∞).(−∞,∞). Покажите, что ряд Маклорена сходится к cosxcosx для всех действительных чисел x . В этом проекте мы используем полиномы Маклорена для e x , чтобы доказать, что e иррационально. Доказательство основано на предположении, что e рационально, и приходит к противоречию. В следующих упражнениях найдите полиномы Тейлора второй степени, приближающие заданную функцию с центром в заданной точке. 116. f(x)=1+x+x2f(x)=1+x+x2 при a=1a=1 117. f(x)=1+x+x2f(x)=1+x+x2 при a=-1a=-1 118. f(x)=cos(2x)f(x)=cos(2x) при a=πa=π 119. f(x)=sin(2x)f(x)=sin(2x) при a=π2a=π2 120. f(x)=xf(x)=x при a=4a=4 121. f(x)=lnxf(x)=lnx при a=1a=1 122. f(x)=1xf(x)=1x при a=1a=1 123. f(x)=exf(x)=ex при a=1a=1 В следующих упражнениях проверьте, что данный выбор n в оценке остатка |Rn|≤M(n+1)!(x−a)n+1,|Rn|≤M(n+1)! (x−a)n+1, где M — максимальное значение |f(n+1)(z)||f(n+1)(z)| на интервале между и и указанной точкой дает |Rn|≤11000. 124. [Т] 10;а=9,n=310;а=9,n=3 125. [Т] (28)1/3;а=27,n=1(28)1/3;а=27,n=1 126. [T] sin(6);a=2π,n=5sin(6);a=2π,n=5 127. [Т] и 2 ; а=0,n=9а=0,n=9 128. [T] cos(π5);a=0,n=4cos(π5);a=0,n=4 129. [T] ln(2);a=1,n=1000ln(2);a=1,n=1000 130. Интегрировать аппроксимацию sint≈t−t36+t5120−t75040sint≈t−t36+t5120−t75040, оцененную в πt для приближения к ∫01sinπtπtdt. 131. Проинтегрируйте аппроксимацию ex≈1+x+x22+⋯+x6720ex≈1+x+x22+⋯+x6720, оцененную как − x 2 , чтобы получить аппроксимацию ∫01e−x2dx.∫01e−x2dx. В следующих упражнениях найдите наименьшее значение n такое, что оценка остатка |Rn|≤M(n+1)!(x−a)n+1,|Rn|≤M(n+1)! (x−a)n+1, где M — максимальное значение |f(n+1)(z)||f(n+1)(z)| на интервале между и и указанная точка дает |Rn|≤11000|Rn|≤11000 на указанном интервале. 132. f(x)=sinxf(x)=sinx на [−π,π],a=0[−π,π],a=0 133. f(x)=cosxf(x)=cosx на [−π2,π2],a=0[−π2,π2],a=0 134. f(x)=e−2xf(x)=e−2x на [−1,1],a=0[−1,1],a=0 135. f(x)=e−xf(x)=e−x на [−3,3],a=0[−3,3],a=0 В следующих упражнениях максимум правой части оценки остатка |R1|≤max|f″(z)|2R2|R1|≤max|f″(z)|2R2 на [a−R, a+R][a−R,a+R] встречается в положении a или a±R. 136. [T] e x округляется как 1+x,a=01+x,a=0 137. [T] sinxsinx аппроксимировано x , a=0a=0 138. [T] lnxlnx аппроксимируется как x−1,a=1x−1,a=1 139. [T] cosxcosx аппроксимировано 1,a=01,a=0 В следующих упражнениях найдите ряд Тейлора заданной функции с центром в указанной точке. 140. x4x4 при a=−1a=−1 141. 1+x+x2+x31+x+x2+x3 при a=-1a=-1 142. sinxsinx при a=πa=π 143. cosxcosx при a=2πa=2π 144. sinxsinx при x=π2x=π2 145. cosxcosx при x=π2x=π2 146. exex в a=-1a=-1 147. exex при a=1a=1 148. 1(x−1)21(x−1)2 при a=0a=0 ( Подсказка: Дифференцировать 11−x.)11−x.) 149. 1(x−1)31(x−1)3 при a=0a=0 150. F(x)=∫0xcos(t)dt;f(t)=∑n=0∞(−1)ntn(2n)!F(x)=∫0xcos(t)dt;f(t)= ∑n=0∞(−1)ntn(2n)! at a=0a=0 ( Примечание : ff — ряд Тейлора для cos(t).)cos(t).) В следующих упражнениях вычислите ряд Тейлора для каждой функции в районе x=1.x=1. 151. f(x)=2−xf(x)=2−x 152. f(x)=x3f(x)=x3 153. f(x)=(x−2)2f(x)=(x−2)2 154. f(x)=lnxf(x)=lnx 155. f(x)=1xf(x)=1x 156. f(x)=12x−x2f(x)=12x−x2 157. f(x)=x4x−2×2−1f(x)=x4x−2×2−1 158. f(x)=e−xf(x)=e−x 159. f(x)=e2xf(x)=e2x [T] В следующих упражнениях определите значение x так, чтобы данный ряд ∑n=0∞an∑n=0∞an был значением ряда Маклорена f(x)f(x ) в х.х. Аппроксимируйте значение f(x)f(x), используя S10=∑n=010an.S10=∑n=010an. 160. ∑n=0∞1n!∑n=0∞1n! 161. ∑n=0∞2nn!∑n=0∞2nn! 162. ∑n=0∞(−1)n(2π)2n(2n)!∑n=0∞(−1)n(2π)2n(2n)! 163. ∑n=0∞(−1)n(2π)2n+1(2n+1)!∑n=0∞(−1)n(2π)2n+1(2n+1)! В следующих упражнениях используются функции S5(x)=x−x36+x5120S5(x)=x−x36+x5120 и C4(x)=1−x22+x424C4(x)=1−x22+x424 на [ −π,π].[−π,π]. 164. [T] Постройте sin2x−(S5(x))2sin2x−(S5(x))2 на [−π,π].[−π,π]. Сравните максимальную разницу с квадратом оценки остатка Тейлора для sinx.sinx. 165. [T] Постройте график cos2x−(C4(x))2cos2x−(C4(x))2 на [−π,π].[−π,π]. Сравните максимальную разницу с квадратом оценки остатка Тейлора для cosx.cosx. 166. [T] График |2S5(x)C4(x)−sin(2x)||2S5(x)C4(x)−sin(2x)| на [−π,π].[−π,π]. 167. [T] Сравните S5(x)C4(x)S5(x)C4(x) на [−1,1][−1,1] с tanx.tanx. Сравните это с оценкой остатка Тейлора для аппроксимации tanxtanx с помощью x+x33+2×515.x+x33+2×515. 168. [T] Постройте ex-e4(x)ex-e4(x), где e4(x)=1+x+x22+x36+x424e4(x)=1+x+x22+x36+x424 на [ 0,2].[0,2]. Сравните максимальную ошибку с оценкой остатка Тейлора. 169. (Приближения Тейлора и нахождение корней.) Напомним, что метод Ньютона xn+1=xn−f(xn)f′(xn)xn+1=xn−f(xn)f′(xn) аппроксимирует решения f(x )=0f(x)=0 вблизи входа x0.x0. В следующих упражнениях используйте тот факт, что если q(x)=∑n=1∞an(x−c)nq(x)=∑n=1∞an(x−c)n сходится в интервале, содержащем c ,c, затем limx→cq(x)=a0limx→cq(x)=a0 для оценки каждого предела с использованием ряда Тейлора. 170. limx→0cosx−1x2limx→0cosx−1×2 171. limx→0ln(1−x2)x2limx→0ln(1−x2)x2 172. limx→0ex2-x2-1x4limx→0ex2-x2-1×4 173. limx→0+cos(x)−12xlimx→0+cos(x)−12x Использование ряда Маклорена/Тейлора для аппроксимации определенного интеграла с требуемой точностью. Контрольно-пропускной пункт
6.14
 f(x)=1x=11−(1−x).
f(x)=1x=11−(1−x). limn→∞Rn(x)=0.
limn→∞Rn(x)=0. Теорема
6,8
Сходимость ряда Тейлора

Пример
6.16
Нахождение ряда Маклорена
Решение
Для определения интервала сходимости мы используем критерий соотношения. Так как
имеем
для всех x . Следовательно, ряд сходится абсолютно для всех x , и, таким образом, интервал сходимости равен (−∞,∞).(−∞,∞). Чтобы показать, что ряд сходится к e x для всех x , мы используем тот факт, что f(n)(x)=exf(n)(x)=ex для всех n≥0n≥0 и e x — возрастающая функция на (−∞,∞).(−∞,∞). Следовательно, для любого действительного числа b максимальное значение e x для всех |x|≤b|x|≤b равно e b . Таким образом,
Следовательно, ряд сходится абсолютно для всех x , и, таким образом, интервал сходимости равен (−∞,∞).(−∞,∞). Чтобы показать, что ряд сходится к e x для всех x , мы используем тот факт, что f(n)(x)=exf(n)(x)=ex для всех n≥0n≥0 и e x — возрастающая функция на (−∞,∞).(−∞,∞). Следовательно, для любого действительного числа b максимальное значение e x для всех |x|≤b|x|≤b равно e b . Таким образом,
Поскольку мы только что показали, что
сходится для всех x , по критерию расходимости мы знаем, что
для любого действительного числа x . Комбинируя этот факт с теоремой о сжатии, получаем limn→∞Rn(x)=0.limn→∞Rn(x)=0.
Комбинируя этот факт с теоремой о сжатии, получаем limn→∞Rn(x)=0.limn→∞Rn(x)=0.
Чтобы применить тест отношения, рассмотрим
Поскольку
для всех x , мы получить интервал сходимости в виде (−∞,∞).(−∞,∞). Чтобы показать, что ряд Маклорена сходится к sinx,sinx, посмотрите на Rn(x).Rn(x). Для каждого x существует действительное число c между 0 и x так, что
Так как |f(n+1)(c)|≤1|f(n+1)(c)|≤1 для всех целых чисел n и всех действительных чисел c , мы имеем
для всех действительных чисел x . Используя ту же идею, что и в части а., результат limn→∞Rn(x)=0limn→∞Rn(x)=0 для всех x , и, следовательно, ряд Маклорена для sinxsinx сходится к sinxsinx для всех вещественных х .
Используя ту же идею, что и в части а., результат limn→∞Rn(x)=0limn→∞Rn(x)=0 для всех x , и, следовательно, ряд Маклорена для sinxsinx сходится к sinxsinx для всех вещественных х . Контрольно-пропускной пункт
6.15
Студенческий проект
Доказательство того, что
e иррационально Поэтому на следующих шагах мы предполагаем, что e=r/se=r/s для некоторых целых чисел r и s , где s≠0.s≠0.
Поэтому на следующих шагах мы предполагаем, что e=r/se=r/s для некоторых целых чисел r и s , где s≠0.s≠0. n=0 ,1,2,3,4.
n=0 ,1,2,3,4.
Раздел 6.3 Упражнения
 |Rn|≤11000. Найти значение многочлена Тейлора p n функции ff в указанной точке.
|Rn|≤11000. Найти значение многочлена Тейлора p n функции ff в указанной точке. ∫01sinπtπtdt.
∫01sinπtπtdt. a±R. Оцените максимальное значение R такое, что max|f″(z)|2R2≤0,1max|f″(z)|2R2≤0,1 на [a−R,a+R][a−R,a+R ] путем построения этого максимума как функции R .
a±R. Оцените максимальное значение R такое, что max|f″(z)|2R2≤0,1max|f″(z)|2R2≤0,1 на [a−R,a+R][a−R,a+R ] путем построения этого максимума как функции R .



 ln(2).
ln(2). Использование ряда Маклорена/Тейлора для аппроксимации определенного интеграла
 В этом видео я использую ряды Маклорена/Тейлора и теорему об оценке чередующихся рядов для аппроксимации определенного интеграла с требуемой точностью.
В этом видео я использую ряды Маклорена/Тейлора и теорему об оценке чередующихся рядов для аппроксимации определенного интеграла с требуемой точностью. Курсовые лекции
Что такое последовательность? Основная информация о последовательности
Патрик ДжонсЧто такое последовательность? Основная информация о последовательности. В этом видео я рассказываю, что такое последовательность, что означает сходимость или расхождение последовательности, и привожу несколько примеров.
Последовательности — примеры, показывающие конвергенцию или дивергенцию
Патрик ДжонсПоследовательности — Примеры, показывающие конвергенцию или дивергенцию.
Обозначение суммирования
Патрик ДжонсОбозначение суммирования — Обозначение суммирования объясняется на множестве примеров!
Что такое серия
Патрик ДжонсЧто такое серия? Я пытаюсь дать общее представление о том, что такое серия.
 Я также кратко обсуждаю геометрические ряды и тест на дивергенцию.
Я также кратко обсуждаю геометрические ряды и тест на дивергенцию.Геометрические ряды и критерий расходимости. Часть 1
Патрик ДжонсГеометрический ряд и тест на дивергенцию — В этом видео есть дополнительные примеры!
Геометрические ряды и критерий расходимости. Часть 2
Патрик ДжонсГеометрический ряд и тест на дивергенцию — Часть 2. В этом видео я заканчиваю задачу, которую обрезали!
Геометрический ряд. Выражение десятичной дроби в виде рационального числа
Патрик ДжонсГеометрический ряд — Выражение десятичной дроби в виде рационального числа.
 В этом видео я покажу как преобразовать число 5.1212121212….. в дробь с помощью геометрического ряда.
В этом видео я покажу как преобразовать число 5.1212121212….. в дробь с помощью геометрического ряда.Телескопическая серия Пример
Патрик ДжонсПример телескопического ряда. Нахождение суммы телескопического ряда.
Отображение расходимости ряда с использованием частичных сумм
Патрик ДжонсОтображение расходимости ряда с использованием частичных сумм
Использование интегрального теста для серии
Патрик ДжонсИспользование интегрального теста для рядов — один полный пример. Я ВСЕ оправдываю!
Оценка остатка для интегрального теста
Патрик ДжонсОценка остатка для интегрального теста.
 В этом видео я показываю оценку остатка для интегрального теста, показываю, что ряд сходится с помощью интегрального теста, а затем оцениваю ошибку этого ряда, используя первые 10 членов.
В этом видео я показываю оценку остатка для интегрального теста, показываю, что ряд сходится с помощью интегрального теста, а затем оцениваю ошибку этого ряда, используя первые 10 членов.Предельное сравнительное испытание и прямое сравнительное испытание (часть 1)
Патрик ДжонсТест предельного сравнения и тест прямого сравнения — Использование теста предельного сравнения и теста прямого сравнения для определения сходимости или расходимости ряда.
Предельное сравнительное испытание и прямое сравнительное испытание (часть 2)
Патрик ДжонсИспользование критерия предельного сравнения для определения, сходится ряд или расходится.
Чередующиеся серии
Патрик ДжонсОсновная идея того, как показать, что чередующийся ряд сходится.
 Показан очень ПРОСТОЙ пример!
Показан очень ПРОСТОЙ пример!Дополнительные примеры чередующихся рядов
Патрик ДжонсДополнительные примеры чередующихся рядов — определение того, сходится или расходится заданный чередующийся ряд.
Теорема об оценке чередующихся рядов
Патрик ДжонсТеорема об оценке чередующихся рядов. Показана основная идея вместе с парой примеров.
Использование теста отношений для определения сходимости ряда #1
Патрик ДжонсИспользование теста отношения для определения сходимости или расходимости ряда — показаны два примера. В другом видео показаны еще два примера!
Использование теста отношений для определения сходимости ряда #2
Патрик ДжонсИспользование теста отношений для определения сходимости ряда № 2.
 Показаны еще два примера использования теста отношений.
Показаны еще два примера использования теста отношений.Использование теста отношений для определения сходимости ряда #3 (факториалы)
Патрик ДжонсИспользование теста отношения для определения сходится ли ряд № 3 — Еще один пример использования теста отношения ряда, содержащего факториалы.
Корневой тест для серии
Патрик ДжонсКорневой тест для ряда — Использование корневого теста для определения сходимости или расходимости ряда! Показан тест вместе с 3 полными примерами!
Серия «Стратегия тестирования» — серия практических задач
Патрик ДжонсСтратегия тестирования серии — Серия практических задач.
 В этом видео я рассматриваю 14 серий задач, обсуждая, что бы я сделал, чтобы показать, что они сходятся или расходятся. Я пытаюсь показать, о чем я думаю, когда смотрю сериал, и что мне «прилипает» к тому, как я должен оправдывать происходящее.
В этом видео я рассматриваю 14 серий задач, обсуждая, что бы я сделал, чтобы показать, что они сходятся или расходятся. Я пытаюсь показать, о чем я думаю, когда смотрю сериал, и что мне «прилипает» к тому, как я должен оправдывать происходящее.Абсолютная сходимость, условная сходимость и дивергенция
Патрик ДжонсАбсолютная сходимость, условная сходимость и расходимость рядов. В этом видео я даю основной результат и делаю 3 примера!
Серия Power Представление функций
Патрик ДжонсПредставление функций в степенном ряду. В этом видео я использую представление степенного ряда 1/(1-x) для получения представления степенного ряда других функций
Степенной ряд — нахождение интервала сходимости
Патрик ДжонсPower Series — Нахождение интервала сходимости — показаны два полных примера!
Радиус сходимости для серии Power
Патрик ДжонсРадиус сходимости для степенного ряда.
 В этом видео я обсуждаю, как найти радиус сходимости. Это легко после того, как вы найдете ИНТЕРВАЛ сходимости.
В этом видео я обсуждаю, как найти радиус сходимости. Это легко после того, как вы найдете ИНТЕРВАЛ сходимости.Серия дифференциации и интеграции Power
Патрик ДжонсДифференциация и интегрирование степенных рядов. Показаны два примера интегрирования или дифференцирования известного степенного ряда для получения представления степенного ряда для новой функции.
Нахождение суммы ряда дифференцированием
Патрик ДжонсНахождение суммы ряда дифференцированием. Хорошо, я думаю, что это своего рода «сложная» проблема! Здесь мы находим сумму ряда путем дифференцирования известного степенного ряда, чтобы получить исходный ряд в более узнаваемой форме.
Нахождение степенного ряда путем дифференцирования — 3 примера
Патрик ДжонсНахождение степенного ряда путем дифференцирования — 3 примера.
 В этом видео я беру производную степенного ряда для 1/(1-x), чтобы создать новые представления степенного ряда.
В этом видео я беру производную степенного ряда для 1/(1-x), чтобы создать новые представления степенного ряда.Интеграция серии Power
Патрик ДжонсВ этом видео я делаю простой пример интегрирования степенного ряда. Это полезный трюк, так как мы часто делаем это, чтобы найти новые представления степенных рядов, интегрируя известные представления степенных рядов.
Интеграция серии Power, пример 2
Патрик ДжонсЕще один пример интегрирования степенного ряда для поиска нового представления степенного ряда.
Нахождение интервала сходимости для заданного представления степенного ряда
Патрик ДжонсНахождение интервала сходимости для заданного представления степенного ряда.
 В этом видео мы находим интервал сходимости для заданного степенного ряда.
В этом видео мы находим интервал сходимости для заданного степенного ряда.Интервал и радиус сходимости ряда, пример 3
Патрик ДжонсИнтервал и радиус сходимости для ряда, пример 3. В этом видео я показываю еще один пример нахождения интервала и радиуса сходимости для ряда.
Интервал и радиус сходимости ряда, пример 4
Патрик ДжонсИнтервал и радиус сходимости для ряда, упр. 4. Еще один пример, где я нахожу радиус и интервал сходимости для степенного ряда.
Интервал и радиус сходимости для ряда, пример 5
Патрик ДжонсИнтервал и радиус сходимости для ряда, пример 5.
 Еще один пример нахождения радиуса и интервала сходимости для степенного ряда.
Еще один пример нахождения радиуса и интервала сходимости для степенного ряда.Интервал и радиус сходимости ряда, пример 6
Патрик ДжонсИнтервал и радиус сходимости для ряда, пример 6. Еще один пример нахождения радиуса и интервала сходимости для степенного ряда.
Интервал и радиус сходимости ряда, пример 7
Патрик ДжонсИнтервал и радиус сходимости для ряда, упр. 7. Еще один пример нахождения радиуса и интервала сходимости для степенного ряда
Интервал и радиус сходимости для ряда, пример 9
Патрик ДжонсИнтервал и радиус сходимости для ряда, упр.
 x, и мы используем его, чтобы найти новый степенной ряд.
x, и мы используем его, чтобы найти новый степенной ряд.Нахождение представлений степенного ряда путем манипулирования 1/(1-x) — еще один пример 1
Патрик Джонс1/(1-x) — Еще один пример 1. Здесь я иллюстрирую идею создания новых степенных рядов путем манипулирования известными степенными рядами.
Нахождение нового степенного ряда путем манипулирования известным степенным рядом, пример 2 92.
Поиск расширения ряда Маклорена — еще один пример 1
Патрик ДжонсПоиск расширения ряда Маклорена — еще один пример 1. В этом видео я нахожу расширение ряда Маклорена для 1/(1-x).
Теорема Тейлора об остатке.
 Нахождение остатка, пример 1 Патрик Джонс
Нахождение остатка, пример 1 Патрик ДжонсТеорема Тейлора об остатке. Нахождение остатка, упр. 1. В этом примере я использую теорему Тейлора об остатке, чтобы найти выражение для остатка.
Теорема Тейлора об остатке. Нахождение остатка, пример 2
Патрик ДжонсТеорема Тейлора об остатке. Нахождение остатка, упр. 2. В этом примере я использую теорему Тейлора об остатке, чтобы найти выражение для остатка.
Теорема Тейлора об остатке. Нахождение остатка, пример 3
Патрик ДжонсТеорема Тейлора об остатке. Нахождение остатка, упр. 3. В этом примере я использую теорему Тейлора об остатке, чтобы найти выражение для остатка.

Нахождение полинома Маклорена — упр. 1 9(4 раза).
Нахождение полинома Маклорена — пример 2
Патрик ДжонсНахождение полинома Маклорена — Упр. 2. В этом примере я нахожу полином Маклорена третьей степени для аппроксимации функции.
Нахождение полинома Тейлора для аппроксимации функции, пример 1
Патрик ДжонсВ этом видео я нахожу полином Тейлора степени 3 для аппроксимации sin(x).
Корневой тест — еще один пример, №3
Патрик ДжонсКорневой тест — еще один пример, №3.
 Просто еще один пример, показывающий, что ряд сходится или расходится с использованием корневого теста.
Просто еще один пример, показывающий, что ряд сходится или расходится с использованием корневого теста.Нахождение полинома Тейлора для аппроксимации функции, пример 2
Патрик ДжонсНахождение полинома Тейлора для аппроксимации функции, пример 2. В этом видео я нахожу полином Тейлора степени 4 для аппроксимации функции.
Нахождение полинома Тейлора для аппроксимации функции, пример 3
Патрик ДжонсНахождение полинома Тейлора для аппроксимации функции, пример 3. В этом примере я нахожу полином Тейлора третьей степени для аппроксимации заданной функции.
Нахождение полинома Тейлора для аппроксимации функции, пример 4
Патрик ДжонсНахождение полинома Тейлора для аппроксимации функции, пример 4.
 В этом примере я нахожу полином Тейлора степени 2 для аппроксимации кроватки (x).
В этом примере я нахожу полином Тейлора степени 2 для аппроксимации кроватки (x).Корневой тест — еще один пример, № 2
Патрик ДжонсКорневой тест — еще один пример, №2. Просто еще один пример, показывающий, что ряд сходится или расходится с использованием корневого теста.
Тест соотношения, еще один пример #1
Патрик ДжонсТест соотношения , еще один пример №1. Просто еще один пример использования теста отношения, чтобы определить, сходится ряд или расходится.
Тест соотношения, еще один пример #2
Патрик ДжонсТест соотношения, еще один пример №2.
 Просто еще один пример использования теста отношения, чтобы определить, сходится ряд или расходится.
Просто еще один пример использования теста отношения, чтобы определить, сходится ряд или расходится.Тест соотношения, еще один пример #3
Патрик ДжонсТест соотношения, еще один пример №3. Просто еще один пример, показывающий, что ряд сходится или расходится с использованием теста отношения.
Тест соотношения, еще один пример #4
Патрик ДжонсТест соотношения , еще один пример №4. Просто еще один пример, показывающий, что ряд сходится или расходится с использованием теста отношения.
Абсолютная сходимость, Условная сходимость, Другой пример 1
Патрик ДжонсАбсолютная сходимость, условная сходимость, еще один пример 1.
 Здесь мы рассмотрим еще несколько примеров, чтобы определить, является ли ряд абсолютно сходящимся, условно сходящимся или расходящимся.
Здесь мы рассмотрим еще несколько примеров, чтобы определить, является ли ряд абсолютно сходящимся, условно сходящимся или расходящимся.Абсолютная сходимость, Условная сходимость, Другой пример 2
Патрик ДжонсАбсолютная сходимость, условная сходимость, еще один пример 2. Здесь мы рассмотрим еще несколько примеров, чтобы определить, является ли ряд абсолютно сходящимся, условно сходящимся или расходящимся.
Абсолютная сходимость, Условная сходимость, Другой пример 3
Патрик ДжонсАбсолютная сходимость, условная сходимость, еще один пример 3. Здесь мы рассмотрим еще несколько примеров, чтобы определить, является ли ряд абсолютно сходящимся, условно сходящимся или расходящимся.

Чередующиеся ряды — еще один пример 1
Патрик ДжонсПеремежающийся ряд — еще один пример 1. В этом видео я показываю, что знакопеременный ряд сходится или расходится.
Чередующиеся ряды — еще один пример 2
Патрик ДжонсПеремежающийся ряд — Другой пример 2. В этом видео я показываю, что знакопеременный ряд сходится или расходится.
Чередующиеся серии — еще один пример 3
Патрик ДжонсПеремежающийся ряд — еще один пример 3. Еще один пример, показывающий, что чередующийся ряд сходится или расходится.
Чередующиеся ряды — еще один пример 4
Патрик ДжонсЧередующийся ряд — еще один пример 4.
 Еще один пример, показывающий, что чередующийся ряд сходится или расходится.
Еще один пример, показывающий, что чередующийся ряд сходится или расходится.Введение в нотацию суммирования и бесконечные ряды, пример 1
Патрик ДжонсВведение в нотацию суммирования и бесконечные ряды, пример 1. Забыли нотацию суммирования? Вот небольшой освежающий пример! Обратите внимание, что «i» не имеет ничего общего с комплексными числами.
Сравнительный тест предельных значений для серий — другой пример 1
Патрик ДжонсПредельный сравнительный тест для рядов — еще один пример 1. В этом видео я использую предельный сравнительный тест, чтобы определить, сходится или расходится данный ряд.
Сравнительный тест предельных значений для серий — еще один пример 2
Патрик ДжонсПредельный сравнительный тест для рядов — еще один пример 2.
 В этом видео я использую предельный сравнительный тест, чтобы определить, сходится или расходится данный ряд.
В этом видео я использую предельный сравнительный тест, чтобы определить, сходится или расходится данный ряд.Сравнительный тест предельных значений для серий — другой пример 3
Патрик ДжонсПредельный сравнительный тест для рядов — еще один пример 3. В этом видео я использую предельный сравнительный тест, чтобы определить, сходится или расходится данный ряд.
Сравнительный тест предельных значений для серий — другой пример 4
Патрик ДжонсПредельный сравнительный тест для рядов — еще один пример 4. В этом видео я использую предельный сравнительный тест, чтобы определить, сходится или расходится данный ряд.
Предельный сравнительный тест для серий — еще один пример 5
Патрик ДжонсПредельный сравнительный тест для рядов — еще один пример 5.
 В этом видео я использую предельный сравнительный тест, чтобы определить, сходится или расходится данный ряд.
В этом видео я использую предельный сравнительный тест, чтобы определить, сходится или расходится данный ряд.Введение в монотонные и ограниченные последовательности, Пример 1
Патрик ДжонсВведение в монотонные и ограниченные последовательности, пример 1. Небольшой вопрос, чтобы решить, является ли последовательность монотонной и/или ограниченной.
Теорема сжатия и теорема об абсолютном значении, №1
Патрик ДжонсТеорема сжатия и теорема об абсолютном значении, №1. Здесь мы рассмотрим нахождение пределов некоторых последовательностей с помощью теорем сжатия и/или абсолютного значения.
Теорема сжатия и теорема об абсолютном значении, № 2
Патрик ДжонсТеорема сжатия и теорема об абсолютном значении, №2.
 Просто еще один пример нахождения предела последовательности с использованием теоремы сжатия и/или абсолютного значения.
Просто еще один пример нахождения предела последовательности с использованием теоремы сжатия и/или абсолютного значения.Теорема сжатия и теорема об абсолютном значении, № 3
Патрик ДжонсТеорема сжатия и теорема об абсолютном значении, №3. Здесь мы находим предел другой последовательности, используя теорему сжатия.
Нахождение предела последовательности, еще 3 примера
Патрик ДжонсНахождение предела последовательности, еще 3 примера, №1. Просто еще один пример нахождения предела последовательности, когда n приближается к бесконечности.
Умножение и деление степени, ряд
Патрик ДжонсУмножение и деление степенных рядов — Использование умножения и деления степенных рядов для получения представлений степенных рядов для других функций!
Серия Тейлора и Маклорена – Пример 1
Патрик ДжонсРяд Тейлора и Маклорена — Показан пример нахождения ряда Маклорена для функции.
 В другом видео я найду продолжение серии Тейлор, так что ищите и его!
В другом видео я найду продолжение серии Тейлор, так что ищите и его!Серия Taylor / Maclaurin для Sin (x)
Патрик ДжонсСерия Тейлора / Маклорена для греха (x). В этом видео я показываю, как найти представление в степенной ряд для sin(x), используя разложение в ряд Тейлора/Маклорена.
Серия Тейлора и Маклорена — пример 2
Патрик ДжонсРяды Тейлора и Маклорена. Показан полный пример нахождения ряда Тейлора для функции ln(x) с центром в точке a = 2.
Использование рядов для оценки пределов
Патрик ДжонсИспользование ряда для оценки пределов.
 В этом примере я показываю, как можно использовать разложение в ряд и немного алгебры для вычисления предела.
В этом примере я показываю, как можно использовать разложение в ряд и немного алгебры для вычисления предела.Использование ряда Маклорена/Тейлора для аппроксимации определенного интеграла
Патрик ДжонсИгра
Использование ряда Маклорена/Тейлора для приближения определенного интеграла к желаемой точности. В этом видео я использую ряды Маклорена/Тейлора и теорему об оценке чередующихся рядов для аппроксимации определенного интеграла с требуемой точностью.
Биномиальный ряд — пример 1
Патрик ДжонсИспользование биномиального ряда для получения представления степенного ряда для другой функции. Показан один пример!
Биномиальный ряд — пример 2
Патрик Джонс 92) ] / x путем интегрирования соответствующего степенного ряда для функции.
Нахождение представления степенного ряда для логарифмической функции
Патрик ДжонсНахождение представления степенного ряда для логарифма. Здесь мы находим представление в виде степенного ряда для функции, включающей функцию натурального логарифма.
Поиск функции, соответствующей заданному степенному ряду, путем интегрирования
Патрик ДжонсВ этом примере нам дано представление степенного ряда для cos(x) и мы используем его, чтобы найти функцию, которая соответствует новому заданному расширению ряда.
Нахождение степенного ряда дифференцированием
Патрик ДжонсВ этом видео нам дается представление степенного ряда для sin(x) и мы используем его, чтобы найти представление степенного ряда для: xcos(x) – sin(x)
Интервал и радиус сходимости для ряда, пример 2
Патрик ДжонсИнтервал и радиус сходимости для ряда, пример 2.
 В этом видео я показываю еще один пример нахождения интервала и радиуса сходимости для ряда.
В этом видео я показываю еще один пример нахождения интервала и радиуса сходимости для ряда.Тест прямого сравнения — другой пример 2
Патрик ДжонсТест прямого сравнения — еще один пример 2. В этом видео я показываю, что другой ряд сходится или расходится, используя теорему прямого сравнения.
Тест прямого сравнения — другой пример 1
Патрик ДжонсТест прямого сравнения — еще один пример 1. В этом видео я показываю, что другой ряд сходится или расходится, используя теорему прямого сравнения.
Тест прямого сравнения — другой пример 3
Патрик ДжонсТест прямого сравнения — еще один пример 3.
 В этом видео я показываю, что другой ряд сходится или расходится, используя теорему прямого сравнения.
В этом видео я показываю, что другой ряд сходится или расходится, используя теорему прямого сравнения.Серия P
Патрик ДжонсВ этом видео я рассматриваю несколько ОЧЕНЬ простых р-серий. Я привожу формулу, показывающую, какие р-ряды сходятся, а какие расходятся. НИЧЕГО ТЯЖЕЛОГО!!! Вы можете обосновать эти результаты, используя интегральный тест.
Интегральный тест для оценки серии, Ex 4
Патрик ДжонсИнтегральный тест для оценки ряда, пример 4. Еще один пример использования интегрального теста для оценки ряда.
Интегральный тест для оценки серии, Ex 3
Патрик ДжонсИнтегральный тест для оценки ряда, пример 3.
 В этом видео я показываю, что другой ряд сходится или расходится, используя интегральный тест для ряда.
В этом видео я показываю, что другой ряд сходится или расходится, используя интегральный тест для ряда.Интегральный тест для оценки серии, Ex 2
Патрик ДжонсИнтегральный тест для оценки ряда, пример 2. В этом видео я показываю другой пример использования интегрального теста, чтобы показать, сходится или расходится ряд. Обосновываю все шаги (непрерывный, положительный, убывающий).
Интегральный тест для оценки серии, Ex 1
Патрик ДжонсИнтегральный тест для оценки ряда, пример 1. В этом видео я показываю, как оценивать ряд с помощью интегрального теста.
Телескопическая серия, показывающая расхождение с использованием частичных сумм
Патрик ДжонсТелескопическая серия, показывающая расхождение с использованием частичных сумм.
 Здесь я нахожу формулу частичной суммы геометрического ряда и показываю, что этот ряд расходится.
Здесь я нахожу формулу частичной суммы геометрического ряда и показываю, что этот ряд расходится.Телескопическая серия, нахождение суммы, пример 1
Патрик ДжонсТелескопический ряд , Нахождение суммы, Пример 1. Здесь я нахожу формулу для телескопического ряда, использую частичные дроби для разложения формулы, смотрю на частичные суммы и беру предел, чтобы найти сумму.
Сумма бесконечного геометрического ряда, пример 3
Патрик ДжонсСумма бесконечного геометрического ряда, пример 3. В этом видео я делаю еще один пример нахождения суммы сходящегося бесконечного ряда.
Сумма бесконечного геометрического ряда, пример 2
Патрик ДжонсСумма бесконечного геометрического ряда, пример 2.
 В этом видео я показываю, как найти значение суммы двух сходящихся бесконечных рядов.
В этом видео я показываю, как найти значение суммы двух сходящихся бесконечных рядов.Сумма бесконечного геометрического ряда, пример 1
Патрик ДжонсСумма бесконечного геометрического ряда, пример 1. В этом видео я показываю, как найти сумму сходящегося бесконечного ряда.
Запись геометрического ряда с использованием сигма/суммирования, пример 2
Патрик ДжонсНаписание геометрического ряда с использованием сигма/суммирования, пример 2. В этом видео показано, как написать бесконечный геометрический ряд с использованием сигма/суммирования. Я не нахожу фактической суммы для этого конкретного сходящегося геометрического ряда.
Нахождение формулы частичной суммы телескопического ряда
Патрик ДжонсНахождение формулы частичной суммы телескопического ряда.
 Чтобы оценить телескопический ряд, обычно находят выражение для частичной суммы, а затем берут предел этой частичной суммы. В этом видео я покажу, как найти формулу частичной суммы. Я не беру предел, чтобы получить значение соответствующего бесконечного ряда (хотя вы можете сделать это, просто беря предел в бесконечности конечного выражения, которое я нахожу)
Чтобы оценить телескопический ряд, обычно находят выражение для частичной суммы, а затем берут предел этой частичной суммы. В этом видео я покажу, как найти формулу частичной суммы. Я не беру предел, чтобы получить значение соответствующего бесконечного ряда (хотя вы можете сделать это, просто беря предел в бесконечности конечного выражения, которое я нахожу)Запись геометрического ряда с использованием сигмы/суммирования
Патрик ДжонсНаписание геометрического ряда с использованием сигмы/суммирования. В этом видео показано, как записать бесконечный геометрический ряд: 1 + 0,1 + 0,01 + 0,001+ ….используя сигму/суммирование. Я не нахожу фактической суммы для этого конкретного сходящегося геометрического ряда.
Тест на расходимость рядов, два примера
Патрик ДжонсТест на расходимость рядов, два примера.
 В этом видео я обсуждаю тест на расхождение и показываю два примера рядов, которые расходятся с помощью теста на расхождение.
В этом видео я обсуждаю тест на расхождение и показываю два примера рядов, которые расходятся с помощью теста на расхождение.Тест прямого сравнения — другой пример 4
Патрик ДжонсТест прямого сравнения — еще один пример 4. В этом видео я показываю, что другой ряд сходится или расходится, используя теорему прямого сравнения.
Тест прямого сравнения — другой пример 5
Патрик ДжонсТест прямого сравнения — еще один пример 5. В этом видео я показываю, что другой ряд сходится или расходится, используя теорему прямого сравнения.
Корневой тест — еще один пример, № 1
Патрик ДжонсКорневой тест — еще один пример, №1.
 Просто еще один пример, показывающий, что ряд сходится или расходится с использованием корневого теста.
Просто еще один пример, показывающий, что ряд сходится или расходится с использованием корневого теста.Чередующиеся серии — оценка ошибки № 2
Патрик ДжонсЧередование серий — оценка ошибки №2. В этом видео я суммирую первые несколько членов переменного ряда, а затем нахожу максимальную ошибку.
Чередующиеся серии — оценка погрешности
Патрик ДжонсЧередующийся ряд — оценка погрешности. В этом примере я нахожу необходимое количество членов, чтобы мы могли оценить значение нашего сходящегося чередующегося ряда с точностью до двух знаков после запятой.
Сравнительный тест предельных значений для серий — другой пример 6
Патрик ДжонсПредельный сравнительный тест для рядов — еще один пример 6.
 В этом видео я использую предельный сравнительный тест, чтобы определить, сходится или расходится данный ряд.
В этом видео я использую предельный сравнительный тест, чтобы определить, сходится или расходится данный ряд.Предельный сравнительный тест для серий — еще один пример 7
Патрик ДжонсПредельный сравнительный тест для рядов — еще один пример 7. В этом видео я использую предельный сравнительный тест, чтобы определить, сходится или расходится данный ряд.
Сравнительный тест предельных значений для серий — другой пример 8
Патрик ДжонсПредельный сравнительный тест для рядов — еще один пример 8. В этом видео я использую предельный сравнительный тест, чтобы определить, сходится или расходится данный ряд.
Исчисление II — серия Тейлора
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-16: Серия Taylor
В предыдущем разделе мы начали рассматривать запись функции в виде степенного ряда. Проблема с подходом в этом разделе заключается в том, что все сводилось к необходимости каким-то образом связать функцию с
. \[\frac{1}{{1 — x}}\]
, и хотя есть много функций, которые могут быть связаны с этой функцией, есть еще много других, которые просто не могут быть связаны с этой.
Итак, ничего не отвлекая от процесса, который мы рассмотрели в предыдущем разделе, нам нужно придумать более общий метод записи представления степенного ряда для функции. 94} + \cdots\]
94} + \cdots\]
Далее нам нужно будет предположить, что функция \(f\left( x \right)\) имеет производные любого порядка и что мы можем найти их все.
Теперь, когда мы предположили, что представление в виде степенного ряда существует, нам нужно определить, каковы коэффициенты \({c_n}\). Это проще, чем может показаться на первый взгляд. Давайте сначала просто оценим все в \(x = a\). Это дает,
\[f\влево( а \вправо) = {c_0}\] 92} + \cdots \\ f»\left( a \right) & = 2{c_2}\end{align*}\]
Итак, похоже,
\[{c_2} = \frac{{f»\left( a \right)}}{2}\]
Использование третьей производной дает,
\[\begin{align*}f»’\left( x \right) & = 3\left( 2 \right){c_3} + 4\left( 3 \right)\left( 2 \right){c_4 }\left( {x — a} \right) + \cdots \\ f»’\left( a \right) & = 3\left( 2 \right){c_3}\hspace{0. i}} \]
9п}} \]
i}} \]
9п}} \]
\(n\) -й -й степени многочлена Тейлора является просто частичной суммой ряда.
Далее, остаток определяется как
\[{R_n}\влево( x \вправо) = f\влево( x \вправо) — {T_n}\влево( x \вправо)\]
Таким образом, остаток на самом деле просто ошибка между функцией \(f\left( x \right)\) и \(n\) полиномом Тейлора -й степени для заданного \(n\).
Обратите внимание, что с этим определением мы можем записать функцию как
\[f\влево( x \вправо) = {T_n}\влево( x \вправо) + {R_n}\влево( x \вправо)\]
Теперь у нас есть следующая Теорема.
Теорема
Предположим, что \(f\left( x \right) = {T_n}\left( x \right) + {R_n}\left( x \right)\). Тогда если,
\[\ mathop {\lim}\limits_{n \to \infty} {R_n}\left( x \right) = 0\] 9п}\]
Хорошо, теперь нам нужно обработать несколько примеров, которые не включают экспоненциальную функцию, так как они, как правило, требуют немного больше работы. {\ left ( 6 \ right)} }\left( 0 \right) = — 1\\ \vdots \,\,\,\,\,\,\,\,\,\, & & \hspace{0.5in} & \,\,\, \,\,\,\, \vdots \end{align*}\]
9{2n}}}}{{\left( {2n} \right)!}}} \]
{\ left ( 6 \ right)} }\left( 0 \right) = — 1\\ \vdots \,\,\,\,\,\,\,\,\,\, & & \hspace{0.5in} & \,\,\, \,\,\,\, \vdots \end{align*}\]
9{2n}}}}{{\left( {2n} \right)!}}} \]
Эта идея перенумерации членов ряда, как мы сделали в предыдущем примере, используется не так часто, но иногда очень полезна. Есть еще одна серия, где нам нужно это сделать, поэтому давайте посмотрим на нее, чтобы мы могли получить еще один пример перенумерации членов серии.
Пример 6. Найдите ряд Тейлора для \(f\left( x \right) = \sin \left( x \right)\) относительно \(x = 0\).
Показать решение 9{2n + 1}}}}{{\left( {2n + 1} \right)!}}} \]
Нам действительно нужно поработать еще один или два примера, в которых \(f\left( x \right)\) не относится к \(x = 0\).
Пример 7. Найдите ряд Тейлора для \(f\left( x \right) = \ln \left( x \right)\) относительно \(x = 2\). 2}}}\) относительно \(x = — 1\).
93}\конец{выравнивание*}\]
2}}}\) относительно \(x = — 1\).
93}\конец{выравнивание*}\]
При нахождении ряда Тейлора многочлена мы не делаем никакого упрощения правой части. Оставляем как есть. На самом деле, если бы мы все перемножили, мы просто вернулись бы к исходному многочлену!
Хотя не очевидно, что запись ряда Тейлора для многочлена полезна, бывают случаи, когда это необходимо сделать. Проблема в том, что они выходят за рамки этого курса и поэтому здесь не рассматриваются. Например, есть одно приложение к рядам в области дифференциальных уравнений, где это нужно делать время от времени.
Итак, к этому моменту мы видели довольно много примеров ряда Тейлора, и во всех из них мы смогли найти общие формулы для ряда. Так будет не всегда. Чтобы увидеть пример того, у которого нет общей формулы, посмотрите последний пример в следующем разделе.
Прежде чем покинуть этот раздел, остановимся на трех важных рядах Тейлора, которые мы получили в этом разделе и которые мы должны обобщить в одном месте.



 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления

 8):
8): Отсюда получаем или .
Отсюда получаем или .
 Итак, .
Итак, .
 Признаки сходимости знакопостоянных рядов. 7
Признаки сходимости знакопостоянных рядов. 7 Сущность недвижимости
Сущность недвижимости
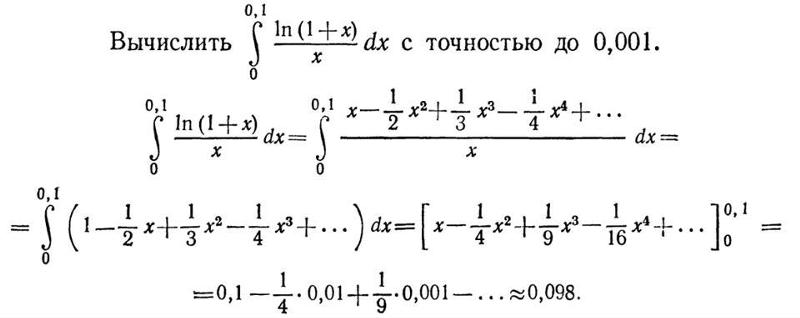 Следовательно,
Следовательно, f(x)=sinxf(0)=0f′(x)=cosxf′(0)=1f″(x)=−sinxf″(0)=0f‴(x)=−cosxf‴( 0)=−1f(4)(x)=sinxf(4)(0)=0.
f(x)=sinxf(0)=0f′(x)=cosxf′(0)=1f″(x)=−sinxf″(0)=0f‴(x)=−cosxf‴( 0)=−1f(4)(x)=sinxf(4)(0)=0. f(x)=cosxf(0)=1f′(x)=−sinxf′(0)=0f″(x)=−cosxf″(0)=−1f‴(x)=sinxf‴ (0)=0f(4)(x)=cosxf(4)(0)=1.
f(x)=cosxf(0)=1f′(x)=−sinxf′(0)=0f″(x)=−cosxf″(0)=−1f‴(x)=sinxf‴ (0)=0f(4)(x)=cosxf(4)(0)=1.

 |R2(11)|≤0,00114683!(11−8)3≈0,0065104.
|R2(11)|≤0,00114683!(11−8)3≈0,0065104.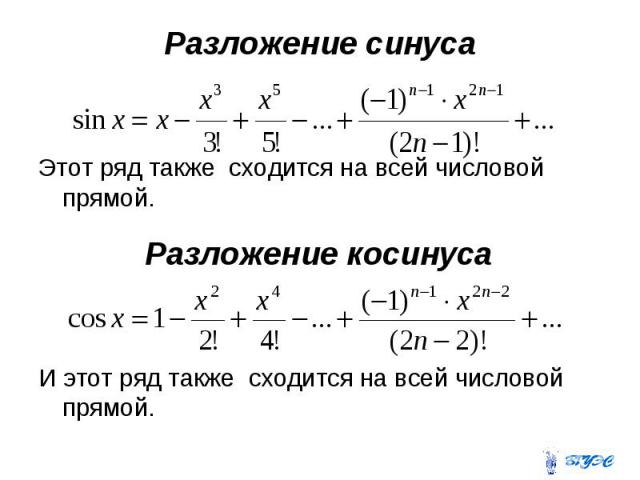 p5(x)=x−x33!+x55!.
p5(x)=x−x33!+x55!.