Arctg что это такое: Арктангенс, арккотангенс — свойства, графики, формулы

Содержание

Арктангенс, арккотангенс — свойства, графики, формулы

Арктангенс, arctg

Определение и обозначения

Арктангенс ( y = arctg x ): – это функция, обратная к тангенсу ( x = tg y ). Он имеет область определения и множество значений .
tg(arctg x) = x ;
arctg(tg x) = x .

Арктангенс обозначается так:
.

График функции арктангенс

График функции y = arctg x.

График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.

Арккотангенс, arcctg

Определение и обозначения

Арккотангенс ( y = arcctg x ): – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения и множество значений .
ctg(arcctg x) = x ;
arcctg(ctg x) = x .

Арккотангенс обозначается так:
.

График функции арккотангенс

График функции y = arcctg x.

График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.

Четность

Функция арктангенс является нечетной:
arctg(–x) = arctg(–tg arctg x) = arctg(tg(–arctg x)) = – arctg x

Функция арккотангенс не является четной или нечетной:
arcctg(–x) = arcctg(–ctg arcctg x) = arcctg(ctg(π–arcctg x)) = π – arcctg x ≠ ± arcctg x.

Свойства – экстремумы, возрастание, убывание

Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x. (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.

	y = arctg x	y = arcctg x
Область определения и непрерывность	– ∞ < x < + ∞	– ∞ < x < + ∞
Множество значений
Возрастание, убывание	монотонно возрастает	монотонно убывает
Максимумы, минимумы	нет	нет
Нули, y = 0	x = 0	нет
Точки пересечения с осью ординат, x = 0	y = 0	y = π/2
	–	π
		0

Таблица арктангенсов и арккотангенсов

В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.

x	arctg x		arcctg x
	град.	рад.	град.	рад.
– ∞	– 90°	–	180°	π
–	– 60°	–	150°
– 1	– 45°	–	135°
–	– 30°	–	120°
0	0°	0	90°
	30°		60°
1	45°		45°
	60°		30°
+ ∞	90°		0°	0

≈ 0,5773502691896258
≈ 1,7320508075688772

Формулы

См. Вывод формул обратных тригонометрических функций

Формулы суммы и разности

     при

     при

     при

Выражения через логарифм, комплексные числа

См. Вывод формул
,
.

Выражения через гиперболические функции

Производные

См. Вывод производных арктангенса и арккотангенса > > >

Производные высших порядков:
Пусть . Тогда производную n-го порядка арктангенса можно представить одним из следующих способов:
;
.
Символ означает мнимую часть стоящего следом выражения.

См. Вывод производных высших порядков арктангенса и арккотангенса > > >
Там же даны формулы производных первых пяти порядков.

Аналогично для арккотангенса. Пусть . Тогда
;
.

Интегралы

Делаем подстановку x = tg t и интегрируем по частям:
;
;
;

Выразим арккотангенс через арктангенс:
.

Разложение в степенной ряд

При |x| ≤ 1 имеет место следующее разложение:
;
.

Обратные функции

Обратными к арктангенсу и арккотангенсу являются тангенс и котангенс, соответственно.

Следующие формулы справедливы на всей области определения:
tg(arctg x) = x
ctg(arcctg x) = x .

Следующие формулы справедливы только на множестве значений арктангенса и арккотангенса:
arctg(tg x) = x при
arcctg(ctg x) = x при .

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов. Опубликовано: 14-07-2014 Изменено: 23-12-2018

Обратные тригонометрические функции и их графики

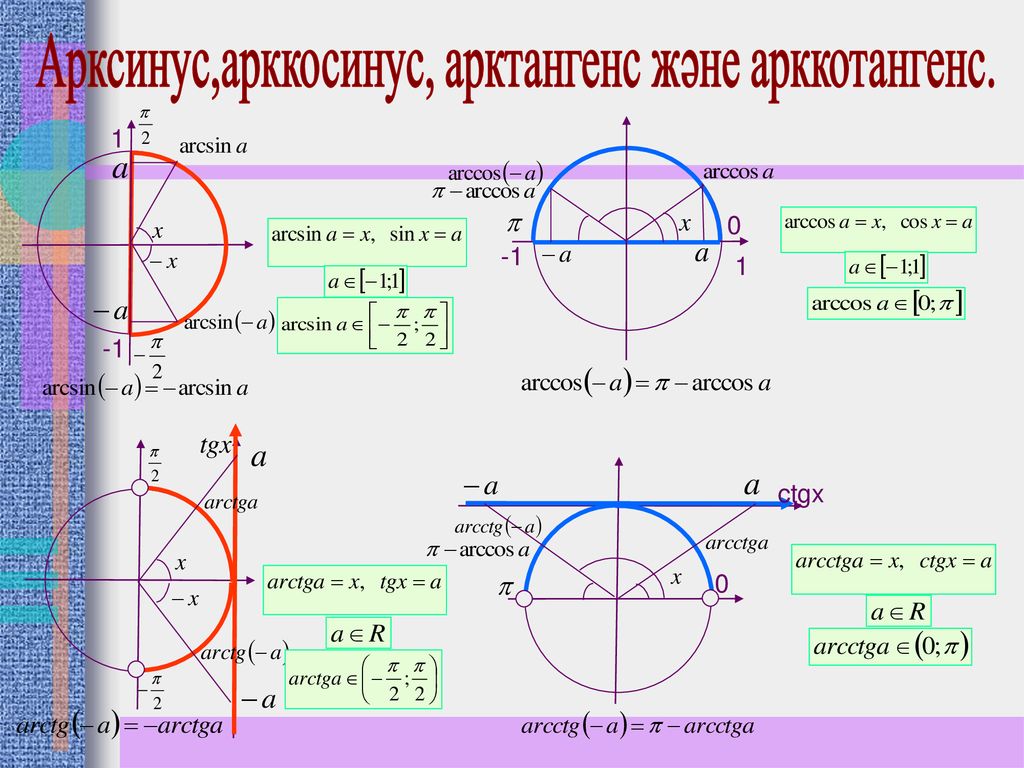
Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс.

Сначала дадим определения.

Арксинусом числа а называется число , такое, что Или, можно сказать, что это такой угол , принадлежащий отрезку , синус которого равен числу а.

Арккосинусом числа а называется число , такое, что

Арктангенсом числа а называется число , такое, что

Арккотангенсом числа а называется число , такое, что

Расскажем подробно об этих четырех новых для нас функциях — обратных тригонометрических.

Помните, мы уже встречались с обратными функциями.

Например, арифметический квадратный корень из числа а — такое неотрицательное число, квадрат которого равен а.

Логарифм числа b по основанию a — такое число с, что

При этом

Мы понимаем, для чего математикам пришлось «придумывать» новые функции. Например, решения уравнения — это и Мы не смогли бы записать их без специального символа арифметического квадратного корня.

Понятие логарифма оказалось необходимо, чтобы записать решения, например, такого уравнения: Решение этого уравнения — иррациональное число Это показатель степени, в которую надо возвести 2, чтобы получить 7.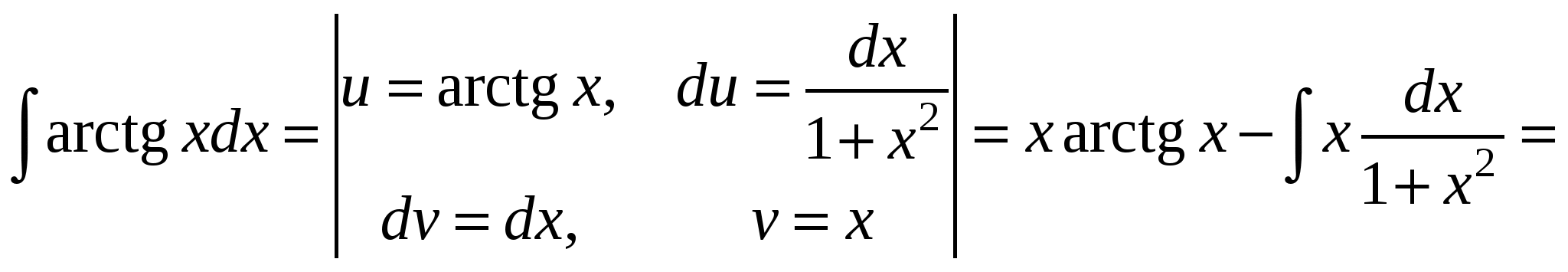

Так же и с тригонометрическими уравнениями. Например, мы хотим решить уравнение

Ясно, что его решения соответствуют точкам на тригонометрическом круге, ордината которых равна И ясно, что это не табличное значение синуса. Как же записать решения?

Здесь не обойтись без новой функции, обозначающей угол, синус которого равен данному числу a. Да, все уже догадались. Это арксинус.

Угол, принадлежащий отрезку , синус которого равен — это арксинус одной четвертой. И значит, серия решений нашего уравнения, соответствующая правой точке на тригонометрическом круге, — это

А вторая серия решений нашего уравнения — это

Подробнее о решении тригонометрических уравнений — здесь.

Осталось выяснить — зачем в определении арксинуса указывается, что это угол, принадлежащий отрезку ?

Дело в том, что углов, синус которых равен, например, , бесконечно много. Нам нужно выбрать какой-то один из них. Мы выбираем тот, который лежит на отрезке .

Взгляните на тригонометрический круг.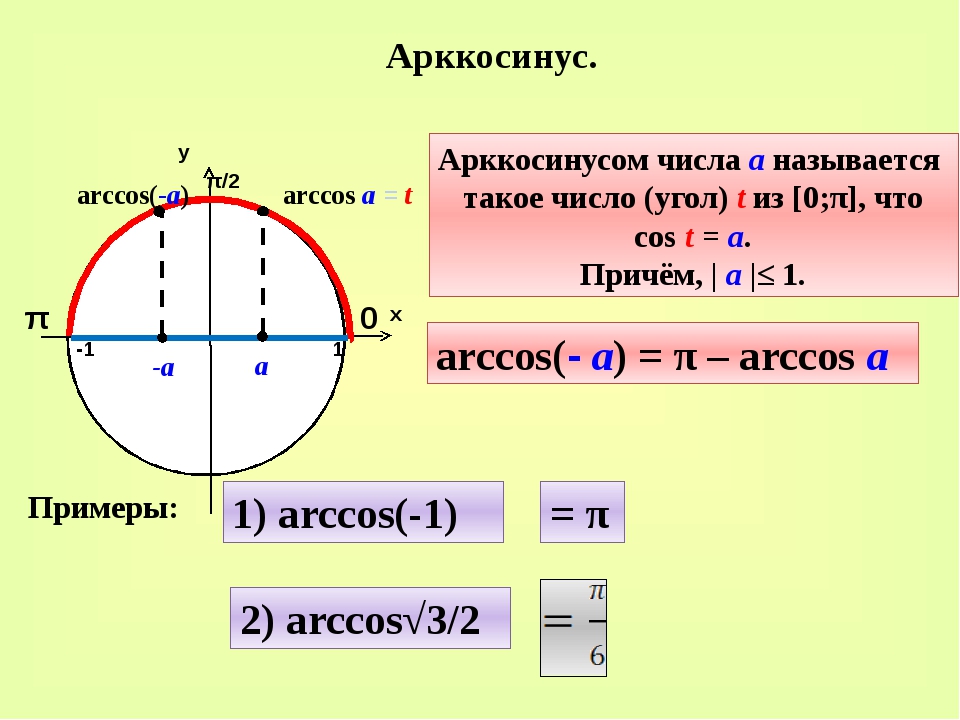 Вы увидите, что на отрезке каждому углу соответствует определенное значение синуса, причем только одно. И наоборот, любому значению синуса из отрезка отвечает одно-единственное значение угла на отрезке . Это значит, что на отрезке можно задать функцию принимающую значения от до

Повторим определение еще раз:

Арксинусом числа a называется число , такое, что

Обозначение: Область определения арксинуса — отрезок Область значений — отрезок .

Можно запомнить фразу «арксинусы живут справа». Не забываем только, что не просто справа, но ещё и на отрезке .

Мы готовы построить график функции

Как обычно, отмечаем значения х по горизонтальной оси, а значения у — по вертикальной.

Поскольку , следовательно, х лежит в пределах от -1 до 1.

Значит, областью определения функции y = arcsin x является отрезок

Мы сказали, что у принадлежит отрезку . Это значит, что областью значений функции y = arcsin x является отрезок .

Заметим, что график функции y=arcsinx весь помещается в области, ограниченной линиями и

Как всегда при построении графика незнакомой функции, начнем с таблицы.

По определению, арксинус нуля — это такое число из отрезка , синус которого равен нулю. Что это за число? — Понятно, что это ноль.

Аналогично, арксинус единицы — это такое число из отрезка , синус которого равен единице. Очевидно, это

Продолжаем: — это такое число из отрезка , синус которого равен . Да, это

Строим график функции

Свойства функции

1. Область определения

2. Область значений

3. , то есть эта функция является нечетной. Ее график симметричен относительно начала координат.

4. Функция монотонно возрастает. Ее наименьшее значение, равное — , достигается при , а наибольшее значение, равное , при

5. Что общего у графиков функций и ? Не кажется ли вам, что они «сделаны по одному шаблону» — так же, как правая ветвь функции и график функции , или как графики показательной и логарифмической функций?

Представьте себе, что мы из обычной синусоиды вырезали небольшой фрагмент от до , а затем развернули его вертикально — и мы получим график арксинуса.

То, что для функции на этом промежутке — значения аргумента, то для арксинуса будут значения функции. Так и должно быть! Ведь синус и арксинус — взаимно-обратные функции. Другие примеры пар взаимно обратных функций — это при и , а также показательная и логарифмическая функции.

Напомним, что графики взаимно обратных функций симметричны относительно прямой

Аналогично, определим функцию Только отрезок нам нужен такой, на котором каждому значению угла соответствует свое значение косинуса, а зная косинус, можно однозначно найти угол. Нам подойдет отрезок

Арккосинусом числа a называется число , такое, что

Легко запомнить: «арккосинусы живут сверху», и не просто сверху, а на отрезке

Обозначение: Область определения арккосинуса — отрезок Область значений — отрезок

Очевидно, отрезок выбран потому, что на нём каждое значение косинуса принимается только один раз. Иными словами, каждому значению косинуса, от -1 до 1, соответствует одно-единственное значение угла из промежутка

Арккосинус не является ни чётной, ни нечётной функцией. Зато мы можем использовать следующее очевидное соотношение:

Построим график функции

Нам нужен такой участок функции , на котором она монотонна, то есть принимает каждое свое значение ровно один раз.

Выберем отрезок . На этом отрезке функция монотонно убывает, то есть соответствие между множествами и взаимно однозначно. Каждому значению х соответствует свое значение у. На этом отрезке существует функция, обратная к косинусу, то есть функция у = arccosx.

Заполним таблицу, пользуясь определением арккосинуса.

Арккосинусом числа х, принадлежащего промежутку , будет такое число y, принадлежащее промежутку , что

Значит, , поскольку ;

, так как ;

, так как ,

Вот график арккосинуса:

Свойства функции

1. Область определения

2. Область значений

Эта функция общего вида — она не является ни четной, ни нечетной.

4. Функция является строго убывающей. Наибольшее значение, равное , функция у = arccosx принимает при , а наименьшее значение, равное нулю, принимает при

5.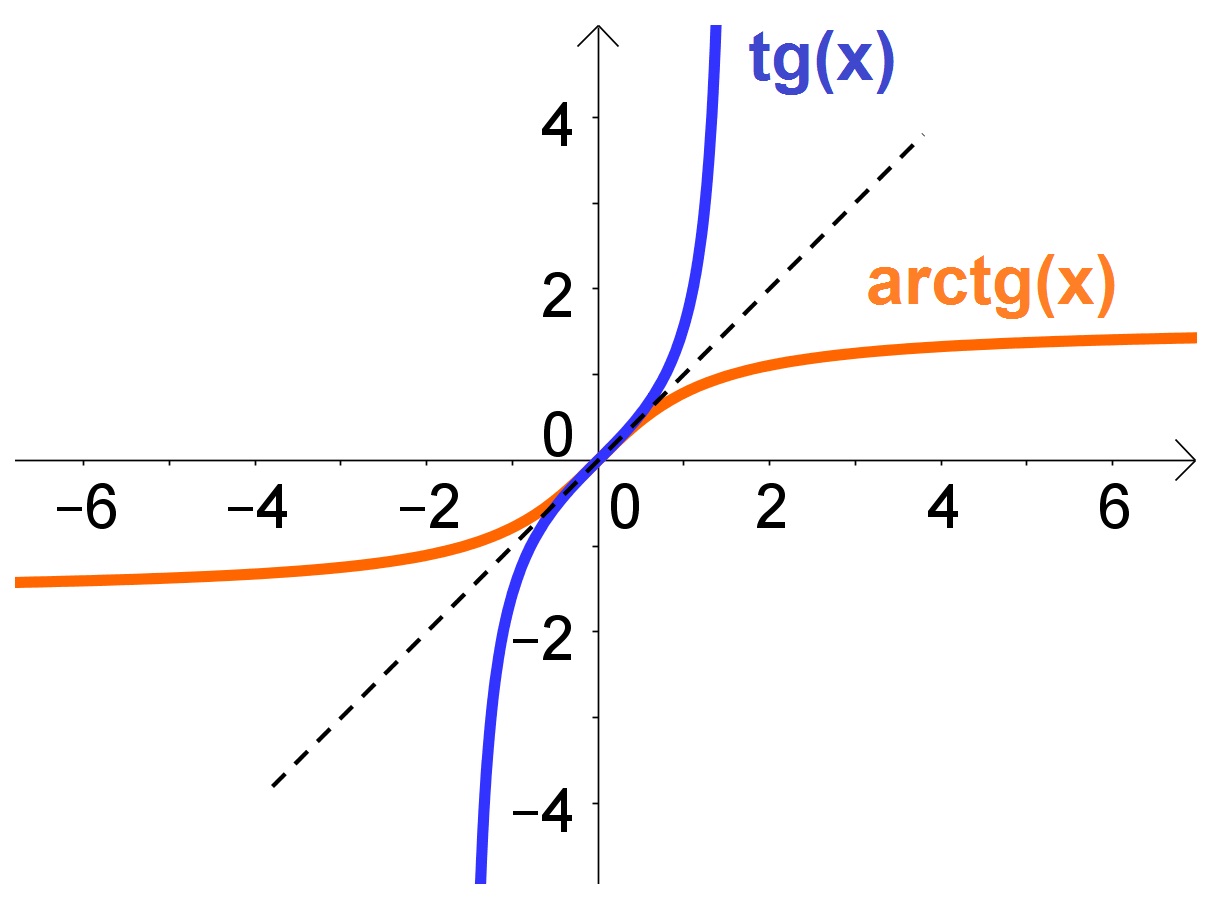 Функции и являются взаимно обратными.

Следующие — арктангенс и арккотангенс.

Арктангенсом числа a называется число , такое, что

Обозначение: . Область определения арктангенса — промежуток Область значений — интервал .

Почему в определении арктангенса исключены концы промежутка — точки ? Конечно, потому, что тангенс в этих точках не определён. Не существует числа a, равного тангенсу какого-либо из этих углов.

Построим график арктангенса. Согласно определению, арктангенсом числа х называется число у, принадлежащее интервалу , такое, что

Как строить график — уже понятно. Поскольку арктангенс — функция обратная тангенсу, мы поступаем следующим образом:

— Выбираем такой участок графика функции , где соответствие между х и у взаимно однозначное. Это интервал Ц На этом участке функция принимает значения от до

Тогда у обратной функции, то есть у функции , область, определения будет вся числовая прямая, от до а областью значений — интервал

Дальше рассуждаем так же, как при построении графиков арксинуса и арккосинуса.

, значит,

А что же будет при бесконечно больших значениях х? Другими словами, как ведет себя эта функция, если х стремится к плюс бесконечности?

Мы можем задать себе вопрос: для какого числа из интервала значение тангенса стремится к бесконечности? — Очевидно, это

А значит, при бесконечно больших значениях х график арктангенса приближается к горизонтальной асимптоте

Аналогично, если х стремится к минус бесконечности, график арктангенса приближается к горизонтальной асимптоте

На рисунке — график функции

Свойства функции

1. Область определения

2. Область значений

3. Функция нечетная.

4. Функция является строго возрастающей.

5. Прямые и — горизонтальные асимптоты данной функции.

6. Функции и являются взаимно обратными — конечно, когда функция рассматривается на промежутке

Аналогично, определим функцию арккотангенс и построим ее график.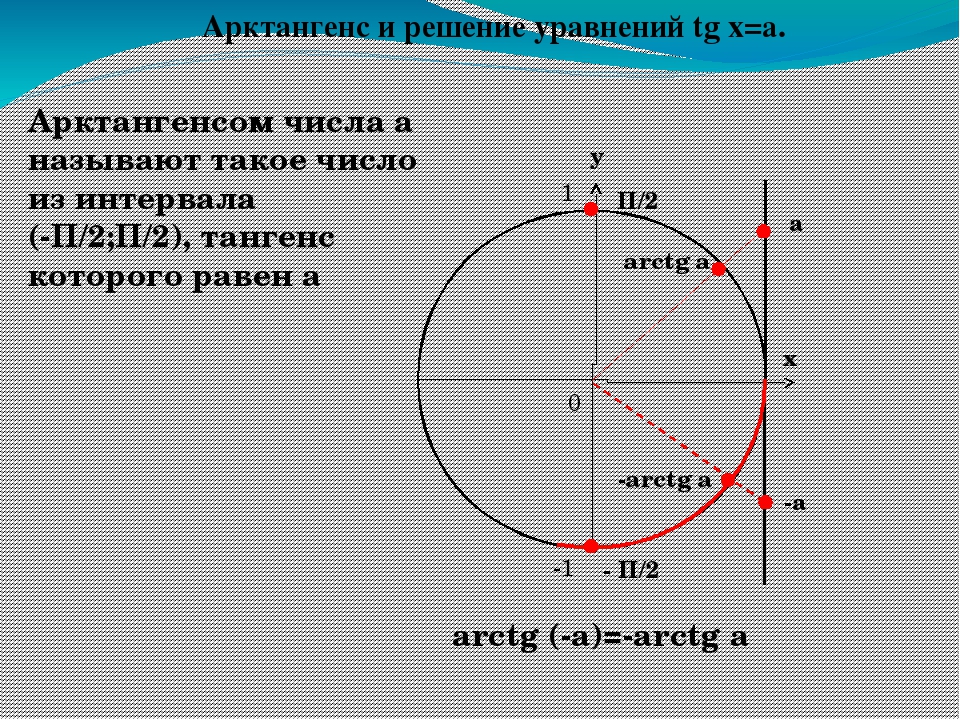

Арккотангенсом числа a называется число , такое, что

График функции :

Свойства функции

1. Область определения

2. Область значений

3. Функция — общего вида, то есть ни четная, ни нечетная.

4. Функция является строго убывающей.

5. Прямые и — горизонтальные асимптоты данной функции.

6. Функции и являются взаимно обратными, если рассматривать на промежутке

Внеклассный урок — Арктангенс и арккотангенс

Арктангенс и арккотангенс

Арктангенс и арккотангенс, так же как и арксинус и арккосинус, являются обратными тригонометрическими функциями.

Арктангенс.

Арктангенс числа а – это такое число из отрезка от –π/2 до π/2, тангенс которого равен а.

Обозначается так: arctg a.

Говоря иначе:

arctg a = x,

следовательно tg x = a.

Условие: x больше –π/2, но меньше π/2

(–π/2 < x < π/2)

Формулы.

(1)

x = arctg a + πk

где k – любое целое число (k ∈ Z)

(2)

arctg (–a) = –arctg a

Пример: Вычислить arctg 1.

Решение.

Решая, следуем буквально по таблице над примером.

Итак, в нашем примере а = 1. Значит:

arctg 1 = х.

Следовательно, tg x = 1. При этом x ∈ [–π/2; π/2].

Находим значение x:

Координату 1 имеет tg π/4. Значит:

x = π/4.

При этом π/4 ∈ [–π/2; π/2].

Ответ: arctg 1 = π/4.

Арккотангенс.

Арккотангенс числа а – это такое число в интервале (0; π), котангенс которого равен а.

Обозначается так: arcctg a.

Говоря иначе:

arcctg a = x,

следовательно ctg x = a.

Условие: x больше 0, но меньше π

(0 < x < π)

Формулы.

(1)

x = arcctg a + πk

(k ∈ Z)

(2)

arcctg (–a) = π – arcctg а

Пример: Вычислить arcctg 1.

Решение.

Опять следуем по таблице над нашим примером.

а = 1.

Следовательно:

ctg x = 1.

Осталось найти значение x (либо вычислить самим, либо посмотреть таблицу котангенсов):

x = π/4.

arcctg 1 = π/4.

Все полученные результаты не выходили из рамок интервала (0; π).

Пример решен.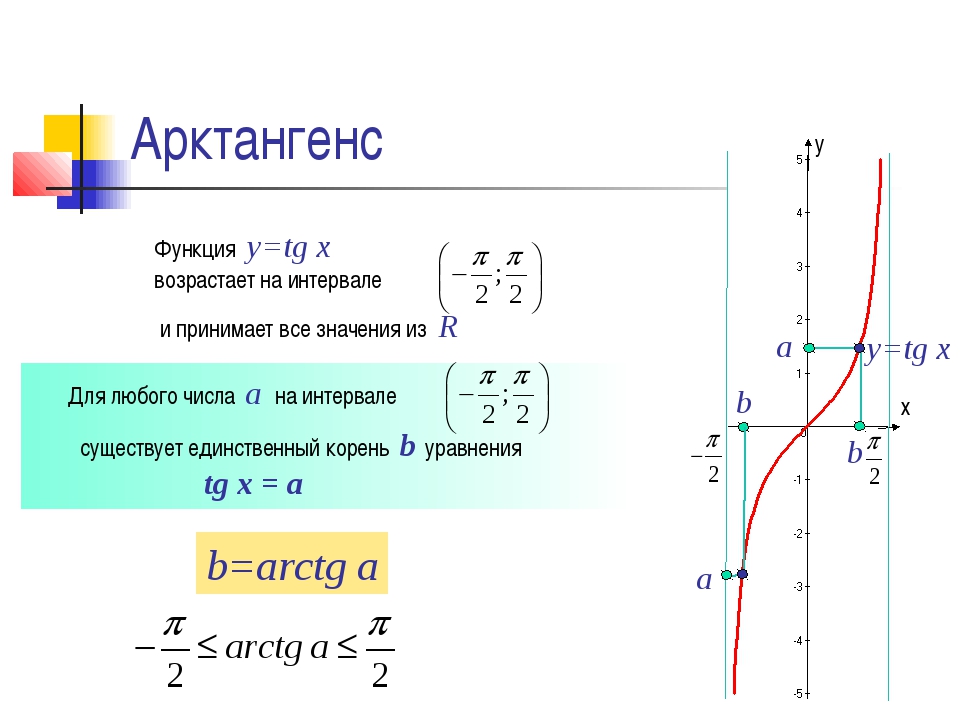

Значения обратных тригонометрических функций y=arctg(x) и y=arcctg

Значения обратных тригонометрических функций \(arctg(x)\) и \(arcctg(x)\):

Вычислим значения \( \text{arcctg}\left( \frac{\sqrt{3}}{3} \right) \text{ },\text{ } \text{arcctg}\left( -\sqrt{3} \right) \).

Вычислить угол \(\alpha\) на промежутке \(\left( 0;\pi \right)\) такой, что \(\text{ctg}\alpha =\frac{\sqrt{3}}{3}\). Из таблицы значение котангенса \(\alpha =\frac{\pi }{3}\) значение \(\text{ctg}\alpha =\frac{\sqrt{3}}{3}\) этому значению соответствует угол \(\alpha =\frac{\pi }{3}\). Найденный угол принадлежит промежутку \(\left( 0;\pi \right)\). Следовательно:

\( \text{arcctg}\left( \frac{\sqrt{3}}{3} \right)=\frac{\pi }{3}\).

Для того чтобы найти \(\text{arcctg}\left( -\sqrt{3} \right)\) используем формулу:

\(\text{arctg}\left( -\sqrt{3} \right)=\pi -\text{arctg}\sqrt{3}\)

Найдем значение \(\text{arcctg}\sqrt{3}\) из таблицы котангенсов: \(\alpha =\frac{\pi }{6}\). Итого имеем:

\(\text{arcctg}\left( -\sqrt{3} \right)=\pi -\frac{\pi }{6}=\frac{5\pi }{6}\)

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Наши преподаватели

Оставить заявку

Репетитор по математике

Белорусский государственный педагогический университет им. М. Танка

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-4 классов. Математика — отличный тренажер! Только тренирует он не мышцы, а наш ум! А я могу Вам помочь с тренировками, ведь изучать математику не всегда бывает легко. На занятиях будем развивать память и мышление, используя различные интересные задания и игры!

Оставить заявку

Репетитор по математике

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 5-11 классов. Люблю математику и стараюсь привить эту любовь учащимся. Учу учащихся искать нестандартные решения, рассуждать, не бояться ошибок, делать выводы. Показываю связь математики с жизнью.

Оставить заявку

Репетитор по математике

Харьковский государственный университет им. А.М. Горького

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-11 классов. Имею высшую квалификационную категорию и педагогическое звание «Учитель — методист». В работе использую технологии развивающего, личностно-ориентированного обучения, успешно готовлю выпускников к итоговому независимому оцениванию. Я с детства люблю решать задачи. Мне кажется, что любой человек, который делает открытие, испытывает такое сильное чувство, которое хочется повторить. Любая задача, особенно трудная, позволяет испытать это чувство. Люди, которые увлекаются математикой более успешные в жизни. Ведь вся наша жизнь — это решение задач.

Математика 10 класс

— Индивидуальные занятия
— В любое удобное для вас время
— Бесплатное вводное занятие

Математика 10 класс

— Индивидуальные занятия
— В любое удобное для вас время
— Бесплатное вводное занятие

Записаться на бесплатный урок

Тригонометрия arctg.

Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс? Ограничения на арксинус, арккосинус, арктангенс, арккотангенс

Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса данного числа. Сначала мы внесем ясность, что называется значением арксинуса, арккосинуса, арктангенса и арккотангенса. Дальше получим основные значения этих аркфункций, после чего разберемся, как находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса. Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.

Навигация по странице.

Значения арксинуса, арккосинуса, арктангенса и арккотангенса

Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса ».

Таблицы синусов и косинусов, а также тангенсов и котангенсов Брадиса позволяют найти значение арксинуса, арккосинуса, арктангенса и арккотангенса положительного числа в градусах с точностью до одной минуты. Здесь стоит оговориться, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(−a)=−arcsin a , arccos(−a)=π−arccos a , arctg(−a)=−arctg a и arcctg(−a)=π−arcctg a .

Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса. Будем это делать на примерах.

Пусть нам требуется найти значение арксинуса 0,2857 . Находим это значение в таблице синусов (случаи, когда это значение отсутствует в таблице, разберем ниже). Ему соответствует синус 16 градусов 36 минут. Следовательно, искомым значением арксинуса числа 0,2857 является угол 16 градусов 36 минут.

Часто приходится учитывать и поправки из трех справа столбцов таблицы. К примеру, если нам нужно найти арксинус 0,2863 . По таблице синусов это значение получается как 0,2857 плюс поправка 0,0006 , то есть, значению 0,2863 соответствует синус 16 градусов 38 минут (16 градусов 36 минут плюс 2 минуты поправки).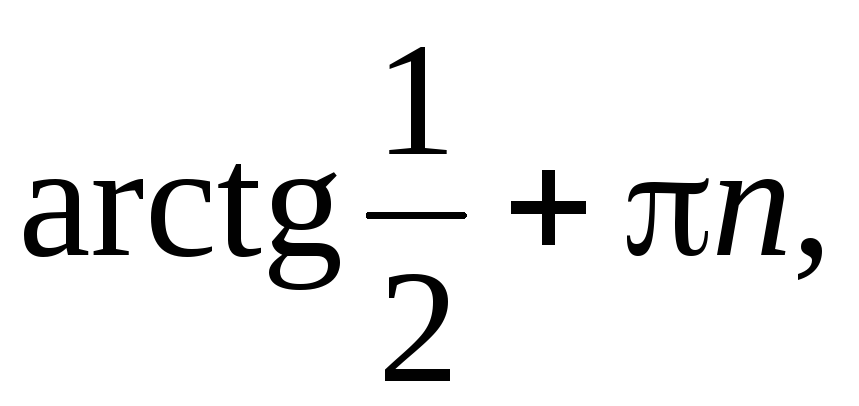

Если же число, арксинус которого нас интересует, отсутствует в таблице и даже не может быть получено с учетом поправок, то в таблице нужно отыскать два наиболее близких к нему значения синусов, между которыми данное число заключено. Например, мы ищем значение арксинуса числа 0,2861573 . Этого числа нет в таблице, с помощью поправок это число тоже не получить. Тогда находим два наиболее близких значения 0,2860 и 0,2863 , между которыми исходное число заключено, этим числам соответствуют синусы 16 градусов 37 минут и 16 градусов 38 минут. Искомое значение арксинуса 0,2861573 заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1 минуты.

Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).

Нахождение значения arcsin через arccos, arctg, arcctg и т.

п.

Например, пусть нам известно, что arcsin a=−π/12 , а нужно найти значение arccos a . Вычисляем нужное нам значение арккосинуса: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12 .

Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a требуется найти значение арктангенса или арккотангенса этого числа a или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.

Пусть нам известно, что арккосинус числа a равен π/10 , и нужно вычислить значение арктангенса этого числа a . Решить поставленную задачу можно так: по известному значению арккосинуса найти число a , после чего найти арктангенс этого числа. Для этого нам сначала потребуется таблица косинусов, а затем – таблица тангенсов.

Угол π/10 радиан – это угол 18 градусов, по таблице косинусов находим, что косинус 18 градусов приближенно равен 0,9511 , тогда число a в нашем примере есть 0,9511 .

Осталось обратиться к таблице тангенсов, и с ее помощью найти нужное нам значение арктангенса 0,9511 , оно приближенно равно 43 градусам 34 минутам.

Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg .

Список литературы.

Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2

Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!

Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.

Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.

Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…

Что означает выражение

arcsin 0,4 ?

Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.

И всё.

Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:

arc sin 0,4
угол, синус которого равен 0,4

Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.

Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.

Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.

Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.

Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!

Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)

Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)

Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.

А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)

Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)

Например: что такое arcsin 0,5?

Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:

arcsin 0,5 = 30°

Или, более солидно, через радианы:

Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.

Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)

Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!

Достаточно сообразить, что:

Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:

и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.

Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!

Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:

Нужно вам, скажем, определить значение выражения:

Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:

Внутри арккосинуса справа уже положительное значение. То, что

вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:

Вот и всё.

Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.

С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)

Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.

Значения арксинуса, арккосинуса, арктангенса и арккотангенса

Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».

Определения арксинуса, арккосинуса, арктангенса и арккотангенса числапомогут разобраться в вычислении заданных функций. Значение тригонометрических функций угла равняется числу a , тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.

Для четкого понимания рассмотрим пример.

Если имеем арккосинус угла равного π 3 , то значение косинуса отсюда равно 1 2 по таблице косинусов. Данный угол расположен в промежутке от нуля до пи, значит, значение арккосинуса 1 2 получим π на 3 . Такое тригонометрическое выражение записывается как a r cos (1 2) = π 3 .

Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно ). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °

Основные значения arcsin, arccos, arctg и arctg

Благодаря таблице синусов, косинусов, тангенсов и котангенсов, мы имеет точные значения угла при 0 , ± 30 , ± 45 , ± 60 , ± 90 , ± 120 , ± 135 , ± 150 , ± 180 градусов. Таблица достаточно удобна и из нее можно получать некоторые значения для аркфункций, которые имеют название как основные значения арксинуса, арккосинуса, арктангенса и арккотангенса.

Таблица синусов основных углов предлагает такие результаты значений углов:

sin (- π 2) = — 1 , sin (- π 3) = — 3 2 , sin (- π 4) = — 2 2 , sin (- π 6) = — 1 2 , sin 0 = 0 , sin π 6 = 1 2 , sin π 4 = 2 2 , sin π 3 = 3 2 , sin π 2 = 1

Учитывая их, можно легко высчитать арксинус числа всех стандартных значений, начиная от — 1 и заканчивая 1 , также значения от – π 2 до + π 2 радианов, следуя его основному значению определения. Это и является основными значениями арксинуса.

Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.

Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:

cos 0 = 1 , cos π 6 = 3 2 , cos π 4 = 2 2 , cos π 3 = 1 2 , cos π 2 = 0 , cos 2 π 3 = — 1 2 , cos 3 π 4 = — 2 2 , cos 5 π 6 = — 3 2 , cos π = — 1

Следуя из таблицы, находим значения арккосинуса:

a r c cos (- 1) = π , arccos (- 3 2) = 5 π 6 , arcocos (- 2 2) = 3 π 4 , arccos — 1 2 = 2 π 3 , arccos 0 = π 2 , arccos 1 2 = π 3 , arccos 2 2 = π 4 , arccos 3 2 = π 6 , arccos 1 = 0

Таблица арккосинусов.

Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.

a r c sin , a r c cos , a r c t g и a r c c t g

Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют т аблицу синусов, косинусов, тангенсов и котангенсов Брадиса.

Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin (- α) = — a r c sin α , a r c cos (- α) = π — a r c cos α , a r c t g (- α) = — a r c t g α , a r c c t g (- α) = π — a r c c t g α .

Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.

Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.

Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.

Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.

Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .

Чтобы найти арксинус через известный арккосинус данного числа, нужно применить тригонометрические формулы a r c sin α + a r c cos α = π 2 , a r c t g α + a r c c t g α = π 2 (не обходимо просмотреть тему формул сумм ы арккосинуса и арксинуса, суммы арктангенса и арккотангенса ).

При известном a r c sin α = — π 12 необходимо найти значение a r c cos α , тогда необходимо вычислить арккосинус по формуле:

a r c cos α = π 2 − a r c sin α = π 2 − (− π 12) = 7 π 12 .

Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.

Если дан арккосинус числа а равный π 10 , а вычислить арктангенс данного числа поможет таблица тангенсов. Угол π 10 радиан представляет собой 18 градусов, тогда по таблице косинусов видим, что косинус 18 градусов имеет значение 0 , 9511 , после чего заглядываем в таблицу Брадиса.

При поиске значения арктангенса 0 , 9511 определяем, что значение угла имеет 43 градуса и 34 минуты. Рассмотрим по таблице ниже.

Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.

Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.

Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.

Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.

Свойства арксинуса:

Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.

Арккосинус

Arccos числа а — это значение угла α, косинус которого равен а.

Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.

Рассмотрим функцию арккосинуса более подробно:

Функция определена на отрезке [-1; 1].
ОДЗ для arccos — .
График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
Y = 0 при x = 1.
Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.

Некоторые свойства арккосинуса совпадают с функцией косинуса.

Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.

Задание 1. Укажите функции изображенные на рисунке.

Ответ: рис. 1 – 4, рис.2 — 1.

В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.

Арктангенс

Arctg числа a – это такое значение угла α, что его тангенс равен а.

Если рассмотреть график арктангенса, можно выделить следующие свойства:

График бесконечен и определен на промежутке (- ∞; + ∞).
Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
Y = 0 при x = 0.
Кривая возрастает на всей области определения.

Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.

Арккотангенс

Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.

Свойства функции арккотангенса:

Интервал определения функции – бесконечность.
Область допустимых значений – промежуток (0; π).
F(x) не является ни четной, ни нечетной.
На всем своем протяжении график функции убывает.

Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.

Задание 2. Соотнести график и форму записи функции.

Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,

Ответ: рис. 1 – 1, рис. 2 – 4.

Тригонометрические тождества arcsin, arcos, arctg и arcctg

Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.

Также существуют соотношения для arctg и arcctg:

Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.

Примеры решения задач

Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.

При решении первого типа задач необходимо придерживаться следующего плана действий:

При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.

Допустим в ЕГЭ необходимо найти ответ для уравнения типа:

Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.

Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:

Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.

(круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям .

Арктангенс — обозначение: arctg x или arctan x .

Арктангенс (y = arctg x ) — обратная функция к tg (x = tg y ), которая имеет область определения и множество значений . Другими словами возвращает угол по значению его tg .

Функция y = arctg x непрерывна и ограничена на всей своей числовой прямой. Функция y = arctg x является строго возрастающей.

Свойства функции arctg .

График функции y = arctg x .

График арктангенса получают из графика тангенса, меняя местами оси абсцисс и ординат. Чтоб избавиться от многозначности, множество значений ограничивают интервалом , на нем функция монотонна. Это определение называется главным значением арктангенса.

Получение функции arctg .

Есть функция y = tg x . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arctg x не является функцией. Поэтому рассматриваем отрезок, на котором она только возрастает и принимает все значения лишь 1 раз — . На таком отрезке y = tg x только возрастает монотонно и принимает все значения лишь 1 раз, то есть, на интервале есть обратная y = arctg x , график ее симметричен графику y = tg x на отрезке относительно прямой y = x .

Электронный справочник по математике обратные тригонометрические функции арксинус арккосинус арктангенс арккотангенс определение свойства графики значения

ОПРЕДЕЛЕНИЕ 1. Пусть число a удовлетворяет неравенству . Число x называют арксинусом числа a и обозначают x = arcsin a, если выполнены два условия:

ОПРЕДЕЛЕНИЕ 2. Пусть число a удовлетворяет неравенству . Число x называют арккосинусом числа a и обозначают x = arccos a, если выполнены два условия:

ОПРЕДЕЛЕНИЕ 3. Рассмотрим произвольное число a . Число x называют арктангенсом числа a и обозначают x = arctg a, если выполнены два условия:

ОПРЕДЕЛЕНИЕ 4. Рассмотрим произвольное число a . Число x называют арккотангенсом числа a и обозначают x = arcctg a, если выполнены два условия:

Арксинус, арккосинус, арктангенс и арккотангенс удовлетворяют, в частности, следующим соотношениям:

arcsin (– a) = – arcsin a ,

arccos (– a) =
= π – arccos a ,

arctg (– a) = – arctg a ,

arcctg (– a) =
= π – arcctg a .

Обратными тригонометрическими функциями называют функции:

Графики этих функций изображены на рисунках 1, 2, 3, 4.

Рис. 1. График функции y = arcsin x

ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ y = arcsin x

Рис. 2. График функции y = arccos x

ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ y = arccos x

Рис. 3. График функции y = arctg x

ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ y = arctg x

Рис. 4. График функции y = arcctg x

ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ y = arcctg x

ПРИМЕР. Решить уравнение

2 arcsin 2x = arccos 7x .

РЕШЕНИЕ. Возьмём косинус от обеих частей уравнения. Тогда в левой части уравнения получим:

cos ( 2 arcsin 2x ) = 1 – 2sin²( arcsin 2x ) = 1 – 2 ( 2x )² = 1 – 8x² .

cos ( 2 arcsin 2x ) =
= 1 – 2sin²( arcsin 2x ) =
= 1 – 2 ( 2x )² = 1 – 8x² .

В правой части уравнения получим:

cos ( arccos 7x ) = 7x.

Следовательно, возникает квадратное уравнение:

В силу того, что область определения обратных тригонометрических функций y = arcsin x и y = arccos x имеет вид: , второй корень должен быть отброшен.

ОТВЕТ:

Где на окружности находится arctg 1 3. Арксинус, формула, график функции арксинус, урок и презентация

Ранее по программе учащиеся получили представление о решении тригонометрических уравнений, ознакомились с понятиями арккосинуса и арксинуса, примерами решений уравнений cos t = a и sin t = a. В этом видеоуроке рассмотрим решение уравнений tg x = a и ctg x = a.

В начале изучения данной темы рассмотрим уравнения tg x = 3 и tg x = — 3. Если уравнение tg x = 3 будем решать с помощью графика, то увидим, что пересечение графиков функций y = tg x и y = 3 имеет бесконечное множество решений, где x = x 1 + πk. Значение x 1 — это координата x точки пересечения графиков функций y = tg x и y = 3. Автор вводит понятие арктангенса: arctg 3 это число, tg которого равен 3, и это число принадлежит интервалу от -π/2 до π/2. Используя понятие арктангенса, решение уравнения tg x = 3 можно записать в виде x = arctg 3 + πk.

По аналогии решается уравнение tg x = — 3. По построенным графикам функций y = tg x и y = — 3 видно, что точки пересечения графиков, а следовательно, и решениями уравнений, будет x = x 2 + πk. С помощью арктангенса решение можно записать как x = arctg (- 3) + πk. На следующем рисунке увидим, что arctg (- 3) = — arctg 3.

Общее определение арктангенса выглядит следующим образом: арктангенсом а называется такое число из промежутка от -π/2 до π/2, тангенс которого равен а. Тогда решением уравнения tg x = a является x = arctg a + πk.

Автор приводит пример 1. Найти решение выражения arctg.Введем обозначения: арктангенс числа равен x, тогда tg x будет равен данному числу, где x принадлежит отрезку от -π/2 до π/2. Как в примерах в предыдущих темах, воспользуемся таблицей значений. По этой таблице тангенсу данного числа соответствует значение x = π/3. Запишем решение уравнения арктангенс заданного числа равен π/3, π/3 принадлежит и интервалу от -π/2 до π/2.

Пример 2 — вычислить арктангенс отрицательного числа. Используя равенство arctg (- a) = — arctg a, введем значение x. Аналогично примеру 2 запишем значение x, которое принадлежит отрезку от -π/2 до π/2. По таблице значений найдем, что x = π/3, следовательно, — tg x = — π/3. Ответом уравнения будет — π/3.

Рассмотрим пример 3. Решим уравнение tg x = 1. Запишем, что x = arctg 1 + πk. В таблице значению tg 1 соответствует значение x = π/4, следовательно, arctg 1 = π/4. Подставим это значение в исходную формулу x и запишем ответ x = π/4 + πk.

Пример 4: вычислить tg x = — 4,1. В данном случае x = arctg (- 4,1) + πk. Т.к. найти значение arctg в данном случае нет возможности, ответ будет выглядеть как x = arctg (- 4,1) + πk.

В примере 5 рассматривается решение неравенства tg x > 1. Для решения построим графики функций y = tg x и y = 1. Как видно на рисунке, эти графики пересекаются в точках x = π/4 + πk. Т.к. в данном случае tg x > 1, на графике выделим область тангенсоиды, которая находится выше графика y = 1, где x принадлежит интервалу от π/4 до π/2. Ответ запишем как π/4 + πk

Далее рассмотрим уравнение ctg x = a. На рисунке изображены графики функций у = ctg x, y = a, y = — a, которые имеют множество точек пересечения. Решения можно записать как x = x 1 + πk, где x 1 = arcctg a и x = x 2 + πk, где x 2 = arcctg (- a). Отмечено, что x 2 = π — x 1 . Из этого следует равенство arcctg (- a) = π — arcctg a. Далее дается определение арккотангенса: арккотангенсом а называется такое число из промежутка от 0 до π, котангенс которого равен а. Решение уравнения сtg x = a записывается в виде: x = arcctg a + πk.

В конце видеоурока делается еще один важный вывод — выражение ctg x = a можно записать в виде tg x = 1/a, при условии, что a не равно нулю.

ТЕКСТОВАЯ РАСШИФРОВКА:

Рассмотрим решение уравнений tg х = 3 и tg х= — 3. Решая первое уравнение графически, мы видим, что графики функций у = tg х и у = 3 имеют бесконечно много точек пересечения, абсциссы которых запишем в виде

х = х 1 + πk, где х 1 — это абсцисса точки пересечения прямой у = 3 с главной ветвью тангенсоиды (рис.1), для которой было придумано обозначение

arctg 3 (арктангенс трех).

Как же понимать arctg 3?

Это число, тангенс которого равен 3 и это число принадлежит интервалу (- ;). Тогда все корни уравнения tg х = 3 можно записать формулой х = arctg 3+πk.

Аналогично решение уравнения tg х = — 3 можно записать в виде х = х 2 + πk, где х 2 — это абсцисса точки пересечения прямой у = — 3 с главной ветвью тангенсоиды (рис.1), для которой было придумано обозначение arctg(-3) (арктангенс минус трех). Тогда все корни уравнения можно записать формулой: х = arctg(-3)+ πk. По рисунку видно, что arctg(- 3)= — arctg 3.

Сформулируем определение арктангенса. Арктангенсом а называется такое число из промежутка (-;), тангенс которого равен а.

Часто используют равенство: arctg(-а) = -arctg а, которое справедливо для любого а.

Зная определение арктангенса, сделаем общий вывод о решении уравнения

tg х= a: уравнение tg х = a имеет решение х = arctg а + πk.

Рассмотрим примеры.

ПРИМЕР 1.Вычислить arctg.

Решение. Пусть arctg = х, тогда tgх = и хϵ (- ;). Показать таблицу значений Следовательно, х =, так как tg = и ϵ (- ;).

Итак, arctg =.

ПРИМЕР 2. Вычислить arctg (-).

Решение. Используя равенство arctg(- а) = — arctg а, запишем:

arctg(-) = — arctg . Пусть — arctg = х, тогда — tgх = и хϵ (- ;). Следовательно, х =, так как tg = и ϵ (- ;). Показать таблицу значений

Значит — arctg=- tgх= — .

ПРИМЕР 3. Решить уравнение tgх = 1.

1. Запишем формулу решений: х = arctg 1 + πk.

2. Найдем значение арктангенса

так как tg = . Показать таблицу значений

Значит arctg1= .

3. Поставим найденное значение в формулу решений:

ПРИМЕР 4. Решить уравнение tgх = — 4,1(тангенс икс равно минус четыре целые одна десятая).

Решение. Запишем формулу решений: х = arctg (- 4,1) + πk.

Вычислить значение арктангенса мы не можем, поэтому решение уравнения оставим в полученном виде.

ПРИМЕР 5. Решить неравенство tgх 1.

Решение. Будем решать графически.

Построим тангенсоиду

у= tgх и прямую у = 1(рис.2). Они пересекаются в точках вида х = + πk.

2. Выделим промежуток оси икс, на котором главная ветвь тангенсоиды расположена выше прямой у = 1, так как по условию tgх 1. Это интервал (;).

3. Используем периодичность функции.

Своийство 2. у=tg х — периодическая функция с основным периодом π.

Учитывая периодичность функции у= tgх, запишем ответ:

(;). Ответ можно записать в виде двойного неравенства:

Перейдем к уравнению ctg х = a. Представим графическую иллюстрацию решения уравнения для положительного и отрицательного а (рис.3).

Графики функций у= ctg х и у =а а также

у= ctg х и у=-а

имеют бесконечно много общих точек, абсциссы которых имеют вид:

х = х 1 + , где х 1 — это абсцисса точки пересечения прямой у =а с главной ветвью тангенсоиды и

х 1 = arcсtg а;

х = х 2 + , где х 2 — это абсцисса точки пересечения прямой

у = — а с главной ветвью тангенсоиды и х 2 = arcсtg (- а).

Заметим, что х 2 = π — х 1 . Значит, запишем важное равенство:

arcсtg (-а) = π — arcсtg а.

Сформулируем определение: арккотангенсом а называется такое число из интервала (0;π), котангенс которого равен а.

Решение уравнения ctg х = a записываются в виде: х = arcсtg а + .

Обратим внимание, что уравнение ctg х = a можно преобразовать к виду

tg х = , за исключение, когда а = 0.

Свойства арксинуса:

Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.

Арккосинус

Arccos числа а — это значение угла α, косинус которого равен а.

Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.

Рассмотрим функцию арккосинуса более подробно:

Функция определена на отрезке [-1; 1].
ОДЗ для arccos — .
График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
Y = 0 при x = 1.
Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.

Некоторые свойства арккосинуса совпадают с функцией косинуса.

Задание 1. Укажите функции изображенные на рисунке.

Ответ: рис. 1 – 4, рис.2 — 1.

Арктангенс

Arctg числа a – это такое значение угла α, что его тангенс равен а.

Если рассмотреть график арктангенса, можно выделить следующие свойства:

График бесконечен и определен на промежутке (- ∞; + ∞).
Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
Y = 0 при x = 0.
Кривая возрастает на всей области определения.

Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.

Арккотангенс

Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.

Свойства функции арккотангенса:

Интервал определения функции – бесконечность.
Область допустимых значений – промежуток (0; π).
F(x) не является ни четной, ни нечетной.
На всем своем протяжении график функции убывает.

Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.

Задание 2. Соотнести график и форму записи функции.

Ответ: рис. 1 – 1, рис. 2 – 4.

Тригонометрические тождества arcsin, arcos, arctg и arcctg

Также существуют соотношения для arctg и arcctg:

Примеры решения задач

При решении первого типа задач необходимо придерживаться следующего плана действий:

Допустим в ЕГЭ необходимо найти ответ для уравнения типа:

Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:

Навигация по странице.

Значения арксинуса, арккосинуса, арктангенса и арккотангенса

Нахождение значения arcsin через arccos, arctg, arcctg и т.п.

Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg .

Список литературы.

Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2

Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Тригонометрическая функция arctan () — арктангенс — определение математического слова
Тригонометрическая функция arctan () — арктангенс — определение математического слова — Math Open Reference
Функция арктангенса — это функция, обратная касательной.
Возвращает угол, тангенс которого является заданным числом.
Попробуй это Перетащите любой вершине треугольника и посмотрите, как вычисляется угол C с помощью функции arctan ().
Для каждой тригонометрической функции существует обратная функция, которая работает в обратном порядке.Эти обратные функции имеют то же имя, но с дугой впереди. (На некоторых калькуляторах кнопка arctan может быть помечена как атан, а иногда загар ^-1.) Таким образом, загар — это арктангенс, обратный величине и т. Д. Когда мы видим арктангенс х, мы понимаем его как «угол, тангенс которого равен х».
загар 30 = 0,577 Означает: тангенс 30 градусов равен 0,577
арктан 0,577 = 30 означает: угол, тангенс которого равен 0,577, равен 30 градусам.
Используйте arctan, если вы знаете тангенс угла и хотите узнать фактический угол.
См. Также Обратные функции — тригонометрия
Пример — использование arctan для нахождения угла
На рисунке выше нажмите «Сброс». Нам известны длины сторон, но нам нужно найти величину угла C.
Мы знаем, что поэтому нам нужно знать угол, тангенс которого равен 0,577, или формально: С помощью калькулятора находим arctan 0,577 равным 30 °.
Большие и отрицательные углы
Напомним, что мы можем применить Триггерные функции на любой угол, включая большие и отрицательные углы.Но когда мы Рассмотрим обратную функцию, мы столкнемся с проблемой, потому что существует бесконечное количество углов, имеющих одинаковую касательную. Например, 45 ° и 360 + 45 ° будут иметь одинаковую касательную. Подробнее об этом см. Обратные тригонометрические функции.
Чтобы решить эту проблему, диапазон обратных триггерных функций ограничены таким образом, чтобы обратные функции были взаимно однозначными, то есть для каждого входного значения был только один результат.
Ареал и владение arctan
Напомним, что область определения функции — это набор допустимых входных данных для нее.Диапазон — это набор возможных выходов.
Для y = arctan x:
Диапазон
Домен Все вещественные числа
Условно диапазон arctan ограничен от -90 ° до + 90 ° * .
Итак, если вы используете калькулятор для вычисления, скажем, arctan 0,55, из бесконечного числа возможностей он вернет 28,81 °, тот, который находится в диапазоне функции.
* На самом деле, -90 ° и + 90 ° сами по себе не входят в диапазон.Это потому, что функция tan имеет значение бесконечность при этих значениях. Но значения чуть ниже них находятся в диапазоне, например +89.9999999. Но для простоты объяснения мы говорим, что диапазон составляет ± 90 °.
Что попробовать
На рисунке выше нажмите «Сброс» и «Скрыть детали».
Отрегулируйте треугольник до нового размера
Используя функцию arctan, вычислите значение угла C из длин сторон
Нажмите «Показать подробности», чтобы проверить ответ.
Другие темы по тригонометрии
Уголки
Тригонометрические функции
Решение задач тригонометрии
Исчисление
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Arctan: определение, функция и формула — видео и стенограмма урока
Когда использовать Arctan
Тригонометрические функции можно использовать для определения значений, относящихся к прямоугольному треугольнику.На практике эти функции можно использовать для определения высоты объектов или расстояний, которые трудно измерить. Эти измерения определяются с использованием меры одного угла (не прямого) и отношения двух сторон треугольника. Тригонометрические функции определяются по сторонам треугольника, которые используются в соотношении этих формул:
синус = противоположный / гипотенуза
косинус = смежный / гипотенуза
касательная = противоположная / смежная
Обратные к этим функциям можно использовать для определения углов, когда известны стороны треугольника.Вы можете использовать arctan для определения меры угла, когда известны противоположная сторона и сторона, прилегающая к углу. Arctan имеет практическое применение в архитектуре, строительстве, ландшафтном дизайне, физике и инженерии, а также в других научных и математических областях.
Лучший метод для определения арктана — научный калькулятор . Кнопка arctan должна находиться над касательной на калькуляторе. Таблица данных также может использоваться для определения арктангенса; однако это может быть утомительным и громоздким методом, но он эффективен, если научный калькулятор недоступен.
Далее мы рассмотрим несколько примеров, в которых арктангенс используется для определения меры угла.
Первый пример
В этом первом примере давайте найдем угловую меру θ:
Помните, что арктангенс — это тригонометрическая функция, которую вы можете использовать для определения меры угла, если вы знаете сторону, противоположную и сторону, примыкающую к измеряемому углу, которое вы пытаетесь найти.
Уравнение будет выглядеть так:
arctanθ = напротив / рядом
arctanθ = 15/23
arctanθ = 0.65
θ = 33 °
Второй пример
В этом втором примере мы найдем меру угла θ:
arctanθ = напротив / рядом
arctanθ = 3/2
arctanθ = 1,5
θ = 56 °
Пример 3
В нашем последнем примере мы будем использовать пандус для инвалидных колясок, который поднимается на 6 футов вертикально. на расстоянии 25 футов. Каков угол наклона пандуса?
arctanθ = напротив / рядом
arctanθ = 6/25
arctanθ = 0.24
θ = 13 °
Резюме урока
arctan — это обратная тригонометрическая функция функции касательной , которая представляет собой отношение стороны, противоположной углу, к стороне, прилегающей к углу. Функция arctan используется для определения углов прямоугольного треугольника, когда известны катеты треугольника. Он имеет практическое применение в архитектуре, инженерии и физике, а также в других науках. Арктангенс рассчитывается с помощью научного калькулятора или таблицы данных.
Arctan
Арктангенс, записанный как arctan или tan ^-1 (не путать с) — это функция арктангенса. Касательная имеет обратную функцию только в ограниченной области
Область должна быть ограничена, потому что для того, чтобы функция имела инверсию, функция должна быть взаимно однозначной, что означает, что ни одна горизонтальная линия не может пересекать график функции более одного раза.Поскольку касательная является периодической функцией, без ограничения области определения, горизонтальная линия будет периодически пересекать функцию бесконечно много раз.
Одно из свойств обратных функций состоит в том, что если точка (a, b) находится на графике функции f, точка (b, a) находится на графике обратной функции. Это фактически означает, что график обратной функции является отражением графика функции через линию y = x.
График y = arctan (x) показан ниже.
Как видно из рисунка, y = arctan (x) является отражением tan (x) в ограниченной области
Калькулятор Arctan
Ниже приведен калькулятор для определения значения арктангенса числа или значения тангенса угла.
С помощью специальных углов найти arctan
Хотя мы можем найти значение арктангенса для любого значения x в интервале [-∞, ∞], существуют определенные углы, которые часто используются в тригонометрии (0 °, 30 °, 45 °, 60 °, 90 ° и их кратные и радианные эквиваленты), значения тангенса и арктангенса которых, возможно, стоит запомнить.Ниже приведена таблица, в которой показаны эти углы (θ) как в радианах, так и в градусах, а также их соответствующие значения тангенса, tan (θ).
θ -90 ° -60 ° -45 ° -30 ° 0 ° 30 ° 45 ° 60 ° 90 °
тангенс (θ) undefined -1 0 1 undefined
Чтобы найти tan (θ), нам нужно либо просто запомнить значения, либо запомнить, что tan (θ) = и определите значение tan (θ) на основе значений синуса и косинуса, которые следуют шаблону, который может быть легче запомнить.Обратитесь к соответствующим страницам, чтобы просмотреть метод, который может помочь с запоминанием значений синуса и косинуса.
После того, как мы запомнили значения или если у нас есть какая-то ссылка, становится относительно просто распознать и определить значения тангенса или арктангенса для специальных углов.
Обратные свойства
Как правило, функции и их обратные показывают взаимосвязь
f (f ^-1 (x)) = x и f ^-1 (f (x)) = x
При условии, что x находится в области определения функции.То же самое верно для tan (x) и arctan (x) в их соответствующих ограниченных доменах:
tan (arctan (x)) = x, для всех x
и
arctan (tan (x)) = x, для всех x в (,)
Эти свойства позволяют нам оценивать состав тригонометрических функций.
Состав арктангенса и тангенса
Если x находится в пределах домена, оценить композицию arctan и tan относительно просто.
Примеры:
Состав других тригонометрических функций
Мы также можем составлять композиции, используя все другие тригонометрические функции: синус, косинус, косеканс, секанс и котангенс.
Тот же процесс можно использовать с выражением переменной.
Пример:
Найдите грех (arctan (3x)).
Учитывая arctan (3x) = θ, мы можем найти, что tan (θ) =, и построить следующий треугольник:
Чтобы найти синус, нам нужно найти гипотенузу, так как sin (θ) =. Пусть c — длина гипотенузы. Используя теорему Пифагора,
(3x) ² + 1 ² = с ²
9x ² + 1 = с ²
с =
и
sin (arctan (3x)) = sin (θ) =
Использование arctan для решения тригонометрических уравнений
Арктангенс также можно использовать для решения тригонометрических уравнений, включающих функцию тангенса.
Примеры:
Решите следующие тригонометрические уравнения относительно x, где 0≤x
1. 3tan (x) =
3tan (x) =
тангенс (x) =
x = arctan ()
Касательная положительна в двух квадрантах, I и III, поэтому есть два решения: x = и x =. Это единственные два угла в пределах 0≤x <2π, значение тангенса которых равно.
2. tan ² (x) — tan (x) = 0
загар ² (x) — загар (x) = 0
tan (x) (tan (x) -) = 0
tan (x) = 0 или tan (x) — = 0
tan (x) = 0 или tan (x) =
x = 0, π или x =
математических слов: обратная касательная
Обратный тангенс
tan ^-1
Tan ^-1
arctan
Arctan
Функция, обратная касательной.
Основная идея : Найти загар ^-1 1, мы спрашиваем, «какой угол имеет тангенс, равный 1?» Ответ составляет 45 °. В результате мы говорим, что tan ^-1 1 = 45 °. В радианах это tan ^-1 1 = π / 4.
Еще : На самом деле существует много углов, касательная равна 1. Мы действительно спрашиваем, «что самое простое, самый основной угол, тангенс которого равен 1? «Как и прежде, ответ — 45 °.Таким образом, загар ^-1 1 = 45 ° или tan ^-1 1 = π / 4.
Подробности : Что такое загар ^-1 (–1)? Выбираем ли мы 135 °, –45 °, 315 °, или под другим углом? Ответ –45 °. Обратной тангенсой выбираем угол на правой половине единицы круг, имеющий размер как можно ближе к нулю. Таким образом, загар ^-1 (–1) = –45 ° или тангенциальный угол ^-1 (–1) = –π / 4.
В другими словами, диапазон tan ^-1 равен ограничено (–90 °, 90 °) или.
Примечание : arctan относится к «арктангенсу» или радианной мере дуга на окружности, соответствующая заданному значению касательной.
Техническое примечание : Поскольку ни одна из шести триггерных функций синус, косинус, тангенс, косеканс, секанс и котангенс не взаимно однозначны, их обратные не являются функциями. Каждая триггерная функция может иметь свой домен ограничен, однако, чтобы сделать его инверсию функцией.Некоторые математики пишут эти ограниченные триггерные функции и их перевернутое с заглавной буквы (например, Tan или Tan ^-1). Однако большинство математиков не следуют этой практике. Этот веб-сайт не делает различий между заглавными и не заглавными буквами триггерные функции.
См. также
обратный тригонометрия, обратная триггерные функции, интервальное обозначение
Формула Arctan — Cuemath
В тригонометрии тангенс определяется как отношение противоположной стороны к смежной стороне определенного угла прямоугольного треугольника, тогда как arctan является обратной функцией касательной и используется для найти угол.{2} \ right) \) + C
Формулы арктангенса для π
π / 4 = 4 арктангенс (1/5) — арктангенс (1/239)
π / 4 = арктангенс (1/2) + арктангенс (1/3)
π / 4 = 2 арктангенс (1/2) — арктангенс (1/7)
π / 4 = 2 арктангенса (1/3) + арктангенса (1/7)
π / 4 = 8 арктангенс (1/10) — 4 арктангенса (1/515) — арктангенс (1/239)
π / 4 = 3 arctan (1/4) + arctan (1/20) + arctan (1/1985)
π / 4 = 24 арктангенса (1/8) + 8 арктангенса (1/57) + 4 арктангенса (1/239)
Решенные примеры с использованием формулы арктана
Пример 1
В прямоугольном треугольнике ABC основание 23 и высота 15.Найдите базовый угол.
Решение
Найти: базовый угол
По формуле арктана
θ = arctan (напротив ÷ смежный)
θ = арктангенс (15 ÷ 23) = арктангенс (0,65)
θ = 33 градуса или 33 ^o.
Ответ: Угол 33 ^o.
Пример 2
В прямоугольном треугольнике ABC, если основание треугольника равно 2 единицам, а высота треугольника равна 3 единицам.Найдите базовый угол.
Решение
Найти: базовый угол
По формуле арктана
θ = arctan (напротив ÷ смежный)
θ = arctan (3 ÷ 2) = arctan1,5
θ = 56 ^o
Ответ: Угол 56 ^o.
Определение арктангенса по Merriam-Webster
дуга · загар · гент | \ (ˌ) ärk-ˈtan-jənt \
варианты: или реже арктангенс
арктангенсы множественного числа также арктангенсы
: функция, обратная касательной если y — тангенс угла θ, то θ — арктангенс угла y — сокращение arctan
Функция арктангенса — исчисление
Эта статья посвящена конкретной функции от подмножества действительных чисел до действительных чисел.Информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференциации и интеграции, представлена в статье.
Посмотреть полный список определенных функций в этой вики
Для функций, включающих углы (тригонометрические функции, обратные тригонометрические функции и т. Д.), Мы следуем соглашению, согласно которому все углы измеряются в радианах. Так, например, угол измеряется как.
Определение
Функция арктангенса , обозначенная или, является функцией, определяемой следующим образом: for, — это уникальный номер в открытом интервале, такой что.
Эквивалентно, функция арктангенса является функцией, обратной ограничению функции касательной к интервалу.
Основные данные
График
Вот график из уменьшенного положения, где горизонтальные асимптоты четкие.
Вот более крупный вариант с проведенной касательной через начало координат (линия), указывающей, что начало координат является точкой перегиба графика:
Дифференциация
Первая производная
ЧТО МЫ ИСПОЛЬЗУЕМ : теорема обратной функции и касательная функция # Первая производная, которая, в свою очередь, зависит от синусоидальной функции # Первая производная, функция косинуса # Первая производная и правило частного для дифференцирования
Мы используем теорему об обратной функции, и тот факт, что производная от равна.
По теореме об обратной функции имеем:
Если, то и получаем:
Подключив это к вышесказанному, мы получим:
Вторая производная
ЧТО МЫ ИСПОЛЬЗУЕМ : цепное правило дифференцирования и правило дифференцирования для степенных функций
Вторая производная определяется как:
Высшие производные
Для высших производных мы используем правило частного дифференцирования в сочетании с цепным правилом дифференцирования для работы со степенями.
Интеграция
Первая первообразная
Мы можем проинтегрировать это, используя метод интегрирования обратной функции, и получить:
Это становится:
Имеем, и получаем:
Если говорить более подробно, мы можем выполнить интеграцию, используя интеграцию по частям, принимая как часть для дифференциации и как часть для интеграции:
Для второй интеграции мы интегрируем, используя формулировку для получения.
Высшие первообразные
Функция может быть антидифференцирована любое количество раз с помощью интеграции по частям. Причина этого в том, что производная функции является рациональной функцией, а рациональные функции могут многократно интегрироваться в элементарно выражаемые функции.
Все первообразные можно выразить в виде:
где — полиномиальные. Обратите внимание, что это неоднозначно с точностью до сложения многочленов степени, если мы интегрируем времена.
Высшие первообразные
Функция может быть антидифференцирована любое количество раз с помощью интеграции по частям.
Серия
Power и серия Тейлора
Расчет степенного ряда
Степенный ряд для функции около 0 может быть получен следующим образом.
Мы знаем, что для функции у нас есть степенной ряд:
Интегрируя с определенным интегралом, получаем:
Левая часть, поэтому получаем:
По теореме о чередующемся ряду мы отмечаем, что степенной ряд справа сходится для и для, поэтому по теореме Абеля мы заключаем, что он сходится от к соответствующих входных данных.
No related posts.