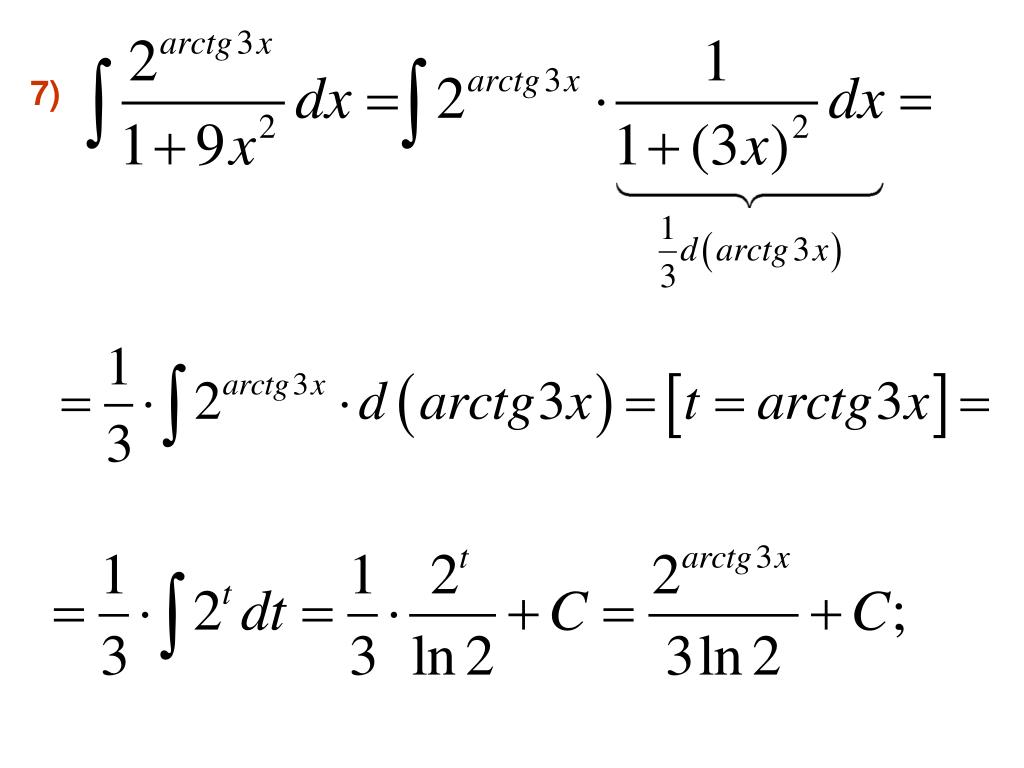арктан (х) | функция обратной тангенса
арктан (х) | функция обратной тангенсаГлавная / Математика / Тригонометрия /Arctan
Arctan (x), tan -1 (x), функция обратной тангенса .
- Определение слова arctan
- График арктана
- Правила Арктана
- Стол Arctan
- Калькулятор Arctan
Определение арктана
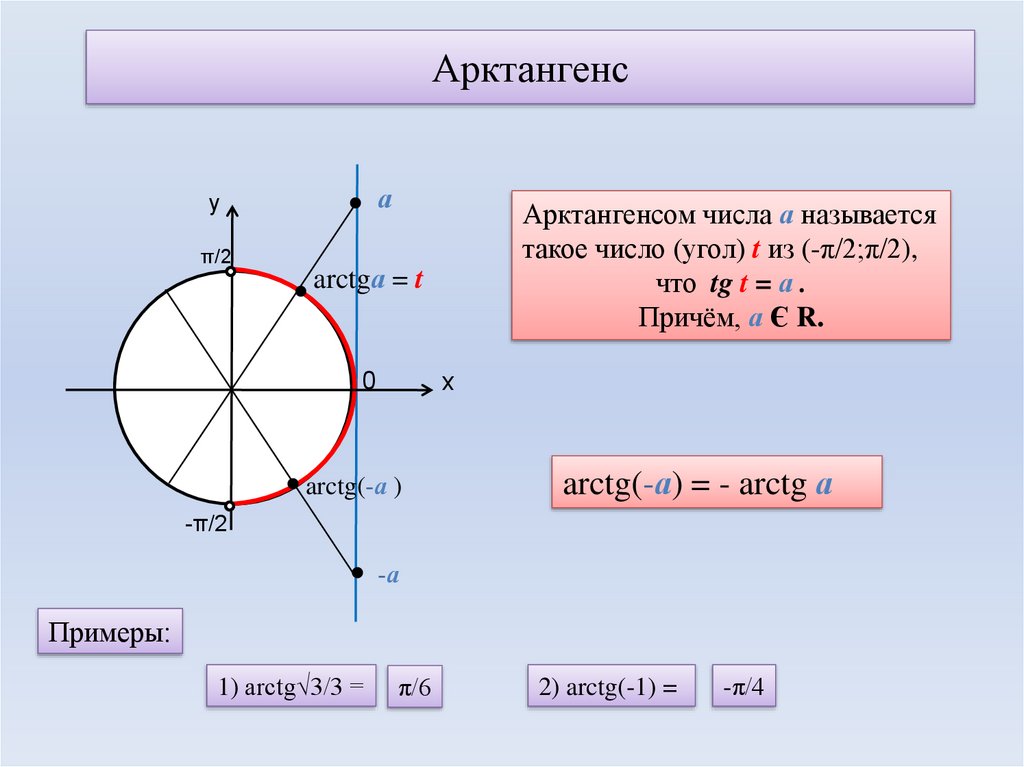
Арктангенс x определяется как функция, обратная касательной к x, когда x является вещественным (x ∈ℝ ).
Когда тангенс y равен x:
загар у = х
Тогда арктангенс x равен функции арктангенса x, которая равна y:
arctan x = tan -1 x = y
пример
arctan 1 = тангенс -1 1 = π / 4 рад = 45 °
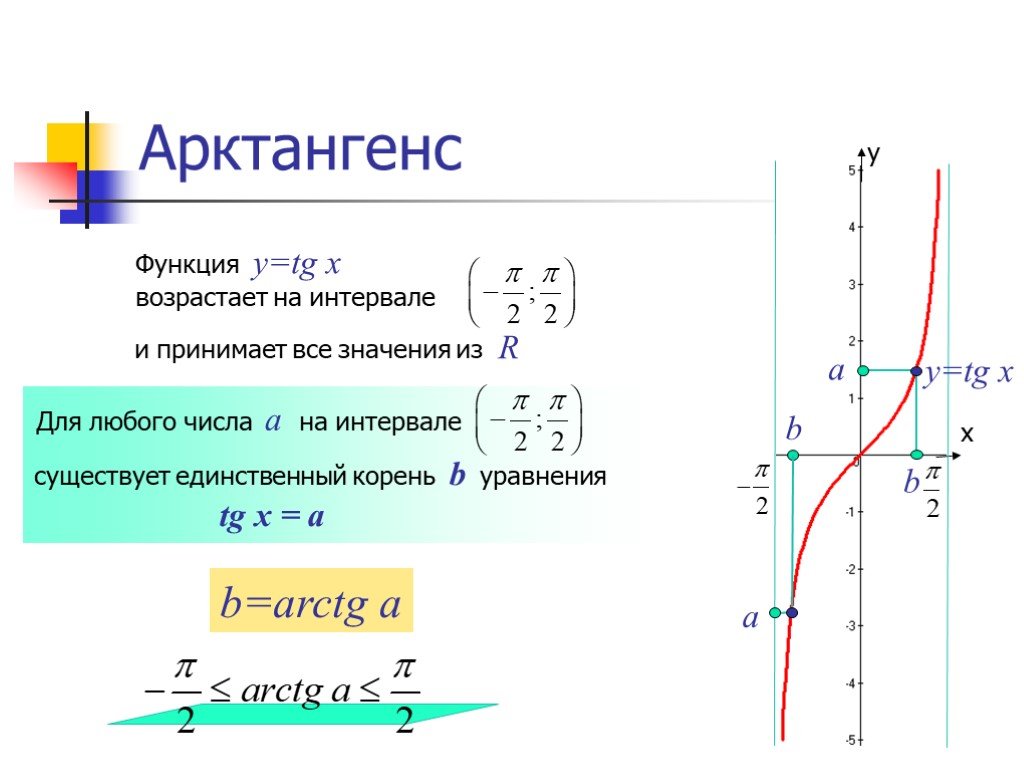
График арктана
Правила Арктана
| Название правила | Правило |
|---|---|
| Тангенс арктангенса | загар (arctan x ) = x |
| Арктан отрицательного аргумента | arctan (- x ) = — arctan x |
| Арктановая сумма | arctan α + arctan β = arctan [( α + β ) / (1- αβ )] |
| Арктанская разница | arctan α — arctan β = arctan [( α — β ) / (1+ αβ )] |
| Синус арктангенса | |
| Косинус арктангенса | |
| Взаимный аргумент | |
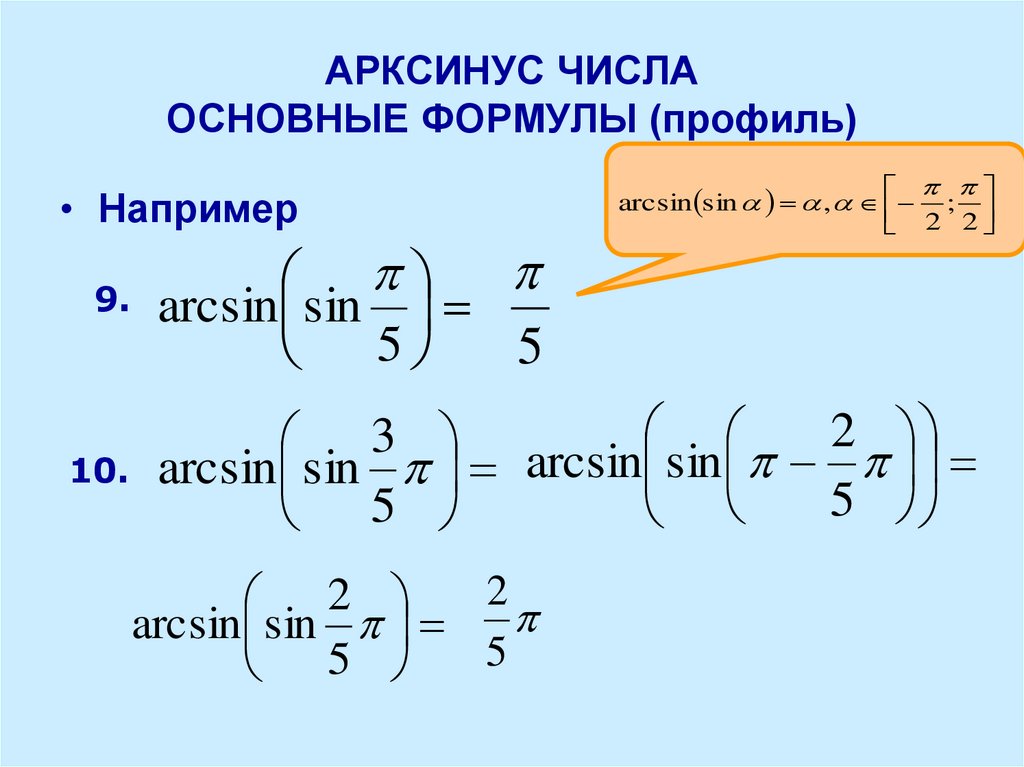
| Арктан из арксина | |
| Производное от arctan | |
| Неопределенный интеграл от arctan |
Стол Arctan
| х | арктан (х) (рад) | арктан (х) (°) |
|---|---|---|
| -∞ | -π / 2 | -90 ° |
| -3 | -1,2490 | -71,565 ° |
| -2 | -1,1071 | -63,435 ° |
| -√ 3 | -π / 3 | -60 ° |
| -1 | -π / 4 | -45 ° |
| -1 / √ 3 | -π / 6 | -30 ° |
| -0,5 | -0,4636 | -26,565 ° |
| 0 | 0 | 0 ° |
| 0,5 | 0,4636 | 26,565 ° |
| 1 / √ 3 | π / 6 | 30 ° |
| 1 | π / 4 | 45 ° |
| √ 3 | π / 3 | 60 ° |
| 2 | 1,1071 | 63,435 ° |
| 3 | 1,2490 | 71,565 ° |
| ∞ | π / 2 | 90 ° |
- Касательная функция
- Функция арккосинуса
- Функция арксинуса
- Арктан из 0
- Арктан из 1
- Арктан из 2
- Арктан бесконечности
- Производное от arctan
- Интеграл арктана
- Синус арктана
- Косинус арктана
- График арктана
- Калькулятор Arctan
- Конвертер градусов в радианы
Advertising
ТРИГОНОМЕТРИЯ
- Функция Arccos
- Функция Arcsin
- Функция арктана
- Функция косинуса
- Функция синуса
- Касательная функция
БЫСТРЫЕ ТАБЛИЦЫ
- Рекомендовать сайт
- Отправить отзыв
- О нас
Выражение для тригонометрической функции : Дискуссионные темы (М)
Сообщения без ответов | Активные темы | Избранное
| Skipper |
| ||
24/03/09 |
| ||
| |||
| gris |
| |||
13/08/08 |
| |||
| ||||
| Skipper |
| ||
24/03/09 |
| ||
| |||
| meduza |
| |||
03/06/09 |
| |||
| ||||
| venco |
| |||
04/05/09 |
| |||
| ||||
| Skipper |
| ||
24/03/09 |
| ||
| |||
| venco |
| |||
04/05/09 |
| |||
| ||||
| Skipper |
| ||
24/03/09 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Garik2 |
| |||
03/08/09 |
| |||
| ||||
| AKM |
| |||||
18/05/09 |
| |||||
| ||||||
| Garik2 |
| |||
03/08/09 |
| |||
| ||||
| AKM |
| |||||
18/05/09 |
| |||||
| ||||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 14 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
arctan(x), функция арктангенса
Arctan(x), тангенс -1 (x), функция арктангенса.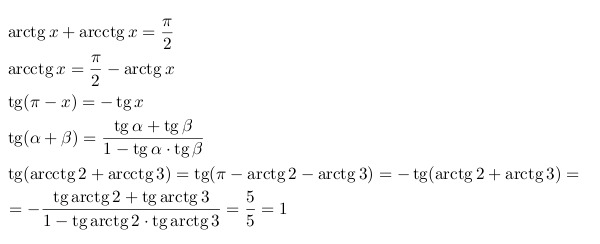
- Арктан определение
- График арктана
- f (х) = арктангенс (х)
- Арктан правила
- Арктан стол
Определение арктангенса
Арктангенс x определяется как функция арктангенса x, когда x является действительным (x∈ℝ).
Когда тангенс y равен x:
tan y = x
Тогда арктангенс x равен функции арктангенса x, которая равна y:
arctan x = TAN -1 X = Y
Например:
Реклама
Арктан 1 = TAN -1 1 = π/4 RAD = 45 °
График Arctan
F (График Arctan
F ((Arctan
F 6 ((Arctan
F (. х ) = арктангенс ( х )
Правила ARCTAN

. -x) = — arctan x
Стол Arctan
| x | Арктан (x) (RAD) | Arctan (x) (°) |
| -Ch | 565°» data-order=»-71.565°»> -71.565° | |
| -2 | -1.1071 | -63.435° |
| -√3 | -π/3 | -60° |
| -1 | -π/4 | -45° |
| -1/√3 | -π/6 | -30° |
| 5″ data-order=»-0.5″> -0.5 | -0.4636 | -26.565° |
| 0 | 0 | 0° |
| 0.5 | 4636″ data-order=»0.4636″> 0.4636 | 26.565° |
| 1/√3 | π /6 | 30° |
| 1 | π/4 | 45° |
| √3 | π/3 | 60° |
| 2 | 1071″ data-order=»1.1071″> 1.1071 | 63.435° |
| 3 | 1.2490 | 71.565° |
| ∞ | π/2 | 90° |
Advertisements
Inverse Trigonometric Function: Arctangent
Перед изучением этого раздела рекомендуется прочитать
Попытка «отменить» тригонометрические функции.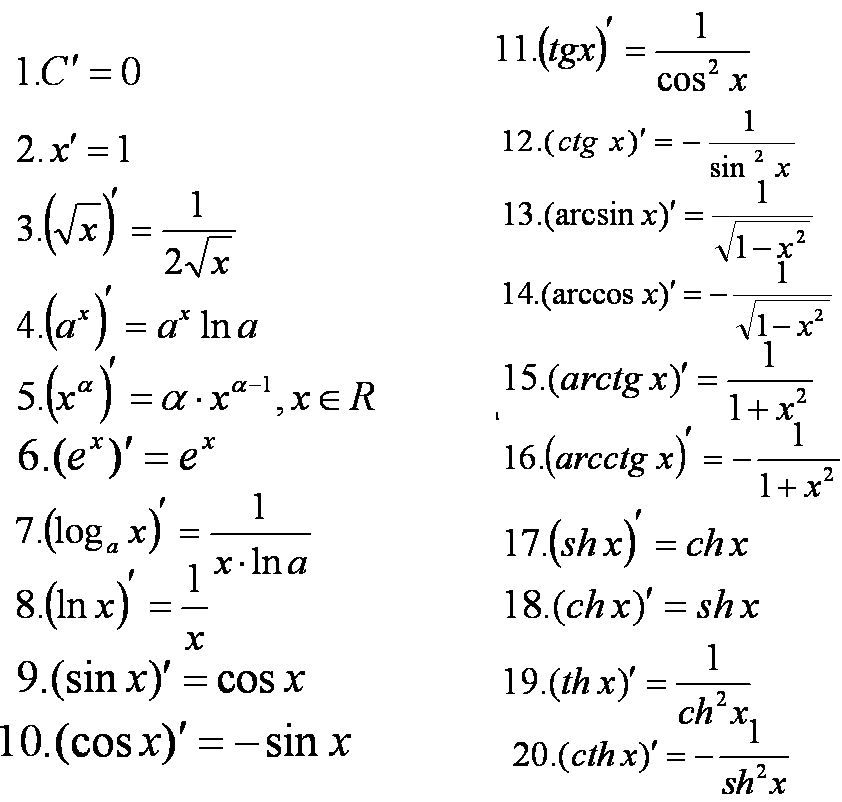
Этот раздел является копией книги «Обратная тригонометрическая функция: арксинус» с соответствующими изменениями.
Если вы освоили раздел арксинуса, то этот должен быть быстрым и легким!
Функция арктангенса (точное определение ниже) — это лучшее, что мы можем сделать, пытаясь получить обратную функцию
касательная функция.
Функция арктангенса равна , а на самом деле — обратная зеленая фигура, показанная выше!
Вот функциональная панель того, что происходит:
Функция тангенса принимает действительное число
(исключая $\,\frac{\pi}{2} + k\pi\,$ для целых чисел $\,k\,$)
в качестве входа. Это дает действительное число на выходе. Например (как показано ниже), | Когда мы пытаемся использовать поле касательной функции «назад»,
мы попадаем в беду. Вывод $\,0.5\,$ мог прийти | Однако,
когда мы используем зеленый кусок касательная кривая, проблема решена! Теперь их работает только один вход . Обратите внимание, что $\,\color{green}{x}\,$ находится в интервале $\,(- \frac{\pi}2,\frac{\pi}2)\,$. |
Это немного неправильное название, но функция арктангенса (точное определение ниже) часто упоминается как
как «функция арктангенса».
Лучшее название было бы что-то вроде «обратная функция касательной с соответствующими ограничениями».
(Однако неудивительно, что люди не говорят ничего такого длинного и громоздкого.)
Итак, что же такое $\,\arctan 0.5\,$?
$\,\arctan 0,5\,$ — число в интервале $\,(-\frac{\pi}{2},\frac{\pi}{2})\,$, тангенс которого равен $\,0,5 \,$
Что такое $\,\arctan x\,$?
В более общем случае пусть $\,x\,$ будет любым действительным числом.
Затем:
$\,\arctan x\,$ — число в интервале $\,(-\frac{\pi}{2},\frac{\pi}{2})\,$, тангенс которого равен $\,x \,$
В моем собственном уме (здесь говорит автор доктор Кэрол Бернс) я произношу следующие слова:
$\,\arctan x\,$ — это число между $\,-\frac{\pi}{2}\,$ и $\,\frac{\pi}{2}\,$, тангенс которого равен $\ ,х\,$
Я лично знаю конечные точки не включены , так что это меня не смущает.
Однако слово «между» неоднозначно — оно может включать или не включать конечные точки, в зависимости от контекста.
Можно уточнить, сказав:
$\,\arctan x\,$ — число между $\,-\frac{\pi}{2}\,$ и $\,\frac{\pi}{2}\,$ (не включая конечные точки )
, тангенс которого равен $\,x\,$
. .. но тогда он теряет свою простоту.
Проблемы с языком.
Выберите слова, которые работают на вас!
.. но тогда он теряет свою простоту.
Проблемы с языком.
Выберите слова, которые работают на вас!
Точное определение функции арктангенса
Далее следует точное определение функции арктангенса.
Это может выглядеть немного пугающе — примечания, следующие за определением, должны помочь.
9{-1}\,$
Пусть $\,x\,$ — действительное число.
Используя обозначение ‘$\,\arctan\,$’ для функции арктангенса: $$ \cssId{s63}{y = \arctan x}\ \ \ \ \ \cssId{s64}{\text{если и только если}}\ \ \ \ \bigl(\ \cssId{s65}{\тангенс у = х}\ \ \cssId{s66}{\text{И}}\ \ \cssId{s67}{-\frac{\pi}{2} \lt y\lt \frac{\pi}{2}}\ \bigr) $$ 9{-1} х}\ \ \ \ \ \cssId{s70}{\text{если и только если}}\ \ \ \ \bigl(\ \cssId{s71}{\тангенс у = х}\ \ \cssId{s72}{\text{И}}\ \ \cssId{s73}{-\frac{\pi}{2} \lt y\lt \frac{\pi}{2}}\ \bigr) $$
Примечания к определению функции арктангенса:
- ПОНИМАНИЕ ОПРЕДЕЛЕНИЯ:
Определение точно отвечает на вопрос: «Каково число $\,\arctan x\,$?»
Вот как:- Напомним, что «если и только если» означает то же самое, что и эквивалентно.

Эквивалентные предложения имеют одинаковые значения истинности:
если одно верно, то верно и другое; если одно ложно, то и другое. - Таким образом, если предложение $\,y = \arctan x\,$ истинно,
затем сложное предложение ‘$\,\tan y = x\ \ \text{AND}\ \ -\frac{\pi}{2} \lt y\lt \frac{\pi}{2}\,$’ тоже должно быть правдой. - Если ‘$\,y = \arctan x\,$’ истинно, затем ‘$\,y\,$’ — это просто другое название для ‘$\,\arctan x\,$’. 9{\ text {находясь в интервале $ \ strut \, (- \ frac {\ pi} {2}, \ frac {\ pi} {2}) \, $}}} \ \ bigr) $$
- То есть:
$\,\arctan x\,$ — число в интервале $\,(-\frac{\pi}{2},\frac{\pi}{2})\,$, тангенс которого равен $\,x \,$
- Напомним, что «если и только если» означает то же самое, что и эквивалентно.
Ваш браузер не поддерживает аудио элементы.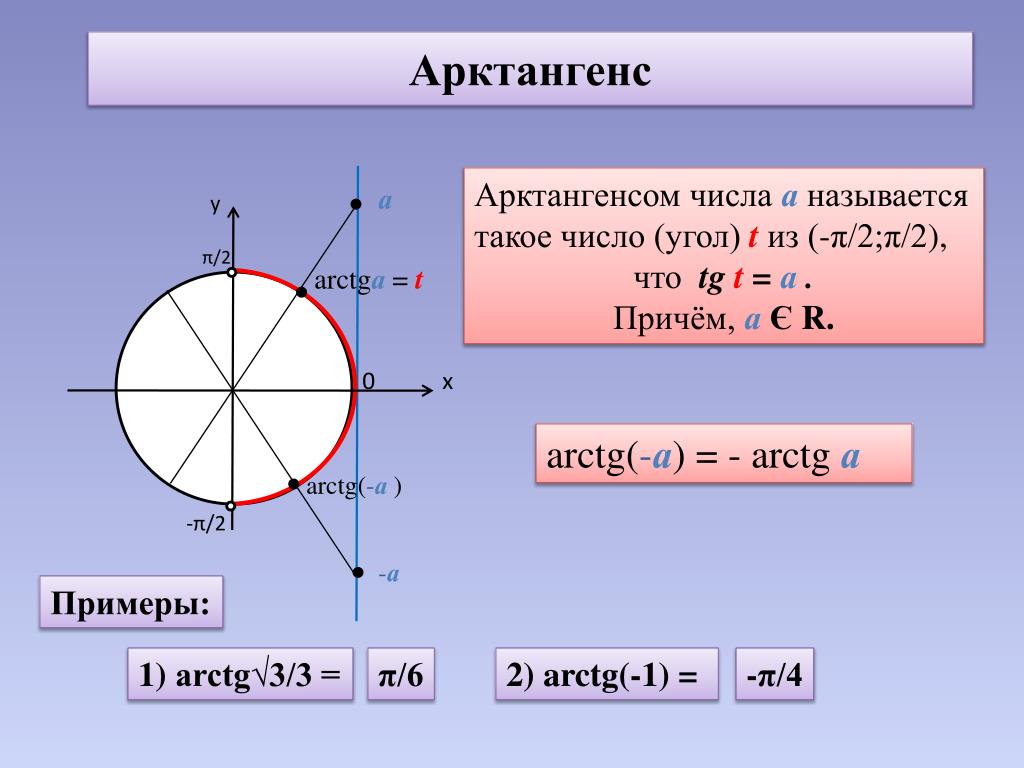
ПРОЧТЕНИЕ, ЧАСТЬ 2
- ОФИЦИАЛЬНОЕ НАЗВАНИЕ В ОТНОШЕНИИ ФУНКЦИИ ОБОЗНАЧЕНИЯ СОКРАЩЕНИЯ:
Формальное название функции, обсуждаемой в этом разделе, — «арктангенс».
Произносится как ARC-tan-gent. 9{-1}\,$’ вводит в заблуждение и дает себя к ошибкам.
Этот автор настоятельно предпочитает обозначение ‘$\,\arctan\,$’. - АЛЬТЕРНАТИВНОЕ ОПРЕДЕЛЕНИЕ, С ИСПОЛЬЗОВАНИЕМ ГРАДУСОВ ВМЕСТО РАДИАНОВ:
Входные данные для тригонометрических функций можно рассматривать как действительные числа (радианы) или градусы.
Например, $\,\tan \frac{\pi}{4} = 1\,$: здесь $\,\frac{\pi}{4}\,$ — мера в радианах. 9\circ)\,$, тангенс которого равен $\,x\,$ - НАВЫКИ КАЛЬКУЛЯТОРА:
Если калькулятор находится в режиме градусов, то $\,\arctan x\,$ сообщается в градусах.
Если калькулятор работает в радианном режиме, то значение $\,\arctan x\,$ отображается в радианах. - ГРАФИК ФУНКЦИИ АРКТАНГЕНСА: 9{-1}\,$,
находится путем отражения графика $\,f\,$
относительно прямой $\,y = x\,$.
Ниже этот прием используется для построения графика функции арктангенса:Вот часть касательной кривой
который используется для определения функции арктангенса:
домен: $\,(-\frac{\pi}{2},\frac{\pi}{2})\,$диапазон: $\,(-\infty,\infty)\,$
Вот та же кривая,
вместе со своим отражением относительно линии $\,\color{red}{y = x}\,$График функции арктангенса
домен: $\,(-\infty,\infty)\,$диапазон: $\,(-\frac{\pi}{2},\frac{\pi}{2})\,$
Обратите внимание, что домен и область значений функции и ее обратной функции меняются местами!
Домен одного является диапазоном другого. 9{-1}\,$ что-то делает, а $\,f\,$ отменяет действие Поскольку функции тангенса и арктангенса являются , а не истинными обратными друг другу,
9{-1}\,$ что-то делает, а $\,f\,$ отменяет действие Поскольку функции тангенса и арктангенса являются , а не истинными обратными друг другу,
отношения между ними немного сложнее.Вот направление, в котором они делают красиво «отменяют» друг друга: начните с числа, сначала примените функцию арктангенса, затем примените функцию тангенса, и в конечном итоге там, где вы начали. Вот подробности:
Для всех $\,x\in \Bbb R\,$, $$ \cssId{sb65}{\tan(\arctan x) = x} $$
- начните с $\,\color{red}{x}\in \Bbb R\,$
- функция арктангенса переводит $\,\color{red}{x}\,$ в $\,\color{green}{\arctan x}\,$ в интервале $\,(-\frac{\pi} 2,\frac{\pi}2)\,$
- функция касательной возвращает
$\,\color{green}{\arctan x}\,$ обратно в $\,\color{red}{x}\,$
Вот направление, где они не обязательно красиво «отменять» друг друга: начните с числа, сначала примените функцию тангенса, затем примените функцию арктангенса.  Если число, с которого вы начали, находится вне интервала $\,(-\frac{\pi}2,\frac{\pi}2)\,$,
тогда вы не окажетесь там, где начали!
Если число, с которого вы начали, находится вне интервала $\,(-\frac{\pi}2,\frac{\pi}2)\,$,
тогда вы не окажетесь там, где начали!Вот подробности:
Для всех $\,x\in (-\frac{\pi}2,\frac{\pi}2)\,$, $$ \cssId{sb75}{\arctan(\tan x) = x} $$
(См. верхний график справа.) Для всех $\,x\,$ в области определения функции тангенса, но не в $\,(-\frac{\pi}2,\frac{\pi}2)\,$, $$ \cssId{sb78}{\arctan(\tan x) \ne x} $$
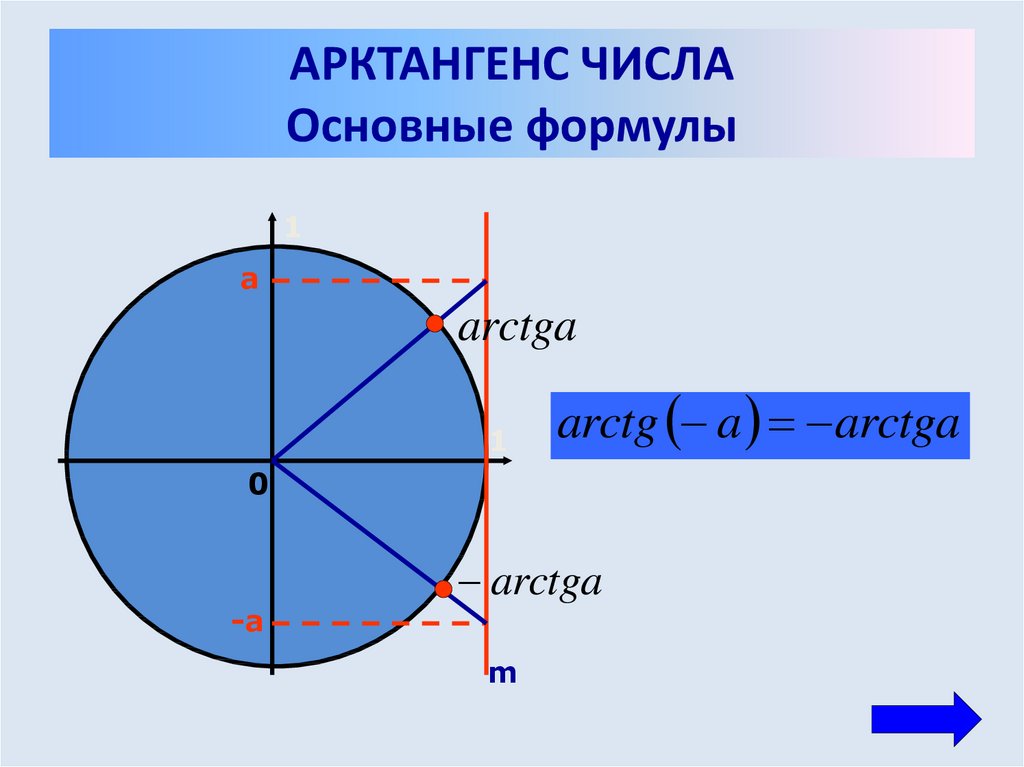
(См. нижний график справа.) Пример: Найдите точное значение $\,\arctan(-1/\sqrt 3)\,$ 9\circ\,$, тангенс которой равен $\,-\frac{1}{\sqrt 3}\,$.

- По мере необходимости, просмотреть информацию о размере и знаке касательная функция.
9\circ\,$, тангенс которого равен минус , угол находится в квадранте IV.
Так как нам нужен угол, тангенс которого имеет размер $\,\frac{1}{\sqrt 3} \приблизительно 0,58\,$, сделайте красный сегмент имеет эту длину.
Таким образом, показанный (отрицательный) угол равен $\,\arctan(-1/\sqrt 3)\,$. 9\цирк\,$.

 08.2010, 21:32
08.2010, 21:32 
 08.2010, 21:46
08.2010, 21:46  08.2010, 21:47
08.2010, 21:47  08.2010, 21:49
08.2010, 21:49  08.2010, 21:57
08.2010, 21:57  08.2010, 21:59
08.2010, 21:59  08.2010, 22:05
08.2010, 22:05  08.2010, 22:20
08.2010, 22:20 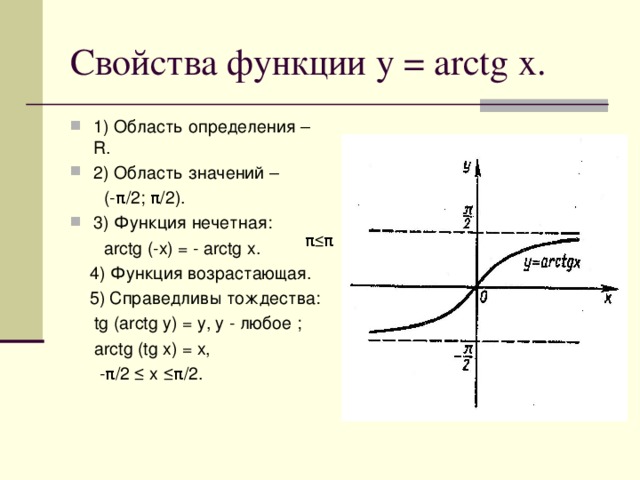 08.2010, 10:47
08.2010, 10:47 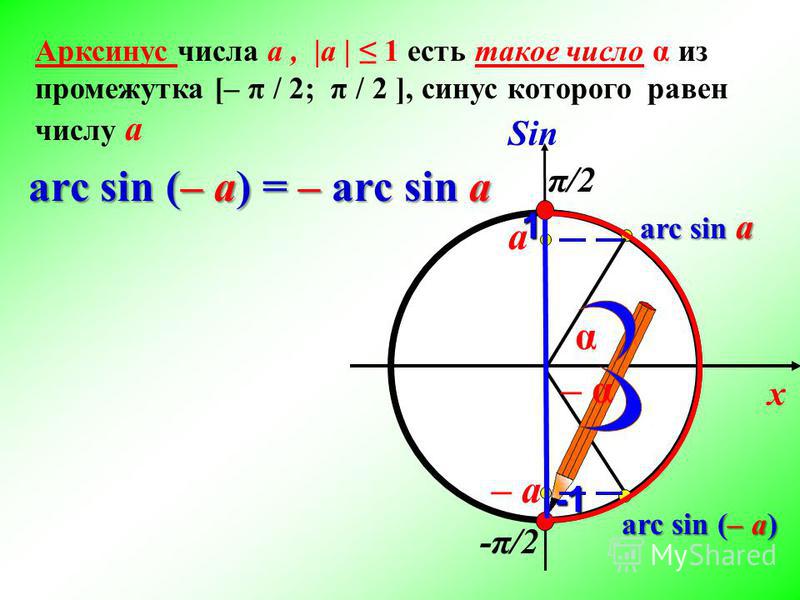 08.2010, 12:01
08.2010, 12:01  08.2010, 22:25
08.2010, 22:25 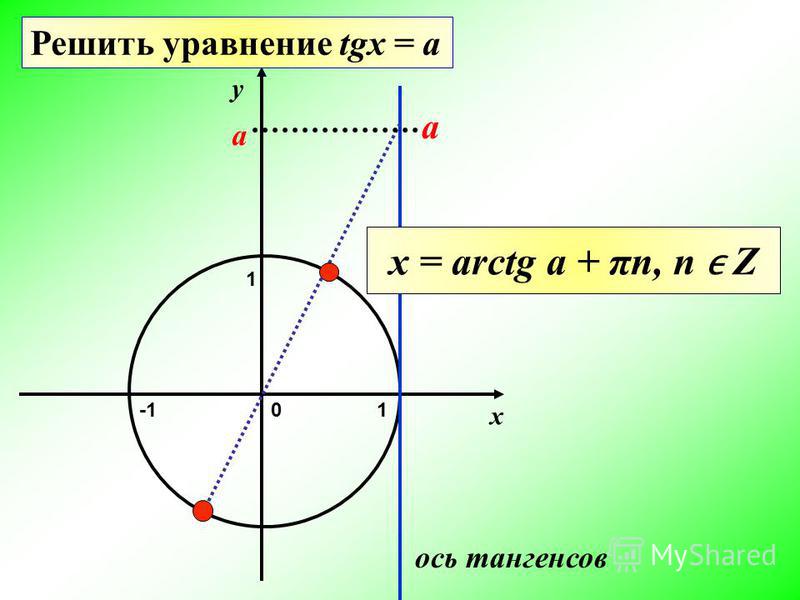 Почему-то мне кажется, что он не будет возражать. Если возражения появятся, я перенесу эту часть в какую-нибудь отдельную тему типа «Глупо аппроксимировать арктангенс полиномом». Или «Глупо или не глупо аппроксимировать арктангенс полиномом?».
Почему-то мне кажется, что он не будет возражать. Если возражения появятся, я перенесу эту часть в какую-нибудь отдельную тему типа «Глупо аппроксимировать арктангенс полиномом». Или «Глупо или не глупо аппроксимировать арктангенс полиномом?».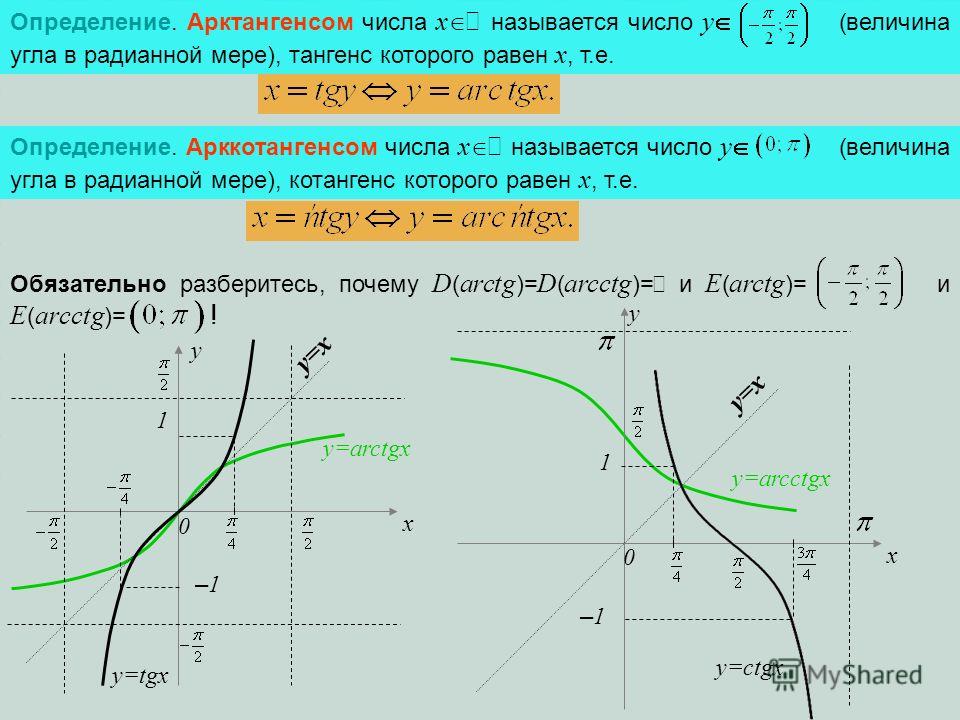


 9{-1}\,$ что-то делает, а $\,f\,$ отменяет действие Поскольку функции тангенса и арктангенса являются , а не истинными обратными друг другу,
9{-1}\,$ что-то делает, а $\,f\,$ отменяет действие Поскольку функции тангенса и арктангенса являются , а не истинными обратными друг другу, 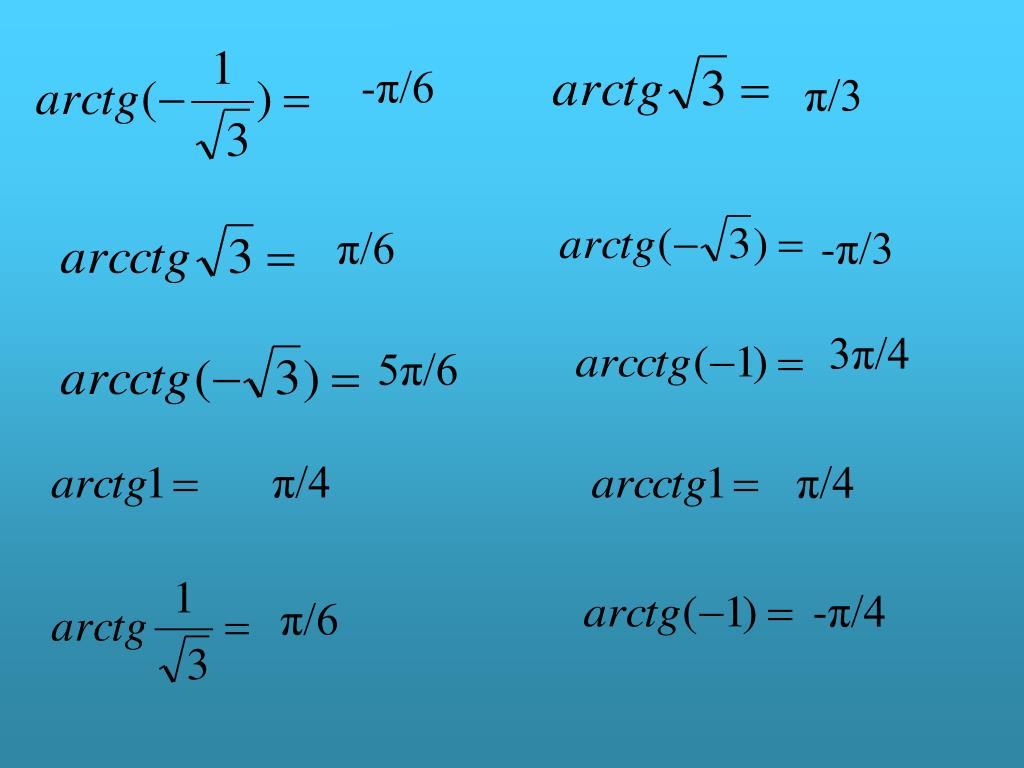 Если число, с которого вы начали, находится вне интервала $\,(-\frac{\pi}2,\frac{\pi}2)\,$,
тогда вы не окажетесь там, где начали!
Если число, с которого вы начали, находится вне интервала $\,(-\frac{\pi}2,\frac{\pi}2)\,$,
тогда вы не окажетесь там, где начали!