Другие примеры:
Квадратный корень из комплексного числа
sqrt(1-24*i)
Деление комплексных чисел
(1-2i)/(1+4i)
Кубический корень
cbrt(1-7*i)
Умножение комплексных чисел
(5+4i)*(8-2i)
Корни четвертой и пятой степени
(1-11*i)^(1/4)
(1-11*i)^(1/5)
Комплексно-сопряженное число
conj(1 + 4j)
(3/2-3*sqrt(3)/2*i)/conj(-5/2-1/3*i)
Реальная часть комплексного числа
re(1+I)
Комплексные уравнения
z - |z| = 2 + i
(i + 5)*z - 2*i + 1 = 0
Возведение в степень
i^15
(1 - 2*i)^32
Мнимая и действительная часть
im(re(x) + y)
Мнимая часть
im(1+I)
Модуль комплексного числа
absolute(1+I)
Аргумент
arg(1+I)
Комплексный знак числа
sign(1+I)
Можно использовать следующие функции от z (например, от z = 1 + 2. 2
2
Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Аргумент комплексного числа — справочник для студентов и школьников
ОПРЕДЕЛЕНИЕ
Угол \(\ \varphi \) (измеренный в радианах) радиус-вектора точки, который соответствует комплексному числу \(\ z \) на комплексной плоскости, называется аргументом числа \(\ z : \varphi=\arg z \) . В этом случае вещественные числа \(\ \mathbf{X} \), \(\ y \) комплексного числа \(\ z=x+i y \) могут быть выражены через модуль \(\ \mathbf{r} \) и аргумент \(\ \varphi : x=r \cos \varphi, y=r \sin \varphi \).
Геометрическая интерпретация комплексного числа
Если мы рассмотрим плоскость с прямоугольной системой координат, то любое комплексное число \(\
z=x+i y
\) можно связать с точкой на этой плоскости с соответствующими координатами: \(\
\{x, y\}
\) и радиус-вектор \(\
\mathbf{F}
\) комплексного числа, т.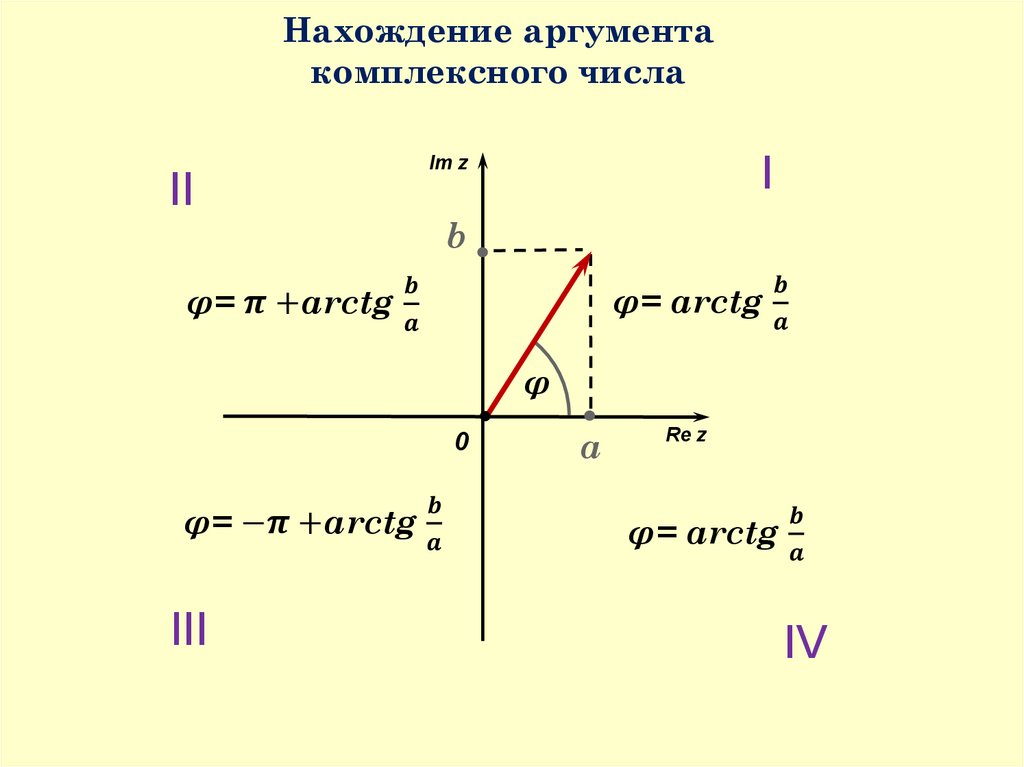 {2}}=\sqrt{1+3}=\sqrt{4}=2
\)
{2}}=\sqrt{1+3}=\sqrt{4}=2
\)
Следовательно, тригонометрическая форма комплексного числа:
\(\ z=2\left(\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}\right) \)
\(\ \frac{\pi}{3} \)
Тригонометрическая форма комплексного числа:\(\ z=2\left(\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}\right) \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Возведение в степень комплексного числа Комплексно сопряженные числа Модуль комплексного числа Показательная форма записи комплексного числа
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое Принимаю Политику конфиденциальностиПодпишись на рассылку, чтобы не пропустить информацию об акциях
Аргумент комплексного числа
Легко увидеть, что комплексные числа и векторы имеют много общего, если изобразить их на диаграмме Аргана. Например, сложение и вычитание комплексных чисел — это то же самое, что сложение и вычитание векторов с точки зрения геометрии. У вектора есть две характеристики: его направление и величина. Комплексное число также должно иметь эти две характеристики. Важно помнить, что размер комплексного числа называется его модулем. Чтобы выяснить направление комплексного числа, посмотрите на его аргумент.
Например, сложение и вычитание комплексных чисел — это то же самое, что сложение и вычитание векторов с точки зрения геометрии. У вектора есть две характеристики: его направление и величина. Комплексное число также должно иметь эти две характеристики. Важно помнить, что размер комплексного числа называется его модулем. Чтобы выяснить направление комплексного числа, посмотрите на его аргумент.
Комплексные числа
Помимо действительных чисел существует набор чисел из a+ib. Этот тип числа называется комплексным числом. Он используется для представления квадратного корня из отрицательных чисел. Научные исследования, гидродинамика, квантовая механика и обработка сигналов — вот примеры того, где могут быть полезны комплексные числа.
Комплексное число можно представить как сумму воображаемого числа и фактического числа, например: a+ib можно записать как a+z. Каждое число в этом предложении является точным числом, как «а» и «б»; a называется основной частью, а b называется мнимой частью, которая называется Im (z). Это также число, которое не является реальным. В данном случае комплексными числами являются 2+3i и -2-5i, примеры. (i) называется йотой и используется для обозначения мнимой части комплексных чисел, которая записывается с (i) в ней.
Это также число, которое не является реальным. В данном случае комплексными числами являются 2+3i и -2-5i, примеры. (i) называется йотой и используется для обозначения мнимой части комплексных чисел, которая записывается с (i) в ней.
Определение: Аргумент комплексного числа
Это угол в радианах между положительной действительной осью и линией между началом координат и комплексным числом, измеренный против часовой стрелки. Аргумент называется Arg (z), что является сокращением от «arg».
Обычно аргумент комплексного числа задается в следующем диапазоне: (-Π,Π)
Однако мы также можем говорить о комплексном числе с точки зрения, что оно больше или меньше. Это основной аргумент для комплексного числа в диапазоне [-π, π]. Некоторые люди используют содержание от нуля до двух для основной идеи. Однако это не очень распространено.
В тригонометрии прямоугольного треугольника мы можем вычислить аргумент комплексного числа, если дана декартова форма числа a + ib.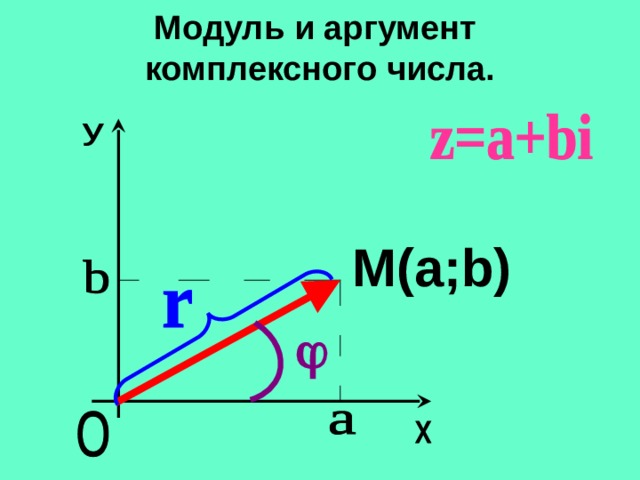
Угол определяется как tan-1(b/a), а главный аргумент лежит только между (-Π,Π).
Нахождение аргумента комплексного числа в радианах
Комплексное число имеет «аргумент»: угол между положительной действительной осью и линией, соединяющей его начало с комплексным числом в радианах. Аргумент комплексного числа по соглашению задается в диапазоне между [-π, π].
На первом этапе мы записываем комплексное число на диаграмме Аргана.
Мы назвали аргумент комплексного числа на диаграмме Аргана выше. Вот так надо писать. Мы видим, что это комплексное число имеет угол в прямоугольном треугольнике, стороны которого представляют собой синие, зеленые и фиолетовые линии. Этот угол является аргументом этого числа.
Этот угол можно найти, используя тригонометрические свойства прямоугольного треугольника.
Свойства аргумента комплексного числа
Давайте поговорим о нескольких вещах, общих для всех аргументов комплексных чисел. Если подумать об этом таким образом, предположим, что z — комплексное число, а n — какое-то число. Тогда предположим, что z — ненулевое комплексное число и
Тогда предположим, что z — ненулевое комплексное число и
arg(nz) = n arg(z)
Когда мы думаем о комплексных числах z1 и z2, это следующие:
- arg (z 1 / z 2 )= arg ( z 1 ) – arg ( z 2 )
- arg ( z 1 /* z 2 ) = arg ( z 1 ) + arg ( z 2 )
Основной и общий аргумент комплексного числа
Угол, образованный линейным представлением комплексного числа с положительной осью x называется аргументом комплексного числа. Этот угол называется углом комплексного числа. Эти значения делают этот угол «главным значением», что означает, что он имеет «общее значение», что означает, что он имеет «главный аргумент» и «общий аргумент». Тригонометрическое значение Tan используется для нахождения аргумента комплексного числа, которое основано на общем ответе на тригонометрическую функцию тангенса, поэтому оно называется Tan.
Применение аргумента комплексного числа
Аргумент комплексного числа можно использовать для преобразования комплексного числа в полярную форму, а также для выяснения того, как действительные и мнимые части комплексного числа связаны. Используя угол, вы можете сказать, является ли фундаментальный фактор более значительным или мнимая часть более значительной. Значением аргумента комплексного числа является угол. Когда действительная и мнимая части равны, основной множитель имеет большее значение, чем мнимая часть. Когда действительная и мнимая части одинаковы, существенный элемент важнее мнимой части. Когда действительная и мнимая части равны, фундаментальный фактор более значителен.
Используя угол, вы можете сказать, является ли фундаментальный фактор более значительным или мнимая часть более значительной. Значением аргумента комплексного числа является угол. Когда действительная и мнимая части равны, основной множитель имеет большее значение, чем мнимая часть. Когда действительная и мнимая части одинаковы, существенный элемент важнее мнимой части. Когда действительная и мнимая части равны, фундаментальный фактор более значителен.
Заключение
Каждый многочлен с комплексными коэффициентами имеет корни в комплексных числах, потому что комплексные числа были добавлены в математику. Это введение также помогло открыть дверь для создания нового типа чисел, которые можно было использовать для решения и объяснения множества различных типов задач.
1.4: Основной аргумент — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 76203
- Хуан Карлос Понсе Кампусано
- Университет Квинсленда
В этом тексте обозначение \(arg(z)\) используется для обозначения произвольного аргумента \(z\), что означает, что \(arg(z)\) – это набор, а не число.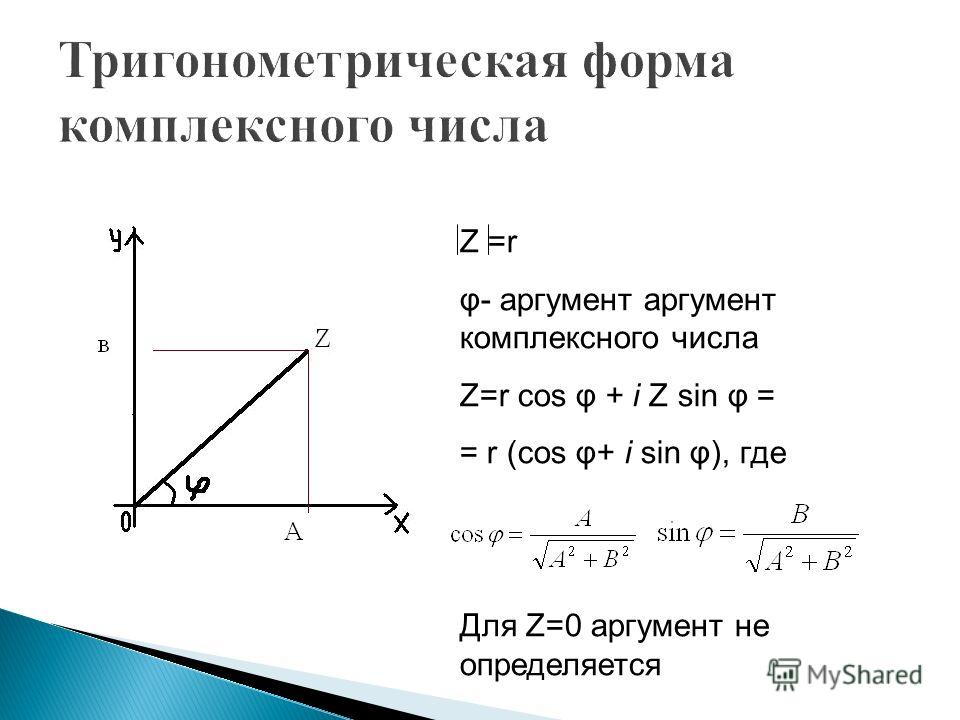 В частности, соотношение
В частности, соотношение
\(arg(z_{1})=arg(z_{2})\)
не является уравнением, а выражает равенство двух множеств.
Как следствие, два ненулевых комплексных числа \(r_{1}(cos\varphi _{1}+isin\varphi _{1})\) и \(r_{2}(cos\varphi _{ 2}+isin\varphi _{2})\) равны тогда и только тогда, когда
\(r_{1}=r_{2}\) и \(\varphi _{1}=\varphi _{2 }+2k\pi \),
, где \(k\in \mathbb{Z}\).
Чтобы сделать аргумент \(z\) четко определенным числом, его иногда ограничивают интервалом \((-\pi ,\pi ]\). Этот особый выбор называется главное значение или основная ветвь аргумента и записывается как \(Arg(z)\).
Обратите внимание, что не существует общего соглашения об определении главного значения, иногда предполагается, что его значения находятся в интервале \([0 ,2\pi )\). Эта двусмысленность является постоянным источником недоразумений и ошибок.
Главное значение \(Arg(z)\) комплексного числа \(z=x+iy\) обычно определяется как
\(\Theta = arctan(\frac{y}{x})\ ),
, где \(y/x\) – это наклон, а arctan преобразует наклон в угол. Но это верно только тогда, когда \(x>0\), поэтому частное определено, а угол лежит между \(-\pi/2\) и \(\pi/2\). Нам нужно распространить это определение на случаи, когда \(x\) не является положительным, рассматривая главное значение аргумента отдельно в четырех квадрантах.
Но это верно только тогда, когда \(x>0\), поэтому частное определено, а угол лежит между \(-\pi/2\) и \(\pi/2\). Нам нужно распространить это определение на случаи, когда \(x\) не является положительным, рассматривая главное значение аргумента отдельно в четырех квадрантах.
Функция \(Arg(z):\mathbb{C}\setminus \left \{ 0 \right \}\rightarrow (-\pi ,\pi ]\) определяется следующим образом:
\(Arg( г) = \ влево \ {\ {начать матрицу}
arctan\frac{y}{x} & if x>
arctan\frac{y}{x}+\pi &ifx< 0,y\geq 0 \\
arctan\frac{y}{x}-\pi & ifx< 0,y< 0 \\
\frac{\pi }{2}& ifx=0,y>0\\
-\frac{\pi } {2} & ifx= 0,y< 0\\
undefined& ifx=0,y= 0
\end{matrix}\right.\)
Таким образом, если \(z=r(cos\Theta +isin\ Theta )\), с \(r>0\) и \(-\pi <\Theta <\pi \), тогда
\(arg(z)=Arg(z)+2n\pi\), \ (н\в \mathbb{Z}\).
Мы можем визуализировать многозначный характер \(\), используя 90 155 римановых поверхностей 90 156 .

 3
3 14159..
14159..