Арифметический квадратный корень это: Арифметический квадратный корень — урок. Алгебра, 8 класс.

Содержание

Арифметический квадратный корень

Если а больше или равно 0 и n – натуральное число, которое больше 1, то будет существовать только лишь одно, неотрицательно число х, при котором выполняется равенство . Именно это число х и называется арифметическим квадратным корнем n-ой степени из неотрицательного числа а. Число а называют подкоренным числом, а n – показателем корня . Если n = 2, то показатель корня обычно опускают и называют такое выражение арифметическим квадратным корнем. Стоит отметить, что довольно-таки часто вместо слова «корень» употребляют слово «радикал».

А теперь давайте рассмотрим, как можно извлечь квадратный корень из натурального числа.

Например, нам необходимо извлечь корень из натурального числа к, причем нам точно, известно, что корень извлекается. Чтобы сделать это довольно удобным способом, следует воспользоваться следующими правилами:

Разбить число к на грани (начинать с последней цифры и справа налево) и включить в каждую грань по две рядом стоящие цифры. При этом стоит обратить внимание, что если к состоит из четного числа цифр, то в первой левой грани будет 2 цифры, если же число цифр в к нечетное, то в первой левой грани будет 1 цифра. Количество наших граней показывает количество цифр результата. На первый взгляд все просто и понятно.
Далее нам необходимо подобрать наибольшую цифру, но такую, чтобы ее квадрат не превосходил числа, которое находится в первой грани. Эта цифра и будет первой цифрой результата.
Полученную первую цифру результата возводим в квадрат и вычитаем полученное из первой грани число, а затем припишем к найденной разности справа вторую грань. У нас выйдет какое-то число А. Удваиваем часть результата, которую имеем и получаем число а. Теперь следует подобрать такую наибольшую цифру х, чтобы произведение числа ах на х не было больше числа А. Цифра х – вторая цифра результата.
Следующий шаг практически повторяет весь третий пункт. Продолжать находить следует до тех пор, пока не используется последняя грань.

Свойства квадратного (арифметического) корня

√a * √b = √ab

√a	= √	a
√b	= √	b

(√a)^m = √a^m

√ab = √|a| * √|b|

√	a	=	√\|a\|
	b		√\|b\|

√a^m = (√a)^m

ⁿ√a = ^nm√a^m

ⁿ√a * ⁿ√b = ⁿ√ab

ⁿ√a	= ⁿ√	a
ⁿ√b	= ⁿ√	b

(ⁿ√a)^m = ⁿ√a^m

ⁿ√

^m√a

= ^nm√a

Урок.

«Квадратные корни. Арифметический квадратный корень»

Урок № 3 § 12

Тема: Квадратные корни. Арифметический квадратный корень.

Цель урока:

Образовательная: ввести понятие квадратного корня. Дать учащимся свойства арифметического квадратного корня. Умение находить квадратные корни из чисел.

Развивающая: развитие устного счета при возведении в квадрат и при извлечении квадратного корня.

Воспитательная: воспитание трудолюбия и коллективизма.

Тип урока: урок усвоения новых знаний и умений

Оборудование: мел, доска, плакаты, карточки с заданием.

Х о д у р о к а

Организационный момент.

— проверка готовности класса к уроку;

— проверка готовности учащихся к уроку;

— приветствие

— проверка Д. З.

Анализ домашних заданий (устный опрос):

№ 356(1). Как найти координаты точек пересечения?

№ 354. Умение решать уравнение графически.

№ 372 и 373. Подготовка к новому материалу

2. Мотивация. Рациональные числа, с которыми мы ознакомились в предыдущих классах — это лишь малая часть множества чисел. На числовой прямой кроме рациональных ещё больше не рациональных чисел. Без знания этих чисел, без умения выполнять действия с ними невозможно в дальнейшем изучать математику и другие науки.

Рассказ учителя об исторической предпосылке возникновения понятия арифметического квадратного корня. Возникновение понятия «квадратного числа».

Вывешиваем плакат №1.

Древнегреческие математики представляли целые числа и любые величины, соизмеримые и несоизмеримые, геометрически, с помощью отрезков, прямоугольников и других фигур. Отсюда у них появились такие названия, как:

1) «плоские числа» для чисел вроде 6 = 2 • 3, 14 = 7 • 2, являющихся произведениями двух сомножителей и выражающих площадь прямоугольника, построенного на соответствующей паре отрезков;

2) «квадратные числа»: 4(= 2 • 2), 81 (= 9 • 9) и т. д. Это название употребляется и поныне;

3) «телесные числа»: 24( = 2 • 3 • 4), 210( = 5 • 6 • 7) и т. д., являющиеся произведениями трех чисел и изображаемые с помощью параллелепипедов;

4) «кубические числа

»: 8(=2 • 2 -2), 125(=5 • 5 • 5) и т.п.

Задание классу:

Представьте в виде квадрата числа

Это же задание формулируем по другому: «Какие числа удовлетворяют уравнениям х² = 25; х² = 1; х² = 144?»

«Темринг» (к доске выходят три ученика, с каждого ряда по одному)

Задание: Найдите значение выражения, и записать на доске.

8² = 10² = 6² =

(-8)² = (-10)² = (-6)² =

-8² = -10² = -6² =

Вопрос «как называются числа 8² и -8²?» ( противоположными)

Эстафета 1

Ученики заполняют карточки, передавая друг другу (каждый заполняет только одну клетку).

0,8

1,3

-5

а²

0,9

1,2

-7

а²

0,7

1,1

-9

а²

3. Подача нового материала.

Ещё в древности у египтян, из практической деятельности, возникла задача «Как, зная площадь поля квадратной формы, определить сторону?»

Пусть сторона квадрата х. Тогда х² = S. Решим эту задачу с точки зрения математики. Зададим себе вопрос, например для уравнения х² = 25, а каковы корни уравнения?

х₁ = 5 т.к. 5² = 25, но и

х₂ = -5_{т.к. (-5)² = 25.}

5 и -5 называются квадратными корнями из числа 25;

7 и -7 называются квадратными корнями из числа 49;

0,3 и -0,3 называются квадратными корнями из числа 0,09 и т.п.

Даем определение квадратного корня из числа a.

Плакат 2.

Квадратным корнем из числа а называется число, квадрат которого равен а

Например:

Квадратным корнем из числа 81 есть числа 9 и -9,

так как 9² = 81 и (-9)² = 81.

Эстафета 2

Каждому ряду раздаем следующие карточки

Уравнение

х²=16

х²=0,25

х²=1,44

х²=100

х²= -9

Корни

уравнения

х₁=

х₂=

х₁=

х₂=

х₁=

х₂=

х₁=

х₂=

х₁=

х₂=

х₁=

х₂=

Уравнение

х²=64

х²=0,16

х²=1,21

х²=225

х²= -16

Корни

уравнения

х₁=

х₂=

х₁=

х₂=

х₁=

х₂=

х₁=

х₂=

х₁=

х₂=

х₁=

х₂=

Неотрицательные корни этих уравнений принято называть арифметическим квадратным корнем из числа a.

Плакат 3.

Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а

Например:

— знак арифметического квадратного корня.

Выражение читают так: «квадратный корень из числа а ».

Знак арифметического квадратного корня впервые ввел в 1525 году немецкий математик Х.Рудольф.

Вводим знак радикала

И так = 10, т.к. 10 > 0 и 10² = 100.

= 4; = 12; =46; = 81.

Наименьшее число, которое может быть под корнем – это 0.

= 0

Арифметический квадратный корень из отрицательного числа не существует

— не определено

Практическая работа – как с помощью таблицы квадратов находить квадратные корни из чисел. Например:

= 81 = 810

= 8,1 = 8100

= 0,81 = ?

= 0,081 = ?

Последние два значения можно найти приближенно с помощью калькулятора.

Эстафета 3. Работа по нахождению арифметического квадратного корня из чисел.

а	4	81		0,64	625	10,24

a	9	64		0,49	441	12,25

а	16	25		0,36	400	10,89

4. Динамическая пауза. ( Направлена на профилактику остеохондроза.)

Сесть на краешек стула.

Поднять руки, потянуться, напрячь мышцы.

Вытянуть руки перед грудью, потянуться.

Руки в стороны, потянуться, напрячь мышцы.

Обхватить себя руками, выгнуть спину.

Принять рабочее положение.

5. Закрепление материала.

Весь класс работает, в устной форме, с заданиями № 377, 378, 379(1,5,9,13).

Потом, всем классом, повторяем свойства арифметического квадратного корня.

Плакат 4

Из свойства арифметического квадратного корня имеем:

1) равенство = в имеет место, если

а) a 0 б) в² = a;

2) если a < 0, то не имеет смысла.

6. Итоги урока. Рефлексия.

Оценивание результатов работы: устной, практической и с карточками.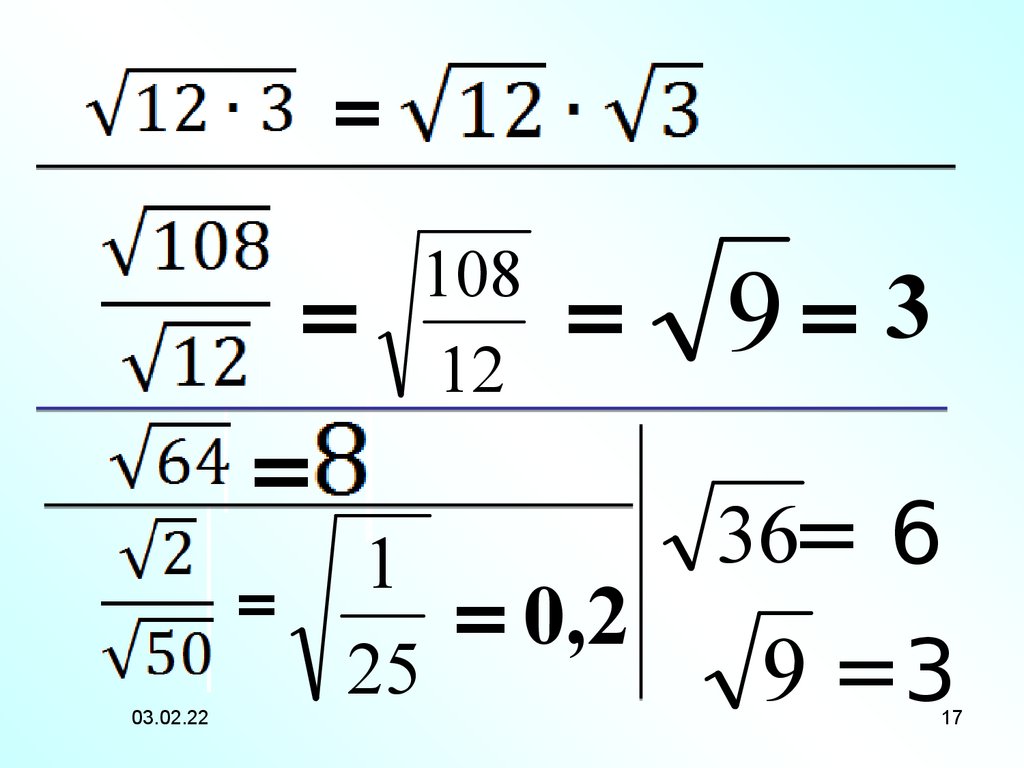

Над какой темой мы сегодня на уроке работали?
Трудным ли для тебя был материал урока?
На каком из этапов урока было труднее всего, а на каком легче всего?
Что нового ты узнал на уроке?

7. Домашнее задание § 12, № 380, 381, 382, 383.

Как найти квадратный корень из 24?

Арифметическое значение, которое используется для представления количества и используется в расчетах, определяется как Числа. Такой символ, как «4,5,6», который представляет число, известен как цифра. Без цифр мы не можем вести подсчет вещей, даты, времени, денег и т. д., эти цифры также используются для измерения и используются для маркировки.

Свойства чисел делают их полезными при выполнении над ними арифметических операций. Эти числа могут быть записаны в числовой форме, а также в словах.

Например, 3 записывается как три прописью, 35 записывается как тридцать пять прописью и т. д. Учащиеся могут записывать числа от 1 до 100 прописью, чтобы узнать больше.

Существуют разные типы чисел, которые мы можем выучить. Это целые и натуральные числа, нечетные и четные числа, рациональные и иррациональные числа и т. д.

Что такое система счисления?

Система счисления — это метод записи чисел, представляющий собой математический способ представления чисел данного набора с использованием чисел или символов математическим способом. Система записи для обозначения чисел с использованием цифр или символов логическим образом определяется как система счисления.

Мы можем использовать цифры от 0 до 9, чтобы составить все числа. С помощью этих цифр любой может составить бесконечное число.

Например, 156,3907, 3456, 1298, 784859 и т. д.

Что такое квадратный корень?

Значение числа квадратных корней, которое при умножении само на себя дает исходное число. Предположим, что a — это квадратный корень из b, тогда он представляется как a = √b, или мы можем выразить то же уравнение как a ² = b. Здесь, ’√’ этот символ, который мы использовали для обозначения корня чисел, называется радикалом. Положительное число, когда его нужно умножить само на себя, представляет собой квадрат числа. Квадратный корень из квадрата любого положительного числа дает исходное число.

Например, квадрат 4 равен 16, 4 ² = 16, а квадратный корень из 16 √16 = ±4. Так как 4 — совершенный квадрат, то найти квадратный корень из таких чисел несложно, но для несовершенного квадрата это действительно сложно.

Квадратный корень представлен как «√». Его называют радикальным символом. Чтобы представить число «а» в виде квадратного корня, с помощью этого символа можно записать как: «√a», где a — это число.

Число здесь под подкоренным символом называется подкоренным. Например, квадратный корень из 4 также представлен как радикал 4. Оба представляют одно и то же значение.

Формула для нахождения квадратного корня: a = √b

Свойства квадратных корней

Он определяется как функция «один к одному», которая принимает положительное число в качестве входных данных и возвращает квадратный корень из заданного входного числа.

f(x) = √x

Например, здесь, если x = 9, функция возвращает выходное значение как 3.

Свойства квадратного корня следующие:

Если число является совершенным квадратным числом, то точно существует совершенный квадратный корень.
Если число заканчивается четным числом нулей (0), то у нас может быть квадратный корень.
Можно перемножить два значения квадратного корня. Например, √3 можно умножить на √2, тогда получится √6.
При умножении двух одинаковых квадратных корней результатом должно быть радикальное число. Он показывает, что результат не является квадратным корнем. Например, если √7 умножить на √7, получится 7.
Квадратный корень из отрицательных чисел не определен. Следовательно, полный квадрат не может быть отрицательным.
Некоторые числа оканчиваются на 2, 3, 7 или 8 (в разряде единиц), тогда идеальный квадратный корень не существует.
Некоторые числа заканчиваются на 1, 4, 5, 6 или 9 в разряде единиц, тогда число будет иметь квадратный корень.

Легко найти квадратный корень из числа, которое является полным квадратом.

Совершенные квадраты — это положительные числа, которые можно записать как произведение числа на себя, или можно сказать, что совершенный квадрат — это число, равное степени 2 любого целого числа.

Число, которое можно представить как произведение двух равных целых чисел. Например, 16 — это совершенный квадрат, потому что это произведение двух равных целых чисел, 4 × 4 = 16. Однако 24 не является идеальным квадратом, потому что его нельзя выразить как произведение двух равных целых чисел. (8 × 3 = 24).

Число, полученное возведением целого числа в квадрат, называется полным квадратом.

Если предположить, что N является полным квадратом целого числа y, это можно записать как N = произведение y и y = y ²

Итак, формула идеального квадрата может быть выражена как:

N = Y ²

Воспользуемся формулой со значениями.
Если y = 9 и N = y ² .
Это означает, что N = 9 ² = 81,
Здесь 81 — это полный квадрат 9, потому что это квадрат целого числа.
, так что упрощенный квадратный корень из 81 равен 9.

С помощью квадратных корней мы можем определить, является ли число полным квадратом или нет, и вычислим ли мы квадратный корень из данного числа.

Если квадратный корень представляет собой целое число, то данное число будет полным квадратом, а если значение квадратного корня не является целым числом, то данное число не является полным квадратом.

Например, , чтобы проверить, является ли 34 полным квадратом или нет, мы вычислим его квадратный корень. √34 = 5,83095…. Как мы видим, 5,83905… не является целым числом, поэтому 34 — не полный квадрат.

Возьмем другой пример

Число 49. √49 = ±7. Мы видим, что 7 — целое число, следовательно, 49 — полный квадрат.

Что такое упрощенный квадратный корень 24?

Решение:

квадратный корень из 24
Здесь квадратный корень из 24 равен 4,8989
или упрощенно как 4,8999

Аналогичные вопросы 90

Решение:

квадратный корень из 999
квадратный корень из 999 равен 31,606

Вопрос 2. Найдите квадратный корень из 1024?

Решение:

квадратный корень из 1024 9{\раз} /\{\pm 1\}. $$ Его порядок $|G| = (p — 1)/2$ четен, что означает, что $G$ содержит хотя бы один элемент $g$ порядка $2$. Пусть $x$ находится в прообразе $g$ при фактор-отображении. Порядок $x$ может быть только $2$ или $4$. Если бы это было $2$, то $x = -1$, что означало бы противоречие с тем, что $g = 1$.
No related posts.

Арифметический квадратный корень

Свойства квадратного (арифметического) корня

Урок.

Как найти квадратный корень из 24?

Добавить комментарий Отменить ответ