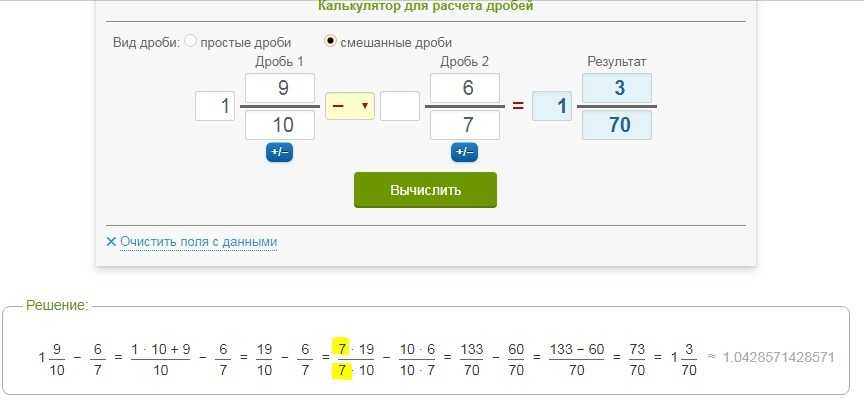
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т.
е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Math Symbols
| Symbol | Symbol name | Symbol Meaning | Example |
|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 |
| — | знак минус | вычитание | 1 1/2 — 2/3 |
| * | asterisk | multiplication | 2/3 * 3/4 |
| × | times sign | multiplication | 2 /3 × 5/6 |
| : | division sign | division | 1/2 : 3 |
| / | division slash | division | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
more math problems »
Использование калькуляторов для более глубокого вовлечения учащихся в математикуЛюбим мы их или ненавидим, калькуляторы никуда не денутся — прошли те времена, когда мы могли говорить учащимся: « У вас не всегда будет калькулятор». Мы должны переосмыслить, что значит учить детей основам математики в эпоху калькуляторов. Я потратил годы на то, чтобы выяснить, как внедрить калькуляторы в свое обучение таким образом, чтобы мои ученики средней школы могли научиться таким важным навыкам, как чувство чисел, оценка и решение задач. Путем проб и ошибок я создал и провел уроки, в которых калькуляторы используются как центральный инструмент для развития у учащихся математической любознательности, концептуального понимания и беглости процедур. ПроцентыНа этом уроке я всегда начинаю с того, что говорю учащимся, что я даю им несколько процентных задач, а также ответы . Первое, что интересует студентов, это почему я даю им ответы. Разве они не должны их вычислить? Не в этом случае, говорю я им: цель не в том, чтобы получить ответ, а в том, чтобы выяснить, как он был получен. Первая проблема, которую мы решаем, довольно проста: чему равно 50% от 24? Студенты обычно могут выкрикнуть «12!» прежде чем я закончу писать задачу на доске. «Отлично!» Я отвечаю. «Ну, как вы могли вычислить это на калькуляторе?» В этот момент ученики берут простой калькулятор с четырьмя функциями. Я хожу и прошу студентов показать мне свои методы, а я говорю им, что деление 24 на 2 — это не то, чего я хотел. «Но 50% — это половина», — протестуют они. — Значит, ты делишь на 2. «Конечно, — говорю я. «Но у нас не всегда будет что-то столь же хорошее, как 50%, поэтому мы должны найти другой способ». Раздраженные, мои ученики пытаются понять, чего я хочу. Предоставив им возможность продуктивно бороться, я подвожу их к идее, что мы можем использовать числа 50 и 24, чтобы получить 12. Вскоре у них появляются такие идеи, как умножение чисел, в результате чего получается 1200. «Это вроде как 12», — скажет кто-то. «Но я должен избавиться от этих нулей». Мои ученики начинают понимать, что для получения ответа мы можем умножить процент на целое число, а затем разделить на 100. Некоторые ученики даже предлагают просто превратить одно из чисел в десятичное перед умножением (50 умножить на 0,24 или 0,50 умножить на 24). Другие говорят, что вы ставите десятичную точку в оба числа, но только по одной цифре в каждом (5,0 умножить на 2,4). Некоторые предлагают использовать кнопку % на калькуляторе, что также превращает их число на экране в десятичное число. Вскоре мои ученики участвуют в математической дискуссии о взаимосвязях между десятичными дробями и процентами, о том, как число 100 присуще всем вычислениям и почему 50%, 0,50 и ½ — это одно и то же. Продолжаю урок с более сложными задачами. Попытка решить что-то вроде 17,35% от 8,4 с помощью бумаги и карандаша утомительна, но с калькуляторами мои ученики уверенно подходят даже к таким, казалось бы, страшным задачам, вооруженные знанием того, что отношения остаются постоянными независимо от сложности чисел. Используя такие идеи, как процентно-десятичная эквивалентность, а также эффективные алгоритмы, такие как «% × n ÷ 100», мои ученики развивают с помощью калькуляторов концептуальное понимание и беглость процедур. Операции с дробями Расширяя новое понимание моих учеников эквивалентности рациональных чисел, я использую калькуляторы, чтобы научить их умножению и делению дробей и десятичных знаков. Предлагаю задачу на умножение: ½ × ½. Я прошу студентов посмотреть, смогут ли они использовать свою стратегию конверсии, чтобы упростить эту задачу. После продуктивной борьбы студенты приходят к 0,25, которую они обычно признают равной ¼. Вскоре они вступают в дискуссию о том, как они могли просто умножить знаменатели без всех этих десятичных дробей. «А как же числители?» Я спрашиваю. Ну, может, они и размножаются, но мои ученики не уверены. Тогда мы решим еще одну задачу: ¾ × ⅖. Учащиеся сначала предполагают, что они перемножают числители и знаменатели, в результате чего получается 6 «Но как мы можем быть уверены?» Я спрашиваю. А что, если мы преобразуем наш ответ в десятичную дробь? В конце концов учащиеся могут убедиться, что 6/20 является решением, поскольку ¾ × ⅖ = 0,75 × 0,4, что дает 0,3, а 6 ÷ 20 = 0,3. На протяжении урока я даю ученикам разные задачи, в том числе с неправильными дробями и смешанными числами, и все их работы можно проверить с помощью калькуляторов; им больше не нужно, чтобы я постоянно проверял их работу, что приводит к большей самостоятельности в решении проблем. Самым большим удивлением, с которым я столкнулся, было то, как легко ученики могли работать с повторяющимися десятичными дробями. Хотя на это ушло некоторое время и еще более продуктивная борьба, мои ученики решали задачи на умножение и деление со всевозможными дробями, имеющими повторяющиеся закономерности. Они начали осознавать, что набор троек для представления 0,3 довольно близко приблизил их к фактическому ответу для ⅓ ÷ ¼ (0,3333333 ÷ 0,25 = 1,3333332, очень близкое приближение к фактическому ответу 1⅓). |
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме.
Два моих любимых урока охватывают то, что многие считают базовыми понятиями средней школы: операции с процентами и дробями.
Затем я прошу студентов высказать предположения о том, почему все эти стратегии работают и что у них общего.
Как и в случае с задачами на проценты, я начинаю с того, что показываю учащимся известные эквивалентные дроби и десятичные дроби, такие как ½ = 0,5 и ¾ = 0,75. Студенты изучают, как использовать числитель и знаменатель для создания десятичных форм. В конце концов, они открывают алгоритм деления (числитель ÷ знаменатель). Как только они освоят этот метод, начнется настоящее веселье.
