Ошибка
Перейти к основному содержанию
Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+)
Извините, не удалось найти запрашиваемый Вами файл
Подробнее об этой ошибке
Перейти на…
Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ).
 Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»Примеры решения задач по теме «Непрерывность функции»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления.
Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»Примеры решения задач по теме «Непрерывность функции»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления.
 Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий.
Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий.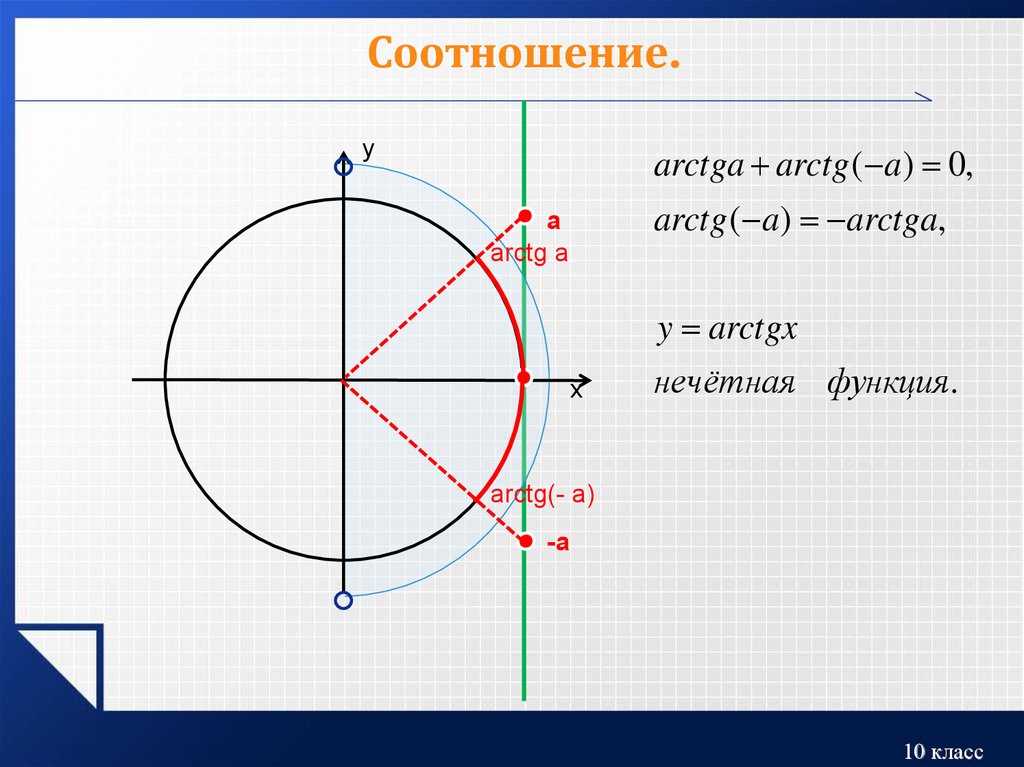
 Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа.
Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Лекционный материал по теме «Системы массового обслуживания»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа.
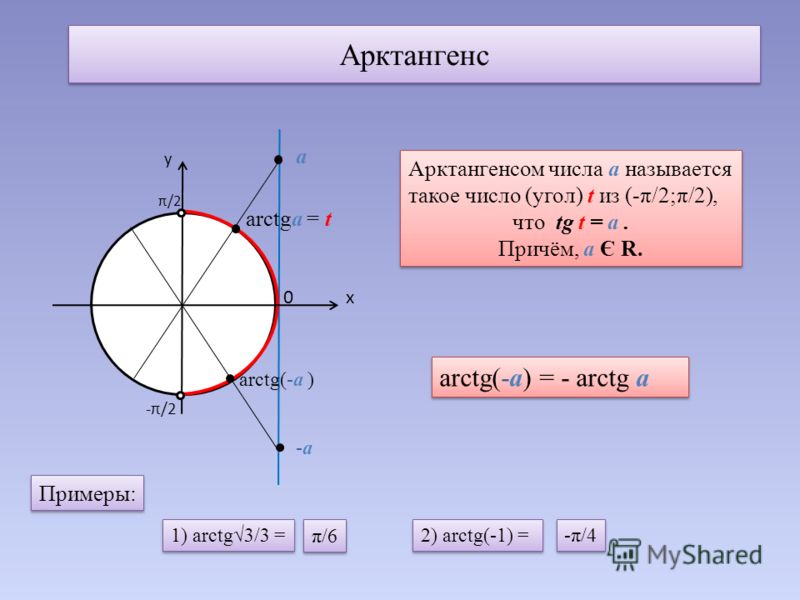
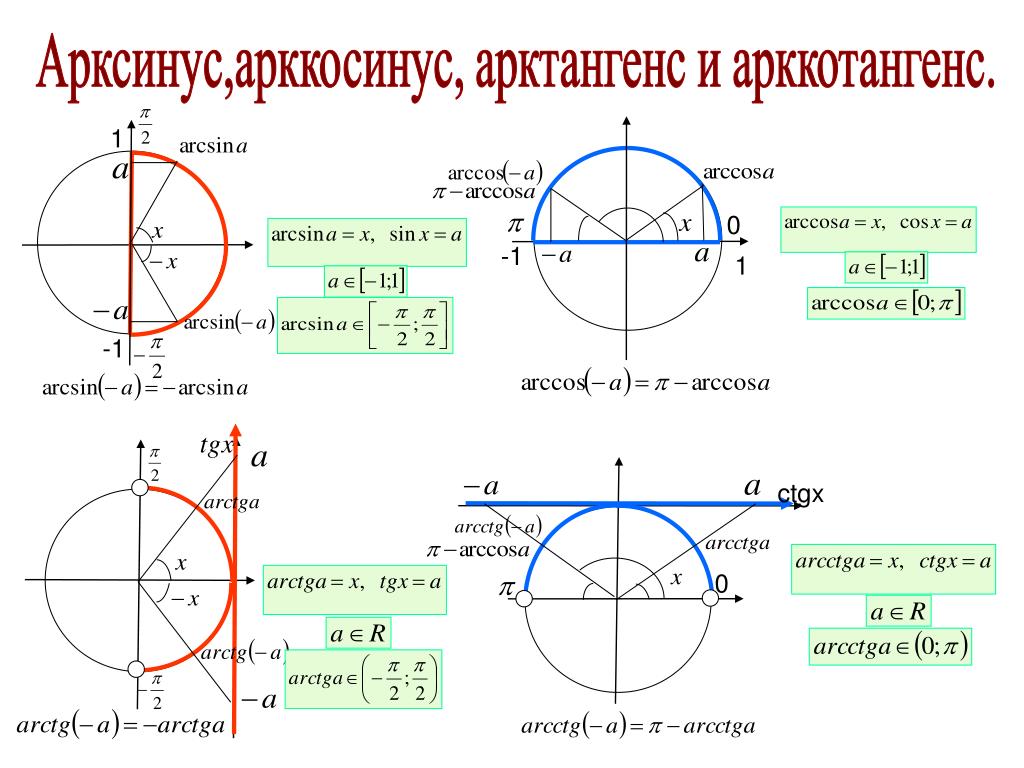
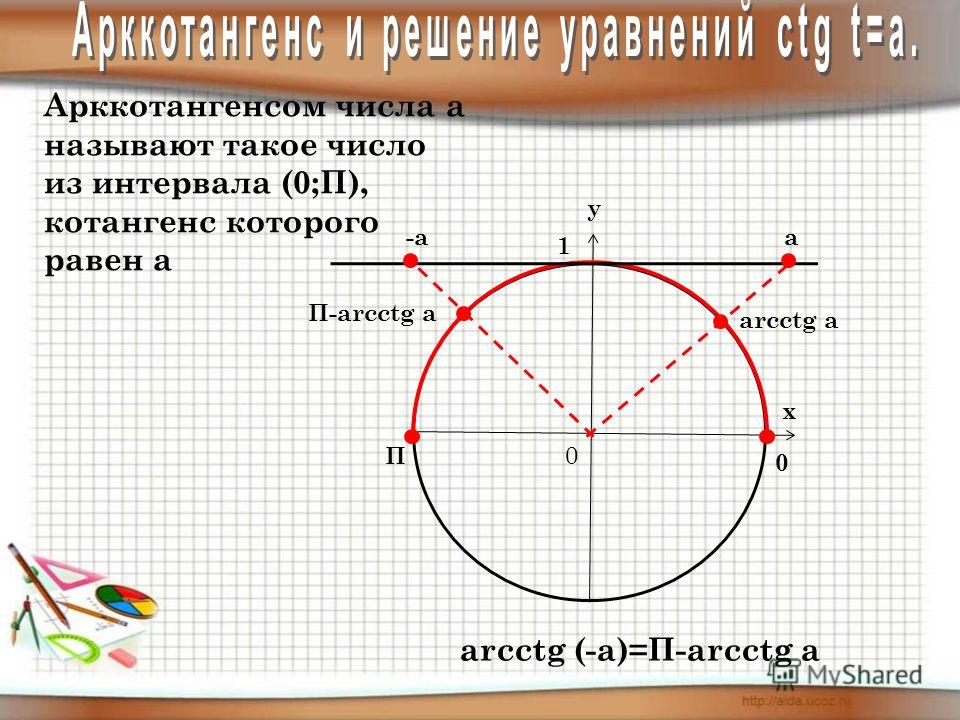
Главная → Видеоуроки → Алгебра. Описание видеоурока: В видеоуроке дано определение обратных тригонометрических функций: арктангенс и арккотангенс. Арктангенс — обозначение: arctg x или arctan x. Арктангенс (y = arctg x) – обратная функция к tg (x = tg y) Арккотангенс — обозначение: arcctg x или arccot x или arccotan x. Арккотангенс (y = arcctg x) – обратная функция к ctg (x = ctg y). Валерий Волков 3 15.01.2016 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
Функция ATAN2 — служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Дополнительно. .. Меньше
.. Меньше
В этой статье описаны синтаксис формулы и использование функции ATAN2 в Microsoft Excel.
Описание
Возвращает арктангенс или арктангенс указанных координат x и y. Арктангенс — это угол от оси x до линии, содержащей начало координат (0, 0) и точку с координатами (x_num, y_num). Угол дается в радианах между -pi и pi, исключая -pi.
Синтаксис
ATAN2(x_num, y_num)
Синтаксис функции ATAN2 имеет следующие аргументы:
Замечания
Положительный результат представляет угол против часовой стрелки от оси x; отрицательный результат представляет угол по часовой стрелке.
ATAN2(a,b) равно ATAN(b/a), за исключением того, что a может равняться 0 в ATAN2.

Если x_num и y_num равны 0, ATAN2 возвращает #DIV/0! значение ошибки.
Чтобы выразить арктангенс в градусах, умножьте результат на 180/PI( ) или используйте функцию ГРАДУСЫ.
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
Формула | Описание | Результат |
=АТАН2(1, 1) | Арктангенс точки 1,1 в радианах, пи/4 | 0,785398163 |
=АТАН2(-1, -1) | Арктангенс точки -1,-1 в радианах, -3*pi/4 | -2. |
=ATAN2(-1, -1)*180/PI() | Арктангенс точки 1,1 в градусах | -135 |
=ГРАДУСЫ(АТАН2(-1,-1)) | Арктангенс точки 1,1 в градусах | -135 |
arctan с двумя аргументами
При обращении полярных координат требуется функция загара дуги (http://planetmath.org/CyclometricFunctions) загар дуги с двумя аргументами. Если (x,y)∈ℝ2∖{0}, то арктан(х,у) определяется как угол (x, y) образующий с положительная ось x.
Обычно встречаются такие выражения, как arctan(y/x),
который равен arctan(x,y), когда (x,y) находится в первом квадранте. Однако arctan(y/x) не дает правильного угла, когда (x,y)
находится в третьем квадранте (поскольку y/x=(-y)/(-x)).
Кроме того, частное y / x включает деление на ноль, когда x = 0,
что наносит ущерб как в численном, так и в математическом отношении.
Однако arctan(y/x) не дает правильного угла, когда (x,y)
находится в третьем квадранте (поскольку y/x=(-y)/(-x)).
Кроме того, частное y / x включает деление на ноль, когда x = 0,
что наносит ущерб как в численном, так и в математическом отношении.
В большинстве математических программ и языков программирования арктангенс с двумя аргументами реализуется непосредственно.
В языке Python функции atan(x) и atan2(x,y) являются соответственно версиями arctan с одним и двумя аргументами. Смысл наличия версии с двумя аргументами состоит в том, чтобы определить правильный квадрант точки. Например, 1/1=1=-1/-1, поэтому atan(x) не может различать (1,1) и (-1,-1), но atan2(x,y) может, как показано в следующем Python код иллюстрирует:
\PMlinkescapetext{
>>> из математического импорта *
>>> печатать атан(1)
0,785398163397
>>> напечатать atan2(1,1)
0,785398163397
>>> напечатать atan2(-1,-1)
-2,3619449019
}
, потому что (1,1) имеет аргумент π/4=0,7853… но (-1,-1) имеет аргумент -3π/4=-2,3619….
В математических работах arctan(x,y) просто обозначается через θ(x,y). Символ θ, очевидно, относится к углу, но на самом деле это функция h3, где
| г(r,θ)=(rcosθ,rsinθ),h(x,y)=g-1(x,y)=(r,θ). |
Функция g:ℝ2→ℝ2 представляет собой преобразование полярных координат в декартовы. По теореме об обратной функции функция h (преобразование декартовых координат в полярные) существует и является гладкой везде, где она определена. Обратите внимание, что h не может быть определено непрерывно везде, из-за многозначного характера θ — (r, θ) и (r, θ + 2πn) всегда отображаются в одну и ту же точку под g. (Аналогично, θ не может быть определено, когда r=x2+y2=0.) Это означает, что если гоняться по петле (скажем, по кругу) вокруг начала координат, θ будет двигаться от 0 до 2π, даже если точка изображения g(r,θ) возвращается к исходной точке.
Технически «наибольшей» возможной областью значений h (и θ) можно считать только некоторое односвязное открытое подмножество ℝ2∖{0}.

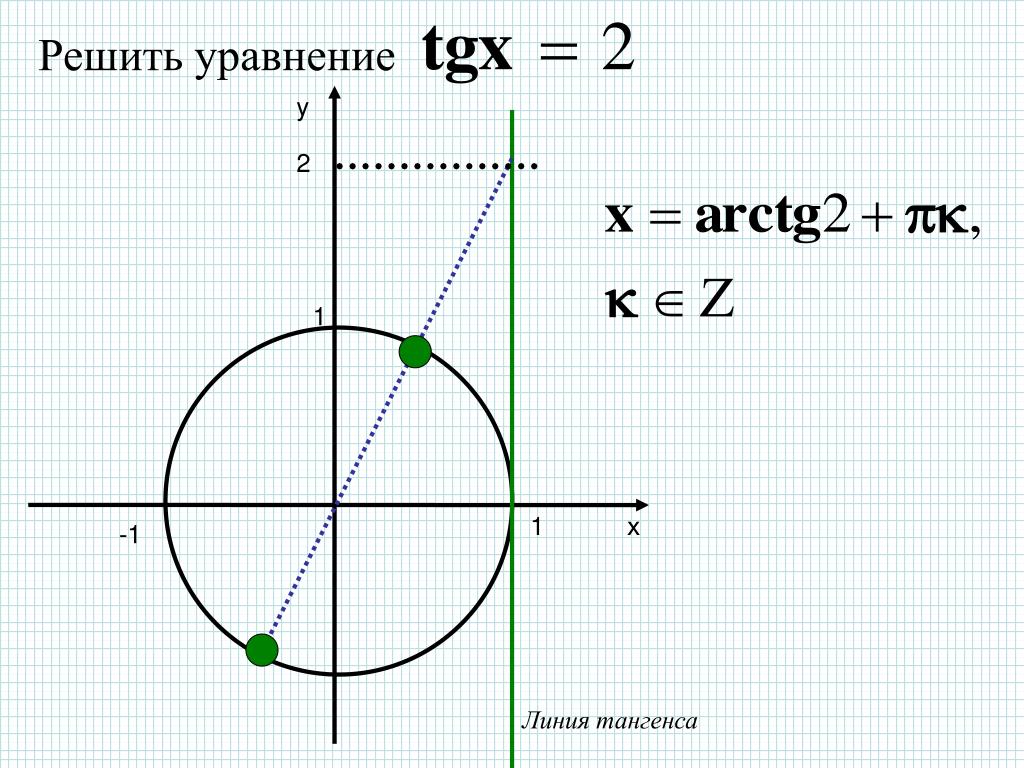 10 класс. Тригонометрические функции.
10 класс. Тригонометрические функции. 5 класс.
5 класс.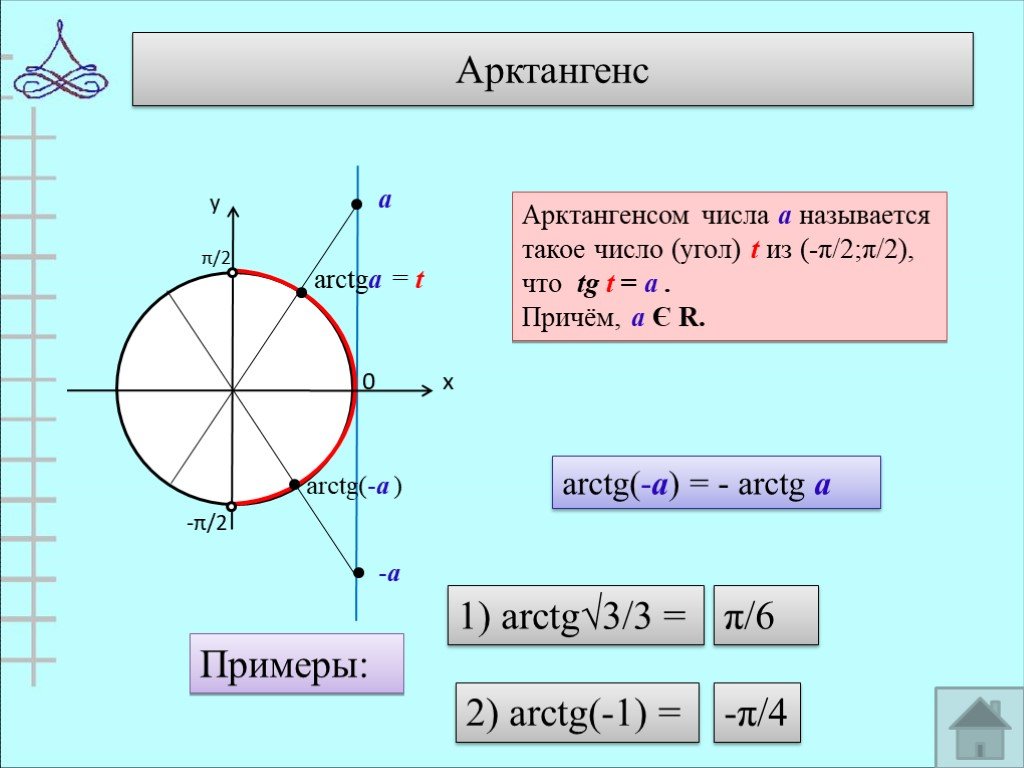 10 — 11 класс.
10 — 11 класс.

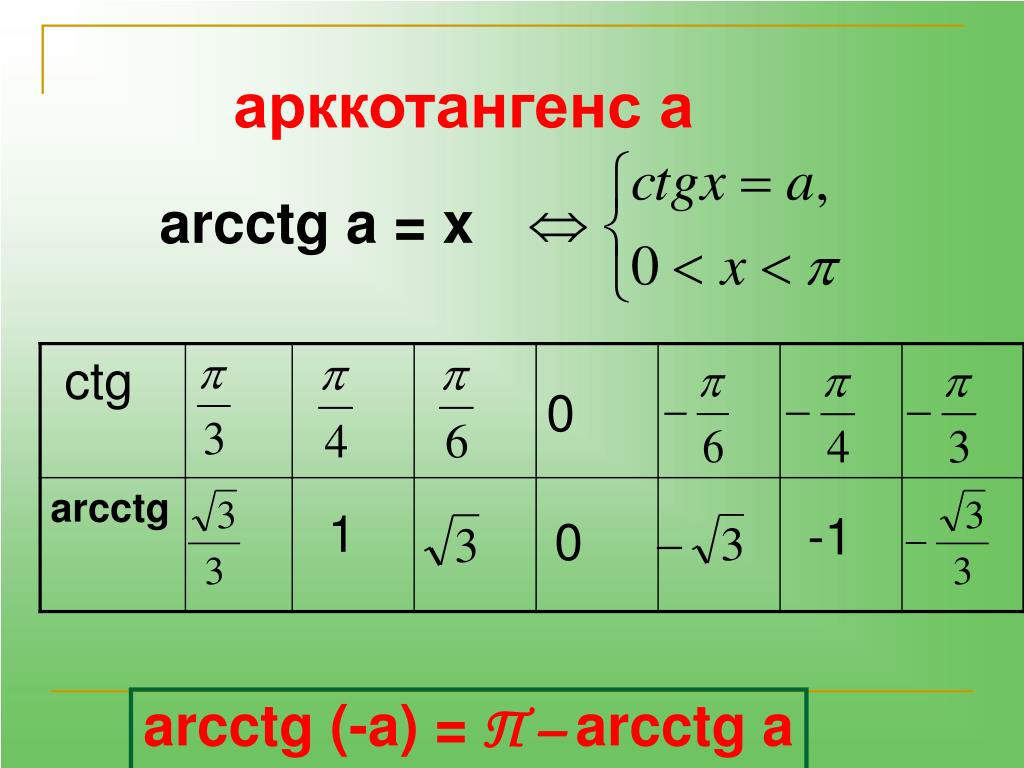 35619449
35619449