Вывод производных arctg(x) и arcctg(x)
Вывод производной арктангенса
Здесь мы полагаем, что нам известна производная тангенса:
.
Далее мы выводим формулу производной арктангенса, учитывая, что арктангенс является функцией, обратной к тангенсу.
По формуле производной обратной функции
Рассмотрим функцию арктангенс:
y = arctg x.
Здесь независимая переменная x может принимать любые действительные значения:
.
Зависимая переменная y может принимать значения от – π/2 до + π/2:
.
Арктангенс является функцией, обратной к тангенсу:
x = tg y.
Для определения его производной, применим формулу производной обратной функции:
(1) .
Производная тангенса нам известна:
.
Здесь .
Поменяем местами обозначения переменных x и y. Тогда
,
где .
Подставим в формулу (1):
(2) .
Здесь
y = arctg x;
x = tg y.
Теперь выразим правую часть формулы (2) через переменную x. Для этого воспользуемся формулой и выполним преобразования:
Для этого воспользуемся формулой и выполним преобразования:
.
Отсюда
.
Подставим в (2):
.
Тем самым мы вывели формулу производной арктангенса:
.
Второй способ
Поскольку арктангенс и тангенс являются взаимно обратными функциями, то
(3) .
Продифференцируем это уравнение по переменной x. То есть найдем производные левой и правой части и приравняем их друг к другу:
(4) .
Из таблицы производных имеем:
.
Производную левой части находим по формуле производной сложной функции:
.
Здесь .
Далее выполним преобразования:
.
Тогда
.
Подставим в (4):
.
Отсюда
.
Вывод производной арккотангенса
Используя связь между арктангенсом и арккотангенсом
Производную арккотангенса можно получить из производной арктангенса, если воспользоваться связью между арктангенсом и арккотангенсом:
.
Отсюда
.
По формуле производной обратной функции
Рассмотрим функцию арккотангенс:
y = arcctg x.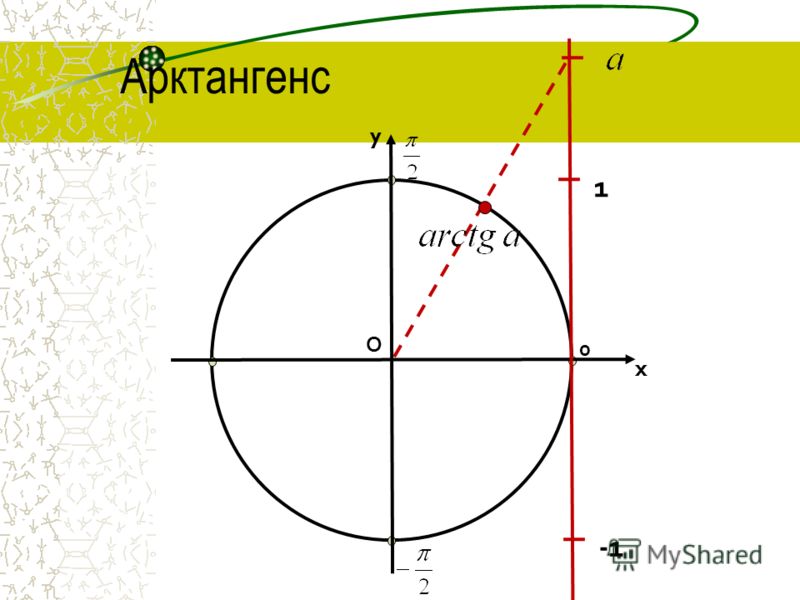
Здесь независимая переменная x может принимать любые действительные значения:
.
Зависимая переменная y может принимать значения от 0 до π:
.
Арккотангенс является функцией, обратной к котангенсу:
x = ctg y.
Для определения его производной, применим формулу производной обратной функции:
(1) .
Считаем, что производная котангенса нам известна:
.
Здесь .
Поменяем местами обозначения переменных x и y. Тогда
,
где .
Подставим в формулу (1):
(5) .
Здесь
y = arcctg x;
x = ctg y.
Выразим правую часть формулы (5) через переменную x. Для этого выполним преобразования:
.
Отсюда
.
Подставим в (5):
.
Таким образом, мы вывели формулу производной арккотангенса:
.
Второй способ
Поскольку арккотангенс и котангенс являются взаимно обратными функциями, то
(6) .
Продифференцируем это уравнение по переменной x:
(7) .
Из таблицы производных находим:
.
Производную левой части находим по формуле производной сложной функции:
.
Здесь .
Далее выполним преобразования:
.
Тогда
.
Подставим в (7):
.
Отсюда
.
Калькулятор — arctan(1/2) — Солуматы
Арктан, расчет онлайн
Резюме:
Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
arctan онлайн
Описание:
Функция arctan является обратной функцией касательная функция, это вычисляет арктангенс числа онлайн .
- Расчет арктангенса
- Пределы арктангенса Пределы арктангенса существуют при `-oo` (минус бесконечность) и `+oo` (плюс бесконечность):
Чтобы вычислить арктангенс числа, просто введите число и примените арктанг функция.
Например, чтобы вычислить арктангенс следующего числа 10, введите
arctan(`10`), или сразу 10, если
кнопка arctan уже появляется, возвращается результат 1.
- Функция арктангенса имеет предел в `-oo`, который равен `pi/2`.
- Функция арктангенса имеет предел в `+oo`, который равен `-pi/2`.
- `lim_(x->-oo)arctan(x)=pi/2`
- `lim_(x->+oo)arctan(x)=-pi/2`
| arctan(`-1`) | `3*pi/4` | |
| arctan(`-sqrt(3)/3`) | `5*pi/6` | `2*pi/3` |
| arctan(`0`) | `0` | |
| arctan(`sqrt(3)`) | `/3` | |
| arctan(`1`) | `pi/4` | |
| arctan(`sqrt(3)/3`) | `pi/6` |
Syntax :
arctan(x) , x — число. 92)`
Предельный арктангенс :
Калькулятор пределов позволяет вычислить пределы функции арктангенса.
предел арктангенса(x) is limit(`»arctan»(x)`)
Обратная функция арктангенса :
обратная функция арктангенса представляет собой функцию тангенса, отмеченную как тангенс.
Графический арктангенс :
Графический калькулятор может строить график функции арктангенса в интервале ее определения.
Свойство функции арктангенс :
Функция арктангенса является нечетной функцией.
Расчет онлайн с арктангенсом (арктангенсом)
См. также
Список связанных калькуляторов:
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.- Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
Напоминания о курсах, калькуляторы, упражнения и игры: Тригонометрические функции, Вещественные функции
- numpy.arctan( x , /, out = none , * , , где = true , Casting = ‘some_kind’ , , ride = ‘k’ , ‘, =’ k ‘, ‘ , .
 [ подпись , extobj ]) =
[ подпись , extobj ]) = Тригонометрический арктангенс, поэлементный.
Инверсия tan, так что если
y = tan(x), тоx = arctan(y).- Параметры
- x массив_подобный
- out ndarray, None или кортеж из ndarray и None, необязательный
Местоположение, в котором сохраняется результат. Если он предусмотрен, он должен иметь форма, на которую транслируются входные данные. Если не указано или Нет, возвращается только что выделенный массив. Кортеж (возможен только как аргумент ключевого слова) должен иметь длину, равную количеству выходов.
- где array_like, необязательный
Это состояние передается по входу. В местах, где условие равно True, массив из будет установлен в результат ufunc. В другом месте массив из сохранит исходное значение.
 Обратите внимание, что если неинициализированный массив из создается по умолчанию
Обратите внимание, что если неинициализированный массив из создается по умолчанию out=None, места внутри него, где условие равно False, будут остаются неинициализированными.- **kwargs
Другие аргументы, содержащие только ключевые слова, см. документы ufunc.
- Возвращает
- out ndarray или скаляр
Out имеет ту же форму, что и x . Его реальная часть находится в
[-pi/2, pi/2](arctan(+/-inf)возвращает+/-pi/2). Это скаляр, если x — скаляр.
См. также
-
arctan2 Четырехквадрантный арктангел угла, образованный ( x , y ) и положительную ось x .
-
угол Аргумент сложных значений.
Примечания
arctan— многозначная функция: для каждого x существует бесконечное число много чисел z таких, что tan( z ) = x . Конвенция заключается в том, чтобы вернуться
угол z , действительная часть которого лежит в [-pi/2, pi/2].
Конвенция заключается в том, чтобы вернуться
угол z , действительная часть которого лежит в [-pi/2, pi/2].Для вещественных типов входных данных
arctanвсегда возвращает реальный результат. Для каждого значения, которое не может быть выражено как действительное число или бесконечность, это даетДля входных данных с комплексным знаком
arctanпредставляет собой комплексную аналитическую функцию, которая имеет [1j, infj] и [-1j, -infj] как ответвления и является непрерывным слева на первом и справа на втором.Арктангенс также известен как 9{-1}.
Ссылки
Абрамовиц, М. и Стегун, И. А., Справочник по математическим функциям , 10-е издание, Нью-Йорк: Довер, 1964, стр. 79. https://personal.math.ubc.ca/~cbm/aands/page_79.htm
Примеры
Мы ожидаем, что арктангенс 0 будет равен 0, а арктангенс 1 будет пи/4:
>>> np.


 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.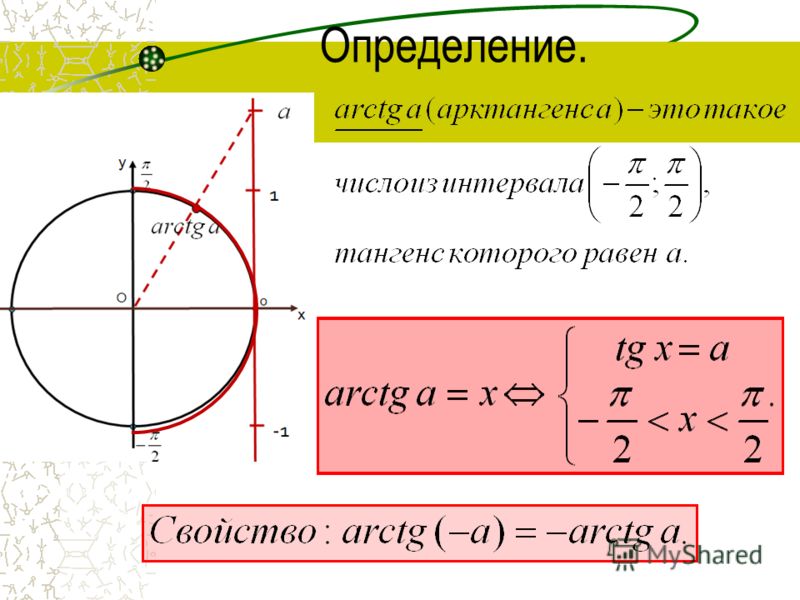 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения.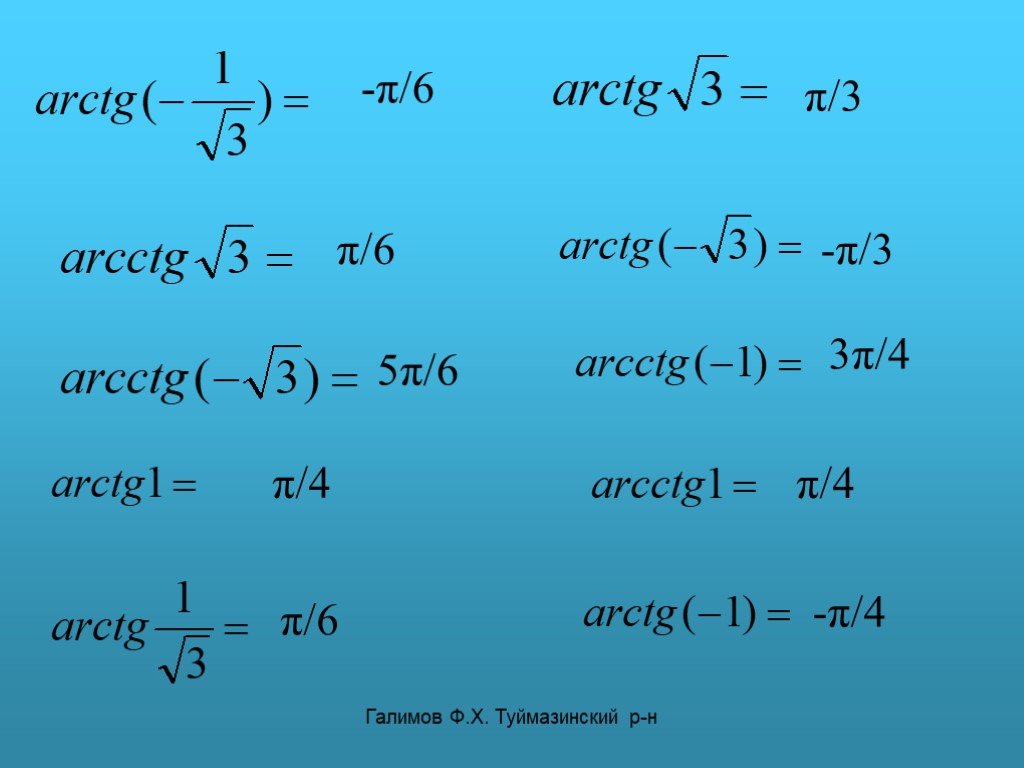 [ подпись , extobj ]) =
[ подпись , extobj ]) = 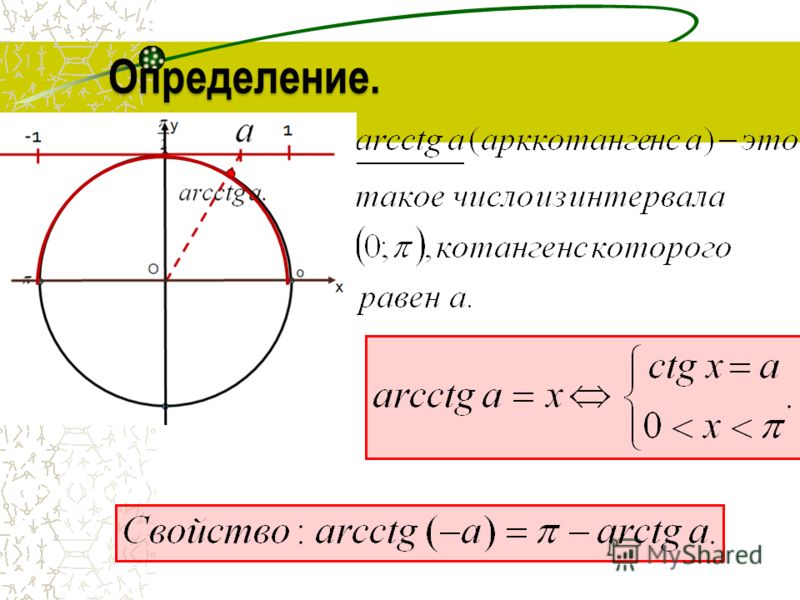 Обратите внимание, что если неинициализированный массив из создается по умолчанию
Обратите внимание, что если неинициализированный массив из создается по умолчанию  Конвенция заключается в том, чтобы вернуться
угол z , действительная часть которого лежит в [-pi/2, pi/2].
Конвенция заключается в том, чтобы вернуться
угол z , действительная часть которого лежит в [-pi/2, pi/2].