Формула бинома Ньютона. Свойства биномиальных коэффициентов
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Министерство образования и науки Алтайского края
КГБПОУ «Алтайская академия гостеприимства»
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
Тема проекта: Формула бинома Ньютона. Свойства биномиальных коэффициентов.
Выполняла студентка гр. Т-1812
Ложкина Виктория
Тема проекта актуальна на данный момент, потому что бином
Ньютон применяется для решения примеров и задач, в том
математической статистике и логике; к исследованию функций
и приближенным вычислениям.
 Изучение обобщающих
Изучение обобщающихформул развивает дедуктивное-математическое мышление и
общие мыслительные способности.
Цель исследования: обобщить формулы сокращенного умножения,
показать их применение к решению задач.
Задачи исследования:
1) изучить применении бинома Ньютона.
2) привести примеры задач на применение бинома Ньютона и формул
суммы и разности степеней.
Объекты исследования: бином Ньютона, формулы суммы и
разности степеней.
Предмет исследования: применение бинома Ньютона и формул
суммы и разности при решении примеров.
Слово «бином» означает двучлен, т.е. сумму двух слагаемых. Из
школьного курса известны так называемые формулы сокращенного
умножения:
(а + b)2 = a2 + 2ab + b2,
(a + b)3 = a3 +3a2b + 3ab2 + b3.
Обобщением этих формул является формула, называемая формулой
бинома Ньютона. Используются в школе и формулы разложения на
множители разности квадратов, суммы и разности кубов.
Слово «бином» в переводе с латыни означает и двучлен.
 Формула
Формулаэта имеет прямое отношение к комбинаторике.
Для удобства в выражении (a + b)n вынесем bn за скобки и обозначим a/
b через x. Получается bn(x + 1)n. На время забудем про множитель bn и
будем искать формулу для (x + 1)n. Нетрудно догадаться, что после
раскрытия скобок перед нами предстанет многочлен n-й степени.
Вывод формулы бинома Ньютона
Рассмотрим степени двучлена а + b.
n = 0, (а +b)0 = 1
n = 1, (а +b)1 = 1а+1b
n = 2, (а + b)2 = 1а2+ 2аb +1b2
n = 3, ( а + b)3 = 1 а3 + 3а2b + 3аb2+1 b3
n = 4, ( а + b)4 = 1а4 + 4а3b + 6а2b2+4а b3 +1b4
n = 5, (а + b)5 = 1а5+ 5а4b+ 10а3b2+ 10а2b3+ 5аb4+ 1b5
Заметим следующие закономерности:
— показатель степени первого слагаемого убывает от n до 0, показатель степени второго слагаемого
возрастает от 0 до n;
— степени всех одночленов равны степени двучлена в условии;
— каждый одночлен является произведением первого и второго выражения в различных степенях и
некоторого числа — биномиального коэффициента;
— биномиальные коэффициенты, равноотстоящие от начала и конца разложения, равны.

Обобщением этих формул является следующая формула, называемая формулой бинома Ньютона:
(a + b)n = C0n anb0+ C1n an-1b + C2n a n-2b2 + … + Cn-1n abn-1 + Cnn a0bn. (6)
Треугольник Паскаля
Связь ряда простых чисел и треугольника Паскаля.
Подумаешь, Бином Ньютона
Оскар Хуторянский
«Подумаешь, Бином Ньютона»
Кот промяукал Бегемот
(Он Воланда слуга покорный),
Предсказывая жизни ход.
Все это только подтверждает
Ньютона гений, но давно
Бином известен был в Китае,
Арабы знали про него.
Но обобщил Ньютон решение,
Возвёл он в степень многочлен…
Избавил нас от всех сомнений
Других же нет у нас проблем.
Скажите нам совсем без прений
Зачем нам нужен тот бином?
Комбинаторику явлений
Мы без бинома не найдём.
English Русский Правила
Курс высшей математики, Т.1
Курс высшей математики, Т.1
ОглавлениеПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ 1. Величина и ее измерение. 2. Число. 3. Величины постоянные и переменные. 4. Промежуток. 5. Понятие о функции. 6. Аналитический способ задания функциональной зависимости. 7. Неявные функции. 8. Табличный способ. 9. Графический способ изображения чисел. 10. Координаты. 11. График и уравнение кривой.  12. Линейная функция. 13. Приращение. Основное свойство линейной функции. 14. График равномерного движения. 15. Эмпирические формулы. 16. Парабола второй степени. 17. Парабола третьей степени. 18. Закон обратной пропорциональности. 19. Степенная функция. 20. Обратные функции. 21. Многозначность функции. 22. Показательная и логарифмическая функции. 23. Тригонометрические функции. 24. Обратные тригонометрические, или круговые, функции. § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 25. Упорядоченное переменное. 26. Величины бесконечно малые. 27. Предел переменной величины. 28. Основные теоремы. 29. Величины бесконечно большие. 30. Монотонные переменные. 31. Признак Коши существования предела. 32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью. 33. Примеры. 34. Непрерывность функции. 35. Свойства непрерывных функций. 36. Сравнение бесконечно малых и бесконечно больших величин. 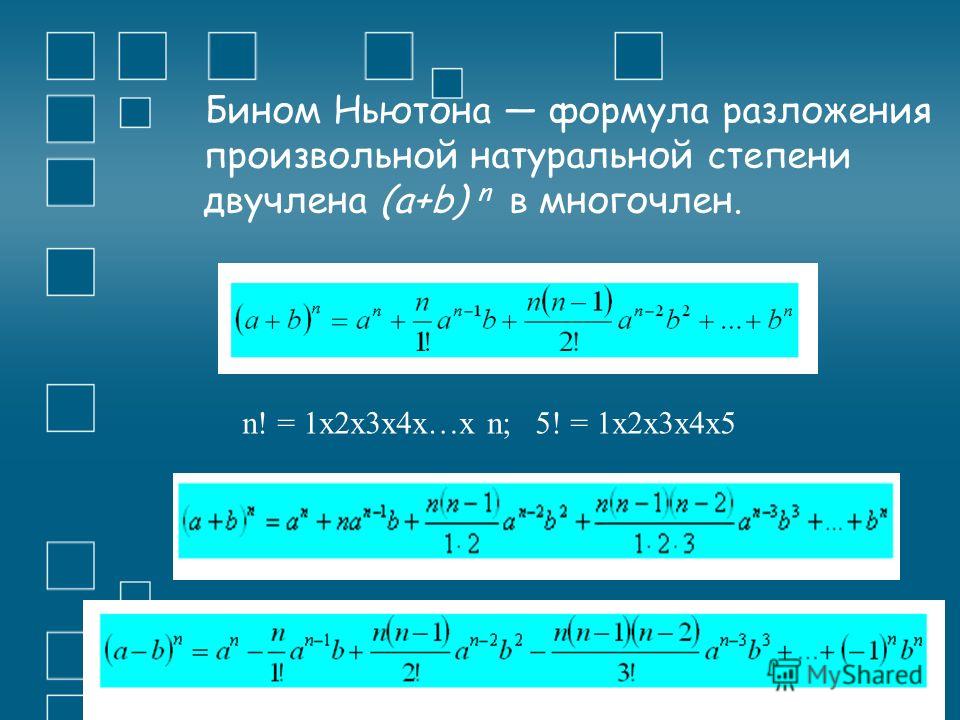 37. Примеры. 38. Число е. 39. Недоказанные предложения. 40. Вещественные числа. 41. Действия над вещественными числами. 42. Точные границы числовых множеств. Признаки существования предела. 43. Свойства непрерывных функций. 44. Непрерывность элементарных функций. ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ 45. Понятие о производной. 46. Геометрическое значение производной. 47. Производные простейших функций. 48. Производные сложных и обратных функций. 49. Таблица производных и примеры. 50. Понятие о дифференциале. 51. Некоторые дифференциальные уравнения. 52. Оценка погрешностей. § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 53. Производные высших порядков. 54. Механическое значение второй производной. 55. Дифференциалы высших порядков. 56. Разности функций. § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ 57. Признаки возрастания и убывания функций. 58. Максимумы и минимумы функций.  59. Построение графиков. 60. Наибольшее и наименьшее значения функций. 61. Теорема Ферма. 62. Теорема Ролля. 63. Формула Лагранжа. 64. Формула Коши. 65. Раскрытие неопределенностей. 66. Различные виды неопределенностей. § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ 68. Частные производные и полный дифференциал функции двух независимых переменных. 69. Производные сложных и неявных функций. § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ 70. Дифференциал дуги. 71. Выпуклость, вогнутость и кривизна. 72. Асимптоты. 73. Построение графиков. 74. Параметрическое задание кривой. 75. Уравнение Ван-дер-Ваальса. 76. Особые точки кривых. 77. Элементы кривой. 78. Цепная линия. 79. Циклоида. 80. Эпициклоиды и гипоциклоиды. 82. Кривые в полярных координатах. 83. Спирали. 85. Овалы Кассини и лемниската. ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ 86. Понятие о неопределенном интеграле.  87. Определенный интеграл как предел суммы. 88. Связь определенного и неопределенного интегралов. 89. Свойства неопределенного интеграла. 90. Таблица простейших интегралов. 91. Правило интегрирования по частям. 92. Правило замены переменных. Примеры. 93. Примеры дифференциальных уравнений первого порядка. § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 94. Основные свойства определенного интеграла. 95. Теорема о среднем. 96. Существование первообразной функции. 97. Разрыв подынтегральной функции. 98. Бесконечные пределы. 99. Замена переменной под знаком определенного интеграла. 100. Интегрирование по частям. § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 101. Вычисление площадей. 102. Площадь сектора. 103. Длина дуги. 104. Вычисление объемов тел по их поперечным сечениям. 105. Объем тела вращения. 106. Поверхность тела вращения. 107. Определение центров тяжести. Теоремы Гульдина. 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций.  109. Формула касательных и формула Понселе. 110. Формула Симпсона. 111. Вычисление определенного интеграла с переменным верхним пределом. 112. Графические способы. 113. Площади быстро колеблющихся кривых. § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 115. Разбиение промежутка на части и образование различных сумм. 116. Интегрируемые функции. 117. Свойства интегрируемых функций. ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 118. Понятие о бесконечном ряде. 120. Ряды с положительными членами. Признаки сходимости. 121. Признаки Коши и Даламбера. 122. Интегральный признак сходимости Коши. 123. Знакопеременные ряды. 124. Абсолютно сходящиеся ряды. 125. Общий признак сходимости. § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ 126. Формула Тейлора. 127. Различные виды формулы Тейлора. 128. Ряды Тейлора и Маклорена. 129. Разложение exp(x). 130. Разложение sin x и cos x.  131. Бином Ньютона. 132. Разложение log(1+x). 133. Разложение arctg x. 134. Приближенные формулы. 135. Максимумы, минимумы и точки перегиба. 136. Раскрытие неопределенностей. § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 137. Свойства абсолютно сходящихся рядов. 138. Умножение абсолютно сходящихся рядов. 139. Признак Куммера. 140. Признак Гаусса. 141. Гипергеометрический ряд. 142. Двойные ряды. 143. Ряды с переменными членами. Равномерно сходящиеся ряды. 144. Равномерно сходящиеся последовательности функций. 145. Свойства равномерно сходящихся последовательностей. 146. Свойства равномерно сходящихся рядов. 147. Признаки равномерной сходимости. 148. Степенные ряды. Радиус сходимости. 149. Вторая теорема Абеля. 150. Дифференцирование и интегрирование степенного ряда. ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 152. О предельном переходе. 153. Частные производные и полный дифференциал первого порядка.  154. Однородные функции. 155. Частные производные высших порядков. 156. Дифференциалы высших порядков. 157. Неявные функции. 158. Пример. 159. Существование неявных функций. 160. Кривые в пространстве и поверхности. § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных. 162. Необходимые условия максимума и минимума функции. 163. Исследование максимума и минимума функции двух независимых переменных. 164. Примеры. 165. Дополнительные замечания о нахождении максимумов и минимумов функции. 166. Наибольшее и наименьшее значения функции. 167. Относительные максимумы и минимумы. 168. Дополнительные замечания. 169. Примеры. ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ 170. Комплексные числа. 171. Сложение и вычитание комплексных чисел. 172. Умножение комплексных чисел.  173. Деление комплексных чисел. 174. Возвышение в степень. 175. Извлечение корня. 176. Показательная функция. 177. Тригонометрические и гиперболические функции. 178. Цепная линия. 179. Логарифмирование. 180. Синусоидальные величины и векторные диаграммы. 181. Примеры. 182. Кривые в комплексной форме. 183. Представление гармонического колебания в комплексной форме. § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ 185. Разложение многочлена на множители. 186. Кратные корни. 187. Правило Горнера. 188. Общий наибольший делитель. 189. Вещественные многочлены. 190. Зависимость между корнями уравнения и его коэффициентами. 191. Уравнение третьей степени. 192. Решение кубического уравнения в тригонометрической форме. 193. Способ итерации. 194. Способ Ньютона. 195. Способ простого интерполирования. § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ 196. Разложение рациональной дроби на простейшие. 197.  {n-k}$$ 9{(n-k)}$$ {n-k}$$ 9{(n-k)}$$Обе формулы могут быть получены просто по индукции; Бином Ньютона также имеет комбинаторное доказательство (вот соответствующая страница в Википедии). Поразительно, насколько похожи эти формулы; возможна ли между ними связь? Я думал, что может быть общее правило Лейбница можно получить и с помощью комбинаторного рассуждения (отсюда и биномиальные коэффициенты)…0025 биномиальные коэффициенты $\endgroup$ 2 $\begingroup$ Вот один комбинаторный способ взглянуть на обе формулы. Пусть в первом случае $M$ будет оператором, который съедает полином $f(x,y)$ и возвращает полином $(x+y)f(x,y)$. Обратите внимание, что $M$ линейно, так как умножение является дистрибутивным. Мы хотим начать с $1$, применить $M$ $n$ раз и посмотреть, что получится. Дело в том, что $M$ переводит любой моном $x^r y^s$ в сумму двух родственных:
$$M : x^r y^s \to x^{r+1}y^s + x^r y^{s+1}. $\endgroup$ $\begingroup$ Основная особенность закона Лейбница $f(x)g(x)’ = f'(x)g(x) + f(x)g'(x)$ состоит в том, что он превращает произведение в сумму. Другой способ написать это, чтобы показать, что это более явно: $$ \ frac {d} {dx} \ left (f (x) g (x) \ right) = \ left (\ left. \ frac {\ partial {\ partial s} \ right \ rvert_ {s, t = x }+\left.\frac{\partial}{\partial t}\right\rvert_{s,t=x}\right)\left(f(s)g(t)\right)=\frac{df} {dx}g(x)+f(x)\frac{dg}{dx} $$ или, если вам не нравится введение отдельных фиктивных переменных только для того, чтобы затем снова заменить их на $x$, вы можете написать с тензорным произведением, например $$ \frac{d}{dx}\left(f(x)\otimes g(x)\right) = \left(1\otimes \frac{d}{dx} + \frac{d}{dx}\otimes 1\вправо)\влево(f(x)\otimes g(x)\вправо). $$ Как бы мы ни думали об этом, суть в том, что производная произведения на самом деле является суммой двух дифференциальных операторов, примененных к этому произведению. А как вычислить $n$-ю степень суммы двух коммутирующих переменных? Почему с биномиальной теоремой, конечно. Формула 9{н-и}} $$ что при применении к произведению $f(s)g(t)$ и вычислении при $s=t=x$ дает вам желаемую обобщенную формулу Лейбница. Итак, мы рассматриваем эту формулу как частный случай биномиальной теоремы. Ведь биномиальная теорема — это всего лишь бухгалтерия комбинаторики применения дистрибутивного закона $n$ раз. А дифференциальные операторы распределяют по сложению точно так же, как это делает умножение. Вот почему $n$-е правило производного произведения — это всего лишь $n$ приложений закона распределения. Комбинаторика этого хорошо объяснена в ответе Тэда. Таким образом, вопрос здесь не в том, почему $n$-кратная производная, которая на самом деле является суммой, имеет ту же форму, что и $n$-я степень суммы. Теперь это очевидно: первое — всего лишь частный случай второго. Вместо этого возникает вопрос: почему производная произведения вообще является суммой? Какова интуиция, стоящая за необобщенным законом Лейбница для первой производной? Графика в Википедии полезна. Добавлю, что в физике и обработке сигналов и в других местах, где вы проводите свои дни в преобразованиях Фурье, очень естественно думать о дифференцировании и умножении на нашу независимую переменную как о двух сторонах одной медали. Каждая функция допускает двойственное представление в конфигурационном пространстве и в импульсном пространстве. Умножение в конфигурационном пространстве — это то же самое, что и дифференцирование представления в импульсном пространстве, и наоборот. Так что, конечно, $n$ приложений одного равно $n$ приложений другого. Бьюсь об заклад, эта точка зрения может быть конкретизирована в полный ответ на вопрос. $\endgroup$ 2 Биномиальная формула расширения – важные термины, свойства, практическое применение и пример задачи Биномиальная теорема – это быстрый способ умножить или расширить биномиальное выражение. Что такое биномиальное расширение и как оно работает?Биномиальная теорема — это математическое выражение, описывающее расширение степеней бинома. Согласно этой теореме многочлен (x + y)n можно разложить в ряд сумм, содержащих слагаемые типа an xbyc. Показатели степени b и c — целые неотрицательные числа, а b + c = n — условие. Кроме того, в зависимости от n и b коэффициент каждого члена представляет собой отдельное положительное целое число. Для n = 4 рассмотрим следующее: 9k\] Также помните, что n! является факториальной записью. Ниже приведены некоторые расширения: (x+y)1=x+y (x+y)2=x²+2xy+y² (x+y)3=x³+3x²y+3xy²+y³ (x+y)n Свойства биномиального разложения
Биномиальная теорема Общий терминБиномиальное расширение — это один из методов, используемых для расширения биномов со степенями в алгебраических выражениях. В алгебре бином — это алгебраическое выражение, состоящее ровно из двух членов (приставка «би» относится к числу 2). Если биномиальное выражение (x + y)n должно быть расширено, можно использовать формулу биномиального расширения, чтобы выразить это через более простые выражения формы ax + by + c, в которых «b» и «c» не равны. -отрицательные целые числа. Значение «а» полностью зависит от значения «n» и «b». Этот раздел дает более глубокое понимание того, что такое общий термин биномиального расширения и как биномиальное расширение связано с треугольником Паскаля. Математическая форма общего члена биномиального разложения Любой бином вида (a + x) можно разложить в любую степень, скажем, «n», используя приведенную ниже формулу биномиального разложения. ( a + x )n = an + nan-1x + \[\frac{n(n-1)}{2}\] an-2 x2 + …. + xn Приведенная выше формула более благоприятна, когда значение «x» намного меньше, чем значение «a». Это связано с тем, что в таких случаях первые несколько членов разложения дают лучшее приближение к значению выражения. Расширение всегда имеет (n + 1) членов. Общий член биномиального разложения можно также записать как: 9k\] Обратите внимание, что факториал равен N! = 1 . 2 . 3 … п 0! = 1 Важные термины, связанные с биномиальным расширениемРасширение бинома, возведенного в некоторую степень, дается биномиальной теоремой. Это наиболее широко известно как биномиальное расширение. Различные термины, используемые в биномиальном расширении, включают:
Биномиальная теорема и треугольник Паскаля: . Биномиальное разложение терминов можно представить с помощью треугольника Паскаля. Чтобы понять, как это сделать, возьмем пример двучлена (a + b), возведенного в степень «n», и пусть «n» — любое целое число. Для присвоения значений «n» как {0, 1, 2 …..} биномиальные разложения (a + b) n для разных значений «n», как показано ниже. Биномиальное разложение терминов можно представить с помощью треугольника Паскаля. Чтобы понять, как это сделать, возьмем пример двучлена (a + b), возведенного в степень «n», и пусть «n» — любое целое число. Для присвоения значений «n» как {0, 1, 2 …..} биномиальные разложения (a + b) n для разных значений «n», как показано ниже.
При таком представлении необходимо сделать следующие наблюдения.
Свойства биномиальной теоремыБиномиальные теоремы обладают многочисленными свойствами, полезными в математических вычислениях. Вот несколько важных свойств биномиальных коэффициентов:
Формула биномиального расширения Практическое применениеБиномиальное расширение используется в различных математических и научных расчетах, которые в основном связаны с различными темами, включая
. Ответ на этот вопрос — большое ДА!! Некоторые алгебраические тождества могут быть получены или доказаны с помощью биномиального расширения. Следующие тождества можно доказать с помощью биномиальной теоремы.
Примеры задач на биномиальное разложение1. Вычислить (3 + 7)3 с помощью биномиальной теоремы. Решение: Формула биномиального разложения имеет вид: (x+y)n = xn + nxn-1y + n(n-1)2! xn-2y2 +…….+ yn В данной задаче х = 3 ; у = 7; п = 3 (3 + 7)3 = 33 + 3 х 32 х 7 + (3 х 2)/2! x 31 x 72 + 73 = 27 + 189 + 441 + 343 (3 + 7)3 = 1000 Интересные факты
|

 И.Смирнов Курс высшей математики, Т.1.: Изд-во «Наука». 1974. — 479 с.
И.Смирнов Курс высшей математики, Т.1.: Изд-во «Наука». 1974. — 479 с.
 $$ 9{(n-i)}(x)$$
$$ 9{(n-i)}(x)$$
 В этой теме есть несколько хороших ответов. Я предложу следующее: производная — это линейный отклик функции на небольшое изменение входных данных. Имеет смысл, что когда вы вычисляете линейный отклик произведения двух функций, вы получаете произведение сумм, которые вы распределяете. Но в основном это, наверное, тема для отдельного вопроса.
В этой теме есть несколько хороших ответов. Я предложу следующее: производная — это линейный отклик функции на небольшое изменение входных данных. Имеет смысл, что когда вы вычисляете линейный отклик произведения двух функций, вы получаете произведение сумм, которые вы распределяете. Но в основном это, наверное, тема для отдельного вопроса. Интенсивность выразительности была значительно усилена. Как мы все знаем, умножение таких высказываний на большие степени и фразы всегда затруднено. Однако биномиальные разложения и формулы чрезвычайно полезны в этой области. Биномиальная теорема и формула биномиальной теоремы будут обсуждаться в этой статье. Давайте начнем с нескольких примеров, чтобы понять концепцию.
Интенсивность выразительности была значительно усилена. Как мы все знаем, умножение таких высказываний на большие степени и фразы всегда затруднено. Однако биномиальные разложения и формулы чрезвычайно полезны в этой области. Биномиальная теорема и формула биномиальной теоремы будут обсуждаться в этой статье. Давайте начнем с нескольких примеров, чтобы понять концепцию. В данном случае он отражает произведение всех целых чисел от 1 до n.
В данном случае он отражает произведение всех целых чисел от 1 до n.




