Астроида
Астроидой называется кривая, которую описывает точка окружности радиуса R/4, когда окружность катится без скольжения внутри окружности радиуса R.
Параметрические уравнения астроиды
где
В декартовых координатах уравнение астроиды
x2/3+y2/3=R2/3.
Длина астроиды L=6R, а площадь, ограниченная астроидой S=3R2/8.
IV. ПоверхносТи второго порядка
Алгебраической поверхностью второго порядка называется поверхность, уравнение которой в декартовой системе координат имеет вид:
Ax2+By2+Cz2+2Dxy+2Exz+2Fyz+gx+Hy+Iz+K=0,
где
не все коэффициенты при членах второго
порядка равны одновременно нулю (в
противном случае получаем алгебраическую
поверхность первого порядка, т.
В зависимости от значений коэффициентов возможны случаи, когда уравнение определяет вырожденную поверхность (пустое множество, точку, плоскость, пару плоскостей).
Например, уравнение не имеет решений и задает пустое множество, уравнение задает точку с координатами (0,0,0), уравнение задает плоскость х = 1, уравнение задает пару плоскостей х = у и х = у.
Исследование формы поверхностей второго порядка по их каноническим уравнениям
Основным методом исследования формы поверхности по ее уравнению является метод сечений, когда о форме поверхности судят по форме кривых, которые получаются при пересечении данной поверхности плоскостями
Эллипсоид
Эллипсоидом называется поверхность второго порядка с каноническим уравнением
.
Рассмотрим сечение эллипсоида плоскостью . Линия пересечения эллипсоида и плоскости задается системой уравнений
Г – эллипс с полуосями а и b в плоскости .
Рассмотрим сечение эллипсоида плоскостью . Линия пересечения задается системой уравнений
где Таким образом, если , то Г – эллипс с полуосями в плоскости Если , Г – точка с координатами Если , система решений не имеет, т.е. исследуемая поверхность не имеет общих точек с рассматриваемой плоскостью.
Далее, так как переменная z содержится в уравнении во второй степени, плоскость является плоскостью симметрии
Аналогично рассматриваются сечения поверхности плоскостями
Эллипсоид — замкнутая овальная поверхность, имеющая три плоскости симметрии:
Если , каноническое уравнение эллипсоида принимает вид . При этом линиями пересечения эллипсоида с плоскостями , где –с < h < c, являются окружности, центры которых лежат на оси OZ и, следовательно, в этом случае эллипсоид является фигурой вращения с осью OZ.
Если , каноническое уравнение принимает вид
и задает сферу с центром в начале координат и радиусом R.
Гиперболоиды Однополостный гиперболоид
Однополостным гиперболоидом называется поверхность второго порядка с каноническим уравнением
.
Линия пересечения гиперболоида и плоскости задается системой уравнений
и
определяет эллипс с полуосями а и b.
В сечении плоскостью получаем эллипс:
с большими, чем в предыдущем случае полуосями
Сечение поверхности плоскостью дает уравнение линии пересечения в виде:
и представляет гиперболу, пересекающую ось OY.
Сечение плоскостью задает гиперболу, пересекающую ось OX.
Однополостный гиперболоид
Большая Энциклопедия Нефти и Газа, статья, страница 3
Cтраница 3
Построить гипоциклоиду при К 4г ( астроиду) и найти обычное, не параметрическое уравнение астроиды. [31]
Эпициклоида и гипоциклоида описываются точкой на окружности круга, когда этот последний катится без скольжения по основной окруж-чости вне ( фиг.
[32]
Эпициклоиды и гипоциклоиды могут быть образованы с помощью перекатывания без скольжения одного круга по неподвижному другому. Если точка М находится на окружности производящего круга, то получаются обыкновенные эпициклоиды и гипоциклоиды в зависимости от того, располагается ли производящий круг с наружной или с внутренней стороны окружности неподвижного круга; при расположении точки М вне или внутри производящего круга эта точка вычертит соответственно удлиненную или укороченную эпициклоиду или гипоциклоиду. [33]
Астроида — гипоциклоида, у которой радиус направляющей окружности равен двум диаметрам производящей окружности. [34]
Эпициклоиды и гипоциклоиды, определяемые модулем, выраженным рациональным числом, являются алгебраическими кривыми. В нашей работе рассматриваются механизмы, разработанные для воспроизведения только таких линий. Формы эпициклоид и гипоциклоид, если их модуль представляет собой иррациональное число, не подчиняются приведенным закономерностям.
В механизме, построенном для вычерчивания такой кривой, точка В звена АВ, выйдя из начального положения, никогда уже в него не вернется. Кривая будет иметь нарастающее с каждым оборотом кривошипа число ветвей с бесконечным числом точек самопересечения и точек возврата и все же останется не замкнутой.
[35]
Построение очерка гипоциклоиды аналогично построению очерка эпициклоиды и понятно из чертежа. [36]
Построение очерка гипоциклоиды аналогично построению очерка эпициклоиды. [37]
Нормаль EN гипоциклоиды в точке Е проходит через точку N соприкасания центроид. Касательная ЕТ проходит через точку, диаметрально противоположную точке соприкасания центроид. [38]
Эпициклоиду и гипоциклоиду можно рассматривать как частные случаи циклоиды, когда направляющая прямая ААХ превращается в дугу окружности. [39]
Построение. а — эпициклоиды. б — гипоциклоиды.
[40] |
Эпициклоиду и гипоциклоиду можно рассматривать как частные случаи циклоиды, когда направляющая прямая ААг превращается в дугу окружности. [41]
| Построение циклоиды. [42] |
Эпициклоиду и гипоциклоиду можно рассматривать как частные случаи циклоиды, когда направляющая прямая AAt превращается в дугу окружности. [43]
Задача о гипоциклоидах и эпициклоидах может быть обобщена на две произвольные кривые Г и Г рассмотрением пути произ-вольн. [44]
Кривой Штейиера называется гипоциклоида, которая получается в том слу чае, когда радиус производящего круга в три раза меньше радиуса неподвижного круга. [45]
Страницы: 1 2 3 4
Создание астероидов | astroEDU
Что такое астероид? Астероиды — это валуны, вращающиеся вокруг Солнца, размером от нескольких сотен метров до нескольких километров.
Астероид называется метеоритом, если он упадет на Землю. Если он полностью испаряется в атмосфере Земли, прежде чем упасть на поверхность, его называют метеором. Люди обычно называют метеоры «падающими звездами». Большинство метеоритов состоят из силикатов или смеси железа и никеля. В прошлом на Землю падали огромные метеориты. Шестьдесят пять миллионов лет назад, почти 90% видов животных были уничтожены (включая динозавров), когда метеорит упал на Юкатан, Мексика. К счастью, это случается очень редко! Этим мы обязаны Юпитеру, который своим гравитационным притяжением притягивает множество астероидов.
Изображение: Астероид Ида (см. вложения)
Как образуются астероиды?
Частицы пыли в ранней Солнечной системе столкнулись, образовав более крупные скопления, известные как планетезимали. Они могли расти, привлекая больше пыли своими гравитационными полями; некоторые выросли достаточно большими, чтобы образовать планеты.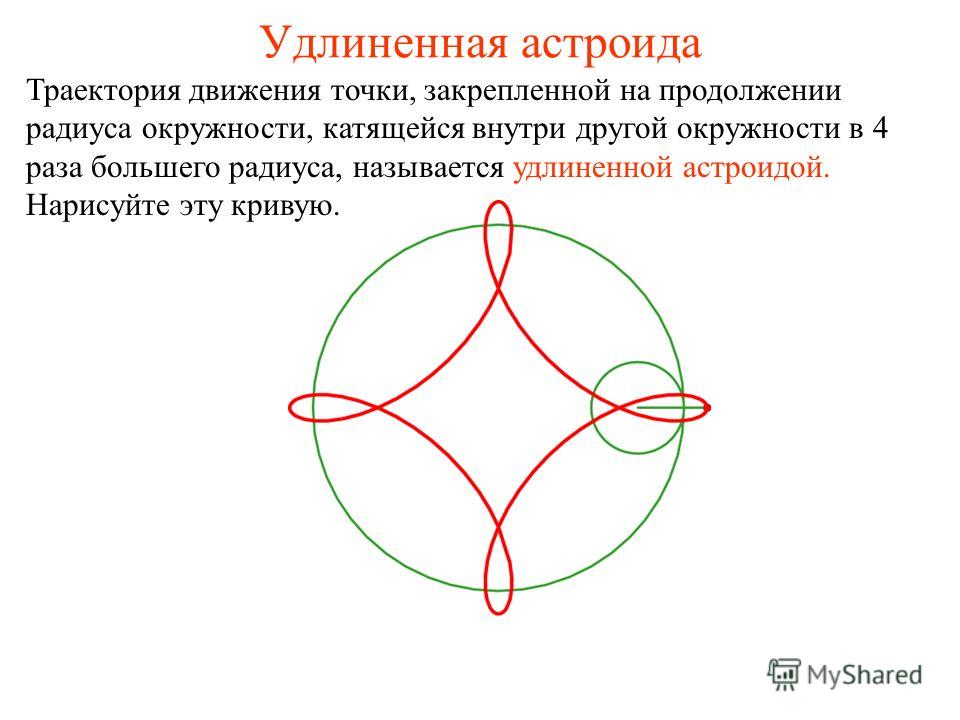
Остальные остались, превратившись в астероиды. Некоторые из этих астероидов столкнулись друг с другом (и с ранними планетами), разделившись на более мелкие астероиды. Некоторые столкновения были настолько медленными, что астероиды сливались, образуя астероиды странной формы.
Изображение: Дублет Антиопы (см. вложения)
Где находятся астероиды?
Многие астероиды образуют большие кольца или пояса вокруг Солнца. В нашей Солнечной системе есть два пояса астероидов: главный пояс (или просто пояс астероидов) между Марсом и Юпитером, содержащий тысячи астероидов (см. область, которая простирается за пределы орбиты Нептуна и содержит бесчисленное количество астероидов и множество карликовых планет, из которых Плутон является самой известной. 900:25 Большинство астероидов находится в поясе астероидов; однако есть астероиды, которые не находятся на этой орбите, и они называются объектами, сближающимися с Землей (NEO).
Иногда эти ОСЗ могут достигать нашей планеты Земля.
Изображение: Пояс астероидов
Почему важно изучать астероиды?Астероиды относятся к группе малых тел. Астероиды, кометы и метеороиды могут предоставить ценную информацию об эволюции нашей Солнечной системы. Кроме того, существуют небольшие тела, называемые метеороидами, остатки образования Солнечной системы. Эти метеороиды могут быть размером с рисовое зерно. Метеороиды постоянно встречаются с Землей, производя то, что мы видим на Земле как «падающие звезды».
Правда ли, что астероид может столкнуться с Землей?Астероид диаметром 10 километров упал на Землю 65 миллионов лет назад. Предполагается, что это падение астероида на Землю стало одной из причин вымирания динозавров.
Кометы Вы также можете рассказать ученикам о кометах.
Кометы подобны грязным снежкам или ледяным комкам грязи. Они состоят из смеси льда (как из воды, так и из замерзших газов) и пыли. Как и астероиды, кометы вращаются вокруг Солнца. Однако их орбиты сильно вытянуты по сравнению с планетами. То есть они иногда очень близко подходят к Солнцу, а иногда очень далеко. Когда они пересекают орбиту планеты, они могут столкнуться с ней. Это произошло, например, в 1994 года, когда комета Шумейкера-Леви столкнулась с планетой Юпитер и разбилась на части. Когда кометы приближаются к Солнцу по своей орбите, лед в их ядре тает и испаряется. В результате получается красивый хвост, который хорошо виден на ночном небе, если комета пройдет достаточно близко к Земле. В 2061 году комета Галлея вновь приблизится к Земле. Он обращается вокруг нашего Солнца раз в 76 лет. Не забудьте отметить его прибытие в своем календаре!
Изображение: Комета Галлея
Как смоделировать астероид своими руками
«Сделай сам» традиционно означает «сделай сам» и относится к культуре строительства или создания вещей, которые можно купить.
На DIY.org мы даем несколько более широкое определение «сделай сам».
Наша миссия — создать безопасное интернет-сообщество, которым дети смогут пользоваться самостоятельно, без присмотра родителей, место, где они смогут «сделать это сами». В этом сообществе мы поощряем их создавать, делиться и взаимодействовать друг с другом по общим интересам, не опасаясь негатива, запугивания или хищнического поведения, ограничивающих их. Для нас DIY означает расширение возможностей. С помощью нашего бесплатного сайта и приложения мы надеемся дать миллионам детей по всему миру возможность стать творцами, строителями и, самое главное, ответственными гражданами мира. 9№ 0007
Набор «Сделай сам» идеально подходит для детей в возрасте от 6 до 13 лет. Учитывая, что это одни из самых важных лет развития, мы пытаемся затронуть как можно больше детей с положительным содержанием и практическим обучением.
Мы стремимся поощрять развитие навыков, воспитывая здоровый дух соперничества и создавая сообщество активных, уверенных в себе, стремящихся к обучению и, прежде всего, добрых детей.
Вы можете создать свой профиль DIY на https://diy.org/register. Единственные данные, которые нам нужны, это ваше имя, день рождения и адрес электронной почты. Если у вас есть приложение «Сделай сам», вы можете использовать его для создания своего профиля.
Чтобы взаимодействовать и делиться на DIY, дети должны подтвердить свою учетную запись DIY. Проверка — это способ получить согласие родителей в соответствии с COPPA. После подтверждения своей учетной записи дети могут:
