Какие существуют виды дисперсии: Виды дисперсий

Содержание

суть, история открытия, причины и свойства дисперсии света

Изучение явления

Сложный состав солнечного света был обнаружен Исааком Ньютоном. Он направлял из круглого отверстия на призму тонкий луч белого света, при этом свет разлагался на спектр, и на экране появлялась линия из цветных круглых пятен.

Недостаток такого способа состоял в том, что цветные пятна перекрывали друг друга и давали четкий спектр только по краям. Чтобы доказать, что не сама призма окрашивает световые лучи, Ньютон собирал второй призмой разложенные цветные лучи, и получал луч белого цвета. Когда Ньютон направлял на призму монохроматический свет, разложения не происходило.

Только в 1802 году английский ученый Уильям Волластон впервые использовал в качестве источника луча не круглое отверстие, а узкую щель, и благодаря этому получил непрерывный четкий спектр.

Определение дисперсии света, суть явления, объяснение

Определение 1

Дисперсия света — это совокупность явлений, обусловленных зависимостью абсолютного показателя преломления от частоты колебаний (длины волны) света.

Источник: ru.123rf.com

Явление дисперсии возникает в связи с тем, что световые лучи с разной длиной волны имеют различную скорость распространения в оптической среде.

Формула 1

n=cv,

где n — относительный показатель преломления,

с — скорость света в вакууме,

v — скорость света данной частоты в среде.

Так как скорость распространения волн света в воздухе и вакууме (имеющем абсолютный показатель преломления, равный 1) всегда одинакова, независимо от длины волны и, следовательно, цвета, то относительный показатель преломления зависит от скорости света в среде и обратно пропорционален ей.

Обычно, чем меньше длина световой волны, тем больше показатель преломления среды для нее и тем меньше скорость распространения волны в среде:

в видимом спектре красный свет имеет максимальную фазовую скорость распространения в среде и минимальную степень преломления;
у фиолетового цвета фазовая скорость распространения в среде минимальна, а степень преломления — максимальна.

Дисперсионный спектр выглядит растянутым в коротковолновой части. Это связано с тем, что волны разной длины проходят разный путь сквозь призму. Наибольшие отклонение и путь внутри призмы имеют лучи с высокой частотой: соответственно, дисперсионный спектр растянут в фиолетовой части.

Дисперсия света: примеры в природе

Радуга — это результат отражения и дисперсии света в капельках воды. Именно дисперсия ответственна за то, что радуга имеет вид спектра, а не белой дуги. Так как капельки воды могут отличаться только размерами, то расположение радуги всегда примерно одинаково. Центр окружности, которую описывает радуга, всегда лежит на прямой, проходящей через Солнце и глаз наблюдателя, то есть одновременно видеть солнце и радугу без использования зеркал невозможно.

Источник: mirtesen.ru

Источник: center-axioma.vsite.biz

Дисперсия света в парящих кристаллах льда лежит в основе такого атмосферного оптического явления, как гало. Ледяные кристаллы могут быть разного размера, формы и по-разному ориентированы в воздухе, поэтому гало бывает очень разнообразным. Существует около сотни разных видов гало.

Источник: paikea.ru

Световые столбы, ложные солнца (паргелии) по некоторым классификациям также относятся к гало. Их вид обусловлен дисперсией света в ледяных кристаллах.

Источник: camminanelsole.com

«Призрак Броккена». Явление, получившее название «броккенский призрак», представляет собой тень наблюдателя, падающую на нижележащее облако, и обычно наблюдается в горах.

Источник: flickr.com

Применение дисперсии света

Дисперсия в ограненном бриллианте, которую демонстрирует картинка ниже.

Источник: lubikamni.ru

На явлении дисперсии основано применение жидких кристаллов, обладающих свойствами как жидкостей (текучесть), так и кристаллов (анизотропия).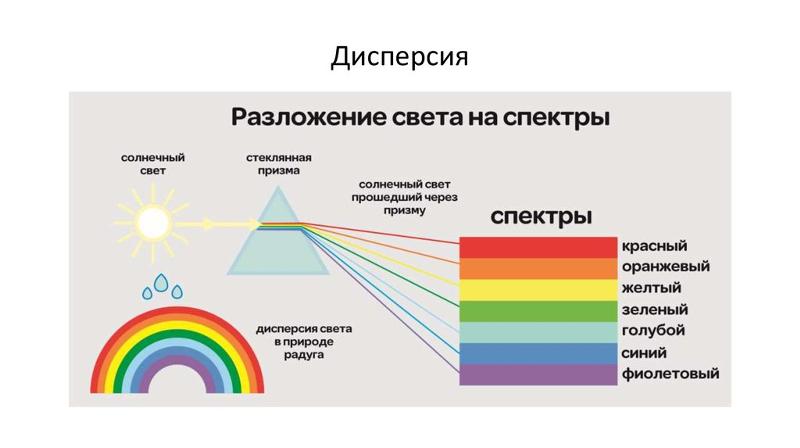 Проходя через жидкий кристалл, свет распадается на два луча: распространяющийся обычно и преломленный. С их помощью обнаруживают пары вредных химических соединений, гамма- и ультрафиолетовые излучения.

Применяют в информационной технике (жидкокристаллические индикаторы и экраны), в медицине, в микросхемах, на производстве. Например, жидкие кристаллы применяются в производстве «умного стекла», способного изменять опалесценцию и коэффициенты светопропускания и поглощения тепла.

Источник: easyladys.com

В «кольце настроения» под слоем стекла или пластика находятся жидкие кристаллы, поэтому оно меняет цвет в зависимости от температуры.

Виды дисперсии. Правило сложения дисперсии — Студопедия

Одних только средних недостаточно для оценки тех или иных явлений, так как средние уравнивают, сглаживают индивидуальные особенности отдельных единиц совокупности, показывают типичный для данных условий уровень варьирующих признаков, и тем самым могут затушевывать различные тенденции в развитии. В этом случае исчисляют показатели вариации, характеризующие средние отклонения каждой единицы совокупности от среднего значения признака в целом.

Вариация имеет объективный характер и помогает познать сущность изучаемого явления.

Для измерения вариации в статистике применяют несколько способов, описательная характеристика которых представлена в табл. 5.6.

Дисперсия имеет ряд математических свойств, упрощающих технику ее расчета.

1. Если из всех вариант отнять какое-то постоянное число А, то дисперсия от этого не изменится.

2. Если все значения вариант разделить на какое-то постоянное число h, то дисперсия уменьшится от этого в h²раз, а среднее квадратическое отклонение – в h раз.

Таблица 5.6.

Показатели вариации

Название показателя	Обозначение и методика расчета	Сущностная храктеристика
по несгруппированным данным	по сгруппированным данным
Размах вариации		Улавливает только крайние отклонения значений признака, но не отражает отклонений от средней всех вариант в ряду. Чем больше размах вариации, тем менее однородна исследуемая совокупность
Среднее линейное отклонение			Представляет собой среднее арифметическое значение абсолютных отклонений признака от его среднего уровня. Чем меньше среднее линейное отклонение, тем более однородны значения признака изучаемого явления
Дисперсия			Представляет собой средний квадрат отклонений значений признака от его среднего уровня
Среднее квадратическое отклонение		Является абсолютной мерой вариации и зависит не только от степени вариации признака, но и от абсолютных уровней вариант и средней, что не позволяет непосредственно сравнивать средние квадратические отклонения вариационных рядов с разными уровнями. Оно выражается в тех именованных числах, в которых выражены варианта и средняя
Коэффициент вариации		Является относительной мерой вариации. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна (типична) средняя

Методика расчета показателя дисперсии упрощенными способами показана на рис.

5.4. Отметим, что способ моментов применим в том случае, если задан интервальный ряд с равными интервалами, а способ разности применяется в любых рядах распределения: дискретных и интервальных с равными и неравными интервалами.

Вариация признака определяется различными факторами, в результате чего различают общую дисперсию, межгрупповую дисперсию и внутригрупповую дисперсию.

Общая дисперсия (σ²) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Вместе с тем, благодаря методу группировок можно выделить и измерить вариацию, обусловленную группировочным признаком, и вариацию, возникающую под влиянием неучтенных факторов.

Межгрупповая дисперсия (σ²_м.гр) характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака – фактора, положенного в основание группировки.

Рис. 5.4. Упрощенные способы расчета дисперсии

где k – количество групп, на которые разбита вся совокупность;

m_j – количество объектов, наблюдений, включенных в группу j;

– среднее значение признака по группе j;

– общее среднее значение признака.

Внутригрупповая дисперсия (σ²_j,вн.гр) отражает случайную вариацию, т.е. часть вариации, возникающую под влиянием неучтенных факторов и независящую от признака фактора, положенного в основание группировки.

, или, на основе метода разностей ,

где x_ij – значение i-ой варианты в группе j.

Если в сформированных группах отдельные данные встречаются не один раз, то для расчета внутригрупповой дисперсии используется формула средней арифметической взвешенной.

Среднее значение внутригрупповых дисперсий рассчитывается по формуле:

Существует закон согласно которому, общая дисперсия, возникающая под воздействием всех факторов, равна сумме дисперсии, возникающей за счет группировочного признака и дисперсии, появляющейся под влиянием всех прочих факторов. Этот закон связывает три вида дисперсии.

Правило сложения дисперсий: .

Правило сложения дисперсии широко применяется при исчислении тесноты связей между признаками (факторным и результативным). Для этого определяют эмпирический коэффициент детерминации и эмпирическое корреляционное отношение.

Эмпирический коэффициент детерминации (η²) показывает, какая доля всей вариации признака обусловлена признаком, положенным в основание группировки. (η – греческая буква «эта»).

Эмпирическое корреляционное отношение (η) показывает тесноту связи между признаками — группировочным и результативным.

Оно изменяется в пределах от 0 до 1. Если η = 0, то группировочный признак не оказывает влияния на результативный, если η =1,то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторов равно нулю. Характеристика связи между признаками при соответствующих значениях эмпирического корреляционного отношения приведена в табл. 5.7.

Таблица 5.7

Качественная оценка связи между признаками

Значение η		0-0,2	0,2-0,3	0,3-0,5	0,5-0,7	0,7-0,9	0,9-0,99
Характеристика связи	отсутствует	очень слабая	слабая	умеренная	заметная	тесная	очень тесная	функцио нальная

Что такое дисперсия в оптике?

Опубликовано Шейла Рейнольдс на 29 мая 2019 г. 9:00 | Оставить комментарий

В оптике дисперсия относится к свету, который разделяется на отдельные цвета при прохождении через объект. Радуги являются наиболее распространенным примером этого события. Радуга образуется, когда белый свет разделяется на компоненты разных длин волн (или цветов). Дисперсия может привести к ухудшению качества сигнала во многих приложениях, особенно на больших расстояниях.

Дисперсия в оптических волокнах

Существует три типа дисперсии: модальная, хроматическая и материальная.

Модальная дисперсия

Модальная дисперсия относится к пути, по которому проходит луч света. Многие передатчики излучают несколько типов мод. Некоторые световые лучи проходят через волокно, в то время как другие отражаются от границы сердцевины волокна, вместо этого двигаясь по непрямому пути в волноводе. Они составляют два типа мод: моды высокого порядка и моды низкого порядка.

Моды высокого порядка входят в волокно под острыми или тупыми углами, и для прохождения через волокно требуется значительно больше времени, чем для мод низкого порядка.
Моды низкого порядка входят в волокно напрямую и проходят через него быстрее.

Модовая дисперсия может быть устранена с помощью одномодового волокна. Эти волокна передают только одну моду света, поэтому сигнал не будет распространяться за счет модовой дисперсии.

Хроматическая дисперсия

Хроматическая дисперсия является результатом ширины спектра излучателя, которая определяет количество излучаемых длин волн — чем меньше ширина спектра, тем меньше длин волн. Длинные волны движутся быстрее, чем короткие, поэтому они быстрее достигают конца волокна, распространяя сигнал. Хроматическая дисперсия может быть уменьшена путем сужения ширины спектра передатчика. Монохроматический излучатель имеет только одну длину волны, поэтому он не способствует хроматической дисперсии.

Хроматическая дисперсия важна для исследователей, разрабатывающих оптическое оборудование, включая камеры, оптические микроскопы и телескопы. Система в таком оборудовании должна быть тщательно спланирована, включая использование комбинации линз из разных материалов с разными показателями преломления, чтобы свести к минимуму хроматические аберрации и получить оптимальное изображение.

Дисперсионный материал

Дисперсия материала возникает, когда длина волны зависит от показателя преломления материала сердцевины волокна. Дисперсия материала является фактором, способствующим ряду явлений, в том числе:

Дисперсия задержки волновода
Хроматические аберрации в линзах
Искажение групповой задержки
Цветоделение в призмах
Разброс многомодовой групповой задержки
Задержка дифференциального режима

Производители метрологии полагаются на стеклянные призмы для рассеивания света в точном оборудовании, таком как спектрометры.

Изготовление стекла из Swift Glass

Если вы хотите узнать больше об оптической дисперсии, вы можете получить нашу бесплатную электронную книгу «Понимание оптических свойств стекла». Он обеспечивает углубленный анализ ключевых свойств, влияющих на оптические характеристики вашего стеклянного материала, включая показатель преломления, хроматическую дисперсию и пропускание/пропускание.

Знание этой информации особенно важно для инженеров, работающих в отраслях, в которых оптические характеристики стекла являются ключом к соответствию спецификациям применения.

Swift Glass – сертифицированная по стандарту ISO 9001:2015 и зарегистрированная в ITAR компания с почти 100-летним опытом работы в отрасли. Изготовление стекла на заказ — наша специализация, и мы известны своей приверженностью всей компании к предоставлению качественных решений для производителей оригинального оборудования. Мы работаем с ведущими производителями стекла, включая Corning и Schott, и располагаем широким ассортиментом материалов, что позволяет нам быстро реагировать на ваши потребности. Мы предоставили решения для компаний биомедицинской, промышленной, оптической и аэрокосмической промышленности.

Если вам нужны услуги по изготовлению стекла, обязательно свяжитесь с нашей командой, чтобы запросить расценки сегодня.

Волоконная и оптическая дисперсия – Обзор – Fosco Connect

Дисперсия в оптических волокнах

В оптической среде, такой как волокно, существует три типа дисперсии: хроматическая, модальная и материальная.

Хроматическая дисперсия

Хроматическая дисперсия определяется шириной спектра излучателя. Ширина спектра определяет количество различных длин волн, излучаемых светодиодом или лазером. Чем меньше ширина спектра, тем меньшее количество длин волн излучается. Поскольку более длинные волны распространяются быстрее, чем более короткие волны (более высокие частоты), эти более длинные волны будут достигать конца волокна раньше более коротких, распространяя сигнал.

Одним из способов уменьшения хроматической дисперсии является сужение ширины спектра передатчика. Лазеры, например, имеют более узкую ширину спектра, чем светодиоды. Монохроматический лазер излучает только одну длину волны и, следовательно, не способствует хроматической дисперсии.

Модальная дисперсия

Модовая дисперсия касается пути (моды) каждого светового луча. Как упоминалось выше, большинство передатчиков излучают множество различных мод. Некоторые из этих световых лучей будут проходить прямо через центр волокна (аксиальная мода), в то время как другие будут неоднократно отражаться от границы оболочки и сердцевины, зигзагообразно двигаясь вдоль волновода, как показано ниже.

Моды, которые входят под острыми углами, называются модами высокого порядка. Этим модам требуется гораздо больше времени, чтобы пройти через волокно, чем модам низкого порядка, и поэтому они вносят свой вклад в модовую дисперсию. Одним из способов уменьшения модовой дисперсии является использование волокна с плавным показателем преломления. В отличие от двух разных материалов в волокне со ступенчатым показателем показателя преломления, оболочка волокна с плавным показателем преломления легирована таким образом, что показатель преломления постепенно уменьшается во многих слоях. Соответствующие сечения типов волокон показаны ниже.

В волокне с градуированным показателем преломления свет движется по более искривленному пути. Моды высокого порядка проводят большую часть времени в слоях оболочки с более низким показателем преломления около
за пределами волокна. Эти основные слои с более низким показателем преломления позволяют свету распространяться быстрее, чем в центральных слоях с более высоким показателем преломления. Следовательно, их более высокая скорость компенсирует более длинные пути этих мод высокого порядка. Хорошая конструкция волновода заметно уменьшает модовую дисперсию.

Модовая дисперсия может быть полностью устранена при использовании одномодового волокна. Как следует из названия, одномодовое волокно передает только одну моду света, поэтому нет 9 мод.0089 расширение сигнала из-за модовой дисперсии. Монохроматический лазер с одномодовым волокном полностью устраняет дисперсию в оптическом волноводе, но обычно используется на очень больших расстояниях из-за его сложности и дороговизны.

Материальная дисперсия

Материальная дисперсия обусловлена зависимостью показателя преломления от длины волны от материала сердцевины волокна, тогда как волноводная дисперсия возникает из-за зависимости постоянной распространения моды от параметров волокна (радиуса сердцевины и разницы между показатели преломления в сердцевине и оболочке волокна) и длина волны сигнала.

Материальная дисперсия вносит вклад в искажение групповой задержки, наряду с волноводным искажением задержки, задержкой дифференциального режима и разбросом многомодовой групповой задержки.

Волоконно-оптические устройства компенсации дисперсии

Управление дисперсией — это процесс проектирования волокна и компенсирующих элементов на пути передачи для уменьшения общей дисперсии. Как правило, элементы компенсации дисперсии размещаются примерно через каждые 100 км.

На приведенном ниже рисунке показаны характеристики оптоволоконного пути с чередующимися длинами (+D) NZ-DSF и (-d) NZ-DSF каждые 20 км. Первые 20 км длины волокна представляют собой (+D) NZ-DSF, поэтому дисперсия увеличивается на этой длине до 60 пс/нм. Следующие 20 км волокна относятся к типу (-D) NZ-DSF, поэтому дисперсия постепенно уменьшается до нуля. Эта схема повторяется еще два раза. В конце 120-километрового оптоволоконного пути дисперсия вернулась почти к нулю.

Но в большинстве реальных приложений волокно уже есть, и есть вероятность, что это волокно типа NDSF.